129. (Diciembre 2022) Grafos Parsimónicos para una Selección de Escalas Heptatónicas y Pentatónicas (1/2)
129. (Diciembre 2022) Grafos Parsimónicos para una Selección de Escalas Heptatónicas y Pentatónicas (1/2) |
 |
 |
 |
| Escrito por Luis Nuño (Universidad Politécnica de Valencia) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Lunes 12 de Diciembre de 2022 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Tenemos otra vez más el placer de contar como autor invitado a Luis Nuño, que ya ha escrito en esta columna anteriormente. Luis Nuño es catedrático de universidad en la Universidad Politécnica de Valencia y autor de la Rueda Armónica. Es un gran investigador de la teoría matemática y computacional de la música así como un divulgador de la misma. Ha publicado varios artículos de investigación en la prestigiosa revista Journal of Mathematics and Music. Siguiendo con su trabajo de grafos parsimónicos, esta vez estudia dichos grafos sobre escalas heptatónicas y pentatónicas. Este trabajo que trae a Divulgamat consta de dos partes; la segunda la veremos en enero. De nuevo, estamos ante un artículo iluminador y profundo. Espero que los lectores de esta columna lo disfruten tanto como lo he hecho al leerlo. Paco Gómez Martín
1. IntroducciónEl presente artículo fue presentado en junio de este año 2022 en la Conferencia Internacional de Matemáticas y Computación en Música, celebrada en Atlanta (GA, USA). Para facilitar su difusión entre un conjunto de lectores lo más amplio posible se ha simplificado en cierta medida su parte más teórica, pero se han mantenido en su totalidad los resultados obtenidos. En todo caso, el artículo completo puede consultarse en la referencia indicada al final de este artículo (Nuño 2022a). La escala mayor es la base de la música occidental. Por ello, aunque pueda parecer superfluo, conviene revisar algunas de sus principales características. Se trata de un conjunto de siete notas que guardan entre sí una gran afinidad acústica, de manera que es muy “completo y versátil”. Así, muchas canciones populares – y no tan populares – están compuestas en una tonalidad mayor. Nuestra notación musical, basada en el pentagrama y las armaduras, es idónea para escribir música en las tonalidades mayores. El piano, considerado el “instrumento rey”, está perfectamente adaptado para tocar en la tonalidad de Do mayor. Los nombres de las notas son siete – en lugar de doce –, precisamente las de la escala de Do mayor. El término octava (derivado de “ocho”) indica su extensión (repitiendo la tónica al final), mientras que los términos tono y semitono describen los intervalos entre dos de sus notas sucesivas. Así mismo, la calificación de los intervalos (justo, mayor, menor, etc.) se establece tomando como referencia una escala mayor. En resumen, la escala mayor es fundamental en teoría de la música y composición. Además, a partir de la escala mayor pueden obtenerse directamente otros tipos de escalas. Por ejemplo, tomando cualquiera de sus notas como como tónica, obtenemos siete modos, de los cuales el eólico constituye la escala menor, que es también característica de la música occidental. En este caso, sus grados sexto y séptimo pueden ser naturales o alterados (elevados un semitono), lo que da lugar a las escalas menores natural, melódica y armónica. Por otra parte, la escala complementaria de una escala mayor (es decir, la formada por el resto de las doce notas) es una escala pentatónica mayor. En general, las escalas pentatónicas – y no solo la pentatónica mayor – han sido utilizadas por diferentes culturas desde la antigüedad. Aunque son predominantes en los países del este (China, Japón, India, Java, etc.), también se han empleado en diferentes estilos occidentales, tanto en la música clásica como en la escocesa, andina, jazz, etc. Este estudio está basado en el sistema de afinación temperado de doce notas, utilizándose como nomenclatura los nombres de Forte y las clases de conjuntos (Forte 1973), que aquí llamaremos clases de escalas. De entre ellas, las no inversionalmente simétricas se dividen en dos tipos de escalas relacionados entre sí por inversión, llamados a y b, de acuerdo con Nuño (2021c o, en español, 2020 y 2021a). Con respecto a las escalas mayor y pentatónica mayor podemos decir que son las escalas de siete y cinco notas, respectivamente, que tienen sus notas más uniformemente espaciadas. Y, además, poseen una propiedad exclusiva: aparte de los casos triviales de las escalas de una u once notas, son las únicas que pueden transformarse en otras de su mismo tipo mediante una transformación monosemitonal (es decir, cambiando una sola nota y solo un semitono, que puede ser ascendente o descendente). Por ejemplo, subiendo en la escala de Do mayor la nota Fa un semitono obtenemos la escala de Sol mayor. Esta propiedad, para el caso de las escalas mayores, da lugar al orden de los sostenidos y los bemoles, así como al ciclo de quintas (Balzano 1980, Cohn 1996), que es fundamental en la teoría de la modulación, es decir, el cambio de una tonalidad a otra. En este sentido, dada una tonalidad, las más “cercanas” a ella son las que tienen un sostenido o un bemol de más o de menos en su armadura (Schönberg 1983, Piston 1988). Esto también es aplicable a las tonalidades menores, ya que sus armaduras son las mismas que las de sus relativas mayores. El concepto de transformación parsimónica es algo más general, ya que, en este caso, son una o más notas las que cambian en uno o dos semitonos (en la práctica, no más de dos semitonos en total), mientras el resto permanecen fijas (Douthett y Steinbach 1998). A este respecto, el Tonnetz es una primera representación de este tipo de transformaciones para las tríadas mayores y menores, mientras que Douthett y Steinbach (1998) presentan otros grafos más complejos e interesantes. En el s. XIX, diversos compositores hacen un uso extensivo de este tipo de transformaciones, varias de cuyas obras son analizadas por Cohn (2012). Por su parte, Tymoczko (2011) sigue un planteamiento distinto, representando los conjuntos de notas en unos espacios particulares denominados orbifolds. En cambio, Nuño (2021b o, en español, 2021d) desarrolla unos grafos cíclicos circulares, llamados Cíclopes, que relacionan los tricordos y tetracordos “más comunes”, mediante los cuales se puede analizar de forma práctica un buen número de dichos tipos de obras. En este artículo se presentan dos nuevos grafos similares a ellos para relacionar diferentes escalas heptatónicas y pentatónicas. En cada caso, se han seleccionado ocho tipos de escalas siguiendo unos criterios puramente musicales. Además, muestran de forma gráfica un resultado anteriormente mencionado: el ciclo de quintas para las escalas mayores, que es complementado con el ciclo de cuartas para las escalas pentatónicas mayores, los cuales corresponden a las únicas circunferencias posibles que conectan escalas del mismo tipo en estas clases de grafos (Balzano 1980, Cohn 1996). Este trabajo consta de dos partes, la primera de las cuales se dedica a las escalas heptatónicas y la segunda a las pentatónicas, en la cual se estudiará también la relación acústica existente entre ambas y se incluye, además, un ejemplo de análisis musical con escalas heptatónicas. En caso de duda sobre alguno de los conceptos utilizados aquí, se recomienda consultar los artículos de Nuño (2020, 2021a y 2021d), anteriormente publicados en esta misma página Web. 2. Selección de las Escalas HeptatónicasLa música tonal está basada en las escalas mayor, menor melódica y menor armónica (Schönberg 1983, Piston 1988), cuyos nombres de Forte “extendidos” son 7-35, 7-34 y 7-32a, respectivamente. Para completar esta serie numérica podemos considerar también las escalas 7-32b (mayor armónica) y 7-33 (napolitana mayor, según la nomenclatura de Ring 2022). Estas son, además, las escalas heptatónicas cuyas notas están más uniformemente espaciadas, sobre todo la escala mayor (7-35). Para obtener otras escalas heptatónicas a partir de ellas podemos, simplemente, descomponerlas en tetracordos (entendidos ahora como grupos de cuatro notas consecutivas) y combinar dos de ellos. Este es el procedimiento utilizado, por ejemplo, en la música tradicional de India para obtener las escalas heptatónicas denominadas “Melakarta ragas” (Popley 1921). Otra opción es partir de una escala mayor y elevar o rebajar una o más notas un semitono, tal como se hace con la escala menor natural para obtener las escalas menores armónica y melódica. En este caso, lo lógico es tomar las notas alteradas de las tonalidades más cercanas a la considerada. A continuación, usaremos ambos procedimientos para obtener un número “razonable” de escalas heptatónicas que nos permitan obtener unos grafos de complejidad aceptable y que pueden ser de interés para teóricos y compositores. Por otra parte, en adelante emplearemos la notación inglesa para las notas musicales (C=Do, D=Re, E=Mi, F=Fa, G=Sol, A=La y B=Si). 2.1. Combinaciones de dos Tetracordos Consideremos la escala de C mayor. Podemos ver que está compuesta por los tetracordos C – D – E – F y G – A – B – C, donde el primero de ellos comienza por la nota C y el segundo por G. En ambos casos, sus “estructuras interválicas”, en semitonos, son iguales: 221, siendo el intervalo entre los dos tetracordos de 2 semitonos. Por tanto, podemos escribir la estructura interválica de la escala completa como 221 2 221 y al tetracordo 221 lo llamaremos “mayor”. Si empezamos esa misma escala por las notas D o A, las primeras cuatro notas formarán un tetracordo de la forma 212, que llamaremos “menor”. Si, en cambio, empezamos por las notas E o B, resulta un tetracordo del tipo 122, que llamaremos “frigio”. Y, por último, si empezamos por la nota F, obtenemos un tetracordo del tipo 222, que llamaremos “lidio”. Así, podemos obtener diferentes escalas heptatónicas combinando dos cualesquiera de estos cuatro tetracordos. Pero, para obtener las escalas armónicas, tanto mayores como menores, necesitamos otro tipo de tetracordo: el 131, que llamaremos “armónico”. La Tabla 1 muestra las 25 posibles combinaciones de dos de estos cinco tipos de tetracordos. Se indican también las estructuras interválicas de las escalas resultantes, así como los nombres y símbolos usados para representarlas. Los nombres menos comunes se han tomado de Ring (2022) y se ha utilizado el mismo nombre para todos los modos de una misma escala. Además, en todos los casos, el intervalo entre los dos tetracordos se ha elegido de manera que la primera y la última nota de cada escala sea la misma. Es decir, que la suma de todos los semitonos en cada escala sea igual a 12. Tabla 1. Tipos de escalas heptatónicas obtenidas combinando dos de los cinco tetracordos considerados aquí, junto con sus correspondientes estructuras interválicas. Los símbolos utilizados para representar las escalas son: M: mayor, mm: menor melódica, hm: menor armónica, hM: mayor armónica, NpM: napolitana mayor, Npm: napolitana menor, hL: lidia armónica, hh: doble armónica o húngara y WT: escala de tonos.
Como podemos ver, la combinación de dos tetracordos lidios da lugar a la escala de tonos (WT), que solo tiene seis notas, por lo que no la incluiremos en este estudio. El resto de las combinaciones dan lugar a ocho tipos diferentes de escalas, entre las que se encuentran las cinco mencionadas al principio de la Sección 2, siendo, además, un número adecuado (ni muy grande ni muy pequeño) para desarrollar los grafos parsimónicos deseados. La Tabla 2 muestra estos tipos de escalas con sus nombres de Forte extendidos, los símbolos para representarlas y sus estructuras interválicas. La última columna es el vector de clases de intervalos, que consta de seis dígitos que indican correlativamente cuántos intervalos de cada clase (de 1 a 6 semitonos) contiene la escala considerada. Así, por ejemplo, este vector indica que la escala mayor (7-35) contiene “2” intervalos de 1 semitono, “5” intervalos de 2 semitonos, “4” intervalos de 3 semitonos, “3” intervalos de 4 semitonos, “6” intervalos de 5 semitonos y “1” intervalo de 6 semitonos. Tabla 2. Tipos de Escalas Heptatónicas considerados aquí.
2.2. Combinaciones de las Notas Alteradas pertenecientes a las Tonalidades más Cercanas Consideremos de nuevo la escala de C mayor. Sus dos tonalidades más cercanas, siguiendo tanto el orden de los sostenidos como el de los bemoles, dan lugar a las notas alteradas F♯, C♯, B♭ y E♭. Así, partiendo de la escala de C mayor y utilizando estas cuatro notas, bien naturales o alteradas, resultan 16 combinaciones, las cuales se muestran en la Tabla 3, junto con las escalas resultantes. Como puede verse, obtenemos los mismos ocho tipos de escalas heptatónicas que con el procedimiento anterior. Además, de acuerdo con el studio de Hook (2011), estas son justamente las escalas que tienen un “span” menor o igual que 10. Por todo ello, estos serán los tipos de escalas heptatónicas que consideraremos en este estudio y cuyas principales características están recogidas en la Tabla 2. Tabla 3. Escalas Heptatónicas obtenidas a partir de CM combinando dos notas alteradas.
2.3. Características Armónicas de las Escalas Heptatónicas Seleccionadas Para analizar las características armónicas de las escalas heptatónicas seleccionadas podemos utilizar dos generalizaciones del vector de clases de intervalos: el vector de tipos de tricordos y el vector de tipos de tetracordos, los cuales indican, respectivamente, cuántos tricordos y tetracordos de cada tipo contiene la escala considerada. La Tabla 4 muestra estos vectores para las escalas seleccionadas, donde cada uno de sus dígitos corresponde a un tipo de acorde en el orden establecido por Nuño (2021c o, en español, 2020 y 2021a). Así, por ejemplo, los primeros dígitos del vector de tipos de tricordos, de derecha a izquierda, corresponden a las tríadas aumentada, mayor, menor y disminuida. Y los primeros dígitos del vector de tipos de tetracordos, también de derecha a izquierda, corresponden al acorde de séptima disminuida, acorde de séptima de dominante, acorde semidisminuido (o de séptima de sensible) y acorde menor con séptima menor. Los dígitos en negrita corresponden a los tricordos y tetracordos “más comunes”, según el artículo de Nuño (2021b o, en español, 2021d). Tabla 4. Vectores de Tipos de Tricordos y de Tetracordos para las Escalas Heptatónicas.
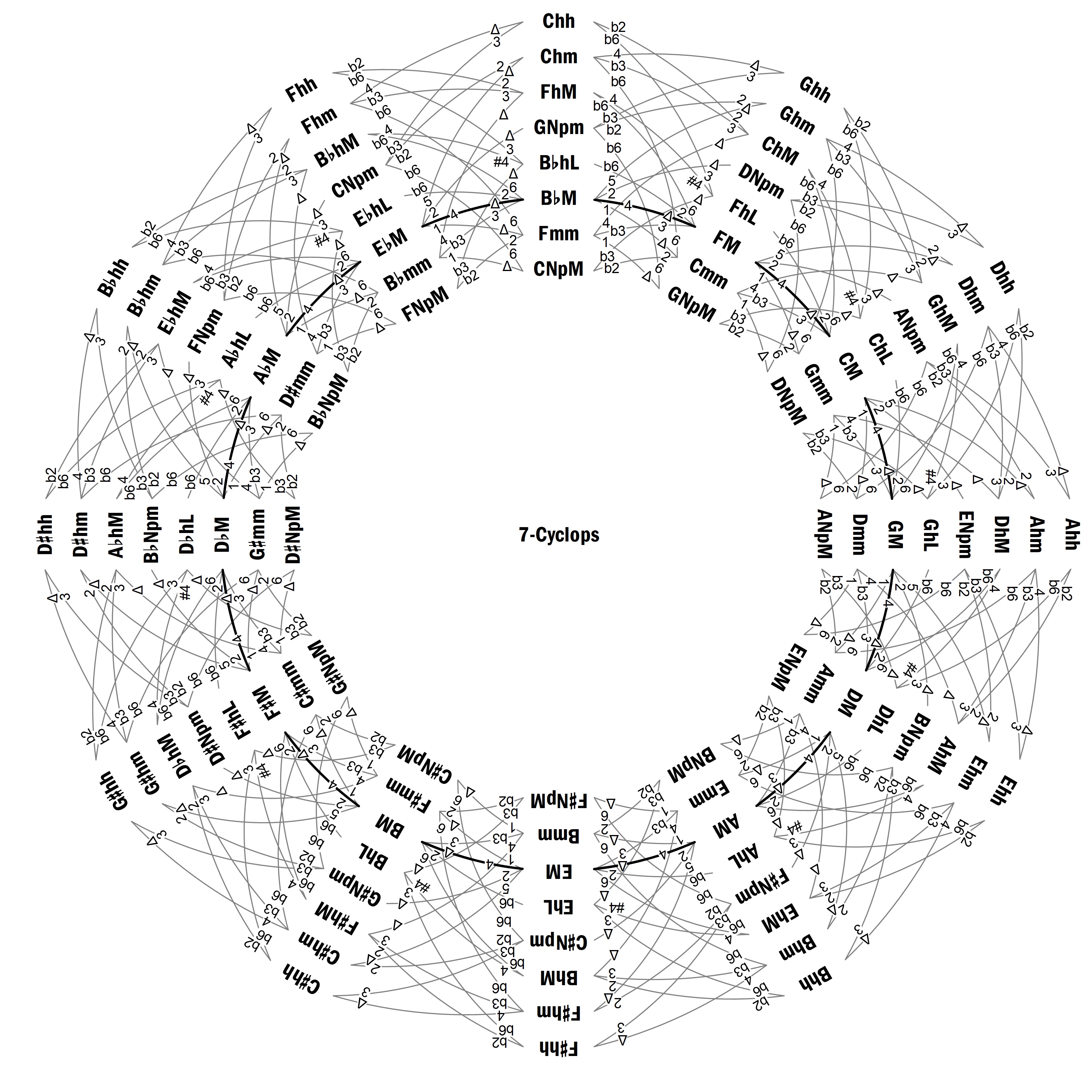
3. Grafo Parsimónico para las Escalas Heptatónicas SeleccionadasLa Figura 1 es un grafo cíclico circular que he denominado 7-Cíclope, que muestra todas las escalas heptatónicas de los tipos considerados en la Tabla 2, conectadas mediante transformaciones monosemitonales. Así, se pasa de una escala a otra adyacente cambiando una nota un semitono, el cual puede ser ascendente, si giramos en sentido horario, o descendente, si lo hacemos en sentido antihorario. Los números que hay en los extremos de las líneas que conectan las escalas indican las notas inicial y final referidas a las tónicas de estas escalas, donde 1 a 6 representan intervalos justos o mayores, que pueden alterarse mediante ♯ o ♭, mientras que las séptimas mayores y menores se representan mediante Δ y 7, respectivamente. Haciendo una analogía con la carátula de un reloj, cada acorde se ha colocado en una “zona”, que viene definida por “la suma de sus notas”, módulo 12 (Cohn 2012, p. 102). Así, por ejemplo, la escala CM = (C, D, E, F, G, A, B) está en la zona 0 + 2 + 4 + 5 + 7 + 9 + 11 = 2 (mod 12) y, análogamente, la escala B♭ M = (B♭ , C, D, E♭, F, G, A) está en la zona 0. De esta manera, si se sube o baja un semitono una nota de una escala, pasamos a la siguiente zona girando en sentido horario o antihorario, respectivamente. Y las escalas relacionadas por movimiento puramente contrario, como CM y Dhm = (D, E, F, G, A, B♭ , C♯) están en la misma zona (en este caso, 2). Puesto que los números 7 y 12 son coprimos, en cada zona tenemos justamente una escala de cada tipo. Nótese que las escalas mayores son las únicas que pueden transformarse en otras de su mismo tipo, a la vez que los enlaces entre ellas forman el ciclo de quintas, que es la única circunferencia posible en este grafo (la línea gruesa).
Fig. 1. El 7-Cíclope, con los tipos de escalas heptatónicas considerados en la Tabla 2. En cuanto a otros diagramas similares, tenemos el desarrollado por Tymoczko (2011, p. 136), el cual incluye las escalas mayores (que llama diatónicas), las menores melódicas (que llama acústicas y cuya tónica es la cuarta justa de la correspondiente escala menor melódica), las menores y mayores armónicas, más otras tres escalas no heptatónicas y con simetría transposicional: la escala de tonos (6-35), la hexatónica (6-20, también llamada aumentada) y la octatónica (8-28, también llamada disminuida semitono/tono), cuyas estructuras interválicas son, respectivamente, 222222, 131313 y 12121212. En este caso, para colocar adecuadamente todas estas escalas se utilizan 36 posiciones angulares que, lógicamente, no pueden coincidir con las zonas consideradas aquí, a la vez que no se indican las notas que cambian de una escala a otra. Así mismo, algunas de estas escalas están repetidas varias veces dentro del diagrama. Otro trabajo relevante es el publicado por Žabka (2014), que está basado en lo que denomina “series de transición comática”, y que incluye, además de las escalas de la Tabla 2, el par 7-31a/7-31b y las escalas de tonos con una nota enarmónica adicional. Estas escalas las distribuye en tres diagramas diferentes, por lo que no se muestran las conexiones existentes entre algunas de ellas, a la vez que tampoco se indican las notas que cambian de una escala a otra. Por otra parte, la nomenclatura utilizada para algunas de estas escalas es distinta de la empleada aquí. 4. ConclusionesSiguiendo unos criterios puramente musicales se han seleccionado ocho tipos de escalas heptatónicas. Sus características armónicas se han analizado mediante los vectores de clases de intervalos, de tipos de tricordos y de tipos de tetracordos. Además, se ha desarrollado un nuevo grafo parsimónico, denominado 7-Cíclope, que relaciona todas esas escalas mediante transformaciones monosemitonales. En este grafo destaca claramente el ciclo de quintas, que es la única circunferencia posible que conecta escalas del mismo tipo en este grafo. En la segunda parte de este trabajo se llevará a cabo un proceso análogo para las escalas pentatónicas y se estudiará la relación acústica existente entre las escalas heptatónicas y pentatónicas consideradas aquí. Además, se incluirá un ejemplo de análisis musical con escalas heptatónicas. Finalmente, para los lectores interesados en un estudio más general de los vectores empleados en este estudio, se recomienda el artículo de Nuño (2022b), recientemente publicado.
ReferenciasBalzano, G. 1980. “The Group-Theoretic Description of 12-Fold and Microtonal Pitch Systems”. Computer Music Journal 4 (4), 66–84. Cohn, R. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions”. Music Analysis 15 (1), 9–40. Cohn, R. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. New York: Oxford University Press. Douthett, J., Steinbach, P. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition”. Journal of Music Theory 42 (2), 241–263. Forte, A. 1973. The Structure of Atonal Music. New Haven: Yale University Press. Hook, J. 2011. “Spelled Heptachords”. En: Agon, C., et al. (eds.) Mathematics and Computation in Music 2011, pp. 84–97. Heidelberg: Springer. Nuño, L. 2020. “La Tabla Periódica Musical (1/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 111. Diciembre 2020. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18500&directory=67 Nuño, L. 2021a. “La Tabla Periódica Musical (2/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 112. Enero 2021. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18516&directory=67 Nuño, L. 2021b. Parsimonious Graphs for the Most Common Trichords and Tetrachords. Journal of Mathematics and Music 15(2), 125–139 (2021). Nuño, L. 2021c. A Detailed List and a Periodic Table of Set Classes. Journal of Mathematics and Music 15(3), 267–287. Nuño, L. 2021d. “Grafos Parsimónicos para los Tricordos y Tetracordos más Comunes.” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 119. Octubre 2021. https://divulgamat.net/index.php?option=com_content&view=article&id=18666&directory=67 Nuño, L. 2022a. “Parsimonious Graphs for Selected Heptatonic and Pentatonic Scales”. En: Montiel, M., Agustín-Aquino, O.A., Gómez, F., Kastine, J., Lluis-Puebla, E., Milam, B. (eds) Mathematics and Computation in Music. MCM 2022. Lecture Notes in Computer Science, vol 13267. Springer, Cham. https://doi.org/10.1007/978-3-031-07015-0_3 Nuño, L. 2022b. “Type and Class Vectors and Matrices in ℤn. Application to ℤ6, ℤ7 and ℤ12.” Journal of Mathematics and Music. https://www.tandfonline.com/doi/full/10.1080/17459737.2022.2120214 Piston, W. 1988. Harmony. 5th edn. New York: W. W. Norton and Co. Popley, H. A. 1921. The Music of India. London: Oxford University Press. Ring, I. 2022 (15 marzo). The Exciting Universe of Music Theory, https://ianring.com/musictheory/scales/ Schönberg, A. 1983: Theory of Harmony. 3rd edn. Berkeley, Calif.: University of California Press. Tymoczko, D. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press. Žabka, M. 2014. “Dancing with the Scales: Subchromatic Generated Tone Systems”. Journal of Music Theory 58 (2), 179–233. |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |