130. (Enero 2023) Grafos Parsimónicos para una Selección de Escalas Heptatónicas y Pentatónicas (2/2)
130. (Enero 2023) Grafos Parsimónicos para una Selección de Escalas Heptatónicas y Pentatónicas (2/2) |
 |
 |
 |
| Escrito por Luis Nuño (Universidad Politécnica de Valencia) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Domingo 01 de Enero de 2023 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1. IntroducciónEl presente artículo fue presentado en junio de este año 2022 en la Conferencia Internacional de Matemáticas y Computación en Música, celebrada en Atlanta (GA, USA). Para facilitar su difusión entre un conjunto de lectores lo más amplio posible se ha simplificado en cierta medida su parte más teórica, pero se han mantenido en su totalidad los resultados obtenidos. En todo caso, el artículo completo puede consultarse en la referencia indicada al final de este artículo (Nuño 2022a). La primera parte de este trabajo se ha dedicado a la selección de ocho tipos de escalas heptatónicas, al análisis de sus características armónicas y a la obtención de un grafo parsimónico, denominado 7-Cíclope, que relaciona dichas escalas mediante transformaciones monosemitonales. A continuación, se llevará a cabo un proceso análogo para las escalas pentatónicas y se estudiará la relación acústica existente entre las escalas heptatónicas y pentatónicas consideradas aquí. Finalmente, se incluye un ejemplo de análisis musical con escalas heptatónicas. En caso de duda sobre alguno de los conceptos utilizados aquí, se recomienda consultar los artículos de Nuño (2020, 2021a y 2021d), anteriormente publicados en esta misma página Web. Al igual que se hizo en la primera parte de este estudio, emplearemos la notación inglesa para las notas musicales (C=Do, D=Re, E=Mi, F=Fa, G=Sol, A=La y B=Si). 2. Escalas PentatónicasEn esta sección se va a realizar la selección, análisis armónico y desarrollo de un grafo parsimónico para escalas pentatónicas, mediante un proceso totalmente análogo al seguido para las heptatónicas. 2.1. Selección de las Escalas Pentatónicas Para mantener un completo paralelismo con las escalas heptatónicas previamente seleccionadas, tomaremos ahora como escalas pentatónicas las complementarias de aquellas. La Tabla 5 muestra estos tipos de escalas con sus nombres de Forte extendidos, los símbolos para representarlas, sus estructuras interválicas y sus vectores de clases de intervalos. Los símbolos de la forma “m…P” y “7…P” representan, respectivamente, variantes de las escalas pentatónica menor (mP) y pentatónica “dominante” (7P), cuyas estructuras interválicas son 32232 y 22332. Nótese que la escala “mP” es un modo de la escala pentatónica mayor (MP). Tabla 5. Tipos de Escalas Pentatónicas considerados aquí.
Estos ocho tipos de escalas también pueden obtenerse de forma análoga a como se obtuvieron las escalas heptatónicas combinando las cuatro notas alteradas más cercanas a la tonalidad de partida. Sin embargo, dado que las escalas pentatónicas no definen tonalidades, hablaremos ahora de notas modificadas en lugar de alteradas. Así, si partimos de la escala de C pentatónica mayor, debemos determinar, en primer lugar, cuáles de sus notas, modificadas en un semitono, dan lugar a otras escalas pentatónicas mayores. Un sencillo análisis nos revela que hay únicamente dos posibilidades: elevar E a F, obteniendo FMP, o bien rebajar C a B, obteniendo GMP. Y, a continuación, repetimos este proceso para hallar las siguientes escalas pentatónicas más cercanas a ellas, obteniendo así la Tabla 6, que es análoga a la Tabla 3 de la primera parte de este estudio, pero para las escalas pentatónicas. Podemos comprobar que, efectivamente, obtenemos los mismos ocho tipos de escalas de la Tabla 5. Tabla 6. Escalas Pentatónicas obtenidas a partir de CMP combinando dos notas modificadas.
Las características armónicas de estas escalas se muestran en la Tabla 7, utilizando para ello los vectores de tipos de tricordos y de tetracordos. Esta tabla es análoga a la Tabla 4 de la primera parte de este estudio, pero para las escalas pentatónicas, y en ambas se han aplicado los mismos criterios. Tabla 7. Vectores de Tipos de Tricordos y de Tetracordos para las Escalas Pentatónicas.
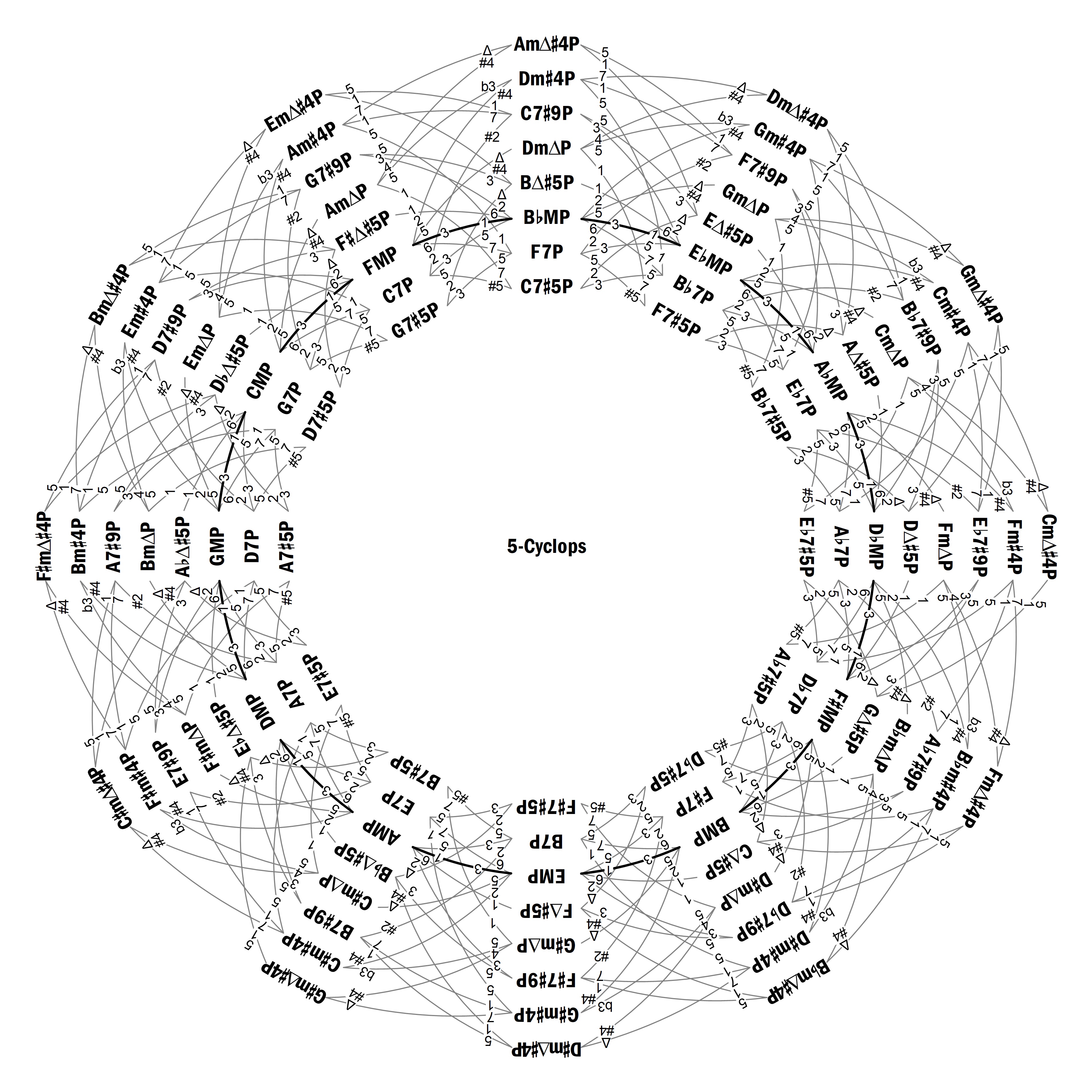
2.2. Grafo Parsimónico para las Escalas Pentatónicas Seleccionadas La Figura 2 es un grafo cíclico circular que he denominado 5-Cíclope, que muestra todas las escalas pentatónicas de los tipos incluidos en la Tabla 5, conectadas mediante transformaciones monosemitonales. Dado que, si dos escalas están relacionadas mediante una transformación monosemitonal, también lo estarán sus complementarias, resulta que esta figura es completamente análoga a la Figura 1, y en ambas se han aplicado los mismos criterios. Puesto que los números 5 y 12 también son coprimos, en cada zona tenemos justamente una escala de cada tipo. Nótese que las escalas pentatónicas mayores son las únicas que pueden transformarse en otras de su mismo tipo, a la vez que los enlaces entre ellas forman ahora el ciclo de cuartas, que es la única circunferencia posible en este grafo (la línea gruesa).
Fig. 2. El 5-Cíclope, con los tipos de escalas pentatónicas considerados en la Tabla 5. 2.3. Relación entre las Escalas Heptatónicas y Pentatónicas Seleccionadas Aparte de la relación de complementariedad que tenemos entre las escalas heptatónicas y pentatónicas consideradas aquí, existen entre ellas unas relaciones acústicas muy interesantes que pueden observarse mediante el vector de tipos de pentacordos, que es otra generalización del vector de tipos de intervalos. Este nuevo vector indica cuántos pentacordos (o escalas pentatónicas) de cada tipo contiene una escala dada. La Tabla 8 muestra este vector para las escalas heptatónicas incluidas en la Tabla 2 de la primera parte de este estudio, más el par 7-31a/7-31b considerado por Žabka (2014). En dicho vector, cada dígito corresponde a un tipo de escala pentatónica en el orden establecido por Nuño (2021c o, en español, 2020 y 2021a). Se han representado en negrita los dígitos correspondientes a las escalas pentatónicas consideradas aquí. Así, de izquierda a derecha, el primer dígito en negrita corresponde a la escala 5-22 y los últimos nueve dígitos (que están después de un espacio en blanco) corresponden a las escalas 5-30a, 5-30b, 5-31a, 5-31b, 5-32a, 5-32b, 5-33, 5-34 y 5-35. Tabla 8. Vector de Tipos de Pentacordos para diversas Escalas Heptatónicas.
Como podemos ver en la tabla, la escala 7-35 contiene tres escalas del tipo 5-35. Este es, además, el máximo número de escalas 5-35 contenidas en cualquiera de las diferentes escalas heptatónicas (no solo las incluidas en la tabla), ya que en el resto de los casos este número no es superior a dos. Así mismo, las escalas 7-34, 7-33 y 7-22 contienen, respectivamente, el máximo número de escalas 5-34, 5-33 y 5-22, que son 2, 6 y 2 (el resto de las escalas heptatónicas no contienen más de una en cada caso). En cuanto a los pares de escalas formados por un tipo a y un tipo b, debemos tener en cuenta que la complementaria de un tipo a es un tipo b y viceversa (Nuño 2021c o, en español, 2020 y 2021a). Entonces, las escalas 7-30a y 7-30b contienen, respectivamente, el máximo número de escalas 5-30a y 5-30b (es decir, las inversas de sus complementarias), que es dos (el resto de las escalas heptatónicas no contienen más de una), mientras que no contienen ninguna de sus correspondientes escalas complementarias. Así mismo, las escalas 7-31a y 7-31b contienen, respectivamente, el máximo número de escalas 5-31a y 5-31b, que es tres (el resto de las escalas heptatónicas no contienen más de dos) y tampoco contienen a sus correspondientes escalas complementarias. Pero, en cuanto al contenido en escalas 5-32a y 5-32b, resulta que son las escalas heptatónicas 7-31a y 7-31b las que contienen, respectivamente, el máximo número de ellas, que es dos (el resto de las escalas heptatónicas no contienen más de una). Por su parte, las escalas 7-32a y 7-32b contienen, respectivamente, una escala 5-32a y una 5-32b (de nuevo, las inversas de sus complementarias) y no contienen a sus correspondientes escalas complementarias. Por tanto, en todos estos casos existe, en mayor o menor medida, una clara relación acústica entre cada tipo de escala heptatónica y la inversa de su complementaria (que es pentatónica). 3. Ejemplo de Análisis MusicalŽabka (2014) incluye en su artículo el análisis de un pasaje cromático muy interesante: la Fantasía en C menor, K. 475, de Mozart, compases 1–25. Para ello, determina cuáles son las escalas heptatónicas utilizadas en cada caso, aunque algunas de ellas aparecen de forma incompleta. Con la nomenclatura usada en el presente artículo, estas escalas son:
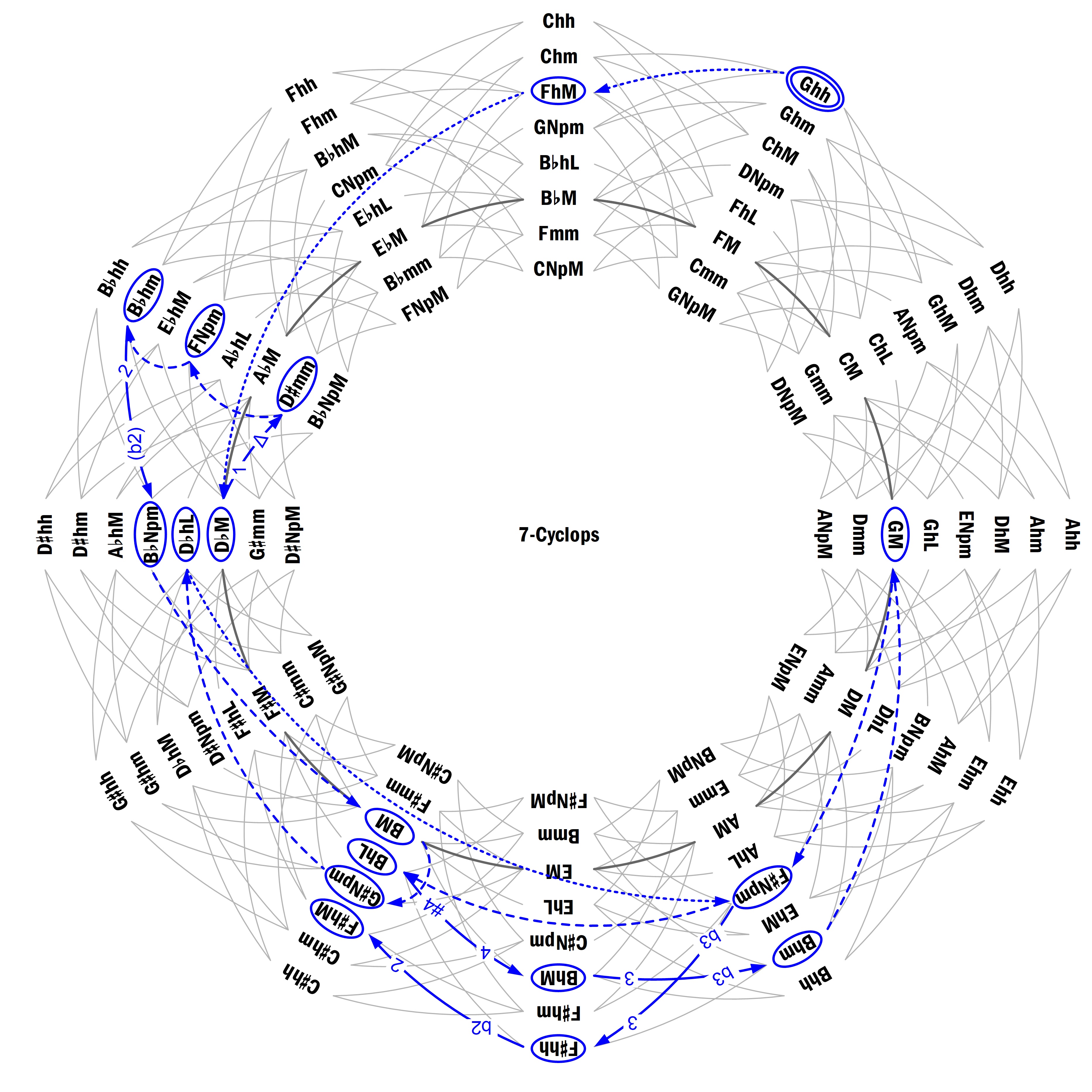
Ghh % FhM % D♭M E♭mm FNpm B♭hm B♭Npm BM % G♯Npm D♭hL F♯Npm C♭hL BhM Bhm GM % % F♯Npm–F♯hh F♯hM % % % donde cada escala o cada pareja de escalas unidas por un guión dura un compás y el símbolo “%” significa repetir el compás anterior. Las representaciones de este pasaje realizadas por Žabka (2014) presentan algunas complicaciones y pueden compararse con la que se muestra en la Figura 3 en el 7-Cíclope, el cual contiene todas las escalas requeridas, y donde la primera de ellas se ha indicado con una línea doble. Aunque la composición está en C menor, Mozart no incluye ninguna alteración en la armadura; y, como se aprecia en la Figura 3, no se utiliza ninguna de las escalas Chm, Cmm o C menor natural (E♭M). No obstante, la escala inicial, Ghh, contiene el acorde de C menor, cuyo arpegio se ejecuta empezando justamente por la nota C (cuarto modo de Ghh). A partir de ahí, las escalas se mueven en el diagrama en sentido antihorario, es decir, en la dirección de los bemoles (con algunos movimientos hacia delante y hacia atrás), hasta llegar a GM, cuya tónica (en el bajo) es la dominante de C. Sin embargo, la resolución no se hace sobre una escala de C menor, sino sobre varias escalas de tónica F♯, que está a un intervalo de tritono de C, y los últimos cuatro compases están basados, de hecho, en el acorde de F♯ mayor.
Fig. 3. Mozart, Fantasía en C menor, K. 475, compases 1–25. Análisis con el 7-Cíclope. 4. Conclusiones e Información AdicionalComo conclusiones del artículo completo, podemos decir que, siguiendo unos criterios puramente musicales, se han seleccionado ocho tipos de escalas heptatónicas y sus complementarias pentatónicas. Sus características armónicas se han analizado mediante los vectores de clases de intervalos, de tipos de tricordos y de tipos de tetracordos. Además, se han desarrollado dos nuevos grafos parsimónicos, denominados 7-Cíclope y 5-Cíclope, que relacionan cada uno de estos tipos de escalas mediante transformaciones monosemitonales. En estos grafos destacan, respectivamente, los ciclos de quintas y de cuartas, que son las únicas circunferencias posibles que conectan escalas del mismo tipo en esta clase de grafos (aparte de los casos triviales de escalas de una u once notas). Por otra parte, se ha encontrado una relación acústica entre cada escala heptatónica y la inversa de su complementaria, utilizando para ello el vector de tipos de pentacordos. Finalmente, se ha incluido un ejemplo de aplicación al análisis musical de una obra bastante compleja, por lo que toda esta información se estima que puede ser de interés tanto para teóricos como para compositores. Los lectores interesados en los tipos de vectores utilizados aquí, tanto para el caso del sistema de afinación temperado de doce notas como para otros sistemas más generales, pueden encontrar información adicional en Nuño (2022b). En ese artículo se presenta un riguroso estudio considerando la división de la octava en un número arbitrario de notas n y se incluyen diferentes teoremas que proporcionan una visión global y un conocimiento detallado de estos tipos de vectores.
ReferenciasBalzano, G. 1980. “The Group-Theoretic Description of 12-Fold and Microtonal Pitch Systems”. Computer Music Journal 4 (4), 66–84. Cohn, R. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions”. Music Analysis 15 (1), 9–40. Cohn, R. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. New York: Oxford University Press. Douthett, J., Steinbach, P. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition”. Journal of Music Theory 42 (2), 241–263. Forte, A. 1973. The Structure of Atonal Music. New Haven: Yale University Press. Hook, J. 2011. “Spelled Heptachords”. En: Agon, C., et al. (eds.) Mathematics and Computation in Music 2011, pp. 84–97. Heidelberg: Springer. Nuño, L. 2020. “La Tabla Periódica Musical (1/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 111. Diciembre 2020. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18500&directory=67 Nuño, L. 2021a. “La Tabla Periódica Musical (2/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 112. Enero 2021. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18516&directory=67 Nuño, L. 2021b. Parsimonious Graphs for the Most Common Trichords and Tetrachords. Journal of Mathematics and Music 15(2), 125–139 (2021). Nuño, L. 2021c. A Detailed List and a Periodic Table of Set Classes. Journal of Mathematics and Music 15(3), 267–287. Nuño, L. 2021d. “Grafos Parsimónicos para los Tricordos y Tetracordos más Comunes.” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 119. Octubre 2021. https://divulgamat.net/index.php?option=com_content&view=article&id=18666&directory=67 Nuño, L. 2022a. “Parsimonious Graphs for Selected Heptatonic and Pentatonic Scales”. En: Montiel, M., Agustín-Aquino, O.A., Gómez, F., Kastine, J., Lluis-Puebla, E., Milam, B. (eds) Mathematics and Computation in Music. MCM 2022. Lecture Notes in Computer Science, vol 13267. Springer, Cham. https://doi.org/10.1007/978-3-031-07015-0_3 Nuño, L. 2022b. “Type and Class Vectors and Matrices in ℤn. Application to ℤ6, ℤ7 and ℤ12.” Journal of Mathematics and Music. https://www.tandfonline.com/doi/full/10.1080/17459737.2022.2120214 Piston, W. 1988. Harmony. 5th edn. New York: W. W. Norton and Co. Popley, H. A. 1921. The Music of India. London: Oxford University Press. Ring, I. 2022 (15 marzo). The Exciting Universe of Music Theory, https://ianring.com/musictheory/scales/ Schönberg, A. 1983: Theory of Harmony. 3rd edn. Berkeley, Calif.: University of California Press. Tymoczko, D. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press. Žabka, M. 2014. “Dancing with the Scales: Subchromatic Generated Tone Systems”. Journal of Music Theory 58 (2), 179–233. |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |