Su obra

A efectos de un resumen podemos clasificar los trabajos matemáticos de Chebyshev en las cuatro ramas siguientes: Mecanismos y Teoría de la Aproximación de Funciones, Teoría de los Números, Teoría de Probabilidades y Teoría de Integración. Sin embargo  escribió acerca de muchos otros temas: formas cuadráticas, construcción de mapas, cálculo geométrico de volúmenes, etc.

Mecanismos  y  Teoría de la Aproximación de Funciones Durante su estancia en el extranjero en el año 1852, Chebyshev visitó varias factorías de construcción de maquinaria, interesándose especialmente por  las máquinas de vapor construidas por el escocés James Watt (1736-1819). Dedicó mucha atención al perfeccionamiento del mecanismo, llamado paralelogramo de Watt, que convierte el movimiento circular en rectilíneo. Este mecanismo, fundamental en las máquinas de vapor, resultaba tan imperfecto que la varilla del pistón realizaba un recorrido curvilíneo en vez del rectilíneo deseado,  dando lugar a muchas fricciones que estropeaban las máquinas. El propio Watt y las siguientes generaciones de ingenieros intentaron mejorarlo sin mucho éxito durante los 75  primeros años después de su invención. Chebyshev, con su nueva teoría de aproximación de funciones, no solo resuelve el paralelogramo de Watt, sino que sus fórmulas generales permiten la resolución de otros tipos de mecanismos y problemas. Este descubrimiento quedó plasmado en sus trabajos [4,5],  los cuales marcan el comienzo de sus 40 años de investigación sobre aproximación y el estudio de mecanismos. Chebyshev fue el creador de otros muchos mecanismos y máquinas que asombraron a sus contemporáneos por su ingenio. Por ejemplo, construyó una máquina que andaba, imitando el movimiento de un animal. Su mecanismo más elaborado fue un aritmómetro, construido por la firma Gautier en París. El movimiento paralelo de Chebyshev son tres barras articuladas  AB, BC, AD cuyo punto de trazado P se aproxima al movimiento rectilíneo. En total construyó más de 40 mecanismos distintos y cerca de 80 modificaciones más de los mismos. En 1893, con motivo del 400 aniversario del descubrimiento de América por Cristóbal Colón,  se realizó una exposición mundial en Chicago, exhibiéndose siete de sus inventos mecánicos,  incluyendo su invento de una bicicleta especial para mujeres.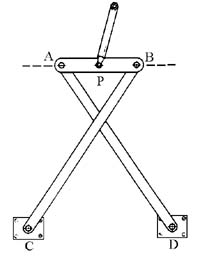

Es en [4] donde sienta las bases de la teoría de aproximación formulando el siguiente problema: Dada una función continua ƒ(x), encontrar un polinomio de  grado dado, tal que el máximo de su desviación de f(x) en un intervalo dado, sea más pequeño que el de los otros polinomios del mismo grado. En este trabajo también aparece su famoso polinomio por primera vez. Temáticamente, el trabajo total de Chebyshev sobre aproximación incluye la teoría de polinomios ortogonales, interpolación, teoría de momentos, método de cuadraturas y fracciones continuas.

Teoría de los Números: Además de la citada y premiada obra  sobre Teoría de Congruencias presentada como defensa de su tesis, y de su colaboración con el académico Bunyakovsky, en la publicación de los trabajos de Euler sobre teoría de los números, los trabajos de Chebyshev sobre números primos incluyen la determinación del número de primos que no exceden un número dado, y una prueba de la conjetura de Bertrand. En 1845 Bertrand conjeturó, que siempre existe al menos un número primo entre  n y 2n-2 para n>3. Chebyshev probó esta conjetura en 1850.

También estuvo cerca de demostrar el Teorema del Número Primo (T. N. P.): Sea π(x) la cantidad de números primos menores o iguales que x. Evidentemente π(x) → ∞ cuando x → ∞ puesto que existe una infinidad de números primos ("Elementos" libro IX, Euclides, 300 a. C.). El comportamiento de π(x) como función de x ha sido objeto de estudio de muchos matemáticos  ilustres a partir del siglo XVIII. Usando tablas de números primos, Gauss (1792) y Legendre (1798) observaron que para x grande, el cociente π(x)log(x)/x era próximo a 1 y conjeturaron que este cociente tendía a 1 cuando x tiende a ∞ (T. N. P.).

En 1848 fue Chebyshev quien demostró, que si dicho cociente tenía límite, este límite debía ser 1. Sin embargo, no fue capaz de demostrar que el cociente tenía límite. La prueba de este resultado fue completada solamente dos años después de la muerte de Chebyshev, por Hadamard y por de la Vallée Poussin, independientemente uno del otro.

Teoría de Probabilidades: Chebyshev se dedicó desde su juventud a la teoría de probabilidades siendo el objeto de su primera tesis. Escribió en total cuatro trabajos sobre teoría de probabilidades, en los años 1845, 1846, 1867 y 1887; según el reconocimiento universal, estos trabajos llevaron la teoría de probabilidades nuevamente al rango de ciencia matemática y sirvieron de base para la creación de toda una escuela matemática. Es sabido que se le atribuyen las leyes principales de esta teoría, como la ley de los grandes números y el teorema central del límite, aunque quizás su contribución más conocida a la teoría de la probabilidad es la llamada desigualdad de Chebyshev: 
Si una variable aleatoria x tiene media μ y varianza σ² finitas, entonces ∀ k ≥ 0,  

Estos trabajos dieron un fuerte impulso a la escuela probabilística rusa, siendo especificados sus resultados por sus alumnos, en particular  A. A. Márkov y Liapunov.

Teoría de Integración: En su segunda tesis  establece una conjetura de Abel de 1826: Si la integral , con P(x), R(x) polinomios, es expresable mediante logaritmos, entonces se verifica

donde p y q son funciones enteras y c es una constante. En 1852, Chebyshev, a instancias de Liouville y Hermite, consideró la integral general donde f(x) es una función racional y R(x) es un polinomio. Además generaliza la función Beta y examina integrales de la forma  ∫x^m(a+bxⁿ)^p dx donde m, n, p son números racionales. Más precisamente encontró que los únicos casos de integrabilidad se dan  cuando: p es entero; (m+1)/n o ((m-1)/n)+p son  números enteros.