 Chebyshev, P. L. (1821-1894)
Chebyshev, P. L. (1821-1894) |
 |
 |
 |
| Escrito por Francisco Luquin (Universidad del País Vasco) | ||||||
Su vida
Pafnuty Lvovich Chebyshev nació el 16 de Mayo de 1821 en una finca de su padre en Okatovo, región de Kaluga, al oeste de Rusia, en el seno de una familia de rancio abolengo. Su padre, Lev Pavlovich Chebyshev, fue un oficial militar que combatió contra Napoleón. Alguno de sus nueve hermanos siguió la tradición militar de su padre; Vladimir, el más pequeño, fue general y profesor en la Academia de Artillería de San Petersburgo. Existe un artículo [8] sobre la historia de la familia de Chebyshev, en el que figura como descendiente del líder militar tártaro del siglo XVIII, Khan Chabysh. La educación primaria la recibió en casa. Su madre, Agrafena Ivánovna, le enseñó a leer y escribir, mientras que su prima Sújarieva le enseñó la aritmética y el idioma francés, el cual le sería de gran utilidad. En el año de 1832 la familia Chebyshev se trasladó a Moscú, donde Pafnuty siguió completando su educación secundaria también en casa, pero teniendo como tutor en Matemáticas a P. N. Pogorelsky, reconocido en su día como el mejor profesor de matemáticas elementales de Moscú. Pogorelsky escribió alguno de los más populares textos de matemáticas elementales de la época, que ciertamente inspiraron a su discípulo dándole además una sólida formación matemática. Así pues, Chebyshev estaba muy bien preparado para el estudio de las Ciencias Matemáticas a su ingreso, en 1837, en la Universidad de Moscú. Fue el profesor N. D. Brashman quien prácticamente dirigió los estudios universitarios de Chebyshev que finalizaron en el año 1841. Chebyshev siempre expresó un gran respeto por su profesor, atribuyéndole una gran influencia en su posterior desarrollo matemático. El departamento de física y matemáticas en el que Chebyshev estudiaba convocó un premio en el curso 1840-41. Chebyshev presentó un trabajo sobre el cálculo de las raíces de las ecuaciones, en el que resolvía la ecuación y=f(x) usando el desarrollo en serie de la función inversa de f. El trabajo, no publicado en su momento, fue premiado sólo con la medalla de plata, cuando seguramente fuese merecedor del oro. Su primera tesis magistral “Experiencia sobre el análisis elemental de la teoría de probabilidades” fue defendida en el verano del año 1846 en la Universidad de Moscú, siendo su supervisor, de nuevo, el profesor Brashman. Puesto que Chebyshev no encontró un trabajo satisfactorio en Moscú, se trasladó a la Universidad de San Petersburgo, donde en 1847 defiende su segunda tesis “Sobre la integración mediante logaritmos” consiguiendo con ello el título de profesor adjunto. En el año 1849 defiende su tercera tesis doctoral “Teoría de Congruencias”, obra muy importante en el siglo XIX. Con ella, Chebyshev obtiene el grado científico de Doctor. Esta obra obtuvo un premio de la Academia de Ciencias y durante mucho tiempo sirvió como libro de texto en las universidades, reeditándose en los años 1879 y 1907. En el año 1888 fue traducida al alemán y en 1895 al italiano.
Chebyshev trabajó como profesor en la Universidad de San Petersburgo durante 35 años. Desde el año 1847 hasta el 1853 fue profesor adjunto, desde el año 1853 hasta el 1857 fue profesor extraordinario y desde el año 1857 hasta el 1882 fue profesor ordinario, fecha en que se retiró de la enseñanza para dedicarse exclusivamente a la investigación. En este tiempo, acostumbraba a recibir visitas una vez por semana, a unas horas determinadas. Las puertas de su casa estaban abiertas a todos aquellos que necesitasen una consulta o deseasen informar sobre sus investigaciones o recibir algún consejo sobre algún tema. Chebyshev dejó de existir sentado en su escritorio a los 73 años de edad, el 8 de Diciembre de 1894, al día siguiente de la consulta ordinaria con los visitantes. No quiso celebrar sus 25 años y tampoco su 50 aniversario de actividades científicas.
Aunque nunca se casó, Chebyshev tuvo una hija, a la que no reconoció oficialmente pero sí ayudó económicamente. Más tarde se encontraría con ella y su esposo, el coronel Leer, y la hija de ambos, en la casa de su hermana Nadiejda en Rudakovo. Las “dos jóvenes y hermosas hijas" vistas en el funeral de Chebyshev (de acuerdo con las notas autobiográficas de Grave [2]) fueron, presumiblemente, su hija y nieta. A Chebyshev se le reconoce como el creador de la escuela matemática de San Petersburgo cuyo eco e influencia ha llegado hasta nuestro tiempo en muchas ramas de la matemática. Esta escuela se distinguía por la tendencia a relacionar los problemas teóricos de la matemática con los problemas de la técnica y de la naturaleza. Según el propio Chebyshev “la unión de la teoría y la práctica proporciona los resultados más provechosos. Con ello, no sólo gana la práctica, sino que también salen beneficiadas las ciencias. La práctica descubre a la teoría nuevos objetivos de investigación o nuevas facetas en los objetos ya conocidos”. En otra ocasión escribe: “Entre la inmensa cantidad de problemas que plantea a la humanidad la actividad práctica del hombre, se destaca el siguiente: Cómo deben disponerse los medios para alcanzar el máximo provecho posible”, y añade más adelante: “La mayor parte de los problemas prácticos se reducen a problemas de máximo y mínimo que son nuevos para la ciencia y sólo su resolución puede satisfacer a la práctica, que siempre busca lo mejor y más ventajoso”. Los méritos de Chebyshev fueron debidamente reconocidos en su tiempo. Fue miembro honorífico de todas las universidades rusas, así como de la Academia de Artíllería. Fue elegido miembro correspondiente de la Real Sociedad de las Ciencias de Lieja y de la Sociedad Philomathique en 1856, de la Academia de Ciencias de París en 1860 y miembro extranjero de esta en 1874, en 1871 miembro correspondiente de la Academia de Ciencias de Berlín, de la Academia de Bolonia en 1873, miembro de la Real Sociedad de Londres en 1877, de la Academia Real de Italia en 1880 y de la Academia de Ciencias de Suecia en 1893. En el año 1890, y a petición del Presidente de la Academia de Ciencias de París, el conocido matemático francés Ch. Hermite, se concede a Chebyshev la orden de la Legión de Honor. Con el objeto de obtener un mayor reconocimiento, Chebyshev creía necesario publicar también fuera de su país y, por ende, en otra lengua distinta de la rusa, que debido a su formación fue el francés. Su primer trabajo fue sobre integrales múltiples y lo remitió en 1842 al "Journal des mathématiques pures y appliquées", fundado por Liouville en 1836, y llamado familiarmente "Liouville's Journal", apareciendo en la revista en 1843. No se sabe con certeza cómo llegó el manuscrito a las manos de Liouville. El trabajo presentaba una fórmula sin demostrar y sorprendentemente la revista contenía un trabajo de Catalan (1814-1894) dando una demostración de dicha fórmula. Explicaciones sobre este hecho pueden verse en [3]. Su segundo y tercer trabajo, también en francés, fueron dedicados a la convergencia de las series de Taylor y a la teoría de la probabilidad, respectivamente, y fueron publicados por Crelle en su "Journal für Reine und Angewandte Mathematik" (1844, 1846). De nuevo se desconoce cómo hizo llegar los trabajos a la editorial. Chebyshev publicó un solo trabajo más en "Crelle Journal", fue en 1855, año de la muerte de Crelle. Después publicaría en el recién creado Bulletin de la Société Mathématique de France. Chebyshev realizó múltiples giras científicas por Europa, destacando sus estancias en Francia, sobre todo las de París. Aquí se solía hospedar en el hotel Corneille, enfrente de Odeón, comía en restaurantes baratos y viajaba en los omnibuses. En Francia estuvo al menos en los años 1852, 1856, 1864, 1873, 1875, 1876, 1878, 1882, 1884, 1893. Nunca hizo referencias a estas giras, exceptuando la del año 1852, de la que existe una detallada descripción. Durante estos viajes, tuvo contactos con los matemáticos franceses Liouville, Hermite, Bienaymé, Serret, Lebesgue, Poncelet (si no directamente con él, sí con el círculo de sus ideas), con los matemáticos ingleses Cayley y Silvester, y con el matemático alemán Dirichlet, disfrutando tanto de las discusiones científicas como de la atmósfera de libertad reinante por Europa. Por último señalemos que en 1868 apoyó sin éxito el ingreso de Sonia Kovalévskaya en la Facultad de Matemáticas de San Petersburgo y que ella, discípula de Weierstrass, por medio de sus frecuentes contactos con Chebyshev, ejerció de transmisora entre ellos y entre sus respectivas escuelas matemáticas. Su obra
A efectos de un resumen podemos clasificar los trabajos matemáticos de Chebyshev en las cuatro ramas siguientes: Mecanismos y Teoría de la Aproximación de Funciones, Teoría de los Números, Teoría de Probabilidades y Teoría de Integración. Sin embargo escribió acerca de muchos otros temas: formas cuadráticas, construcción de mapas, cálculo geométrico de volúmenes, etc. Mecanismos y Teoría de la Aproximación de Funciones Durante su estancia en el extranjero en el año 1852, Chebyshev visitó varias factorías de construcción de maquinaria, interesándose especialmente por las máquinas de vapor construidas por el escocés James Watt (1736-1819). Dedicó mucha atención al perfeccionamiento del mecanismo, llamado paralelogramo de Watt, que convierte el movimiento circular en rectilíneo. Este mecanismo, fundamental en las máquinas de vapor, resultaba tan imperfecto que la varilla del pistón realizaba un recorrido curvilíneo en vez del rectilíneo deseado, dando lugar a muchas fricciones que estropeaban las máquinas. El propio Watt y las siguientes generaciones de ingenieros intentaron mejorarlo sin mucho éxito durante los 75 primeros años después de su invención. Chebyshev, con su nueva teoría de aproximación de funciones, no solo resuelve el paralelogramo de Watt, sino que sus fórmulas generales permiten la resolución de otros tipos de mecanismos y problemas. Este descubrimiento quedó plasmado en sus trabajos [4,5], los cuales marcan el comienzo de sus 40 años de investigación sobre aproximación y el estudio de mecanismos. Chebyshev fue el creador de otros muchos mecanismos y máquinas que asombraron a sus contemporáneos por su ingenio. Por ejemplo, construyó una máquina que andaba, imitando el movimiento de un animal. Su mecanismo más elaborado fue un aritmómetro, construido por la firma Gautier en París. El movimiento paralelo de Chebyshev son tres barras articuladas AB, BC, AD cuyo punto de trazado P se aproxima al movimiento rectilíneo. En total construyó más de 40 mecanismos distintos y cerca de 80 modificaciones más de los mismos. En 1893, con motivo del 400 aniversario del descubrimiento de América por Cristóbal Colón, se realizó una exposición mundial en Chicago, exhibiéndose siete de sus inventos mecánicos, incluyendo su invento de una bicicleta especial para mujeres. 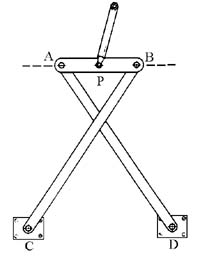 Es en [4] donde sienta las bases de la teoría de aproximación formulando el siguiente problema: Dada una función continua ƒ(x), encontrar un polinomio de grado dado, tal que el máximo de su desviación de f(x) en un intervalo dado, sea más pequeño que el de los otros polinomios del mismo grado. En este trabajo también aparece su famoso polinomio por primera vez. Temáticamente, el trabajo total de Chebyshev sobre aproximación incluye la teoría de polinomios ortogonales, interpolación, teoría de momentos, método de cuadraturas y fracciones continuas. Es en [4] donde sienta las bases de la teoría de aproximación formulando el siguiente problema: Dada una función continua ƒ(x), encontrar un polinomio de grado dado, tal que el máximo de su desviación de f(x) en un intervalo dado, sea más pequeño que el de los otros polinomios del mismo grado. En este trabajo también aparece su famoso polinomio por primera vez. Temáticamente, el trabajo total de Chebyshev sobre aproximación incluye la teoría de polinomios ortogonales, interpolación, teoría de momentos, método de cuadraturas y fracciones continuas.Teoría de los Números: Además de la citada y premiada obra sobre Teoría de Congruencias presentada como defensa de su tesis, y de su colaboración con el académico Bunyakovsky, en la publicación de los trabajos de Euler sobre teoría de los números, los trabajos de Chebyshev sobre números primos incluyen la determinación del número de primos que no exceden un número dado, y una prueba de la conjetura de Bertrand. En 1845 Bertrand conjeturó, que siempre existe al menos un número primo entre n y 2n-2 para n>3. Chebyshev probó esta conjetura en 1850. También estuvo cerca de demostrar el Teorema del Número Primo (T. N. P.): Sea π(x) la cantidad de números primos menores o iguales que x. Evidentemente π(x) → ∞ cuando x → ∞ puesto que existe una infinidad de números primos ("Elementos" libro IX, Euclides, 300 a. C.). El comportamiento de π(x) como función de x ha sido objeto de estudio de muchos matemáticos ilustres a partir del siglo XVIII. Usando tablas de números primos, Gauss (1792) y Legendre (1798) observaron que para x grande, el cociente π(x)log(x)/x era próximo a 1 y conjeturaron que este cociente tendía a 1 cuando x tiende a ∞ (T. N. P.). En 1848 fue Chebyshev quien demostró, que si dicho cociente tenía límite, este límite debía ser 1. Sin embargo, no fue capaz de demostrar que el cociente tenía límite. La prueba de este resultado fue completada solamente dos años después de la muerte de Chebyshev, por Hadamard y por de la Vallée Poussin, independientemente uno del otro. Teoría de Probabilidades: Chebyshev se dedicó desde su juventud a la teoría de probabilidades siendo el objeto de su primera tesis. Escribió en total cuatro trabajos sobre teoría de probabilidades, en los años 1845, 1846, 1867 y 1887; según el reconocimiento universal, estos trabajos llevaron la teoría de probabilidades nuevamente al rango de ciencia matemática y sirvieron de base para la creación de toda una escuela matemática. Es sabido que se le atribuyen las leyes principales de esta teoría, como la ley de los grandes números y el teorema central del límite, aunque quizás su contribución más conocida a la teoría de la probabilidad es la llamada desigualdad de Chebyshev:
Si una variable aleatoria x tiene media μ y varianza σ2 finitas, entonces ∀ k ≥ 0, Estos trabajos dieron un fuerte impulso a la escuela probabilística rusa, siendo especificados sus resultados por sus alumnos, en particular A. A. Márkov y Liapunov.
Teoría de Integración: En su segunda tesis establece una conjetura de Abel de 1826: Si la integral donde p y q son funciones enteras y c es una constante. En 1852, Chebyshev, a instancias de Liouville y Hermite, consideró la integral general
BIBLIOGRAFÍA
En la Web:
Nota: 1 La primera dificultad que encontramos al iniciar su estudio es como escribir su nombre. Habiéndose contabilizado hasta nueve formas distintas, un comité internacional creado a tal efecto, tuvo que decidir sobre el deletreo estándar del nombre de Chebyshev. Philip J. Davis ha escrito un gracioso libro con este problema como tema central. Nosotros, de acuerdo con E. Aparicio, lo escribiremos de esta forma, por ser la transcripción letra a letra del nombre ruso a nuestro alfabeto. |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






 Chebyshev
Chebyshev