Plücker y las curvas algebraicas

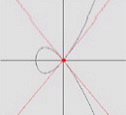
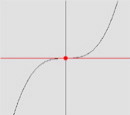
También hizo Plücker importantes descubrimientos en geometría algebraica. En su System der analytischen Geometrie, publicado en 1834, abordó el problema de los puntos de intersección de dos curvas algebraicas. Representó todas las curvas que pasan por los puntos de corte de dos curvas de idéntico grado C* y C** de la forma siguiente (ya propuesta por G. Lamé, pero a la que Plücker extrajo mayor rendimiento): C=C*+λC**, donde λ es un número cualquiera. Mediante este esquema aclaró la siguiente paradoja (llamada de Cramer). Sabemos que una curva algebraica de grado n queda determinada por n(n+3)/2 puntos, pero sabemos también que dos curvas de grado n se cortan en n² puntos. Pero, cuando n>3,  n²>n(n+3)/2, de modo que por n(n+3)/2 de los n² puntos en los que se cortan dos curvas de grado n, pasa más de una curva con dicho grado. Para explicar esto, pensemos en [n(n+3)/2]-1 puntos y busquemos dos curvas C* y C** de grado n que los contengan. Si completamos la colección con un punto más, podemos encontrar un valor de λ que proporcione una curva C de grado n que pase por todos ellos. Las curvas C, C* y C** tienen en común, no solo el conjunto original, sino los n² que comparten C* y C**. Esto quiere decir que para todo conjunto de [n(n+3)/2]-1 puntos existe otro (dependiente del primero) cuya cardinalidad es n²-[[n(n+3)/2]-1]-[(n-1)(n-2)/2], y tales que cualquier curva de grado n que pase por los primeros pasa también por los dependientes. De este modo, cualquier cúbica que pase por ocho puntos de corte de otras dos, pasa también por el noveno.

Otra importante aportación de Plücker, quizás la más conocida, fue dada a conocer en su Theorie der algebraischen Curven, publicada en 1839. Consiste en cuatro fórmulas que ligan entre sí las constantes asociadas a una curva. Si una curva pasa varias veces por un punto, diremos que dicho punto es múltiple o singular. Si pasa dos veces se llama punto doble. Un punto doble es un nodo si la curva tiene en él dos tangentes distintas (ver en la figura de la izquierda la curva de ecuación y²=x³+x²), y una cúspide si las tangentes están superpuestas (figura del medio, curva de ecuación y²=x³). En cambio, un punto no singular es una inflexión si el orden de contacto entre la curva y su tangente en dicho punto es mayor que tres (figura de la derecha, curva y=x³).

La clase de una curva es el número de tangentes que se pueden trazar desde un punto cualquiera del plano. Pues bien, si una curva tiene grado n, clase m, i inflexiones, t bitangentes (esto es tangentes a la curva en dos puntos diferentes), d nodos, r cúspides y ningún otro punto singular, se cumplen las siguientes relaciones:

m + 2d + 3r = n(n-1)
i + 6d + 83 = 3n(n-2)
n + 2t + 3i = m(m-1)
r + 6t + 8i = 3m(m-2)

Estas son las célebres fórmulas de Plücker. De ellas se deduce que para toda curva de grado n sin puntos singulares, sucede lo siguiente: