[Howad Eves. An introduction to the history of Mathematics]

Stevin, paladín de la lengua vernácula

Uno de los grandes objetivos de Stevin fue el hacer llegar los conocimientos científicos de su época al mayor número de sus compatriotas. Para ello, atendiendo especialmente a aquellos ciudadanos que no habían tenido acceso a una educación escolar (impartida en latín) y, en consecuencia, estaban condenados a no poder participar en actividad científica alguna, escribió la mayor parte de su obra en lengua vernácula. Con ello, además de acercar la ciencia a un público no científico, consiguió que sus libros fuesen poco o nada  leídos por investigadores contemporáneos de otros países.

Otra razón por la que Stevin se decantó por el uso del holandés como lenguaje científico fue la convicción de que esta lengua era la más idónea para expresar y transmitir ideas, especialmente las científicas, a causa de sus palabras cortas y su gran potencial combinatorio.

Además de estos dos argumentos racionales a favor del uso del holandés en la generación y transmisión de los conocimientos científicos, Stevin contaba con una justificación que entra en el terreno de lo fantástico. Veamos.

En la “Era de los Sabios”, todo lo que nosotros conocemos en estado deficiente e incompleto estaba en orden. ¿Era posible volver a aquella situación ideal? ¿Cuáles eran los medios para ello? Según Stevin, el principal recurso consistía en el estudio sistemático de la ciencia natural. Para ello, era necesaria la colaboración organizada de todas las personas capacitadas para desarrollar un trabajo científico, independientemente de su status social. Esto sólo era posible si todos los razonamientos e ideas científicas se enunciaban y transmitían en lengua vernácula. Dado que el holandés era el idioma que permitía  esta formulación y comunicación de forma más precisa, ergo el holandés era la lengua de los “Sabios”.

Este desvarío nacionalista, impropio de un científico que se precie, ejemplifica de forma contundente que, en ocasiones, las mentes más privilegiadas incurren en desatinos mayúsculos cuando se alejan imprudentemente de los terrenos en que son competentes.   

Stevin y la aritmética comercial

Desde que la complejidad de los problemas de carácter mercantil (cálculo del interés simple o compuesto, anualidades, descuentos,...) se hizo  mayor, los profesionales capaces de realizar este tipo de cómputos se convirtieron en empleados indispensables en todas las empresas dedicadas a negociar con dinero. No obstante, los expertos que podían resolver satisfactoriamente este tipo de cuestiones eran pocos. Recordemos que, en pleno siglo XVI, la multiplicación y la división eran operaciones que no estaban al alcance de la mayoría de los mortales. No debe extrañarnos, pues, que los bancos dispusiesen de tablas para facilitar los cálculos y que éstas se guardasen como información confidencial. Este ocultismo se mantuvo hasta que el número de calculadores hábiles aumentó de forma considerable. Este incremento se vio favorecido por la publicación de estupendas aritméticas comerciales en las que se desarrollaban los contenidos teórico-prácticos imprescindibles para que el lector pudiese detectar cualquier error (¿fraude?) en la aplicación de descuentos, cálculo de anualidades, etc.

Durante buena parte del siglo XVI los centros monetarios más importantes de la Europa Occidental estuvieron localizados en Lyón y Amberes. Precisamente en dichas ciudades se imprimieron los primeros manuales con Tablas de Interés. El primero, escrito por Jean Trenchant en 1558, y el segundo por Simon Stevin (Tafelen van Interest, midtsgaders de constructie der selver) en 1582. Las primeras Tafelen se publicaron en lengua vernácula y se reeditaron con algunas correcciones en 1590. También se tradujeron al francés y aparecieron en L’Arithmétique (1585).

En ellas Stevin no sólo incluyó una introducción teórica del interés simple y compuesto, acompañada de numerosas ejemplificaciones, sino que también presentó una serie de tablas con las reglas necesarias para calcularlas.

Los problemas de geometría

Los contenidos matemáticos de carácter geométrico están incluidos en Problematum geometricorum (1583), única obra de Stevin escrita en latín, estructurada en cinco libros.

El primero contiene la teoría clásica de razones y proporciones así como su aplicación a la división de figuras en partes que estén en una razón dada.

En el segundo, Stevin aplica la “regla de falsa posición” (procedimiento que gozó de gran popularidad en los manuales de aritmética del siglo XVI  y que se usaba para resolver algunos problemas de primer grado con una incógnita, sin necesidad de recurrir al simbolismo algebraico) a la resolución de cuestiones geométricas como la siguiente:

En primer lugar, Stevin construye un cuadrado cualquiera (falsa suposición) y determina la diferencia entre la diagonal y el lado. Si esta diferencia coincide con la dada, el problema está resuelto. En caso contrario, mediante una proporción se determina el lado del cuadrado requerido.

El tercer libro, el más interesante de todos, se consagra al estudio de los sólidos platónicos, poliedros semirregulares o arquimedianos y  poliedros estrellados. En él, además de los siete arquimedianos conocidos por Durero [Underweysung der Rechnung mit dem Zirckel und Richtscheyt (1525)], Stevin descubre otros tres: el truncato icosaedro per laterum media, con doce pentágonos regulares y veinte  triángulos equiláteros, el truncato dodecaedro per laterum divisiones in tres partes, con doce decágonos regulares y veinte triángulos equiláteros, y el truncato icosaedro per laterum tertias, con veinte hexágonos regulares y doce pentágonos regulares.

Por último, en los libros cuarto y quinto, se resuelven, respectivamente, los dos problemas siguientes:

• Dados dos sólidos S₁ y S₂, construir un tercer sólido S₃ equivalente a S₁ y semejante a S₂.
• Dados dos sólidos semejantes S₁ y S₂ (S₁ > S₂), construir un sólido S₃ semejante a S₁ y S₂ y equivalente a:
  1) S₁ + S₂
  2) S₁ – S₂

Décimas, centésimas, milésimas,...

En el opúsculo De Thiende (1585), escrito en lengua vernácula y  dedicado a los astrónomos, agrimensores, tapiceros, vinateros, geómetras, banqueros y todo tipo de mercaderes, Stevin introdujo el uso sistemático de las fracciones decimales en las matemáticas europeas. Dicho tipo de fracciones ya se habían utilizado por los matemáticos chinos (s. XIII), por el rabino Immanuel Bonfils de Tarascón (ca. 1350), por  el matemático alemán Christoff Rudolff (1530), y por el francés F. Viète en 1579. Además, en dicho folleto, Stevin planteó la unificación del sistema de pesas y medidas mediante un método basado en la división decimal de la unidad.

El contenido del libro está estructurado en dos partes y un apéndice.

En la primera, a lo largo de cuatro definiciones, el autor define los números decimales y presenta un código para representarlos. Hagamos notar que el sabio de Brujas utilizó su notación de diversas formas (véase el cuadro adjunto):

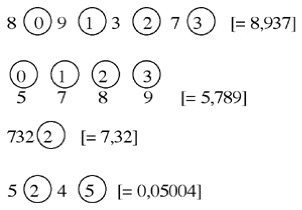Advirtamos también que el simbolismo de Stevin es deficiente, recuerda la notación sexagesimal y también el simbolismo algebraico de R. Bombelli (1572).

En la segunda parte se estudian las operaciones elementales con números decimales (adición, sustracción, multiplicación, división y extracción de raíces).

Por  último, en el apéndice se presentan diferentes aplicaciones prácticas de los números decimales en distintos ámbitos (agrimensura, estereometría, cálculo astronómico, etc.).

La mayor parte del álgebra de Simone Stevino Brugense se desarrolla en L’Arithmetique, texto escrito en francés y publicado en 1585, que contiene además un apéndice (La Pratique d’Arithmetique), Les Tables d’Interest (versión francesa de Tafelen van Interest, midtsgaders de constructie der selver), La Disme (traducción al francés de  De Thiende), los cuatro primeros libros de álgebra de Diofanto y un tratado de magnitudes inconmensurables con la explicación del décimo de Euclides.

En  L’Arithmetique, Stevin consideró tres tipos de “números”:

1) Los aritméticos, que eran los números abstractos.
2) Los geométricos, asociados a segmentos rectilíneos, cuadrados, cubos y bloques rectangulares, que nosotros denotaríamos por a, a², a³,. . ., a^1/2, a^1/3,etc.
3) Los algebraicos, combinaciones lineales de números geométricos.

En su intento de establecer analogías entre la geometría (números geométricos) y la aritmética (números aritméticos), el álgebra (teoría de ecuaciones) de Stevin consistió en la aplicación de la regla de tres a los números algebraicos. Por tanto, el álgebra de Stevinius forma parte de su aritmética general.

Stevin introdujo algunas simplificaciones en la notación algebraica. Así, usó el signo + para la adición y el símbolo – para la sustracción, la letra M para la multiplicación y la letra D para la división; sin embargo, no dispuso de un símbolo especial para la igualdad. Para la raíz cuadrada y la raíz cúbica también utilizó caracteres especiales, parecidos a los actuales.

En su teoría de ecuaciones, para representar las sucesivas potencias de la incógnita, Stevin adoptó un simbolismo similar al del matemático boloñés Rafael Bombelli. No hizo uso de los números complejos (introducidos por el autor italiano) pero si de los negativos. En el tratamiento de las ecuaciones de tercer y cuarto grado con una incógnita se inspiró en los trabajos de Girolamo Cardano (1501 – 1576) y  Ludovico Ferrari (1522 – 1565).

En el Appendice Algebraique (1594), opúsculo de seis páginas publicado en Leiden, Stevin (mediante las cúbicas x³ = 300x + 33915024  y  x³ = 300x + 33900000) presentó un método general para el cálculo aproximado de las soluciones reales de una ecuación de cualquier grado.

Stevin y el cálculo infinitesimal

El libro segundo del tratado de Estática De Beghinselen der Weeghconst (1586), se dedica al cálculo de centros de gravedad. En él, Stevin sustituye el método indirecto de exhausción (utilizado por Arquímedes y otros insignes matemáticos griegos) por un método directo que representa un gran paso hacia el concepto matemático de límite.

El método de exhausción Cuando Arquímedes quería demostrar que una cierta magnitud Q, por ejemplo el volumen de un segmento parabólico, era igual a A, probaba que las hipótesis Q < A y Q > A eran absurdas y, por tanto, Q = A era la única opción posible. El método de Stevin Si la diferencia entre dos magnitudes B y A se puede hacer menor que cualquier cantidad arbitrariamente pequeña, entonces B = A.

El procedimiento de Stevin se puede ejemplificar en la demostración de la proposición siguiente: El centro de gravedad de un triángulo pertenece a su mediana.

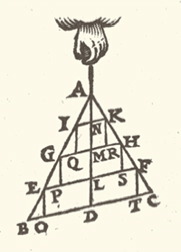Sea ABC un triángulo cualquiera y AD el segmento que une el vértice A con el punto medio del lado BC.

Dibújense los segmentos EF, GH e IK paralelos a BC y que cortan a AD en los puntos L, M y N respectivamente. Dibújense los segmentos EO, GP, IQ, KR, HS y FT paralelos a AD.

Dado que EF es paralelo a BC , y EO y FT lo son a LD, el cuadrilátero EFTO es un paralelogramo en el que EL es igual a LF y también a OD y DT. Entonces, en virtud de la primera proposición de este libro (el centro geométrico de cualquier figura plana también es su centro de gravedad), el centro de gravedad de EFTO está en DL. Por la misma razón, el centro de gravedad del paralelogramo GHSP está en LM y el de IKRQ en MN.

Por tanto, el centro de gravedad de la figura IKRHSFTOEPGQ, formada por los antedichos cuadriláteros, estará en el segmento ND o AD. Ahora bien, del mismo modo que se han inscrito tres cuadriláteros en el triángulo, también se puede inscribir un número infinito de ellos y el centro de gravedad de la figura inscrita estará en el segmento AD. Además, cuantos más cuadriláteros se inscriban, la diferencia entre el triángulo ABC y la figura compuesta por ellos se podrá hacer menor que cualquier figura plana por pequeña que sea. Si los “pesos” de los triángulos ABD y ACD no fuesen iguales, entonces tendrían una diferencia fija. Pero no puede haber una tal diferencia dado que cada uno de dichos triángulos difiere de la suma de los paralelogramos inscritos en él (que en ambos triángulos son iguales) en una figura plana tan pequeña como se quiera. En consecuencia, los “pesos” de ABD y ACD son iguales y, por tanto, el centro de gravedad del triángulo ABC está en la mediana AD.

En las líneas precedente hemos presentado las aportaciones más significativas de Simon Stevin al campo de las Matemáticas. Sin embargo, la actividad científica del sabio de Brujas no se redujo solamente a esta parcela del saber.

Se pueden encontrar contribuciones originales de Stevinius, que se mueven en la frontera de lo teórico y lo práctico, en terrenos tan diversos como Mecánica, Hidrostática, Astronomía, Geografía, Navegación, Tecnología, Arquitectura militar, Arquitectura civil, Música, Política y Lógica.

Si a esto se añade su obsesión por divulgar los conocimientos científicos a todos los estratos sociales, no resulta descabellado afirmar que Simone Stevinio fue uno de los científicos más notables del siglo XVI.

a) Fuentes

• Tafelen van Interst, midtsgaders de constructie derselver. Amberes, Christoffel Plantijn, 1582.
• Problematum geometricorum. Amberes, Ioannem Bellerum, 1583.
• De Thiende. Leiden, Christoffel Plantijn, 1585.
• L’Arithmetique. Leiden, Christophle Plantin, 1585.
• De Beghinselen der Weeghconst. Leiden, Christoffel Plantijn, 1586.

b) Literatura secundaria

• BOYER, C. B. (1959). The history of the Calculus and its conceptual development. New York, Dover.
• EVES, H (1983). An introduction to the history of Mathematics. New York, Saunders College Publishing.
• WAERDEN, B. L. van der (1985). A history of Algebra. Berlín, Springer-Verlag.

c) Bibliografía on line

• Principal works van Simon Stevin.