 126. EL POLIGONO ENTERO - Página 2: Solución
126. EL POLIGONO ENTERO - Página 2: Solución |
 |
 |
 |
Página 2 de 2
Es sabido que un polígono de n lados puede descomponerse en n-2 triángulos. Por tanto la suma de todos los ángulos interiores del polígono es igual a : (n-2) .180º. Si el polígono es regular y tiene n lados, la medida de cada ángulo interior de dicho polígono será igual a : 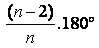 - Naturalmente si n es impar, n debe ser un divisor de 180. - Mientras que si n es par, podemos poner que n = 2k y la expresión 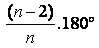 toma la forma, 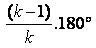 para que esta expresión sea un número natural se ha de cumplir que k debe ser un divisor de 180. Resumiendo : n es un divisor impar de 180 o el doble de un divisor cualquiera de 180. Pero los divisores de 180 son 1, 2, 3, 4, 5, 6, 9, 10, 12,15, 18, 20, 30, 36, 45, 60, 90 y 180. Teniendo en cuenta que n tiene que ser mayor o igual que 3, los posibles n impares son 3, 5, 9, 15 y 45. Los posibles n pares son 4, 6, 8, 10, 12, 30, 36, 40, 60, 72, 90 y 180. |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






