1. (2004-2005) Afinación - Afinación pitagórica
1. (2004-2005) Afinación - Afinación pitagórica |
 |
 |
 |
| Escrito por Vicente Liem | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Jueves 01 de Enero de 2004 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Página 5 de 8
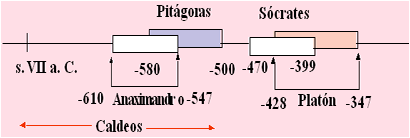
4.1. Afinación pitagórica Es muy probable que Pitágoras de Samos (580 –500 a. de C.), tras un largo periodo de estudio en las escuelas mesopotámicas, llevase las teorías de la música y los principios de la afinación a Grecia. Tal y como hacían los caldeos, estableció que el sonido musical producido por una cuerda vibrante varía en razón inversa a su longitud, esto es:
Además, estableció cuatro intervalos, o relaciones entre las longitudes de las cuerdas que producían las únicas consonancias admitidas:
Para producir todos los sonidos afinados (notas musicales) sólo se dispone de estos cuatro intervalos y sus combinaciones. Expresado de forma axiomática, el sistema de afinación pitagórico se obtiene de la forma siguiente:
En lugar de manejar la longitud de las cuerdas estudiaremos las frecuencias producidas por éstas. El axioma P2 sube quintas cuando se multiplica por 3 y las baja cuando se divide y el axioma P3 sube o baja octavas cuando se multiplica o divide por 2.
Ya estamos en condiciones de obtener de forma práctica las notas de la afinación pitagórica. Todas las notas de la afinación pitagórica se obtienen aumentado o disminuyendo quintas, es decir, dada una frecuencia f multiplicamos o dividimos por 3/2 cualquier número de veces.
Para llevar esta nota a la misma octava que f (hacer que el factor que multiplica a f esté en el intervalo [1,2] debemos dividir por 2. Es decir que la nueva nota afinada será:
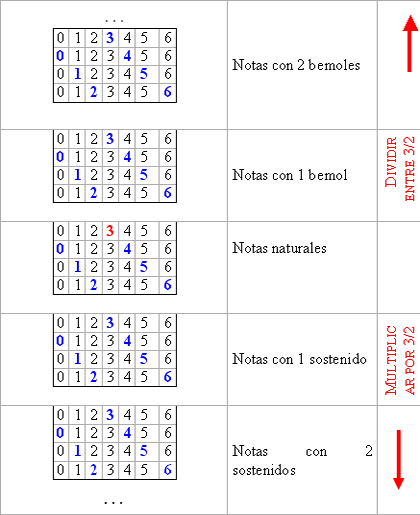
Método para obtener las notas 1.- Asociamos cada una de las notas con un número, es decir 0 = Do, 1 = Re, 2 = Mi, 3 = Fa, 4 = Sol, 5 = La, 6 = Si 2.- Escribimos tablas de 7 columnas y 4 filas:
En la primera fila marcamos la nota central (3)
A partir de la nota 3 marcamos las notas que se obtienen contando 5 casillas (OJO porque la casilla de partida también se cuenta)
Cada vez que hemos marcado una casilla nueva hemos aumentado una quinta, y repitiendo el proceso siete veces obtenemos las notas naturales en el orden siguiente: Fa – Do – Sol – Re - La - Mi - Si Para obtener más notas ampliamos el número de matrices o tablas. Con ellas aparecerán, en un sentido, las notas con un sostenido, con dos, etc y en el sentido contrario las notas con 1 bemol, 2 bemoles, etc.
Cada vez que vamos de una nota marcada a otra bajando en la tabla multiplicamos por 3/2 tantas veces como notas marcadas haya. Y en el sentido contrario lo que haremos es dividir por 3/2 . Ejemplo: A partir de un Do (natural), ¿cómo se obtiene un Fa# y un Mib? a) Desde el Do (natural) al Fa# hay que subir 6 quintas (hemos contado 6 casillas de las que hemos marcado previamente) por tanto se obtiene de la forma siguiente:
Para que el Do (natural) y el Fa# estén en la misma octava debemos dividir por una potencia de 2 , en concreto 2 3, es decir:
b) Desde el Do (natural) al Mib hay que bajar 3 quintas (hemos contado 3 casillas de las que hemos marcado previamente) por tanto se obtiene de la forma siguiente:
Para que el Do (natural) y el Mib estén en la misma octava debemos multiplicar por una potencia de 2 , en concreto 2 2, es decir :
Las fracciones para obtener las notas más frecuentes son las siguientes:
Para el sistema pitagórico, por ejemplo un Lab y un Sol# son dos notas diferentes:
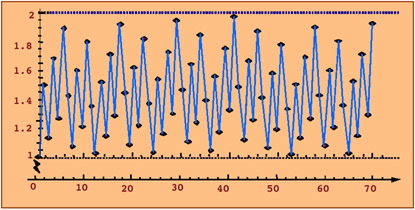
¿Cuántas notas deben aparecer dentro de una octava? Con el método que hemos descrito podríamos generar una cantidad infinita de notas dentro de una misma octava, por tanto debemos añadir algún criterio que permita detenernos cuando se tiene una cantidad razonable de ellas. Sería lógico pensar que un buen momento para parar es cuando empiecen a repetirse los sonidos. Sin embargo, como se puede demostrar que esto no va a ocurrir nunca, deberemos conformarnos con aceptar como iguales sonidos que sean “muy parecidos”. En la gráfica siguiente hemos representado las 70 primeras notas de la afinación pitagórica. En el eje de abcisas se representa el orden en el que aparecen y en el de ordenadas la fracción con la que se obtiene. Por ejemplo, la primera nota es el punto (0,1). Cuando obtengamos una nota cuya ordenada esté muy próxima al 1 nos detendremos.
La primera vez que nos acercamos al sonido inicial es cuando tenemos 12 notas, y ésta es la razón por la que la inmensa mayoría de la música que se escucha en la actualidad está hecha para el Temperamento Igual de 12 notas del que más tarde hablaremos. Si queremos mayor precisión necesitamos 53 notas, y si continuásemos 665 notas, etc., pero sin duda estas cantidades resultarían poco prácticas. Como se ve, el hecho de fijar 7, 12 u otro número de notas por octava no es una cuestión trivial y depende de la precisión que se exija en el parecido con la nota de partida. De hecho, esta elección no siempre se ha hecho con éxito. Por ejemplo, Robert Smith, en Harmonics, or the Philosophy of Musical Sounds (1749), propone 21 divisiones por octava para el temperamento de 5/18 de coma zarliniana y, como se apreciaría más tarde desde el punto de vista práctico, esto no tenía sentido. |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |