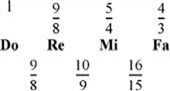4.2. Justa entonación

Con el nombre de afinación justa o de los físicos se conocen varios sistemas de afinación que añaden el intervalo 5/4 a la afinación pitagórica para representar la tercera. La forma de incorporarlo es ajustando algunas notas de la afinación pitagórica, por tanto deben considerarse correcciones a la afinación pitagórica.

En la afinación pitagórica, la tercera no se considera un intervalo consonante, sino que aparece subiendo cuatro quintas.

Tercera pitagórica	Tercera justa
Do->Mi	Do->Mi

Oyéndolas juntas se percibe bien la diferencia:

De todos los intentos por incorporar el intervalo de tercera a la afinación pitagórica, el que se utiliza en la práctica es el de Aristóxeno-Zarlino. No obstante, a continuación citamos otras propuestas bastante conocidas.

Modificaciones de Arquitas

Arquitas de Tarento (430-360 a.C.) es un discípulo de Pitágoras que dedicó gran parte de su investigación a la afinación. Advirtió que los intervalos pitagóricos 2/1, 3/2 y 4/3 son de la forma

Teniendo en cuenta esto, propuso dividir la cuarta en tres intervalos que verifiquen esta relación, para lo cual propuso añadir tres nuevas proporciones:

Así aparecen los valores siguientes:

entre los que, por primera vez, se tiene el intervalo de tercera 5/4 que había estado prohibido por los primeros pitagóricos.

Modificaciones de Tolomeo

Claudio Tolomeo (100-170) parte de los conceptos pitagóricos de afinación y en su obra Harmónicos expone una teoría matemática de los sonidos en las que aparecen dos tipos de escala una fija, tética, y una móvil, dinámica. A pesar de que su sistema de afinación es más complejo que los dos anteriores, en él siempre aparece el intervalo de tercera.

Como ocurría con los pitagóricos, los sonidos que consideran afinados están relacionados con su modelo del Universo.

Modificaciones de Zarlino y Delezenne

Gioseffo Zarlino (1517-1590) justificó los acordes con razones matemáticas que resultaron totalmente premonitorias de los armónicos. Estableció que había una afinidad entre los sonidos cuyas frecuencias son proporcionales a 1, 2, 3, 4, 5, 6 y comprobó que éstos eran emitidos por cuerdas de longitudes

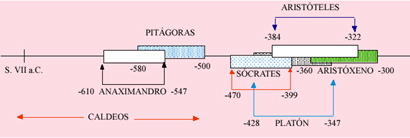
Delezenne (1776-1866) modificó la afinación de Zarlino y de hecho en la actualidad es habitual que en la afinación justa se mezclen notas de Zarlino con las de Delezenne.

Ha habido otras muchas más propuestas, como la de Johannes Kepler (1571-1630) que, a pesar de resultar muy ingeniosas, no han supuesto aportaciones considerables a la consolidación de la Justa Entonación.

Afinación de Aristóxeno-Zarlino

Arsitóxeno de Tarento (360-300 a.C.) es un discípulo de Aristóteles que estudió con profundidad las doctrinas pitagóricas. Rechaza asociar las consonancias naturales de quinta, cuarta y tercera con relaciones numéricas y sostiene que basta con el oído para conseguir la afinación.

A pesar de que históricamente no se introdujo como se expondrá a continuación, una forma sencilla de presentar la afinación de Aristóxeno-Zarlino es la siguiente: Consideramos una aproximación de la quinta pitagórica (3/2) dada por

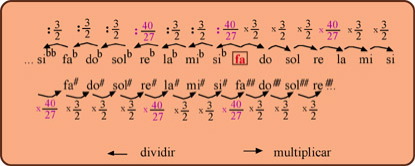
A partir de aquí (y en todos los tratados de música), como conviene distinguir entre ambos intervalos, se les da nombres diferentes. La quinta dada por 3/2 se llama quinta natural y la quinta dada por 40/27 se llama quinta sintónica.

Una vez fijada esta aproximación, la afinación de Aristógeno-Zarlino es una afinación hecha por quintas naturales (como la de Pitágoras) pero en la que algunas de ellas han sido sustituidas por quintas sintónicas. En la tabla siguiente marcamos sólo las sintónicas y entenderemos que el resto son naturales:

Teniendo en cuenta estas correcciones a la afinación pitagórica, las notas más frecuentes se obtendrían con las siguientes fracciones:

A pesar de la diferencia entre las fracciones que aparecen en la afinación pitagórica y la de Aristóxeno-Zarlino, podéis comprobar que el resultado es parecido:

Escala Pitagórica	Escala Justa Entonación

En la afinación de Aristóxeno-Zarlino, al aparecer dos tipos de quinta, aparecen dos tipos de tono:

Tono grande: 9/8 Ejemplo: Do-Re
Tono pequeño: 10/9 Ejemplo: Re-Mi

y tres tipos de semitono:

Semitono diatónico grande: 27/25 Ejemplo:Do-Re^b
Semitono diatónico pequeño: 16/15 Ejemplo:Mi-Fa
Setinono cromático: 25/24 Ejemplo: Do-Do#

Sin duda, esta circunstancia dificulta enormemente el uso de la justa entonación en la música polifónica.

Comentario

Desde un punto de vista meramente aritmético podemos decir que el sistema pitagórico sólo maneja sonidos que se pueden obtener mediante potencias de 2 y de 3 a partir de una frecuencia dada f₀. La justa entonación añade al sistema pitagórico las potencias del 5. Vista esta secuencia lógica, la pregunta es evidente: ¿por qué no seguir con las potencias de 7 y de 9, etc.?

Las razones para detenernos en el 5 son de diversa índole. En primer lugar hay razones estéticas: el intervalo de séptima convive con dificultad con los intervalos de la afinación de Zarlino. Por otro lado, cada vez que se añaden nuevas frecuencias se están incrementando los inconvenientes de los sistemas de afinación. Sirva como resumen de estos razonamientos el fragmento de la carta, fechada el de 3 de mayo de 1760, que Leonhard Euler (1077-1783) escribió a Federica Carlota Ludovica von Brandenburg Schwedt, princesa de Anhalt Dessau (1745 – 1808), para instruirla sobre temas de música (Euler, 1990):

Carta VII: De los doce tonos del clavecín:

“Mi intención era presentar a Vuestra Alteza el verdadero origen de los sonidos empleados en la música, casi totalmente desconocido para los músicos; pues no es la Teoría lo que los ha conducido al conocimiento de los tonos, lo deben más bien a la fuerza oculta de la verdadera Armonía, actuando tan eficazmente en sus oídos que, por así decirlo, los forzó a recibir los tonos actualmente en uso, aunque no estén suficientemente decididos sobre su justa determinación. Ahora bien, los principios de la Armonía se reducen en último término a números, [...] el número 2 produce sólo octavas [...]. Después el número 3 produce los tonos

que difieren de los anteriores en una quinta. Pero introduzcamos también el número 5 y veamos cuál sería el tono que produce 5 vibraciones, mientras que el F no hace más que una. [...] los músicos lo indican con la letra , [...] es llamado una tercera mayor y produce una consonancia muy agradable, estando contenido en una proporción de números bastante pequeña, 4 y 5. [...] (Así ) tendréis las teclas principales del clavecín que según los antiguos, constituye la escala llamada diatónica que deriva del número 2, del número 3 repetido tres veces y del número 5. No admitiendo más que estos tonos, se está en condiciones de componer muy bellas melodías, cuya belleza se fundamenta únicamente en la simplicidad de los números que producen estos tonos. [...]
Si se quisiera también introducir el número 7, el número de tonos de una octava sería mayor, y se llevaría toda la música a un grado más alto. Pero aquí la Matemática abandona la armonía a la Música.”

3 de mayo de 1760

Ventajas e inconvenientes de las afinaciones

Ventajas

En las afinaciones, como los sonidos afinados se obtienen con números racionales, los intervalos que aparecen son naturales, es decir, que las notas musicales se corresponden con armónicos de la serie natural. Por ejemplo, en el sistema pitagórico están afinados todos los armónicos que son múltiplos de 2 y de 3, mientras que en el sistema de Zarlino, están afinados los múltiplos de 2, de 3 y de 5. Dicho de otro modo, el primer armónico que no está afinado en el sistema de Pitagóras es el quinto, mientras que en el sistema de Zarlino es el séptimo.

Inconvenientes

Para determinar el número de notas por octava hemos supuesto que dos notas son iguales cuando en realidad son muy parecidas. Esto hace que al sonar dos o más instrumentos diferentes simultáneamente las afinaciones resulten poco prácticas. Veámoslo en el siguiente ejemplo.

Ejemplo: Un cantante tiene dificultades para interpretar los tonos graves y prefiere que se suba toda la música una quinta. A esto se le llama transposición.