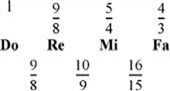1. (2004-2005) Afinación
1. (2004-2005) Afinación |
 |
 |
 |
| Escrito por Vicente Liem | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Jueves 01 de Enero de 2004 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1. Introducción 2. Afinaciones y Temperamentos 4. Sistemas de afinación 4.1. Afinación pitagórica 5. Bibliografía 1. Introducción Para estudiar un sonido hay, al menos, tres cualidades que debemos tener en cuenta:
En esta sección, como vamos a estudiar la afinación, sólo estamos interesados en el tono, y por tanto vamos a identificar cada sonido con la frecuencia que nos da el tono. Como muestra intuitiva de la importancia que tiene en la música la “forma de afinar”, a continuación analizamos dos fragmentos en los que se puede observar y escuchar dos tipos de música de estilos muy diferentes. Sin embargo, obviando las grandes diferencias técnicas (la primera es una grabación del año 2002 hecha en Estambul y la segunda una grabación del año 1929 extraída de un disco de pizarra), ambos fragmentos comparten muchas características fundamentales.
La primera es obra de un compositor contemporáneo turco y la segunda de una interpretación de de “cançò d’estil” de Paterna -Valencia. En ellas, aunque se desconozca su origen, y con independencia de la cultura musical de cada uno, cualquiera puede apreciar que se trata de música popular. Las razones que nos permiten situarlas dentro de la música folclórica son, básicamente las siguientes: En estos momentos, a nosotros nos interesa especialmente el segundo aspecto: Se utilizan muchas más notas que en la música occidental sinfónica. ¿Significa esto que hemos escuchado notas que están desafinadas?. Sin duda, la respuesta es no. Lo que ocurre es que no están afinadas en el sistema temperado al que está habituado nuestro oído. Analicemos más detenidamente los dos primeros compases del primer pentagrama:
2. Afinaciones y Temperamentos
Si los interpretamos en el sistema temperado de 12 notas (el más extendido en la música occidental actual) y en el sistema de afinación pitagórico comprobamos que hay diferencias claramente perceptibles:
Escuchemos, por ejemplo, la cuarta nota (Si b) en cada uno de los sistemas y luego juntas para apreciar la diferencia
El objetivo de esta sección es entender situaciones como ésta e intentar responder con argumentos matemáticos a preguntas como las siguientes:
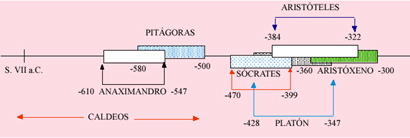
El esquema que seguiremos será el siguiente: 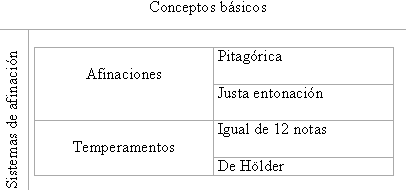 A lo largo de la Historia han aparecido centenares de afinaciones de las que sólo se siguen utilizando alrededor de media docena. La razón por la que trataremos estas cuatro formas de afinar es que éstas son las cuatro afinaciones que conviven en la orquesta clásica actual. 3. Conceptos básicos
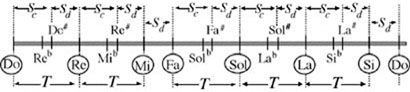
Una afinación o un sistema de afinación es el conjunto de los sonidos que utiliza la Música. En el conjunto de las frecuencias de todos los sonidos, R+ tenemos que elegir aquellos que sirven para hacer música y descartar el resto. Los sonidos admitidos por el sistema de afinación se denominarán sonidos afinados o notas musicales. Según sea la naturaleza de los números elegidos se tiene dos tipos de sistemas de afinación: las afinaciones y los temperamentos. En las primeras todos los números son racionales mientras que en los temperamentos algunos (o todos) son irracionales. Ahora bien, a pesar de que esta clasificación cada día se usa más en los tratados de música lo cierto es que tanto histórica como conceptualmente los temperamentos han surgido como aproximaciones a las afinaciones sin que, normalmente, se tuviese en cuenta el tipo de números utilizados. Una vez introducido, aunque sea grosso modo, el concepto de afinación, cabe preguntarse si éste puede ser todavía un tema de interés para alguien que no se dedique al estudio de la Historia. La aparición esporádica de artículos en revistas de física o matemáticas tratando temas de música podrían dar una contestación a esta pregunta. Sin embargo, las necesidades de músicos y musicólogos proporcionan un respuesta mucho más convincente. "uno de los principales problemas que se presentan en la praxis de la música antigua para tecla es el de la elección del temperamento adecuado" Revista de Musicología, 22 (1999) Entendiendo por adecuado aquel temperamento para el que fue concebida. De hecho, incluso la expresión "buen temperamento", empleada al menos a partir de la obra Clave bien temperado (Das wohltemperierte Klavier I, 1721) de J. S. Bach, resulta imprecisa. Como aclara J. J. Goldáraz buen temperamento no designa una única forma de afinar y continúa siendo un tema de discusión conocer si se trataba realmente del sistema de afinación de 12 notas por octava o se tratataba de otro temperamento de los que en la época se utilizaban en Alemania. La octava En todos los sistemas de afinación aparece el concepto de octava. Un sonido de frecuencia f1 se dice que es una octava más grave que otro f2 si f2 = 2·f1. Hasta tal punto es intuitiva esta idea, que se usa de forma natural aunque no se tenga formación musical. Piénsese, por ejemplo, cuando cantan juntos un hombre y una mujer. El hombre suele cantar una octava más grave y sin embargo cualquiera reconoce que están interpretando las mismas notas. A partir del concepto de octava, lo que se hace es partir el intervalo de frecuencias audibles por octavas: … [f, 2f], [2f, 4f], [4f, 8f], … e identifican las notas que están a diferente octava. Es decir, hablaremos de un Do sin importarnos la octava en la que se encuentra. Por tanto, es mucho más cómodo suponer que las notas están en el intervalo [1,2].
Siete notas Al menos desde el primer milenio antes de Cristo, los caldeos relacionaron muy estrechamente la música con la astrología y las matemáticas. De hecho, el destino de los hombres y la armonía del Universo se explicaba usando especulaciones matemáticas a las que atribuían multitud de propiedades. Parece ser que esto dio lugar a que numerosos fenómenos cósmicos fuesen representados por la comparación entre las longitudes de cuerdas tirantes. De este modo aparecieron cuatro relaciones asociadas con las cuatro estaciones del año que, por su importancia, tomaron nombres propios:
Entre los números cuyas propiedades eran especialmente útiles en la predicción de sucesos destacaban el 4 y el 7. De hecho, probablemente la antigua escala caldea era de siete notas. En occidente, a partir de los caldeos y sobre todo de los pitagóricos (siglo VI. a. C.) se ha considerado que las notas fundamentales eran 7 y que el resto eran alteraciones de estas notas. A las alteraciones se les llama sostenidos ( # ) si aumentan la frecuencia y bemoles ( b ) si la disminuyen. Pero no precisaremos más en la definición de las alteraciones porque, como se verá más adelante, dependiendo del sistema de afinación significarán una cosa u otra. Tonos y semitonos Se trata de intervalos que en la práctica se emplean más que los dados anteriormente. Dadas dos notas f1, f2 se tienen las siguientes relaciones: Hay sistemas de afinación en los que aparecen varios tipos de quinta, por tanto la distancia de tonos y semitonos dependerá del sistema. Algunas de estas afinaciones verifican: T=Sc+Sd 4.1. Afinación pitagórica Es muy probable que Pitágoras de Samos (580 –500 a. de C.), tras un largo periodo de estudio en las escuelas mesopotámicas, llevase las teorías de la música y los principios de la afinación a Grecia. Tal y como hacían los caldeos, estableció que el sonido musical producido por una cuerda vibrante varía en razón inversa a su longitud, esto es:
Además, estableció cuatro intervalos, o relaciones entre las longitudes de las cuerdas que producían las únicas consonancias admitidas:
Para producir todos los sonidos afinados (notas musicales) sólo se dispone de estos cuatro intervalos y sus combinaciones. Expresado de forma axiomática, el sistema de afinación pitagórico se obtiene de la forma siguiente:
En lugar de manejar la longitud de las cuerdas estudiaremos las frecuencias producidas por éstas. El axioma P2 sube quintas cuando se multiplica por 3 y las baja cuando se divide y el axioma P3 sube o baja octavas cuando se multiplica o divide por 2.
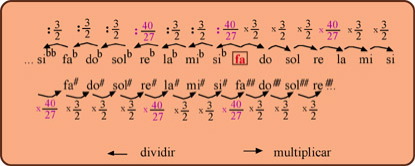
Ya estamos en condiciones de obtener de forma práctica las notas de la afinación pitagórica. Todas las notas de la afinación pitagórica se obtienen aumentado o disminuyendo quintas, es decir, dada una frecuencia f multiplicamos o dividimos por 3/2 cualquier número de veces.
Para llevar esta nota a la misma octava que f (hacer que el factor que multiplica a f esté en el intervalo [1,2] debemos dividir por 2. Es decir que la nueva nota afinada será:
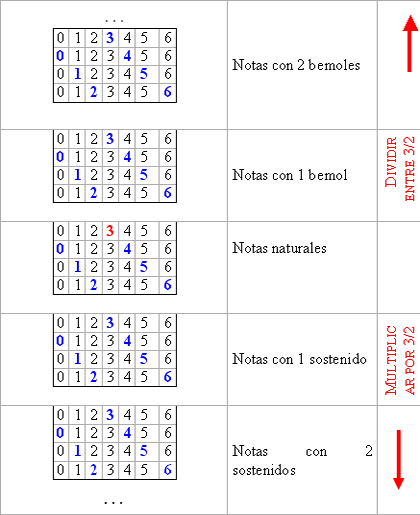
Método para obtener las notas 1.- Asociamos cada una de las notas con un número, es decir 0 = Do, 1 = Re, 2 = Mi, 3 = Fa, 4 = Sol, 5 = La, 6 = Si 2.- Escribimos tablas de 7 columnas y 4 filas:
En la primera fila marcamos la nota central (3)
A partir de la nota 3 marcamos las notas que se obtienen contando 5 casillas (OJO porque la casilla de partida también se cuenta)
Cada vez que hemos marcado una casilla nueva hemos aumentado una quinta, y repitiendo el proceso siete veces obtenemos las notas naturales en el orden siguiente: Fa – Do – Sol – Re - La - Mi - Si Para obtener más notas ampliamos el número de matrices o tablas. Con ellas aparecerán, en un sentido, las notas con un sostenido, con dos, etc y en el sentido contrario las notas con 1 bemol, 2 bemoles, etc.
Cada vez que vamos de una nota marcada a otra bajando en la tabla multiplicamos por 3/2 tantas veces como notas marcadas haya. Y en el sentido contrario lo que haremos es dividir por 3/2 . Ejemplo: A partir de un Do (natural), ¿cómo se obtiene un Fa# y un Mib? a) Desde el Do (natural) al Fa# hay que subir 6 quintas (hemos contado 6 casillas de las que hemos marcado previamente) por tanto se obtiene de la forma siguiente:
Para que el Do (natural) y el Fa# estén en la misma octava debemos dividir por una potencia de 2 , en concreto 2 3, es decir:
b) Desde el Do (natural) al Mib hay que bajar 3 quintas (hemos contado 3 casillas de las que hemos marcado previamente) por tanto se obtiene de la forma siguiente:
Para que el Do (natural) y el Mib estén en la misma octava debemos multiplicar por una potencia de 2 , en concreto 2 2, es decir :
Las fracciones para obtener las notas más frecuentes son las siguientes:
Para el sistema pitagórico, por ejemplo un Lab y un Sol# son dos notas diferentes:
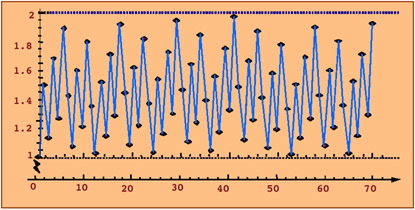
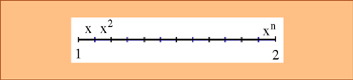
¿Cuántas notas deben aparecer dentro de una octava? Con el método que hemos descrito podríamos generar una cantidad infinita de notas dentro de una misma octava, por tanto debemos añadir algún criterio que permita detenernos cuando se tiene una cantidad razonable de ellas. Sería lógico pensar que un buen momento para parar es cuando empiecen a repetirse los sonidos. Sin embargo, como se puede demostrar que esto no va a ocurrir nunca, deberemos conformarnos con aceptar como iguales sonidos que sean “muy parecidos”. En la gráfica siguiente hemos representado las 70 primeras notas de la afinación pitagórica. En el eje de abcisas se representa el orden en el que aparecen y en el de ordenadas la fracción con la que se obtiene. Por ejemplo, la primera nota es el punto (0,1). Cuando obtengamos una nota cuya ordenada esté muy próxima al 1 nos detendremos.
La primera vez que nos acercamos al sonido inicial es cuando tenemos 12 notas, y ésta es la razón por la que la inmensa mayoría de la música que se escucha en la actualidad está hecha para el Temperamento Igual de 12 notas del que más tarde hablaremos. Si queremos mayor precisión necesitamos 53 notas, y si continuásemos 665 notas, etc., pero sin duda estas cantidades resultarían poco prácticas. Como se ve, el hecho de fijar 7, 12 u otro número de notas por octava no es una cuestión trivial y depende de la precisión que se exija en el parecido con la nota de partida. De hecho, esta elección no siempre se ha hecho con éxito. Por ejemplo, Robert Smith, en Harmonics, or the Philosophy of Musical Sounds (1749), propone 21 divisiones por octava para el temperamento de 5/18 de coma zarliniana y, como se apreciaría más tarde desde el punto de vista práctico, esto no tenía sentido. 4.2. Justa entonación Con el nombre de afinación justa o de los físicos se conocen varios sistemas de afinación que añaden el intervalo 5/4 a la afinación pitagórica para representar la tercera. La forma de incorporarlo es ajustando algunas notas de la afinación pitagórica, por tanto deben considerarse correcciones a la afinación pitagórica.
En la afinación pitagórica, la tercera no se considera un intervalo consonante, sino que aparece subiendo cuatro quintas.
Oyéndolas juntas se percibe bien la diferencia: De todos los intentos por incorporar el intervalo de tercera a la afinación pitagórica, el que se utiliza en la práctica es el de Aristóxeno-Zarlino. No obstante, a continuación citamos otras propuestas bastante conocidas. Modificaciones de Arquitas Arquitas de Tarento (430-360 a.C.) es un discípulo de Pitágoras que dedicó gran parte de su investigación a la afinación. Advirtió que los intervalos pitagóricos 2/1, 3/2 y 4/3 son de la forma
Así aparecen los valores siguientes:
entre los que, por primera vez, se tiene el intervalo de tercera 5/4 que había estado prohibido por los primeros pitagóricos. Modificaciones de Tolomeo Claudio Tolomeo (100-170) parte de los conceptos pitagóricos de afinación y en su obra Harmónicos expone una teoría matemática de los sonidos en las que aparecen dos tipos de escala una fija, tética, y una móvil, dinámica. A pesar de que su sistema de afinación es más complejo que los dos anteriores, en él siempre aparece el intervalo de tercera. Como ocurría con los pitagóricos, los sonidos que consideran afinados están relacionados con su modelo del Universo. Modificaciones de Zarlino y Delezenne Gioseffo Zarlino (1517-1590) justificó los acordes con razones matemáticas que resultaron totalmente premonitorias de los armónicos. Estableció que había una afinidad entre los sonidos cuyas frecuencias son proporcionales a 1, 2, 3, 4, 5, 6 y comprobó que éstos eran emitidos por cuerdas de longitudes
Delezenne (1776-1866) modificó la afinación de Zarlino y de hecho en la actualidad es habitual que en la afinación justa se mezclen notas de Zarlino con las de Delezenne. Afinación de Aristóxeno-Zarlino Arsitóxeno de Tarento (360-300 a.C.) es un discípulo de Aristóteles que estudió con profundidad las doctrinas pitagóricas. Rechaza asociar las consonancias naturales de quinta, cuarta y tercera con relaciones numéricas y sostiene que basta con el oído para conseguir la afinación.
A pesar de que históricamente no se introdujo como se expondrá a continuación, una forma sencilla de presentar la afinación de Aristóxeno-Zarlino es la siguiente: Consideramos una aproximación de la quinta pitagórica (3/2) dada por
A partir de aquí (y en todos los tratados de música), como conviene distinguir entre ambos intervalos, se les da nombres diferentes. La quinta dada por 3/2 se llama quinta natural y la quinta dada por 40/27 se llama quinta sintónica. Una vez fijada esta aproximación, la afinación de Aristógeno-Zarlino es una afinación hecha por quintas naturales (como la de Pitágoras) pero en la que algunas de ellas han sido sustituidas por quintas sintónicas. En la tabla siguiente marcamos sólo las sintónicas y entenderemos que el resto son naturales:
Teniendo en cuenta estas correcciones a la afinación pitagórica, las notas más frecuentes se obtendrían con las siguientes fracciones:
A pesar de la diferencia entre las fracciones que aparecen en la afinación pitagórica y la de Aristóxeno-Zarlino, podéis comprobar que el resultado es parecido:
En la afinación de Aristóxeno-Zarlino, al aparecer dos tipos de quinta, aparecen dos tipos de tono:
y tres tipos de semitono:
Sin duda, esta circunstancia dificulta enormemente el uso de la justa entonación en la música polifónica. Comentario Desde un punto de vista meramente aritmético podemos decir que el sistema pitagórico sólo maneja sonidos que se pueden obtener mediante potencias de 2 y de 3 a partir de una frecuencia dada f0. La justa entonación añade al sistema pitagórico las potencias del 5. Vista esta secuencia lógica, la pregunta es evidente: ¿por qué no seguir con las potencias de 7 y de 9, etc.? Las razones para detenernos en el 5 son de diversa índole. En primer lugar hay razones estéticas: el intervalo de séptima convive con dificultad con los intervalos de la afinación de Zarlino. Por otro lado, cada vez que se añaden nuevas frecuencias se están incrementando los inconvenientes de los sistemas de afinación. Sirva como resumen de estos razonamientos el fragmento de la carta, fechada el de 3 de mayo de 1760, que Leonhard Euler (1077-1783) escribió a Federica Carlota Ludovica von Brandenburg Schwedt, princesa de Anhalt Dessau (1745 – 1808), para instruirla sobre temas de música (Euler, 1990): Carta VII: De los doce tonos del clavecín:
Ventajas e inconvenientes de las afinaciones Ventajas En las afinaciones, como los sonidos afinados se obtienen con números racionales, los intervalos que aparecen son naturales, es decir, que las notas musicales se corresponden con armónicos de la serie natural. Por ejemplo, en el sistema pitagórico están afinados todos los armónicos que son múltiplos de 2 y de 3, mientras que en el sistema de Zarlino, están afinados los múltiplos de 2, de 3 y de 5. Dicho de otro modo, el primer armónico que no está afinado en el sistema de Pitagóras es el quinto, mientras que en el sistema de Zarlino es el séptimo. Inconvenientes Para determinar el número de notas por octava hemos supuesto que dos notas son iguales cuando en realidad son muy parecidas. Esto hace que al sonar dos o más instrumentos diferentes simultáneamente las afinaciones resulten poco prácticas. Veámoslo en el siguiente ejemplo.
Si los instrumentos afinaban en el sistema pitagórico con 12 notas: Mib Sib Fa Do Sol Re La Mi Si Fa# Do# Sol# cuando en la partitura aparece un Sol# , al subir una quinta el efecto será Sol#·(3/2) = (38/212)·(3/2) = 39/213 = Re# Sin embargo, esta nota no aparece entre las 12 que hemos seleccionado. La más parecida es Mib = 25 / 33 Así, cuando se interpreta Mib en lugar de Re# el error que se está cometiendo es el que ya habíamos escuchado cuando distinguíamos entre Lab y Sol# :
4.3. Temperamentos cíclicos regulares Los temperamentos cíclicos surgen en la práctica para evitar, entre otros, los problemas que acabamos de analizar. Lo que se hace es disminuir las quintas “templar” de manera que se repita la primera nota, pero claro está, de manera que el resultado sea aceptable.
Con este proceso lo que aseguramos es que si multiplicamos el 1 por x n veces debemos obtener el 2, es decir xn x 1 = 2 => x = Por tanto, las notas afinadas en un temperamento cíclico de n notas serán:
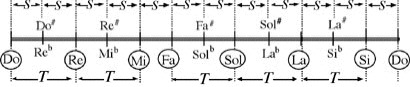
Temperamento igual de 12 notas Divide la octava en 12 semitonos iguales. Fue el español Bartolomé Ramos de Pareja (1440 - 1491) quien lo sistematizó en 1482, cuando ejercía como profesor de Música en la Universidad de Salamanca y en Bolonia. En su tratado Música Práctica (1482) se encuentran teorías renovadoras y maneras de calcular diferentes clases de intervalos. Este sistema, que tardó mucho tiempo en imponerse, lo consagró J. S. Bach (1685 - 1750) en su obra El Clave Bien Temperado donde realiza 48 Preludios y fugas (en dos libros) en todas las tonalidades.
Temperamento de Holder William Holder (1614-1697) utiliza un procedimiento mediante el cual divide la octava en 53 partes, notas o comas, de esta forma un tono contiene 9 comas, el semitono cromático 5 y el diatónico 4. El sistema utilizado por Holder no es más que una adaptación del sistema Pitagórico y, de hecho, cuando se compara ambos sistemas dan resultados prácticamente iguales.
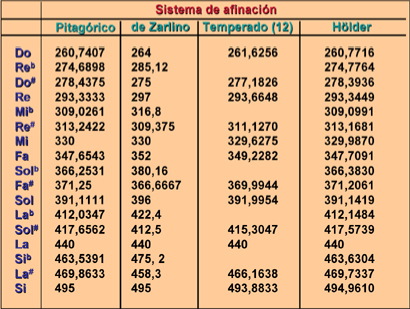
Ventajas y desventajas de los temperamentos El Temperamento de 12 notas Ventajas Inconvenientes El Temperamento de Holder Desde el trabajo del profesor Robert Dussaut, Explicación de las comas en los distintos sistemas acústicos (Chailley, Challan, 1965), el sistema de Holder se ha considerado como un sistema de afinación idóneo para trabajar con la afinación pitagórica. Ventajas Inconvenientes Como muestra de las diferencias entre los sistemas que hemos analizado, podemos observar las frecuencias de las notas más habituales en los cuatro sistemas de afinación:
5. Bibliografía
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |