Mayo 2009: Combinatoria de colores (publicado en la revista SUMA, nº 53, 2006)
Mayo 2009: Combinatoria de colores (publicado en la revista SUMA, nº 53, 2006) |
 |
 |
 |
| Escrito por Grupo Alquerque |
| Miércoles 06 de Mayo de 2009 |
|
Introducción En los años que llevamos con esta sección hemos hablado muchas veces de puzzles, de su diseño, de su construcción y del estudio de sus posibilidades de manipulación. Hoy queremos presentar uno basado en la combinatoria. Aprovechando la propuesta polícroma de la nueva etapa de SUMA, queremos jugar con colores viendo todas las formas de ordenarlos para obtener piezas distintas y conseguir figuras con colorido. Vamos a dedicar especial atención, como hemos hecho muchas veces, al diseño y estudio preliminar de las piezas que se pueden construir, antes de pasar a jugar con ellas. Como surgió la actividad Estábamos trabajando en clase la división de figuras en partes iguales (sobre lo que ya hablamos en el número 45 –Dividir en partes iguales- de SUMA) y habíamos comenzado con lo más simple, dividir un cuadrado en cuatro partes iguales y entonces apareció el reto, ¿de cuántas formas distintas podemos dividir un cuadrado en cuatro piezas que sean exactamente iguales (es decir si las recortamos y las colocamos una sobre otra coinciden)? La pregunta dio lugar a una actividad frenética, cada uno quería encontrar “su división”. A continuación mostramos algunas de las que aparecieron: 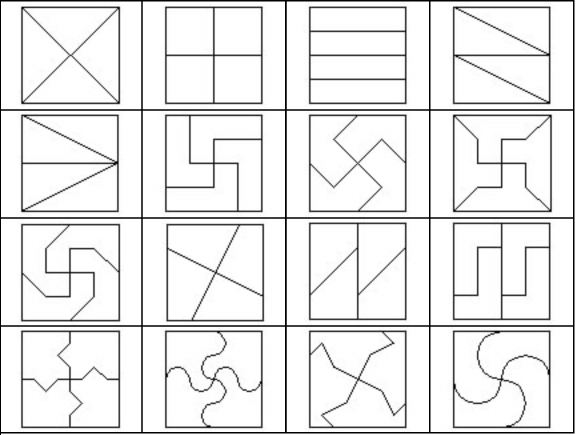 Como el colorear es la debilidad de los alumnos de primero de ESO cuando fueron apareciendo las distintas divisiones, alguien pregunto: “Maestro, ¿las podemos colorear?” Y entonces cambió la línea de trabajo, pues el problema era ahora cómo colocar los colores y por tanto surgió una nueva actividad de investigación con los siguientes apartados:
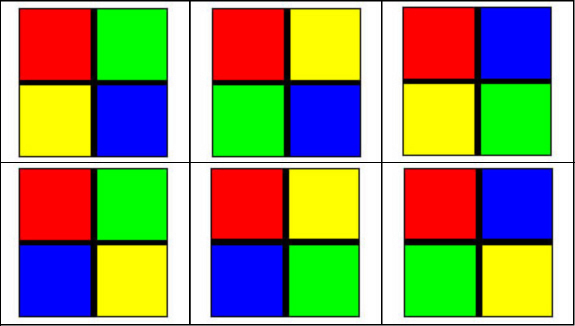
A partir de esta idea surgieron tres trabajos distintos dependiendo de la figura base de la que se partía, que como veremos, influye en los resultados. Primer puzzle de combinatoria a) Construcción La respuesta a la pregunta base del coloreo de la pieza ya dividida ha dado más de un quebradero de cabeza a nuestros alumnos. Ellos no conocen nada de Combinatoria por lo que las soluciones iban saliendo por ensayo y error, por intuición y por el poco o mucho factor visual desarrollado. Muchos de ellos (y de nosotros) para distinguir claramente dos piezas diferentes las tenemos que dibujar, recortar y superponer para ver claramente si son piezas iguales o distintas. Se les insistió en buscar algún procedimiento para no dibujar figuras repetidas, por ejemplo, fijar uno de los colores siempre en la misma posición. Analizando el problema desde el punto de vista de la Combinatoria deducimos que la situación planteada es una permutación circular de cuatro elementos (los cuatro colores) alrededor del centro del cuadrado. El número de ordenaciones posibles en una permutación circular de n elementos se obtiene por el factorial de n-1; P(n) = (n-1)! En nuestro caso es P(4) = (4-1)! = 3·2·1 = 6 Por lo que nuestro primer puzzle de combinatoria tendrá seis piezas distintas. Para demostrar que las piezas son distintas o para deducir cuál es la que falta hacemos un análisis comparativo entre ellas. Después del estudio detallado aparecen las seis posibilidades:
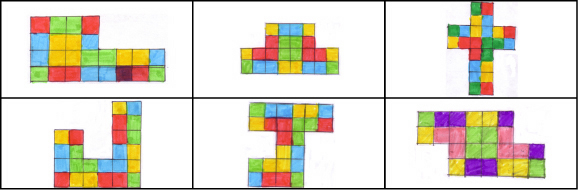
b) Juegos Una vez que teníamos las piezas no quisimos quedarnos ahí. Comenzamos a jugar con ellas y se planteó cómo construir composiciones con las seis piezas que tiene el puzzle con las condiciones de que las piezas tengan un lado común y correspondan a un triángulo del mismo color. Incluimos a continuación algunas de las figuras más llamativas que realizaron los alumnos.
Segundo puzzle de combinatoria Partiendo de la división del cuadrado en cuatro cuadrados iguales y escogiendo cuatro colores podemos construir el segundo puzzle. Las ordenaciones posibles de los cuatro colores es también una permutación circular de cuatro elementos, por lo que tenemos otras seis piezas diferentes:
Juegos y composiciones Como en el primer puzzle, para la realización de las composiciones, las piezas han de unirse por un lado que tenga el mismo color. A simple vista puede parecer que estamos en el mismo caso que el puzzle anterior, pero aquí se plantea una nueva dificultad. Anteriormente al unir los dos lados del cuadrado sólo había que hacer coincidir un color, pero en este segundo caso un lado equivale a una combinación de dos colores coincidiendo a la vez. Esto dificulta más la construcción de figuras con las seis piezas. El primer reto a plantear es: Con este puzzle ¿se puede formar un rectángulo de 2x3 piezas?
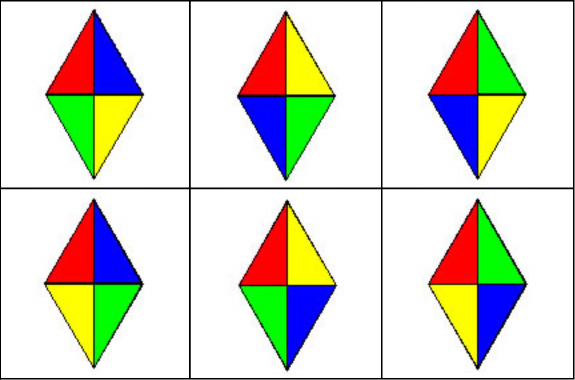
Tercer puzzle: rombos de colores Ya metidos en faena, decidimos modificar un poco las condiciones iniciales. Íbamos a seguir jugando a colorear piezas pero en este caso la pieza no sería tan regular como un cuadrado. Decidimos elegir un rombo con la característica de que su lado coincidía con su diagonal menor, es decir, sería un rombo formado por dos triángulos equiláteros (esta restricción influye sólo en la regularidad de las figuras que se pueden construir al final, no en el estudio combinatorio de piezas que se hace previamente). Con ese rombo dividido en cuatro partes iguales (triángulos rectángulos) por sus diagonales, comenzamos a trabajar. Si cada una de las divisiones del rombo la pintamos de un color ¿Cuántos rombos distintos se formarán? Volcando aquí el estudio hecho en los dos casos anteriores nos encontramos rápidamente con los siguientes seis casos:
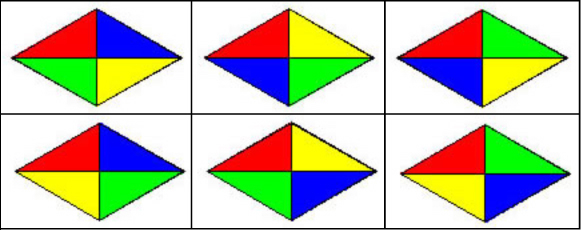
En los rombos los cuatro lados son iguales, pero los cuatro ángulos no son todos iguales, por lo que se nos plantea la siguiente cuestión, ¿son iguales estos dos rombos?
Con sólo superponerlo comprobamos que son rombos diferentes, y por tanto este puzzle tiene otras seis piezas más (nuestros alumnos las nombran “los rombos tendidos”).
Este puzzle esta compuesto al final por 12 rombos diferentes que pueden generar todas las composiciones que nuestra imaginación y mucho mejor la que nuestros alumnos quieran poner en el juego. Enigmas y composiciones ¿Si tenemos 12 rombos podremos formar romboides con todos ellos cumpliendo la regla de que los lados coincidan exactamente y los colores que se toquen sean iguales? Después de estudiar la cuestión aparecen romboides de distintas dimensiones, luego la siguiente pregunta es, ¿de qué dimensiones pueden ser los romboides obtenidos? ¿Con los 12 rombos (24 triángulos equiláteros) podemos construir un hexágono regular con las restricciones de hacer coincidir los colores que están en contacto?
Como siempre un paso más Al hablar de puzzles siempre nos gusta tratar el tema de la construcción por parte de los alumnos de las piezas que se utilizan, pues pensamos que es un escalón más en el proceso educativo. En primer lugar hace que los alumnos personalicen su material, ya que están trabajando con un puzzle que ellos se han construido y además entran en juego una serie de procedimientos que pueden desarrollarse en otras áreas, por ejemplo en Tecnología. En este caso es muy fácil la construcción del material, basta entregar en cartulina los dibujos de varios cuadrados o rombos y que los alumnos los dividan y coloreen. Posteriormente se plastifican y recortan o incluso mejor, se pegan previamente sobre una superficie más rígida como panel o cartón pluma, ya que ambas son fáciles de cortar con un simple cutter. Una vez plastificado ¡a jugar! |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






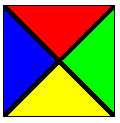 Dibujemos un cuadrado y dividámoslo trazándole las dos diagonales (suele ser de las primeras en aparecer), entonces el cuadrado contiene cuatro triángulos rectángulos isósceles.
Dibujemos un cuadrado y dividámoslo trazándole las dos diagonales (suele ser de las primeras en aparecer), entonces el cuadrado contiene cuatro triángulos rectángulos isósceles.