Septiembre 2012: Múltiplos y divisores (publicado en la revista SUMA, nº 62, 2009)
Septiembre 2012: Múltiplos y divisores (publicado en la revista SUMA, nº 62, 2009) |
 |
 |
 |
| Escrito por Grupo Alquerque | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Miércoles 12 de Septiembre de 2012 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
INTRODUCCIÓN. No hace mucho que comentábamos en esta sección que siempre que preparamos una nueva entrega nos gusta incluir al menos uno de los artículos sobre juegos de conocimiento, puesto que suelen ser los de más directa implicación en el desarrollo normal de nuestra asignatura en las aulas. Hasta ahora hemos tocado varias partes de la asignatura, pero nunca habíamos repetido un tema y creemos que este puede ser un buen momento. Pueden pensar que es debido a la edad, al deterioro mental imparable o al cansancio después de 10 años de sección, pero la verdad es que lo hacemos porque es un tema que nos gusta y que nos suele funcionar bastante bien con nuestros alumnos. El tema que inauguró esta sección, en los estertores del siglo pasado, fue un juego de tablero donde se trabajaban los conceptos de múltiplo y divisor de un número: el salto del factor. Pensamos que no está de más el recuperar ese tema que da mucho de sí. Por eso en esta entrega vamos a continuar con ese concepto con una serie de juegos que pueden trabajarse en Primaria y Secundaria. COLOCANDO EL DIVISOR. En este juego cada alumno juega individualmente y se enfrenta al resto de la clase. Cada alumno copia el tablero siguiente que es sobre el que se juega.
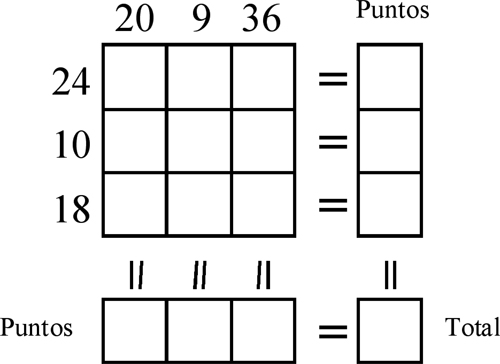
El profesor dispone de un dado cúbico normal y lo lanza nueve veces. A medida que va diciendo los resultados, los alumnos deben escribirlos en una de las nueve casillas libres centrales. El número que se coloca no puede cambiarse y en cada casilla sólo puede figurar un número. El proceso se continúa hasta completar los nueve cuadros. Una vez relleno el tablero, se anotan a la derecha, tantos puntos como divisores del número que aparece a la izquierda hay en cada fila. Se trabaja igual por columnas, anotando un punto por cada uno de los números que hayamos escrito en la columna que sea divisor del número que aparece en la parte superior de la columna. Por último se suman las seis casillas de puntos para obtener la puntuación total. Quien tenga la máxima puntuación gana. Como la dinámica de este juego es muy rápida, pues se tardan pocos minutos en realizarlo, solemos repetirlo varias veces, y para no perder tiempo en copiar reiteradamente el tablero hacemos que los alumnos lo dibujen con bolígrafo y las partidas las señalen con lápiz, por lo que para jugar de nuevo basta borrar la partida anterior. Seguimos el siguiente proceso. 1) La primera partida la realizamos sin haber explicado como se anotarán los puntos. Por lo que en su resultado sólo influye el azar. 2) Repetimos la partida cuando ya conocen la forma de puntuar. De todos modos aún depende mucho del azar pues, aunque los primeros números se pueden elegir donde se quiera, al final está forzado el situar los números en los huecos que quedan. 3) En tercer lugar lanzamos los dados las nueve veces y posteriormente es cuando se colocan sobre el tablero, por lo que en este caso ya intervienen más los conocimientos y la inteligencia de quien coloca los valores. 4) En todos los casos solemos sacar un alumno a la pizarra a colocar su distribución y siempre estudiamos si se podría haber conseguido mayor puntuación variando de lugar algún número. Por eso solemos hacer una cuarta partida en la que se les da los números 1, 2, 2, 3, 4, 4, 5, 6 y 6. Una vez colocados se plantea si es posible conseguir la máxima puntuación, 18 puntos, con esos valores. Nuestra experiencia es que siempre hay quien deduce que no es posible y explica los motivos. 5) Por último, con el pretexto de ayudar a los que siempre sacan menos puntuación que los demás, les volvemos a plantear que coloquen los números del apartado anterior pero ahora para ver quién consigue menos puntuación. Este proceso, como ya hemos dicho, lleva poco tiempo, la mayor parte del mismo en los debates que se pueden generar en cada caso. Uno de los más interesantes es el elaborar una estrategia para optimizar la colocación en las celdas. Si partimos de que la máxima puntuación se consigue cuando todos los números colocados son divisores simultáneos de los que ocupan la cabecera de su respectiva columna y fila, llegamos a que las celdas han de estar ocupadas por divisores comunes de los números exteriores; y por tanto por los divisores de su máximo común divisor que estén entre 1 y 6 (porque se obtienen lanzando un dado). Por ello la tabla de optimización de la puntuación debe estar conformada de la siguiente forma:
La estrategia óptima consiste en colocar el valor que salga al lanzar el dado en la casilla en que aparezca que tenga menos números (porque la probabilidad de ser ocupada es menor). Por ejemplo, el primer 1 que salga debe colocarse en la casilla de la segunda fila y segunda columna (casilla (2,2)); el primer 2 lo podemos poner, indiferentemente en la casilla (2,3) o en la (3,1); el primer 5 ha de ir forzosamente a la casilla (2,1). ¿Y si vuelve a salir otro 5? Como ya no hay casilla en la que podamos sumar los dos puntos, deberíamos ponerlo en una en la que al menos aseguremos uno, y eso ocurre en la primera columna, por lo que deberíamos colocarlo en la tercera fila que tiene menos números (dos) que la primera (que tiene tres). Se pueden introducir en este juego otras variantes como cambiar los números que aparecen en el tablero para trabajar con otros múltiplos distintos o plantear tableros con otras dimensiones, aunque no es conveniente aumentar mucho el número de filas y columnas; un tablero de 4x4 ya pierde la efectividad de la rapidez y puede desconectar a algunos alumnos. BÚSQUEDA DE DIVISORES. El siguiente juego lo tomamos de un artículo de Fátima Esteves y João Cámara, editado en el número 22 (2º trimestre de 1992) de la revista Educação e Matemática, editada por la Asociación de Profesores de Matemáticas de Portugal. Es un juego para dos jugadores que disponen cada uno de un marcador de un color diferente y de una tabla para anotar sus puntos. En lugar del marcador se pueden utilizar un tablero común y fichas de dos colores distintos para ir tapando los números. Se juega sobre el siguiente tablero.
El modo de jugar es el siguiente: 1) El jugador A tacha un número sobre el tablero y lo anota en su tabla de puntuación. 2) El jugador B tacha todos los divisores del número tachado por el compañero que estén sobre el tablero y va anotando esos números en su tabla de puntuación. Una vez terminado tacha cualquier otro número no tachado del tablero y lo anota en su tabla. 3) Se invierte el turno; ahora el otro jugador (el A en este caso) repite el paso 2. 4) Se van alternando los turnos hasta que no quede ningún número sin tachar sobre el tablero. 5) Si un jugador olvida tachar un divisor y su contrincante se da cuenta, el contrario puede tacharlo y anotarlo en su cuenta aunque no sea su turno. 6) Gana el jugador que sume más puntos en su tabla de puntuación. Como estrategia para este juego está el conocimiento de los números primos, que suelen ser los primeros que se agotan para impedir que el contrario anote muchos valores en su tabla. JUEGO DE LOS NÚMEROS PRIMOS. Veamos ahora un juego tomado del Grupo Cero de Valencia, de sus libros de Matemáticas para la ESO editados por M.E.C. y Narcea. Es un juego para dos jugadores donde usaremos un dado cúbico, fichas de distinto color para cada jugador y un tablero como el siguiente también para cada jugador.
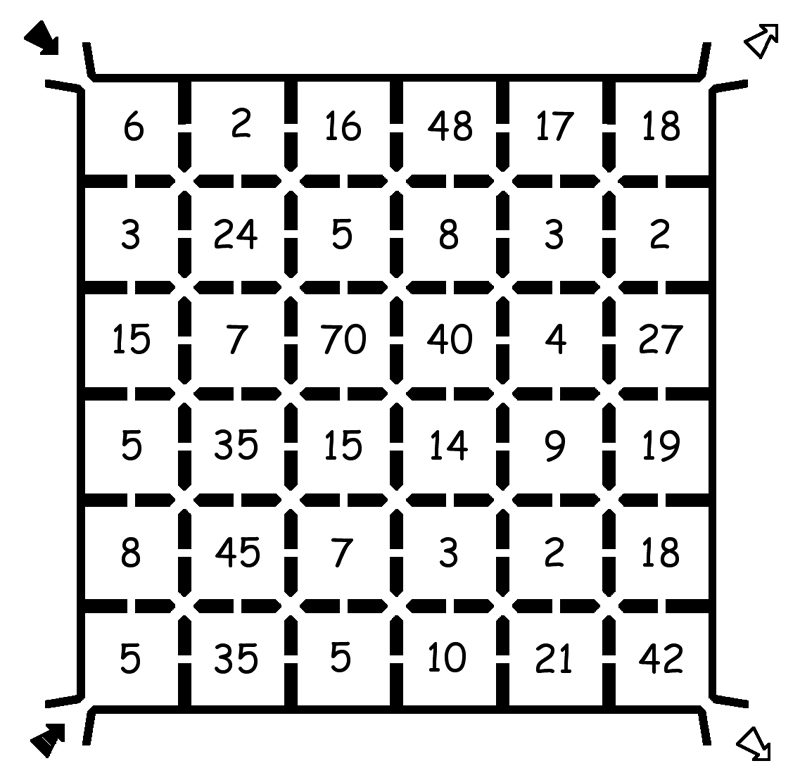
Reglas del juego: 1) Un jugador, en su turno, lanza dos veces el dado y compone un número de dos cifras en el orden en que han salido los números, por ejemplo el 36. Coloca una ficha sobre un divisor de ese número, por ejemplo el 2, en su propio tablero. Se queda con el cociente de la división 36:2 = 18 y vuelve a repetir el proceso con el 18. Por ejemplo coloca una ficha sobre un 3 y se queda con el valor 18:3 = 6. Continua hasta que no encuentre más divisores y en ese caso pasa el turno al otro jugador. 2) Si el número inicial que construye es primo, no está sobre el tablero y el jugador lo descubre tirará de nuevo, pero si no lo hace pasa el turno al otro jugador. Si el jugador dice que el número es primo, pero no lo es, el otro jugador puede poner en su tablero las fichas de los divisores que descubra y a continuación coger el turno. 3) Gana quien primero llene una fila y una columna. Es posible modificar algunas restricciones del juego. Por ejemplo, si se pueden formar los números de dos cifras en el orden que se quiera sólo quedan sobre el tablero números primos como el 11 o el 13, ya que los restantes primos pueden cambiarse las cifras y obtener un número compuesto. Entonces si el jugador compone un número primo (distinto del 11 y 13) directamente pierde el turno. También es posible recortar alguna fila y columna para que el juego sea más dinámico. Nosotros pensamos que es mejor que se juegue más de una vez antes de que el juego se eternice y no dé, a la mayoría, tiempo de terminarlo en una clase. Aunque no suele ser el caso de este juego, si vemos que hay parejas que tardan mucho en acabar, puede ponerse como restricción que gana el primero en rellenar una fila o una columna completa. Hay que tener en cuenta que el azar siempre puede influir negativamente en una buena estrategia. Está también la posibilidad de que cada jugador juegue con un tablero diferente, para que de esa manera no utilicen los resultados del contrario y tengan que buscar una estrategia distinta. LABERINTO DE MÚLTIPLOS Y DIVISORES. En este caso presentamos un laberinto en el que hay que moverse de una casilla a otra en cualquier dirección, pero siempre con la condición de que se pase a una casilla donde haya un múltiplo o divisor de la casilla anterior. Es posible encontrar caminos que entren por alguno de los extremos de la izquierda y salgan por alguno de la derecha, por lo que pueden hacerse cuatro recorridos distintos por lo menos.
Hay caminos que tienen distinto recorrido, por ejemplo para entrar por el 5 y salir por el 42 podemos encontrar, entre otros, los caminos distintos siguientes: 5 – 35 – 5 – 10 – 2 – 42 5 – 35 – 7 – 14 – 2 – 42 5 – 45 – 15 – 3 – 21 – 42 5 – 45 – 15 – 3 – 9 – 18 – 2 – 42 Por ello podemos plantear encontrar el camino más largo o el más corto para llegar de una entrada a una salida. Por ejemplo el camino anterior puede hacerse pasando por 25 casillas, ¿será el más largo?, pero para eso están nuestros lectores y sus alumnos, para investigar. EL CAMINO EN EL TABLERO. Para terminar vamos a darnos un gusto personal. Ya que tenemos una sección fija (mientras dure) nos podemos permitir el lujo de citar a los amigos y hoy lo vamos a hacer con una persona que es miembro honoraria del Grupo Alquerque y que a pesar de su lejanía en otro continente sigue estando siempre a nuestro lado. En la línea del juego anterior vamos a terminar con otro laberinto de nuestra querida amiga Ana García Azcarate, tomado de su libro “Pasatiempos y juegos en clase de matemáticas. Números y álgebra”. En el siguiente tablero debemos entrar por la esquina superior izquierda y salir por la inferior derecha. Podemos pasar de una casilla a otra contigua en horizontal, vertical o diagonal con la única condición de que el número anterior y el posterior deben tener algún divisor común, lógicamente distinto de 1.
En el libro de nuestra colega y amiga viene una indicación como ayuda por si al principio hay alguien que se bloquea con la dificultad. Dice textualmente: “Empieza marcando con un punto de color rojo todas las casillas con números múltiplos de 2. A continuación, con un punto de otro color, marca las casillas de los múltiplos de 3 y después las de los múltiplos de 5. ¡¡Puedes ya escoger un camino!!” Dado que hay varios caminos que pueden recorrer el tablero volvemos a plantear el buscar el que pasa por menos casillas o por más. También se puede imponer que el camino pase por una casilla determinada, por ejemplo por el número 99 o plantear el camino que al sumar las casillas por donde se pasa se obtiene el número mayor. Etc. Y por esta ocasión: ¡Esto es todo amigos! |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |