11. 176. El drama personal de X

Un nuevo y reciente cortometraje con aspectos matemáticos como telón de fondo. Aunque pudiera parecer dirigido a público infantil, es probable que los adultos encuentren algún que otro “zasca” sobre la sociedad que han construido. Ficha Técnica: Título Original: Finding X. Nacionalidad: Australia, 2022. Dirección: Benjamin Zaugg. Guion: Toby Hendy. Música: Cassie To. Asesor Científico: Petr Lebedev. Asesor Literario: Dan Simpson. Producción: Toby Hendy y Cedric Scheerlinck. Duración: 11 min. Ficha artística: Intérpretes: Voz de Toby Hendy Argumento En el mundo de los números, la vida estaba claramente definida, las cosas bastante bien organizadas; todo el mundo conocía su valor numérico. Un día, sin embargo, todos los patrones se desbocaron al nacer x, a partir de una ecuación demasiado difícil de analizar. Según fue creciendo, x fue descubriendo como todos lo rechazaban, al no saber dónde encuadrarlo. Hasta que un día, harto de desprecios, decide ir a la busqueda de su identidad. Breve Comentario Encontrando a x es un simpático cortometraje, plagado de referencias matemáticas elementales (anímese el lector a localizarlas todas, que hay más de las que parecen tras un primer visionado), con mensaje (no solo matemático sino también humano, aplicable a todos los que por alguna razón se hayan sentido distintos o desplazados de su entorno social en alguna ocasión). En esta ocasión no voy a describir el argumento al pie de la letra, para que sea una sorpresa lo que podéis encontrar. Toby Hendy, el alma mater de este corto, tiene una destacada carrera con un montón de méritos. Se graduó en matemáticas y física por la Universidad de Canterbury (Nueva Zelanda), logrando una beca de astronomía Aurora que le permitió pasar largas temporadas entre semestres en el Observatorio de la Universidad de Monte John en Tekapo, además de diferentes estancias en la Universidad de California en Los Angeles (concretamente en el laboratorio de Propulsión a Chorro de la NASA), en el Observatorio Macdonald de Texas, en la Universidad de Columbia Británica, en el Observatorio NRC (National Research Council) Victoria en Canadá y en el telescopio CHFT (siglas de Canada, Francia, Hawái) en Hawaii. Posteriormente se doctoró en la Universidad Nacional de Australia, en Canberra, con un tesis titulada “Examen de la respuesta mecánica de la Arabidopsis thaliana usando nanoindentación y modelado de elementos finitos”, con una calificación ciertamente sobresaliente (93 puntos de 100 posibles). Paralelamente, participó en el certamen Famelab de divulgación científica de su país quedando en un digno segundo lugar. Esto la animó a comenzar una segunda carrera como Youtuber científica. En la actualidad tiene un canal propio con más de 100000 suscriptores, y ha dejado un poco de lado la parte academica formal para dedicarse de lleno a la comunicación con un montón de trabajos y experiencias positivas (colaboración con Vsauce3, Physics Girl, Cody'sLab, Andrew Dotson, Flammable Maths, Up and Atom, Knowing Better, RiverTechJess y Science Petr). Ha realizado videos sobre exámenes difíciles de todo el mundo, explicando conceptos matemáticos sobre una pizarra junto a otros de historia de la ciencia. Volviendo al corto, aunque la realización parezca muy sencilla, se han empleado diferentes técnicas en su elaboración. Entre ellas, se han hecho cientos de fotografias, así como la inclusión de elementos de stop-motion y de animación digital. El cortometraje puede verse integramentte (y subtitulado en español; ojo con alguna palabra, como cuadratura por cuadratics, que se refiere a las ecuaciones de segundo grado, no a la cuadratura, o línea de números en vez de recta real) en este enlace.  La página principal del mismo es https://findingxfilm.com/, donde se puede ampliar la información sobre la autora y sobre todo disfrutar con otro trabajos, como el que describe la trayectoria profesional de Terence Tao, realmente interesante (éste no está traducido). Os dejo un par de imágenes del corto, en el que seguro localizareis algunos elementos matemáticos curiosos. Disfrutad del corto, y sobre todo pensad en su conclusión, sobre el verdadero significado de las matemáticas. ¡¡Felices Navidades para todos!!

Miércoles, 07 de Diciembre de 2022 | Imprimir | PDF |  Correo electrónico

12. 88. (Diciembre 2022) La eclosión moderna de la medida

(Girolamo Mazzola. Pitágoras. Palacio Farnesio. Piacenza) Tú lo has dispuesto todo con medida, número y peso. Biblia. Libro de la sabiduría. Los filósofos pitagóricos.. supusieron que las cosas existentes son números Aristóteles. Metafísica. Est modus in rebus [Hay medida en todas las cosas] Horacio. Sátiras. La sociedad medieval estaba regida por la tradición y la costumbre. El naciente capitalismo procede racionalmente. Se calcula y se mide, introduce la contabilidad y usa maquinas. Edgar Zilsel Medir, contar y pesar son actividades humanas desde tiempos inmemoriales, pero en los inicios de la modernidad occidental se convierten en la característica de la época. Los historiadores hacen de la cuantificación una de las expresiones de los inicios de la revolución científica. The Measure of Reality (1998) de Alfred W. Crosby, The Sociological Roots of Science (1942) de Edgar Zilsel o In Measure, Number and Weight (1994) de Jens Hoyrup son algunos de los testimonios los estudios actuales. Los artistas del Renacimiento y el Barroco fueron conscientes de que estaba emergiendo una mentalidad que hacía de la medida una de sus señas de identidad. Repasemos algunas pinturas y grabados que lo ponen de manifiesto. “Los medidores” de Hendrick van Balen El History of Science Museum de Oxford, abigarrado de instrumentos matemáticos, ha incorporado a su colección una pintura que en sí misma contiene todo un programa iconográfico con algunas razones para la enseñanza de la matemática. Hendrick van Balen el Joven (Amberes, 1623–1661) fue un pintor historicista que aprendió el arte de su padre y que colaboró con otra gran saga flamenca, la de los Breughel. El Museo de Oxford tuvo el acierto de adquirir Los medidores, un interesantísimo cuadro atribuido a Van Balen. (Hendrick van Balen. Los medidores. Oxford) No son hombres de ciencia, son trabajadores artesanos, hombres y mujeres, los que realizan la actividad de medir y calcular como una necesidad para ser buenos en su trabajo: una modista mide su tela, un carpintero dibuja su obra con todo tipo de instrumentos, unos cargadores al fondo pesan en una balanza, unos vinateros miden líquidos,… Mientras se desarrolla tanta actividad, un niño aprende apaciblemente geometría consciente de su importancia: todo lo que le rodea lo requiere. Pocas veces encontramos algo que de forma tan explicita nos da cuenta de la matematización del trabajo. La pintura de Van Balen reproduce un grabado anterior, obra de Frans Floris. (Frans Floris. Los medidores) Con medida, número y peso en El Escorial La espectacular Biblioteca del Monasterio de El Escorial reproduce las siete Artes Liberales en sus bóvedas y en los laterales muestra ejemplos de sus aplicaciones. El fresco de Salomón y la Reina de Saba de Bartolomeo Carducci reproduce en hebreo el “con medida, número y peso” bíblico. (Bartolomeo Carducci .  Salomón y la Reina. San Lorenzo de El Escorial) Los números, la balanza y la regla sobre la mesa. Las vasijas con medidas precisas ilustran la importancia determinante de la Aritmética en la vida cotidiana. Resulta curioso que dos reyes se comuniquen con la lengua de los signos matemáticos. Los escultores medidores de Lugo La sillería del coro de a Catedral de Santa María en Lugo tiene una hermosa muestra de la importancia de la medición en los nuevos tiempos. La modernidad se caracteriza tanto por el paso de un mundo estático a otro dinámico como por la hegemonía de lo cuantitativo frente a lo cualitativo. (Francisco de Moure.  Escultores medidores. Catedral de Lugo) Los artistas matemáticos se reivindican y lo reflejan en sus obras con toda rotundidad. Es el caso del escultor gallego Francisco de Moure (1595 – 1636), que siguiendo el estilo de Juan de Juni y Alonso Berruguete, expone una gran lección de geometría en un dosel de sitial del coro inferior (último en la esquina izquierda). Dos escultores atienden las explicaciones de otro que está ¡midiendo un pie!, mientras un cuarto talla un crucifijo y el quinto utiliza un compás para medir una calavera. La filacteria trata de dar un mensaje religioso a lo que es orgullo profesional: entre los santos hay sitio para el artista que modela. Si Santa Teresa opinaba que Dios podía estar ente los pucheros, Moure lo encuentra en el taller del ebanista que no descuida los detalles. Pitágoras y Euclides en el Palacio Farnesio de Piacenza El Museo Cívico de Piacenza utiliza el Palazzo Farnese, parte de la fortaleza de los Visconti,  para mostrar su rica pinacoteca, el museo de carruajes, las esculturas y el archivo. Girolamo Mazzola Bedoli (1500-1569) es el pintor de Parma que decoró las dos planchas que formando un díptico cierran el órgano de una familia noble de la ciudad y donde fueron representados Euclides y Pitágoras. Pitágoras aparece muy a menudo como creador de la música. Los martillos crean el sonido mientras que la balanza y el compás ponen medida para hacerlo armonioso. El Museo del Prado archiva un dibujo de Bedoli representando a Pitágoras que contiene similares elementos iconográficos: martillo con yunque, una romana y una cítara al fondo. La música era aritmética aplicada. (Girolamo Mazzola. Pitágoras. Museo del Prado) De proprietatibus rerum Bartholomaeus Anglicus (1203 – 1272) fue el autor medieval de una exitosa enciclopedia: De proprietatibus rerum. Se conservan muchos manuscritos bellamente iluminados ; reproducimos una ilustración del siglo XIV que muestra como la medida y el número son esenciales. Un monarca se dedica a a música, un tendero a pesar y medir, y un escolar usa la escuiadra. (Bartholomaeus Anglicus  De proprietatibus rerum) Los medidores del Palacio Zwinger Los electores y las cortes imperiales alemanas, como ocurría  con los príncipes renacentistas italianos y  anteriormente con los reinos de taifas andalusíes, también competían por el arte y la ciencia. Los museos del Palacio Zwinger de Dresde son muestras espectaculares de cómo belleza y matemáticas van unidas. El Salón Matemático Físico exhibe los objetos de mayor tamaño, los demás están repartidos formando una unidad con el mobiliario y el arte. Durante el recorrido palaciego iremos encontrando lujosos instrumentos de cálculo como los compases de proporción, las calculadoras mecánicas y hasta cifradoras de mensajes secretos. Seleccionamos un lujoso cuadrante de agrimensor y arquitectura por estar ribeteado por multitud de detalles en miniatura de las aplicaciones del instrumento. ¡Todo hay que medirlo! (Cuadrante. Palacio Zwinger Drede) La Templanza y la Medida La Templanza es la más matemática entre las Virtudes y muchas veces va acompañada de un compás como símbolo. Un grabado de Pieter Brueghel el Viejo (1525 - 1569) va más allá y reproduce todo un mundo de personajes que se afanan en medir y calcular por doquier. Los astrónomos miden el cielo; sus alcances, los artilleros; los comerciantes, su contabilidad; sus obras, los artistas; los geógrafos, las distancias;... (Pieter Brueghel el Viejo. La Templanza. 1560)

Jueves, 01 de Diciembre de 2022 | Imprimir | PDF |  Correo electrónico

13. Diciembre 2022: Regla de Laplace. La baraja

1. Introducción. Dentro del ambiente familiar y social siempre han existido muchas actividades lúdicas para llenar los ratos de ocio, y permitir socializar y aprender una serie de valores y aptitudes necesarios para la vida cotidiana en todos los aspectos. A través de esas actividades podemos acostumbrarnos al trabajo en equipo, potenciar la agilidad mental, fortalecer la memoria, practicar la concentración y la observación, aprender a seguir unas normas establecidas, etc… Dentro de esas actividades tienen un lugar especial los llamados juegos de mesa. Existen muchos juegos que son aprendidos y desarrollados en edades tempranas, y que quedan en nuestro anclaje cultural aunque con la edad vayamos alejándonos de ellos. Ejemplo de estas actividades son: los rompecabezas, los juegos de tablero y fichas, laberintos, juegos de dados, de lápiz y papel, dominós, cartas, etc… Muchos de ellos son adaptables a situaciones diferentes. Entre los juguetes infantiles no es raro encontrar juegos de cartas o de dominós adaptados a los personajes infantiles de la época. Esa versatilidad es lo que permite que muchos de estos juegos se hayan utilizado en la didáctica de la matemática, desde hace décadas, para trabajar contenidos matemáticos de una forma más atractiva, planteando las prácticas, que pueden llegar a ser tediosas en determinadas situaciones, como un juego. Una de esas adaptaciones a un juego de cartas es lo que se va a proponer en este artículo. Entre los recursos didácticos de grupos como el Cero de Valencia o el Azarquiel de Madrid, o recientemente en los libros de una de los componentes de éste último como Ana García Azcárate, pueden encontrarse muchas barajas de cartas adaptadas a muchos contenidos, desde números y álgebra hasta geometría o azar. En la sección de juegos aparecida en la revista SUMA se incluyó una baraja de funciones que creamos el Grupo Alquerque[i]. La ventaja de estos juegos fácilmente adaptables a ítems nuevos, es que ver uno de ellos nos puede dar ideas para crear material para nuestros alumnos, Como además suelen ser fáciles de construir, pues cualquier tratamiento de texto aceptable nos da mucha potencialidad para la creación, no cuesta mucho trabajo crear juegos nuevos y adaptarlos después de haber practicado en el aula con ellos. La idea de la creación de esta baraja me llegó después de consultar un material que encontré en internet cuando documentaba otro artículo sobre juegos de azar. En la página Teaching Ideas[ii] aparecía un juego de cartas de probabilidad, aunque en ese caso eran cartas para ordenar sucesos donde aparecían situaciones tales como la probabilidad de que hoy nieve o que el fin de semana haga sol. Basada en esa idea pensé en crear una baraja de cartas para trabajar la Regla de Laplace. La cuestión era trabajar con las mismas actividades que se pueden encontrar en cualquier libro de texto, para hallar probabilidades sencillas, pero planteándolas en forma de juego. Y así surgió el siguiente conjunto de naipes y las reglas para este juego. 2. La baraja de la Regla de Laplace. 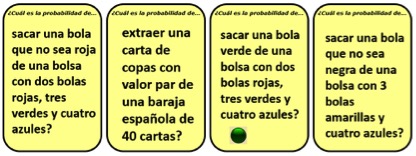Todas las actividades que se plantean en las cartas son experimentos simples cuya probabilidad puede calcularse con una aplicación directa de la Regla de Laplace. No aparecen probabilidades condicionadas ni experimentos compuestos como lanzar una moneda y un dado, salvo un solo caso. En todos los demás son situaciones simples en las que se lanzan uno o varios dados o monedas, se extraen cartas de barajas española o francesa, se extraen bolas de una bolsa con bolas numeradas o de colores y cosas similares. Aparte del cálculo de probabilidades hay que manejar conceptos numéricos como la divisibilidad o las fracciones, sobretodo porque el objetivo es ordenar las fracciones resultantes de la Regla de Laplace. Tal como se presenta, la baraja se compone de 40 cartas que son las siguientes. 3. Formas de jugar. Este es un juego pensado para que jueguen de dos a cuatro jugadores. Se necesita una baraja como la que hemos visto, y una moneda que puede ser sustituida por un dado. Las reglas básicas para este juego son las siguientes. 1) Uno de los jugadores baraja el mazo de cartas, reparte cinco cartas a cada jugador y el resto lo coloca boca abajo sobre la mesa. Levanta una carta del mazo y la expone boca arriba y a partir del jugador a su derecha y siguiendo el sentido contrario a las agujas del reloj, comienza propiamente el juego. 2) Cada jugador en su turno lanza la moneda o el dado. Si sale cara o par, debe colocar sobre la anterior una de sus cartas cuya probabilidad sea mayor que la última expuesta. En caso de cruz o impar la carta nueva debe tener menor probabilidad que la anterior. 3) Si un jugador en su turno no dispone de ninguna carta para satisfacer la regla anterior, toma una carta del mazo sobrante. Si puede la coloca y si no se queda con ella y pasa el turno. 4) Entre las cartas aparece una con el suceso seguro y otra con el suceso imposible. Si el jugador que le toca jugar observa que la última carta expuesta es una de esas dos, y lo comenta, entonces no debe lanzar la moneda, sino que coloca una probabilidad posible, es decir, mayor que el suceso imposible o menor que el suceso seguro. 5) Gana el primer jugador que se queda sin cartas anotándose cinco puntos. Si se acaba el mazo, sin llegar a esta situación, se puede seguir jugando hasta que algún jugador lo consiga aunque no se robe al no poder poner. Lo ideal es jugar varias partidas y que en cada una sea un jugador distinto el que baraja y reparte. Se puede fijar un tiempo límite para acabar la partida, a decisión del profesor, y entonces gana el que tenga menos cartas. Si hay varios jugadores con la misma cantidad mínima de cartas todos se anotan los cinco puntos. Si en algún momento de la partida se observa que un jugador ha puesto una carta incorrecta, se retira la carta que ha puesto y ese jugador debe tomar una carta del mazo. Si puede la pone según el ritmo del juego y si no pasa su turno. Las preguntas de las cartas son variadas desde la más simple sobre la probabilidad de obtener cruz al lanzar una moneda hasta la más complicada, que se puede considerar un experimento compuesto, que consiste en extraer una carta de bastos si antes se ha sacado una de oros y no se ha reemplazado. Por ello, a veces es interesante que, una vez con las cartas en la mano, los jugadores calculen en su cuaderno, y sin que los contrarios lo observen, las probabilidades de sus cartas. Para que los alumnos practiquen de otra forma antes de jugar tal como se ha explicado, hay otro modo de jugar. Se reparten cinco cartas a cada jugador y deben calcular sus probabilidades y ordenar las cartas de menor a mayor probabilidad. Una vez que cada jugador lo ha hecho con sus cartas, cada uno de ellos que tenga correcta la ordenación se anota cinco puntos. Si en algún jugador se observa un fallo, si es posible quitar una carta de forma que las cuatro restantes están bien ordenadas, se anota tres puntos. Si aun así, las cuatro no están bien, pero quitando una quedan tres cartas bien ordenadas, entonces se anota un punto. En cualquier otro caso no se anota nada. En este juego, se descartan las cartas utilizadas y se vuelve a repetir el proceso con las cartas restantes. Si juegan cuatro jugadores pueden realizar dos jugadas cada uno. Con este proceso se trabaja la regla de Laplace y se calculan la mayoría de las probabilidades. Según decida el profesor, para pasar a jugar según las reglas originales, los cálculos que han hecho los alumnos pueden tenerlos a la vista por si les cae alguna de las cartas, o puede decidir que deben guardarse. 4. Variaciones sobre el mismo tema. Revisando los enunciados de las cartas, es necesario que el alumnado conozca unos conceptos básicos de los materiales que se utilizan en los experimentos. Deben saber cuántas fichas tiene un dominó y como están construidos, los distintos tipos de dados que se utilizan en los juegos de rol, los números que aparecen en la cartas de una baraja, según sean española o francés, etc… En este aspecto he utilizado siempre la baraja española de 40 cartas porque suele ser la más corriente, pero se pueden proponer también sucesos con una baraja de 48 cartas. La primera vez que hice el diseño de la baraja, ésta constaba de sólo 24 cartas, con idea de que se repartieran 6 cartas por cada jugador y no sobrara ninguna para coger. Simplemente se pasaba si no se podía poner carta. Posteriormente la amplié para tener más juego. Esto permite que si el profesor estima que algunas de ellas pueden ser muy complicadas para su alumnado, pueda descartarlas a la hora de jugar. Otra posibilidad, para apoyar a los alumnos con más dificultades, es que se repartan siete cartas, y el alumno que quiera puede llegar a descartarse de hasta dos de ellas cuyo cálculo le pueda parecer muy complicado. Otra forma de simplificar el juego es aprovechar las cartas que tienen igual probabilidad. Hay seis sucesos que repiten probabilidad dos o tres veces, por ejemplo la de obtener cruz al lanzar una moneda o la de obtener cara y cruz al lanzar dos monedas. Se puede permitir la opción de que un alumno, tras lanzar la moneda y observar que no puede poner un suceso con una probabilidad mayor o menor, pueda poner uno con una probabilidad igual. Hay que dar esta posibilidad como opción final, pues si no, el alumno al ver que tiene una carta con la misma probabilidad no hace el intento siquiera de buscar una mayor o menor. En total hay, entre las 40 cartas, 31 probabilidades diferentes. Si se desea se pueden modificar los sucesos de forma que haya más sucesos con probabilidades iguales. Debe quedar claro que no es mi intención “vender” esta baraja sino más bien la idea del juego, por lo que cada profesor puede elegir los sucesos y construirse su baraja. El diseño no tiene por qué ser muy rebuscado, pues por ejemplo las cartas presentadas están hechas con el Power Point. Hay una actividad que, si se tiene tiempo, es interesante y es que sean los propios alumnos, colocados en grupos de tres o cuatro, los que propongan las cuestiones que deberán llevar las tarjetas. Como es natural aparecerán en muchos grupos el mismo suceso, para obligar a que piensen en sucesos más rebuscados se hace lo siguiente. Se van colocando los sucesos en la pizarra apuntando la cantidad de grupos que lo proponen y cuando ya estén todos, cada grupo se anota un punto por haber propuesto una actividad que no haya aparecido en más de tres grupos y al final el grupo que tenga más puntos gana la competición. Como no es raro que para ganar se planteen sucesos con enunciados totalmente barrocos, un grupo que proponga un suceso retorcido debe indicar cuál sería exactamente su probabilidad. Si no es correcta se desecha esa propuesta. Resumiendo, la idea es trabajar el cálculo básico de la probabilidad en un ambiente más lúdico que el de resolver una hoja de ejercicios de aplicación de la Regla de Laplace.   Notas: [i] Puede accederse al artículo en la página de divulgamat https://www.divulgamat.net/index.php?option=com_content&view=article&id=15661&directory=67 [ii] https://www.teachingideas.co.uk/probability/probability-cards

Lunes, 05 de Diciembre de 2022 | Imprimir | PDF |  Correo electrónico

14. Las anamorfosis de Brusspup

Brusspup es un mago de las ilusiones ópticas. Esta es la mesa de su despacho, con objetos variados… alguno de ellos un tanto fuera de lugar… … pero no todo es lo que parece… Usando la técnica de la anamorfosis, Brusspup ha elaborado un cubo de Rubik, una cinta azul y un zapato un tanto deformados: http://i.imgur.com/ffAnX.jpg http://i.imgur.com/GUU2b.jpg http://i.imgur.com/J8VNL.jpg Y colocando estas imágenes -o la cámara- con el ángulo adecuado, se observan las figuras como si fueran de dimensión 3: ¡Impresionante! Visto en Colossal Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Jueves, 24 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico

15. ¡Utilicemos el plátano como unidad de medida!

El plátano no es una unidad de la medida ni estándar ni científica… Ni siquiera es una medida precisa… Pero, no todo el mundo necesita tantísima exactitud a la hora de conocer el tamaño de ciertos objetos… http://www.howtobeadad.com/2012/11903/banana-added-for-scale-origin Para estimar el tamaño de un pez, la altura de un niño o la longitud de un bolso, el plátano parece una buena unidad de medida ¿no? Tampoco somos muy precisos en otros aspectos de nuestras vidas: ‘echa a la sopa una pizca de sal’, ‘llego enseguida’, ‘tengo mucha hambre’… ¿Necesitas saber ‘al milímetro’ el tamaño de todo lo que te rodea? Si quieres abandonar la rigidez impuesta por cálculos exactos, las normas excesivamente rigurosas que no llevan a ningún lugar… ¡mide en plátanos! ¡Desde luego, yo lo voy a intentar! Por supuesto, esto es una broma –¿o no?– que he leído y adaptado de Banana Added for Scale (A New, More Forgiving Unit of Measure). En esta entrada del blog How to be a dad explican además el origen de la ‘gansada’. Y recuerda que si no tienes una regla graduada a mano… un plátano podría ayudarte a salir del paso… Visto en The Meta Picture Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 24 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico

16. There Will Be Blood… a través de los números

There Will Be Blood. Through Numbers es un video de Ali Shirazi: el artista toma la película There Will Be Blood de Paul Thomas Anderson y superpone números, razones y curvas… relacionadas con las técnicas cinematográficas utilizadas. http://vimeo.com/80654617 ¡Es una auténtica delicia! http://vimeo.com/80654617 http://vimeo.com/80654617 http://vimeo.com/80654617 http://vimeo.com/80654617 http://vimeo.com/80654617 http://vimeo.com/80654617 http://vimeo.com/80654617 Puedes ver el video completo aquí: Visto en Kuriositas Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Miércoles, 23 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico

17. Vestidos… muy geométricos

La diseñadora Amila Hrustic ha creado una curiosa colección de vestidos denominada Plato’s Collection. La presenta con esta sugerente frase: Geometry existed before the creation. La colección está basada en los sólidos platónicos: cinco vestidos hechos a mano con materiales textiles y papel… verdaderas esculturas para llevar puestas. Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Miércoles, 16 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico

18. Escaleras infinitas

Esta escalera infinita es una escultura del artista David McCracken llamada Diminish and Ascend. http://www.sculpturebythesea.com/Home.aspx Esta escultura de aluminio tiene nueve metros y medio de longitud y casi cinco de altura. Una escalera que parece un ‘camino infinito’ que pretende ‘alcanzar el cielo’. Su nombre –y el concepto de infinitud que incluye– recuerda al Ascenso y descenso de Maurits Cornelis Escher, basado en la escalera infinita de Penrose, una de las más conocidas figuras imposibles: http://www.planetperplex.com/nl/item/klimmen-en-dalen/ Bonus: Os dejo la fantástica animación Hallucii, de Goo-Shun Wang. El pobre hombre lucha, desesperado, por salir de la escalera infinita de Penrose: ¿Os habéis fijado en la imagen que aparece en la etiqueta de la botella de marca Hallucii? http://youtu.be/hhfhgbmZe9s Si… es otra conocida paradoja visual: ¿Vieja o joven? Visto en Colossal (la primera escalera) Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Miércoles, 16 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico

19. El planímetro de Jacob Amsler

El matemático, físico e ingeniero Jacob Amsler (1823-1912) nació un 16 de noviembre. Perfeccionó y llevó a su forma moderna el planímetro polar (1854), un instrumento que permite la medida mecánica directa de superficies planas siguiendo el contorno por medio de un brazo articulado. También inventó el integrador y el freno diferencial. Escribió varios trabajos sobre magnetismo y las leyes de conductividad del calor en cuerpos sólidos.     http://ids.si.edu/ids/dynamic?container.fullpage&id=NMAH-AHB2013q009207 El planímetro polar de Amsler http://en.wikipedia.org/wiki/File:Amsler-Polarplanimeter-2.jpg Más información: Jakob Amsler, Über die mechanische Bestimmung des Flächeninhaltes, der statischen Momente und der Trägheitsmomente ebener Figuren, Schaffhausen, 1856 Jakob Amsler: Anwendung des Integrators (Momentenplanimeters) zur Berechnung des Auf- und Abtrages bei Anlage von Eisenbahnen, Strassen und Kanälen. Zürich, 1875 Los planímetros originales de Amsler Amsler’s polar planimeter, Harvard University Bill Casselman y John Eggers, The Mathematics of Surveying: Part II. The Planimeter, AMS Charles Care, Illustrating the History of the Planimeter, 2003-2004 Francis Ziegeltrum, Planimètre polaire à compensation N°36 Los planímetros de Amsler, Linealis.org The polar planimeter, Universidad de Amsterdam Planimeters The polar planimeter Planimeters – Polar–Amsler, National Museum of American History Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Miércoles, 16 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico

20. Ilusión óptica: ¿el cubo se hunde en la mesa?

Esto es una lámpara, la lámpara Urbicande del diseñador Cédric Dequidt. Lámpara Urbicande Diseñada para quedar colocada sobre una superficie plana, parece parcialmente incrustada en ella… Lámpara Urbicande Los ángulos y la perspectiva provocan esta curiosa ilusión… Lámpara Urbicande Visto en Neatorama Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Lunes, 14 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico