121. La increíble vida de Luis Raluy, el payaso matemático fascinado por la 'Teoría de Números'

ABC, 28 de Febrero de 2022 CIENCIA - El ABCdario de las matemáticas Pedro Alegría

Lunes, 28 de Febrero de 2022 | Imprimir | PDF |  Correo electrónico | Leer más

122. 81. (Marzo 2022) El ábaco

(Ábaco Salamis. Museo epigráfico. Atenas) El ábaco en sus múltiples formas ha sido el instrumento de computación aritmética más universal. Unas líneas y unas cuentas, guijarros (calculi), bolas o fichas, facilitan las operaciones. La adición y la substracción son los cálculos habituales para el instrumento, además con cierta maestría se puede incluso multiplicar, dividir o extraer raíces. El ábaco decayó en occidente ante el empuje del algoritmo indo-árabe al que se sumaron dispositivos como los huesos de Neper que hacían innecesaria  la memorización de las tablas de multiplicar. En Asía y Europa Oriental se mantuvo hasta la aparición de las calculadoras electrónicas baratas en los años sesenta. Hagamos un rápido recorrido histórico. El Ábaco Salamis en Atenas En 1846 se encontró en la isla de Salamis una gran piedra de mármol con líneas paralelas, marcas y letras que dan testimonio de un primitivo ábaco. En sentido estricto es una tablilla de cuentas. La loseta se encuentra en el recibidor del Museo Epigráfico de Atenas, un lugar adosado al lateral del bullicioso Museo Arqueológico y que tiene pocos visitantes. Las letras se corresponden con los números griegos (penta, deca, hecto,…) y con las unidades de medida o monedas en uso del siglo III a.C. El historiador Herodoto (485–425) ya daba cuenta de la utilización de instrumentos que usaban cuentas: dejó constancia de que los egipcios las movían de derecha a izquierda, al revés que los griegos. Las líneas están poco marcadas y son poco visibles. Una vieja fotografía de alto contraste nos da mejor detalle. El abaquista romano de los Capitolinos en Roma Los Museos Capitolinos de la Piazza del Campidoglio ocupan el Palazzo dei Conservatori y parte del Palazzo Nuovo. Los Capitolinos albergan una pinacoteca y una colección de escultura grecorromana de gran interés, en ella se puede disfrutar del Dálmata herido, la Venus capitolina o el original de la estatua ecuestre de Marco Aurelio. Destacamos el abaquista de una sepultura. (Ábaco de fichas. Museos capitolinos. Roma) Al subir a la planta primera del Palazzo Nuovo, a la derecha (y a media altura) se encuentra empotrado el frontal de una tumba con la representación de un calculista con ábaco de fichas. No conocemos otra reproducción similar. Hay varios museos con pequeños ábacos que se han conservado, pero quizá sea el único bajorrelieve que de cuenta de las operaciones aritméticas con calculi. El ábaco romano del British Museum (Ábaco romano de bronce. British Museum. Londres) El British Museum no se queda atrás respecto a los otros museos de Londres en cuanto a interés matemático. La parte instrumental puede parecer poca cosa si la comparamos con la riqueza arqueológica griega o mesopotámica pero no es nada despreciable: armarios y armarios con estanterías repletas de instrumentos de dibujo, astronómicos, gnomónicos, ábacos, o de laboratorio. Entre los ábacos de bolsillo destacamos uno romano de bronce. Ábacos similares se pueden encontrar en otros lugares como Roma y Aosta. No han sobrevivido muchos pero estar hechos en bronce y el pequeño tamaño facilitan su conservación. El sistema de numeración romano mixto entre quinario y decimal se adapta muy bien al ábaco. Curiosamente el paralelismo con el ábaco japonés (soroban) es casi completo: utiliza cuatro bolas para las unidades y una quinaria en cada decena. Tanto en la Grecia Clásica como en el Imperio Romano los cálculos no formaban parte de la aritmética sino de una disciplina no liberal, la logística.  Los árabes y el ascenso del comercio cambiaron el paradigma. Aritmética con ábaco en la Casa Julius de Helmstedt (Alegoría de la Aritmética. Casa Julius. Helmstedt) La recuperación del comercio en la Europa Medieval necesita calcular. El ábaco era el instrumento útil compitiendo con el algorítmico. Precisamente Leonardo Pisano, Fibonacci, hijo de mercader, llama a su tratado Liber abaci (1202) cuando se trata de uno de los manuales de extensión de las cifras indias. Hay muchas representaciones del ábaco pero no se han conservado los antiguos. Elegimos una bella alegoría de la Aritmética. La residencia de los príncipes obispos de Brunswick-Wolfenbüttel es coherente con la Universidad que fundaron en 1576: el Juleum. La Academia Julia fue la primera universidad protestante del norte de Alemania y tiene una puerta espectacular de filigrana policroma. La universidad de Helmstedt tuvo sus momentos de esplendor desde 1575 hasta 1625, cuando la peste y la guerra de los treinta años diezmaron la población. Giordano Bruno impartió clases en Helmstedt en los años de esplendor, y cuando ya era una decadente universidad provinciana tuvo por alumno a Gauss. La Casa Julius se encuentra en pleno centro al lado del Ayuntamiento. Se trata de una casa renacentista de entramados de madera. La iconografía de la planta superior son las Alegorías de las Artes Liberales y la de la inferior los escudos de los duques. La inscripción de la flecha en números romanos es 1568, anterior al portal de la Academia Julia. Cada disciplina es representada con un niño que la complementa. La Aritmética calcula con  un ábaco pero el erote usa el algoritmo. La Margarita Phylosophica El monje cartujo Gregor Reisch (1467 – 1525) fue un humanista alemán que escribió una enciclopedia de saberes en doce libros llamada Aepitoma Omnis Phylosophiae alias  Margarita Phylosophica (1503). La obra tenía numerosas láminas y alcanzó gran popularidad como manual. Los siete primeros libros de la Margarita estaban dedicadas a las artes liberales, la Aritmética era el cuarto libro. Su conocido grabado se ha convertido e la referencia de la coexistencia del ábaco y el algoritmo. La alegoría de la Aritmética está acompañada de dos personajes, Boecio y Pitágoras, el primero calcula con las cifras árabes y el segundo con el ábaco. Se trata de una recreación inventada pues el latino Boecio no conocía el algoritmo ni el griego Pitágoras dejó constancia del uso del ábaco. Ambos autores son los citados habitualmente en los libros medievales y quizá no sean los representados sino dos mercaderes, el joven se ha pasado al cálculo indo-árabe mientras que el  mayor sigue apegado al ábaco. (Gregor Reisch. Margarita Phylosophica Alegoría de la Aritmética) Un ábaco Ming en Chapel Hill El Ackland Art Museum de la Universidad de Carolina del orte en Chapel Hill exhibe en la zona dedicada a la porcelana de la Dinastía Ming un ábaco tradicional chino del siglo XVI. (Ábaco chino de porcelana Ming. Ackland Art Museum Chapel Hill) El ábaco chino, suanpan, utiliza cinco cuentas de valor unidad y dos quinarías por cada decena, no está optimizado como el romano o el japonés. La época de la Dinastía Ming (siglos XIV – XVII) fue un periodo de prosperidad que se pone de manifiesto en su porcelana azul y blanca. Los ábacos no son ajenos a ella. Nos son extremadamente raros pero no suelen verse en museos. El British Museum tiene uno en almacén sin cuentas pero no se haya expuesto. Los ábacos suelen ser de madera y los pequeños en metal. La porcelana es frágil y aún no siendo el material adecuado sería apreciado por su belleza. Algunos ábacos tenían pequeños cajones, como el que mostramos. (Ilustración de 1820 sobre la práctica del suanpan) Un ábaco singular del Museo Británico El British Museum exhibe un curioso ábaco inglés del siglo XVII que muestra la pervivencia del instrumento. Cada línea tiene nueve cuentas, tres blancas, tres negras y tres blancas. Como el ruso pero ahorrando una ficha. Se trata de una curiosidad. El stchoty, el ábaco ruso (ábaco ruso moderno) Los viajeros por la  Unión Soviética todavía tuvieron la oportunidad de  contemplar el uso generalizado del ábaco de diez bolas sobre marco de madera. Las dos bolas centrales eran más oscuras. El soroban , el ábaco japonés (Ábaco japonés moderno) El soroban japonés es muy similar al chino pero eliminando las fichas superfluas. Con cuatro unidades y una cuenta quinaria es suficiente. El ábaco estaba tan extendido y tenía tantos partidarios que la compañía SHARP de calculadoras vio una oportunidad comercial en la incorporación de uno a sus calculadoras. O fue solo un experimento curioso pues se fabricaron varias series. (Híbrido de calculadora electrónica y ábaco) Ábacos escolares en Huesca El Museo Pedagógico de Aragón quizá albergue la colección de mayor interés dedicada a la institución escolar de la Península Ibérica. El Museo comparte instalación con la Oficina de Turismo de la céntrica Plaza de Luís López Allué de Huesca. La educación de la infancia se remonta a los orígenes de la humanidad. La institución de la Escuela y los principios de Enseñanza General y Obligatoria son muy recientes. La Ley de Instrucción Pública (1857) del Ministro Moyano marcó para España el inicio de la modernidad educativa. (Ábacos escolares. Museo Pedagógico. Huesca) La recuperación de las viejas aulas y los antiguos materiales escolares están en el origen de este museo. Aunque esté muy extendido la idea de que la Escuela es la institución que menos ha cambiado (maestra/o con pizarra y escolares en su pupitre) la realidad es que basta entrar en el museo de Huesca para desmontar el tópico. En Huesca veremos varias aulas con ábacos de diez bolas como material didáctico obligado. ¿Tiene futuro el ábaco? El viejo ábaco se resiste a desaparecer, las posiciones que pierde en oriente intenta ganarlas en occidente. Algunos centros escolares europeos introducen el ábaco para mejor comprensión del concepto de número y para desarrollar el cálculo mental. Quien esto escribe lleva siempre consigo su vieja regla de cálculo logarítmica y entiende a las familias chinas o japonesas que se educaron con el ábaco. En un mundo donde los teléfonos son potentísimas calculadoras de bolsillo puede parecer dudoso que quede sitio para este bastidor con cuentas perforadas. ¿Tras miles de años de prestar buen servicio se convertirán los ábacos en meros objetos de museo? Terminamos con un poema de Jacob Bronowski (1908-1972) – matemático y poeta polaco -  que fue publicado en un diálogo titulado precisamente El ábaco y la rosa: La fuerza que al invierno mueve a dar suaves hexágonos de nieve que lleva a vivir a las abejas en sus bien calculadas colmenas, es ábaco y rosa conjuntamente Una helada dulzura invade mi mente.

Martes, 01 de Marzo de 2022 | Imprimir | PDF |  Correo electrónico

123. El teorema de Fermat-Wiles para probar… la irracionalidad de la raíz n-ésima de 2

Pierre de Fermat En el blog The Dude Minds… comentan una demostración de la irracionalidad de la raíz n-ésima de 2… un poco ‘sofisticada’.  TEOREMA: La raíz n-ésima de 2 es irracional para n ≥ 3. Demostración: Suponemos que la propiedad no es cierta, con lo que existen dos enteros coprimos p y q, tales que: Elevando a la n ambos miembros de la ecuación, queda: y por lo tanto que puede reescribirse como Pero, el teorema de Fermat-Wiles asegura que esta ecuación no tiene solución para p y q enteros si n ≥ 3. Así, la raíz n-ésima de 2 es necesariamente irracional para  n ≥ 3. CQD ¡Toma herramienta fuerte! Visto en The Dude Minds… Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Martes, 22 de Febrero de 2022 | Imprimir | PDF |  Correo electrónico

124. «Surface detail», inspeccionando un fractal

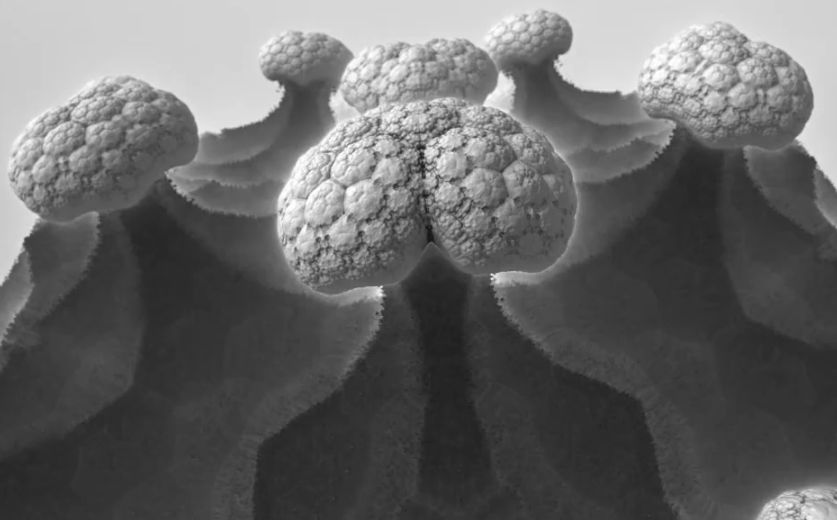
No es la primera vez que hablamos del físico y diseñador Tom Beddard –conocido como subBlue– en DivulgaMAT (ver Frax, fractales en tu mano). Captura de pantalla de Surface detail Esta vez, traemos otro de sus espectaculares fractales: Surface detail. No dejes de visitar su galería de fractales  2D y 3D… Visto en Le blog-notes mathématique du coyote Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Lunes, 21 de Febrero de 2022 | Imprimir | PDF |  Correo electrónico

125. Las matemáticas 'ocultas' tras la Catedral de Burgos

ABC, 21 de Febrero de 2022 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 21 de Febrero de 2022 | Imprimir | PDF |  Correo electrónico | Leer más

126. Qué es blockchain y por qué puede llevar a un mundo sin corrupción

ABC, 14 de Febrero de 2022 CIENCIA - El ABCdario de las matemáticas Lierni Ortiz Elorza

Lunes, 14 de Febrero de 2022 | Imprimir | PDF |  Correo electrónico | Leer más

127. Georg Joachim Rheticus, el primer copernicano

El matemático, astrónomo, teólogo, cartógrafo, constructor de instrumentos musicales y médico Georg Joachim Rheticus (1514-1574) nació un 16 de febrero. Contribuyó considerablemente a la expansión del pensamiento copernicano, como su único discípulo. En su Narratio prima de libris revolutionum Copernici (1540) dio las primeras noticias sobre la obra copernicana. Más tarde, Rheticus pubilicó Ephemeris ex fundamentis Copernici (1550). Gráfico de «Narratio prima» Rheticus elaboró unas cuidadas tablas de funciones trigonométricas, realizadas con una exactitud de 10 segundos; su cálculo fue terminado por su discípulo Valentinus Otho, que las editó en Opus palatinum de triangulis (1596). Bartholomaeus Pitiscus mejoró las tablas trigonométricas y el Magnus Canon doctrinæ triangulorum (1551) de Rheticus. http://www.feldkirch.at/stadt/bildung-kultur/rheticus-jahr-2014 Más información: Rheticus Jahr 2014 (el año de Georg Joachim Rheticus) Rheticus 500 Hommage à Georg Joachim Rheticus, né le 16 février 1514, Luminisciences, 2014 Rheticus http://rheticus.able-network.com/ Notas biográficas de Georg Joachim Rheticus. Importancia de Rheticus en la difusión de la obra de Copérnico Dennis Danielson, The First Copernican: Georg Joachim Rheticus and the Rise of the Copernican Revolution,Walker & Company 2006 Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Miércoles, 16 de Febrero de 2022 | Imprimir | PDF |  Correo electrónico

128. Pierre-François Verhulst y la ecuación logística

El matemático Pierre-François Verhulst (1804-1849) falleció un 15 de febrero. Se le conoce principalmente por la ecuación logística que lleva su nombre, que publicó en 1838 [Verhulst, Pierre-François, Notice sur la loi que la population poursuit dans son accroissement, Corresp. Math. Phys. 10, 113–121, 1838], después de haber leído An Essay on the Principle of Population de Thomas Malthus. Su interés en la teoría de las probabilidades comenzó por un juego de lotería, y con el apoyo de Adolphe Quételet comenzó a aplicarla a las áreas de la economía política y las estadísticas demográficas. Su obra principal es el Traité des fonctions elliptiques (1841), con la que fue aceptado como miembro de la Academia Real de Bélgica, siendo Presidente a partir de 1848. Más información: Bernard Delmas, Pierre-François Verhulst and the logistic law of population, Math. & Sci. hum. Mathematics and Social Sciences 167, 51-81, 2004 Miguel A. F. Sanjuán, Pierre-François Verhulst, Robert M. May y la aplicación logística, Madri+d, 2009 José Luis López Fernández, La ecuación diferencial logística (o de Verhulst), 2011 N. Bacaër, Verhulst and the logistic equation (1838), A Short History of Mathematical Population Dynamics, 35-39, 2011 Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Martes, 15 de Febrero de 2022 | Imprimir | PDF |  Correo electrónico

129. 121. (Febrero 2022) Modelos matemáticos de la función tonal (II)

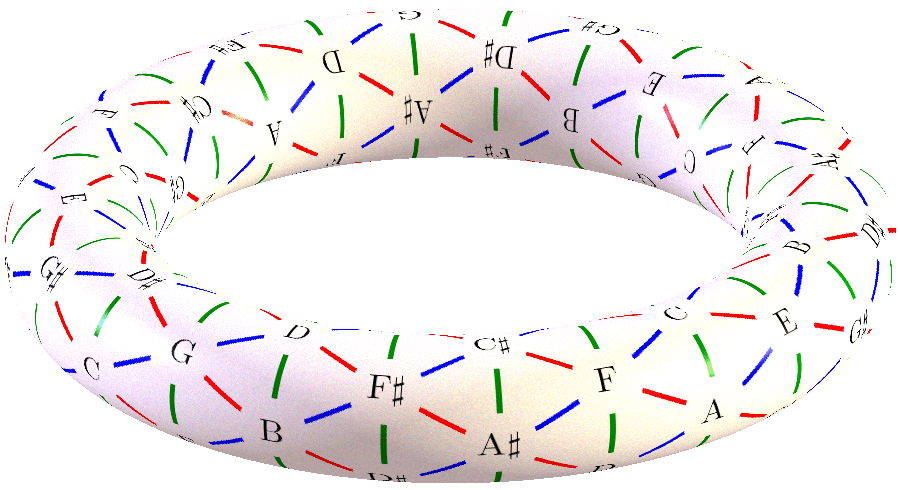
1. La función tonal y el tonnetz En esta última entrega de la serie sobre modelos matemáticos de la función tonal vamos a estudiar un modelo de naturaleza geométrica: el tonnetz. Es un modelo que se basa en la clasificación clásica de los acordes en tónica, dominante y subdominante y que proporciona una visualización bella y elegante de la función tonal y de las relaciones entre los acordes. Una de sus visualizaciones es en forma de toro, como muestra la figura 1 (esta visualización es su interpretación moderna en términos de teoría neoriemanniana, que veremos más adelante en este artículo). Figura 1: El tonnetz como un toro geométrico El tonnetz fue definido por primera vez por Euler en 1739 en su obra Tentamen novae theoriae musicae ex certissismis harmoniae principiis dilucide expositae [Eul22]. Dado un acorde, Euler se fijó en tres relaciones respecto a ese acorde: el movimiento por quintas, el movimiento por terceras mayores y el movimiento por terceras menores. Fijado un acorde, la organización geométrica del tonnetz es entonces como sigue: Los saltos por quintas a partir de ese acorde se representan en línea horizontales; Los acordes a una tercera menor por arriba está en la diagonal superior derecha y los de tercera menor por abajo en la diagonal superior izquierda; Análogamente, los acordes a distancia de tercera mayor están por debajo; los de tercera mayor ascendente se sitúan en la diagonal derecha y los de tercera mayor descendente en la diagonal izquierda. Si fijamos el acorde de do, en la figura de abajo vemos los acordes relacionados con este por el modelo tonnetz. En la línea horizontal vemos un trozo del círculo de quintas, do–sol; en la línea inmediatamente superior están las notas que forman el acorde menor con do, la–do–mi, las cuales a su vez forman otro círculo de quintas; y en la línea inferior a do, vemos los notas a distancia de tercera mayor, también ordenadas por quintas ascendentes hacia la derecha. Las triadas en este modelo forman triángulos. Figura 2: Acordes relacionados entre sí por el modelo tonnetz Las triadas mayores son los triángulos formados por la nota de la diagonal superior derecha y la inmediatamente a la derecha; en la figura do–mi–sol sería el triángulo con la m mayúscula. Las triadas menores son el reflejo respecto al eje x de dicho triángulo; en la figura el triángulo do–mi♭–sol marcado con una m minúscula. El modelo inicial de Euler estaba basado en la entonación justa (véanse las columnas de esta sección sobre afinación, [Góm21a], [Góm21b], [Lie04]). Por tanto, las quintas eran justas y el modelo se extendía hasta el infinito. De hecho, todos los intervalos del tonnetz en el modelo de Euler eran puros (las terceras y los demás intervalos también). Más de un siglo después, el modelo de Euler llama la atención del físico y teórico de la música Arthur von Oettingen. El trabajo de este teórico a su vez llama la atención de Hugo Riemann, quien lo sistematiza y usa en sus análisis de las conducciones de voces y las progresiones armónicas. El cambio que se produce en el uso moderno del tonnetz es que se hace finito al establecer el sistema temperado como sistema de afinación. Esto es, al dividir la octava en 12 partes iguales, el tonnetz pierde su carácter infinito (de ahí la representación finita en forma de toro que vimos más arriba). A la luz de la teoría neoriemanniana, el tonnetz se usa como modelo matemático de los acordes y las funciones tonales, donde las notas del tonnetz son ahora clases de alturas. En dicha teoría se definen tres tipos de operaciones o transformaciones: La operación P, de paralelo, donde un acorde mayor se transforma en su versión menor y viceversa. Esto ocurre por el movimiento de la tercera bien ascendente o descendente. La transformación R, donde un acorde mayor se transforma en su relativo menor y viceversa. En el acorde mayor la quinta sube un tono y en el acorde menor la fundamental baja medio tono. La operación L (de leading-tone exchange en sus siglas inglesas) transforma un acorde mayor en el acorde menor a distancia de una tercera mayor bajando la fundamental medio tono. Así, por ejemplo, do mayor se transforma en mi menor bajando do a si. A la inversa, un acorde menor, como do menor, se transforma en mi♭ mayor bajando do a si♭. En el tonnetz, estas operaciones se identifican con cuadrados como se muestra en la figura de abajo. Figura 3: Versión moderna del modelo del tonnetz (figura tomada de [Wik22]) El tonnetz ha servido para modelizar música de la práctica común extendida y el jazz. Para una ilustración muy clara del uso del tonnetz en la música de jazz, véase [Wel20]. En los vídeos que se muestran a continuación, se muestran explicaciones más detalladas y visuales sobre el tonnetz. En el primero, se explica el tonnetz con ejemplos musicales en el piano. Figura 4: Tonnetz explicado por Daniel Lewis En el siguiente vídeo se oye un preludio de Chopin y se visualiza cómo evolucionan los acordes en el tonnetz. Figura 5: Tonnetz explicado por Daniel Lewis En el último vídeo se visualiza la Gimnopédie número 1 de Satie en el tonnetz. Figura 6: Tonnetz explicado por Daniel Lewis Por ultimo, recomendamos al lector la visita a la página de Imaginary [Ima22], donde puede encontrar una versión interactiva del tonnetz.   Bibliografía [Eul22] Leonard Euler. Tentamen novae theoriae musicae ex certissismis harmoniae principiis dilucide expositae. http://eulerarchive.maa.org/backup/E033.html, Accedido en enero de 2022. Published on Euler archive. [Góm21a] Paco Gómez. Afinamiento y temperamento (I). http://www.divulgamat.net/index.php?option=com_content&view=article&id=18644&directory=67, accedido el 20 de julio de 2021. [Góm21b] Paco Gómez. Afinamiento y temperamento (II). http://www.divulgamat.net/index.php?option=com_content&view=article&id=18645&directory=67, accedido en agosto de 2021. [Ima22] Imaginary.org. Tonnetz. https://www.imaginary.org/es/node/1523, accedido en enero de 2022. [Lie04] Vicente Liern. Afinación. http://www.divulgamat.net/index.php?option=com_content&view=article&id=8747&directory=67, enero de 2004. [Wel20] John Welsh. Using Tonnetz Tone Mesh To Understand Jazz Harmony. https://jazz-library.com/articles/tonnetz/, Abril de 2020. [Wik22] Wikipedia. Tonnetz. https://en.wikipedia.org/wiki/Tonnetz, accedido en enero de 2022.

Lunes, 14 de Febrero de 2022 | Imprimir | PDF |  Correo electrónico

130. Números primos de 9 cifras diferentes

Con los dígitos 1, 2, 3, 4, 5, 6, 7, 8 y 9 se pueden formar 362.880 números de 9 cifras –son las permutaciones de 9 elementos P(9)=9!– diferentes. ¿Cuántos de ellos son primos? SOLUCIÓN (piensa antes un poquito) Visto en Futility Closet Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Jueves, 10 de Febrero de 2022 | Imprimir | PDF |  Correo electrónico