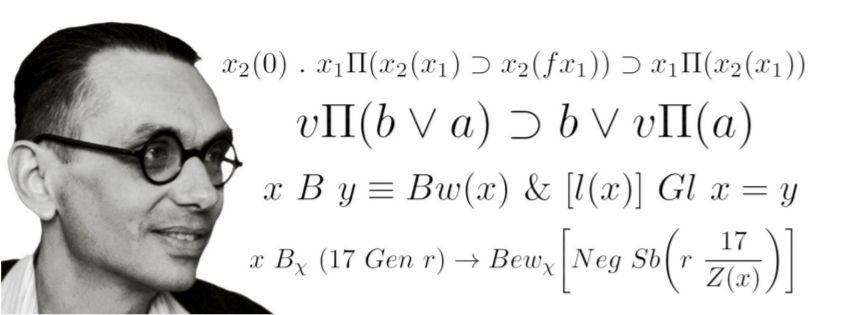171. Desafío matemático de la Lotería de Navidad 2021: una suerte que se comparte

El País, 17 de Diciembre de 2021 LOTERÍA DE NAVIDAD Adolfo Quirós

Viernes, 17 de Diciembre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

172. Solución al desafío matemático de la Lotería de Navidad: un número muy variable de segmentos

El País, 21 de Diciembre de 2020 LOTERÍA DE NAVIDAD Adolfo Quirós

Lunes, 21 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

173. Desafío matemático de la Lotería de Navidad: un décimo rayado

El País, 16 de Diciembre de 2020 LOTERÍA DE NAVIDAD Adolfo Quirós

Miércoles, 16 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

174. Trigonometría, el puente que une todas las matemáticas

ABC, 13 de Diciembre de 2021 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 13 de Diciembre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

175. 166. El conocimiento, ¿es poder?

Acercándonos a un periodo vacacional, en el que teóricamente disponemos de más tiempo para hacer actividades menos usuales, puede ser propicio dedicar algunos minutos a la reflexión, guiados por una película atípicamente poco comercial. Ficha Técnica: Título: Senderos de la mente. Título Original: Mindwalk. Nacionalidad: EE. UU., 1990. Dirección: Bernt Amadeus Capra. Guion: Floyd Byars y Fritjof Capra, basado en el libro The Turning Point, de Bernt Amadeus Capra. Fotografía: Karl Kases, en Color. Montaje: Jean Claude Piroué. Música: Philip Glass. Producción: Adrianna A.J. Cohen. Duración: 112 min. Ficha artística: Intérpretes: Liv Ullmann (Sonia Hoffman), Sam Waterston (Jack Edwards), John Heard (Thomas Harriman), Ione Skye (Kit Hoffman), Emmanuel Montes (Romain), Jean Boursin (Sacristán), Gabrielle Danchick (Guia turística), Jeanne Van Phue (Turista), Penny White (Turista). Argumento Jack Edwards es un político norteamericano en horas bajas que se siente completamente bloqueado ante los resultados electorales. Tratando de cambiar el chip, telefonea a un amigo periodista que fue colaborador suyo en campañas electorales en el pasado. Éste le propone que pase unos días junto a él en la región francesa de Normandía, a los pies del Monte de Saint-Michel (de lo cual se arrepiente a los dos minutos, recordando su forma de ser). Una típica visita turística los hará coincidir con una física en año sabático. El encuentro hará plantearse a cada uno aspectos de su vida personal artificialmente cerrados. Comentario En esta ocasión no vamos a encontrar matemáticas explícitas (miento: se menciona y enuncia el teorema de Pitágoras), pero sí un montón de referencias a matemáticos y físicos, y su aportación a la forma de entender el mundo, y cómo su visión modificó la del resto de la humanidad. Llegué a esta película preparando una reciente charla sobre Matemáticas, Filosofía y Cine, en el Salón de Actos del Museo Patio Herreriano de Valladolid, a la que gentilmente fui invitado por la organización del Festival Valladolid Piensa,  aunque finalmente no incluí ninguna de sus escenas en la presentación. Me resultó complicado seleccionar un momento concreto, ya que toda la película de inicio a fin proporciona momentos interesantes que comentar, y hubiera necesitado una hora más, dada la cantidad de escenas que ya tenía seleccionadas. En cualquier caso, la película aparece íntegramente en el siguiente enlace, subtitulada, ya que está en versión original (lo que es de agradecer en determinados momentos, aunque, en general está bastante fielmente traducida). Aunque la película va recorriendo a lo largo de un día diversos puntos de la abadia del Monte de Saint Michel (el islote y la bahía fueron declarados patrimonio de la humanidad en el año 1979, siendo un lugar espectacular para visitar), lo cierto es que perfectamente podía haberse rodado en una sala cerrada con los tres personajes principales, ya que sobre ellos recae todo el desarrollo del metraje. No obstante, el director ha seleccionado perfectamente los rincones del lugar para introducir los temas que abordan (el reloj y su engranaje para el universo mecanicista de Descartes, la cámara de tortura para el pensamiento de Francis Bacon, el uso de la luz en otras estancias con Isaac Newton, etc.). Como suele ser habitual en este tipo de obras, la tesis defendida por cada personaje es cuestionada por los otros (en este caso, uno de ellos, las pocas veces que define su pensamiento, toma partido siempre por la perspectiva de otro de ellos), produciendose un fecundo intercambio de ideas, todas ellas bastante bien traidas, que además tienen un perfecto reflejo en nuestra sociedad actual, en nuestro modo de vida. Por supuesto no se da por finalizada ninguna de las cuestiones (en la mayor parte de las ocasiones no es posible), sino que como los que las exponen, el espectador tomará partido por unas u otras. Probablemente haya un sesgo hacia la parte científica frente a la visión del político, no se puede negar, e incluso de la primera frente a la “idilica” visión poética del periodista (al menos eso es lo que me ha parecido a mí), pero los diálogos intentan contrarrestar de una u otra manera todas las perspectivas para que al final pueda declararse un “empate a los puntos” (por supuesto, no para los que estén plenamente convencidos de alguna de las posturas). No piense el lector que todo es absolutamente filosófico-teórico (el inicio comienza de ese modo, con la postura mecanicista frente a la teológica). Como hemos indicado llega un momento en el que se plantean temas polémicos de plena actualidad como el control de natalidad, el cambio de hábitos como freno al cambio climático (obsérvese que la película es de 1990, y ya se veía este problema como uno de los más relevantes al que hacer frente; sin embargo, aquí seguimos, haciendo nada al respecto), el reemplazo de Dios por el cientifismo, ¿es lícito arrasar los bosques amazónicos para saldar la deuda del país?, ¿es la medicina actual un negocio?, la nueva visión de la llamada teoría de sistemas (concebir todo el Universo como un todo uniforme), entre otros. En la imagen, el libro en el que se basa, cuyo título, El punto crucial, es bastante gráfico, aunque, desde un punto de vista matemático, hubieramos puesto El punto de inflexión. En suma, una propuesta de cine diferente (por momentos cercano al documental) para el que hay que estar advertido y preparado (el que espere cualquier tipo de acción comercialona de pegolete, tipo tortazos, cuernos, persecuciones, etc., claramente que se abstenga), y seguramente dosifique su visionado en varias tandas porque lo que prima es claramente el diálogo y la reflexión. Obviamente al que le gusten este tipo de propuestas, seguramente se le hará corta y le parecerá magnífica. Y por supuesto, nuestro más fraternal saludo para estos días que, indefectiblemente para algunos, y anheladamente para otros, se aproximan. 2022 está ya llamando a la puerta.

Lunes, 13 de Diciembre de 2021 | Imprimir | PDF |  Correo electrónico

176. El grupo ‘Luzitania’

El matemático Nikolai Nikolaevich Luzin (1883-1950) nació un  9 de diciembre. Trabajó en teoría descriptiva de conjuntos y en aspectos de análisis matemático relacionados con la topología. Él es el epónimo de Luzitania, grupo de jóvenes matemáticos de Moscú interesados en la investigación. Estudió matemáticas en la Universidad de Moscú y Dimitri Egorov fue su director de tesis, titulada Integral and trigonometric series (1915). Entre sus alumnas y alumnos se encuentran muchos de los más famosos matemáticos soviéticos: Pavel Aleksandrov, Nina Bari, Aleksandr Khinchin, Andrey Kolmogorov, Alexander Kronrod, Mikhail Lavrentyev, Alexey Lyapunov, Lazar Lyusternik, Pyotr Novikov, Lev Schnirelmann, Mikhael Suslin o Pavel Urysohn. Llevan su nombre el teorema de Denjoy–Luzin, el teorema de Denjoy–Luzin–Saks, el teorema de Luzin y los espacios de Luzin. El libro de Loren Graham y Jean-Michel Kantor, El nombre del infinito. Un relato verídico de misticismo religioso y creatividad matemática (El Acantilado, 2012), los autores hablan de las relaciones entre matemáticas y religión en dos escuelas matemáticas de la primera mitad del siglo XX: la de París de teoría de funciones y la de Moscú, cuyos fundadores –Egorov y Luzin– eran profundamente religiosos. La portada del libro (portada del libro en inglés, 2009) representa a Pável Florenski (amigo y condiscípulo de Luzin) paseando y conversando con el filósofo Sergei Bulgakov También se habla del asunto Luzin de 1936:  chantajes, acusaciones falsas, uso de la vida privada, etc. que destruyeron brutalmente el mundo alrededor de Egorov —que falleció en 1931, tras una huelga de hambre en prisión—, Pável Florenski —fusilado en 1937— y Luzin —criticado de manera anónima en el periódico Pravda por diferentes motivos—. Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 09 de Diciembre de 2021 | Imprimir | PDF |  Correo electrónico

177. 199. (Diciembre 2021) Ilusiones mágicas

Llevamos más de 17 años dando muestras mensuales de la estrecha relación que existe entre la magia y la matemática. Después de este recorrido tan extenso, es posible que hayas tenido la impresión de que toda la magia es matemática o de que toda la matemática es mágica pero, a poco que conozcas algo más de cualquiera de estas dos disciplinas, concluirás que hay vida más allá de ambas. Digo esto porque hoy quiero dedicar nuestra reunión mensual en este rincón a explorar algunas relaciones de la magia con otras ciencias, concretamente con las ciencias cognitivas. Esto tampoco nos aleja de las matemáticas porque el estudio de la lógica del cerebro y la lógica de la razón están lógicamente relacionados, por pura lógica. Así que voy a realizar un pequeño recorrido por algunos juegos más o menos clásicos en los que el razonamiento lógico choca contra la percepción sensorial. (1) LA HIPERCARTA El primer ejemplo es el que aparece en la imagen que encabeza el artículo: ¿crees que es posible que esta figura se haya construido con una sola carta sin haberla roto completamente? Parece imposible que la sección vertical corresponda exactamente con los dos huecos contrapuestos que se han formado en la parte horizontal. Pues, contrariamente a la razón, es posible y muy fácil de realizar. El acertado nombre comercial de esta ilusión es "hipercarta" debido a que, aparentemente, se debe viajar a la cuarta dimensión para conseguir que los dos huecos se conviertan en un solo trozo. Se desconoce el origen de esta ilusión pero, en el capítulo 8 del libro Fractal Music, Hypercards and More ... (Freeeman, 1992), Martin Gardner señala que la construcción de este modelo fue propuesta como examen de ingreso para la escuela de arquitectura en la Universidad de Leningrado (la actual San Petersburgo). En ese mismo capítulo, Gardner explica el método para construir la hipercarta y desvela algunas ideas elaboradas por varios magos para convertir esta ilusión en juego de magia. Un estudio riguroso y completo, realizado por Tom Frame, culminó con el libro titulado The Hypercard Project (2006), donde se pueden encontrar diferentes variaciones y muchas sorpresas. A modo de ejemplo, van estas dos figuras: la imagen de la izquierda consiste en una banda de Möbius con aspecto de hipercarta, ideada por Paul Merva y Alexis Gilliand y la imagen de la derecha (¿te animas a construirla?) es una sorprendente construcción realizada por Jack Botermans, especialista en puzles y problemas de ingenio, como aparece en su libro Paper Capers (1986). Aunque la propia ilusión ya produce en sí misma una sorpresa mágica, una estupenda adaptación como juego de magia la ofreció el mago californiano Daryl Easton (fallecido en 2017 bajo extrañas circunstancias) con el juego Hyper-Bent-Elation. Una última sugerencia: no dejes de consultar el artículo "Impossible Folding Font", firmado por Erik Demaine, Martin Demaine, Tomoko Taniguchi y Ryuhei Uehara, que fue presentado para la edición de 2019 de las Conferencias Bridges, en las que se exploran las conexiones de las matemáticas con el arte, la música, la arquitectura y la cultura. En ese trabajo crean todo un alfabeto con figuras «imposibles» como las que vemos en las imágenes de aquí abajo. (2) EL BOOMERANG El segundo ejemplo que quiero mostrar recibe el nombre de «ilusión del boomerang». Consiste en dos láminas o tiras de cartón u otro material con forma de rectángulo curvado, como se ve en estas dos imágenes. Si nos fijamos en la imagen de la izquierda, parece evidente que la pieza A es de menor tamaño que la pieza B. Ahora bien, si intercambiamos las posiciones de las dos piezas, resulta que la pieza B tiene ahora menor tamaño que la pieza A, como se puede apreciar en la imagen de la derecha. La realidad es que ambas plantillas son exactamente iguales. Sólo la posición relativa entre ellas y la forma curvada de su construcción produce la sensación de que una de ellas es mayor que la otra (al alinearse las dos piezas por los lados cortos de su izquierda, la figura superior queda desplazada hacia la izquierda de forma inapreciable por el subconsciente). En este videoclip de la página Mighty Optical Illusions se muestran las distintas posiciones relativas de las piezas y la ilusión óptica que hace variar nuestra sensación sobre su tamaño relativo. Se dice por ahí que esta ilusión óptica fue ideada por el psicólogo estadounidense —de origen polaco — Joseph Jastrow en 1892, razón por la cual se conoce popularmente como "ilusión de Jastrow". Sin embargo, aparece impresa —¿por primera vez?— en la enciclopedia "The world of wonders: a record of things wonderful in nature, science, and art", publicada alrededor del año 1882, bajo el título Wonderful optical delusion, como se muestra en la imagen de la izquierda. Esta misma ilusión fue publicada por el psicólogo alemán Felix Müller-Lyer para la revista Archiv fur Anatomie und Physiologie en 1889 junto a una selección de ilusiones similares (que se muestran en la imagen central) y por Wilhelm Wundt unos años más tarde. El estudio de la forma que deben tener las figuras para maximizar la ilusión fue estudiado por otro psicólogo, el japonés Shogu Imai en 1960. Aquí intervinieron las matemáticas pues la conclusión de Imai fue que los bordes curvos de las láminas debían tener forma de arcos de circunferencia, que la razón entre los radios debía ser 3/5 y el ángulo central ideal debía medir 80 grados. No pasó mucho tiempo para que la ilusión se convirtiera en un juego de magia. La referencia más temprana que se conoce corresponde al libro de Will Goldston titulado Simple Conjuring Tricks That Anyone Can Perform y publicado en 1913. Un completo y documentado estudio sobre esta ilusión ha sido escrito recientemente por Peter Prevos (quien se autodefine como ingeniero civil y científico social con incursiones esporádicas a la magia teatral) bajo el título The Jastrow Illusion in Magic, publicado en 2016. Él mismo escribió en 2017 una breve reseña del folleto en el artículo titulado "The science of the boomerang illusion", publicado en el número 8 de la revista Journal of Magic Research (de la que hablaremos más adelante). Muchas y variadas versiones de la ilusión del boomerang se han desarrollado como juegos de magia. Una de mis preferidas se debe al ingenio de Terri Rogers (ya citada en este rincón en el número 152 de septiembre de 2017), con el juego titulado Top of the bill, donde van cambiando de tamaño los carteles con los nombres de Stan Laurel y Oliver Hardy, los famosos "el gordo y el flaco". Otro enfoque interesante es el juego comercializado en 2006 por Chuck Leach bajo el título Boomerang Card Across; éste consiste en un sorprendente viaje de una carta pensada desde un paquete de cartas hacia otro con la ayuda de la ilusión del boomerang. Las imágenes sin palabras que muestro aquí abajo corresponden a otras versiones ingeniosas del juego. También puedes ver un video donde el mago japonés Mizoguchi realiza el juego titulado Arch Illusion y, si quieres adquirir un modelo barato, el matemago reinounidense Andrew Jeffrey comercializa la ilusión que titula la mariposa creciente. (3) UNO ES MAYOR QUE TRES La tercera y última ilusión paradójica que quiero comentar ya no se trata de un efecto óptico ni visual sino táctil. Antes de entrar en detalles, quiero que la experimentes personalmente para lo cual basta que sigas las instrucciones que leerás a continuación. Necesitarás tres barajas de cartas, aunque lo importante no son las cartas sino sus estuches de cartón. En su defecto, valen tres cajas iguales de dimensiones similares a las de los estuches de cartas, como las cajas grandes de cerillas. Vacía dos de las tres cajas y deja la tercera llena (puede ser con las propias cartas o con muchas monedas o llena de granos de arroz o de tornillos). Cuanto mayor sea su peso, más sorprendente será el efecto. Coloca las tres cajas apiladas, una sobre otra, pero dejando la más pesada encima de las otras dos. Agarra las tres cajas desde arriba con una mano, colocando el dedo pulgar en la parte interior y el resto de los dedos en la parte exterior y levanta todo el conjunto. Toma nota mental de su peso. Deja todo el conjunto sobre la mesa y agarra ahora solamente la caja superior. Levanta la caja y observa su peso. Por arte de magia, resulta que esta única caja pesa más que la suma de las tres. ¿Menos es más? Si no crees lo que has sentido, repite el experimento todas las veces que quieras, incluso empezando por levantar primero el paquete superior y después los tres juntos. ¡Increíble pero cierto! Si te ha parecido interesante el experimento, puedes construir tus propias cajas con el diseño que ha realizado Mark Fuller, el cual está disponible en el portal www.thingiverse.com, y que puedes reproducir con una impresora 3D. Si te parece más cómodo, puedes adquirir el juego en la tienda online Grand Illusions o una versión con ingredientes adicionales y material de gran calidad en Vanishing Magic. Este juego me lo enseñó Fernando Blasco (citado ya en este rincón en varias ocasiones) quien, a su vez, lo conoció en una de las famosas reuniones Gathering for Gardner, que se celebran cada dos años en Atlanta (capital del estado norteamericano de Georgia) reuniendo todo tipo de personas que comparten con Martin Gardner tres de sus grandes pasiones, la magia, las matemáticas y los juegos de ingenio. El efecto está basado en la conocida por los psicólogos como ilusión peso/tamaño de Charpentier, por haber sido el oftalmólogo francés Augustin Charpentier el primero en realizar el experimento y mostrar la ilusión creada en el artículo titulado "Analyse experimentale: De quelques elements de la sensation de poids" y publicado en 1891 (se puede leer un resumen de dicho artículo, así como otros aspectos históricos de la ilusión, en el trabajo de 1999 titulado "Charpentier (1891) on the size-weight illusion", firmado por David Murray, Robert Ellis y Christina Bandomir). El experimento inicial consistía en disponer de varios objetos, todos del mismo peso pero de distintas formas y tamaños, y estimar su peso levantándolos individualmente. La conclusión que se obtenía era que el objeto más pequeño parecía que fuera el más pesado. El fenómeno sigue suscitando debates entre los especialistas ya que no queda completamente resuelta la causa que origina esta ilusión. Intervienen aspectos físicos —como la diferencia de tamaño—, aspectos fisiológicos —como la dificultad de agarrar el objeto más grande o que la mano ejerce más presión sobre la parte superior del objeto que es la más pesada— o aspectos psicológicos —como la idea preconcebida de que más grande equivale a más pesado—, aunque es posible que la respuesta esté en la suma de todos ellos. Muchos artículos científicos se han publicado en relación con esta ilusión y es fácil encontrarlos gracias a la existencia de buscadores virtuales tan eficientes como veloces. Sólo citaré el artículo titulado "The size-weight illusion", al que puedes acceder desde el portal Science is Fun, mantenido por Bassam Shakhashiri, profesor de Química de la Universidad de Wisconsin-Madison, y que presidió en 2012 la American Chemical Society. La revista electrónica The Journal of Magic Research, disponible bajo registro en el portal Ask Alexander (la mayor biblioteca virtual sobre magia del mundo), está dedicada a promocionar la investigación científica en la magia; su lema es: "cuando mides cualquier cosa y lo expresas con números, entonces ya sabes algo sobre ella". En la revista se pueden encontrar artículos que relacionan la magia con las matemáticas, la neurociencia, psicología, biología, física, química y otras disciplinas científicas. Pues bien, en el número 5 de dicha revista (que apareció en febrero de 2014), Gerry Hayes escribe el artículo titulado "Can you fool yourself?" en el que cita este juego a partir de la descripción dada por Ian Rowland en la revista Magic Circular, que es el órgano de difusión del longevo y selecto club londinense «Magic Circle». Hayes pide a los lectores de la revista que se pronuncien sobre el fenómeno y propongan respuestas a las causas que lo originan. En el siguiente número de la revista podemos encontrar un par de contribuciones de magos que comentan sus propios métodos para realizar el juego, sin profundizar en la posible explicación. Independientemente de las causas que originan esta ilusión, puede presentarse ante el público como juego de magia, bien para demostrar los poderes de sugestión que tiene el mago, bien para hacer creer que existen fuerzas ocultas que se ejercen por la voluntad del mago, o mediante cualquier explicación pseudocientífica que se te ocurra. La buena noticia es que nadie descubrirá el truco porque ... ¡no hay truco! Para saber más Como podrás imaginar, hay muchos otros ejemplos que se podrían proponer en la línea de los citados aquí. Para no extenderme demasiado en el tema, terminaré indicando algunos enlaces en los que puedes empezar a navegar si te interesa el tema de la psicología en la magia. La ilusión del vaso de tubo era uno de los juegos favoritos de Martin Gardner (como puedes comprobar en la imagen) y está descrito en uno de los artículos de la revista digital Computer Science for Fun, de la Universidad Queen Mary de Londres. En el portal Psychology of magic, del grupo formado por investigadores de las Universidad McGill y British Columbia, aparecen publicados algunos resultados de investigación realizados con el objetivo de entender cómo la magia actúa sobre nuestra mente. El artículo de Susan Krauss (Universidad de Massachusetts Amherst), titulado 5 amazing psychology magic tricks (2012), enseña cinco juegos de magia como ejemplos de demostraciones científicas que pueden ser utilizados en institutos o escuelas de psicología. Diversos trabajos del mago y psicólogo Richard Wiseman, como los libros "Magic in Theory", "Blink and you'll miss it" o "Magic and wellbeing", abundan en el tema de la relación entre la magia y la psicología. Han sido (y son) muy populares en la red sus ilusiones ópticas y otros efectos mágicos, que se pueden disfrutar en el canal de YouTube titulado Quirkology. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Jueves, 02 de Diciembre de 2021 | Imprimir | PDF |  Correo electrónico

178. Lo que las matemáticas han cambiado nuestras vidas

ABC, 29 de Noviembre de 2021 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 29 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

179. 78. (Diciembre 2021) Simetrías en las tapas de fundición con teselaciones periódicas

(Decoración doméstica con una tapa del grupo p4g) Las tapas de registro en hierro fundido de los distintos suministros urbanos tienen un especial atractivo. Muchos fotógrafos y diseñadores han prestado la debida atención al modesto objeto. Decoran vestidos y hasta las viviendas como puede verse en la foto inicial. No es algo que nos deje indiferentes. Para la educación matemática es un objeto de contemplación y estudio por sus variadas regularidades. Las tapas circulares tan habituales del alcantarillado presentan a veces simetrías de rotación pero aquí nos vamos a dedicar solo a las tapas que contienen teselaciones periódicas del plano en su limitada superficie. De los 17 grupos posibles de teselado periódico del plano vamos a mostrar que en las tapas de fundición encontraremos al menos 13. Los diecisiete grupos de teselaciones periódicas del plano A finales del siglo XIX, el matemático ruso Fedorov (1891) sistematizó los grupos cristalográficos que aplicados al plano reducen a diecisiete las posibles teselaciones periódicas del plano desde el punto de vista de sus simetrías. Más tarde el húngaro-americano Pólya  reprodujo los resultados. Los movimientos que definen el tipo de simetría son las traslaciones, los giros, las reflexiones y las reflexiones deslizantes. La traslaciones están incluidas al observar la periodicidad. Cinco son los giros posibles para las teselaciones periódicas: orden 1 (vuelta completa, 360º) orden 2 (media vuelta, 180º) orden 3 (tercio de vuelta, 120º) orden 4 (cuarto de vuelta, 90º) y orden 6 (sexto de vuelta, 60º). Las reflexiones vienen dadas por sus ejes de simetría que hacen de espejos. Los ejes de reflexión deslizante actúan como espejo tras una traslación con deslizamiento sobre el propio eje. La nomenclatura que vamos a usar es la de la Unión Internacional de Cristalografía (IUCr) que se inicia con p (en 15 casos) y con c (los otros dos), sigue el número de orden del giro, y se termina con m (mirror) si tiene ejes de simetría y/o g (glide) si tiene ejes deslizantes. Así p2mg será una simetría con giros de 180º un eje simetría especular y uno deslizante. Por redundancia se suele suprimir el 2 y queda pmg. Un desarrollo detallado y sencillo de la teoría, con numerosos ejemplos, se puede encontrar el artículo Wallpaper group de la edición inglesa de la Wikipedia. No hemos encontrado ninguna de los tres grupos de orden 3 aunque hay varios diseños con ángulos de 120º que se acercan. Veremos como el p31m está incluido prácticamente pero termina perdiéndose por la colocación. Tampoco hemos localizado la rotación de orden 4 sin simetrías de reflexión. Veamos los ejemplos: Grupo p1 (Tapa del grupo p1) Solo traslaciones, sin centros de giro privilegiados ni ejes de simetría. Si en lugar de una L y una I, hubiera sido una U tendríamos un grupo pm. Grupo pm Existe un reflexión sobre un eje de simetría y todos los paralelos de la estructura periódica. (Tapa del grupo pm) En el ejemplo el eje de simetría es horizontal pasa por el centro y otro y otro por la separación. Grupo pg Existe un reflexión deslizante sobre un eje y todos los paralelos de la estructura periódica. En el ejemplo son verticales, formando 45º con las eles. (Tapa del grupo pg) Grupo cm Existe un reflexión con eje de simetría y paralelo un eje deslizante. Y todos los paralelos de la estructura periódica. En el ejemplo los ejes de simetría especular son los líneas diagonales a 45º que unen los vértices de los catetos. Los ejes deslizantes son paralelos a ellos a mitad de distancia. (Alcorque de Zaragoza con grupo cm) Grupo p2 (Tapa del grupo p2) Existen centros de giros de 180º. Si tomamos un cuadradito cualquiera, ceda base o primitiva, los centros de giro son los cuatro vértices, el centro y los cuatro centros de los lados del cuadrado. No existe simetría de reflexión. Grupo pmm (Tapa del grupo pmm) Teselación muy sencilla. Cada rectángulo pequeño es una celda que se repite. Hay centros de giro de 180º y reflexiones tanto en ejes horizontal como verticales. Grupo pmg (Tapa de Atenas. Grupo pmg) Los ejes de reflexión siguen el palo largo de la T y los deslizantes son perpendiculares, entre los dos sombreros de la T. Los centros de giro de orden 2 se localizan con facilidad. Grupo pgg (Tapa del grupo pgg) Los centros de giro de orden 2 y la periodicidad es fácil de ver. Menos sencillo es ver los ejes deslizantes que van según las dos diagonales. Grupo cmm (Tapa del grupo cmm) El grupo cmm adopta aquí su estructura más sencilla, a base de rombos, sus diagonales son  ejes de reflexión, sus centros son de giro de orden 2 y los ejes deslizantes son paralelos a los de reflexión en su mitad. Grupo p4m (Tapa del grupo p4m) Los giros de orden 4, de 90º, y los ejes de simetría llevan la dirección de lados y las diagonales. En la tapa de ejemplo están hasta marcados la mitad de los centros. El grupo simetría p4m es el más habitual en la azulejería, pero en las tapas se ven muchos del tipo siguiente, el p4g. Grupo p4g (Tapa del grupo p4g. Praga) El grupo p4g tiene centros de giro de orden 4 y ejes de simetría perpendiculares como el p4m. La manera más fácil de distinguirlos es que en el p4g los ejes de simetría especular no pasan por los centros de giro de orden 4. Grupo p6 Mostramos una bonita tapa vista en Santiago de Compostela que no posee ejes de simetría pero si giros de orden 6. Además responde a la ilusión óptica de los cubos. Si no estuviera rayada tendría reflexiones y sería del grupo siguiente, el p6m. (Tapa del grupo p6. Santiago de Compostela) Grupo p6m (Tapa del grupo p6m. Nueva York) La estructura hexagonal permite los giros de orden 6 y existen ejes de simetría que forman ángulos de 120º. Terminamos con otra tapa p6m que con pequeños cambios correspondería al grupo de simetría p31m, bastaría con no contraponer simétricamente las Y griegas. (Tapa del grupo p6m)

Miércoles, 01 de Diciembre de 2021 | Imprimir | PDF |  Correo electrónico

180. 136. (Diciembre 2021) Retrato alfabético de Kurt Friedrich Gödel, por Iker Ruiz de Infante González

Un retrato alfabético es un listado de palabras (eventualmente acompañadas de frases breves) ordenadas en orden alfabético, que dibujan un retrato. Este relato alfabético ha sido una de las propuestas premiadas en el concurso “retrato alfabético-matemático” organizado durante la Zientzia Astea 2021. Axiomas En matemáticas, proposiciones que se asumen ciertas, y de las cuales se deducen el resto de proposiciones, teoremas, etc. Durante su vida Gödel estudió algunos de los sistemas axiomáticos de las matemáticas y analizó sus propiedades. Brno Brünn en alemán, ciudad en la que Gödel nació el 28 de abril de 1906, en lo que entonces era el Imperio Austrohúngaro. Vivió en esta ciudad, en la que se graduó con honores en la escuela secundaria, hasta que a los 18 años ingresase en la Universidad de Viena. Actualmente Brno es la segunda ciudad más grande de la República Checa. Círculo de Viena Movimiento científico y filosófico que abogaba por una concepción científica del mundo. Gödel participó en el mismo junto con Moritz Schlick, Hans Hahn y Rudolf Carnap. Fue disuelto en 1936 debido al ascenso del nazismo en Austria. Desnutrición Causa de la muerte de Gödel. Murió cuando su esposa, Adele Nimbursky Porkert, estuvo hospitalizada y no pudo continuar preparándole la comida. Gödel sufría de un miedo obsesivo a ser envenenado, y solo tomaba la comida preparada por Adele. Einstein, Albert Amigo de Gödel en Princeton. Solían pasear juntos y conversar en el idioma materno de ambos, El alemán. Einstein decía en sus últimos años de vida que su propio trabajo ya no le interesaba tanto, y que le entusiasmaba más compartir el paseo hasta casa con Gödel. Frege, Gottlob Matemático logicista precursor del intento de encontrar un conjunto de axiomas válido para poder deducir del mismo toda la matemática. El trabajo de Gödel terminó con esta idea de Frege, zanjando la discusión con una respuesta negativa a la existencia de este conjunto de axiomas. Gödel Lenguaje de programación informático perteneciente al paradigma de programación lógica. Nombrado así en honor a Kurt Gödel, debido a las aportaciones de este a la lógica, y a los conceptos de computabilidad y de función recursiva. Hilbert, David Matemático que continuó con las ideas de axiomatización de Frege, y que formuló un Programa para definir un conjunto de axiomas finito y completo que fuera suficiente para expresar toda la matemática. El trabajo de Gödel determinó que el Programa de Hilbert era inalcanzable, en el sentido de que con un conjunto tal de axiomas no era posible demostrar la consistencia del sistema desde dentro del mismo. Instituto de Estudios Avanzados Institución privada, situada cerca de la Universidad de Princeton, dedicada a realizar investigaciones avanzadas en ciencia básica. En el mismo han desarrollado su trabajo personajes como Albert Einstein y John von Neumann. Gödel impartió algunas conferencias en esta institución, y finalmente acabo siendo docente en la misma tras su huida de la Alemania nazi. Kleene, Stephen Matemático alumno de Alonzo Church. Asistió a las conferencias de Gödel en el IEA y sentó las bases para la teoría de las funciones recursivas, área que siguió investigando durante el resto de su vida. Fue capaz de ofrecer una demostración alternativa de los Teoremas de Incompletitud de Gödel, usando el concepto de computabilidad, que hacía más fácil entender y enseñar los teoremas. Lógica Ciencia formal a la que Gödel hizo grandes aportaciones. Gödel aprendió lógica de la mano de Hans Hahn y Rudolf Carnap, y contribuyo a la teoría de la demostración clarificando la relación entre distintos sistemas formales. Medalla Nacional de Ciencia Galardón que le fue concedido a Gödel en 1974 por el entonces presidente de los Estados Unidos, Gerald Ford. Anterior a esto, había sido el primer galardonado con el Premio Albert Einstein, junto con Julian Schwinger, en 1951. Numeración de Gödel Idea original de Gödel basada en identificar cada proposición formal de un sistema axiomático con un número natural de forma única. Esto es posible si el sistema axiomático en cuestión es capaz de expresar la noción básica de aritmética necesaria para poder demostrar el Teorema Fundamental de la Aritmética. Ontología Rama de la filosofía por la que Gödel pareció mostrar interés cuando formuló una demostración del argumento ontológico de Leibniz sobre la existencia de Dios. Actualmente dicha demostración se conoce como la prueba ontológica de Gödel. Principia Mathematica Obra realizada por Bertrand Russell y Alfred Whitehead para continuar el trabajo de Gottlob Frege, pero eliminando las inconsistencias derivadas de la paradoja de Russell. Gödel se basó en el sistema descrito en esta obra para formular sus Teoremas de Incompletitud. Recursividad Propiedad fundamental de las funciones y demostraciones que Gödel empleó en su obra. Más concretamente Gödel basó sus teoremas en la recursión primitiva. Es por ello que argumentaba que sus demostraciones eran constructivas y computables. Sobre proposiciones formalmente indecidibles de Principia Mathematica y sistemas relacionados Obra principal de Gödel. En dicha obra formuló y demostró sus Teoremas de Incompletitud. Se publicó originalmente en alemán, con el nombre “Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I”, en la revista Monatshefte für Mathematik. Gödel apuntó que publicaría una segunda parte de la obra, pero esa segunda parte jamás vio la luz. Teoremas de Incompletitud Principal y más importante aportación de Gödel a las matemáticas, consta de dos teoremas. El primer teorema establece las condiciones para que un sistema axiomático sea incompleto, es decir, que contenga proposiciones formales indemostrables e irrefutables al mismo tiempo (proposiciones indecidibles). El segundo teorema señala que dentro de un sistema tal la proposición que indica la consistencia del mismo es indecidible. Universo de Gödel Solución exacta de las ecuaciones de campo de la relatividad general de Einstein propuesta por Gödel. En dicho universo serían posibles los viajes en el tiempo, y este hecho supuso un estímulo para la búsqueda de soluciones exactas más complejas. Viena Ciudad en la que Gödel cursó sus estudios universitarios, se doctoró y vivió hasta su exilio a los Estados Unidos. Fue, sin embargo, en Bolonia donde Gödel asistió a una conferencia de Hilbert sobre completitud y consistencia en matemáticas, hecho que lo marcaría de por vida. Widerspruchsfreiheit En alemán, consistencia. Es la propiedad fundamental que tienen que tener los sistemas axiomáticos como los que estudió Gödel. Se trata de que, si se puede demostrar una proposición formal, no se pueda también demostrar la proposición contraria. El sistema descrito en el Principia Mathematica es consistente, aunque esa consistencia no se pueda demostrar dentro de la lógica del propio sistema. Por el contrario, en un sistema inconsistente toda proposición es demostrable. ZFC Los axiomas de Zermelo-Fraenkel, junto con el axioma de elección, componen el que actualmente es el sistema axiomático estándar para la teoría de conjuntos. Durante la década de 1930 Gödel demostró que el axioma de elección era independiente de los axiomas de Zermelo-Fraenkel, pero consistente con ellos. Los axiomas de ZFC constituyen también uno de los sistemas en los que se cumplen los Teoremas de Incompletitud de Gödel.

Miércoles, 01 de Diciembre de 2021 | Imprimir | PDF |  Correo electrónico