181. Fractales: las formas que simulan a la naturaleza

ABC, 22 de Noviembre de 2021 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 22 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

182. 120. (Noviembre 2021) Modelos matemáticos de la función tonal (I)

1. La función tonal La nueva serie de artículos de esta columna versan sobre los modelos matemáticos de la función tonal. Este primer artículo se dedica a examinar las diferentes definiciones de función tonal en la música clásica y en el jazz. Walter Piston en su libro Armonía4 define función tonal como siguiente (página 50, sus cursivas): La tonalidad no es simplemente una manera de utilizar las notas de una escala particular. Es más bien un proceso de establecimiento de relaciones de estas notas con la nota que representa el centro tonal. Cada grado de la escala tiene su parte en el esquema de la tonalidad, su función tonal. Esta definición resulta demasiado general o incluso vaga. La expresión “una manera de utilizar las notas” necesita más concreción. De hecho, nos resulta sorprendente que muchos manuales de armonía no definan la función tonal con más formalidad (el libro de Piston ha sido una clásica referencia durante largo tiempo). A continuación vamos a revisar las definiciones más comunes; para el lector interesado daremos referencias a los trabajos que profundizan más en el concepto de función tonal. La definición más operativa y a la vez menos ambigua la hemos encontrado en el libro en línea Open Music Theory1, que es la base de un proyecto pedagógico basado fuertemente en el aprendizaje por indagación implementado con clase invertida y discusiones en clase. Este proyecto fue iniciado por un grupo de profesores de música formado por Kris Shaffer, Bryn Hughes y Brian Moseley. Esta definición tiene en cuenta la historia del acorde, esto es, su pasado —los acordes que lo precedieron —, el presente —las notas que forman el acorde y el orden en que se presentan —, y el futuro —las notas que suelen suceder a este acorde—. Las notas que siguen a un acorde dependen fuertemente del estilo y un cierto conjunto de notas son más probables que sucedan a un acorde dado en un estilo que en otro. En vista de lo anterior, el concepto de función tonal se basa en tres principios: (1) Los acordes son conjuntos de grados de escala. (2) Cada grado de la escala tiene sus propias tendencias. (3) La combinación de tendencias de los grados de la escala de las notas de un acorde constituye la función del acorde. Vamos a examinar los conceptos incluidos en esta definición de función tonal para su mejor entendimiento. Fijada una escala (do mayor, mi frigio, etc.), el grado de la escala es la posición de una nota en la escala. Como es sabido, los grados de la escala en orden ascendente son: tónica (I), supertónica (II), mediante (III), subdominante (IV), dominante (V), superdominante (VI) (también submediante), y sensible (VII). Los grados de la escala se suelen designar con números romanos, como aparece en la figura de abajo. Figura 1: Los grados de la escala La ausencia de los conceptos raíz del acorde y calidad del acorde no es casualidad; estos conceptos se discutirán más adelante. Dado que la tendencia de un acorde es función del estilo, empezaremos estudiando la función tonal en la llamada práctica común (el periodo de la música clásica comprendido aproximadamente desde 1600 hasta el principio del siglo XX) y luego seguiremos con otros estilos (pop, rock, la práctica común extendida). Un estudio del estilo y sus leyes se puede acometer a partir del trabajo de Meyer, empezando por sus libro Emoción y significado de la música2 y Style and Music3. Meyer usa tres conceptos para explicar el estilo musical: ley, regla y estrategia. Las leyes son características de orden biológico y cognitivo y tienen una naturaleza universal (muchas de esas leyes se explican a través de la psicología de la forma); la ley de la continuación, por ejemplo, es un ejemplo de leyes. Las reglas son características de tipo cultural y están asociadas a una cultura y a un tiempo histórico particulares; por ejemplo, las reglas de conducción de voces es una regla. Por último, las estrategias son las características propias de la obra de un compositor dado; considérese el lenguaje armónico de Chopin en particular. La función tonal se puede considerar como una clasificación de los acordes en términos de su relación a un centro tonal o tónica. Estos dos últimos términos son equivalentes, pero hay alguna pequeña diferencia de matiz. Fijada una escala, la tónica es la primera nota de la escala. Nótese que la escala es una sucesión ordenada de notas y, por tanto, la tónica siempre está bien definida. La tónica implica estabilidad y resolución de las tensiones armónicas. Cuando hablamos de centro tonal esto comprende la noción de tónica, pero también se puede referir a una nota que se ha convertido en una referencia tonal (bien por medio de dominantes secundarias, cambios de modo, u otros mecanismos) y que no necesariamente tiene que ser la primera nota de la escala. Nosotros usaremos ambos términos de manera equivalente. La teoría de la función tonal surgió de la combinación de dos teorías previas sobre la armonía, la teoría de Hugo Riemann (la llamada teoría alemana) y la teoría de Schenker y otros (la llamada teoría vienesa). Hugo Riemann presentó su teoría en su libro Vereinfachte Harmonielehre en 1893. En él, define los conceptos de tónica, subdominante y dominante y comienza la clasificación de acordes según dicha función. En la teoría vienesa, fueron teóricos como Schenker, Sechter, o el propio Schoenberg quienes la construyeron. Esta teoría se basa en los grados de la escala y se centra en el contexto de las progresiones armónicas. La teoría moderna es una síntesis de ambas escuelas de pensamiento. 2. Las tres funciones tonales de la práctica común En la práctica común se han usado tradicionalmente tres funciones tonales: función de tónica, función de subdominante y función de dominante. Se les designa por T, SD y D, respectivamente. La función de subdominante también recibe el nombre de predominante. Los grados de la escala asociados a estas funciones son: Función de tónica: grados I, III y VI; las triadas formadas sobre estos grados contienen todas al grado I. Función de subdominante: grados II y IV; todas las triadas de esta función contienen el grado IV Función de dominante: grados V y VII. Fijando la escala de do mayor, por ejemplo, si ponemos los grados de la escala por terceras, veremos la relación entre dichos grados y las funciones tonales, como ilustra la figura siguiente: Figura 2: Las tres funciones tonales Una característica de la música clásica del periodo de la práctica común es que las notas del acorde determinan por sí solas la función del acorde, circunstancia que no es cierta en otros estilos musicales, como veremos más adelante en esta serie. En la música pop o rock, por ejemplo, el acorde sobre IV puede tener distintas funciones de acuerdo al contexto en que se encuentre. Otros autores, como Ian Quinn5, dan definiciones más profundas y operativas, que permiten clasificar la función tonal de una variedad más amplia de acordes en un número mayor de contextos. La definición de Quinn se basa en clasificar las notas de un acorde según tres categorías, que aquí llamaremos primarias, secundarias y disonancias (en el inglés original, son llamadas triggers, associates y dissonnace). La tabla siguiente muestra las notas asociadas a cada función tonal: FUNCIÓN NOTAS NOTAS NOTAS PRIMARIAS SECUNDARIAS DISONANTES Tónica Notas I y III Notas V y VI V si VI está presente y 7 Subdominante Notas IV y VI Notas I y II I si II está presente y 3 Dominante Notas V y VII Nota II IV y VI Tabla 1: Funciones tonales según Quinn5 Quinn introduce una excepción en el esquema anterior. Un acorde con los grados VI, I, III lo considera un tipo especial de acorde de tónica, al que llama tónica inestable (destabilized tonic). Para este acorde usa el símbolo especial Tx en lugar de simplemente T. Volveremos a esta cuestión más adelante en esta serie. There is one exception to this (for now): a chord with scale degrees 6, 1, and 3 is a special kind of tonic chord, called a destabilized tonic. Quinn uses the special functional label is Tx, rather than simply T, for this chord. En la siguiente figura vemos un esquema del propio Quinn en que se ilustra la clasificación de las notas por sus funciones tonales. Figura 3: Las funciones tonales definidas por Quinn5 En el próximo artículo veremos modelos de función tonal más avanzados y empezaremos a examinar sus primeros modelos matemáticos. Bibliografía [1] Bry Hughes et al. Harmonic function. http://openmusictheory.com/harmonicFunctions.html. web page. accedido el 1 de noviembre de 2021. url: https://viva.pressbooks.pub/openmusictheory. [2] Leonard Meyer. Emoción y significado de la música. Madrid: Alianza Música, 1956/2000. [3] Leonard Meyer. Style and Music. Nueva York: University of Chicago Press, 1997. [4] Walter Piston. Harmony. London: Gollancz, 1950. [5] Ian Quinn. Harmonic Function without Primary Triads. web page. Artículo presentado en la reunión anual de la Society for Music Theory en Boston. 2005.

Martes, 16 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico

183. Las ecuaciones matemáticas para adelgazar, ¿son fiables?

ABC, 15 de Noviembre de 2021 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 15 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

184. Egmont Colerus y sus matemáticas para todos

ABC, 8 de Noviembre de 2021 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 08 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

185. El clavecín ocular de Castel

El matemático y físico Louis Bertrand Castel (1688-1757) nació un 15 de noviembre. Charles Germain de Saint Aubin: Caricatura del «órgano ocular» de Louis-Bertrand Castel http://en.wikipedia.org/wiki/File:A_caricature_of_Louis-Bertrand_Castel%27s_%22ocular_organ%22.jpg Castel opinaba que hay una relación directa entre los siete colores del arco iris y las siete notas de la escala: pensaba que las vibraciones, además de sonido, producen color. Teorizó sobre el clavecín ocular, que mostraba colores en relación con las notas, incluso se pasó treinta 30 años intentando construirlo, sin éxito. Abbé Louis Bertrand Castel, «Musique oculaire». En «Edme-Gilles Guyot, Nouvelles récréations physiques et mathématiques», Paris, 1770 http://commons.wikimedia.org/wiki/File:Musique_Oculaire_Castel_1770.jpg El clavecín ocular de Castel incorporaba sobre un clavecín normal un marco con ventanas de cristal de diferentes colores. El matemático asignaba un color a cada nota de la escala cromática: Do = azul, Do# = celedón,  Re = verde, Re# = oliva, Mi = amarillo, Fa = león, Fa# = encarnado,  Sol = rojo, Sol# = carmesí, La = violeta, La# = ágata,  Si = gris; al presionar cada tecla, el color asociado parpadeaba. Extraído de «L’optique des couleurs : fondée sur les simples observations & tournée sur-tout à la pratique» (1940) El compositor Georg Philipp Telemann viajó a Francia para ver el instrumento, escribió varias piezas para él y un libro sobre el tema. Comparación de Castel (1740) del color espectral de Newton, con su explicación en términos de la interacción de la luz y la oscuridad. Castel escribió varias obras científicas, entre ellas Traité de physique sur la pesanteur universelle des corps (1724) –explica los fenómenos del universo a través de dos principios: la gravedad de los cuerpos que provocaba que todo tendiera al reposo y la actividad de los espíritus que creaba incesantemente el movimiento: es uno de los opositores principales de la teoría de la gravitación de Isaac Newton–, Mathématique universelle (1728), L’optique des couleurs : fondée sur les simples observations & tournée sur-tout à la pratique (1940) –compara el color espectral de Newton con su explicación en términos de la interacción de la luz y la oscuridad–, y un análisis crítico (1943) sobre la obra de Newton. Más información: Donald Stephen Schier, Louis Bertrand Castel, anti-Newtonian scientist, The Torch press, 1941. Color organ Maarten Franssen, The Ocular Harpsichord of Louis-Bertrand Castel. The Science and Aesthetics of an Eighteenth-Century Cause Célèbre, Tractrix 3, 15-77, 1991 Thomas L. Hankins, The Ocular Harpsichord of Louis-Bertrand Castel; Or, The Instrument That Wasn’t,  Osiris  9, 141-156, 1994 Jean-Marc Warszawski,  Le clavecin pour les yeux du père Castel, Musicologie, 1999 Maura McDonnell, Colour and Sound, 2002 Gilles Chapalain, Les instruments de «musiques des couleurs», 2003 Jean-Marc Warszawski,  Castel Louis-Bertrand. 1688-1757, Musicologie, 2009 Le clavecin oculaire, 2011 Luca Tanzini, Painted music, 2011 SolReSol y arquitectura, CUP, 2012 Françoise Roy-Gerboud, Le piano des Lumières : le grand oeuvre de Louis-Bertrand Castel, l’Harmattan, 2012 Rubén Díaz Caviedes, Cromopianos, órganos de color y cromatófonos: así fracasó la música para los ojos, JotDown, 2013 Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Lunes, 15 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico

186. Fórmulas y ecuaciones: cómo perderle el miedo al lenguaje de las matemáticas

ABC, 2 de Noviembre de 2021 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Martes, 02 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

187. Los límites matemáticos de la amistad, la enemistad y el Big Data

ABC, 25 de Octubre de 2021 CIENCIA - El ABCdario de las matemáticas Ernesto Estrada

Lunes, 25 de Octubre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

188. 165. Proyecto ESC3N4S MA/TEMÁTICAS

Nueva aportación de los profesores Marta Martín Sierra y Abel Martín Álvarez, en esta ocasión en formato fichas, para trabajar en el aula. La revista Making Of es una publicación centrada en la aplicación del cine en actividades de enseñanza-aprendizaje. Trata de ofrecer al profesorado información puntual sobre todos los recursos que sobre el cine se encuentran a su disposición en Internet. De una periodicidad de ocho números al año, incluye en todos una Guía Didáctica de 16 páginas sobre una película específica, junto con un buen número de fichas y sugerencias para desarrollar actividades en el aula a partir de los estrenos que se proyectan en los cines españoles. Editada por el Centro de Comunicación y Pedagogía, a partir del enlace se accede a una amplia información tanto de esta revista como de Comunicación y Pedagogía, y de Revista de Literatura. La revista dedicó un especial a las películas sobre matemáticas en el número doble 124-125, del que ya dimos en esta misma sección cumplida referencia.  Posteriormente, los profesores Abel Martín Álvarez y Marta Martín Sierra han publicado artículos en otros números: Homenaje a Jaime Escalante (revista nº 143; artículo de libre acceso que puede leerse a través del hipervínculo) y José María Sorando Muzás Las matemáticas escolares en el cine (revista nº 150) El pasado mes de octubre, de nuevo los profesores Marta Martín Sierra y Abel Martín Álvarez, comparten con nosotros unas fichas con actividades para trabajar diferentes temas relacionadas con diversas películas.  Marta y Abel mantienen el portal Mathsmovies, un compendio de referencias a las matemáticas en el cine (organizadas en diferentes salas, como si de la asistencia a un cine real se tratara), junto a exposiciones, material didáctico elaborado para llevar al aula, referencias a cursos y conferencias que han impartido, enlaces de interés, etc., y por supuesto, el tema en el que se han especializado: las matemáticas en los Simpson. Descripción de las fichas En esta revista inician una serie de varias entregas que irán apareciendo en números sucesivos de la publicación. En esta primera nos muestran ocho fichas, de libre acceso. Cada una de ellas está orientada a un curso concreto. También se indica cómo distribuir el tiempo para su realización, pensando siempre en la duración de una clase de 55 minutos, así como la descripción de los estándares de aprendizaje tratados. En todas aparece como objetivo motivador la investigación y creatividad de los alumnos, por lo que bastantes cuestiones plantean aspectos relacionados con los temas, pero no habituales en los libros de texto. Después, claramente separado de lo anterior, un pequeño resumen del argumento de la película. Se distinguen seis tipos diferentes de actividades, identificadas con un icono concreto cada una de ellas: Actividades teóricas, Actividades de investigación, Actividades para responder y/o resolver con lápiz y papel, Actividades para resolver con la ayuda de una calculadora/hoja de cálculo, Talleres de creatividad, Actividades de opinión. Se describen a continuación las aparecidas en esta revista: 1.- Los números reales (3º ESO a 1º Bachillerato) a partir de la película Smila, misterio en la nieve (Billie August, 1997).- El planteamiento es puramente conceptual en este caso (entender cuáles son los números reales y reconocerlos en situaciones cotidianas). 2.- Los números reales (3º ESO a 1º Bachillerato) a partir de la película El clan del oso cavernario (Michael Chapman, 1986).- Con un planteamiento nuevamente conceptual, en este caso las cuestiones van más orientadas a la relación de los números con la evolución de la especie humana y de otros animales. Es más antropológica que matemática. 3.- Polinomios. Fracciones algebraicas (3º ESO a 1º Bachillerato) a partir de la película Lecciones Inolvidables (Ramón Menéndez, 1988).- A partir de una escena de la película y lo que aparece parcialmente escrito en un encerado, se proponen factorizaciones de polinomios cuadráticos exclusivamente, tras haber comprobado diferentes maneras de expresar esas factorizaciones. 4.- Ecuaciones. Aplicaciones (2º ESO a 1º Bachillerato) a partir del episodio Las chicas solo quieren sumar (Temporada 17, Episodio 19) de la serie de animación Los Simpson.- En esta ocasión, la actividad está orientada a la educación no sexista de las matemáticas, echando un vistazo a la historia para comprobar cómo ha sido el comportamiento de la sociedad a este respecto. Posteriormente se propone la resolución de ecuaciones lineales y cuadráticas incompletas (similares a la de la escena del episodio) de manera mental, sin papel ni calculadora. 5.- Sistemas de ecuaciones. Aplicaciones (3º ESO a 1º Bachillerato) a partir de la película La habitación de Fermat (Piedahita y Sopeña, 2007).- Se plantean cuestiones a partir de un ejercicio propuesto en la película. De nuevo se incide no tanto en la resolución (aunque se proponen otro par de ellos similares) sino más bien en el contexto en que se describen este tipo de ejercicios. 6.- Inecuaciones y sistemas de inecuaciones (3º ESO a 1º Bachillerato) a partir de la película Una señal invisible (Marilyn Agrelo, 2010).- En realidad la ficha propuesta no trata de inecuaciones, sino exclusivamente de la comprensión de los símbolos menor y mayor que. Evidentemente es un primer paso antes de abordar el tema al completo que probablemente, como en las fichas anteriores, obedezca a un proceso de varias fichas para cada tema. Toda la actividad, salvo una última cuestión, está desarrollada en formato test. 7.- Funciones reales de variable real. Propiedades globales (3º ESO a 1º Bachillerato) a partir del episodio Homr (Temporada 12, Episodio 9) de la serie de animación Los Simpson.- En esta ocasión, la ficha está enfocada al reconocimiento de magnitudes directa e inversamente proporcionales. 8.- Tipos de funciones. Interpretación y representación (3º ESO a 1º Bachillerato) a partir de la película Cadena de favores (Mimi Leder, 2000).- A partir de los primeros valores, se trata de concluir que la gráfica que mejor se ajusta a ellos es una función exponencial. Una vez determinada, se pregunta por algunas de sus propiedades. Siete de estas ocho fichas son la primera de los diferentes temas, por lo que es difícil hacernos a la idea de cómo proseguirán desarrollándolos. En éstos el enfoque es totalmente conceptual e introductorio de lo que pudiera entenderse en un desarrollo usual de los temas planteados, potenciando más la creatividad que la comprensión de las técnicas y resultados matemáticos. Será necesario estar pendiente de cómo proseguirán las siguientes entregas para poder valorar en conjunto el proyecto. En todo caso siempre son de agradecer las nuevas propuestas y los distintos puntos de vista que traten de motivar a los alumnos y de dinamizar las clases, tendiendo además puentes a otras asignaturas que se han ido desligando (artificialmente, por cierto) progresivamente de lo que debe ser una enseñanza interdisciplinar y completa.

Miércoles, 03 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico

189. 198. (Noviembre 2021) Primos estrellados

Seguro que ya sabes lo que pasa cuando se dibujan 5 puntos equidistantes sobre una circunferencia y se une, empezando por uno de ellos, cada uno de los puntos con el siguiente, hasta volver al punto de partida. Cierto, se obtiene un pentágono regular. También sabrás que este procedimiento es completamente general: si se dibuja cualquier otra cantidad de puntos —digamos n— equidistantes sobre una circunferencia, al unir puntos consecutivos hasta volver al punto de partida se obtiene un polígono regular de n lados. En la siguiente figura se muestran los casos del pentágono y el heptágono regulares. Creo que no es difícil tampoco adivinar lo que ocurre cuando se unen los vértices del pentágono anterior no de forma consecutiva sino saltando un punto cada vez. Haz la prueba, numera los cinco puntos (por ejemplo, en el sentido de las agujas del reloj), traza un segmento uniendo el 1 con el 3 (saltando el 2), luego el 3 con el 5 (saltando el 4), luego el 5 con el 2 (saltando el 1), éste con el 4 y, por último, el 4 con el 1. Efectivamente, conseguirás la famosa estrella de cinco puntas o pentagrama, que fue símbolo de la escuela pitagórica y que oculta numerosas sorpresas matemáticas. Ahora bien, a diferencia del proceso de construcción de los polígonos regulares, si el número de puntos no es cinco, no se puede asegurar que la figura obtenida sea una estrella. Por ejemplo, con seis puntos, empieza trazando un segmento uniendo el 1 con el 3, luego el 3 con el 5 y el 5 con el 1; no hay forma de pasar por los puntos numerados con el 2, 4 ni 6. Ahora bien, si se empieza uniendo el punto 2 con el 4, el 4 con el 6 y el 6 con el 2, se consigue un segundo triángulo que, junto con el anterior, forman también una estrella, símbolo que la religíón judía conoce como sello de Salomón o estrella de David. La estrella pentagonal es un ejemplo de polígono estrellado (figura que se obtiene al unir de forma alterna, ya sea de dos en dos, de tres en tres, etc., los vértices de un polígono regular) y la estrella hexagonal es un ejemplo de falso polígono estrellado (figura que se obtiene superponiendo varios polígonos girados entre sí). En la figura se muestran las estrellas poligonales de cinco, seis, siete y ocho vértices, entre las cuales hay dos que son falsos polígonos estrellados. La pregunta que te surge ahora es: ¿cuántos lados debe tener un polígono para que se pueda dibujar una estrella poligonal y cuántas estrellas poligonales se pueden construir sobre un mismo polígono? La clave para dar con la respuesta es que, al unir los vértices, no se vuelva al punto de partida hasta que se hayan recorrido todos. Matemáticamente, esto significa que el número de lados y el salto entre vértice y vértice sean números primos entre sí. Por esta razón, sólo hay una estrella pentagonal pues 5 y 2 son primos entre sí (claro, también lo son 5 y 3 pero la figura resultante al saltar de dos en dos que de tres en tres es la misma) y no hay ninguna estrella hexagonal (vale, 6 y 5 son primos entre sí pero no sale ninguna estrella saltando de cinco en cinco pues es lo mismo que saltar de uno en uno, pero en sentido contrario). Como no quiero profundizar en estas interesantes y entretenidas cuestiones, citaré un par de referencias por si quieres aprender un poco más: el apartado "Polígonos estrellados" del blog Matemáticas en tu mundo de José María Sorando, ilustrado con gran variedad de originales fotografías, y el trabajo de Inmaculada Fernández Benito titulado "Polígonos estrellados, estrellas y formas estrelladas", presentado en la sexta reunión nacional de Estalmat (marzo de 2009). Te estarás preguntando qué relación tiene esta extensa introducción con el juego de magia que estás esperando. Para prolongar un poco más el misterio, hagamos primero el juego y, si nos queda tiempo (a mí) y paciencia (a ti), daremos las pertinentes justificaciones. Prepara siete cartas, del as al siete de cualquier palo y ordénalas de menor a mayor formando un paquete (el as es el que quedará a la vista, si las cartas están cara arriba). Quedará algo así como esta figura: Cierra la extensión de cartas y, manteniendo el paquete con las cartas cara abajo, reparte dos montones sobre la mesa, dejando alternativamente una carta en el montón de la izquierda y una carta en el montón de la derecha. Recoge los dos montones colocando uno de ellos sobre el otro. Ahora puedes cortar y completar el corte para no saber cuál es la posición de las cartas. Muy bien, gira cara arriba la carta superior y déjala nuevamente como carta superior. ¿Es el siete? Lo sabía. ¡Ah!, que no es el siete (lástima, habría sido la predicción perfecta). Pasa entonces de arriba abajo del paquete tantas cartas como indique dicho número (el as corresponde al uno, claro). Por ejemplo, si es un tres, pasa tres cartas de arriba abajo del paquete (el tres seguirá estando cara arriba pero las demás quedarán cara abajo). Gira ahora cara arriba la nueva carta superior y repite el proceso indicado en el paso anterior con este nuevo número. En este momento habrá dos cartas cara arriba y cinco cartas cara abajo. Vuelve a repetir el mismo proceso anterior hasta encontrar que la nueva carta superior ya está cara arriba. Podría apostar a que, en este momento, sólo queda una carta cara abajo. Además, sé incluso de qué carta se trata: ahora sí es el siete. Como podrás apreciar, el juego tiene un aire similar a los de tipo combinatorio que citamos en el número 193 (mayo de 2021) de este rincón, y seguro que sería muy del gusto del genio mágico John Conway. Para comprender el fundamento de este juego, debemos detenernos en el efecto que producen los dos pasos clave del proceso: el reparto inicial de los dos montones y la secuencia numérica de las cartas que se van girando. Con el primer reparto se han separado las cartas pares de las impares. El hecho de cortar el paquete puede alterar la posición de las cartas pero no el orden cíclico (si pensamos que las cartas están colocadas en los vértices de un heptágono regular, veremos las cartas pares de menor a mayor seguidas de las cartas impares, también de menor a mayor). En este momento, independientemente del valor de la primera carta, sólo hay una posible secuencia de cartas que se van girando cara arriba: 1 - 3 - 2 - 6 - 4 - 5. Hay que entender de nuevo que esta secuencia es cíclica, es decir, si la carta superior es, por ejemplo, el 5, la secuencia de cartas giradas es 5 - 1 - 3 - 2 - 6 - 4. Así pues, se recorren todas las cartas excepto el siete de modo que la predicción es infalible. Esto conduce inexorablemente a plantearse la siguiente pregunta: ¿el juego se puede realizar con cualquier cantidad de cartas? La respuesta inmediata es ¡NO! Haz la prueba con seis cartas. Recuerda el proceso: ordénalas de menor a mayor, reparte dos montones, reúnelos, corta y gira la carta superior: si es un seis, se acaba el juego. Si no, pasa de arriba abajo tantas cartas como indique su valor, repite el proceso. Verás que aparece una cara cara arriba antes de girar todas. El juego no funciona. ¿Y con cinco cartas? Ahora sí, la secuencia de cartas giradas es 1 - 3 - 4 - 2 (o cualquier reordenación cíclica de ésta). ¡Vaya!, resulta que con cinco y siete vértices se podía construir un polígono estrellado pero con seis no. ¿Tendrá algo que ver? Sigamos investigando, pero antes quiero citar el artículo donde se detallan las ideas fundamentales que he rescatado aquí: se trata del titulado "Les secrets du pentacle", escrito por Ludovic Simonet en el número 46-47 (año 2003) de la revista Hyper Cube, cuya portada se muestra en la imagen. En dicho artículo, el autor atribuye al mago George Sands (1920-2006), el mismo que inventó-descubrió-ideó-creó el principio del número primo que protagonizó el número 76 (octubre de 2010) de este rincón, el origen del método de adivinación descrito. Misteriosamente, los números primos también van a aparecer aquí. Este es el enfoque desarrollado por Ludovic Simonet (y quizá también por George Sands (ver comentarios finales)): Dibuja un número impar arbitrario de puntos equidistantes en una circunferencia, digamos 2n + 1; Escribe el número 1 junto a uno cualquiera de los puntos; Saltando n puntos en el sentido de las agujas del reloj, escribe el número 2 en el punto al que has llegado; Repite el paso anterior y escribe el número 3 en el nuevo punto al que has llegado; Sigue recorriendo los puntos marcados como se ha indicado y escribiendo números de forma consecutiva; Por último, traza un segmento uniendo el punto 1 con el 2, luego el 2 con el 3, el 3 con el 4 y así hasta volver al punto de partida. 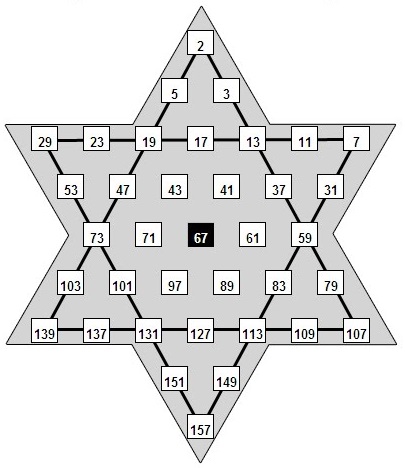¡Acabas de construir un polígono estrellado de 2n + 1 puntas! Has recorrido todos los puntos sin repetir ninguno de ellos debido a que los números 2n + 1 y n son primos entre sí, sea cual sea el valor de n (¿sabrías demostrar esta propiedad?). Además, si recorres los vértices de la estrella en el sentido de las agujas del reloj, aparecen los números impares, en orden creciente, y, a continuación, los números pares, también en orden creciente (precisamente, como se debían colocar para realizar el juego anterior). Esto significa que podíamos plantear el juego utilizando una estrella con los vértices numerados de esta forma en lugar de cartas, tachando los números a los que se llega después del recorrido por la estrella. El único punto que no quedará tachado sería siempre el número 2n + 1. En la figura puedes ver la disposición de los números y la forma de las estrellas con siete y nueve puntas. ¡Última sorpresa! Sería un poco aburrido que el juego se pudiera realizar con cualquier estrella que tenga un número impar de vértices. Ya hemos visto que funciona con 5 y 7 vértices pero no sale con 9, 11, 13 ni 15. Sí funciona con 17 (número que utiliza Ludovic Simonet en su artículo), con 19, 29, 31 y 43. ¿Cuál es el siguiente? ¿Sólo vale con algunos números primos? Como yo no sé las respuestas, planteo estas cuestiones a mi amigo Juan Carlos Ruiz de Arcaute —mago, matemático e informático, entre otras habilidades— y, como resultado de sus indagaciones, me devuelve la lista de los primeros valores, resumida en esta tabla: Pues sí, son todos primos, que podríamos bautizar como "primos estrellados" si no fuera porque ya estaban bautizados previamente (con otro nombre): se trata de la sucesión catalogada como A019334 en la "Enciclopedia de Sucesiones de Números Enteros", fundada en 1964 por el inagotable matemático Neil Sloane. Resulta que se trata de la sucesión de números primos con raíz primitiva 3, lo cual conduce a nuevas e inquietantes preguntas, como por ejemplo: ¿qué tienen que ver estos números con el proceso de conteo que se lleva a cabo en el juego descrito? Comentarios finales Un precursor del juego que aquí hemos mostrado es el titulado "Prime choice", ideado por George Sands y publicado por Karl Fulves en el número 8 de la revista The Chronicles (1978). En primer lugar nos hace aprender la frase mnemotécnica "A furry kitten fights seven to try at joinning six queens" (algo así como "Un gatito peludo pelea contra siete para tratar de unirse a seis reinas") como regla para recordar el orden As-4-K-10-5-7-2-3-8-J-9-6-Q. Por ejemplo, "furry" recuerda a "four", "fight" a "five", etc. Ahora basta tener preparadas trece cartas con esa ordenación, dar a elegir una carta del resto de la baraja, sustituirla por la K en la preparación anterior y dejar las trece cartas en las manos de tu asistente. Esta persona corta el paquete, completa el corte y gira cara arriba la carta superior. Ya sabes el resto: si es la carta elegida, perfecto; si no, pasa de arriba abajo tantas cartas como indica el valor de la carta girada (el as cuenta como 1, la J como 11 y la Q como 12), repite el proceso hasta que sólo quede una carta cara arriba. Será la elegida. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Martes, 02 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico

190. 77. (Noviembre 2021) Huellas de Gabrielle Émilie

(Marianne Loir. Portrait de Gabrielle Émilie. Museo de Bellas Artes. Burdeos) ¿Alguien duda de la contribución de la matemática a la felicidad? Quizá quien no se haya leído el Discours sur la bonheur de Gabrielle Émilie Le Tonnelier de Breteuil (1706-1749), que firmaba como Marquise de Châtelet. La sabiduría debe hacer siempre bien sus cálculos: porque quien dice sabio dice feliz, al menos en mi diccionario. Gabrielle Émilie es una figura fascinante. Un espíritu libre que defiende con sano orgullo su autonomía personal y su pensamiento: Juzgadme por mis propios méritos, o por la falta de ellos, pero no me consideréis como un mero apéndice de este gran general o de aquel renombrado estudioso, de tal estrella que relumbra en la corte de Francia o de tal autor famoso. Soy yo misma una persona completa, responsable sólo ante mí por todo cuanto soy, todo cuanto digo, todo cuanto hago. Puede ser que haya metafísicos y filósofos cuyo saber sea mayor que el mío, aunque no los he conocido. Sin embargo, ellos también no son más que débiles seres humanos, y tienen sus defectos; así que, cuando sumo el total de mis gracias, confieso que no soy inferior a nadie. Estudiar matemática no ha sido un camino de rosas para muchas mujeres. Desde la propia familia a las instituciones: todo eran obstáculos casi imposibles de salvar. La humanidad se ha mutilado a sí misma. Gabrielle Émilie lo tuvo algo más fácil: su padre la educó en igualdad y pertenecía a la clase privilegiada en una época de revolución intelectual que anticipaba la política. Del atractivo imperecedero de la brillante matemática francesa dan cuenta el estreno de dos dramas teatrales con su figura como protagonista en EEUU durante el 2010 y una opera representada en Lyon en el 2008. Un asteroide y un cráter de Venus también la distinguen. Las dos obras de teatro basadas en su vida son Legacy of Light de Karen Zacarías y Emilie: La Marquise Du Châtelet Defends Her Life Tonight de Lauren Gunderson. La ópera Émilie (2008), de Kaija Saariaho, trata de los últimos momentos de la vida de la marquesa de Châtelet, donde la soprano Karita Mattila hizo de Émilie, y la letra fue redactada por Amin Maalouf. (Karita Mattila haciendo de Émilie. Opera de Lyon) Lo anecdótico, más o menos verídico, ha llenado la historia popular y sigue teniendo atractivo didáctico. El manzano de Newton, la noche anterior al duelo mortal de Galois o el Eureka de un Arquímedes desnudo forman parte de la mitología. Émilie tiene también los suyos, uno es la lucha por acabar la traducción francesa de los Principia de Newton antes de una probable muerte por embarazo tardío: no sobrevivió al parto. La vida académica francesa estaba dominada a inicios del XVIII por la física cartesiana pero un pequeño grupo se quitó el provincianismo identitario y divulgó la obra de Newton. La polémica se resolvería científicamente: si la Tierra era un melón tendría razón Descartes y Newton si fuera sandía. Las expediciones a Laponia y Ecuador dieron el triunfo al inglés: la Tierra resultó achatada en los polos. La expedición a Ecuador fue una bendición para España: los jóvenes marinos Jorge Juan y Antonio de Ulloa se impregnaron de ciencia. Maupertuis, Voltaire y Émilie tomaron partido por Newton. Lo maravilloso de Émilie es que rápidamente se da cuenta de la mejora de Leibniz: el papel de la vis viva, la energía cinética, y su conservación frente a la cantidad de movimiento (impulso). Ironías de la historia: será Emmy Noether, otra insigne matemática, quien en el siglo XX formulará el importantísimo teorema de que cada ley de conservación física se corresponde con una simetría: la energía con el tiempo, el impulso con el espacio. Muchas colegas han hecho magníficas semblanzas de figura tan destacada. Nos limitamos modestamente a hacer un breve recorrido por los espacios que la recuerdan como sencillo homenaje. (Edición póstuma de la traducción de los Principia) Gabrielle Émilie en el Château de Breteuil Gabrielle Émilie Le Tonnelier de Breteuil es una figura imprescindible de la Ilustración. Si Moliere hubiera conocido a la Marquesa de Châtelet su sátira sobre Las mujeres sabias quizá hubiera sido muy distinta. El Château de Breteuil, situado en la zona residencial de Chevreuse, treinta kilómetros al suroeste de París, fue la casona familiar de los barones y después marqueses de Perrault. Como tantos castillos franceses, se pueden visitar tanto los jardines como la mansión que está llena de recuerdos de la brillante pensadora. Nos interesan especialmente el ambiente y las pinturas, originales y copias, de la pensadora en pleno trabajo matemático, sobre todo la conocida de Quentin de La Tour, o la copia de la realizada por Marianne Loir (original en Burdeos). Algunas escenas de la actividad científica se han reproducido con muñecas de cera. (Quentin de La Tour.  Gabrielle Émilie. Château de Breteuil) Existe un tercer gran retrato de Émilie, el realizado por Nicolas de Largillière y que pertenece a una colección privada. (Nicolas de Largillière. Gabrielle Émilie. Colección particular) Los tres retratos son muy similares, el compás en la mano derecha, esfera armilar en dos de ellos y globo terráqueo en el otro. La más convencional es la pintura de De Largillière pues Émilie parece Urania mirando el cielo. El más matemático es el de De La Tour pues la muestra en pleno trabajo. El más sensible, y el que más le hace honor, es el de Loir. Un compás y una flor definen la plenitud de quien podía traducir a Newton, la terrible y amoral Fábula de las abejas de Mandeville o escribir el Discurso sobre la felicidad. (Imagen de cera.  Gabrielle Émilie. Château de Breteuil) La marquesa de Châtelet en Burdeos La reapertura, tras años de obras, de las dos alas del Museo de Bellas Artes de Burdeos permite ya contemplar el delicioso Portrait de Gabrielle Émilie Le Tonnelier de Breteuil, Marquise du Châtelet (1749) realizado por la pintora Marianne Loir. Retrato menos conocido que el realizado por Maurice Quentin de La Tour pero que es, si cabe, mucho más interesante. Como hemos dicho La Tour pintó a Émilie sobre una mesa y un libro de matemáticas abierto, Marianne Loir conserva la esfera armilar y el compás, coloca los libros en el lateral, quita la mesa y pone una flor en la mano izquierda. La condición de mujer, a la vez sensible y sabía, es resaltada de forma primorosa. Émilie no es una rara avis sino una mujer plena. El retrato de Burdeos muestra las barreras intelectuales que estaba barriendo la Ilustración. Cirey sur Blaise: refugio de las artes Voltaire y Gabrielle Émilie Le Tonnelier de Breteuil protagonizaron en el Château de Cirey sur Blaise uno de los episodios más productivos para la extensión de la física newtoniana en el continente. La marquesa ofreció refugio a Voltaire en su castillo próximo a la frontera alemana y durante unos años (1734-1738) tuvieron allí su lugar de residencia. (Émilie como musa de Voltaire. Elémens de la philosophie de Newton. 1738) Cirey fue punto de encuentro de sabios y foco de correspondencia con los principales científicos del momento. Una inmensa biblioteca, hoy desaparecida, y un bello teatro, que se puede visitar, dan cuenta de la actividad de una pareja cuya respeto intelectual se mantuvo intacto tras su relación sentimental. Émilie fue clave para la edición de Voltaire de los Elémens de la philosophie de Newton (1738), por ello no extraña la dedicatoria: Minerva de Francia, inmortal Émilie, discípula de Newton y de la Verdad. Durante su estancia en Cirey, Voltaire diseñó la puerta principal de acceso, decorándola con motivos alegóricos a las ciencias y las artes. Así, en la parte derecha vemos una esfera armilar para la astronomía y un conjunto de regla, transportador y compás para la matemática. El interior tiene motivos marinos para reflejar el origen de la vida y la unidad del conocimiento. (Puerta diseñada por Voltaire. Château de Cirey sur Blaise)

Martes, 02 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico