191. Noviembre 2021: Raíces de un polinomio

1. Introducción. Suele ser una máxima, con la que mucha gente está de acuerdo, que para dominar de una forma aceptable un procedimiento en matemáticas, es necesario practicarlo a conciencia hasta poder repetirlo sin equivocaciones, salvo un despiste que puede ocurrirle a cualquiera, por mucha experiencia que se tenga. Esta insistencia en el procedimiento a veces se hace aburrido y tedioso sobre todo si son cálculos repetitivos que se realizan fuera de un contexto determinado. A veces, para poder resolver un problema, necesitamos aplicar un procedimiento que debemos haber asimilado previamente trabajándolo fuera de una situación concreta. Y eso se hace pesado. Especialmente eso suele ocurrir cuando nos encontramos en algunas parcelas de las matemáticas como el álgebra. Por ello, no es extraño que muchas personas hayan investigado como hacer ese trabajo rutinario más atractivo utilizando juegos. Desde grupos de profesores como el Grupo Cero de Valencia o el Azarquiel de Madrid, hasta profesores de forma individual, muchas personas han inventado o adaptado todo tipo de juegos para realizar esa labor repetitiva de una forma más lúdica y mucho más atractiva para un gran grupo del alumnado. En esta ocasión queremos plantear una actividad realizada en el aula y mostrar como con un mismo juego podemos cambiar las reglas para poder volver a jugar y practicar el mismo procedimiento de una forma algo distinta y, por tanto, no repetir el proceso anterior. La actividad tiene por objetivo trabajar las raíces de un polinomio, trabajando con su valor numérico. Como además vamos a trabajar con un tablero donde sólo aparecen ecuaciones de segundo grado, se puede complementar con la resolución de ecuaciones de segundo grado y además trabajar con la relación entre las raíces del polinomio y los coeficientes de ese polinomio. 2. Cuatro en raya. El juego inicial está previsto para dos jugadores. Como material necesitamos una moneda y un dado y 18 fichas para cada jugador, de colores distintos para diferencias las fichas de cada jugador. Además necesitaremos un tablero como el siguiente. Imagen 1: Tablero base de polinomios. 2.1. Reglas del juego. a) Cada jugador lanza el dado y comienza el que obtenga mayor puntuación. b) El jugador, en su turno, lanza la moneda y el dado y construye una raíz correspondiente al valor obtenido en el dado con el signo más o menos según que la moneda haya salido cara o cruz. A continuación, coloca una de sus fichas en una casilla donde haya un polinomio que tenga ese valor como raíz. c) Se fija un tiempo máximo, por ejemplo 30 segundos, para encontrar el polinomio y colocar la ficha. Si se agota el tiempo el jugador pierde su turno. d) Una vez colocada o acabado el margen de tiempo pasa el turno al otro jugador. e) No se pueden colocar una ficha donde ya existiese otra, tanto propia como del contrario. f) Si todos los polinomios que tienen raíz el número obtenido estuviesen ya ocupados, se da la opción de que el jugador en activo vuelva a realizar otro lanzamiento. g) Si un jugador se equivoca al colocar la ficha y su contrincante se da cuenta, se retira la ficha del tablero y su error se penaliza permitiendo al contrario realizar dos tiradas consecutivas. h) Gana el jugador que consigue colocar en primer lugar cuatro fichas consecutivas en horizontal, vertical o diagonal. i) Si tras ocupar todos los polinomios ninguno de los jugadores ha conseguido colocar cuatro de sus fichas en línea, el juego termina en tablas. 2.2. Complementos. Es interesante que el alumnado escriba en su cuaderno una tabla con el número que ha sustituido, la ecuación que ha elegido y los cálculos que ha realizado para confirmar que es cierto que es una raíz del polinomio. Esta tabla puede servir además para repasar y para utilizarla en sucesivos juegos, bien si se repite el proceso o se utilizan los restantes métodos que vamos a comentar. Hay variaciones que se pueden plantear en la metodología. Por ejemplo, si no hay moneda el mismo dado puede utilizarse para el signo. Se lanza primero el dado para obtener, por ejemplo, el número y después se vuelve a lanzar el dado de forma que si sale impar se le añade un signo menos al número o un signo más si sale par. Las primeras veces que se juega se pueden simplificar alguna de la reglas del juego, se puede dejar más tiempo para buscar la solución, no es conveniente más de un minuto pues se hace desesperante la espera. Se puede permitir colocar nuestra ficha donde ya hubiese una del contrario, aunque está opción permite que un jugador copie la jugada del contrario. Otra posibilidad es no hacer tan restrictiva la opción g y si se comete un error sólo se retira la ficha y se pierde el turno, no dos tiradas seguidas del contrario. Otra posibilidad es trabajar con ruletas. Si disponemos de copias de ruletas como la de la imagen, basta utilizar un bolígrafo, colocado en el centro, que sostenga a un clip semiabierto para, al girar el clip, poder obtener directamente el valor que necesitamos sustituir en el polinomio que elijamos. Imagen 2: Ruleta como alternativa al dado y moneda. Si estudiamos todos los polinomios que aparecen en el tablero podemos comprobar que todos ellos tienen dos soluciones comprendidas entre 1 y 6, una de ellas positiva y la otra negativa. Según el grupo de alumnos que tengamos podemos modificar los polinomios ampliándolos o reduciéndolos, reduciendo también las posibles soluciones que aparezcan. 3. La misma raíz. Podemos utilizar otra metodología en el juego trabajando con el mismo tablero y con la misma dinámica para colocar las fichas, únicamente cambiando el objetivo del juego. En esta segunda modalidad los jugadores van colocando sus fichas en los polinomios que han ido eligiendo por tener como raíz el valor que les ha salido con el dado y la moneda. La única diferencia es que el objetivo del juego es conseguir cuatro polinomios que tengan una raíz en común. Por ejemplo, un jugador obtiene los siguientes valores y selecciona los siguientes polinomios: Valor a sustituir Ecuación elegida 5 x² – 4x – 5 3 x² – 2x – 3 –1 x² – 1 2 x² – x – 2 El jugador gana pues sus cuatro polinomios tienen como solución –1, aunque no sea el valor que ha sustituido para seleccionar la casilla correspondiente. Con este enfoque el alumnado tiene que ir controlando, no solamente el valor que sustituye sino, cuál es la otra raíz del polinomio. 4. De lado a lado. La siguiente propuesta es una versión de un juego que hemos utilizado en otras ocasiones y que llamamos “Atraviesa el panal”, aunque cambiando el sistema de obtener los valores. En este caso, no necesitamos moneda ni dado sino únicamente el tablero ampliado con una regleta de valores. Cada jugador tendrá una serie de fichas de distinto color. El tablero será de la forma: Imagen 3: Tablero con regleta de valores. El objetivo del juego es conseguir una línea continua de fichas propias que conecten los dos lados paralelos que elijamos. Las fichas que forman esa línea pueden estar en casillas que sean consecutivas bien horizontal, vertical o diagonalmente. 4.1. Reglas del juego. a) Se sortea quien será el que comience a jugar. b) El primer jugador elije los valores positivos o los negativos y coloca una de sus fichas en uno de esos valores. El contrincante colocará una de las suyas en uno de los valores con distinto signo que el primer jugador. c) El primer jugador elegirá también si quiere conectar las líneas superior o inferior o bien la izquierda con la derecha, quedando la opción no elegida para el segundo jugador. d) El que comienza el juego, busca el polinomio que tenga como raíces las dos elegidas, tanto por él como por el contrario, y si su casilla está libre, coloca una de sus fichas en la casilla correspondiente. e) El segundo jugador, y a partir de él cada jugador en su turno, puede cambiar de sitio en la regleta la ficha propia, nunca la del contrario, y de nuevo busca el polinomio que tenga esos dos valores como raíces y coloca una ficha, si puede. f) Gana el primer jugador que consigue unir los dos extremos que le corresponden mediante una línea continua. 4.2. Complementos. Si nos fijamos en la imagen, el jugador con las fichas verdes gana la partida porque consigue unir sus dos extremos, en este caso los laterales, mediante una línea continua de fichas. Imagen 4: Gana el jugador de fichas verdes. 5. Para terminar. Los juegos que hemos visto suelen son atractivos pues son rápidos de realizar y permiten trabajar varias partidas en una clase. Antes de los dos últimos puede ser interesante estudiar las distintas soluciones de los polinomios, cuya pareja de raíces no se repite nunca, pues lógicamente no hay ningún polinomio repetido. También suele ayudarles en el juego el estudiar qué relación hay entre los coeficientes del polinomio y las dos raíces que tienen, por ejemplo, saber que el producto de las dos raíces es el término independiente, pues eso les ayuda a buscar más rápidamente cuál es el polinomio que les interesa. Volviendo a retomar el hilo inicial, con estas actividades sólo hemos pretendido que los alumnos practiquen el valor numérico de un polinomio y sepan encontrar sus raíces de una forma más atractiva, pues el plantearlo en forma de juego hace, con el objetivo de ganar al contrario, realicen más operaciones que planteadas de otra forma.

Lunes, 01 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico

192. 119. (Octubre 2021) Grafos Parsimónicos para los Tricordos y Tetracordos más Comunes

Una vez más tengo el placer de contar como autor invitado a Luis Nuño, catedrático de universidad en la Universidad Politécnica de Valencia y autor de la Rueda Armónica, página web que presenta herramientas para el aprendizaje de la teoría de la música con una base matemática. Esta vez nos trae un fascinante artículo sobre grafos parsimónicos en triadas y tetracordos. Estamos ante un artículo profundo y bello a la vez. Espero que los lectores de esta columna lo disfruten tanto como lo he hecho al leerlo. Paco Gómez Martín 1. Introducción La prestigiosa revista internacional Journal of Mathematics and Music ha publicado este año 2021 un número especial titulado “Pattern in Music” (Patrones en Música), que incluye ocho artículos. A continuación se va a explicar resumidamente uno de ellos, titulado “Parsimonious graphs of the most common trichords and tetrachords” (Nuño, 2021b). La referencia completa de este artículo se encuentra en la Sección 6. Con el objetivo de que esta exposición sea de la máxima utilidad y para una variedad de lectores lo más amplia posible, se ha simplificado sustancialmente la parte teórica, pero se ha mantenido íntegramente la parte práctica. Así mismo, los acordes se han representado mediante la notación inglesa y con los símbolos más comúnmente utilizados. Entre las estructuras que se repiten de manera recurrente en las composiciones musicales tenemos las denominadas “transformaciones parsimónicas”, las cuales han sido ampliamente utilizadas en épocas y estilos musicales tan diferentes como el período Clásico, el Romanticismo, la música Latina o el Jazz, siendo por tanto unos patrones musicales perfectamente establecidos. Su análisis puede llevarse a cabo mediante la “teoría neo-riemanniana”, que surgió en la década de los años 1980 para analizar ciertos pasajes cromáticos de determinados compositores del s. XIX y está todavía en proceso de evolución gracias a las aportaciones del álgebra y la geometría. Según Gollin (2005), esta teoría se caracteriza por tres elementos: grupos matemáticos de transformaciones, conducción parsimónica de las voces y sus representaciones gráficas. El ejemplo por excelencia lo constituyen el grupo “PLR” y el Tonnetz, aunque se limitan únicamente a las tríadas mayores y menores. P, L y R son las operaciones básicas “Paralelo”, “Cambio de Sensible” (en inglés, Leading-tone exchange) y “Relativo”, las cuales transforman, respectivamente, por ejemplo, C mayor en C menor, C mayor en E menor y C mayor en A menor; y viceversa. Como punto de partida podemos tomar una regla básica en Armonía para conectar unos acordes con otros, que es la “ley del camino más corto” (Schönberg 1983, p. 39, citando a Bruckner). Esto significa mantener las notas comunes y mover las demás según los mínimos intervalos posibles. A este respecto, Douthett y Steinbach (1998) establecen que dos acordes de la misma “cardinalidad” (es decir, con el mismo número de notas) guardan entre sí una relación “Pm,n” si uno de ellos puede transformarse en el otro manteniendo las notas comunes y, en cuanto a las demás, moviendo m notas un semitono y n notas un tono. Entonces, diremos que dicha relación es “parsimónica” si los valores de m y n son bajos, generalmente m + 2n ≤ 2. El caso más simple es, lógicamente, P1,0, que denominaremos “monosemitonal” (en inglés, single-semitonal). Además, Douthett y Steinbach (1998) aportan también varios grafos parsimónicos de especial relevancia, como el “Chicken-Wire Torus” (grafo dual del Tonnetz) y el “Cube Dance” para los tricordos “más uniformes” (es decir, en los que los intervalos entre cada dos notas consecutivas son similares) o el “Towers Torus” y el “Power Towers” para los tetracordos más uniformes. Veinte años antes, sin embargo, Waller (1978) ya publicó un toroide equivalente al Chicken-Wire, pero que, además, mostraba claramente su división en hexágonos, así como los ciclos PL, PR y – aunque algo más difíciles de visualizar – los LR. Estas y otras relaciones PLR compuestas han sido estudiadas exhaustivamente por Cohn (2012). Por su parte, Tymoczko (2006) hace un planteamiento diferente, desarrollando una teoría para representar los acordes de n notas en una especie de banda de Möbius generalizada, que llamaremos “n-orbifold”. Además, proporciona las figuras del 2-orbifold y parte del 3-orbifold, antes de “torcerlos y doblarlos” para obtener los verdaderos orbifolds. Callender, Quinn y Tymoczko (2008) aportan nuevas representaciones de este tipo, aunque, en la práctica, dada su especial complejidad, solo se suelen representar las regiones centrales de los orbifolds. En este trabajo se presentan unos nuevos grafos circulares cíclicos, que he denominado “Cíclopes”, que incluyen un mayor número de tricordos y tetracordos que las representaciones anteriores, donde estos están conectados entre sí mediante transformaciones monosemitonales. Así mismo, proporcionan una visión más amplia de las regiones centrales de los correspondientes orbifolds. Por consiguiente, permiten representar un mayor número de obras musicales de una forma práctica y pueden utilizarse tanto para el análisis musical como para la composición. Se asume que el lector está familiarizado con los “nombres de Forte” (Forte 1973) y las “clases de conjuntos”, también llamadas “clases de acordes”. En este trabajo, las clases de acordes “no inversionalmente simétricas” se dividen en dos “tipos de acordes” relacionados entre sí por “inversión”, llamados “a” y “b”, de acuerdo con las definiciones dadas por Nuño (2020a). Todos estos conceptos pueden, de forma alternativa, consultarse en español en Nuño (2020b) y Nuño (2021a). Por otra parte, este estudio trata también, en gran medida, sobre la “geometría de los acordes” (Tymoczko 2011) y las “transformaciones de los acordes más uniformes” (Cohn 2012), aunque los principales conceptos se explican también aquí. 2. Selección de los Tricordos y Tetracordos Tal como se explica en las anteriores referencias, hay 12 clases diferentes de acordes de 3 notas, los tricordos, 5 de los cuales son inversionalmente simétricos, mientras que cada uno de los restantes 7 se puede dividir en dos tipos de acordes relacionados por inversión, lo que hace un total de 19 tipos de acordes. Y hay 29 clases diferentes de acordes de 4 notas, los tetracordos, 15 de los cuales son inversionalmente simétricos; y, dividiendo en dos los restantes 14, obtenemos un total de 43 tipos de acordes. En ambos casos, el número de tipos de acordes es demasiado elevado como para poder relacionarlos en unos grafos que sean visualmente sencillos y de utilidad práctica. Por tanto, nos centraremos únicamente en los tricordos y tetracordos “más comunes”. Veamos cómo podemos seleccionarlos. En el período de la práctica común (aproximadamente, 1650-1900), las armonías se forman mediante superposición de terceras sobre los siete grados de las escalas mayor, menor armónica y menor melódica (veáse, por ejemplo, Schönberg 1983 o Piston 1988). De aquí resultan las 4 tríadas y los 7 acordes de séptima básicos, cuyos nombres de Forte son 3-10, 3-11a, 3-11b, 3-12 y 4-19a, 4-19b, 4-20, 4-26, 4-27a, 4-27b, 4-28, respectivamente. A estos hay que añadir los acordes de sexta aumentada 3-8a (italiana) y 4-25 (francesa). Todos estos tipos de acordes son, por tanto, predominantes en la música occidental. Para una cardinalidad dada (3 o 4 notas en nuestro caso), las clases de acordes están ordenadas desde la que tiene las notas lo más juntas posible, es decir, en secuencia cromática hasta la que las tiene separadas lo más uniformemente posible (tríadas aumentadas y acordes de séptima disminuida, según se trate de acordes de 3 o de 4 notas). Así, el criterio seguido aquí ha sido seleccionar “series completas de tipos de acordes”, desde los “más cromáticos” de los grupos anteriores (3-8 y 4-19) hasta los más uniformes (3-12 y 4-28). Tabla 1. Tipos de tricordos y tetracordos considerados aquí. Un superíndice en los nombres de Forte indica el grado de simetría transposicional, en caso de ser mayor que 1. Un asterisco (*) significa “omit 5” y un doble asterisco (**) “omit b3”. Los acordes mayores (M) se representan, normalmente, mediante su fundamental, sin ningún símbolo adicional. El símbolo “(9)” significa “add 9”, mientras que el símbolo “9” significa añadir tanto la séptima menor como la novena mayor. Las formas interválicas empiezan desde la fundamental. Tricordo Símbolo Forma Int. Tetracordo Símbolo Forma Int. 3-8a 7* 462 4-19a mΔ 3441 3-8b Ø** 642 4-19b Δ#5 4431 3-9 sus4 525 4-20 Δ 4341 3-10 dim 336 4-21 9* 2262 3-11a m 345 4-22a (9) 2235 3-11b M 435 4-22b m4 3225 3-123 + 444 4-23 7sus 5232 4-24 7#5 4422 4-252 7b5 4242 4-26 m7 3432 4-27a Ø 3342 4-27b 7 4332 4-284 O 3333 La Tabla 1 muestra esos tricordos y tetracordos con los símbolos empleados aquí para representarlos y sus “formas interválicas” (Nuño 2020a) empezando desde la fundamental. La forma interválica de un tipo de acorde es la secuencia de intervalos, en semitonos, entre cada dos notas adyacentes, incluyendo el intervalo entre la última nota y la primera; o cualquiera de sus permutaciones circulares. Los acordes añadidos a los grupos anteriores son los siguientes: 3-8b, 3-9, 4-21, 4-22a, 4-22b, 4-23 y 4-24, los cuales se interpretan, en ocasiones, como acordes cromáticos, incompletos o de paso. En otros estilos musicales, como el Pop, la música latina o el Jazz se utilizan con frecuencia todos los tipos de acordes de la tabla (véase, por ejemplo, el listado de acordes proporcionado por Sher 1991, p. iv). Por tanto, la selección realizada de esta manera contiene un número razonable de tipos de acordes, a la vez que incluye, en todo caso, los más relevantes. 3. Grafos Parsimónicos Las Figuras 1 y 2 son unos grafos circulares que he denominado 3-Cíclope y 4-Cíclope, que muestran, respectivamente, los tricordos y tetracordos de la Tabla 1 conectados mediante transformaciones monosemitonales. Así, en cada grafo se pasa de un acorde a otro cambiando una nota un semitono, el cual puede ser ascendente, si giramos en sentido horario, o descendente, si lo hacemos en sentido antihorario. Los números que hay en los extremos de las líneas que conectan los acordes indican las notas inicial y final referidas a las fundamentales de dichos acordes, donde 1, 3, 4 y 5 representan intervalos justos o mayores, que pueden alterarse mediante # y b, mientras que las séptimas mayores, menores y disminuidas se representan mediante Δ, 7 y d7, respectivamente. Haciendo la analogía con la carátula de un reloj, cada acorde se ha colocado en una “zona”, que viene definida por “la suma de sus notas”, módulo 12 (Cohn 2012, p. 102). Así, por ejemplo, el acorde de C mayor está en la zona 0 + 4 + 7 = 11 del 3-Cíclope y el acorde BØ en la zona 11 + 2 + 5 + 9 = 27 = 3 (módulo 12) del 4-Cíclope. De esta manera, si se sube un semitono una nota de un acorde, pasamos a la siguiente zona girando en sentido horario. Además, esto hace que, en el 3-Cíclope, los tricordos del mismo tipo cuyas fundamentales están a distancia de 4 semitonos estén situados en la misma zona. Y lo mismo ocurre en el 4-Cíclope con los tetracordos del mismo tipo cuyas fundamentales están a distancia de 3 semitonos. Por otra parte, los acordes que tienen un grado de simetría transposicional “s” mayor que uno tienen, lógicamente, conexiones múltiples a acordes del mismo tipo. Este es el caso de las tríadas aumentadas (s = 3), los acordes de sexta aumentada francesa (s = 2) y los acordes de séptima disminuida (s = 4). Entre los grafos parsimónicos desarrollados hasta la fecha cabe destacar, para el caso de los tricordos, el “Cube Dance” de Douthett y Steinbach (1998), que muestra las transformaciones monosemitonales entre las tríadas aumentada (3-12), menor (3-11a) y mayor (3-11b), el cual contiene solo un tipo de acorde por zona. Tymoczko (2011, p. 105) representa estos mismos acordes en un cubo. Pero con anterioridad a ambos tenemos el Tonnetz, que es una representación de los acordes mayores y menores conectados mediante transformaciones PLR. Por su parte, el 3-Cíclope puede considerarse como un Cube Dance o un Tonnetz “de orden superior”, ya que incluye también los tipos de acordes 3-8 a 3-10. En total, contiene 7 tipos de acordes frente a los 3 del Cube Dance o los 2 del Tonnetz. Además, en él se visualizan claramente las transformaciones básicas PLR: P y L son líneas “oblicuas” con respecto a las circunferencias centradas en el grafo, y R son líneas que “atraviesan” las tríadas aumentadas, entrando y saliendo por la misma letra (“a”, “b” o “c”). Simbólicamente, P = /, L = \ y R = ^. Figura 1. El 3-Cíclope, con los tricordos considerados en la Tabla 1. Con respecto a los grafos parsimónicos para los tetracordos tenemos el “Power Towers” de Douthett y Steinbach (1998), que muestra las transformaciones monosemitonales entre los acordes disminuido (4-28), semidisminuido (4-27a), de séptima de dominante (4-27b) y menor con séptima (4-26), el cual contiene también solo un tipo de acorde por zona. Cannas (2018) añade a ellos los acordes mayores con séptima mayor (4-20), obteniendo el “Clover graph”. En cambio, tanto el “4-Cube Trio” de Douthett (Cohn 2012, p. 158), como la representación de Tymoczko en el 4-orbifold (2011, p. 106), lo que añaden son los acordes de sexta aumentada francesa (4-25), completando de esta manera un hipercubo en cuatro dimensiones o “teseracto” (tipos de acordes 4-25 a 4-28). Por su parte, el 4-Cíclope puede considerarse como un 4-Cube Trio “de orden superior”, ya que incluye también los tipos de acordes 4-19 a 4-24. En total, contiene 13 tipos de acordes frente a los 5 del 4-Cube Trio o el Clover graph, un número bastante alto que hace que este grafo sea más complejo que el 3-Cíclope. Figura 2. El 4-Cíclope, con los tetracordos considerados en la Tabla 1. 4. Patrones de Acordes Tanto el 3-Cíclope como el 4-Cíclope son especialmente adecuados para representar ciertos patrones de acordes que aparecen en determinadas composiciones musicales, los cuales se indican en la Tabla 2. Estos patrones también pueden representarse en el Tonnetz, pero solo hasta cierto punto, ya que este solo contiene las tríadas menores (3-11a) y mayores (3-11b); y, cuando se utilizan acordes de séptima de la clase 4-27, lo normal es reducirlos eliminando la séptima en los acordes “7” y la tónica en los acordes “Ø”. Cohn (2012) y Tymoczko (2011) analizan muchos ejemplos de este tipo, pero incluyen también las tríadas aumentadas (3-12); y, con respecto a los tetracordos, ambos consideran los cinco tipos más uniformes (4-25 a 4-28). Sin embargo, el 3- y el 4-Cíclope incluyen más del doble de tipos de acordes (3-8 a 3-12 y 4-19 a 4-28, respectivamente), por lo que permiten analizar un mayor número de piezas musicales, así como obtener unas representaciones más simples y compactas. Tabla 2. Patrones de acordes idóneos para ser representados en el 3- y el 4-Cíclope.   3-Cíclope   4-Cíclope     Progresiones Parsimónicas de Tricordos   Progresiones Parsimónicas de Tetracordos     Mismos Tipos de Tricordos a distancia de tercera mayor   Mismos Tipos de Tricordos a distancia de tercera menor   Consideremos, en primer lugar, varios ejemplos basados en tricordos a distancia de tercera mayor, los cuales están situados en la misma zona del 3-Cíclope, y que incluyen también progresiones parsimónicas. En cuanto a los acordes “7” y “Ø”, consideraremos sus formas incompletas, “7*” y “Ø**”, que son mejores aproximaciones a los acordes reales que las utilizadas en el Tonnetz y, lo que es muy ventajoso, conducen a representaciones mucho más compactas. Comencemos por la Sonata para Violín y Piano en Fa mayor, Op. 24 de Beethoven. Las armonías en el segundo movimiento, compases 38-54, son las siguientes:         donde cada acorde o cada pareja de acordes unidos por un guión dura un compás y el símbolo “%” significa repetir el compás anterior. Los acordes relacionados con una misma tríada consonante se han agrupado mediante llaves. Esta progresión de acordes se ha representado en la Figura 3 en el 3-Cíclope, donde el acorde inicial se ha marcado de manera especial. Los tres acordes menores (Bbm, F#m, Dm) están a distancia de tercera mayor descendente, al igual que los tres acordes mayores relacionados con ellos mediante operaciones L y P (Gb, D, Bb). Estos últimos se afirman mediante cadencias con acordes de séptima de dominante y de subdominante, estando cada uno de estos tipos de acordes situados en una misma zona. Debido a la utilización de los acordes “7” en su forma incompleta, es decir, “7*”, el resultado es muy compacto y solo ocupa tres zonas cercanas entre sí: 4, 5 y 8. Si hubiéramos usado los acordes “7” sin la séptima, como se hace en el Tonnetz, entonces estarían localizados en la zona 2 de la Figura 1. En cuanto a sus formas completas con 4 notas, estarían situadas en zonas diferentes (1, 5, 9) de la Figura 2, dejando de estar agrupados. Analicemos ahora la Consolación en Re bemol mayor, Op. 102, No. 3 de Liszt, compases 23-43, cuyas armonías son         donde algunos acordes se tocan sobre una nota pedal, lo cual se representa mediante una barra seguida de la nota pedal. Esta progresión de acordes se ha representado en la Figura 4 en el 3-Cíclope (sin los pedales) y se puede comparar con Cohn (2012, p. 187), quien aporta, además, una animación Web. Ahora los tres acordes mayores (Db, F, A) están a distancia de tercera mayor, pero ascendente, y solo hay dos acordes menores (Fm, Am) relacionados con ellos mediante operaciones L y P, los cuales se afirman mediante cadencias más largas. Hay, además, un acorde “Ø”, cuya forma incompleta (es decir, Ø**), junto con las de los acordes “7” (es decir, 7*), dan lugar a una representación muy compacta, que se extiende únicamente sobre dos zonas consecutivas (1 y 2). De hecho, el 3-Cíclope es también especialmente adecuado para representar las cadencias V7–I(m) y IIØ–V7–I(m), con acordes tónicos mayores o menores. En particular, el tema de Jazz “Giant Steps” de Coltrane (Sher 1991) está estrechamente relacionado con esto, ya que consta únicamente de cadencias V7–IΔ y IIm7–V7–IΔ a distancia de tercera mayor.   Figura 3. Beethoven, Sonata para Violín y Piano en Fa mayor, Op. 24, segundo movimiento, compases 38-54.   Figura 4. Liszt, Consolación en Re bemol mayor, Op. 102, No. 3, compases 23-43. En cuanto a ejemplos con el 4-Cíclope, consideremos el Concierto para Piano No. 2 en Do menor, Op. 18 de Rachmaninoff. En el primer movimiento, compases 1-8, hay una progresión puramente monosemitonal, representada en la Figura 4 en el 4-Cíclope mediante una simple línea: [Fm(5)]  DbΔ  DØ Fm7  F7  Fm7  DØ DbΔ Aquí, una nota entre paréntesis significa añadir dicha nota al acorde. Así, Fm(5) es Fm con la quinta duplicada (C). Este acorde se ha escrito entre corchetes porque no aparece en el 4-Cíclope, pero se ha incluido en la figura para ilustrar mejor el ejemplo. Son precisamente esos dos C los que suben y bajan por semitonos a lo largo de la progresión, excepto al pasar por F7. Hay un pedal F–C (en triple octava), que pertenece a todas las armonías y que da robustez a toda la progresión. También hay otro pedal Ab (en doble octava), excepto en F7. El primer acorde, Fm(5), pasa a DØ a través de DbΔ en lugar de DO, posiblemente porque este último no incluye el pedal C y además contiene dos tritonos, mientras que DbΔ no contiene ninguno. El siguiente ejemplo es Indudable (Bossa Nova) de Nuño (2012), cuyos compases 19-27 constan de los siguientes acordes (algunos de los cuales, en realidad, contienen más tensiones) G#m7  C#Δ  Fm7  BbΔ  Dm7  G6  Bm7  E7sus  G#m7 Esta progresión de acordes se ha representado en la Figura 6 en el 4-Cíclope. Los cuatro acordes menores con séptima (G#m7, Fm7, Dm7, Bm7) están a distancia de tercera menor, por lo que están situados en la misma zona. En cuanto a los demás acordes, sus tónicas están también a distancia de tercera menor, pero en lugar de tener la secuencia homogénea C#Δ, BbΔ, GΔ, EΔ, los dos últimos acordes (marcados con línea discontinua en la Figura 6) se han sustituido por G6 (enarmónico de Em7) y E7sus, respectivamente. En todo caso, la representación es nuevamente simple y compacta.   Figura 5. Rachmaninoff, Concierto para Piano No. 2 en Do menor, Op. 18, primer movimiento, compases 1-8.   Figura 6. Nuño, Indudable (Bossa Nova), compases 19-27. Como último ejemplo tomaremos el Preludio en Mi menor, Op. 28, No. 4 de Chopin, una de las piezas más interesantes analizadas por Tymoczko (2011, pp. 287-293) y Cohn (2012, pp. 160-166), los cuales aportan, además, animaciones Web. La figura 7 es una partitura simplificada con los compases 1-12. Figura 7. Chopin, Preludio en Mi menor, Op. 28, No. 4, compases 1-8. Melodía y estructura armónica. Figura 8. Chopin, Preludio en Mi menor, Op. 28, No. 4, compases 1-8. Armonías de las tres voces inferiores. Como se verá, esta composición se entiende mejor analizando primero las armonías de las tres voces inferiores, representadas en la Figura 8 en el 3-Cíclope, las cuales pasan por todos los tipos de tricordos considerados en este grafo, excepto las tríadas aumentadas (¿quizás son demasiado disonantes?). Chopin incluye, además, los tipos de acordes “m7*” (3-7a) y “Δ*” (3-4a), definidos por las formas interválicas y , que son los acordes tónicos de séptima incompletos de las tonalidades menor natural y mayor, respectivamente. Desde el segundo acorde (F#m7*), las tres voces inferiores realizan estrictamente una progresión monosemitonal (P1,0) descendente, que cubre algo más de una vuelta completa en el grafo. Después, se utilizan otras transformaciones parsimónicas para terminar la frase, las cuales se indican en la partitura. Figura 9. Chopin, Preludio en Mi menor, Op. 28, No. 4, compases 1-8. Armonías completas. Por su parte, la austera melodía describe también una línea descendente, B–A–G#–F#, que completa las armonías y conduce a una representación más compleja en el 4-Cíclope (Figura 9). Aparte de los acordes considerados en este grafo, Chopin también incluye el “(b9)” (4-18a) y el “Δb5” (4-16a), definidos por y , respectivamente. 5. Conclusiones Se han presentado dos nuevos grafos, denominados Cíclopes, que relacionan los tricordos y tetracordos más comunes mediante transformaciones monosemitonales. Ambos incluyen más del doble de tipos de acordes que los grafos publicados hasta la actualidad, por lo que permiten analizar un repertorio más extenso de forma práctica. Estos grafos son especialmente adecuados para representar progresiones de acordes parsimónicas, tricordos a distancia de tercera mayor y tetracordos a distancia de tercera menor, así como las cadencias V7–I(m) y IIØ–V7–I(m), con acordes tónicos mayores o menores. En todos estos casos, los resultados que se obtienen son simples y compactos, lo que nos permite visualizar claramente las relaciones entre los acordes involucrados y entender mejor los patrones de composición utilizados, a la vez que constituyen un excelente recurso mnemotécnico. Por todo ello, podemos concluir que estos grafos son unas herramientas de gran utilidad tanto para el análisis musical como para la composición. 6. Referencias Callender, Clifton, Ian Quinn, and Dmitri Tymoczko. 2008. “Generalized Voice-Leading Spaces.” Science 320 (5874): 346–348. Cannas, Sonia. 2018. “Geometric Representation and Algebraic Formalization of Musical Structures.” Ph.D. dissertation, Université de Strasbourg and Università degli Studi di Pavia e di Milano-Bicocca. Cohn, Richard. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. New York: Oxford University Press. Douthett, Jack, and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42 (2): 241–263. Forte, Allen. 1973. The Structure of Atonal Music. New Haven: Yale University Press. Gollin, Edward. 2005. “Neo-Riemannian Theory.” Zeitschrift der Gesellschaft für Musiktheorie (ZGMTH) 2 (2–3): 153–155. Nuño, Luis. 2012. Puesta de Sol. Vol. 1. Madrid: Acordes Concert, S.L. Nuño, Luis. 2020a. “A Detailed List and a Periodic Table of Set Classes.” Journal of Mathematics and Music 1–21. https://doi.org/10.1080/17459737.2020.1775902 Nuño, Luis. 2020b. “La Tabla Periódica Musical (1/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 111. Diciembre 2020. http://www.divulgamat.net/divulgamat15/index.php?option=com_alphacontent&section=11&category=67&Itemid=67 Nuño, Luis. 2021a. “La Tabla Periódica Musical (2/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 112. Enero 2021. http://www.divulgamat.net/divulgamat15/index.php?option=com_alphacontent&section=11&category=67&Itemid=67 Nuño, Luis. 2021b. “Parsimonious Graphs for the Most Common Trichords and Tetrachords.” Journal of Mathematics and Music 15 (2): 125–139. https://doi.org/10.1080/17459737.2021.1923844 Piston, Walter. 1988. Harmony. 5th ed. New York: W. W. Norton and Co. Schönberg, Arnold. 1983. Theory of Harmony. 3rd ed. Berkeley, Calif.: University of California Press. Sher, Chuck. 1991. The New Real Book. Vol. 2. Petaluma, Calif.: Sher Music Co. Tymoczko, Dmitri. 2006. “The Geometry of Musical Chords.” Science 313 (5783): 72–74. Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press. Waller, Derek A. 1978. “Some Combinatorial Aspects of the Musical Chords.” The Mathematical Gazette 62 (419): 12–15.

Lunes, 11 de Octubre de 2021 | Imprimir | PDF |  Correo electrónico

193. Tape Melbourne

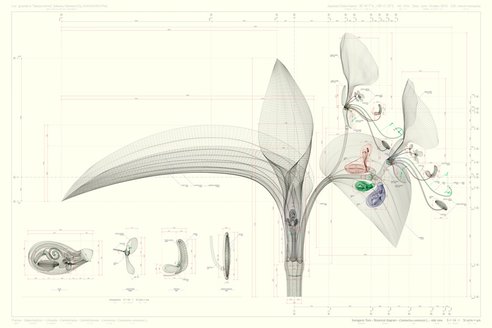
Numen / For Use es un equipo de diseñadores procedentes de Croacia y Austria que trabaja en los campos de la escenografía, el diseño industrial y espacial y el arte conceptual. Su último trabajo es Tape Melbourne, encargado por el principal centro cívico y cultural de Melbourne (Australia). La estructura es una cinta -en realidad una especial y tupida tela de araña- de 16 metros situada en la plaza Federation Square, un espacio público en el que se celebran muchos de los eventos culturales y artísticos de la ciudad. Es la mayor instalación de este tipo realizada hasta el momento. En este enlace pueden verse fotos y videos de la estructura y de su proceso de construcción. Plano de "Tape Melbourne" Un buen ejercicio de geometría… ¡calcular las curvaturas de esta preciosa cinta! Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Martes, 22 de Noviembre de 2011 | Imprimir | PDF |  Correo electrónico

194. Es imposible peinar una bola peluda (¿a tu perro?)

www.mundoperros.es/como-peinar-a-tu-perro/ En el artículo anterior (en Ilusiones y Paradojas) hacíamos un pequeño experimento con gatos -espero que nadie se ponga a hacer burradas con sus mascotas-, y ahora vamos a intentar peinar a un perro sin dejarle remolinos… Tampoco se trata de hacer lo que aparece en la imagen  -pobrecitos-, sino de hablar de un famoso teorema de matemáticas llamado teorema de la bola peluda: Todo campo de vectores tangente a la esfera S2 posee un punto singular. ¿Y que tiene que ver eso con peinar a tu perro? Bueno, vamos a explicar un poco los términos que aparecen en el enunciado del teorema. Un campo de vectores sobre la esfera S2 se dice tangente a la esfera, si para cada punto z en S2, X(z) es ortogonal a z. Podemos pensar un vector ortogonal como un pelo insertado en cada punto de la esfera y peinado. El teorema de la bola peluda -que se demuestra con técnicas de topología- dice que no es posible peinar una bola peluda -bueno, en realidad su superficie frontera, la esfera exterior- sin que aparezcan puntos singulares, es decir, remolinos en términos “peluqueros”. ¿Y qué es un perro más que -topológicamente- una bola? Corolario: No te obsesiones por peinar a tu perro de manera diferenciable, déjale algun remolino, estará igual de estupendo. Nota: El teorema de la bola peluda se cumple en cualquier esfera de grado par. Sin embargo, es posible peinar esferas peludas de dimensión impar -en S2n+1, X(x1, . . . x2n+2) = (−x2, x1,−x4, x3, . . . ,−x2n+2, x2n+1) es un campo de vectores tangente, que verifica la propiedad deseada- y toros peludos… Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Miércoles, 07 de Diciembre de 2011 | Imprimir | PDF |  Correo electrónico

195. El herbario inorgánico de Macoto Murayama

Botanical diagrams es una exhibición del artista -y miembro de la Japanese Association of Botanical Illustration- Macoto Murayama en la galería Frantic de Japón. Macoto Murayama En su web se describe como realiza su impresionante y preciso trabajo… … comenzando por la observación de la flora que desea representar. Secciona las plantas, las fotografía y dibuja bocetos de ellas. Posteriormente, se traslada al plano digital, utilizando diferentes herramientas de modelado 3D. Pueden verse en movimiento algunas de sus creaciones, como Chrysanthemum o C.warneri En sus propias palabras: Generalmente, una planta se considera como una forma orgánica. Sin embargo, es sólo uno de sus aspectos, porque junto a su forma orgánica, una planta posee un elemento contradictorio de estructura geométrica/mecánica. Resaltando esta última, se revela una forma diferente de la planta, y se encuentra una clase distinta de atractivo. Más información: Macoto Murayama’s incredible digital flower diagrams, BoingBoing Artist’s Luminous Botanical Diagrams Reveal Nature’s Inner Intelligence, Treehugger Macoto Murayama y la geometría botánica, Matematicalia Inorganic flora, Pink Tentacle Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Martes, 10 de Enero de 2012 | Imprimir | PDF |  Correo electrónico

196. El puente rodante de Paddington Basin

En 2004, la firma de arquitectos Heatherwick Studio instaló la estructura Rolling Bridge en Paddington Basin (Londres). http://www.heatherwick.com/rolling-bridge/ En lugar de diseñar un único elemento rígido y hacerlo móvil para permitir el tráfico a través del canal, el puente rodante se abre lentamente y se enrolla con delicadeza… … de modo que el  puente recto para peatones sobre el canal se transforma en una bella estructura circular. El puente tiene 12 metros de longitud, y consiste en ocho secciones de acero recubiertas de vigas de madera oscura para aportar calor y comodidad a las personas que lo atraviesan. En este video puedes ver como poco a poco cambia la curvatura del puente… una verdadera lección de geometría: Este mecano muestra con precisión el movimiento de la estructura mientras cambia de forma: Pueden verse más fotografías y videos y los planos del puente en la web de Heatherwick Studio. Visto en Kuriositas Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Jueves, 09 de Febrero de 2012 | Imprimir | PDF |  Correo electrónico

197. 132 5. Issey Miyake

Jun Mitani (Universidad deTsukuba) trabaja en la modelización -asistida por ordenador- de formas geométricas. A partir de un simple trozo de papel y con ayuda del programa informático por él diseñado, es capaz de construir bellas figuras tridimensionales. Jun Mitani Origami Artwork 2010/2011 Issey Miyake es un diseñador de moda, cuyas prendas de vestir se han definido como arquitectura del arte. ¿Y qué tienen que ver estas dos personas? En 2008, uno de los colaboradores del diseñador encontró navegando por la red los trabajos del ingeniero informático Jun Mitani. La firma Miyake solicitó inmediatamente la colaboración del científico para adaptar sus modelos informáticos en la creación de nuevos diseños en su laboratorio de ropa. ¿Cuál fue el resultado? El lanzamiento de la línea 132 5. Issey Miyake, en la que piezas de dimensión dos se transforman en formas geométricas estructuradas -faldas, pantalones y vestidos-. El programa creado por Jun Mitani diseña las formas tridimensionales de las prendas, que se modelan posteriormente en papel, añadiendo cortes y líneas de plegado hasta poder aplanarlas. 132 5. Issey Miyake ¿Y que significan esos números? El 1 alude a la única pieza de tela, el 3 a su forma tridimensional, el 2 muestra como esta estructura puede plegarse hasta obtener una pieza plana, y el 5 -precedido de un espacio- se refiere a la metamorfosis de las formas plegadas cuando una persona las lleva acomodadas sobre su cuerpo. Más información: Visto en La ligne “132 5 d’Issey Miyake” conjugue mathématiques et couture, Culturebox, France Télévisions Jun Mitani Origami Artwork 2009/2010 Jun Mitani Origami Artwork 2010/2011 Algunas fotografías y animaciones de trabajos de Jun Mitani Dana  Thomas, 132 5. ISSEY MIYAKE, Change Observer Nota: No es la primera vez que hablamos de vestidos matemáticos, ver  ¿Y si me visto “de Möbius”? y Vestidos… muy geométricos. PD: Esta entrada participa en la Edición 3.1 del Carnaval de Matemáticas cuyo blog anfitrión es Scientia potentia est. Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Lunes, 27 de Febrero de 2012 | Imprimir | PDF |  Correo electrónico

198. La demostración de tu inocencia… o de como las matemáticas te pueden ayudar a evitar multas

El 1 de abril de 2012, el físico Dmitri Krioukov (University of California, San Diego) subió al repositorio arXiv el artículo -de título bastante dramático- The Proof of Innocence. En el resumen del articulo de puede leer: Una manera de luchar contra tus multas de tráfico. El documento fue galardonado con un premio especial de 400 dólares, que el autor no tuvo que pagar al estado de California. 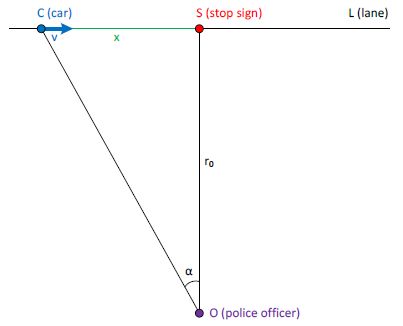Con ese título, ese resumen y ese día para subirlo… tenía “muchas papeletas” para ser una inocentada… En el artículo, Krioukov demuestra lo siguiente: Si un coche se detiene en una señal de STOP, un observador -por ejemplo, un agente de policía que se encuentra a una cierta distancia perpendicular a la trayectoria coche-, tendrá la impresión de que el coche no se detiene, si coinciden las tres circunstancias siguientes: el observador mide la velocidad angular del coche, no la lineal, el vehículo frena y posteriormente acelera relativamente rápido, y hay un corto período de tiempo en el que el observador pierde la visión del coche debido a un objeto externo -por ejemplo, otro coche- en el momento en que ambos se encuentran cerca de la señal de STOP. Parece que este argumento libró a Krioukov de pagar una multa, al recurrirla -argumentando del mismo modo que en el preprint- ante un juez… En un artículo en Physics Central, Krioukov reta a los lectores y lectoras a encontrar un fallo en el argumento… Visto en Boingboing. Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Jueves, 19 de Abril de 2012 | Imprimir | PDF |  Correo electrónico

199. Una máquina de Turing real

Un equipo de estudiantes de máster en el Departamento de Informática de la École Normale Supérieure de Lyon (Francia)  ha construido una máquina de Turing de manera completamente mecánica. Y lo han hecho usando únicamente elementos del juego de construcción LEGO™. La máquina de Turing fue inventada por Alan Turing en 1936 para dar una definición precisa del concepto de algoritmo: se trata de un concepto abstracto cuyo objetivo es definir una máquina -de la manera más elemental posible- capaz de implementar mecanismos de cálculo numéricos y simbólicos. Esta máquina real ha precisado más de 20.000 piezas de LEGO™: 32 cilindros, 1200 engranajes, 23 metros de ejes, 24 palancas y 50 metros de tubos, así como cientos de horas de trabajo de diseño y montaje. Más información: Florent Robic, A real Turing machine en The Alan Turing Year PD: Esta entrada participa en la Edición 3.141 del Carnaval de Matemáticas cuyo blog anfitrión es DesEquiLIBROS. Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Jueves, 26 de Abril de 2012 | Imprimir | PDF |  Correo electrónico

200. Conociendo Planilandia

A través del web cómic The Unspeakable Vault (of Doom) de François Launet podemos apreciar la diferencia entre el 2D y el 3D: http://www.goominet.com/unspeakable-vault/vault/98/ El cultista invoca a Yogzotot en la primera viñeta: ¡Yogzotot! Señor del tiempo y del espacio, ¡déjame visitar alguna dimensión extraña, no conocida por ningún hombre! Yogzotot le concede su deseo: ¡Petición concedida, humano! Pero Yogzotot le envía a Flatland -Planilandia- un mundo de dimensión dos… donde ciertamente, ningún ser humano ha vivido. Los habitantes de este mundo -cuadrados, triángulos, círculos- exclaman asombrados: ¡Oooh! Qué criatura tan extraña. Nota: Se puede descargar Planilandia de Edwin A. Abbott en este enlace. Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Viernes, 18 de Mayo de 2012 | Imprimir | PDF |  Correo electrónico