21. Noviembre 2022: Cuando los dados son las fichas

1. Juegos de mesa. Cuando a una persona no aficionada en su edad adulta a los juegos de mesa se le habla de los juegos de tablero y fichas, o de los juegos de estrategia suelen venir a su mente los juegos que jugaban en su niñez o juventud. Así piensan que los juegos de mesa siguen siendo los que ellos conocieron en su momento, como la oca o el parchís, las damas o el ajedrez, el backgammon, el Monopoly, el Cluedo y similares. Esas personas suelen pensar que en la actualidad no aparecen juegos nuevos en esa línea, pero no hay nada más alejado de la realidad. En la actualidad, a pesar de vivir en una era digital, donde estamos abducidos por la tecnología, existe un auténtico boom lúdico relacionado con los juegos de mesa. Todos los años aparecen juegos nuevos que luchan fieramente por conseguir el título de juego del año. Desde finales del siglo pasado hay una floreciente industria del juego de mesa, que inunda los certámenes que hay sobre el tema y se extiende por todo el mundo. Especialmente por toda Europa irradiando desde su foco principal en Alemania, que celebra desde hace años la Feria de Essen, la más importante del mercado lúdico de juegos, y donde se presentan las novedades de cada año. Son lo que suelen llamarse “eurogames” que son un tipo de juegos en los que el objetivo es conseguir y gestionar una serie de recursos, más que combatir y aniquilar al contrario. Uno de los primeros que tuvo un éxito apoteósico en todo el mundo fue “Los colonos de Catán”,creado por Klaus Tueber en la década de los noventa y que ha tenido multitud de ampliaciones. Este tipo de juegos son también llamados juegos de autor porque a diferencia de otros  más antiguos, en ellos se les da especial importancia a sus creadores. Uno de los más famosos es el alemán Reiner Knizia, doctor en Matemáticas con un master en Ciencias, que acapara premios en sus múltiples creaciones a las que se dedica en exclusiva desde 1997. Con lo anterior quería dejar en evidencia que en los juegos de mesa, podemos hablar de una era dorada y encontrar juegos muy actuales y novedosos. Suelen ser juegos más de estrategia que de azar, como ocurría con el parchís o la oca. Hoy vamos a ver una serie de juegos de estrategia creados en décadas recientes. Como ya se ha insistido en otros artículos de esta sección, los juegos de estrategia son interesantes en el ambiente matemático, ya que en ellos se ponen en acción los mismos procedimientos que se deben utilizar en la resolución de problemas, y estos juegos son una forma ideal de aprender y practicar esos procedimientos o heurísticos. Dentro de la clasificación de los actuales juegos de mesa, los que vamos a ver hoy se engloban dentro de un grupo llamados juegos abstractos, que son aquellos en los que no se recrea un ambiente similar al real, como pueden ser el Cluedo o el Risk. Es decir, las fichas y los tableros no representan ningún elemento que puede considerarse formando parte de un determinado universo, sea real o imaginario. Hoy se va a dedicar el artículo a una serie de juegos que tienen una característica muy especial. Son juegos con dados, pero con un enfoque que no es el habitual. Siempre que pensamos en un juego de mesa o de cálculo donde aparecen los dados, imaginamos que esos elementos sirven para dotar de aleatoriedad al movimiento de las fichas que se utilizan en el juego, o para obtener una serie de valores para operar con ellos, pero que vienen influidos por el azar que queda de manifiesto al hacer rodar esos dados. Sin embargo, los juegos que vamos a ver tienen la característica de que los dados no se utilizan para obtener aleatoriamente el número de casillas que deben avanzar las fichas, sino que los dados son las fichas que se mueven en el juego y sus valores sirven para conseguir puntos y además van variando los valores de las “fichas”, según se van moviendo por el tablero. En definitiva son juegos de estrategia en donde no interviene para nada el azar, a pesar de contar con dados. Antes de comenzar, hay que dejar claras unas características que deben poseer los dados para que no haya dificultades en algunos de los juegos. Hay dos aspectos que deben regir  la distribución de los dados que utilizaremos, la primera es que la suma de cada dos caras opuestas debe dar siempre siete, es decir, el opuesto al 1 debe ser el 6, el opuesto al 2 el 5 y el opuesto al 3 deber ser el valor 4. Esto suele ser uniforme en todos los dados cúbicos que se utilizan para juegos. Pero hay otro aspecto que puede cambiar y que puede afectar al juego. Para que la distribución sea correcta es necesario que en el vértice donde coincidan las caras correspondientes al 1, 2 y 3, estas caras estén situados en el sentido contrario a las agujas del reloj. No es raro encontrar dados que no cumplen esta regla, tal como vemos en la siguiente imagen. Imagen 1: Dados con sentido opuesto. El dado de la izquierda tiene la distribución correcta y suelen corresponder a dados europeos, mientras que el de la derecha tiene la orientación al revés y suele corresponder a países orientales. Hay que tener cuidado porque mezclarlos en un juego puede dar problemas. 2. Artaban: la rebelión de los dados[i]. Vamos a comenzar con el juego más reciente y que, por lo que conozco, no está comercializado. Este juego de dados fue creado en el año 2009 por el suizo Didier Müller[ii], ingeniero informático y profesor de matemáticas e informática en el Liceo cantonal de Porrentruy desde 1996. En varios lugares aparece este juego como una versión o sucedáneo del juego del ajedrez, algo que suele repetirse en otros juegos similares. Es un juego para dos jugadores que se juega sobre un tablero de 8x8. Puede ser un tablero de ajedrez o damas, aunque no tiene por qué haber diferencia de color entre unas casillas y otras. Cada jugador dispone de ocho dados, de colores diferentes para cada jugador. De esos ocho dados hay uno que es un poco más grande que los demás, que se considera el líder de su ejército y que tiene algunas características especiales. Si hay dificultad para encontrar dados de distinto tamaño lo que se suele hacer es utilizar un dado con una variación en el color respecto a los demás Aparte de lo anterior se debe disponer de una pantalla de cartón. Ésta se utiliza para colocarlo en el medio del tablero mientras los jugadores colocan sus dados para jugar, de forma que un jugador no pueda observar como coloca sus dados el contrario. Una vez colocado se retira esa pantalla. Los dados se colocan en la segunda fila del campo de cada jugador, dejando libre la primera fila y se deben de colocar de forma que la suma de las caras superiores sea exactamente 28. Imagen 2: Posible colocación inicial de los dados. El objetivo del juego es llevar la mayor cantidad posible de dados hasta la primera fila del campo contrario, la que ha quedado libre al colocar los dados. Para ello hay cuatro posibles movimientos. 2.1. Mover un dado. Lo primero es tener en cuenta que un dado nunca puede moverse hacia atrás, es decir hacia el inicio de su campo, ni en diagonal, siempre hacia adelante, a la izquierda o la derecha. Tampoco puede ocupar una casilla donde ya exista un dado. Los dados se mueven rotando un cuarto de vuelta sobre una de sus aristas de la cara inferior hacia una casilla adyacente. Una vez que han llegado a la línea final ya no pueden moverse. En la imagen vemos los tres posibles movimientos de un dado suponiendo que avanza hacia el dado superior derecha. Únicamente no puede girar hacia atrás. Imagen 3: Tres posibles resultados al mover el dado central. 2.2. Girar un dado. Se puede girar un dado sobre su eje vertical manteniéndolo en la misma casilla. El giro sería dar un cuarto de vuelta sobre sí mismo bien hacia la izquierda o la derecha. En éste movimiento la cara superior no cambia. En la imagen vemos los dos resultados como puede quedar el dado, siempre manteniéndose en la misma casilla. Imagen 4: Dos resultados posibles al girar el dado central. 2.3. Capturar un dado del contrario. Un dado puede capturar, tras moverse en su turno, a un dado del contrario que tenga una cifra inferior a la que muestra ese dado, y que esté en una casilla adyacente, recordando que nunca se puede capturar ni en diagonal ni hacia atrás. La forma de hacerlo es quitar el dado del contrario del tablero, y colocar el propio en su casilla en la misma posición que estaba en la de ataque. Si el dado que ataca es el líder del grupo, puede capturar a otro dado que tenga una cifra menor o igual que la del dado atacante. El dado líder puede ser capturado por cualquier dado del contrario, siempre que tenga mayor puntuación. En la imagen siguiente, donde la flecha negra indica el sentido de avance del dado, el dado oscuro captura el dado claro que está a su derecha. Si hubiese sido el dado líder hubiese podido capturar en su lugar el dado que se encontraba a su izquierda. Imagen 5: Capturar un dado del contrario. 2.4. Sacrificar un dado. A veces, es interesante acelerar el final del juego si ya tenemos colocados casi todos los dados en la línea de llegada, y no nos interesa que el contrario siga llevando dados a su línea final. Un dado se sacrifica saltando sobre un dado del contrario que tenga el mismo valor que el dado que salta. En este caso el dado atacante se elimina del tablero. La única restricción es que no puede sacrificarse al dado líder. El juego termina cuando uno de los jugadores no puede mover ningún dado, aunque el contrario aún pueda mover. Por ello, a veces es interesante el último movimiento que hemos comentado. Igual que en el ajedrez, en cualquier momento uno de los jugadores puede ofrecer tablas, que pueden ser aceptadas o no por el contrario. 2.5. Ganar la partida. Una vez que se acaba la partida, gana el jugador que tenga mayor valor en la suma de los puntos de sus dados que están en la última línea. Siempre se suma los valores de las caras superiores. En el caso de haber empate, gana quien tenga más dados en la última fila. Si aún así continúa el empate, gana el jugador que tenga más dados sobre el tablero. Si todo lo anterior está igual, se considera que la partida acaba en tablas. En las instrucciones originales del autor se da como posible variante que los dados pueden capturar también en diagonal, en cuyo caso, tal como él mismo indica, el juego es totalmente diferente. Las veces en que yo he propuesto el juego, he cambiado algunos aspectos que me han parecido modificables sin variarlo sustancialmente. Por ejemplo, no suelo jugar con el dado líder, pues aporta poco al juego para las dificultades que provoca tener que conseguir dados más grandes, o con mucha variedad de colores. En las primeras partidas, al menos, no suelo plantear la opción de sacrificar un dado, aunque si se juegan varias partidas, al final si se impone esa regla. Tampoco suelo utilizar la pantalla de cartón inicial, ya que hay que haber jugado mucho para que de un simple vistazo podamos programar nuestros dados, de una forma que vayan a contrarrestar la disposición del contrario El creador propone el juego a partir de los ocho años, pero si se va a jugar con personas de poca edad mi opinión es que es mejor comenzar con un tablero de 6x6 casillas y seis dados por jugador. En este caso es mucho más dinámico, pues se alcanza mucho más rápidamente la fila final. 3. Duelo cara a cara. El juego anterior no deja de ser una curiosidad, por el hecho de utilizar dados como fichas y aprovechar los puntos de las caras, en el caso anterior, para capturar al oponente. Sin embargo, no es un juego totalmente original, pues hay varios juegos que tienen la misma estructura de mover dados sobre un tablero, girando sobre las aristas de la base y según los números de las caras. El más antiguo que conozco recibe el nombre de Duell o también “Head to head”. Fue creado en 1975 por Geoffrey Hayes. Según la empresa que lo comercializaba en distintos países, el nombre variaba. Así se llamó Tactix en Alemania o Conquest en el Reino Unido. Fue comercializado por la empresa Parker Brothers, una empresa de juegos fundada en 1883, y que comercializó juegos tan conocidos como el Monopoly, el Cluedo, el Risk, Boogle, Scrabble, la Fuga de Colditz, etc… Imagen 6: Portada del juego Duell. A diferencia del anterior, en este juego los números de los dados no sirven para capturar, sino para indicar el número de casillas que se moverá en cada momento el dado. El juego Duell está pensado para dos jugadores, y se juega sobre un tablero de 8x9 casillas. Cada jugador dispone de nueve dados de diferente color, ocho de ellos normales y uno especial, llamado pieza clave, que tiene un punto en cada una de las caras. La distribución de los dados en cada campo, sigue la siguiente distribución: las caras superiores se colocan de forma simétrica con los números 5 1 2 6 O 6 2 1 5, donde O es la pieza clave. Todos los dados se colocan de forma que las caras con tres miren al propio jugador, y las caras con cuatro miren hacia dentro del tablero. La pieza clave siempre se coloca en el centro y ese lugar es importante, pues puede hacer ganar la partida. La distribución inicial es la que aparece en la siguiente imagen, sacada de las instrucciones del juego comercializado por la empresa Lakeside. Imagen 7: Distribución inicial de las fichas en el juego Duell. Cada jugador en su turno mueve una de sus “fichas” con las siguientes reglas. a) La pieza clave sólo puede avanzar una casilla en cada jugada. b) Un dado avanza en línea recta la cantidad de puntos que figure en su cara superior. La forma de avanzar es pasar a la casilla contigua rotando un cuarto de vuelta sobre la arista de la base. c) Se puede avanzar en cualquier dirección ortogonal, nunca en diagonal. Mientras se está en movimiento es posible cambiar la dirección de avance con un giro de 90º, pero sólo una vez. Dentro de un mismo movimiento no se puede volver hacia una casilla ya recorrida. d) No se puede pasar por encima de otra ficha, sea propia o del contrario. La forma de capturar una ficha del oponente es llegando a su casilla con el número exacto de movimientos que nos indicaba inicialmente nuestra ficha. La ficha capturada se elimina del tablero. El juego termina cuando la ficha clave del contrario es capturada, o cuando llegamos a colocar nuestra propia ficha clave en la casilla inicial de la ficha clave del contrario. La importancia del movimiento en este juego es que según el camino que recorramos para llegar a una determinada casilla, la posición en que queda el dado puede variar, con lo que la situación en la que queda para el siguiente movimiento cambia en función del valor que quede en la cara superior. Veamos un ejemplo, si movemos un dado cuya cara superior es un tres, podemos llegar a una misma casilla por dos caminos diferentes obteniendo en la cara superior valores muy diferentes. Imagen 8: Resultados según el camino seguido. Por ello, es interesante antes de comenzar a mover, estudiar qué valor nos interesa conseguir y donde colocar el dado. En la imagen anterior vemos lo que se puede obtener según el movimiento llegando a una determinada casilla, pero podemos obtener valores muy diversos según lo que nos interese para el siguiente movimiento. En la siguiente imagen tenemos todos los resultados posibles de mover un dado según los distintos caminos. Imagen 9: Todos los resultados posibles de mover tres casillas. En la imagen aparece la vista superior del dado y hacia donde se puede mover según las vistas laterales que estamos viendo del dado. Este juego suele ser más imprevisto que el anterior por la cantidad de jugadas posibles que puede tener un dado para moverse y, por tanto, capturar un dado del contrario. Conviene recalcar que el valor resultante del movimiento sólo sirve para el siguiente movimiento de esa ficha, mientras que podemos capturar un dado del contrario con cualquier valor de llegada. Para poder construir el juego basta conseguir 18 dados de dos colores diferentes, y a uno de ellos colocarle en cada cara una pegatina con un punto dibujado y ese dado será la ficha clave. 4. Cefalópodo[iii]. Vamos a ver ahora un juego que cambia la dinámica de los anteriores. Ahora los dados no parten de estar colocados en el tablero, sino que se van colocando, y no se mueven en él, simplemente se colocan mostrando distintos números según se capturen otras piezas. Además, en este juego se captura en una jugada piezas tanto propias como del contrario. Este juego lo creó en el año 2006 el californiano Mark Steere, especialista en diseñar juegos abstractos. En su página personal[iv] ofrece las reglas y a veces los tableros, de sus juegos con la única exigencia de no cambiarlos y citar su autoría. Muchos de esos juegos han sido programados y pueden jugarse en internet de forma on-line, algunos incluso descargando el juego en sí. En la página viene la lista de los juegos y los enlaces a las páginas que lo han programado y donde se pueden jugar. Este es un juego para dos jugadores. El tablero es una cuadrícula de 5x5 casillas y cada jugador debe tener 24 dados, de distinto color por jugador. Se comienza con el tablero limpio y se comienzan a colocar dados en cada turno. Una vez que el tablero esté completamente lleno de dados gana el jugador que tenga más dados sobre el tablero. Las dimensiones del tablero hace imposible que pueda haber tablas, pues siempre habrá un jugador que tenga al menos un dado puesto más que el contrario. Esta característica es muy habitual en los juegos abstractos de Mark Steere. La forma de colocar dados en el tablero y capturar piezas es la siguiente. 1) Si un jugador va a colocar un dado en una casilla que no permita capturas, debe colocar el dado con la cara superior mostrando el uno. En la siguiente imagen, el jugador con los dados blancos coloca su ficha en la casilla central inferior y como no puede capturar debe colocarlo con el valor de uno. Imagen 10: Colocar ficha sin captura. 2) Un jugador puede capturar si al colocar un dado en una casilla tiene en casillas adyacentes de forma ortogonal, no vale en diagonal, dados que sumen menos de siete. En ese caso, coloca su dado con un valor de la cara superior igual a la suma de los dados y retira los dados adyacentes del tablero. Esos dados pueden ser propios o del contrario. Los dados retirados se entregan a cada jugador, según su color, para que se puedan utilizar en sucesivas jugadas. Veamos algunos ejemplos de capturas. En la siguiente imagen, la ficha que se coloca en la casilla central inferior captura la ficha superior, y a su derecha y el dado debe mostrar la suma de los dos valores. Imagen 11: Ejemplo de captura. En el segundo ejemplo, la ficha que se coloca en el centro de la tercera columna captura las tres fichas que están alrededor. Imagen 12: Otro ejemplo de captura. A veces, aunque se coloque una ficha en una casilla que tenga otras fichas adyacentes en horizontal o vertical, no se pueden capturar si la suma de esos valores es superior a seis, como vemos en la siguiente imagen. Por eso, la ficha que se coloca nueva vuelve a mostrar el uno en su cara superior. Imagen 13: Jugada sin captura. Para terminar con el juego sólo comentar un detalle. Tal como está diseñado el juego puede tardar horas hasta completarse. Por ello, es conveniente jugar con tableros más pequeños, aunque el autor es bastante reacio a que se modifiquen sus reglas. En concreto, está en contra de jugar en tableros de 4x4, ya que en ellos se pierde la imposibilidad de empate. Mi consejo es comenzar con un tablero de 3x3, aunque se pierde bastante de la estrategia del juego, pero hay también la opción de jugar sobre un tablero de 3x5, que se ajusta más al juego original y es mucho más rápido. Como es de suponer, en cada juego los jugadores deben disponer de un número de dados igual al de casillas del tablero, o quizás uno menos. En la página de Super Duper Games[v], en la que hay muchos juegos para jugar en línea y donde hay que inscribirse, se puede encontrar distintas versiones del Cephalopod en concreto tableros de 5x5, 3x3 y 3x5. Además hay una versión tridimensional de 5x5x3 que ya es para los que se aficionen mucho al juego. 5. Unas posibilidades increíbles. Como me suele pasar a menudo, una vez que comienzo con algún juego que conozco y busco información en internet, para poder ofrecer enlaces y explicaciones en la red, me encuentro con que existen muchos juegos similares de los que no tenía noticia. Y esta vez no podía ser de otra forma. Existen una multitud de juegos donde las fichas son dados. Muchos de ellos se consideran variantes del ajedrez. Hay incluso una versión de ajedrez[vi] donde las fichas están sustituidas por dados de forma que el rey equivale al 6, la dama al 5, la torre corresponde al 4, el caballo es el 3, el alfil el 2 y los peones el 1. El movimiento de las piezas es el mismo que las del ajedrez. Hay otros juegos como el Cublino[vii] que tiene algunas reglas similares al Artaban que hemos visto, aunque es un poco anterior, del 2006, y está comercializado. Lo cierto es que el tema es mucho más amplio de lo que hemos podido recoger en estas páginas, por lo que ya “amenazamos” con dedicar alguna otra entrada a este tipo de juegos. Ya se verá.     Notas: [i] http://www.apprendre-en-ligne.net/jeux/artaban/ [ii] Su página web es http://www.apprendre-en-ligne.net/index.php [iii] En la lista de juegos abstractos del autor se pueden descargar el tablero, las instrucciones del juego y un ejecutable para jugar en el ordenador al cephalopod, en versiones Windows, mac y Linux. http://www.marksteeregames.com/MSG_abstract_games.html [iv] La página del autor http://www.marksteeregames.com/index.html [v] http://www.superdupergames.org/gameinfo.html?game=ceph [vi] Se puede jugar on-line en la dirección https://www.ajedrezeureka.com/ajedrez-con-dados/ [vii] https://boardgamegeek.com/boardgame/85022/cublino

Miércoles, 09 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico

22. 175. Los Oscars® de las matemáticas (y II)

Las matemáticas han motivado procedimientos que, una vez implementados informáticamente, han generado potentes herramientas gráficas que han posibilitado la creación de animaciones espectaculares, logrando no sólo el favor del público. Los premios no se han hecho esperar. En la reseña pasada recordamos que PIXAR fue el primer estudio en realizar una película íntegramente con CGI (Computer Generated Images), Toy Story (Toy Story, John Lasseter, EE. UU., 1995). Partiendo de unos guiones gráficos elaborados por dibujantes al estilo clásico, posteriormente se digitalizaron con el software Avid Media Composer. En promedio se emplearon tres horas para concretar cada una de las 1560 tomas que constituyen la edición definitiva del largometraje, para las que se utilizaron 400 modelos matemáticos que tuvieron que instalarse en cada ordenador. Esta comenzó con el diseño tridimensional de los personajes con el programa informático Modeling Environment (Menv, en siglas). Cada toma era trabajada eventualmente por ocho equipos diferentes. El diseño de cada personaje se realizaba creando una escultura a escala en arcilla, que era digitalizada después mediante el software adecuado (como Polhemus 3 Space Digitizer, por ejemplo, que facilita su manejo tridimensional). Posteriormente, se diseñaron y configuraron los controles de articulación y movimiento de los personajes, a partir de las grabaciones de voz de los actores del reparto. El vaquero Woody resultó ser el más complejo, empleándose 723 controles de movimiento, de los que 212 eran exclusivamente para su rostro y 58 adicionales para su boca. Para sincronizar las voces de los actores con las bocas de los personajes, y que casaran con las expresiones faciales los animadores emplearon una semana. La fase siguiente, el sombreado, utilizó los programas Amazon, Adobe Photoshop y Unwrap, este último desarrollado por los ingenieros de Pixar, mientras que los efectos de iluminación se produjeron de forma similar a un filme con imágenes reales. Finalmente se realizó la renderización y edición con ayuda de software de RenderMan, Avid Technology y Sun, respectivamente. En total, se invirtieron 800000 horas por máquina para producir la película, y un promedio de 2 a 15 horas para renderizar cada toma. El metraje final se envió a Skywalker Sound, en donde se mezclaron los efectos de sonido con la banda sonora. En opinión de su director, John Lasseter, “En la animación computarizada, es fácil lograr que las cosas se muevan, pero es el trabajo minucioso el que hace que parezca real. Cada hoja de césped tuvo que ser creada desde cero. Además, todo ese universo debe parecer realista, y para ello, las puertas tiene que aparecer con golpes y el suelo ha de verse desgastado.”​ Estas nuevas técnicas de animación no han sustituido otras más tradicionales (se siguen produciendo películas al modo tradicional, otras con plastilina y stop motion, etc.), pero sí han captado la atención de los estudios de animación, al punto de que raro es aquel que no los utiliza en alguna de sus producciones. La segunda película, según los historiadores, íntegramente realizada mediante CGI fue HormigaZ (AntZ, Eric Darnell y Tim Johnson, EE. UU., 1998), producida por otro estudio diferente, DreamWorks Animation. Tras el éxito de Toy Story, nadie se quería quedar atrás, y DreamWorks contrató a la empresa Pacific Data Images (PDI) en Palo Alto, California, para tratar al menos de emular a Pixar. Dos fueron los retos no llevados a cabo nunca anteriormente que se plantearon para su película: recrear una escena con más de 10.000 caracteres animados individualmente en varias escenas de multitudes, y simular las propiedades del agua (crear un agua digital, en una inundación). Los fluidos y los gases, debido a su impredecible movimiento y evolución, son difíciles de reproducir verosímilmente en un ordenador. Hasta ese momento, el rodaje en el cine de escenas catastróficas que involucran los elementos de la Naturaleza (inundaciones, vadeo de ríos, salto de cascadas, naufragios, incendios, personas abrasándose, huracanes, etc.), siempre se había realizado mediante el diseño y la construcción de maquetas en las que se recreaba la situación, a veces a escala diferente (que posteriormente se magnificaba o reducía, dependiendo de la situación), a veces a escala real. En cualquier caso, el coste de producción de estas simulaciones era alto (y el riesgo a los accidentes), y en determinados casos (los primeros mencionados, sobre todo) el truco puede notarse en la visualización, lo que perjudica notablemente el resultado final (recuérdense películas como Superman (Richard Donner, EE. UU., 1978), o la pobre impresión que transmiten los hoy artesanos efectos animatrónicos de Ray Harryhausen). Gracias a la informática, y al software desarrollado (detrás del que están ineludiblemente las matemáticas) se han mejorado enormemente los efectos especiales. El segundo de los retos mencionados (la simulación de una inundación) se consiguió recurriendo a las ecuaciones de Navier-Stokes, formuladas independientemente por Claude-Louis Navier en 1822 y George Gabriel Stokes en 1842. Estas ecuaciones modelizan el movimiento de los fluidos incompresibles (aquellos cuya densidad permanece constante con el tiempo y se oponen a la compresión, es decir, ni la masa ni el volumen pueden modificarse; aunque todos los fluidos son compresibles en mayor o menor medida, para simplificar las ecuaciones, se suele considerar que todos los líquidos son incompresibles). Estas ecuaciones se obtienen aplicando los principios de conservación de la mecánica y la termodinámica a un volumen fluido, resultando un conjunto de ecuaciones en derivadas parciales no lineales (ver imagen). Estas ecuaciones gobiernan la atmósfera terrestre, las corrientes oceánicas, el flujo alrededor de vehículos, aeronaves o proyectiles y, en general, cualquier fenómeno en el que se involucren fluidos. El problema es que no se conoce una solución general para este conjunto de ecuaciones (ni siquiera una débil), y salvo para ciertos tipos de flujo y situaciones muy concretas no es posible hallar una solución analítica. Por ello en muchas ocasiones hay que recurrir al análisis numérico para determinar una solución aproximada, o sencillamente como realizó Nick Foster, ingeniero de software de AntZ, obviar algunos de los sumandos que aparecen en el sistema de ecuaciones ya que el espectador no va a percibir la diferencia visualmente. No es exactamente agua, pero se le parece mucho. Obviamente esta simplificación no puede hacerse al azar, ya que las características básicas del fluido deben ponerse de manifiesto. En el caso del agua, uno de los elementos visuales clave que debe permanecer es el de la rotación, o como se conoce en términos de la mecánica de fluidos, la vorticidad. Esta magnitud trata precisamente de cuantificar el grado de rotación de un fluido. En una corriente, bien sea de un líquido o de un gas, la vorticidad aparece siempre que el vector velocidad no sea constante a lo largo del recorrido, tanto por cambios en su módulo como en la dirección que sigue. Matemáticamente para modelizar ese giro dentro de un campo vectorial, se utiliza un operador clásico: el rotacional. El rotacional suele manejarse como el producto vectorial del gradiente por el campo (en el caso de fluidos, la vorticidad se designa por tanto por la expresión , donde es el campo vectorial que designa el movimiento). La ecuación que permite estudiar las variaciones de la vorticidad se obtiene aplicando el rotacional en las ecuaciones de Navier-Stokes. Todas estas consideraciones y conceptos físico-matemáticos, en absoluto elementales, fueron utilizadas en el ordenador para diseñar la inundación de AntZ. El resultado es realmente creíble: lo que vemos parece agua. Y gracias a ello, Nick Foster logró el Oscar® en 1998 (gala 78 delos premios) en la categoría de premios científicos y técnicos. PDI/DreamWorks cuenta con una plantilla de 15 programadores que dan soporte a aproximadamente 200 animadores gráficos. Lo habitual es que los programadores utilicen software comercial en su trabajo; DreamWorks en cambio usa herramientas escritas y desarrolladas por sus propios programadores, para modelar, deformar modelos, renderizar, deformar personajes, y todo tipo de efectos especiales. Y para efectuar cálculo matemático complejos recurren a Maple, según explica Shawn Neely, director senior de I+D de PDI/DreamWorks Neely. Entre las necesidades constantes de los animadores gráficos se encuentra el proceso de sombreado de los objetos que aparecen en la película. Cuando uno hace un dibujo, sabe perfectamente el nivel de sombra que debe dar a la imagen, y si no queda a su gusto, lo modifica manualmente. Sin embargo, hacerlo con el ordenador requiere de muchos cálculos, de muchas pruebas hasta decidir que el resultado es el deseado, que es realista. Esas pruebas (y esos cálculos, por tanto) no pueden hacerse a mano, porque son una cantidad muy grande, además de los posibles errores que una persona puede cometer. Un programa de cálculo de cierta potencia, como Maple en el caso de DreamWorks, es necesario. Shawn Neely lo explicaba mediante un ejemplo concreto: Por ejemplo, ahora estoy trabajando en un renderizador de volumen para un nuevo proyecto, en este caso, técnicas para proporcionar algo que parezca niebla. Los modelos tradicionales dan como resultado una salida que es simple y uniforme: obtienes niebla que aumenta en densidad a medida que la cámara se va alejando. Deseábamos algo que produjera efectos más sutiles: mechones, texturas, el tipo de detalle que diferencia lo extraordinario de lo ordinario. Queríamos hacer una integración directa y eficiente de estos efectos, de modo que tomamos un rayo en el espacio y calculamos la densidad de la niebla en función de los puntos extremos. Usé Maple para ayudarme a resolver algunos de estos problemas, y también resolví algunos casos límite relacionados con la aplicación”. Otro de los usos de Maple es “para generar expresiones en una forma que podemos compilar rápidamente en código C, y luego usamos nuestros propios programas para hacer la visualización". Por otra parte, según Neely, una de las cosas que ha consolidado el uso de Maple por parte de PDI/DreamWorks a largo plazo es el compromiso de Maplesoft con Linux en PC: “Hemos estado usando máquinas SGI que ejecutan Irix, por lo que nuestro desarrollo está basado en Unix", dice. "Nos gustaría seguir así; y como nuestra ruta de migración actual es incorporar más PC, Maple bajo Linux en PC tiene sentido. Otros paquetes no están disponibles o sólo están disponibles bajo Windows". La implementación de las matemáticas ha facilitado que el rodaje actual de este tipo de escenas sea más rápido, más eficiente (no hace falta ser un excelente y paciente dibujante), más económico, y con una imagen final más nítida y realista. No sólo en películas de animación. Muchos de los efectos de las películas de superhéroes de la factoría Marvel han incorporado este tipo de herramientas con unos resultados espectaculares (de hecho, uno de los méritos de los actores que participan en estas películas es mostrar naturalidad ante objetos y situaciones que no existen, que se han añadido en la sala de montaje, cuando en la mayor parte de los casos en todo el rodaje no han salido de una habitación). Desde aquellos años, otras películas han logrado el Oscar® u otros galardones, gracias al software y las ideas generadas por las matemáticas. Un último botón como nueva muestra: el cortometraje animado Bunny (Chris Wedge, EE. UU., 1998) también lo obtuvo en 1999. En este caso, lo produjo Blue Sky Studios, tercera compañía norteamericana destacada en animación en 3D. En este enlace puede visualizarse.

Miércoles, 09 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico

23. Octubre 2022: Juegos de probabilidad con cartas

1. El azar y la probabilidad. Por mucho que nos empeñemos los profesores de la ESO en profundizar en el álgebra y las funciones, si hay una parte de las matemáticas con las que convivimos toda la sociedad es el azar. Aunque no seamos aficionados a los juegos de azar, todos nos encontramos en situaciones en las que nos preguntamos qué será más probable para actuar en consecuencia. La enseñanza de la probabilidad tiene la dificultad de ser una rama de las matemáticas que suele ser complicada de entender en su totalidad, pues muchas veces cosas que pensamos que son evidentes nos sorprenden, al estudiarlas con detenimiento, llevando la contraria a nuestra intuición. Por ello, es conveniente adentrarse en su enseñanza de una forma práctica, realizando muchas actividades englobadas en un entorno reconocible. La ventaja de un primer acercamiento a esa disciplina, es que podemos realizar una gran multitud de experimentos aleatorios con mucho material que podemos manipular de una forma entretenida. Así, podemos extraer cartas de una baraja, lanzar dados de diferentes caras, hacer rodar una ruleta, extraer bolas de distintos color de una bolsa o lanza una o varias monedas, y después de realizar el experimento de una forma empírica pasar a lo interesante, el estudio del fundamento matemático que existe detrás. Lo llamativo es que no se suelen encontrar normalmente en los libros de texto muchos juegos de azar que sean especialmente atractivos, y que permitan también, una vez jugados, investigar las propiedades y en definitiva trabajar el azar que es el objetivo último. Ya en la sesión de juegos hemos dedicado algunos artículos a los juegos de azar. Comenzamos con el que quizás sea el más conocido o difundido, la carrera de caballosi. Justo el último artículo aparecido en la sesión de SUMA, la dedicamos a los juegos de azarii y el primer artículo original que se publicó en la sección de Divulgamat fue dedicada a los juegos de azar no transitivosiii. En la mayoría de los juegos de azar, el material que se utiliza suele ser los dados, bien directamente con sus resultados o a través de tableros, lo que se suele complementar con monedas y con ruletas. Pero no suele ser habitual encontrar juegos de azar que no utilicen esos elementos en su desarrollo, por ello, vamos a dedicar hoy un artículo a unos juegos que se realizan con cartas, (aunque ya incluimos uno en el artículo de los no transitivos) en general con una baraja corriente. En la mayoría de estos juegos se pretende fortalecer la idea del cálculo elemental de probabilidad y la de manejar sucesos que sean equiprobables o saber discernir cuáles tienen más o menos probabilidad de ocurrir. 2. Mayor o menor. Este juego está pensado desde dos hasta cuatro jugadores, y su objetivo es ser consciente de los sucesos que son más o menos probables. Se juega con una baraja francesa y sólo se necesita un papel y lápiz para ir anotando los puntos. Se considera que el as equivale a su valor 1, es decir, sería la primera carta de la escalera hasta el 13. Uno de los jugadores baraja el mazo de cartas y lo coloca boca abajo sobre la mesa. Levanta una de las cartas y la coloca boca arriba. El siguiente jugador, normalmente el que está a la derecha del jugador anterior, hace una predicción, que la siguiente carta que levante será mayor o menor que la que se ha mostrado. A continuación, levanta una carta del mazo y la coloca boca arriba sobre la que se había mostrado en el paso anterior. Si se cumple su predicción se anota un punto, si no coincide no se anota nada y en ambos casos pasa el turno al jugador de su derecha. Suele ser un juego bastante rápido, por lo que se suelen realizar varias partidas seguidas. Se juega de forma que el último jugador que ha levantado la carta y ha acabado el mazo, es el que ahora baraja las cartas y comienza el procedimiento visto anteriormente. Una duda surge cuando el que levanta la carta muestra una con el mismo valor que la que se había mostrado antes. Lo habitual es considerar que esa tirada no vale y el mismo jugador levanta la siguiente carta del mazo. Hay otra versión que es perder el turno si sale la misma carta, aunque en este caso se varían un poco las normas. Un jugador puede predecir que la carta siguiente será mayor o menor que la anterior y si lo logra se anota dos puntos, teniendo en cuenta que si sale carta con el mismo valor pierde el turno. Pero también puede no arriesgarse y decir que su carta será menor o igual que la anterior y si acierta sólo se anota un punto. Lógicamente lo mismo si se plantea mayor o igual. El estudio de este juego es muy complicado pues en cada momento las probabilidades van cambiando según las cartas que vayan saliendo. Pero obliga a estar muy pendiente del juego para ir observando las cartas que han aparecido, lo que influye en nuestra predicción. No creo que éste sea un juego interesante para hacer un estudio completo, pero sí para estudiar las probabilidades de cada valor y estimar en qué casos es más interesante subir o bajar. 3. El compatible. La primera vez que encontré este juego fue en unas fichas que enviaba gratuitamente la editorial SM a los centros educativos con material didáctico. En concreto, el material de matemáticas estaba realizado por el Grupo Azarquiel y se componía de fichas agrupadas en cuatro temas, uno de los cuáles era el de Juegos Matemáticos. Más recientemente, Ana García Azcárate ha recuperado ese juego en su blogiv. 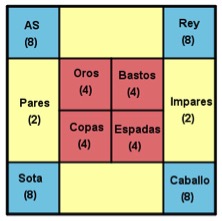Este juego tiene el objetivo de manejar sucesos que sean compatibles e incompatibles. Pueden jugar desde dos hasta cuatro jugadores y se necesita una baraja española de 40 cartas a la que se le apartan los seis y siete, quedando las cartas del as al cinco junto a las figuras. Cada jugador dispondrá también de dos fichas con distinto color por jugador. También se necesita un tablero como el de la imagen y papel y lápiz para apuntar las puntuaciones. Imagen 1: Tablero de El compatible. La dinámica del juego es la siguiente. a) Cada jugador extrae una carta de la baraja y el que tenga la puntuación más alta coloca sus dos fichas en alguno de los recuadros del tablero, con la condición de que deben ser recuadros con distinta puntuación. Siguiendo el turno por su derecha, cada jugador apuesta a dos sucesos de los que queden libres, siempre con la exigencia de que deben tener distinta puntuación. b) Una vez colocadas todas las fichas se baraja el mazo de cartas y se colocan boca abajo sobre la mesa. c) El primer jugador levanta una carta y la coloca boca arriba sobre la mesa. Todos los jugadores que hayan apostado a algún suceso compatible deben decir en voz alta “COMPATIBLE”, y se anotan los puntos correspondientes al recuadro donde tuvieran sus fichas. Por ejemplo, si el jugador saca la sota de bastos, dado que la sota corresponde a un 10 de puntuación, se anotan puntos todos los que hayan apostado a bastos, a sotas o a pares. d) Se sigue el turno sacando cada jugador una nueva carta del mazo. e) Se acaba la partida cuando se haya dado una vuelta completa cinco veces y se suman todos los puntos obtenidos. Gana el que haya ganado más puntos. Tal como he descrito es la propuesta del Grupo Azarquiel, aunque hay aspectos que se pueden modificar sin problemas. Por ejemplo, pueden jugar también cinco jugadores, ya que quedan casillas donde apostar. El número de cartas que se saca de la baraja depende de la cantidad de jugadores. Por ejemplo, si sólo juegan dos pueden seguir extrayendo cartas, mientras no se termine el mazo, como propone Azarquiel. Otra posibilidad es que algún jugador pueda colocar alguna de sus fichas en donde haya ficha de otro jugador, pero no cuando sólo juegan dos. Lo que me parece más interesante del juego es la investigación posterior. Una vez jugado se les plantea a los jugadores a qué creen que se debe la puntuación que hay en cada suceso. No cuesta mucho llegar a estudiar las probabilidades de cada suceso y comprobar que la puntuación es la inversa a la probabilidad ya que, disponiendo de 32 cartas, como nos ha quedado, las probabilidades serían: P(par) = P(impar) = 16/32 = ½ P(oros) = P(copas) = P(bastos) = P(espadas) = 8/32 = ¼ P(as) = P(sota) = P(caballo) = P(rey) = 4/32 = 1/8 Una vez que hemos comenzado con las probabilidades, también es interesante que hallen cuál es la probabilidad de los sucesos que han elegido. Por ejemplo, si un jugador ha elegido as y pares, en total habrá 20 de las 32 cartas de la baraja que nos darán puntos. Si se elige copas y caballos sólo tendremos 11 cartas con las que obtener puntuación, aunque en una de ellas, el caballo de copas, anotaremos puntos por los dos conceptos. Aunque al principio pueda parecer que hay mucha diferencia de cartas, hay que tener en cuenta los puntos que se obtienen en cada caso, pues en el primero podríamos obtener como máximo 32 puntos por pares y 16 por as, es decir, 48, mientras que en el segundo caso podríamos obtener 32 por copas y 16 por caballos, luego volvemos a tener 48 puntos. El juego está pensado para que todos los jugadores tengan la misma probabilidad de anotar. Pero el investigar las posibilidades de cada uno, hace que los alumnos estudien con ansia las probabilidades para intentar elegir los sucesos que le permitan ganar a los contrarios. Otra investigación es completar los dos recuadros del tablero que no tienen asignados sucesos. Se puede proponer, después de los estudios anteriores, que busquen dos sucesos que se puedan colocar en esas casillas libres, y que estudien qué puntuación se podría asignar en ese caso. Una de las que suele salir es similar a la división en pares e impares, y así obtendríamos en una casilla as o figura, y en la otra ni as ni figura y les correspondería dos puntos a cada suceso. Un error muy corriente que cometen las personas que no tienen mucho conocimiento del azar, es pensar que en general, todos los resultados son igualmente probables. Influidos por el hecho de que al lanzar una moneda o un dado, que estén bien construidos, la probabilidad de los resultados es la misma, llevan a hacer extensible ese resultado a otras situaciones, por ejemplo, a pensar que la probabilidad de que salgan dos caras al lanzar dos monedas es la misma de que salga una cara y una cruz. Por eso son interesantes aquellos juegos en que se descubre que no todos los resultados de un experimento aleatorio tienen por qué tener las mismas posibilidades de salir. Sobre todo por el estudio posterior que se hace del juego. Ya vimos un juego en el que queda en evidencia este resultado cuando vimos la carrera de caballos de la que hablamos al principio y ahora vamos a ver un par de juegos en la misma línea. 4. Los cuatro ases. Este juego aparece en el libro de probabilidad de Ana García Azcárate. Está pensado para dos jugadores. Da igual el tipo de baraja que se tome. Se toman los cuatro ases de la baraja, se mezclan y se colocan boca abajo sin que ningún jugador los vea. El primer jugador escoge uno de los cuatro ases, por ejemplo el de oros o el de rombos, el siguiente jugador levanta uno de los cuatro ases y si coincide con el que el otro jugador había elegido, se anota dos puntos, en caso contrario el primer jugador se anota un punto. Se vuelve a barajar las cartas y se colocan, de forma oculta, de nuevo boca abajo y se repite el proceso. Lo normal es mantener la misma elección en toda la partida. Siempre es el segundo jugador el que levanta y se anotan los puntos de la misma forma. Después de diez manos gana el jugador que tenga más puntos. Se pueden jugar varias partidas cambiando los puestos de primer y segundo jugador. Después del terminar el juego se puede plantear si es un juego justo, es decir, si los dos jugadores tienen las mismas posibilidades de ganar. Fácilmente se ve que el primer jugador tiene triple posibilidad de anotarse un punto, frente a la única posibilidad de anotarse dos del segundo jugador. Aunque es un aspecto que no suele verse en secundaria, se puede introducir fácilmente la idea de esperanza matemática o valor medio esperado, pues en los experimentos con resultados discretos es fácil hallarla ya que basta multiplicar la probabilidad de un resultado por la cantidad de veces que puede salir. En nuestro caso, en tres de las cuatro ocasiones el primer jugador se anota un punto y en una de las cuatro se anota dos puntos el segundo jugador. Por ello, la esperanza del primer jugador sería: Como es algo que se entiende fácilmente en este ejemplo, nos puede servir de introducción al estudio de distintas juegos de los llamados socialmente de azar, para ver que, por ejemplo, en un casino siempre tiene mayor esperanza de ganar la empresa. 5. El juego de la cuadrícula. Este juego apareció en los libros de texto del Proyecto Azarquiel para Secundaria que editó, a finales del siglo pasado, Ediciones De La Torre. Concretamente en el texto para 2º de ESO. Posteriormente, Ana García Azcárate, componente original del grupo, lo recuperó hace unos años en su blogv. Aunque en su versión original la propuesta del juego era trabajar con dados, para que tuviese cabida en este artículo lo he adaptado a jugar con una baraja de cartas. En el blog de Ana se puede consultar la versión original. Tal como ella misma indica, éste es un juego de introducción a la probabilidad y a la Ley de los Grandes Números. Es un juego para dos jugadores y se necesita una ficha de distinto color para cada uno, una baraja de cartas española con 40 naipes, y un tablero como el de la imagen. Imagen 2: Tablero para el Juego de la Cuadrícula. La forma de jugar es la siguiente: 1) Se baraja el mazo de cartas y cada jugador extrae una carta. Quien saque la puntuación mayor, escoge la casilla de salida colocando su ficha en dicha casilla. El contrario coloca la suya en la casilla opuesta. Se introducen las cartas extraídas en medio del mazo. 2) Cada jugador en su turno extrae una carta del mazo y mueve esa ficha según la carta extraída. Si la carta es un número (del 1 al 7) mueve la ficha una casilla en vertical y si es una figura en horizontal según el siguiente criterio: Cartas Jugador A Jugador B Números Una casilla hacia arriba Una casilla hacia abajo Figuras Una casilla a la izquierda Una casilla a la derecha 3) Cuando la ficha de cada jugador llega a una casilla coloreada de la diagonal central (lo que ocurre después de extraer cada uno nueve cartas) el jugador se anota los puntos que aparezcan en esa casilla. 4) Acabada la partida, se colocan de nuevo las fichas en la casilla de partida y se vuelve a repetir la partida. Las cartas que se van utilizando se colocan en un montón de descartes. Después de dos partidas, se recogen todas las cartas, se barajan de nuevo y se juegan otras dos partidas más, manteniendo cada jugador la casilla inicial de salida. 5) Tras jugar las cuatro partidas (o más si lo estima el profesor) gana el jugador que haya anotado mayor puntuación. Una vez realizadas las partidas llega el momento de plantear al alumnado si el juego es equitativo, es decir, si los dos jugadores tienen las mismas posibilidades de ganar. Si los alumnos han estado atentos al juego y han visto el movimiento de las fichas, no cuesta mucho que lleguen a advertir que, tal como está diseñado el juego, las fichas se mueven mucho más rápidamente en vertical que en horizontal. La razón es obvia, de cada 10 cartas de un palo, en siete ocasiones se mueven en vertical y en tres en horizontal, por lo que la ficha que está en A se mueve más rápidamente hacia las casillas superiores, con mayor puntuación, mientras que la que sale de B se mueve hacia las casillas inferiores que tienen menor puntuación. Dado que estamos trabajando con el azar, puede ser que lo que esté previsto que pase (que gane el jugador A) no ocurra en realidad, pero como tendremos toda la clase jugando, lo anterior será algún caso aislado, por lo que utilizando la Ley de los Grandes Números, debe salir sin problemas que se cumple las previsiones anteriores. En la versión original del Grupo Azarquiel, además de usar dados el tablero es un poco más pequeño pues sólo llega hasta el 8. Otra variación es que el que primero llega a la diagonal se anota la puntuación y no el otro, pero esto sólo tiene sentido si en cada partida comienza uno distinto de los jugadores, ya que el primero que empieza es siempre el primero que llega a la diagonal. Otra variación es que el que elige casilla de salida coloca su ficha, pero quien empieza el juego es el segundo jugador, por lo que en cada partida hay que elegir la casilla de salida. En las reglas que yo he fijado, cada jugador saca una carta y se mueve según lo extraído. Después de varias partidas, se puede modificar esa regla y entonces el jugador que sea extrae una carta y los dos avanzan según la carta extraída, y se puede observar que el movimiento es simétrico respecto a la diagonal. 6. Referencia. GARCÍA AZCÁRATE, ANA (2013): Probabilidad y Geometría Espacial. Aviraneta, Madrid. Colección Pasatiempos y Juegos en clase de matemáticas.   Notas: [i] Se puede consultar en la sesión de juegos de divulgamat. http://www.divulgamat.net/index.php?option=com_content&view=article&id=10128&directory=67 [ii] http://www.divulgamat.net/index.php?option=com_content&view=article&id=16182&catid=77:juegos-matemcos&directory=67 [iii] http://www.divulgamat.net/index.php?option=com_content&view=article&id=17315&directory=67 [iv] https://anagarciaazcarate.wordpress.com/2015/11/20/probabilidad-el-compatible/ [v] https://anagarciaazcarate.wordpress.com/2017/05/16/el-juego-de-la-cuadricula-probabilidad/

Viernes, 28 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

24. 101 enigmas y misterios para resolver en la oscuridad

Categoría: Divulgación matemática Autor: Miquel Capó Editorial: Montena Año de publicación:  2022 Nº de hojas: 128 ISBN: 978-84-1879-869-6

Jueves, 03 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico | Leer más

25. 87. (Noviembre 2022) Iconografía masónica y matemáticas

(Colgante de ex-venerable. Salamanca) Los orígenes míticos de la Masonería la sitúan entre los constructores del Templo de Jerusalén, de forma que la escuadra y el compás son su emblema característico. La realidad histórica no nos aleja tanto en el tiempo: la francmasonería parece más vinculada a miembros de la Royal Society inglesa, en los inicios de la revolución científica y asociada al cambio de mentalidad que tiene sus frutos en la Ilustración. La simbología geométrica alcanza su máxima expresión en la representación del Teorema de Pitágoras en su versión euclídea, según la figura que acompaña a la proposición 47 del libro 1 de Los elementos. La masonería hace uso de la iconografía geométrica por ser hija del racionalismo que iba a definir su época de esplendor. Plomada, regla, o escuadra son presentadas como emblema de la rectitud de sus acciones y sus objetivos. Presentamos algunas muestras de la vinculación matemática en unos pocos lugares, empezando por el gran templo masónico londinense, paseando por el Cementerio Civil de Madrid o caminando por las calles de Burdeos. El templo pitagórico del Freemasson´s Hall en Londres La iconografía del teorema de Pitágoras según la demostración de Euclides tiende a desaparecer en las imágenes modernas. Una de las pervivencias de la tradición euclídea se encuentra en la simbología masónica. Inglaterra como cuna de la masonería -lugar con gran arraigo y organización- tiene abiertas las puertas de un soberbio edificio Art Decó: el Freemason´s Hall en Great. Queen Street. La construcción actual sustituyó a la logia anterior para rendir homenaje a los fallecidos en los combates durante la primera guerra mundial. Se realizan visitas guiadas a la sala de reuniones, museo, biblioteca, pasillos de iniciación y el gran templo. La escuadra y compás forman parte de toda la decoración desde las lámparas a las vidrieras. Nos detenemos por su interés en los coloristas mosaicos de la bóveda del Gran Templo: en un lado Salomón e Hiran con compás y al otro Euclides y Pitágoras con la ilustración del teorema entre ellos. En muchas iglesias hay representaciones de Euclides y Pitágoras, normalmente acompañando a la Alegoría de la Geometría y la Aritmética o la Música, pero nunca en un lugar tan destacado como en la logia londinense. (Mosaico de Euclides y Pitágoras. Freemasson´s Hall de Londres) Masonería y matemáticas en Salamanca Al depositarse en Salamanca el archivo de la mal llamada “Guerra Civil”, también se ha reproducido una tétrica logia y se dispone la creación de un museo de la disuelta y cruelmente reprimida masonería. Los orígenes míticos de la masonería se sitúan en el templo de Salomón, el rey sabio que ya se reproduce repetidamente en el Monasterio de San Lorenzo de El Escorial. Entre sus fundadores se encuentran matemáticos, por ello no debe extrañarnos que el elemento central del frontispicio de la primera edición (1723) del libro de las “Constituciones masónicas” de Anderson sea el Teorema de Pitágoras. La clásica imagen del triángulo rectángulo con los tres cuadrados de sus lados. (Constituciones masónicas. Museo de la logia de París) El famoso teorema del triángulo rectángulo es el símbolo usado para el ex-venerable masónico. Por ello su medallón reproduce la figura de las proposiciones 47 y 48 con las que se cierra el libro I de los “Elementos” de Euclides. El museo salmantino conserva tres medallones pitagóricos. La unidad entre la filantropía, la teosofía y la matemática se presenta de múltiples formas. Museo masónico en la Logia de París Le musée de la franc-maçonnerie se localiza en un edificio moderno en la Rue Cadet, 16, sede del Gran Oriente de Francia. Las instalaciones no tienen el encanto del Freemasons’ Hall de Londres con su espectacular templo, en cambio, la gran sala de exposición está repleta de objetos y documentos de interés. Incluso el recuerdo del efímero y vilipendiado rey masón José Bonaparte. La masonería está ligada desde los orígenes a la matemática; Euclides y Pitágoras son modelos a seguir. Los símbolos geométricos están siempre presentes. Encabezamos con un mandil con estrella nonágona, compás con arco y triángulo inscrito en circunferencia. (Mandil ceremonial. Museo de la logia de París) El museo contiene gran cantidad de vajillas, cristalerías, relojes, insignias y otros objetos personales. El compás y la escuadra aparecen por doquier: la rectitud geométrica era una forma de vivir. Entre los iniciados se encuentran algunos personajes españoles asentados en París como el cubista Juan Gris. (Insignias masónicas. Museo de la logia de París) Imaginería masónica matemática en las calles de Burdeos La masonería fue muy importante en Burdeos durante su etapa de esplendor del siglo XVIII. La masonería como institución muy emparentada en sus inicios con la Royal Society de Londres -y el mundo de las nuevas ciencias matemáticas- como hemos visto hace gran uso iconográfico de los instrumentos geométricos y del Teorema de Pitágoras. La extensión de la masonería se hace principalmente a través de las ciudades comerciales. El mercantilismo necesita el amparo ético y solidario de personas con los mismos intereses. Filantropía y hermandad van de la mano con las necesidades del comercio. No debe sorprendernos que sean Cádiz en España y Burdeos en Francia dos grandes centros de los caballeros francmasones. (Mascarón masónico. Burdeos) Un aliciente más para pasear por Burdeos es encontrar bajorrelieves en piedra o madera en las fachadas de sus casas. Así, en la Rue Fernand Philippart encontramos el mascarón masónico del compás y la escuadra, en la Rue Tanesse otro compás, al igual que en la Galería Comercial, o los globos del Banco Curtois al lado del Gran Teatro. Geometría masónica en el cementerio civil de Madrid El Cementerio Civil de Madrid quizá sea el rincón más romántico y nostálgico de la ciudad. La otra historia de España late entre sus muros, la de los heterodoxos, hebreos, protestantes, ateos, republicanos, anarquistas, socialistas y comunistas. Mujeres y hombres, cuyos restos sólo tenían cabida en ese lugar. (Tumba masónica. Cementerio civil de Madrid) Un breve recorrido es suficiente para sentir el más profundo sobrecogimiento.  La tumba de Nicolás Salmerón, uno de los presidentes de la primera republica, nos recuerda que dimitió por no firmar una sentencia de muerte. En el Civil podemos encontrar el símbolo del infinito, las estrellas de seis puntas y otros dibujos geométricos, pero concentraremos nuestra mirada -por su abundancia e interés- en los bajorrelieves masónicos. La escuadra, la plomada y el compás acompañan a los masones en su vida y en su muerte: les recuerdan que deben ser constructivos y rectos. La geometría masónica en la loza de Nevers Nevers, en la cabecera del aristocrático río Loira, fue un gran centro de producción cerámica de loza. El Museo Municipal Frédéric Blandin recogía una buena representación de su producción. El palacete que ocupa el museo ha sido remodelado tras un incendio y reconvertido en Museo Nacional de la Cerámica. Entre las miles de piezas expuestas nos quedamos con unas botellas poliédricas y  con los platos masónicos de finales del siglo XIX, elaborados en pleno sueño de liberación redentora de la humanidad. (Plato masónico. Museo de Nevers) El compás, la escuadra, o la recta plomada, son los símbolos del albañil utópico constructor de un nuevo orden más justo. Uno de los platos parece la conmemoración del centenario de la gran revolución de 1789, recogiendo el levantamiento de 1848 y la Comuna de 1870. Marianne con su gorro frigio, y con escuadra y compás, sigue marcando el camino hacia una sociedad de iguales. (Jarra masónica. Museo de Nevers) La cervecería Trindade de Lisboa Una parada obligada en Lisboa debe ser para disfrutar con los azulejos del siglo XIX de la Cervejeria Trindade en el Chiado, el Barrio Alto. Aunque suele estar atestada hay que pasar a su salón para admirar la decoración cerámica. Tampoco debe dejar de verse la azulejería de fachada que se extiende a la calle lateral bajando a la Baixa. Suele asociarse todo el programa iconográfico a la masonería. Hemos escogido como ilustración dos murales masónicos de la Trindade que suelen pasearse por exposiciones temporales por ser los más expresivos. (Panel de azulejos. Lisboa) El compás de San José y Santa Bárbara de Xàtiva El paseo a pie desde el centro de la ciudad de Xátiva hasta su castillo está jalonado de interesantes paradas. La iglesia donde se acumulan más detalles resaltables, tanto técnicos como matemáticos,  es la ermita de San José y Santa Bárbara, reconstruida en el siglo XVIII. Las tumbas de piedra, taracea marmórea y de cerámica son dignas de contemplar. La que no nos podemos perder es la lápida central con su gran compás. Medir la rectitud de las obras que cada uno ha hecho forma parte de la iconografía religiosa tradicional, cuando aparece el compás se tiende a buscar relaciones con la masonería. Quizá no sea una conjetura muy desacertada,  pues los símbolos matemático-arquitectónicos en el templo son insistentes, como la puerta de la sacristía o su lavamanos de mármol de una pieza. La simbología dominante hace gran referencia al gremio de los carpinteros, colectivo vinculado a la ermita. (Lápida en San José y Santa Bárbara. Xàtiva)

Miércoles, 02 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico

26. La ciencia del break dance

El artista gráfico Florian Nicolle –NEO– es el creador de la serie de bocetos titulada Break Dance. http://www.behance.net/gallery/Break-Dance/5340101 La danza captada de manera impecable… expresando posiciones, movimientos, giros y saltos mediante ángulos, alturas, ejes, energías, masas, medidas… Sobran las palabras, es mejor mirarlas y disfrutar con sus muchos detalles de arte y de ciencia. http://www.behance.net/gallery/Break-Dance/5340101 http://www.behance.net/gallery/Break-Dance/5340101 http://www.behance.net/gallery/Break-Dance/5340101 http://www.behance.net/gallery/Break-Dance/5340101 http://www.behance.net/gallery/Break-Dance/5340101 http://www.behance.net/gallery/Break-Dance/5340101 http://www.behance.net/gallery/Break-Dance/5340101 Visto en Stacey Thikx Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Lunes, 24 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

27. Estoy preocupado porque no sé sumar

— Estoy preocupado porque no sé sumar. — Tienes que restarle importancia. — Restar tampoco. — Vaya por dios. — ¡Ni multiplicar!

Viernes, 21 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

28. Examen

El profesor de Matemáticas: - Estoy indignado, más del 80% de la clase no pasó el examen. En eso escucha risas desde la última fila del salón. - ¡Si ni siquiera somos tantos!

Jueves, 24 de Noviembre de 2011 | Imprimir | PDF |  Correo electrónico

29. Ludus Tonalis: simetría musical

Ludus Tonalis (1942) es una obra para piano del compositor Paul Hindemith (1895-1963). Opening and second to last measures of the piece. From the first and final movements, respectively. Excepto por el acorde final, el último movimiento de Ludus Tonalis es el mismo que el primero, pero girado 180 grados. Ludus Tonalis lleva como subtítulo Kontrapunktische, tonale und klaviertechnische Übungen (Estudios o ejercicios de contrapunto, tonales y técnicas para piano) y consta de 25 fragmentos para piano. Esta obra expresaba la nueva teoría tonal del compositor por medio de doce fugas separadas por once interludios y reivindicaba su parentesco histórico con el Clave bien temperado de Johann Sebastian Bach (1685-1750). Más información: Siglind Bruhn, Symmetry and dissymmetry in Paul Hindemith’s Ludus Tonalis, Symmetry: Culture ans Science vol. 7, no. 2 (1996) 116-132 Gabriela Vlahopol, Baroque Reflections in Ludus Tonalis by Paul Hindemith, Recent Advances in acoustics & Music, 171-175, 2010 Wikipedia Visto en Futility Closet Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Martes, 20 de Octubre de 2015 | Imprimir | PDF |  Correo electrónico

30. 128. (Octubre 2022) Retos musicales y matemáticos

1. Introducción En el artículo de este otoñal octubre vamos a proponer al lector una serie de retos matemático-musicales, que están dirigidos principalmente a alumnos de los últimos cursos de primaria y a los de secundaria. Los encontré por pura casualidad en la excelente página web Get the math [DL22] producida por la organización sin ánimo de lucro Next Generation Learning Challenges [Aut22]. Los retos están diseñados por Manny Domínguez and Luis López, que forman el duo DobleFlo (véase su trabajo en Spotify en https://soundcloud.com/dobleflo). En el vídeo que aparece en la página de presentación, Luis López habla de cómo las matemáticas lo empujaron a seguir una carrera musical en hip-hop y achaca tal hecho a la figura del profesor durante sus años de instituto. En su caso, el profesor de matemáticas y el de música era la misma persona (¡hecho bastante inusual!). No cabe duda de que López estuvo en contacto con una persona que supo aunar ambas disciplinas y transmitirlas con la suficiente pasión como para que alguien quisiese seguir el camino de la música (pero con matemáticas). Ese es el verdadero papel de la divulgación. Figura 1: Get the math in the music En ese mismo vídeo, a partir del minuto 3:55 se presenta el primer reto matemático-musical. El reto se le presenta a un grupo de alumnos de instituto y consiste en sincronizar el tempo de dos pistas musicales. Hay varias ideas interesantes que aparecen en el reto. Primero, ha de haber una medida común del tempo para ambas pistas. Una vez fijada, hay que hacer los ajustes necesarios para sincronizar las pistas. El reto se puede encontrar aquí (está en inglés): https://www.thirteen.org/get-the-math/interactives/get-the-math-in-music-take-the-challenge/21/. En esta página se puede meter las soluciones a través de varias pantallas. En la página https://www.thirteen.org/get-the-math/video/get-the-math-in-music-see-how-the-teams-solved-the-challenge/22/ aparece la solución dada por los alumnos, solución que luego es probada en el estudio con DobleFlo. Tras el vídeo de la solución, DobleFlo propone al lector otros retos similares donde hay que mezclar correctamente tres extractos musicales (cada extracto comprende una muestra instrumental y una base rítmica). Esos retos se encuentran en https://www.thirteen.org/get-the-math/interactives/get-the-math-in-music-try-other-music-challenges/23/; véase la figura siguiente. Figura 2: Retos matemático-musicales En otra sección de la página Get the math, encontramos una sección interesante, Math in Special Effects, presentada y escrita por Jeremy Chernick, quien trabaja para la compañía J&M Special Effects. Chernick aparece en un vídeo hablando de su trabajo y su experiencia con las matemáticas durante su vida; el vídeo está en https://www.thirteen.org/get-the-math/video/math-in-special-effects-introduction/243/. Durante el primer minuto, Chernick se queja de lo mal que se le daba aprender matemáticas en la escuela y el instituto. Menciona de hecho un defecto de aprendizaje que le dificulta memorizar hechos, en particular, hechos que presentan nexos lógicos entre sí. También menciona que la enseñanza de las matemáticas que tuvo fue altamente memorística y con poco razonamiento. ¿Cómo es tal cosa posible? ¿Cómo puede algo tan creativo y conceptual enseñarse de una manera memorística e irracional (siento que no hay otra palabra más adecuada aquí)? Más adelante en el vídeo, Chernick afirma que ya no tiene miedo a las matemáticas porque ahora las ve como una herramienta para solucionar los problemas que le surgen en el diseño de efectos especiales. En este vídeo, este diseñador de efectos especiales plantea un reto matemático (ahora ya no musical) que está relacionado con la iluminación de una toma de vídeo. En el reto se investiga la relación entre distancia e iluminación de un sujeto en una toma. El reto está aquí: https://www.thirteen.org/get-the-math/interactives/math-in-special-effects-take-the-challenge/242/. Figura 3: Retos matemático-musicales   Bibliografía [Aut22] Varios Autores. Next Generation Learning. https://www.nextgenlearning.org/, consultado en septiembre de 2022. [DL22] Manny Domínguez and Luis López. Math in music. https://www.thirteen.org/get-the-math/video/get-the-math-in-music-introduction/20/, consultado en septiembre de 2022.

Viernes, 14 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico