201. El concepto matemático de linealidad ¿es innato o se aprende?

¿Son las matemáticas realmente tan universales? Esta es la cuestión que se plantean Rafael Núñez, Kensy Cooperrider y Jürg Wassmann en el artículo Number Concepts without Number Lines in an Indigenous Group of Papua New Guinea [PLoS ONE: Research Article, published 25 Apr 2012, 10.1371/journal.pone.0035662, html y  pdf]. http://www.redorbit.com/news/education/1112522508/study-finds-twist-to-the-story-of-the-number-line/ En este artículo se comenta como los habitantes de la tribu Yupno de Papua (Nueva Guinea) no representan del mismo modo que nosotros el concepto de sucesión regular de números naturales. Esto probaría -según los investigadores- que esta noción se aprende, es decir, no es innata en el ser humano. Algunos estudios habían apuntado que esta capacidad de entender la linealidad está escrita en nuestro ADN desde hace miles de años. Pero este análisis, realizado por investigadores de la Universidad de California en una tribu perdida de Nueva Guinea, parece demostrar que no todos los seres humanos conocen el concepto de linealidad. La tribu de los Yupno está formada por unas 5.000 personas que viven en pequeñas aldeas aisladas.  No tienen ningún tipo de escritura nativa, pero disponen de un sistema numérico y poseen palabras que expresan los números mayores que 20. Su aislamiento hace de estas personas sujetos ideales para estudiar lo innato y lo adquirido con respecto a las matemáticas. Para realizar su estudio, los investigadores reclutaron 14 adultos que nunca habían sido escolarizados y 6 que habían asistido a la escuela al menos durante un tiempo. Además, un grupo de 10 californianos permitió hacer las comparaciones oportunas. El test fue muy simple: se pedía a cada persona colocar los números del 1 al 10 sobre una línea negra de 22 cm dibujada sobre un papel blanco. Los números se presentaban de manera aleatoria, bien mediante sonidos en el dialecto local, mediante sucesiones de sonidos o por medio de puntos. Para los números 3 y 6, se observa la diferencia entre los Yupnos escolarizados (schooled Yupno) que actuaban como los californianos, y los Yupnos no escolarizados (unschooled Yupno) que designaban una de las dos extremidades. Las personas no escolarizadas -entre los Yupno- situaban los números bien completamente a la izquierda  (para el 1, y a veces el 2 y el 3), bien completamente a la derecha (para los números mayores que 3). Los Yupno escolarizados tenían resultados intermedios. Los Yupno no escolarizados ignoraban los puntos intermedios de la línea: de aquí, los investigadores han concluído que es la cultura la que nos inculca la noción de linealidad, es decir, no es un concepto innato. ¿Son las matemáticas realmente un lenguaje tan universal? Esta es la pregunta que plantean estos investigadores… Visto en Le blog-notes mathématique du coyote (información adicional en Futura Sciences y News Center UC San Diego) Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Lunes, 18 de Junio de 2012 | Imprimir | PDF |  Correo electrónico

202. Del 2D al 3D en el antiguo Egipto

En el sistema métrico que utilizamos, la unidad de volumen está basada en el cubo. Esto parecería  indicar que los comerciantes de la antigüedad podían estimar la capacidad de estas jarras redondas -usadas para transportar vino, aceite y otros líquidos- sólo de manera aproximada. Una jarra fenicia globular de Megido (Israel), con una circunferencia máxima externa de 29,2 dedos (unidad de longitud) y el volumen de 0,53 hekat (unidad de volumen egipcia). Pero no es así: recientes estudios realizados por investigadores de la Tel Aviv University (pertenecientes a el Institute of Archaeology y el Department of Geography and Human Environment) y basados en hallazgos arqueológicos, concluyen que estos comerciantes idearon sistemas matemáticos adecuados para determinar el volumen de cada recipiente. La teoría de estos investigadores -publicada en [Zapassky E, Gadot Y, Finkelstein I, Benenson I (2012), An Ancient Relation between Units of Length and Volume Based on a Sphere. PLoS ONE 7(3): e33895. doi:10.1371/journal.pone.0033895, pdf y html]- afirma que los propietarios y los usuarios de las jarras medían los contenidos de los recipientes por medio de un sistema que relacionaba las unidades de longitud y las unidades de volumen. Probablemente se servían de una cuerda para calcular la longitud del perímetro del contenedor esférico, para determinar posteriormente la cantidad precisa de líquido alojada. Los investigadores creen que este sistema fue desarrollado por los antiguos egipcios y se utilizó en el Mediterráneo Oriental entre 1500 AC y 700 AC. La matemática Elena Zapassky se percató de este sistema de medida al construir modelos de jarras en 3D de la excavación arqueológica de Megido (Israel) a partir de una base de datos. Usando métodos estadísticos, el equipo científico midió cientos de ánforas y descubrieron que grandes grupos de estos recipientes de forma esférica o elíptica tenían un perímetro de medida similar. Más información en Phys.org Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Lunes, 18 de Junio de 2012 | Imprimir | PDF |  Correo electrónico

203. Decorando con ecuaciones

En la entrada ¿Demasiadas ecuaciones? hablábamos de un estudio en el que las ecuaciones “no quedan en muy buen lugar“. En este caso, las ecuaciones son las que permiten a Iñigo Quilez realizar los decorados de Brave, el próximo estreno de Pixar. En efecto, los paisajes escoceses de Brave (Indomable) -con los minuciosos detalles de rocas cubiertas de líquen, árboles cubiertos de musgo, etc.- suponían un auténtico quebradero de cabeza para los dibujantes, que decidieron dejar algunos diseños completos -fundamentalmente de elementos vegetales- al ingeniero apasionado por la animación Iñigo Quilez: Mi objetivo ha sido siempre el de no usar ningún software, sino dar al ordenador fórmulas matemáticas para que genere las formas él solo. La gente de Pixar vio mi trabajo y me dijeron: ‘¡Ven!’ La acción de Brave se desarrolla en una Escocia medieval donde la vegetación es onmipresente, y no podían usarse los métodos “tradicionales” de animación por ordenador. Según Iñigo Quilez: Toda la parte de vegetación, hierba y árboles, han sido creados a partir de cero. Hasta ahora, siempre que habíamos hecho árboles o vegetación (en una película de Pixar), un dibujante los hacía a mano. Pero en Brave hay tantos detalles, que una persona se habría pasado años dibujando. Líneas, parábolas, elípses, círculos… han sido los elementos base para generar estos bellos paisajes con ayuda del ordenador… Visto en CinéObs Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Martes, 26 de Junio de 2012 | Imprimir | PDF |  Correo electrónico

204. Fractales biológicos

Cyriak Harris es el director de este video realizado para ilustrar el tema Yellow Bridges de la banda El Ten Eleven. Con un tronco, dos ramas, unas cuantas hojas… y su arte ha conseguido estos espectaculares fractales biológicos. Visto en Neatorama Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Viernes, 14 de Septiembre de 2012 | Imprimir | PDF |  Correo electrónico

205. Reloj cifrado

Este es el reloj Keysay diseñado por José Manuel Otero. Pero es un poco raro… ¿Qué hora es la que marca? = #  ! %  # @ Para averiguarla, hay que conseguir descifrar el mensaje escrito… Pero, ¿qué son esos símbolos? Mira un momento el teclado de tu ordenador… los símbolos y signos corresponden a las teclas de cada número… El reloj tiene otras muchas cualidades y aplicaciones… Para saber rápidamente la hora que es no hace falta ser un as de la criptografía… hay que conocer -y aprender- cual es la correspondencia biyectiva entre cada símbolo y cada número… o cambiar a modo numérico si tienes alguna duda: Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Miércoles, 26 de Septiembre de 2012 | Imprimir | PDF |  Correo electrónico

206. Los números de Tobia Ravà

Tobia Ravà (Padua, 1959) es el pintor de los números… http://www.tobiarava.com/ Los tres videos que siguen son una amplia muestra de las obras de este artista italiano: Perspectivas. Fuga Venecia Caras Más información: Vicente Meavilla Seguí, Tobia Ravà, un pitagórico italiano moderno, Sigma 30, págs. 99-104, 2007 [pdf] Raúl Ibáñez Torres, Tobia Ravà en la publicidad, Divulgamat, Cultura y Matemáticas, Las matemáticas en la publicidad, febrero 2011 Visto en In class able (s) mathématiques 2.0 Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Martes, 09 de Octubre de 2012 | Imprimir | PDF |  Correo electrónico

207. “Caos”, una aventura matemática

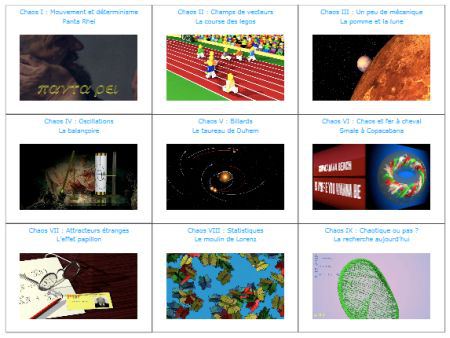
CAOS es un documental matemático sobre sistemas dinámicos, el efecto mariposa y la teoría del caos para todos los públicos. Consta de nueve capítulos de trece minutos cada uno de ellos y pueden verse en varios idiomas. Al igual que DIMENSIONS, Caos está distribuido bajo una licencia de Creative Commons y ha sido producido por el ingeniero y artista Jos Leys, y los matemáticos Étienne Ghys y Aurélien Alvarez. Los nueve capítulos son (están enlazados los videos en su versión en castellano): I: Panta Rhei. Movimiento y determinismo ¿La ciencia puede ayudarnos a conocer el futuro? Formulado por Laplace, el determinismo ha dominado durante mucho tiempo el pensamiento científico. II: La carrera de los legos. Campos de vectores Con el cálculo diferencial e integral, Newton pone a punto una bola de cristal incríblemente eficaz para predecir el futuro. III: La manzana y la luna. Mecánica ¿Por qué una manzana cae del árbol mientras que la luna no lo hace sobre la Tierra? Es la cuestión que se plantea Newton desde los 17 años. IV: El columpio. Oscilaciones La idea de que los movimientos terminan siempre por estabilizarse, deteniéndose u oscilando periódicamente, ha dominado durante mucho tiempo la ciencia. V: El toro de Duhem Comprender el movimiento de los objetos celestes, prever las colisiones entre planetas, predecir tu propio destino… un viejo problema… VI: Smale en Copacabana. El caos y la herradura La herradura: un ejemplo paradigmático del sistema dinámico que busca reducir el caos a su expresión más elemental. VII: El efecto mariposa. Atractores extraños Predictibilidad: ¿el aleteo de una mariposa en Brasil  puede provocar un tornado en Texas? Título de una conferencia de Lorenz en 1972. VIII: El molino de Lorenz. Estadística Debido al problema de la sensibilidad a las condiciones iniciales, Lorenz nos propone centrar nuestros intereses en torno aproblemas estadísticos. IX: Investigando el caos hoy en día Guíados por conjeturas precisas formuladas por Palis, las y los matemáticos intentan comprender los campos de vectores en general. ¡Impresionante trabajo! Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Miércoles, 16 de Enero de 2013 | Imprimir | PDF |  Correo electrónico

208. Henry Segerman: escultura 3D para entender las matemáticas

Henry Segerman (Universidad de Melbourne, Australia) es investigador –especialista en geometría hiperbólica y topología de variedades– y artista –intenta ilustrar la complejidad de la geometría y la topología tridimensional a través de la escultura, usando técnicas de impresión en 3D–. Developing Fractal Curves, Henry Segerman http://blogs.smithsonianmag.com/artscience/files/2013/03/developing-fractal-curves.jpg En este video –Developing the dragon curve– explica la escultura situada en el centro de la anterior imagen, basada en la curva del dragón: Otro bonito ejemplo es Sphere Autologlyph: ¿Quieres intentar visualizar la fibración de Hopf? ¿Deseas tocar una espiral de Arquímedes? ¿Conoces este modelo de la curva de Hilbert? Otros muchos objetos geométricos te esperan en su página web y de YouTube… Más información: Todos los videos de Henry Segerman en YouTube Página matemática de Henry Segerman Página personal de Henry Segerman Henry Segerman, 3D printing for mathematical visualisation Henry Segerman, Recent 3D Printed Sculptures Henry Segerman y Saul Schleimer, Sculptures in S3 Henry Segerman, Some Mathematical Sculptures Visto en Smithsonian Magazine Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Miércoles, 20 de Marzo de 2013 | Imprimir | PDF |  Correo electrónico

209. We Use Math

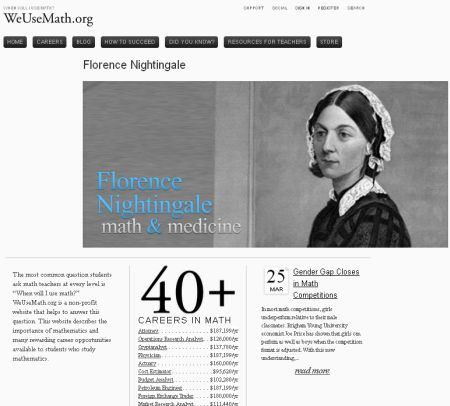
¿Para qué sirven las matemáticas? Seguramente, muchas veces te has hecho –o te han hecho– esta pregunta. We Use Math es una iniciativa del Departamento de Matemáticas de la Brigham Young University que puede ayudarte a responder a esta cuestión. http://www.weusemath.org/ Este sitio web explica la importancia de las matemáticas y las oportunidades que pueden abrirse a cualquier estudiante que curse esta materia. ¿Qué carreras usan las matemáticas? ¿De qué manera? ¿Qué nivel de conocimientos se deben tener? ¿Cómo tener  buenos resultados en matemáticas? ¿Se encuentran matemáticas en nuestra vida cotidiana? ¿Está todo descubierto en matemáticas? ¿Cuáles son los problemas abiertos? Estas y otras preguntas se responden en We Use Math, a través de entrevistas a personas ocupadas en diferentes trabajos.  Además hay recursos disponibles de uso libre, y también puedes contribuir con los tuyos propios. Si quieres dedicarte a la medicina, el control del tráfico aéreo, la arquitectura, la abogacía, la biología, la cartografía, la química, la ingeniería, la climatología, la informática, el criptoanálisis, la economía, la epidemiología, la geografía, la geología, la docencia, la física, el análisis de operaciones, la medicina, la psicometría, la estadística y a otros muchos oficios… ¡necesitarás tener una buena formación en matemáticas! Visto en Math Munch Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Viernes, 05 de Abril de 2013 | Imprimir | PDF |  Correo electrónico

210. Celestial Dynamics

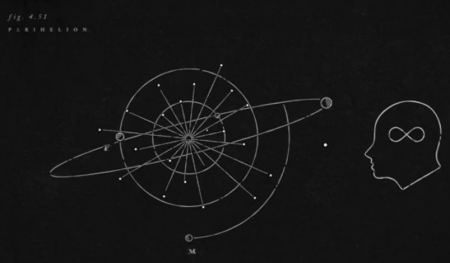
Celestial Dynamics es una animación de Kim Taylor que rinde homenaje a la astronomía -y a la trigonometría- a través de imágenes tomadas de enciclopedias y libros antiguos. Una imagen tomada de la animación Aparecen diagramas, esquemas, cálculos trigonométricos… incluyendo los orígenes “no demasiado científicos” de la astronomía. La pieza musical es Frosti (del álbum Vespertine) de Björk. Visto en AlgoRythmes Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Miércoles, 05 de Junio de 2013 | Imprimir | PDF |  Correo electrónico