Resultados 221 - 230 de 8471
|
Sorpresas Matemáticas/Otros
Autor:Marta Macho Stadler
Menno Dekker (Holanda) inventó el ajedrez de Möbius en 1992.
Un juego de ajedrez de Möbius (no corresponde al que describimos debajo) http://www.neatorama.com/2007/03/31/mobius-chess/
Se considera un tablero de 8 por 8, dibujado en ambas caras de una pieza de papel.
Con esta tira, se construye una banda de Möbius, consiguiendo un tablero con 8 filas y 16 columnas: las primeras ocho columnas forman un tablero normal y las restantes una tabla reflejada.
http://enterthoughts.blogspot.com.es/2013/03/mobius-chess.html
Los cuadrados del tablero reflejado se denotan con un acento para distinguirlos.
Al principio del juego, las piezas se colocan como en una partida estándar. Las reglas son como en el juego normal, pero se añaden algunas más. Por ejemplo, las piezas pueden realizar dos tipos de movimientos: los normales (de este modo se pueden mover sobre todo el tablero de 16 por 8) y los movimientos ‘de fase’. En los desplazamientos de este último tipo, una pieza se mueve de la casilla donde está situada sobre la misma casilla ‘del otro lado del tablero’ –es una forma de hablar, ya sabemos que la banda de Möbius sólo tiene una cara–, es decir, va de una casilla a otra etiquetada del mismo modo, con o sin tilde: por ejemplo, se puede ir de a7′ a a7 y de a7 a a7′.
Su creador impuso como regla el no poder llegar al jaque-mate mediante un movimiento de fase.
¿Te animas a jugar una partida?
Visto en Chess variants
Nota: Brienne Strohl construye uno en papel… y explica como jugar en este video:
Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com
|
|
Sorpresas Matemáticas/Otros
Autor:Marta Macho Stadler
La mesa Fletcher Capstan –mesa cabrestante, de la firma Fletcher– es una joya geométrica y técnica. Mira:
http://www.froot.nl/posttype/froot/6-gifjes-van-uitvindingen-die-we-nu-willen-hebben/
Con un suave movimiento giratorio –de 120 grados–, la mesa duplica prácticamente su superficie.
Esta mesa fue una idea original de Robert Jupe, que patentó su diseño en 1835 –Expandable table. US 6994032 B2–.
http://www.google.com/patents/US6994032
Desde la firma Fletcher, explican la historia de estas mesas, las diferencias con esta primera patente y las características de la mesa en un extenso informe, acompañado de numerosas fotografías.
Puedes ver más imágenes de esta mesa –que no está al alcance de cualquier bolsillo–, algunos videos que explican su funcionamiento y el proceso de construcción, y otros detalles.
Por si alguien no entiende la razón del nombre de la mesa, mirad el funcionamiento de un cabrestante marino:
http://commons.wikimedia.org/wiki/File:Capstan.jpg
Visto en Froot.
Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com
|
|
Sorpresas Matemáticas/Otros
Autor:Marta Macho Stadler
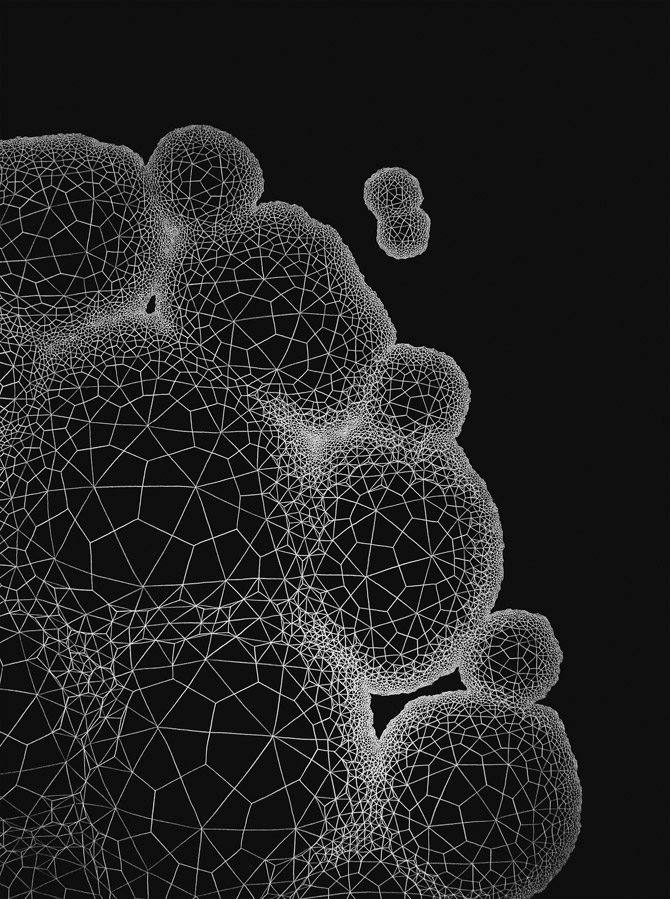
El matemático Georgy Feodosevich Voronoi (1868-1908) nació un 28 de abril.
Clint Fulkerson, “Nebula”, http://www.clintfulkerson.com/
En homenaje al creador de los diagramas de Voronoi, os dejo un poco del arte de Clint Fulkerson:
Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com
|
|
Sorpresas Matemáticas/Otros
Autor:Marta Macho Stadler
El diseñador Erik Åberg es el creador de Ghostcube, un sistema de figuras apilables y plegables de diferentes maneras, que permite crear formas complejas.
http://staceythinx.tumblr.com/post/84333602949/itscolossal-ghostcubes-a-dazzling-system-of
¡Una auténtica belleza!
http://staceythinx.tumblr.com/post/84333602949/itscolossal-ghostcubes-a-dazzling-system-of
http://staceythinx.tumblr.com/post/84333602949/itscolossal-ghostcubes-a-dazzling-system-of
En su web puedes encontrar más información (un tutorial que puede comprarse) sobre la manera de montar estos cubos.
Visto en Colossal
Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com
|
|
Sorpresas Matemáticas/Otros
Autor:Marta Macho Stadler
Suspended stone circle II del artista Ken Unsworth está formada por 103 piedras de río –de unos 15 kilos cada una– en suspensión.
Art Gallery NSW
Las piedras –equidistantes– se cuelgan mediante cables sujetados en tres puntos del techo, de modo que su centro de gravedad cae exactamente en el centro del círculo.
Art Gallery NSW
En este video puede observarse el complejo proceso de construcción:
En este otro video puede verse la construcción de Annulus of Stones, de parecida estructura:
Visto en The Meta Picture
Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com
|
|
Sorpresas Matemáticas/Otros
Autor:Marta Macho Stadler
El puente del diablo (Rakotzbrücke) está situado en el parque Kromlauer (Gablenz, Alemania).
Fotografía: cнαт-ɴoιr/Flickr http://unusualplaces.org/die-rakotzbruck-or-devils-bridge/
Fue construido –en diez años– hacia 1860: el puente y su reflejo en el agua construyen un círculo perfecto, desde cualquier punto de vista.
En esta vista invernal, no se ve el reflejo, pero se observa la belleza del lugar:
Más información:
Die Rakotzbrück or Devil’s Bridge, Unusual Places
Die Rakotzbrücke im Kromlauer Park
El parque de Kromlau
Visto en The Presurfer
Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com
|
|
Sorpresas Matemáticas/Otros
Autor:Marta Macho Stadler
En una clase de primer curso Mattia había estudiado que entre los números primos hay algunos aún más especiales. Los matemáticos los llaman números primos gemelos: son parejas de números primos que están juntos, o mejor dicho, casi juntos, pues entre ellos media siempre un número par que los impide tocarse de verdad. Números como el 11 y el 13, el 17 y el 19, o el 41 y el 43. Mattia pensaba que Alice y él eran así, dos primos gemelos, solos y perdidos, juntos pero no lo bastante para tocarse de verdad.
Fragmento de La soledad de los números primos de Paolo Giordano
El físico y escritor Paolo Giordano (1982-) cumple hoy años.
Dos números primos se dicen gemelos si la diferencia entre el mayor y el menor es 2.
La frecuencia de aparición de pares de primos gemelos va disminuyendo al aumentar el valor de los números; se conjetura que existen infinitos pares de primos gemelos.
Más información:
Los 20.000 primeros pares de primos gemelos
Twin primes, Wolfram Math World
Twin Primes, The Prime Pages
Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com
|
|
Sorpresas Matemáticas/Ilusiones y Paradojas
Autor:Marta Macho Stadler
Mira este video con un fiero dragón como protagonista.
¿Por qué parece que nos sigue con la mirada? Mira la explicación en este enlace.
|
|
Sorpresas Matemáticas/Ilusiones y Paradojas
Autor:Marta Macho Stadler
Fijaos en esta impresionante ilusión creada a través de una anamorfosis:
Para descubrir los pasos previos hasta conseguir este efecto, ir a este enlace.
|
|
Sorpresas Matemáticas/Ilusiones y Paradojas
Autor:Marta Macho Stadler
Hacía tiempo que no hablábamos de anamorfosis… esta vez “va una” de cine:
Un asesino en serie comienza a cometer brutales crímenes dejando una impronta difícilmente olvidable. Los cuerpos de sus víctimas son transformados en reflejos de grotescas obras de arte. El criminal basa el aspecto de sus crímenes en el concepto artístico de la anamorfosis, una técnica pictórica que manipula las leyes de la perspectiva para crear dos puntos de vista diferentes de una misma composición. En una de ellas lo creado toma una forma proporcionada y clara.
Anamorph (2007) es una película dirigida por Henry S. Miller y protagonizada por Willem Dafoe.
Dafoe interpreta al veterano detective Stan Aubray, que se ocupa de un caso cuyo asesino usa la técnica de la anamorfosis para dejar mensajes escondidos al policía: el criminal coloca los cadáveres -descuartizados, manipulados- en posiciones extrañas a primera vista, pero que observados desde el adecuado punto de vista revelan una pista en este juego macabro. Aubray había perseguido con anterioridad a este asesino, pero cometió un error y éste escapó; ahora su compañero, el policía Carl Uffner, intenta ayudarle…
Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |