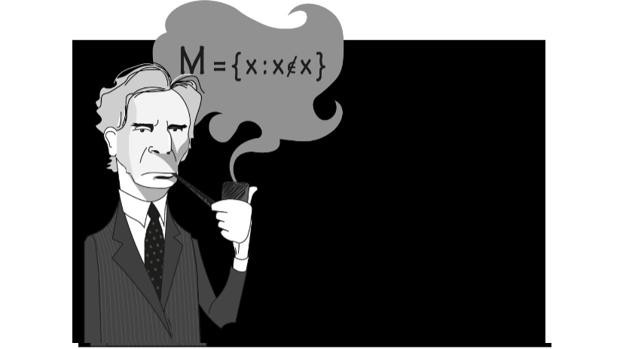231. Bernard Pras, un mago de la anamorfosis

El artista Bernard Pras cultiva el arte de la anamorfosis… http://www.thisiscolossal.com/2013/04/this-anamorphic-portrait-by-bernard-pras-is-an-entire-room-full-of-objects/ Este es su último trabajo, un retrato de Sotigui Kouyaté, referente de la cultura africana: ropa, pintura, madera, caucho y todo tipo de objetos forman parte de esta obra de arte. No es un trabajo sencillo… requiere numerosos cálculos… y mucho arte: Y más arte aún… Guernica, 2010 … fijaos un poco mejor en este Guernica anamórfico: Una bella imagen de este viejo hombre triste… Le vieil homme triste … que no es lo que parece… mira este otro punto de vista: ¿Y qué es esto? Si es… Bugs Bunny… Bugs Bunny ¡Buena imagen de Dalí! Dalí ¿Realmente? Un repaso a algunas de sus obras puede verse en este video: Visto en Colossal Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Viernes, 12 de Abril de 2013 | Imprimir | PDF |  Correo electrónico

232. ¿Se mueven realmente en círculos?

A través de un tuit de Eduardo Saénz de Cabezón, hemos conocido esta impresionante ilusión óptica: Habíamos visto más ilusiones de Brusspup en ::ZTFNews: Las anamorfosis de Brusspup Anamorfosis en tu mesa de trabajo Tyson nos regala diez razones para amar la ciencia (fijaos en la razón número 9) Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Miércoles, 23 de Julio de 2014 | Imprimir | PDF |  Correo electrónico

233. Anamorfosis en tu mesa de trabajo

En esta imagen ya se nota que algo raro pasa… Mira este video hasta el final… una increíble ilusión óptica… una anamorfosis de la mano de una conocida marca de gafas: Ya habíamos visto en ::ZTFNews algunos ejemplos parecidos de figuras planas que detectamos como si fueran en 3D: Las anamorfosis de Brusspup Engañando con papel Visto en Geeks are Sexy Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Martes, 22 de Octubre de 2013 | Imprimir | PDF |  Correo electrónico

234. Bing y su casa con dos habitaciones

El matemático R. H. Bing (1914-1986) cumpliría hoy 100 años. Trabajó en topología geométrica y teoría del continuo, realizando importantes contribuciones. Llevan su nombre el teorema de metrización de Bing o el teorema de reconocimiento de Bing (de variedades de dimensión 3). La casa con dos habitaciones –o casa de Bing– es un ejemplo de 2-complejo contráctil que no es colapsable: todo complejo colapsable es contráctil, la casa con dos habitaciones prueba que el recíproco no es cierto. En los cursos de topología algebraica se suele introducir la casa con dos habitaciones para dar un ejemplo de espacio contráctil, en el que la manera de contraerlo no es para nada evidente. El Mago Moebius tiene una casa de Bing hecha de metacrilato… Más información: Construcción de la casa con dos habitaciones de Bing (símplice a símplice) The Bing House with two rooms Bing’s House with two rooms Bing’s House, Sketches of Topology The deformation retraction of Bing’s house, Sketches of Topology Bing’s House and homotopies, StackExchange David Gillman, Bing’s house and the Zeeman conjecture, Topology and its Applications 24 (1986) 147-151 R. H. Bing, MacTutor History of Mathematics archive, University of St Andrews R. H. Bing, National Academy of Sciences Biographical Memoir R. H. Bing, Mathematics Genealogy Project Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Lunes, 20 de Octubre de 2014 | Imprimir | PDF |  Correo electrónico

235. Investigadores del MIT solucionan un problema matemático de hace 70 años

ABC, 18 de Octubre de 2021 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 18 de Octubre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

236. ¿El portero Buffon es imbatible en 'piedra, papel o tijera'? Una explicación matemática

ABC, 11 de Octubre de 2021 CIENCIA - El ABCdario de las matemáticas Diego Alonso Santamaría

Lunes, 11 de Octubre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

237. La paradoja de Russell o cómo explotar los cimientos de las matemáticas

ABC, 4 de Octubre de 2021 CIENCIA - El ABCdario de las matemáticas Urtzi Buijs y Miriam González

Lunes, 04 de Octubre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

238. 164. Cuando la probabilidad puede traernos problemas legales

El recuerdo de una novela y posterior película sobre el descubrimiento del amor en unos jóvenes superdotados nos permite evocar la existencia de un personaje que trajo de cabeza a las autoridades francesas con su método probabilístico para ganar las apuestas de caballos. Ficha Técnica: Título: Un pequeño romance. Título Original: A Little Romance. Nacionalidad: EE. UU., 1979. Dirección: George Roy Hill. Guion: Allan Burns y Claude Klotz, basado en la novela E = MC² mon amour, de este último bajo el seudónimo Patrick Cauvin. Fotografía: Pierre-William Glenn, en Color. Montaje: William Reynolds. Música: Georges Delerue. Oscar a la mejor música original. Producción: Robert Crawford Jr. y Yves Rousset-Rouard. Duración: 110 min. Ficha artística: Intérpretes: Laurence Olivier (Julius), Diane Lane (Lauren), Thelonious Bernard (Daniel), Arthur Hill (Richard King), Sally Kellerman (Kay King), Broderick Crawford (Brod), David Dukes (George de Marco), Andrew Duncan (Bob Duryea), Claudette Sutherland (Janet Duryea), Graham Fletcher-Cook (Londet), Ashby Semple (Natalie), Peter Maloney (Martin), Claude Brosset (Michel Michon), Jacques Maury (Inspector Leclerc), Argumento Daniel, hijo de un francés de clase media, y Lauren, niña de familia rica norteamericana. Los dos tienen en común algo excepcional: un altísimo coeficiente intelectual, son superdotados. Se gustan y empiezan a verse furtivamente, construyendo una incipiente historia de amor. La novela (y la película) narra sus ilusiones, sus planes, sus problemas con los adultos. Conocen a un anciano que les relata fabulosas historias de su vida viajera, aunque la realidad quizá sea diferente. Los tres se escapan a Venecia, donde Lauren y Daniel vivirán una romántica historia. Comentario, análisis y curiosidades Hace unos días, echando un ojo a los libros de la casa de mis suegros, cogí por casualidad un libro que había visto mil veces, pero que nunca había abierto, dado que aparentemente su argumento no me interesaba lo más mínimo (un libro para adolescentes de los años setenta, nada menos, al estilo de Nacida Inocente o Sara T.; los que han vivido esa época entenderán el tipo de libros que son). En esta ocasión, lo abrí, ¡¡y apareció una fórmula matemática!! (poco usual en las novelas). Lo curioso es que dicha fórmula estaba equivocada. Reproduzco su contenido: “Necesito acostumbrarme a la idea: estoy demasiado adelantada para mi edad. En realidad, hace poco que me he dado cuenta. Nos encontrábamos en la clase de matemáticas, y la tarada que tenemos de profesora me daba la lata desde hacía tres horas con sus ecuaciones, cuando de pronto se equivocó y se puso a relinchar burlonamente, enseñando sus enormes encías rosadas, y diciéndonos para deslumbrarnos: – Craso error de mi parte. Esto nos dará una ecuación de segundo grado, y vosotros no conoceis la fórmula para resolverla. Observé a mis congéneres que babeaban de admiración con sus miradas estúpidas (aborrezco a las norteamericanas), y dije: – Podriamos intentar encontrar esa fórmula … Se puso a reir de tal manera que, además de las encías, nos mostró la faringe y la masa pulmonar. – Adelante -dijo-, encuéntrela y la invito a champán. Ella denomina a eso un rasgo de ingenio. Todos los retrasados me miraron con sus ojos bobalicones y yo comencé a embarullarme con los signos. Al cabo de un rato descubrí el hilo salvador, como si fuera el hilo que sobresale de un ovillo complicado, y que al tirar de él se deshace fácilmente. Entonces dije: – x = , lo que resuelve su problema insoluble. La querida miss Flanaghan se sentó como si acusara una repentina crisis hepática y creí que iba a vomitar sobre su escritorio. Se volvió tan amarilla como diez mil otoños y dijo: – Enseñeme su cuaderno, Lauren. Le alcancé mi borrador y me miró como si yo fuera Frankenstein. […] Entonces tomó el aspecto de una masa repelente de mermelada de manzana y gimoteó: – Es preciso que su madre venga a verme con urgencia. Cuando mamá se presentó, le dio un tratado sobre los niños prodigio. Lo he leido a hurtadillas y ahora sé que no soy muy normal”. Mi primera impresión al leer el párrafo fue que no hace tanto que no nos preocupábamos tanto por lo “políticamente correcto”, teniendo en cuenta además que era un libro dirigido a adolescentes. Pero centrandonos exclusivamente en la parte matemática, desde luego ese alto concepto que la protagonista manifiesta de si misma, no va acompañado de la precisión que supone, ya que es evidente que la fórmula es incorrecta (no por el mas menos de la raíz, ya que podría conformarse con localizar una única solución, sino por el claro error del –b). En páginas posteriores hay más referencias a las matemáticas. Por ejemplo, Lauren afirma un poco más adelante: “… empezaba a secarme como una solterona. Nueve días aquí y ya iba por mi catorceavo libro, uno de los cuales tenía mil doscientas páginas y trataba de cálculo integral”. En otro momento, al inicio del curso escolar, Lauren está cuchicheando con un compañero en clase, y el profesor de matemáticas, molesto, la increpa: – Muy bien. ¿Quiere repetir lo que estaba diciendo a su compañero cuando la he interrumpido? Y no intente inventar. – Le decía que espero que este curso estudiemos con usted la geometría no euclidiana. El adversario vacila ligeramente. Ya no debe de tener la seguridad de antaño para ser profe. Se aferra a la caja de tiza y se lanza al asalto con sarcasmo: – ¿Es usted una especialista del postulado de Riemann? Risas serviles de los tres pelotas de la primera fila. – No, soy partidaria de Lobatchevsky. Hundimiento de Eisenhower; parece que va a perder la segunda guerra mundial. – Sientese. Hablaremos de eso más tarde, exactamente después de las clases de hoy, durante la hora de castigo. ¡Daniel! – Pero ... – Siéntese. Gran silencio. Pertenece a la raza de los que dicen: “Para estar tranquilo durante durante todo el curso, no hay como imponer algún castigo al principio, para que sirva de ejemplo”. El ejemplo soy yo. Tras esa lectura rápida, recordé la película que se hizo sobre este best-seller (fue muy popular y vendió muchos ejemplares), y traté de localizarla por comprobar si aparece algún momento relacionado con las matemáticas. La localicé sin dificultad en este enlace. La película, aún tratando de respetar el espiritu del libro, es más convencional en cuanto a las expresiones, las reacciones de los jóvenes, etc., lógico tratándose de una producción para que su distribución fuera la mayor posible. El libro, como casi siempre, es más rico en cuanto a detalles, descripción de los personajes, y difiere en algunas cosas respecto a la película. Ésta no incluye ninguna de las citas escolares descritas. En un momento dado (digamoslo así para no desvelar demasiado) los protagonistas necesitan dinero para hacer un viaje juntos. El modo de conseguirlo es diferente en novela y película, pero en ambas hay un trasfondo matemático. Describo ambos. En la novela: “Tenemos lo que él ha gando en la radio, pero no es suficiente. A mi me toca ahora arreglármelas. Desde hace mucho tiempo me ronda una idea por la cabeza, pero hasta hoy no había necesitado ponerla en práctica. Los problemas financieros me interesan más bien poco. Pero todo cambia. A grandes rasgos, consiste en lo siguiente: ganar en quince días el máximo de dinero con la mínima inversión. Parecerá idiota, pero estoy segura de poderlo conseguir. Para ello necesito un ordenador. Y no uno pequeño. Por esa razón me encuentro aquí esperando a Agamenón. ¡Ojala comprenda la situación! De todas maneras, no le cuesta mucho prestarme un ordenador durante media hora. Si me explica un poco por encima cómo funciona, creo que me las arreglaré sola para programarlo. No debe ser nada del otro mundo, sobre todo si, como imagino, funciona con sistema binario. Si es así, no hay problema; el negocio está hecho. Sin asomo de vanidad, puedo asegurar que hay pocas cosas que no pueda obtener con ese sistema. He aquí mi idea en líneas generales. Es una hipótesis, por supuesto, pero dada la materialidad de las premisas me parece más que probable. Si abrimos a la vez todos los periódicos del mundo por la página financiera, nos daremos cuenta de que hay una parte cifrada idéntica en todos ellos y que, para mayor comodidad, denominaremos por la letra K. La sección resume todo el mercado interior, los mercados internacionales, la fluctuación de las divisas, el patrón oro, las paridades fijas, la cotización de las acciones ... En una palabra, todo el aspecto numérico que posee la doble propiedad de ser a la vez periodicamente variable y ciclicamente estable. Me explicaré: es evidente desde un punto de vista matemático que un conjunto inestable formado con datos variables, unos con respecto a otros, dentro de unos límites precisos y que oscilan entre una base fija a la que llamaremos P, después de un periodo T más o menos largo, tiene que repetirse de una forma tan ajustada que acaba en una cuasi identidad de su modelo, lo que nos da: P(K/T)– k2 k’ Si tomo con referencia el conjunto k de hace tres años, encontraré en el periodo subsiguiente otro conjunto k’ que será el calco de k. Si entre k y k’ ha transcurrido un tiempo T igual a dieciocho meses, podré conocer el mercado bursatil y financiero de mañana remontandome al que tuvo lugar hace un año y medio. Habrá que maniobrar, por supuesto, tomando en consideración los cambios políticos habidos desde la época en cuestión; o sea, jugar con los componentes no cifrados, aunque de todas maneras podré cuantificar la importancia  precisando los valores exponenciales al utilizar con rigor una axiomática experimental. Resumiendo, un verdadero juego de niños. Entonces, partiendo de una aportación fija –lo que supone, si rompo mi hucha, 75 francos y pico-, y aplicando mi sistema, puedo, dentro de unos límites de tiempo y aprovechando los distintos mercados, multiplicar mi inversión por una cantidad que oscila entre 95 y 105, con un margen de error de 1,5 a 1,8, porcentaje a todas luces despreciable según la escala de las cantidades utilizadas. En conclusión, si todo marcha bien, a final de mes debemos tener Dany boy y yo la simpática suma de 10000 francos. El millón”. Su padre la recibe, cambia algunas impresiones con él, y al poco su secretaria los avisa de que un técnico informático de la empresa la puede atender. Se llama Martin, y lo describe como extremadamente taciturno y de una estatura de metro y medio. “ Le explico con detalle lo que pretendo. Me observa atentamente mientras hablo, lanza un gruñido, intenta por tres veces encender dos cigarrillos con cinco cerillas, cuatro de las cuales ya habían sido utilizadas anteriormente, y concluye: – Gracioso. Tiempo de silencio. – ¿Le parece estúpido mi plan? –pregunto. Se rasca la frente, me sopesa con la mirada, resiste visiblemente a la violenta tentación de meterse un dedo en la nariz, y termina por decir: – ¿Le importa si participo en la aventura con un poco de dinero? – Eso no estaba previsto –le corto. Acusa el golpe. – De acuerdo –me dice-. Le endoso el diez por ciento de mis beneficios. ¿Vale? – Digamos el quince por ciento, y así hacemos los dos un buen negocio. Suspiro intenso de Martin. – De acuerdo, pero hay un enorme trabajo de tratamiento. – No hay mal que por bien no venga –le respondo. Me instalo en seguida en el pupitre. Tal como imaginaba, está basado en el principio binario. Una pequeña maravilla de la técnica. Durante diez días seguidos acudo a la oficina por las tardes, después del colegio. Al final, la hipótesis no parece tan formidable como había supuesto de manera tan rotunda. Además, los imponderables económicos han introducido unas distorsiones que falsean bastante los resultados, sobre todo en lo concerniente a Río Tinto, De Beers y todas las monedas demasiado dependientes del dólar. La cotización del escudo también me ha creado serios problemas. Y el florín no se ha mostrado muy sumiso. Reconozco, pues, sinceramente, que me equivoqué en mis cálculos. Esperaba obtener siete mil quinientos francos y sólo he conseguido seis mil trescientos. Pero, como dice Martin, con una aportación inicial de setenta y cinco francos ha resultado una operación rentable. ¡Puñetero Martin! Los últimos días se ha mostrado inagotable, pero en el fondo no me ha servido de mucho, ya que, a fin de cuentas, si quieren que les diga lo que pienso, se exagera la capacidad de los ordenadores. En la película, vemos desde el inicio que Daniel está muy pendiente de los ganadores de las carreras de caballos. Su taxista padre apuesta diariamente, y pierde dinero. Daniel en cambio parece acertar de acuerdo a un método que ha desarrollado. Va apuntando sus ganancias si hubiera apostado, y comprobamos que llevaría ganados 850.000 francos. Como en la novela, quieren dinero para el viaje. Lauren indica que tiene ahorrados 150 dólares. Daniel está decidido a “invertirlos” en las apuestas con su método. Lauren le pregunta por su frecuencia de ganancia. Daniel le dice que el 45% de las veces. – Y el 55% pierdes. – No soy una computadora. “Un ordenador ayudaría”, comenta, “porque podría tomar las variables de cada caballo en cada carrera, considerar diferentes jockeys, diferentes distancias, etc”. Lauren, igual que en el libro, acude a su padre que le pone en contacto con el informático Martin. El diálogo entre ellos (Martin y Lauren) es como sigue: – ¿Qué información necesitas? – Los tres mejores caballos con probabilidad de ganar mañana en las ocho carreras de Longchamp. Necesito programar los gráficos de rendimiento de cada caballo en el último año y luego cruzar los datos considerando las variables de tiempos y distancias. – Olvidalo. – ¿Por qué? Martin mira a todos los datos para verificar que nadie los escucha. En voz baja, dice: – Hace un año que intento crear ese programa. Ni siquiera ando cerca. – ¿Podría mostrarme su teoría? – ¿Mostrarte mi teoría?¿Quieres que te de 10 meses de cálculos? – Dijo que no funciona. Tal vez pueda ayudarlo. Un tanto reticente inicialmente, finalmente se levanta, abre un cajón y extrae una carpeta, sin dejar de escudriñar a todos los lados, previniendo que no haya curiosos. Saca un montón de hojas de papel continuo. La escena termina, pero acto seguido vemos correr a Lauren en busca de Daniel muy contenta de haber encontrado la solución. Con la colaboración del anciano Julius (ellos no pueden apostar por tener sólo once años), van ganando una y otra vez. A pesar de los consejos de Julius de no arriesgar todo el dinero, Daniel está muy convencido y decidido a ganar el máximo posible. Pero en la última carrera, lo pierden todo. Daniel está muy contrariado. Finalmente, Julius les sorprende porque al final, por una corazonada, no apostó al caballo que Daniel le dijo, sino a otro. Pero esto, lejos de contentar al chaval, lo enfada muchísimo: “Una semana evaluando esos caballos, y ¿usted gana por intuición?” La realidad supera la ficción Seguramente el nombre de Patrice des Moutis (o Monsieur X) no les diga nada a los  lectores. Patrice des Moutis (1921 – 1975) fue un atractivo ingeniero y matemático francés, encantador y bien educado, de familia aristocrática, empleado ejemplar en una empresa de seguros, que desde finales de la década de 1950 y principios de la de 1970, puso en jaque al sistema de apuestas estatal francés, el PMU (Pari Mutuel Urbain), que tuvieron que cambiar varias veces las normas de las apuestas para evitar que continuara ganando las fabulosas cantidades que logró, y sobre todo evitar que cundiera su ejemplo. Con ayuda de aquellos primeros ordenadores, desarrolló un sistema basado en probabilidades bayesianas con el que ganar en todas y cada una de las carreras de caballos y en consecuencia ganar en las apuestas. El 12 de noviembre de 1958, ganó la trifecta (tiercé) 35 veces seguidas y otras 35 veces no seguidas, ganando 5 millones de francos por una apuesta de 294.000 francos (20 veces la apuesta). Se convirtió en un jugador compulsivo y continuó jugando  aumentando las sumas apostadas, y llegando a ganar la trifecta 500 veces seguidas y 2.500 veces más en desorden el 14 de julio de 1961. Esas ganancias (llegó a obtener más de 490 millones de francos; se llevó en más de ocho ocasiones el premio en metálico Arco del Triunfo) le llevaron a ser portada de revistas y medios de comunicación, constituyendose en un héroe para el ciudadano medio, que aplaudia con pasión sus éxitos. Des Moutis se convirtió en asesor de periódicos turfistas (como "Le Meilleur") bajo el nombre de "Monsieur X", que era el nombre con el que el PMU se había referido a él durante mucho tiempo. El 16 de mayo de 1962 apareció un decreto para cambiar las reglas de la trifecta, estipulando que un apostador no podía apostar más de 60 francos en total. El 9 de diciembre de 1962, para el Gran Premio de Burdeos, 83 apostadores (entre los que se encontraban 45 que fueron condenados) de toda Francia apostaron por la misma combinación y ganaron un total de más de 4 millones de francos. La justicia ordenó entonces la incautación del premio, presentando una denuncia contra X. Se le prohibió apostar en Francia, Gran Bretaña e Irlanda, pero lo sigue haciendo, especialmente entre 1967 y 1969 con su familia. En 1973 se le relacionó con un caso de apuestas amañadas; algunos jinetes son acusados ​​de haber perdido deliberadamente la carrera, en beneficio de ciertos apostadores, incluido Des Moutis. Ingresa en la prisión de Fresnes el 21 de febrero de 1975 en prisión preventiva durante 142 días. Poco después de su salida de la cárcel, en la mañana del 17 de octubre de 1975, fue encontrado muerto en su domicilio de Saint-Cloud, sin que se aclararan las circunstancias de su muerte. Des Moutis debía comparecer el 24 de octubre de 1975 ante el Tribunal de Grande Instance de Marsella, sobre el premio Entressem, donde gente influyente había ganado mucho dinero. Algún tiempo después, su hijo, que cuestionó públicamente las circunstancias de la muerte de su padre, también fue encontrado muerto, y la policía también concluyó suicidio ... Conclusión: es peligroso apostar, pero más lo es ganar, al parecer. La novela E = mc2 mon Amour, y su secuela Claude Klotz (1932 – 2010) fue un escritor y guionista francés. Su padre, trabajador ferroviario, lo convirtió en un adicto a la pantalla llevándolo muy temprano a ver multitud de películas estadounidenses. Humphrey Bogart encarna entonces, a sus ojos, la imagen emblemática del cine. Se licenció en Filosofia en La Sorbona en 1954. A su regreso de la guerra de Argelia, enseñó literatura en una escuela secundaria de la región de París, viviendo con cierta humildad en Sarcelles. Marcado por la guerra de Argelia, escribió con su nombre real una serie de trece historias de detectives sangrientas con un héroe recurrente bautizado como Reiner, y posteriormente rebautizado como Raner. Cansado de este duro universo, Claude Klotz crea una historia de amor en 1974. Su editor le aconseja que no la publique con su nombre, utilizando seudónimo de Patrick Cauvin, el apellido de su madre. "Estaba lejos de imaginar que Cauvin ganaría a Klotz, que vendería más libros y que esta doble identidad [...] seguiría confundiendo a la gente". En 1977, mientras Monsieur Papa (publicado en 1976) se estrenaba en las pantallas dirigida por Philippe Monnier, Cauvin publica E = mc2 mon amour, una historia de amor entre dos jóvenes superdotados, éxito rotundo. Un año después, esta historia también será adaptada al cine, la película que estamos comentando. Alternando entre la violencia de Claude Klotz y la ternura de Patrick Cauvin (“Siempre es la historia la que decide quien de ellos toma la pluma”), su fascinación por el cine norteamericano y sus técnicas, está presente en muchas de sus novelas: “Mi ambición es convertir al lector en espectador. Mediante diálogos, que son mi herramienta para componer plano y contraplano”. Sus otras dos pasiones confesadas eran el mar y el fútbol. Veintidós años después de la publicación de E = mc2 mon amour, los dos protagonistas, Lauren y Daniel, se reencuentran en 1999 en Pythagore, je t'adore (Pitágoras, te amo), que vuelve a ser un gran éxito. Aunque el novelista se había prometido no continuar la historia, la nostalgia de sus primeras intrigas lo decide, finalmente, a revivir a sus jóvenes héroes. La trama comienza varios años después de lo sucedido en la historia original: Lauren King se ha mudado de regreso a los EE. UU., y ya no está en contacto con Daniel Michon, aunque vuelven a re-encontrarse. No se ha editado en español.

Martes, 05 de Octubre de 2021 | Imprimir | PDF |  Correo electrónico

239. 197. (Octubre 2021) La magia de Charles Peirce

[Visualización artística de siete "mezclas lecheras" de Roger Antonsen.] Como apéndice al artículo publicado el mes pasado en este rincón (dedicado al principio disléxico) sobre la revisión de las contribuciones a la magia matemática de Charles Peirce realizada por Persi Diaconis y Ron Graham en el artículo "The magic of Charles Sanders Peirce", quiero referirme a la última parte de este artículo, que contiene un descubrimiento reciente y un juego que oculta algunas sorpresas matemáticas. Diaconis y Graham desvelan parte del contenido de una carta que envió Charles Peirce a su amigo y mentor —así como también aficionado a los juegos de magia con cartas— Chauncey Wright el 2 de septiembre de 1865, carta que se encontró recientemente entre los papeles de éste, los cuales están recopilados por la Sociedad Filosófica Americana (y cuya reproducción puedes leer en este enlace). En dicha misiva y después de compartir algunas ideas sobre filosofía, Peirce explica a su colega un nuevo principio matemático relacionado con ciertas mezclas de cartas. Para comprenderlo, propongo que hagamos juntos una versión simplificada del juego con las cartas en la mano. Busca una baraja y sigue leyendo: Selecciona las cartas del as al cinco de los cuatro palos y ordénalas formando un paquete como el de esta figura (el orden de los palos es irrelevante, sólo es importante que todos los palos estén ordenados de la misma forma): Manteniendo las cartas con las caras hacia abajo, realiza una mezcla lechera —también llamada mezcla Klondike— TRES VECES. Si no recuerdas cómo se hace esta mezcla, puedes repasar el número 122 de este rincón, correspondiente a diciembre de 2014. De nuevo con las cartas cara abajo en la mano, cuenta las cuatro primeras, invirtiendo su orden, mientras las pasas de una mano a la otra. Cuenta las cuatro siguientes cartas, sin invertirlas, y las pasas a la otra mano debajo de las cuatro primeras. Repite esta doble mezcla, contar las cuatro cartas superiores invirtiendo su orden y pasarlas sobre las de la otra mano y contar las siguientes cuatro cartas sin invertir su orden y pasarlas bajo las de la otra mano, continuando el mismo proceso hasta que hayas pasado todas las cartas de una mano a la otra. Por último, gira cara arriba el paquete de cartas y reparte sobre la mesa cuatro montones. Observarás que las cartas han vuelto a colocarse en el orden inicial. La secuencia que consiste en pasar grupos de cuatro cartas de una mano a otra, uno de ellos arriba y el otro abajo, es una generalización de la mezcla Monge, que también hemos descrito en este rincón (por ejemplo, en el número 127 de mayo de 2015). En la mezcla Monge original, sólo se pasan las cartas de una en una pero nadie se había planteado antes (que sepamos) el reparto por bloques de cartas. Lo interesante y sorprendente del juego que acabamos de describir es que se puede hacer con cualquier cantidad de cartas que sea múltiplo de cuatro, no necesariamente con cuatro conjuntos de cinco cartas. Pero, además, el número de mezclas lecheras siempre será tres, independientemente del número de cartas con las que se haga el juego. Ya se conocen muchas propiedades de las permutaciones obtenidas al realizar una mezcla Monge (por ejemplo, que después de 12 mezclas, una baraja de 52 cartas recupera su orden inicial) pero —que yo sepa— no se han estudiado, aparte de lo que ocurre en este juego de Peirce, las propiedades de la mezcla Monge generalizada. En la postdata de la carta que Diaconis y Graham analizan en su artículo, Charles Peirce regala a Chauncey Wright un par de juegos relacionados con el anterior, el segundo de ellos adornado con una historia de encuentros y desencuentros. Incluye además las fórmulas y los cálculos realizados para conseguir el resultado deseado. Puedes leer todos los detalles en el citado artículo. Para terminar, quiero compartir mi sorpresa al descubrir que Charles Sanders Peirce sigue entre nosotros, de modo que, si quieres conocer sus pensamientos, sus ideas filosóficas y lógicas y demás aspectos de su vida y obra, puedes seguirle en su perfil de Facebook (aunque, para disimular, haya puesto como foto de portada una recreación de la imagen de Karl Marx). Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Lunes, 04 de Octubre de 2021 | Imprimir | PDF |  Correo electrónico

240. 76. (Octubre 2021) Mercurio matemático

(Mercurio en el Cielo de Roccabianca– Milán) Fuese a Egipto donde a la sazón había varones sabios; y allí con la grandeza de su ingenio, tanto aprovecho en letras principalmente en Aritmética y Astrología, que fue llamado Mercurio. Philosophia secreta (1585) de Juan  Pérez de Moya Los dioses de la gentilidad no desaparecieron tras el triunfo del cristianismo pues toda la cultura clásica estaba impregnada por ellos, desde La Iliada a las Metamorfosis de Ovidio. Los dioses se mutaron en héroes o alegorías morales, y seguirán encontrando cobijo en los astros del cielo. Las constelaciones y los planetas mantienen vivos los mitos astrales de los caldeos y griegos que fueron retomados por Roma. Los nombres de los días de la semana son testimonio actual de la supervivencia. Atenea (Minerva) era la diosa de la sabiduría (y la guerra). Apolo con las musas ocupa su hueco sapiencial. Mercurio el alado es ante todo el veloz mensajero pero en muchas ocasiones tomara el papel de maestro del conocimiento, del alfabeto, la música y sobre todo de la matemática y la astronomía. De alguna manera son los atributos de Nebo, el dios astral Mercurio de los caldeos. Será Marciano Capella en sus Nupcias de Filología y Mercurio (siglo IV) uno de los autores que muestra la relación de Mercurio con las Artes Liberales. Pero aquí Mercurio es comparsa del objeto de sus amores. Será avanzando la Edad Media cuando Mercurio va adoptando otros papeles más vinculados a las matemáticas. Su oficio de viajero y mensajero los vincula a los mercaderes, que tomarán de él su nombre, y la tradición islámica caldea le dará su valor matemático. La representación de Mercurio con instrumentos geométricos y astronómicos se extiende a fines del Medioevo y el Renacimiento.  Mostraremos algunos ejemplos de Mercurios matemáticos. En algunos casos encontraremos a Mercurio con Minerva pero esos no los detallamos. El Mercurio matemático del Castello Sforzesco en Milán El Castello Sforzesco de Milán expone los frescos del cielo astronómico de la fortaleza de los Rossi en Roccabianca, provincia de Parma (1460). Las paredes laterales cuentan la Historia de Griselda, la desventurada esposa puesta cruelmente a prueba una y otra vez en uno de los cuentos del Decamerón de Boccaccio. El conjunto constituye la Camera Picta, un delicioso conjunto de pinturas del Renacimiento temprano. (Mercurio en el Cielo de Roccabianca -Detalle– Milán) El cielo de la bóveda está formado por 24 compartimentos y contiene hasta 87 figuras de planetas, constelaciones y astros; como corresponde a su época tiene valor astrológico. La disposición de las estrellas se ha relacionada con la astronomía antigua de Arato, cuyos manuscritos se superponían a los del Almagesto ptolomeico. Nos fijamos en un Mercurio matemático con cuadrante y compás. Mercurio como el resto de los planetas, la Luna y el Sol es a la vez divinidad pagana, planeta y metal. Mercurio en el Salone de Padua El Salone, la inmensa sala abovedada de carpintería que ocupa la planta superior del Palazzo della Ragione, tiene 81 m de larga y 27 de ancha y de alta. La casualidad ha querido que la razón 3 se haya beneficiado de la lectura en metros y aparezcan potencias de 3 por doquier. La impresionante bóveda estuvo primero decorada con frescos de Giotto, y tras su destrucción por un incendio fueron sustituidos por el ciclo astrológico que aún adorna la sala. Nos fijamos a modo de detalle en la representación de Mercurio  con su esfera armilar por el papel que representaba Hermes como imagen de la sabiduría y sus misterios. (Mercurio en el Palazzo della Ragione – Padua) El programa astrológico está inspirado en el humanista Pietro d´Abano, figura interesante donde las haya y que recuerda algo en inquietudes y en su calvario a nuestro ocultista Enrique de Villena. El Mercurio del Victoria and Albert Museum de Londres Splendor solis es el más bello libro de alquimia hermética que se haya escrito. Sus veintidós laminas iluminadas reflejan las relaciones de la astrología con la alquimia  y la matemática. De las distintas ediciones del siglo XVI destaca la catalogada en la British Librery como manuscrito The Harley 3469. Parece que la ciencia moderna tuvo que pasar una fase no tan racional para desprenderse de otro racionalismo que ahogaba su desarrollo: el aristotélico. (Mercurio en el Victoria & Albert Museum – Londres) La primera sala del Victoria & Albert Museum dedicada al Renacimiento inglés muestra un interesante fresco proveniente de un palacio próximo a Canterbury con las representaciones astrales de la Luna y Mercurio. Debajo de Mercurio en su carro tirado por gallos aparecen un alquimista y un astrólogo. Los dioses astrales solían representarse en los carros que los mueven por el cielo. La iconografía está tomada del Splendor solis que, como vemos más abajo, reproduce en su parte inferior las actividades asociadas con el planeta: aritmética, geometría, astronomía, música y bellas artes. (Mercurio en Splendor solis – Siglo XVI) La lujosa estampa en color, dominada por un matraz que representa a la reina blanca alquimista, contrasta con la sencilla grisalla del mural de la época de Enrique VIII. La vertiente alquimista de Isaac Newton muestra que el despegue de la ciencia moderna no estaba exento de contradicciones. Una curiosa figura de John Dee, contemporánea del mural, importante matemático y ferviente mago, nos dan idea de la compleja realidad renacentista. Atmósfera que recrea muy bien este mural. Tapiz de Mercurio del Museo Nacional Bávaro en Munich El Bayerische Nationalmuseum, fundado por Maximiliano II en 1855, debe contemplarse en toda visita a Munich. La colección es variada y de gran interés, incluido el matemático. No faltan los instrumentos científicos y objetos con representaciones alegóricas a las matemáticas. (Tapiz flamenco de Mercurio – Bayerische Nationalmuseum) Al entrar ya nos encontramos con un tapiz renacentista de los talleres de Bruselas alusivo a Mercurio. El díos mensajero está subido en su carro tirado por gallos en una escena dominada por la música. A la derecha unos sabios hacen geometría y medicina; pudiera ser también una referencia a las artes ocultas tan extendidas en la época: la astrología y la alquimia. Los sabios se corresponden en actitud y tareas con los del Splendor solis. Mercurio matemático en el Palacio de Münster El barroco Palacio del Príncipe Obispo Maximiliano Friderico en Münster, que se construyo en 1767, es hoy el rectorado de su importante Universidad. Detrás del palacio se puede visitar un apacible Jardín Botánico,  rodeado por un gracioso canal pentagonal curvilíneo, y que ha cumplido dos siglos. (Mercurio en el Palacio del Príncipe Obispo – Münster) El palacio se adorna con un elaborado conjunto escultórico tanto en su fachada principal como en los soportes de los balcones. En la parte frontal se encuentran los doce signos del zodiaco con los humores que la superstición atribuye a cada uno, mientras que en la parte trasera se representan las divinidades astrales grecorromanas. Los dioses más proclives a las matemáticas suelen ser Minerva, guerra y sabiduría, Apolo, la razón y el Sol, y Mercurio. A partir del Renacimiento es frecuente encontrar en Mercurio los atributos del geómetra. En el Palacio del Obispo veremos un compás, una escuadra y un transportador de ángulos. Mercurio en el Salón de Nobles de la Reina en Versalles Si en las Grandes Habitaciones del Rey en Versalles nos encontramos a Mercurio con las Artes Liberales, lo mismo ocurre en las Habitaciones de la Reina, incluso con más profusión matemática. (Mercurio en el Salón de Nobles de la Reina – Versalles) El Salón de Nobles de la Reina tiene un techo pintado por Michel II Corneille que representa el esplendor de Mercurio reforzado por Atenea y toda la corte de las Artes Liberales. Lugar especial ocupa la alegoría de la Geometría con el Teorema de Pitágoras. No es el único motivo de gran interés ya que a la derecha podemos ver una escena del Olimpo donde los personajes realizan cálculos geométricos; la estructura de la composición recuerda a los Sacerdotes Egipcios de la Biblioteca de San Lorenzo de El Escorial. Además en las esquinas superiores se localizan grupos de erotes, estucos dorados, que simbolizan las Artes, como el de la Aritmética. Mercurio en los frescos matemáticos del Monasterio Strahov en Praga El Monasterio de Strahov es una antigua fundación del siglo XII remodelada de forma que en su aspecto actual dominan el barroco y el neoclasicismo. Las dos bibliotecas, la Teológica y la Filosófica, son de gran valor tanto por su estética como por su contenido. En ambas hay frescos alegóricos a la actividad matemática. El monasterio se localiza en el alto de Mala Strana, cerca de la plaza con la moderna escultura de Kepler y Brahe. La Biblioteca Filosófica (c. 1779) es más alta y clasicista. Los frescos son continuos y en grandes escenas; en el lateral derecho se puede observar a los sabios Tales, Pitágoras o Euclides trabajando en su actividad con distintos instrumentos y dibujos geométricos. Los focos colocados recortan la visibilidad. La figura inclinada con compás recuerda la Escuela de Atenas de Rafael. Mercurio como inspirador de la actividad matemática está presente en la pintura adjunta. (Mercurio en el Monasterio Strahov - Praga) La Biblioteca Teológica (c. 1670) expone algunos globos, es más baja y los frescos están enmarcados entre estucos. El primero de ellos muestra una discusión entre sabios mientras otro con un compás realiza las mediciones sobre un globo. Curiosamente la cita del Eclesiastés es una de las usadas por Galileo contra los teólogos ortodoxos: Dios entregó el mundo para que fuera debatido. Al fondo se pueden ver los rótulos con el contenido de los libros: aparecen Math y Arith. Mercurio en el Palazzo Rosso de Génova El Palazzo Rosso de Génova es uno de las cuarenta y dos casonas aristocráticas que se han incluido en la lista del Patrimonio de la Humanidad de la UNESCO. La antigua residencia de un dogo es hoy una pinacoteca. Hubo un tiempo como decía Quevedo que el dinero era en Génova enterrado. Los palacios nos dan testimonio. Después todo se desplazó al Atlántico. El Palazzo Rosso no solo exhibe una importante colección, también posee un conjunto de frescos barrocos que permanecen en su lugar original. Destacamos una bóveda de Giovanni Andrea Carlone dedicada a Mercurio y las Artes Liberales. Las Alegorías de la Aritmética y la Geometría se encuentran a los pies de Hermes. Dos niños practican la ciencia tumbados en el suelo. En otra de las lunetas tenemos a la Astronomía y la Música con otra figura con compás y plomada. (Mercurio en el Palazzo Rosso - Génova)

Lunes, 04 de Octubre de 2021 | Imprimir | PDF |  Correo electrónico