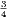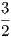241. Franz Reuleaux, sus triángulos y sus mecanismos

El ingeniero mecánico Franz Reuleaux (1829-1905) nació un 30 de septiembre. Con frecuencia se alude a él como el ‘padre de la cinemática‘; realizó contribuciones en diferentes áreas de la ciencia y de la técnica. Supervisó el diseño y la construcción de unos 300 mecanismos simples como el mecanismo de cuatro barras o la manivela. Se le recuerda –al menos entre las gentes de matemáticas–  por el denominado triángulo Reuleaux, un caso particular de polígono Reuleaux: polígono curvilíneo formado por arcos circulares, que en el caso de tener un número impar de lados, es una curva de anchura constante, es decir, la distancia entre dos rectas tangentes paralelas opuestas es siempre la misma. Este triángulo ayudó al ingeniero a desarrollar mecanismos útiles… Y sí que es útil este especial triángulo: el triángulo Reuleaux –y los demás polígonos regulares de Reuleaux, gracias a su anchura constante– es la forma que puede tener la tapa de una alcantarilla –además del círculo– para que no caiga a través del agujero; el rotor de los motores Wankel se parece, pero no es, un triángulo de Reuleaux; el ingeniero James Watt patentó –US-Patent 1241175, US-Patent 1241176 y US-Patent 1241177– una broca con forma de triángulo de Reuleaux, que taladra con forma prácticamente cuadrada; algunos lápices se diseñan con esta sección en vez de la circular o hexagonal habituales; Lápices existen los análogos en dimensión tres de los polígonos de Reuleaux, como el tetraedro de Reuleaux, etc. Para finalizar, os dejo algunas imágenes de estos triángulos (y polígonos de Reuleaux) en diferentes ámbitos cotidianos: Plato Reuleaux Iglesia de San Juan del Hospital (Valencia) Monedas Groot Vleeshuis (Gante, Bélgica) Papelera Guan Baihua y su especial bicicleta (China, 2009) Más información: Reuleaux Collection of Mechanisms and Machines at Cornell University (ver catálogo en pdf) Francis C. Moon, The Reuleaux Collection of Kinematic Mechanisms at Cornell University, 1999 Claudi Alsina, Homenaje a Reuleaux, Revista SUMA 48 (2005) 77-79 Serge Cantat, Le triangle de Reuleaux, Images des Mathématiques, CNRS, 2010 Triángulo de Reuleaux, Wikipedia Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 30 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico

242. Por qué hay más posibilidades en una baraja de cartas que átomos en la Tierra

ABC, 27 de Septiembre de 2021 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 27 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

243. Eustachio Manfredi (1674-1739)

El matemático, astrónomo y poeta Eustachio Manfredi (1674-1739) nació un 20 de septiembre. Su labor científica fue muy amplia. Por ejemplo, el 29 de noviembre de 1707, junto al matemático Vittorio Francesco Stancari, descubrió el cometa C/1707 W1. Entre sus obras científicas se pueden destacar Ephemerides motuum coelestium (1715-1725), De transitu Mercurii per solem anno 1723 (1724), De gnomone meridiano bononiensi (1736) e Instituzioni astronomiche (1749), una obra póstuma. Eustachio Manfredi proporcionó ‘la primera prueba’ –aunque no buscada– de la rotación de la Tierra alrededor del Sol. Casualmente, el 20 de septiembre de 1633, Galileo fue juzgado por defender el heliocentrismo… Por sus numerosos méritos, fue miembro de la Académie des Sciences (1726) y de la Royal Society (1729). Diseño de la Luna, Manfredi, 1703 Más información: Eustachio Manfredi, MacTutor History of Mathematics archive, University of St. Andrews Eustachio Manfredi (1674-1739), Edizione Nazionale Mathematica italiana Bibliografía de Eustachio Manfredi, Scienza Giovane, Università di Bologna Actividad científica de Eustachhio Manfredi, Università di Bologna Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Lunes, 20 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico

244. Etta Zuber Falconer, matemática y educadora

La matemática y educadora Etta Zuber Falconer (1933-2002) falleció un 19 de septiembre. Fue una de las primeras afroamericas en obtener un doctorado en matemáticas: fue en 1969, la Emory University, con una tesis sobre álgebra abstracta, Quasigroup Invariant Under Isotopy, dirigida por Trevor Evans. Durante 37 años enseñó matemáticas y ayudó en la mejora de la educación científica en el Spelman College. En 1995, Falconer recibió el Louise Hay Award de la Association for Women in Mathematics por sus sobresalientes logros en educación matemática. En 2001, recibió un reconocimieto de la American Academy of Arts and Sciences por los logros de toda su carrera. En 1995, en su discurso de aceptación del Louise Hay Award, comentó: I have devoted my entire life to increasing the number of highly qualified African Americans in mathematics and mathematics-related careers. [ ] They have fully justified my beliefs. Perhaps the most rewarding moments have come when younger faculty have undertaken the same goal and have surpassed my efforts, reaching out to the broader community to help minorities and women achieve in mathematics. Más información: Citation for Etta Z. Falconer, 5th Louise Hay Award Etta Zuber Falconer, Biographies of Women Mathematicians, Agnes Scott College Etta Zuber Falconer, MacTutor History of Mathematics archive, University of St. Andrews Etta Zuber Falconer, Mathematical Association of America Etta Zuber Falconer, Black Women in Mathematics Lango Deen, Etta Zuber Falconer, Ph.D. Spelman’s Legendary Math and Science Professor Passes On, Obituario Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Domingo, 19 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico

245. La profesión donde casi no existe el paro en Euskadi

El Correo, 15 de Septiembre de 2021 ECONOMÍA Jorge Murcia

Miércoles, 15 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

246. Partitura palindrómica

EIgnaz Moscheles (1794-1870) fue compositor y pianista. http://commons.wikimedia.org/wiki/File:The_way_of_the_World_Moscheles.png Su obra para piano The Way of the World es palindrómica: la música suena del mismo modo leyendo la partitura como aparece naturalmente, o girándola 180 grados (ver el el pdf de la partitura). En este enlace puede verse un video en el que el pianista Felix Noel toca la pieza en ambos sentidos –es decir, la misma pieza dos veces–: la encontró entre las páginas de una revista. Sobre partituras especiales ya habíamos hablado en: La banda de Möbius y la música Mobius score for violin duet Partitura en forma de cruz… ¿de George Lloyd? Moebius Strip-Tease Los patrones matemáticos de “Clapping Music” Si Fermat hubiese sido compositor… Visto en ConCiencia Musical Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Miércoles, 15 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico

247. Constantin Carathéodory (1873–1950)

El matemático Constantin Carathéodory (1873–1950) nació un 13 de septiembre. Realizó importantes contribuciones a la teoría de funciones de una variable real, al cálculo de variaciones y a la teoría de la medida. El teorema de existencia que lleva su nombre trata sobre la solución de ecuaciones diferenciales ordinarias. En teoría de la medida, el teorema de extensión de Carathéodory es fundamental en teoría moderna de conjuntos. En teoría de funciones de variable compleja, demostró un teorema sobre la extensión de una aplicación conforme a la frontera de un dominio de Jordan: este estudio motivó el inició de la teoría de compactificaciones por finales primos. Se le atribuye la autoría de la conjetura de Carathéodory que afirma que una superficie cerrada y convexa admite al menos dos puntos umbilicales. En 1909, lideró la formulación axiomática de la termodinámica a través de un enfoque puramente geométrico [Untersuchungen ueber die Grundlagen der Thermodynamik, Math. Ann. 67, 355–386, 1909]: su aproximación fue aceptada por Max Born y criticada por Max Planck. Carathéodory realizó también aportaciones en óptica, muy en consonancia con sus métodos de cálculo de variaciones.En 1926 [Über den Zusammenhang der Theorie der absoluten optischen Instrumente mit einem Satz der Variationsrechnung, Ges. Math. Schr. II 181–197, 1926] dió una prueba general de que ningún sistema de lentes y espejos puede evitar la aberración, salvo en el caso trivial de espejos planos. Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Lunes, 13 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico

248. 118. (Septiembre 2021) Afinación y temperamento (III)

1. Introducción En los dos artículos anteriores [4, 5] hicimos un recorrido por los principales sistemas de afinación y por algunos temperamentos. En el primero, cubrimos los fundamentos físicos de la afinación y la afinación pitagórica; en el segundo, la afinación justa y los sistemas mesotónicos. En este tercer artículo, estudiaremos los temperamentos irregulares y el temperamento igual. 2. Temperamentos irregulares Un temperamento irregular —que también recibe el nombre de temperamentos circulares o buenos temperamentos—son temperamentos que partiendo de los sistemas mesotónicos modifican algunas notas para la quinta del lobo desaparezca o al menos se atenúe. Otra manera de expresarlo es que se modifican notas para que la “espiral” de quintas se convierta en un verdadero círculo de quintas donde sea posible la modulación. De hecho, la aparición de los temperamentos irregulares están fuertemente ligados a la necesidad de modulación que de modo creciente se estableció a partir del siglo XVI. Los temperamentos irregulares coexistieron con los sistemas mesotónicos y al menos estuvieron en uso dos siglos antes de que el temperamento igual se generalizara como sistema de afinación estándar. Hay estudios sobre el Clave bien temperado que defienden la idea de que Bach lo escribió para temperamentos irregulares, ya que musicalmente es más rico que si se toca en el sistema mesotónico. Para una buena revisión histórica breve y concisa, véanse el libro de Benson [2] (páginas 206 y siguientes) y el capítulo 7 del libro de Barbour [1]. La quinta del lobo del sistema mesotónico es 35 cents más aguda de lo que debería ser. En general, los temperamentos irregulares se pueden clasificar en función de cómo tal diferencia se distribuye por el resto de las notas. Uno de los temperamentos irregulares más usados fue el llamado Werckmeister III. Siguiendo la notación de Eitz introducida en el artículo anterior y designando por p la coma pitagórica, su diagrama está en la figura de abajo. mi-p si-p fa#-p do#-p sol#-p do0 sol-p re-p la-p mi-p mi♭0 si♭0 fa♭0 do0 Figura 1: Temperamento irregular de Werckmeister III Si miramos a la segunda fila, observaremos que la coma pitagórica está distribuida a partes iguales entre las quintas do-sol-re-la y si-fa♯. A partir del la, la sucesión de notas sigue por quintas puras (pero partiendo desde la-p hasta el si-p, donde ahora salta a fa#-p. Y desde aquí sigue de nuevo por quintas puras. Estos temperamentos permitían obtener resultados más o menos satisfactorios cuando se modulaba a tonalidades relativamente lejanas de la principal. También dieron lugar a “personalidades” en las tonalidades, con frecuencia asignadas de manera subjetiva. Por ejemplo, Daniel Schubart en su obra Ideen zu einer Aesthetik der Tonkunst asigna las personalidades que se ven en la tabla de abajo (la tabla está tomada de la entrada de Wikipedia Tonalidad [6]). En algunos casos las descripciones de estas personalidades resultan algo excesivas. No es el único autor que confeccionó este tipo de tablas de personalidades o características afectivas (piénsese en la teoría de los afectos del periodo barroco). Tonalidad Personalidad Do mayor Alegre, guerrero, completamente puro. Su carácter es de inocencia y de simplicidad. Do menor Oscuro y triste. Declaración de amor y a la vez lamento de un amor no correspondido. Anhelos y suspiros. Do ♯ mayor Miradas lascivas. Pena y éxtasis. No puede reír, pero puede sonreír. No puede aullar, solo puede hacer una mueca de su llanto, bello. Caracteres y sentimientos inusuales. Do ♯ menor Sentimientos de ansiedad, angustia y dolor profundo en el alma, desesperación, depresión, sentimientos sombríos, miedos, indecisiones, escalofríos. Si los fantasmas hablaran se aproximarían a esta tonalidad. Re mayor Feliz y muy guerrero. El triunfo, aleluyas, júbilo, victoria. Re menor Grave y devoto. Melancolía femenina. El rencor. Mi ♭ mayor Crueldad, dureza, amor, devoción, conversación íntima con Dios. Mi ♭ menor Horrible, espantoso. Mi mayor Querellante, chillón, gritos ruidosos de alegría, placer al reírse. Mi menor Afeminado, amoroso, melancólico. Fa mayor Furioso, arrebatado, nostalgia solemne, maravilloso, dulce. Fa menor Oscuro, doliente, depresivo, lamento funerario, gemidos de miseria. Fa ♯ mayor Triunfo sobre la dificultad, libertad, alivio, superación de obstáculos, el eco de un alma que ferozmente ha lidiado y finalmente conquistó. Fa ♯ menor Pesimista, triste, sombrío, oscuro, terco a la pasión, resentimientos, descontentos. Sol mayor Dulcemente jovial, idílico, lírico, calmado, pasión satisfecha, gratitud por la amistad verdadera y el amor esperanzado, emociones gentiles y pacíficas. Sol menor Serio, magnífico, descontento, preocupado por el rompimiento de los esquemas, mal templado, rechinamiento de dientes, disgusto. La ♭ mayor Gravedad, muerte y putrefacción. La ♭ menor Quejándose todo el tiempo, poco complaciente, insatisfecho, corazón sofocado, lamentos, dificultades. La mayor Alegre, campestre, declaración de amor inocente, satisfacción, la esperanza de volver lo que le pertenece a uno de nuevo al regresar de una partida, juventud, aplausos y creencia en Dios. La menor Tierno, lloroso, piedad femenina. Si ♭ mayor Magnífico, alegría, amor alegre, conciencia limpia, metas y deseos por un mundo mejor. Si ♭ menor Oscuro, terrible, criatura pintoresca y curiosa, ropa de noche, tosco, maleducado, burlesco, descortés, descontento con sí mismo, sonidos del suicidio. Si mayor Duro, doliente, deslumbrante, fuertemente coloreado, anunciando pasiones salvajes, enfado, odios y resentimientos. Si menor Solitario, melancólico, ermitaño, paciencia, fe y sumisión esperando el perdón divino. La idea de concentrar la distribución de la coma en ciertas notas y no en otras es la de hacer ciertas tonalidades más aceptables que otras. Con esta estrategia, las terceras de las tonalidades “buenas” suenan casi como las terceras justas, como es el caso de la triada de do mayor do0-mi0-sol-p∕4 del sistema de Werckmeister III (la diferencia es de 4 cents). Si embargo, las terceras construidas sobre do♯ o fa♯ suenan más agudas (ahora la diferencia es de 22 cents, que es una diferencia notable). Para una lista completa y exhaustiva junto con el contexto histórico, consúltense los libros de Goldáraz [3] y Barbour [1]. 3. Temperamento igual Los temperamentos descritos hasta ahora tienen el problema de que la elección de las notas esencialmente favorecía una tonalidad en particular junto a sus vecinas y dejaba el resto con afinaciones deficientes. Los esfuerzos por distribuir la coma pitagórica o sintónica de algunos temperamentos entre las quintas, como en el caso de los temperamentos irregulares, llega a su punto natural con el temperamento igual, cuyo principio consiste en dividir la octava en 12 partes iguales. O dicho de otro modo, hacer que todas las quintas tengan el mismo tamaño. Históricamente y matemáticamente, esto fue difícil. Históricamente, fueron los constructores e intérpretes de instrumentos de afinación fija (órganos, clavecines, laudes, guitarras, etc.) los que empezaron a explorar el temperamento igual. Según Barbour [1] (página 56), Giovanni Maria Lanfranco en 1533 fue el primero en abogar y sistematizar el temperamento igual. Lanfranco recomienda que “las quintas se achiquen de manera que no sean agradables del todo al oído y que las terceras se puedan soportar”. Matemáticamente, la dificultad era construir de manera geométrica (con regla y compás) el número irracional , que es la proporción con que se construye el temperamento igual. En el temperamento igual, una octava se divide en 12 partes iguales; esto equivale a decir que la proporción entre dos notas consecutivas es 2 : 1 o, si se miden en cents, simplemente 100 cents. La tabla siguiente resume la construcción del temperamento igual. Notas Do Do♯ Re Re♯ Mi Fa Fa♯ Proporción 1/1 2 : 1 2 : 1 2 : 1 2 : 1 2 : 1 2 : 1 Cents 0 100 200 300 400 500 600 Notas Sol Sol♯ La La♯ Si Do Proporción 2 : 1 2 : 1 2 : 1 2 : 1 2 : 1 2 Cents 700 800 900 1000 1100 1200 Tabla 1: Temperamento igual Las terceras del temperamento igual son 14 cents más agudas que las terceras justas. Y como dice Benson en su libro [2] (página 204), “suenan nerviosas y agitadas” (estoy de acuerdo con esta afirmación). En la siguiente tabla se ven de nuevo las proporciones de la afinación pitagórica y su comparación con el temperamento igual (medido en cents). Notas Do Sol Re La Mi Si Fa# Do# Sol# Proporción 1/1 3/2 9/8 27/16 81/64 243/128 729/512 Cents 0 701.96 203.91 905.87 407.82 1109.78 611.73 113.68 815.64 Notas Do Fa Si♭ Mi♭ La♭ ~Sol# Proporción 1/1 4/3 9/16 32/27 128/81 Cents 0 498.04 996.09 294.13 792.18 Tabla 2: Afinación pitagórica para la escala cromática En general, la afinación justa y el sistema mesotónico producen terceras con más sensación de calma. Los temperamentos irregulares tienen la ventaja de dotar a cada tonalidad de una personalidad y un color distintos, como consecuencia de la distribución irregular de la coma. En el temperamento igual todas las tonalidades tienen esencialmente la misma personalidad. 4. Para saber más A continuación ponemos algunos vídeos con música en el temperamento Werckmeister III. Empezamos con una sonata de Domenico Scarlatti, la sonata en la menor K. 54. Figura 2: Sonata en la menor K. 54 en el temperamento Werckmeister III Figura 3: Preludio en do mayor del Clave bien temperado de Bach en 7 temperamentos (incluido Werckmeister III)   Bibliografía [1] J. Murray Barbour. Tuning and temperament: a historical survey. New York: Dover Publications, Inc., 1951. [2] D. Benson. Music: A Mathematical Offering. Cambridge University Press, 2006. [3] J. Javier Goldáraz. Afinación y temperamentos históricos. Madrid: Alianza Editorial, 2004. [4] Paco Gómez. Afinación y temperamento (I). http://www.divulgamat.net/index.php?option=com_content&view=article&id=18644&directory=67. web page. accedido el 20 de julio de 2021. [5] Paco Gómez. Afinación y temperamento (II). http://www.divulgamat.net/index.php?option=com_content&view=article&id=18645&directory=67. web page. accedido en agosto de 2021. [6] Wikipedia. Tonalidad_(música). https://es.wikipedia.org/wiki/Tonalidad\_(msica). web page. accedido el 10 de julio de 2021.

Jueves, 09 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico

249. 163. SOLUCIONES CONCURSO DEL VERANO DE 2021

Saludos a todos los lectores de la sección. Empezamos el nuevo curso académico con la publicación de las respuestas al XVII Concurso del verano. Dada la extensión del artículo, sin más preámbulos, vamos con ello. CUESTIONES MATEMÁTICAS M – 1.- La suma es 715663 + 79003 + 781196 = 1575862. Por no extender en demasía la reseña, no indico la solución pormenorizada del criptograma. Si alguien la desea, se la puedo enviar. Por otro lado, al puntuar la cuestión, se han dado los 10 puntos completos a aquellos concursantes que han razonado dicha solución. A aquellos que sólo han dado la solución final, se les ha asignado un 7. M – 2.- Teniendo en cuenta la información del enunciado, llamemos x al número de billetes del que más recibe, y, z las partes de los otros dos, y n el número total de billetes de 5000 cruzeiros. En ese caso, tenemos que x +  + y + z = 5000n Parece razonable que sean y, z los dos cuya suma sea el del que más dinero recibe. Entonces, y + z = x En ese caso la primera ecuación se reduce a + x = 5000n Es decir,  21x = 50000 n. Eso indica que n debe ser un múltiplo de 21. Como nos dicen que el número de billetes debe ser la cantidad mínima posible que cumpla todas las especificaciones, n = 21. En ese caso, x = 50000 (o sea 10 billetes de 5000), x/10 =5000 (es decir, 1 billete), y + z = 50000 (que deben ser 6 y 4 billetes, o 2 y 8, porque ambos han de ser una cantidad par). Finalmente nos dicen que al generoso personaje le sobran tantos billetes como la suma de dos de sus agraciados amigos. Como de nuevo el número de billetes debe ser el mínimo posible, entonces 10 + 1 + 10 (6 + 4, o 2 + 8) = 21 billetes ha entregado Para ver los que le sobran consideramos todas las posibles sumas dos a dos, y tomamos la menor. Ésta surge en el caso 2 + 1. Por tanto, el número de billetes que pide inicialmente es 21 + 3 = 24 billetes. A quien da cada cantidad es subjetivo, aunque a tenor de las imágenes parece que a Chiquita le da los 10 billetes, al dependiente/camarero 1, al cadi 2, y a la señora 8, por ejemplo, aunque se da por válido cualquier otro apaño. M – 3.- Hay dos personajes a los que no se da nombre: una chica (a la que designaremos en principio como C), y un hombre (al que denominaremos como H). En el enunciado se nos dan los siguientes comensales, agrupados en dos frases: Ron, C, H, Joan; y Ann, H, C, H, C, marido de Pam. La chica a la izquierda del marido de Pam, no es Pam, así que debe ser Joan. Por tanto, tenemos Ann, Ron, Pam, H, Joan, marido de Pam. Steve está sentado a la derecha de la chica que está sentada a la derecha de Harry. Así que la configuración debe ser Ann, Ron, Pam, Harry, Joan, Steve. Por tanto, Steve era el marido de Pam. M – 4.- Esta ha sido una de las cuestiones que más quebraderos de cabeza parece haber causado. En efecto, era uno de los más “abstractos”, valga la expresión, y la prueba es más teórica, y con cierta “idea feliz”. Un primer dato importante es que en el enunciado se dice que los números son enteros, por tanto, sí pueden tomar valores negativos. Dos concursantes hallaron la solución correcta, uno de ellos con un razonamiento deductivo impecable (el otro se limitó a dar la solución correcta, supongo que mediante prueba-error). Escribo una demostración “algebraica”: Llamemos x1, x2, …, x100 a los números descritos en sentido horario, con x100 + i = xi, al ser la mesa circular. Tenemos, para i = 1, 2, ...., 100 (he aquí la “idea feliz”: considero todos a partir de uno concreto, el xi, y repito los dos primeros que consideré, xi y xi +1) xi + xi +1 + …. + x100 + x1 + …. xi - 1 + xi + xi +1 = 100 + xi + xi +1 y como hay 102 = 6 x 17 términos en esta suma, agrupándolos cada 6 consecutivos, tenemos 100 + xi + xi +1 ≤ 102 O lo que es lo mismo xi + xi +1 ≤ 2 Entonces, 100 = (x1 + x2) + (x3 + x4) + … + (x99 + x100) ≤ 2 x 50 Dándose la igualdad con x2i - 1 + x2i = 2, si, y sólo si i ≥ 1 Ahora bien, también podemos escribir 100 = (x2 + x3) + (x4 + x5) + … + (x100 + x1) ≤ 2 x 50 De donde x2i + x2i + 1 = 2, si, y sólo si i ≥ 1 Como x1 = 6, entonces x2 = – 4, y por recurrencia, para i = 1, 2, …, 50, x2i - 1 = 6, x2i = – 4, valores que satisfacen las condiciones dadas. M – 5.- 1.- Designemos por a la cantidad de libras, y b la de peniques, de manera que el precio vendrá dado por a.b. De acuerdo con las condiciones del enunciado tenemos entonces que (100a + b) = 100b + a + donde x se encuentra entre los valores , para considerar los posibles redondeos. Simplificando la ecuación tenemos 197a = 298b + x Si x = 0, la solución es a = 298, b = 197, ya que 197 y 298 son primos entre sí. Sin embargo esa solución no sirve ya que b (los peniques), deben cumplir que 0 ≤ b ≤ 99. Si x = 1, encontramos fácilmente la solución mediante el algoritmo de Euclides (recuérdese la conocida como identidad de Bezout; mediante el algoritmo de Euclides obtenemos una combinación lineal de dos números igual a su máximo común divisor, en este caso la unidad al ser primos entre sí): 1 1 1 19 5 → Cocientes 298 197 101 96 5 1 101 96 5 46 0 → Restos 1 = 96 – 19 ‧ 5 = 96 – 19 (101 – 96) = 96 ‧ 20 – 19 ‧ 101 = (197 – 101) ‧ 20 – 19 ‧ 101 = 197 ‧ 20 – 39 ‧ 101 = 197 ‧ 20 – 39 (298 – 197) = 197 ‧ 59 – 298 ‧ 39 Por tanto, a = 59, b = 39 es solución válida, y el precio del libro sería 59.39. Para x = –1, obtenemos el mismo valor, y cantidades mayores exceden de los dos dígitos bien en las libras, bien en los peniques. Varios concursantes han utilizado medios informáticos para encontrar la solución (hojas de cálculo, etc.). He dado la solución como correcta (bueno, lo valoré como 9, en vez de 10), aunque, bueno, desde el punto de vista estrictamente matemático, podría cuestionarse. 2.- La pregunta viene a cuento porque la libra está dividida en 100 peniques desde la decimalización de 1971; anteriormente la libra se dividía en 20 chelines (shilling), y el chelín en 12 peniques (penny, plural pence), por lo que una libra tenía 240 peniques. En este caso, con un razonamiento similar al anterior se comprueba que no hay solución si sólo se consideran dos dígitos para libras y peniques. Necesitaríamos un dígito más, pero un libro como el que vemos en la película, no podría ser tan caro. M – 6.- Son cien lingotes de oro. Si entre todos pesan 495987 libras, cada uno pesa 4959.87 libras. Teniendo en cuenta que una libra (medida de peso) es equivalente a 0.453592 kilogramos, eso supondría que cada uno pesaría 2249.75 kilogramos (o sea 2 toneladas y pico). Difícil que puedan cogerlos. No obstante, bien por error, bien por mostrar las limitaciones de los personajes (eso no lo podemos saber, pero ya sabemos cómo es el humor inglés), es posible que intencionadamente el guionista haya querido jugar con las libras (pounds) no como unidad de peso, sino como libras esterlinas (como valor monetario). En ese caso, como el precio del oro, según dicen en la película, es de 240 chelines la onza, es decir 12 libras esterlinas la onza, dado que 4959.87:12 = 413.32 onzas, un lingote pesaría 413.32:16 = 25.83 kg. (una libra son 16 onzas).  Sin embargo, en joyería, lo usual es trabajar con onzas troy. Una onza troy son 0.37324 kg. Entonces, 0.37324:12 = 0.0311 kg., por lo que un lingote pesaría 413.32 x 0.0311 = 12.85 kg., valor totalmente coherente con el peso de un lingote de 400 onzas troy que es de 12.5 kg. Esa similitud da que pensar que, en efecto, está hecho así adrede. M – 7.- Me ha sorprendido el que bastantes concursantes no respondieran a esta cuestión, una de las más sencillas (bajo mi punto de vista), habida cuenta de que se daba la libertad de que cada uno eligiera los datos que necesitara en base al modelo estándar de lingote de oro. Teniendo en cuenta la forma que suelen presentar los lingotes de oro (en la película también), es determinar las dimensiones de un prisma de base trapezoidal, imponiendo únicamente que el grado de inclinación (del lado oblicuo del trapecio obviamente) fuera de 5º, y que pesara 1 kilogramo. Un modo de hacerlo podría ser el que nos indica Alejandro, uno de los concursantes: Como la densidad del oro puro es 0.01932 kg/cm3, entonces el volumen debe ser Con los nombres dados a los lados del dibujo, el volumen del prisma es Conocido el volumen, tenemos tres valores desconocidos (b, h y L). Fijando dos de ellos, determinamos el tercero. Podemos decidir fijar la altura h y la base menor b, o cualquier otro par, pero cumpliendo con la expresión anterior. M – 8.- La relación entre los volúmenes de los cuerpos semejantes es igual a la que existe entre los cubos de sus alturas respectivas. Si el pisapapeles pesa 7.300.000 veces menos que la torre original (en el caso de un kilogramo), su volumen debe ser 7.300.000 veces menor, luego el pisapapeles debe ser (7300000)^(1/3) =193.9877414 ≈ 194 veces más bajo que el real. Es decir, 300/194 = 1.546 metros (un poco grande para pisapapeles). En el caso de que quisiéramos que pesara ½ kg, la proporción debería ser (7300000 x 2)^(1/3) = 244.4092388 veces más bajo que el real, con lo que sería 300/244.41 = 1.2274 metros, que no es la mitad de alto, precisamente. Afortunadamente, las réplicas no son perfectamente semejantes con el modelo original. M – 9.- La densidad del oro es 19.32 gr/cm3 = 19.32 kg/dm3. Si tuviéramos el oro líquido, un litro pesaría 19.32 kilogramos. A partir de la conocida relación entre densidad, masa y volumen, Y de ahí, la constante de proporcionalidad sería k = 0,0030335. Con ese valor, reproducir la torre de 1 kilogramo de oro puro nos llevaría a una altura de 1.147 metros, y el de medio kilo 91 cm, un tanto grandes en ambos casos. Viendo los pisapapeles de la película, su altura estaría en torno a los 30 cm., de modo que habría que hacer un número excesivo para repartir todo el oro que dicen que roban. M – 10.- Lo primero que a uno se le ocurre es representar gráficamente los puntos dados. En la imagen aparecen en color rojo, junto a los tres en verde de la base. Si quitamos los signos menos de la primera coordenada de los puntos en rojo, completamos por simetría lo que sucedería en la parte positiva del eje OX (puntos azules). Es bastante claro que representa el perfil de una famosa torre (la torre Eiffel, por si aún no lo hemos descubierto de todas las pistas del enunciado del concurso). Para unir los puntos de un modo medianamente realista, se puede hacer en varias etapas (interpolación segmentaria o por partes). En la base (puntos verdes), aproximamos los tres puntos por una parábola (rectificando ligeramente los valores para tener la simetría perfecta; ya se sabe que, si se toman datos de la realidad, a ojo, se pueden cometer pequeños errores que luego “mejoramos” matemáticamente). Los cinco puntos rojos siguientes están unidos también por interpolación (obtenemos un polinomio de grado cuatro; el que aparece en la imagen), pero es igualmente válido hacer un ajuste por mínimos cuadrados a una parábola (un polinomio de segundo grado) quedando bastante realista también. Los tres siguientes idénticamente se pueden unir por interpolación o ajuste, al igual que el tramo final, mediante una recta, por ejemplo. El lado derecho lo completamos por simetría. No incluyo las expresiones de los polinomios obtenidos porque son grandes y lo que importa es el procedimiento, pero si algún lector está interesado, se las mando sin ningún problema. M – 11.- Si designamos por x el peso del primer metal del que está formado el pisapapeles y por y el del segundo, se tiene que x + y = 750. Por otro lado, los volúmenes respectivos con cada metal serán x/19.50 e y/10.50, por lo que Al resolver el sistema lineal, se obtiene que x = 487.50 gr., y = 262.50 gr. M – 12.- En la película se dice que se han perdido 6 pisapapeles valorados en 25000 libras. Cada uno por tanto 12500/3 libras. Antes del 15 de febrero de 1971, ya se ha comentado que la libra eran 240 chelines, por tanto, cada pisapapeles está valorado en 250000/3 chelines. Cada onza vale 240 chelines. Por tanto, cada pisapapeles pesa 250000/(3 x 240) onzas = 25000/(72 x 16) libras de peso (1 libra son 16 onzas), que son aproximadamente  21,7 libras, o sea 21,7 x 0,453592 ≈ 9,84 kg. En el caso de considerar libras troy, serían 25000/(72 x 12) ≈ 28.93 libras troy ≈ 10.7978 Kg. Un poco pesados para que la niña lo maneje con tanta soltura. M – 13.- El ascensor baja a una velocidad de 2 m/seg, y cubre 300 metros, por lo que tarda 150 segundos, que son 2 minutos y medio. En internet se indica que desde arriba había exactamente 1665 escalones (en realidad ellos no bajan tantos, porque lo hacen desde la 2ª planta). Si tuvieran que llegar a la vez, deberían bajar 1665/2.5 = 666 escalones pon minuto (una cantidad “endiablada”, ja ja ja). Eso viene a ser 11.1 escalones por segundo. Sí parece justificado el mareo que tiene, bajando además circularmente. M – 14.- Para calcular el área encerrada por esa curva, pueden utilizarse diferentes procedimientos (aunque para todos necesitamos integrales definidas, obviamente). En cualquier caso, es obvio que podemos aprovechar las simetrías de la figura. Al resolver el ejercicio pensé en las parábolas, todas simétricas. En la imagen adjunta, observamos en rojo tres puntos que me definen todo lo que necesito (cada concursante puede elegir libremente dónde los coloca; la única condición es que la forma final se “parezca” a la propuesta). Esos puntos son (3.5, 1.7), (1.7, 3.5) y (–1.7, 3.5). Con los dos últimos y el (0, 3) (muy obvio de la imagen), obtenemos, por interpolación, la parábola Si quisiéramos dibujar las otras tres parábolas, basta con intercambiar x e y, para las de izquierda y derecha (y un signo menos para una de ellas), y multiplicar por (–1) la dada para la inferior, quedando las siguientes expresiones: pero no son necesarias para el cálculo de la superficie que se pide (sólo para obtener el dibujo de la imagen). Lo que si necesitamos es la ecuación de la recta que une (3.5, 1.7) con (1.7, 3.5), que es Estaremos de acuerdo con que la superficie pedida es cuatro veces al área rayada en morado, más la de verde, menos el trocito que nos pasamos de la parábola de la derecha. Expresándolo mediante integrales será: O sea, unos 38 metros cuadrados, si las medidas fueran en metros. La mayor parte de los concursantes han optado por una resolución teórica en modo exacto, sin medidas concretas, obteniendo (9 – p)r2, siendo r el radio del círculo inscrito entre las parábolas. Por supuesto, también se ha considerado bien resuelto. M – 15.- Todas las formas posibles de elegir un par de alumnos distintos de un conjunto de cinco es De éstos sólo necesitamos eliminar aquellos que tengan como diferencia un año, que son exactamente cuatro: (6, 7), (7, 8), (8, 9) y (9, 10). Por tanto, la probabilidad de seleccionar al menos dos con edades que se diferencien en dos años es 6 de 10, o lo que es lo mismo 3/5. M – 16.- El año de producción Es evidente que el año debe ser de la forma 19** (no es una película muda para que fuera anterior, y tampoco del 2000 en adelante. ¿Qué cuadrados perfectos pueden obtenerse con 10 + x? Sólo 16 o 25, por lo que la suma de las dos cifras desconocidas es 6 o 15. Analicemos todas las posibilidades: Suma 6: pueden ser 1933, 1924, 1942, 1915 o 1951. De ellos sólo son primos 1933 y 1951. Suma 15: pueden ser 1978, 1987, 1969 o 1996.  Sólo es primo 1987. Analicemos con esos tres casos, la última condición que nos dan: al revertir las cifras el número es compuesto. Los números serían 3391, 1591 y 7891. Así descartamos el 1933. Quedan por tanto 1951 y 1987. Pero claramente la película no puede ser de 1987 (blanco y negro, aún existe la escalera de caracol de la Torre Eiffel que se desmontó en 1983, etc.). De modo que el año de producción es 1951. M – 17.- Una palabra clave Se nos dice que el cuadrado de la imagen con las cifras del 1 al 16 es mágico, y que la suma de las casillas de las esquinas (en verde) y las del centro (en rojo) también suman la constante mágica. Al ser un cuadrado de orden cuatro, esa constante mágica es 34 (ya saben (1 + …. + 16)/4). Como los números de la diagonal principal suman ya 26, los otros dos deben ser 1 + 7, o 3 + 5. Por otro lado, la primera fila suma ya 30, de modo que los que restan deben ser 1 + 3 (2 + 2 no puede ser porque no se repite ningún número). Razonemos por reducción al absurdo para ir descartando casos. Supongamos que a11 = 3 y a12 = 1. Entonces, a33 = 5, y de ahí se deduce que a41 = 6, y a21 = 12. En ese caso pueden suceder: 1.- a32 = 10, a42 = 8, de donde a34 = 6. Imposible porque el 6 ya estaba colocado. 2.- a32 = 8, a42 = 10, de donde a34 = 8. Imposible porque el 8 ya estaba colocado. Por tanto, debe ser a11 = 1 y a12 = 3. En esa situación a33 = 7, y por la condición de las cuatro esquinas tenemos que a41 = 8, y de ahí a21 = 12. En la segunda columna tenemos una suma de 18, por lo que a32 + a42 = 16. Teniendo en cuenta los números ya colocados, esa suma sólo podría ser 10 + 6 o 6 + 10. Suponiendo que fuera a32 = 6, entonces a34 = 8. Imposible porque el 8 ya estaba colocado. Por tanto, a32 = 10, y de ahí terminamos el resto de valores sin dificultad (a la derecha el cuadrado mágico terminado; en rojo los valores que hemos ido colocando). En el enunciado se nos indica que “las casillas marcadas con fondo naranja (seis de ellas; una ya se da, la del número 14), encubren esa palabra que puede ser una pista definitiva para desvelar la película en cuestión”. Los números de esas casillas son 1, 14, 12, 5, 7, 9, que en el orden alfabético usual corresponden a las letras A, N, L, E, G, I. Jugando con ellas, nos cuesta encontrar una palabra con sentido en español, hasta que, si somos un poco metódicos damos con EALING. Evidentemente esa palabra no nos dirá nada, salvo que sepamos algo de cine o de geografía londinense (lo siento; era la cuestión rebuscada de esta edición). Ealing es un municipio del oeste de Londres en donde se encontraban los Estudios Ealing que produjeron la película que nos ocupa. M – 18.- La película es Oro en barras (The Lavender Hill Mob, Charles Crichton, Reino Unido, 1951). CUESTIONES CULTURALES C – 1.- Quizá esta cuestión haya confundido a los lectores porque en la película el loro no dice nada. La cuestión simplemente era aprovechar que aparecía el loro para meter el criptograma. De hecho, en el enunciado indica “podría decir”. Lo que se preguntaba era por el significado del criptograma, en resumidas cuentas, por qué le llamaríamos “Polly”. El nombre genérico "Pol" para un loro se remonta a Inglaterra desde al menos principios del siglo XVII. En su comedia de 1606 Volpone, el dramaturgo del Renacimiento y amigo cercano de William Shakespeare, Ben Jonson asignó a muchos de los personajes animales que reflejaban su verdadera naturaleza. El astuto personaje principal, por ejemplo, es un zorro, mientras que su sirviente parasitario es una mosca. Dos personajes cómicos en relieve, Sir Politic Would-Be ("Sir Pol" para abreviar) y su esposa, son visitantes de Inglaterra que están tratando de congraciarse con la sociedad veneciana, y lo hacen simplemente imitando las palabras y el comportamiento de Volpone y sus asociados. Debido a su entrañable ignorancia de lo que realmente están diciendo cuando repiten frases que han aprendido, Jonson los describe como loros. No está claro si Jonson realmente acuñó el término "Pol" como un apodo general para los loros, o si simplemente lo popularizó. En cualquier caso, los indulgentes dueños de mascotas británicos finalmente convirtieron a "Pol" en el diminutivo "Polly", mucho más coloquial, y ambos nombres cruzaron el Atlántico. De hecho, el presidente de los Estados Unidos, Andrew Jackson, tenía un loro gris africano llamado Pol, que era famoso por soltar obscenidades a los dignatarios visitantes. Otra posibilidad que menciona otro concursante es acerca de la canción popular británica Pretty Polly, que narra la tragedia de una joven que es asesinada por un carpintero. Después del crimen, él huye en un barco. El protagonista, Holland, igual que ese carpintero, cometió un crimen y después huyó en barco. Recuerdo un célebre gag de los Monty Python, con un loro muerto, al que llaman Polly. C – 2.- Donald Lowndes fue el fundador del emporio de administración de propiedades Lowndes & Sons S.A. (1936), un emprendedor que provocó una revolución en el mundo empresarial de su tiempo, que persiste hasta nuestros días. Aún no tenía 20 años cuando se fue a estudiar a Inglaterra y allí descubrió empresas que prestaban asistencia a quienes necesitaban alquilar inmuebles, arrendar almacenes o gestionar inmuebles. Desconociendo todo de ese país, le encantó el servicio que le prestaron, recién casado, necesitando ayuda para instalarse en un domicilio mientras permanecía en la ciudad. Se graduó en ingeniería civil y económicas volviendo a su país, Brasil, donde se dispuso a poner en práctica las ideas que había visto. Fue responsable del primer desarrollo de oficinas en condominios en la historia de Brasil, revolucionando el mercado inmobiliario del país. Eso incluyó un banco, el Banco Lowndes (1941). Trasladó a sus empresas su ideal familiar, cercano, humanista, dotando a todas sus empresas de un restaurante para empleados, a los que ofrecía desayuno y almuerzo antes de empezar la jornada laboral, una clínica médica, cuyo uso se ampliaba a familiares de trabajadores, y un club. Para Donald Lowndes era muy importante que estuvieran encantados de trabajar con él. Así lo que vemos en la película no es un restaurante, sino las dependencias del Banco Lowndes de Rio de Janeiro. Mientras el cliente es atendido (fíjense que el protagonista entrega un cheque al presunto camarero, y hace la consulta al superior sobre si darle la cantidad que le pide) disfruta de un trato relajado entre amigos. El banco sigue existiendo en la actualidad, aunque no me consta que esa siga siendo la atención a los clientes. C – 3.- Se trata de Audrey Hepburn, haciendo de Chiquita, una amiga del protagonista. Inicialmente su papel iba a ser más amplio, pero sus compromisos teatrales no lo permitieron. Sir Alec Guinness, impresionado con la joven actriz, logró que al menos apareciera en un pequeño papel. Se considera que esta es su primera aparición en una película importante. C – 4.- En la película vemos que el título es You´d look swell in a shroud (algo así como Te encontrarías hinchado en una mortaja). No he encontrado ningún libro real que tenga ese título. C – 5.- En la versión doblada se dice 495980 libras. C – 6.- El extravío se debe a la diferente pronunciación fonética de la letra “erre” en el inglés y el francés. Se dieron instrucciones de no poner a la venta los souvenirs de la caja que tuviera marcada una “r”. En inglés, la “r” se pronuncia [ar], mientras que en francés es “egue”. En realidad, en francés la “r” se pronuncia de formas diferentes si va delante o detrás de una vocal, o si va delante o detrás de una consonante, y a veces, no se pronuncia. Está claro que en la película han utilizado esa letra no por casualidad, y han tratado de poner de manifiesto que para hacer las cosas bien (en este caso, el delito), hay que tener en cuenta los detalles más nimios, o todo se puede ir al traste. Además, tipográficamente la R y la A, escritas a mano y haciendo la parte superior de la A redondeada, pueden confundirse. C – 7.- Hay una escena en la que el protagonista observa el proceso de modelado de los lingotes de oro. Una mota de oro cae fuera del molde. La recoge con la punta de su paraguas. Indica entonces que “con el oro a 240 chelines la onza, esa partícula tiene un valor de 1 punto 25, y significa una pérdida aproximada de 6 chelines”. En la versión original y en el subtitulado se dice que el valor de la mota es 0.025. Con ese valor, que sí tiene sentido, sale perfectamente la cuenta (240 x 0.025 = 6). La confusión para los dobladores españoles de la época (¡¡unos genios!!), bien de que Alec Guiness pronuncia .025 mediante “point ou twenty-five”, y lo tradujeron como “un punto veinticinco”. Lo dicho: ¡¡unos genios!! Pero los concursantes son más exhaustivos y han descubierto más equivocaciones. Así, Alejandro Apezteguía nos desvela un par de ellos más: Hacia el minuto 26:38, en la planificación del robo, en la versión doblada dicen “tenemos que REMOVER 200 barras”, mientras que en la versión original se dice “MORE THAN 200 BARS” es decir, más de 200 barras (los subtítulos en castellano también salen mal pues lo traducen como “SON 200 BARRAS”. Posteriormente en el minuto 26:56 en ambas versiones se confirman que son exactamente 212 barras que son contadas mientras se cargan en el furgón blindado. Otro error a la inversa, aparece en la versión original pero no en la versión en castellano. En muchas escenas se puede ver la matrícula del furgón LKL238 e incluso la nombran correctamente casi siempre, pero en el minuto 31:27 de la versión original la nombran como LKL638 es decir cambian un 2 por un 6 (y en los subtítulos también parece este error). Esto no ocurre en la versión en castellano donde siempre nombran la matrícula correcta. C – 8.- Se trata de la Torre Eiffel, París, Francia. Aparte de su diseño y medidas arquitectónicas (para las que se precisan bastantes matemáticas), esta torre tiene grabados sobre el friso de sus cuatro caras los nombres de 72 científicos, entre los que figuran 20 matemáticos (eso sí, todos franceses). En https://www.toureiffel.paris/es/el-monumento/torre-eiffel-y-ciencias pueden consultarse. Por otro lado, es relevante, como Gustave Eiffel tuvo que contrarrestar la resistencia al viento. Puso una curva en los bordes exteriores para que la torre no se cayera. En la base de la Torre Eiffel, cuatro pilares curvos se inclinan interiormente en un ángulo de 54 grados. Ese ángulo es el que minimiza la resistencia al viento. A medida que los pilares se elevan y finalmente se unen, el ángulo de cada uno disminuye gradualmente. En la parte superior de la Torre, los pilares fusionados son casi verticales (cero grados). No obstante, la torre se mueve con el viento. En días con vientos fuertes y racheados, el viento puede alcanzar velocidades superiores a 100 mph en la parte superior de la torre. Los visitantes pueden sentir cómo la torre se balancea suavemente en el nivel superior. En tales condiciones de viento, suele estar cerrada al público, aunque siempre hay un ingeniero presente en la cumbre para monitorizar los equipos de telecomunicaciones. La magnitud del balanceo en la torre, en el peor de los casos, es de unas seis pulgadas. No hay peligro de que la torre se dañe por el movimiento inducido por el viento, ya que está diseñada para soportar movimientos fácilmente cinco veces superiores a los producidos por los vientos más fuertes jamás registrados. Hoy, los movimientos son monitorizados por un sistema de alineación láser. C – 9.- Entre otras, París que duerme (Paris qui dort, René Clair, Francia, 1924); El misterio de la torre Eiffel (Le mystère de la tour Eiffel, Julien Duvivier, Francia, 1927); El hombre de la torre Eiffel (The Man on the Eiffel Tower, Burgess Meredith, EE. UU., 1949); Una cara con ángel (Funny Face, Stanley Donen, EE. UU., 1957); Zazie en el metro (Zazie dans le Metro, Louis Malle, Francia, 1959); La torre de los rehenes (The Hostage Tower, Claudio Guzmán, EE. UU., 1980); Superman II. La aventura continúa (Superman II, Richard Lester, EE. UU./Reino Unido, 1980); Panorama para matar (A View to a Kill, John Glen, Reino Unido, 1985). También hay escenas en múltiples películas, aunque tomadas desde la parte turística, más que desde el interior de la estructura, como Ninotchka (Ernst Lubitsch, EE. UU., 1939) o Men in Black International (F. Gary Gray, EE. UU., 2019) por poner dos ejemplos en las antípodas cinematográficas, ja ja ja. C – 10.- En una escena de la película, el protagonista es seguido por un vehículo cuya matrícula se dice que es THX 375. THX es el nombre de una compañía estadounidense con sede en San Francisco, California, fundada en 1983 por George Lucas. Se dedica a desarrollar estándares de audio y video de alta fidelidad para salas cinematográficas, sistemas de sonido caseros, bocinas para computadoras, consolas de videojuegos, sistemas de audio para automóviles y videojuegos. El sistema THX no es una tecnología de grabación y tampoco especifica un formato de grabación; todos los formatos de sonido, ya sea digital o analógico, pueden mostrarse en THX. Básicamente THX es un sistema para garantizar la calidad, de tal manera que salas de cine o sistemas de sonido casero o profesional podrán reproducir el contenido tal cual fue concebido en la sala de mezclas. La segunda relación es obvia: Alec Guinness, el protagonista de esta película, es también Obi Wan Kenobi en la película Star Wars, dirigida por George Lucas. Los concursantes han encontrado otras relaciones, algunas sumamente enrevesadas, aunque se han valorado positivamente todas ellas. Eso sí, cuando sólo se da un detalle (se pedían dos), la puntuación ha sido la mitad, 5. C – 11.- Hacia el minuto 43 de la película, en la oficina de Scotland Yard, aparece un cartel que anuncia una exposición sobre el centenario del fallecimiento de Robert Peel (1850 – 1950). Robert Peel fue un estadista y político británico del Partido Conservador, primer ministro del Reino Unido en dos ocasiones. Introdujo una serie de importantes reformas en la legislación penal británica. La más destacada fue la creación de la London Metropolitan Police, posiblemente el primer cuerpo de policía moderno y precedente de Scotland Yard. Es curioso que inicialmente, a los policías se les denominaba un tanto despectivamente Peelers (peladores, mondadores), y después se transformaran en Bobbies (Bobby es el apodo de Robert), en ambos casos haciendo referencia a Robert Peel. Promovió además cambios en el Código penal para reducir el número de delitos castigados con la pena capital. Al final de la película, los protagonistas entran en la citada exposición, de la que presenciamos una demostración de coche inalámbrico, una muestra del trabajo del Departamento de Investigación Criminal de la policía británica (Criminal Investigation Department; CID, en siglas) sobre casos reales (para los cinéfilos, el actor Robert Shaw aparece como químico especialista en un breve cameo sin acreditar), y parte del Museo del Crimen (Black Museum), inaugurado en 1874, y que sigue existiendo en la actualidad allí mismo, en la sede de Scotland Yard, Londres SW1A 2JL. No está abierto al público, aunque ha aparecido en diferentes películas y programas de radio y televisión. Otra película que recorre alguna de sus salas es Jack, el destripador (The Lodger, John Brahm, EE. UU., 1944). C – 12.- Pregunta de opinión, en la que todos los concursantes han tenido, obviamente la puntuación máxima.   Puntuaciones Finales Este año se ha dado una circunstancia curiosa, que no había sucedido antes. Dos concursantes han alcanzado la misma puntuación máxima (las “penalizaciones” han sido además en cuestiones diferentes). Así que hay un empate técnico, un ganador ex aequo que dicen en los festivales 1.- Alejandro Apezteguia Torres  290 (170 + 120) 2.- Francisco Pi Martínez   290 (180 + 110) 3.- Michel Picquart   241 (131 + 110) 4.- Alba Diez Mariño    220 (110 + 110) 5.- Francisco Javier Morentín  212 (154 + 58) 6.- Celso de Frutos de Nicolás   187 (97 + 90) Como veis, todos ellos han tenido puntuación mayor o igual en la parte matemática (en rojo) que en la parte cultural (en azul). Agradezco a todos su buenísima disposición, la aceptación de la propuesta, y sus elogios. Espero que hayan pasado de verdad un buen rato. En breve recibiréis un mail, algunos para pediros una dirección postal a la que enviaros un pequeño obsequio de DivulgaMAT (ignoro a fecha de hoy el número de obsequios de los que dispone la organización), y a todos para detallaros las puntuaciones de cada cuestión, una vez hayáis leído las soluciones. ¡¡Enhorabuena a todos!!

Miércoles, 08 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico

250. 117. (Agosto 2021) Afinación y temperamento (II)

1. Introducción En el artículo anterior [Góm21], presentamos los conceptos básicos de afinación y temperamento (manejo de frecuencias, división de la octava, cents, la serie armónica) y la afinación pitagórica, cuyos generadores son la octava y la quinta. En este artículo vamos a estudiar los siguientes temas: la afinación justa, en su versión diatónica y cromática junto con algunas afinaciones históricas; hablaremos de los problemas armónicos que se derivan del uso de la afinación justa; continuaremos con los sistemas mesotónicos, de los cuales proporcionaremos los ejemplos más sobresalientes; y, por último, sugeriremos al lector vídeos y referencias para seguir ahondando en ambos; y eso sin olvidar sugerencias de música, por supuesto. 2. Afinación justa 2.1. Escala diatónica justa Si consideramos las proporciones de la afinación pitagórica, las cuales reproducimos por completitud en la tabla 1, observaremos que ciertas notas tienen proporciones complicadas, como pueden ser las notas mi, la y si. En la afinación justa se persigue simplificar estas proporciones. Después de la octava y la quinta, la siguiente proporción más simple es la cuarta 4:3. Sin embargo, concatenar cuartas y quintas, o viceversa, no produce nuevos intervalos. En efecto, si añadimos una cuarta justa a una quinta justa, entonces tenemos que ⋅ = 2 y se genera una octava. Tampoco la concatenación de cuartas a partir de la nota do produce proporciones sencillas para las notas mi, la y si. Notas Do Re Mi Fa Sol La Si Do Proporción 1/1 9/8 81/64 4/3 3/2 27/16 243/128 2/1 Cents 0 203.91 407.82 498.04 701.96 905.87 1109.78 1200 Tabla 1: Afinación pitagórica para la escala diatónica Una opción es usar la proporción 5:4, que es la proporción asociada al quinto armónico, como muestra la serie armónica de la figura 1 (encima de cada armónico aparece la diferencia en cents con respecto a la división igual de la octava redondeado al entero más cercano). Figura 1: Serie armónica (figura adaptada de [Wik21a]) La proporción 5:4 genera una tercera mayor más consonante que la tercera pitagórica, que está dada por la proporción 81:64. Para comprobar esta afirmación, pínchese en el vídeo de más abajo, en que se pueden escuchar dos terceras mayores, la primera pitagórica y la segunda justa. Figura 2: Diferencia entre las terceras pitagórica y justa Si tomamos esta nueva proporción como base de la triada mayor, su proporción es 4:5:6, que significa que 5:4 es la proporción para do–mi y 6:4 = 3:2, la del intervalo do–sol. Saltando por quintas hacia arriba a partir de mi, obtenemos la nota si con una proporción de ⋅ = ; y si en cambio saltamos hacia abajo, entonces llegamos a la nota la mediante el siguiente cálculo: Este sistema de generar las notas de la escala diatónica se llama afinación justa o entonación justa. La tabla 2 muestra las proporciones y los valores en cents de la afinación justa, así como las diferencias entre esta y el temperamento igual y la afinación pitagórica. Obsérvese que la diferencia con las notas mi, la y si son grandes. Notas Do Re Mi Fa Sol La Si Do Proporción 1/1 9/8 5/4 4/3 3/2 5/3 15/8 2/1 Cents 0 203.91 386.31 498.04 701.96 884.35 1088.26 1200 Diferencia con el temperamento igual 0 3.91 -13.68 -1.96 1.96 -15.64 -11.73 1200 Diferencia con la afinación pitagórica 0 0 -21.51 0 0 -21.51 -21.51 0 Tabla 2: Afinación justa para la escala diatónica La diferencia entre las quintas justas (que son iguales que las pitagóricas) y las de temperamento igual no es tan pronunciada. Escúchese el vídeo de más abajo para apreciar las diferencias. Figura 3: Diferencia entre las quintas pitagórica y justa La triada mayor es un acorde que aparece en muchas culturas musicales; en particular, en la música occidental es un acorde fundamental de su armonía. Las afinaciones justas ya eran conocidas por los griegos. Dídimo primero alrededor del siglo I a.C. y más tarde Ptolomeo en el siglo II d.C. estudiaron y desarrollaron estas afinaciones en que la proporción 5:4 aparecen como generador de la afinación o de la escala. La tercer pitagórica tiene una proporción de 81:64 y la justa de 5:4. Su diferencia es = = 1.0125 y esta recibe varios nombres: coma sintónica, coma de Dídimo, coma ptolemaica o coma ordinaria. Si la palabra coma en esta serie aparece sin ningún adjetivo, nos estaremos refiriendo a la coma sintónica. En el audio de abajo aparecen la diferencia entre un do (frecuencia de 261.63 hercios) y un do más una coma sintónica (frecuencia de 264.900375 hercios). Figura 4: Diferencia de una coma sintónica entre dos notas 2.2. Escala cromática justa La afinación justa es en esencia un sistema de afinación en que las triadas mayores siguen la proporción 4:5:6. Las variaciones en las afinaciones justas provienen de cómo generan el resto de las notas hasta conseguir la escala cromática. Con el fin de describir mejor las afinaciones justas cromáticas, vamos a presentar la notación de Eitz; para una buena exposición de su origen y manejo, véanse [Bar51] y [Ben06]. La notación Eitz fue desarrollada por el músico y matemático del mismo nombre en 1891. Se basa en la idea de poner superíndices y subíndices a las notas que indiquen la desviación por comas sintónicas de la quintas puras. Así, la afinación pitagórica se escribe como: do0 - re0 - mi0 - fa0 - sol0 - la0 - si0 - do0 El superíndice 0 significa que todas las quintas son puras. Una nota que diga, por ejemplo, do-1 es un do obtenido por quintas menos una coma sintónica; análogamente, ocurre si nos encontramos do+1. Las notas que están a una coma por debajo se colocan en la fila de arriba y las que están una coma por encima se abajo. Entonces, la afinación justa de la escala diatónica aparece como sigue: la-1 mi-1 si-1 fa0 do0 sol0 re0 Figura 5: Afinación justa en la notación de Eitz La idea de colocar las notas con desviaciones de las quintas puras encima y debajo se debe al teórico de la música y compositor Hugo Riemann (no confundir con el matemático Bernhard Riemann de la hipótesis de Riemann). La notación de Eitz se generalizado en varias direcciones, por ejemplo, poniendo notas con diferentes comas (coma pitagórica, coma septimal, etc.). Siguiendo el libro de Barbour [Bar51] por su excelente exposición, vamos a describir algunas de las afinaciones justas más importantes descritas por su notación de Eitz. Empezamos con la afinación de Ramis de Pareja presentada en su libro Musica Practica de 1482. En sentido descendente de Pareja afina por quintas justas las sucesión sol-la♭ y luego partiendo de re-1 sube por quintas hasta el do#-1. Los acordes que quedan “bien afinados” son los correspondientes a las tonalidades do mayor, fa mayor y si♭ mayor. re-1 la-1 mi-1 si-1 fa#-1 do#-1 la♭0 mi♭0 si♭0 fa0 do0 sol0 Figura 6: Afinación justa de Ramis de Pareja Otra afinación justa interesante es la de Mersenne, publicada en 1637 (figura 7), donde se ven tres sucesiones de notas afinadas por quintas justas donde cada sucesión empieza a distancia respectiva de +1 coma, 0 comas y -1 coma contado desde la línea inferior. En realidad, Mersenne divide el círculo de quintas en tres sectores que afina por quintas justas. Ahora se aprecia que hay más triadas con afinación justa. re-1 la-1 mi-1 si-1 si♭0 fa♭0 do0 sol0 sol♭+1 re♭+1 la♭+1 mi♭+1 Figura 7: Afinación justa de Ramis de Pareja Hay muchas otras afinaciones justas, con frecuencia adaptadas al tipo concreto de instrumento (laúd, vihuela, órgano, etc.). De nuevo, recomendamos el libro de Barbour [Bar51] para un tratamiento riguroso e histórico de estas afinaciones. A modo de resumen, presentamos las principales características de las afinaciones justas: Los semitonos cromáticos son más pequeños que los semitonos diatónicos. Así, por ejemplo, sol# es más grave que la♭. Esto obligaba en los instrumentos de tecla a tener dos teclas diferentes, como se puede ver en la figura 8. Figura 8: Teclados con teclas para los semitonos cromáticos (figura adaptada de [Wik21b]) Como hemos visto más arriba, las terceras mayores justas son más pequeñas que las terceras pitagóricas y que las terceras del temperamento igual. Sin embargo, la situación es la contraria cuando se observan las terceras menores justas, que son más pequeñas que las correspondientes pitagóricas y de igual temperamento. La nota sensible es más grave en la afinación justa que en el caso pitagórico y de temperamento igual. Todos los tonos no tienen el mismo tamaño. Hay tonos grandes, como do–re, fa–sol, la–si, y tonos pequeños, como re–mi y sol–la. Los tonos grandes son mayores que los temperados, pero los tonos pequeños son menores. 3. Problemas armónicos de la afinación justa Volvamos a la afinación justa presentada más arriba: la-1 mi-1 si-1 fa0 do0 sol0 re0 Fijemos como tonalidad de referencia do mayor. Las triadas más importantes son las de los grados I, IV y V. En esta afinación esas triadas son do0-mi-1-sol0, sol0-si-1-re0 y fa0-la-1-do0. Las triadas menores vi y iii y vi, en cambio, tienen otra estructura en términos de afinación, a saber la-1-do0-mi-1 y mi-1-sol0-si-1. El problema aparece con la otra triada menor, la de ii, que es re0-fa0-la-1. En realidad, debería ser re-1-fa0-la-1. Si hiciésemos tal cosa, entonces el acorde del quinto grado se convertiría en sol0-si-1-re-1, y no funcionaría como un auténtico acorde de dominante. Para mayor comprensión de los problemas armónicos de la afinación justa, tomemos una progresión armónica muy común en la música occidental: I – vi – ii – V – I Parece razonablemente musicalmente hablando que cuando dos acordes adyacentes compartan una nota, esta no cambie de altura dentro de la afinación. Suponiendo de nuevo que la tonalidad es do mayor, el grado I es do0-mi-1-sol0. Por la regla que acabamos de establecer, el grado vi es la-1-do0-mi-1. Entonces, el grado ii es ahora re-1-fa0-la-1 porque la-1 es una nota en común y para mantener la distancia de quinta entre la primera nota del acorde y la tercera tenemos que establecer el re como re-1. A continuación, estaría el acorde de sol mayor. Como la nota re-1 es común, obtendremos el acorde sol-1- si-2-re-1. Por último, al caer en el primer grado, llegamos al acorde do-1- mi-2-sol-1. Hemos acabado una coma sintónica más bajo que cuando empezó la progresión. Esto en términos musicales no es aceptable. Escúchese de nuevo el audio de la figura 4. Esta situación se repite en secuencias de acordes tan usuales como I–IV–ii–V–I y I–iii–vi–ii–V–I, entre otras. Por último, recomendamos la lectura el libro de Benson [Ben06], páginas 173–176, para una discusión más profunda sobre los problemas armónicas de la afinación justa. 4. Escalas mesotónicas En esta sección entramos ya en las escalas mesotónicas. Este tipo de escalas pueden deducirse bien por una afinación, esto es, usando siempre proporciones enteras, o por temperamento, introduciendo números irracionales. Mostraremos ambos casos y empezaremos por los temperamentos. La idea esencial del temperamento mesotónico es la de afinar por terceras mayores puras a partir de la proporción 5:4. La escala mesotónica más común es la llamada escala mesotónica clásica o escala mesotónica de cuarto de tono. Las notas que se encuentran entre las notas afinadas por terceras justas se toman equidistantes con el siguiente procedimiento. Empezamos por la primera tercera mayor do–mi, de proporción 5∕4. La nota equidistante, la nota re, se afina con la proporción = ∕2. Esto nos deja la secuencia do–re–mi con las proporciones 1:∕2:5∕4. Con estas proporciones se afinan las secuencias fa–sol–la y sol–la–si. Sin embargo, antes de hacer afinar esas dos secuencias hay que decidir donde empiezan el fa. Hay dos semitonos que fijar, mi–fa y si–do. Las secuencias do–re–mi, fa–sol–la y sol–la–si suman 5 tonos de proporción ∕2 cada uno y, por tanto, quedan dos semitonos. Como hay que hacerlos equidistantes, se dividen por la mitad exacta. Eso en términos de proporciones equivale a extraer la raíz cuadrada. El semitono tiene, pues, el valor de: En esta cuenta estamos restando de la octava (el 2) los 5 semitonos (el 5) y la raíz cuadrada exterior aparece por la división en dos partes iguales. Entonces, para calcular la proporción de la nota fa, tenemos ⋅ = . Las proporciones finales del temperamento mesotónico clásico son: Notas Do Re Mi Fa Sol La Si Do Proporción 1/1 ∕2 5/4 2/1 Cents 0 193.15 386.31 503.42 696.57 884.73 1082.89 1200 Tabla 3: Temperamento mesotónico clásico para la escala diatónica Como se aprecia fácilmente en la tabla, las quintas ya no son puras (500 cents) y las terceras mayores son más pequeñas que en el temperamento igual. La nota sensible es más grave que en el temperamento igual. En cambio el semitono diatónico mi–fa es más grande. En la página web teoria.com [JRA21] el lector puede escuchar el Preludio en la bemol mayor BWV 862 de J. S. Bach en temperamento mesotónico. Una afinación mesotónica se puede conseguir a partir de la afinación pitagórica tomando la serie de quintas sucesivas y bajándolas un cuarto de coma sintónica en cada paso. Si empezamos en do, el diagrama de Eitz de una afinación mesotónica es este: mi-1 si-5∕4 do0 sol-1∕4 re-1∕2 la-3∕4 mi-1 fa+1∕4 do0 En general, una escala cromática se puede completar aplicando los principios anteriores, bien del temperamento o de la afinación. A modo de ejemplo, aquí tenemos la afinación mesotónica de Pietro Aaron del siglo XVI. mi-1 si-5∕4 fai#-3∕2 do#-7∕4 do0 sol-1∕4 re-1∕2 la-3∕4 mi-1 la♭+1 mi♭+3∕4 si♭+1∕2 fa♭+1∕4 do0 Figura 9: Afinación mesotónica de Pietro Aaron Se supone que las notas comunes de ambos extremos del diagrama de Eitz son las mismas (el do0 y el mi-1). La quinta del lobo se produce entre do# y la♭. Haciendo un ejercicio de abstracción, se pueden tomar diferentes divisiones de la coma sintónica. En el ejemplo anterior fue 1∕4, pero en general puede ser un número α ∈ (0,1). Cuando se piensa así, el esquema general de las afinaciones mesotónicas queda como sigue: mi-4α si-5α fa#-6α do#-7α sol#-8α doo sol-α re-2α la-3α mi-4α mi♭+3α si♭+2α fa♭α do0 Figura 10: Afinación mesotónica general 5. Para saber más El catedrático Luis Nuño, de la Universidad Politécnica de Valencia, y autor invitado de pasadas columnas, ha sacado varios vídeos ilustrando las afinaciones justas y pitagóricas. Dejamos dos de ellos a continuación. Figura 11: Entonación Justa: Batidos Figura 12: Entonación Justa: Implementación Práctica Desde la perspectiva histórica, dejamos otro vídeo de Elam Rotem, este sobre la afinación justa en el Renacimiento: Figura 13: Afinación justa en el Renacimiento En este vídeo se puede escuchar las suites y transcripciones para clave de Jean-Henry d'Anglebert, interpretadas por Byron Schenkman en un clave afinado con temperamento mesotónico de cuarto de tono. Figura 14: Suites y transcripciones para clave de Jean-Henry d'Anglebert, interpretadas por Byron Schenkman Una opción más sencilla que el programa de Audacity se puede encontrar en esta web: https://onlinetonegenerator.com/binauralbeats.html   Bibliografía [Bar51] J. Murray Barbour. Tuning and temperament: a historical survey. Dover Publications, Inc., New York, 1951. [Ben06] D. Benson. Music: A Mathematical Offering. Cambridge University Press, 2006. [Góm21] Paco Gómez. Afinamiento y temperamento (I), accedido el 20 de julio de 2021. [JRA21] José José Rodríguez Alvira. 2,500 años de temperamentos musicales, accedido el 20 de julio de 2021. [Wik21a] Wikipedia. Harmonic serie, accedido el 10 de julio de 2021. [Wik21b] Wikipedia. Split sharp, accedido el 20 de julio de 2021.

Domingo, 01 de Agosto de 2021 | Imprimir | PDF |  Correo electrónico