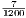251. 116. (Julio 2021) Afinación y temperamento (I)

1. Introducción Este artículo inaugura una serie sobre la afinación y el temperamento. Tras más de diez años de columna nunca habíamos tratado este fascinante e importante tema, cuyas implicaciones matemáticas, como veremos, son notables. Curiosamente, el primer artículo de esta columna, publicado nada menos que en enero de 2004 por Vicente Liern [Lie04], versaba sobre afinaciones y temperamentos. Ha llegado el momento de reparar semejante postergación y zambullirnos con entusiasmo en el fantástico reino de la afinación y el temperamento. Comenzamos aclarando la diferencia entre afinación y temperamento. Un sistema de afinación es la elección de notas en base a proporciones de números enteros entre frecuencias, esto es, en base a números racionales. Por ejemplo, una quinta en el sistema de afinación pitagórico tiene proporción 3:2. Un temperamento es un sistema de afinación en que algunos de los intervalos no se pueden expresar como números racionales. En el temperamento igual una quinta tiene proporción 2, que es claramente un número irracional. Intentar un examen de los sistemas de afinación y temperamento antes de la época de los griegos implica per se una alta cuota de especulación, ya que no han quedado restos escritos, únicamente restos arqueológicos fragmentarios y escasos. Como excepción, un grupo de arqueólogos descubrió en 2008 fragmentos de una flauta hecha perforando huesos de buitre y de mamut la cueva de Hohle Fels, al sur de Alemania [Jon15]. Estas flautas han recibido el nombre de flautas neardentales y su construcción se remontan a una horquilla de 42.000-43.000 años a.C. En el siguiente vídeo se muestra una reconstrucción de la flauta y se ve a un flautista profesional tocarla (véase del minuto 0:50 al 1:32). La flauta tiene 4 agujeros y las notas que emite corresponden aproximadamente a una escala diatónica (como se aprecia en el vídeo). Figura 1: Flauta neardental En este primer artículo vamos a cubrir los conceptos básicos de afinación y temperamento, que requieren solo matemáticas básicas, y a continuación a estudiar la afinación pitagórica. 2. Elementos básicos de la afinación y el temperamento 2.1. Frecuencias Empezaremos a la manera clásica, a partir del monocordio. El monocordio consiste en una cuerda montada sobre una caja de resonancia E como la de una guitarra o un violín. La cuerda está atada en el extremo A. Hay dos puentes movibles, B y C, que se usan para cambiar las frecuencias. D es una rueda movible y W es un peso, el cual se usa para estudiar la relación entre la tensión y la frecuencia; véase la figura 2. Para esta exposición, consideraremos que C está fijo y únicamente moveremos el puente B. El monocordio fue un instrumento con el que se enseñaba teoría de la música, especialmente intervalos y afinación, desde la antigüedad hasta la Edad Media. Figura 2: El monocordo (figura adaptada de [Wik21b]) Si ahora pulsamos la cuerda en algún punto del segmento BC, se producirá un sonido de frecuencia f. Si ahora movemos el puente B hasta la mitad del segmento AC, que es el punto F en la figura 3, y volvemos a pulsar la cuerda, ahora en algún punto intermedio de CF, el sonido producido tendrá frecuencia 2f.   Figura 3: Producción de un sonido una octava más agudo (figura adaptada de [Wik21b]) El sonido de frecuencia 2f lo oiremos como una octava más alto que el sonido de frecuencia f. Este hecho era ya conocido por los griegos y en especial por Pitágoras. Si tomamos la proporción entre la frecuencia del segundo sonido con respecto a la del primero, esta será de 2:1 y se corresponderá también con el cociente . Se pueden explorar otras proporciones, como por ejemplo, 3:2 o 4:3. Si movemos el puente B a un punto F de modo que , el sonido obtenido será el de una quinta perfecta. En general, dados dos sonidos de frecuencias f1,f2 con f1 < f2, el cociente da la diferencia de altura entre ellos. Así, si el cociente es 2, la diferencia es una octava; si el cociente es 3/2, es una quinta perfecta, y así sucesivamente. 2.2. División igual de la octava y cents Para precisar las diferencias entre los intervalos que aparecerán en los distintos sistemas de afinación y temperamento, necesitaremos un método para comparar intervalos. Hay muchos métodos, pero uno que permite una comparación cómoda y precisa es el de los cents. Formalmente, el cent es una unidad de comparación de frecuencias y se basa en la división de una octava en 1.200 partes. Un cent equivale a c = ≈ 1.00057778950655. Nótese que está definición se basa en el hecho de que las diferencias interválicas son factores multiplicativos de las frecuencias, como vimos en la sección anterior. En la escala cromática habitual, un semitono son 100 cents; una quinta, 700; y una octava, 1200. La ventaja de medir las diferencias de frecuencias con cents es que las octavas aparecen igualmente espaciadas y ello es porque los cents es una escala logarítmica. Si esas diferencias de frecuencias se miden en el espacio de las frecuencias, no aparecen igualmente espaciadas y la comparación es mucho más difícil. Dadas dos notas de frecuencias f1,f2, la diferencia en cents entre las dos (suponiendo f1 < f2) es Y, recíprocamente, si la frecuencia de la primera nota f1 es conocida así como el número de cents n hasta la segunda nota es En el temperamento igual, una tercera mayor son 400 cents, mientras que en la afinación pitagórica es de 407.82 cents; esta última cantidad se ha obtenido de introducir en la fórmula anterior la proporción entre las frecuencias, que es de , como veremos más adelante. 2.3. La serie armónica Para terminar esta sección, vamos a tratar la serie armónica, pues tiene importancia notable en los sistema de afinación y temperamentos. Muchos instrumentos musicales están basados en la emisión de frecuencias de una caja de resonancia, como por ejemplo en el caso de las cuerdas o de los instrumentos de viento. El sonido que se oye en esos instrumentos es una combinación de varias frecuencias que suenan a la vez. La frecuencia más grave se llama frecuencia fundamental y el resto de las frecuencias son los armónicos. Los armónicos tienen frecuencias que son múltiplos enteros de la frecuencia fundamental. Este conjuntos de armónicos asociados a una frecuencia fundamental se llama serie armónica. En la figura 4 se puede ver los primeros 20 términos de la serie armónica de un sonido de frecuencia 32.70, el do1 en notación científica. Encima de cada armónico aparece la diferencia en cents con respecto a la división igual de la octava redondeado al entero más cercano. Las notas marcadas en azul son resultan demasiado bajas y las notas en rojo, demasiado altas. En el caso del la♭, la diferencia es de +41 cents, que es casi un cuarto de tono, diferencia que es claramente perceptible por un oído normal. Figura 4: Serie armónica (figura adaptada de [Wik21a]) El segundo armónico es la octava, como se ve en la serie; el tercero es la quinta; el cuarto vuelve a ser la octava; el quinto es la tercera mayor (algo más baja que la tercera mayor de la división igual de la octava, unos 14 cents menos); y el sexto es la quinta. 3. Afinación pitagórica Los griegos tenían múltiples sistemas de afinación, que glosamos brevemente en la siguiente sección, pero la afinación que permaneció en la práctica común fue la afinación pitagórica. La afinación pitagórica establece las notas en base a los dos primeros intervalos de la serie armónica, esto es, la octava y la quinta, que tienen proporciones 2:1 y 3:2, respectivamente. Veamos cómo funciona tal construcción. Empecemos por tomar una nota cualquiera, digamos do. Usar la octava no da ningún intervalo nuevo distinto de la octava, de modo que aplicamos la proporción 3:2 para obtener nuevos intervalos. Como 3:2 es una quinta, llegamos a sol. Si multiplicamos la frecuencia de sol por 3:2, obtenemos re en la segunda octava, de proporción 9:4. Como queremos mantener las notas en una sola octava, pasamos este re a la primera octava dividiendo por 2. Esto da como resultado 9:8 como proporción del intervalo do–re; véase la tabla 1. Continuamos con este procedimiento y saltamos otra quinta desde re, multiplicando por 3∕2, y aterrizamos en la nota la, de proporción 27:16, que se mantiene en la octava de referencia. Damos otro salto, ahora a mi, pero salimos de la octava. Dividimos por dos la proporción y obtenemos 81:64. Por último, llegamos a la nota con otro salto de quinta y llegamos a la nota si, que nos da la proporción 243:128. En la tabla 1 se muestran todas las proporciones de la afinación pitagórica así como sus valores en cents. Se puede apreciar que todos los intervalos no son iguales con respecto al temperamento igual. Nótese además que la nota fa ha sido obtenida dan un salto hacia el registro grave en lugar de hacia el registro agudo. Su proporción se ha conseguido multiplicando por 2∕3 para bajar una quinta y por 2 para subir a la octava, lo que da una proporción de 4:3. Notas Do Re Mi Fa Sol La Si Do Proporción 1/1 9/8 81/64 4/3 3/2 27/16 243/128 2/1 Cents 0 203.91 407.82 498.04 701.96 905.87 1109.78 1200 Tabla 1: Afinación pitagórica para la escala diatónica La afinación pitagórica presenta varios problemas. El primero de ellos es el del tamaño de los semitonos. Un tono tiene proporción 9∕8, por ejemplo, do–re. Si tomamos el semitono si–do, que tiene proporción y formamos un tono con estos dos semitonos, obtenemos  ⋅ = ≈ 1.10985715, que claramente no es igual a 9∕8 = 1.125. El segundo problema viene dado por el círculo de quintas (más bien la espiral de quintas, como veremos). La tabla de arriba se puede completar de modo que incluya las 12 notas de la escala cromática. Se puede partir de un do y subir por quintas hasta el sol# y luego completar las notas que faltan, que son de do hasta la♭, descendiendo por quintas. La tabla de proporciones que resulta siguiendo este procedimiento se muestra a continuación: Notas Do Sol Re La Mi Si Fa# Do# Sol# Proporción 1/1 3/2 9/8 27/16 81/64 243/128 729/512 Cents 0 701.96 203.91 905.87 407.82 1109.78 611.73 113.68 815.64 Notas Do Fa Si♭ Mi♭ La♭ ~Sol# Proporción 1/1 4/3 9/16 32/27 128/81 Cents 0 498.04 996.09 294.13 792.18 Tabla 2: Afinación pitagórica para la escala cromática Si la tabla anterior la ponemos en forma de círculo de quintas, se entenderá el problema más claramente. En efecto, cuando se recorre el círculo de quintas en ambos sentidos las notas la♭ y sol# no coinciden, es decir, el círculo de quintas no se cierra. ¡En realidad, es una espiral de quintas! Y una espiral potencialmente infinita. Figura 5: Círculo de quintas con la afinación pitagórica (figura tomada de [Ben06]) La diferencia entre las notas la♭ y sol# se llama coma pitagórica o coma ditónica (el círculo en la figura) y corresponde a Esto significa que la afinación pitagórica funciona sobre el principio de que subir 12 quintas y bajar 7 octavas nos deja casi en el mismo sitio de que partimos. La diferencia es precisamente la coma pitagórica. Entre todas las quintas que produce el sistema pitagórico, la más desafinada es la quinta sol#-mi♭ (notada como una sexta disminuida). Recibe el elocuente nombre de quinta del lobo (se consideraba que se asemejaba al aullido de un lobo). Dado que los saltos de quinta nunca cierran el círculo, aparecen nuevas notas, como se muestra en la figura 6, donde se aprecia las dos primeras vueltas de la espiral. Figura 6: Espiral de quintas con la afinación pitagórica (figura tomada de [Ben06]) 4. Para saber más En música que no requiere cambios de tonalidad, como puede ser la música modal o la monodia, la afinación pitagórica es factible en la práctica musical; de hecho, ha sido así durante siglos y en muchas tradiciones musicales. A continuación, se mencionan varios ejemplos entre muchos posibles. El primero es del grupo Gothic voices, especializado en música antigua. Figura 7: Gothic voices - Il nome del bel fior El siguiente vídeo es un ejemplo en música instrumental, en este caso con un órgano portátil. Figura 8: Catalina Vicens - Audi Pontus, Audi Tellus, del Códice de Las Huelgas Para el lector ávido de profundizar en los sistemas de afinación y temperamento recomendamos el libro de Goldáraz Afinación y temperamentos históricos [Gol04] y con un sabor más matemático, el libro de Benson A mathematical offering [Ben06]. Un libro que brilla por su erudición es el de Barber [Bar51], de título Tuning and temperament: a historical survey. Recomendamos al lector la exposición de los sistemas de afinación griegos, que no han sido incluidos aquí por su excesiva longitud. Por último, no podemos dejar de recomendar los vídeos de Elam Rotem del proyecto Early Music Sources; el vídeo relevante en la columna de este mes es Temperaments - What you need to know [Rot20].   Bibliografía [Bar51] J. Murray Barbour. Tuning and temperament: a historical survey. Dover Publications, Inc., New York, 1951. [Ben06] D. Benson. Music: A Mathematical Offering. Cambridge University Press, 2006. [Gol04] J. Javier Goldáraz. Afinación y temperamentos históricos. Alianza Editorial, Madrid, 2004. [Jon15] Josh Jones. Hear the World's Oldest Instrument, the "Neanderthal Flute", Dating Back Over 43,000 Years, 10 de febrero de 2015. [Lie04] Vicente Liern. Afinación, enero de 2004. [Rot20] Elam Rotem. Temperaments - What you need to know, 9 de mayo de 2020. [Wik21a] Wikipedia. Harmonic series, accedido el 10 de julio de 2021. [Wik21b] Wikipedia. Monochord, accedido el 10 de julio de 2021.

Viernes, 16 de Julio de 2021 | Imprimir | PDF |  Correo electrónico

252. 196. (Septiembre 2021) El pricnipio deslíxico

La colección de libros The Mathematics of Various Entertaining Subjects (que va ya por su tercer volumen), editados por Jennifer Beineke y Jason Rosenhouse y publicados por Princeton University Press en 2015, 2017 y 2019, recoge las aportaciones de destacados especialistas en el área de la matemática recreativa dictadas en las conferencias MOVES (acrónimo de Mathematics Of Various Entertaining Subjects), organizadas cada dos años por el Museo Nacional de Matemáticas (MoMath) en Nueva York. En el prólogo del tercer volumen de la colección —cuyo subtítulo es precisamente "The magic of mathematics" (en la figura adjunta se muestra un fragmento de la portada)—, el medallista Fields Manjul Bhargava reflexiona sobre el concepto de matemática recreativa y el papel de cohesión que esta disciplina protagoniza para establecer las diferencias y similitudes entre matemática pura y matemática aplicada. Destaca también el gran éxito logrado por Martin Gardner al poner de manifiesto el poder de la matemática recreativa como fuente de inspiración de matemáticos y no matemáticos en su objetivo final de disfrutar de las matemáticas. Justifica con estas palabras la iniciativa de las citadas conferencias MOVES: Debe quedar claro que —con la creciente importancia del enfoque educativo conocido como STEM (acrónimo de Science, Technology, Engineering and Mathematics) para el avance de la sociedad y la humanidad— la matemática recreativa, además de ser divertida, también puede desempeñar un papel fundamental para alentar a la juventud a dedicarse a las matemáticas y campos relacionados. Es con este último objetivo en mente que la conferencia MOVES fue creada en 2013. MOVES reúne a maestros, estudiantes, aficionados y profesionales de todo el mundo para celebrar y compartir ideas y avances en matemática recreativa. En los últimos años, cada conferencia de MOVES ha tenido un tema. En 2017, el tema de MOVES fue "La magia de las matemáticas". Fue un gran placer participar en MOVES 2017 y un verdadero honor ser uno de sus dos oradores principales junto con mi maestro y gran amigo, Persi Diaconis. En el capítulo 12 del libro encontramos el artículo firmado por Persi Diaconis y Ron Graham titulado "The magic of Charles Sanders Peirce" (artículo que también puede encontrarse entre los papeles del recientemente fallecido Ron Graham). En dicho artículo tratan de desentrañar los secretos que ocultan los sofisticados juegos de magia que Charles Peirce publicó en 1908 y 1909 para la revista The Monist bajo el título común "Some amazing mazes". Casi simultáneamente a la conferencia de Diaconis y Graham, ya recogimos en este rincón (en el número 154 de noviembre de 2017) algunos intentos anteriores de comprender el fundamento matemático de la magia de Charles Peirce por parte de ilustres magos como Tom Ranson y Alex Elmsley pero profundizaremos un poco más recogiendo algunas ideas desarrolladas en este nuevo artículo. El artículo es muy extenso y prolijo así que nos limitaremos a describir un original principio contenido en los trabajos de Peirce y aclarado  por Diaconis y Graham, bautizado por estos como "principio disléxico". Lo ilustraremos con un ejemplo para el que necesitarás doce tarjetas o papeles rectangulares. En seis de ellos escribirás las seis primeras letras del alfabeto y en los otros seis escribirás los seis primeros números naturales. Coloca sobre la mesa las tarjetas formando dos filas, donde la fila superior contiene las seis letras, por orden alfabético, y la fila inferior contiene los seis números, en orden creciente. Te quedará algo como esta figura: Elige libremente cualquier tarjeta de la fila superior y cualquier tarjeta de la fila inferior. Luego intercambia sus posiciones; habrá un número en la fila superior y una letra en la fila inferior, pero no puedo saber dónde está cada símbolo. Repite esta misma operación con los otros cinco pares de letras y números. En cada paso elegirás una letra de la fila superior y un número de la fila inferior e intercambiarás sus posiciones. Evidentemente, cada vez la elección será menos libre porque habrá menos letras en la fila superior. Al final del proceso tendrás nuevamente dos filas de tarjetas pero ahora la fila superior tendrá sólo números y la fila inferior tendrá sólo letras. Lo más importante es que nadie puede saber el orden en que han quedado los símbolos en ambas filas. Si quieres sorprenderte a ti mismo, gira caras abajo las tarjetas de la fila inferior. Quedará algo parecido a esta figura (aunque el orden de los números será el que tú has elegido): Voy a tratar de adivinar qué posición ocupa la letra A. Para ello, sólo necesito saber cuál es el primer número de la fila superior. Si es un 1, la letra A será la primera carta de la fila inferior; si es un 2, será la segunda; si es un 3, será la tercera y así sucesivamente. En la imagen anterior, la letra A ocuparía la segunda posición de su fila. Seguro que sabrás encontrar también las posiciones de las demás letras. Por ejemplo, para saber dónde está la letra D, busca el valor de la cuarta carta de la fila superior; dicho valor indicará la posición del cuatro en la fila inferior. En nuestro ejemplo, como la cuarta carta es el 1, la letra D será la primera carta de la fila. Con un poco de reflexión, se comprende fácilmente el fundamento del juego: como sólo se intercambian las tarjetas por parejas, la posición de una de ellas determina el valor de la otra. Esto significa que no importa el número de tarjetas que tiene cada fila, el juego se puede realizar con cualquier cantidad de tarjetas. Además, se puede ocultar un poco el secreto si las tarjetas no se colocan inicialmente en el orden natural: para ello debes ser capaz de llevar la cuenta mental de las posiciones iniciales de cada tarjeta. Incluso, se puede jugar con otro tipo de tarjetas, dos palabras con las mismas letras pero con diferente significado (por ejemplo, ANCESTRO/CARTONES, BOLERAS/ARBOLES, ARSENICO/ESCARNIO, o cualesquiera que puedas descubrir en páginas generadoras de anagramas), dos conjuntos de cartas, digamos rojas y negras, como el juego original de Peirce o la versión de Diaconis y Graham, etc. Más interesante todavía es el resultado matemático del proceso seguido en el juego: resulta que las dos permutaciones obtenidas en las filas de tarjetas son inversas. No vamos a desarrollar aquí la teoría de grupos finitos que contiene el estudio de las permutaciones pero, si tienes ganas, el artículo de Diaconis y Graham detalla un poco más esta analogía. Aprovechando esta propiedad, se comprueba fácilmente que el juego también se puede realizar a partir de dos permutaciones inversas cualesquiera. En resumidas cuentas, los juegos de magia de Charles Peirce podían ser poco prácticos pero los principios matemáticos involucrados fueron muy originales y complejos y todavía no se ha desvelado todo su potencial. El propio Martin Gardner lo evaluaba con estas palabras: No puedo recomendarlo para quien quiera entretener a los amigos a menos que tengan pasión por la teoría de números, pero es excelente para un profesor que quiera motivar el interés de los estudiantes hacia la aritmética de congruencias. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Lunes, 06 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico

253. Israel Gelfand (1913-2009)

El matemático Israel Gelfand (1913-2009) nació un 2 de septiembre. Hizo importantes contribuciones a varias ramas de las matemáticas, incluyendo la teoría de grupos, teoría de la representación y el análisis funcional. Recibió numerosos premios y honores, entre ellos tres veces la Orden de Lenin por su investigación, el Premio Wolf en 1978 o el Premio Kyoto en 1989. Es también conocido por tener generaciones de estudiantes educados e inspirados por su legendario seminario en la Universidad Estatal de Moscú. Algunos de los trabajos o conceptos matemáticos relacionados con Gelfand son: el libro Calculus of Variations (1963), escrito junto a Sergei Fomin; la representación de Gelfand en teoría de álgebras de Banach; el teorema de Gelfand–Mazur en teoría de álgebras de Banach; el teorema de Gelfand–Naimark; la construcción de Gelfand–Naimark–Segal; los espacios de Gelfand–Shilov; la integral de Gelfand–Pettis; conjecturas sobre el teorema del índice de Atiyah–Singer; la cohomología de Gelfand–Fuks en teoría de foliaciones; la dimensión de Gelfand–Kirillov; la teoría de Gelfand–Levitan en ecuaciones diferenciales ordinarias; las ecuaciones de Gelfand–Dikii en el área del cálculo de variaciones; teoría de representación de grupos de Lie clásicos, teoría de distribuciones, geometría integral, functores de Coxeter, y un largo etcétera. Más información: Wikipedia Israel Gelfand en la página de Terence Tao Lista de publicaciones de Israel Gelfand Página en su honor The Unity of Mathematics. In Honor of the Ninetieth Birthday of I.M. Gelfand (proceedings) Israel Moiseevich Gelfand, Notices of the AMS 60, no. 1 y no.2 (parte 1 y parte 2) Obituario en El País (por Manuel de León) Obituario en The Telegraph Obituario en The Guardian Obituario en Los Angeles Times Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 02 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico

254. 75. (Septiembre 2021) Lujosos estuches de instrumentos matemáticos

(Lujosos estuches de instrumentos matemáticos) La Revolución Científica del Renacimiento queda patente en la variedad y calidad de los instrumentos matemáticos. Los reyes, príncipes. aristócratas ilustrados, altos dignatarios y la élite profesional constituyen un mercado para los fabricantes de instrumentos de precisión. En forma de arcón, estuche, caja o armario se hacen juegos completos con variados instrumentos de cálculo, dibujo u observación. Pantómetras, compases, escuadras, astrolabios, transportadores, paralelógrafos, curvígrafos, pantógrafos, cuadrantes y otros objetos son fabricados con delicadeza. El material habitual es el latón, pero también se usaba la plata o el marfil. El cartón o la madera se utilizaba para instrumentos baratos, no nobles. Detallemos algunas de los estuches que pueden visitarse en museos y palacios. Arcón matemático de Carlos II El duque de Medinaceli encargó al padre José Zaragoza un cofre matemático para regalárselo a Carlos II con motivo de sus catorze años en 1675. El eminente matemático y teólogo jesuita cumplió y por ello hoy podemos disfrutarlo, protegido por una urna, dentro del Museo de la Biblioteca Nacional de Madrid. Entendemos que tan extraña ubicación del cofre se debe a la publicación por el padre Zaragoza de un manual de uso de los instrumentos. Libro que pasó por la imprenta y que podemos encontrar en varias bibliotecas, incluso ha sido digitalizado. Lamentablemente algunas copias no contiene las siete láminas desplegables con las figuras de los instrumentos. El arcón contiene instrumentos geométricos con uso para la fortificación, el dibujo, la música y el cálculo. Los instrumentos construidos fueron 14 como los años que cumplía el rey hechizado, la lista de instrumentos es la siguiente: Regla, Pantómetra [compás de Galileo generalizado], Triángulo , Cruz geométrica [ballestina], Rombo gráfico [pantógrafo], Triángulo equilátero mayor, Equilátero menor, Antojo de larga vista, Nomo [Compás armónico], Compás de varilla para la pantómetra, Cadenilla de diez pasos, Mesa de palosanto, Pies para la mesa e instrumentos y Escuadra de una vara. La generalidad de los instrumentos están construidos en latón y son de grandes dimensiones. Quizá el instrumento más interesante es la pantómetra, un gran compás de Galileo, generalizado y ampliado, que permite tanto cálculos al modo euclidiano como dibujar polígonos y también -por detrás- estudiar la armonía musical. Los cálculos con la pantómetra necesitan la ayuda de un compás convencional., (Arcón de Carlos II. 1675. Biblioteca Nacional. Madrid) Caja de Instrumentos de Wilhelm V en Kassel El Gabinete Astronómico-físico del Palacio de la Orangerie es el lugar donde se almacenan los instrumentos del Landgraf Wilhelm IV de Kassel-Hessen, un gobernante que no solo fue mecenas de la ciencia matemática emergente sino que el mismo fue fervoroso practicante. Tycho Brahe y Jost Bürgi dejaron su huella en Kassel. Destacamos el Estuche de Instrumentos Matemáticos de 1628 que perteneció a Wilhelm V, nieto de Wilhelm el Sabio. Los instrumentos son de bella factura de latón: pantógrafo, reglas, escuadras, inclinómetros, etc. Rodearse de instrumentos de observación, cálculo y dibujo se convirtió en algo habitual para los príncipes del Renacimiento y la tradición se conservó. (Estuche de Wilhelm V . 1628. Palacio de la Orangerie. Kassel) La caja de instrumentos matemáticos de Maguncia El Landesmuseum de Mainz muestra en exposición una lujosa caja de instrumentos matemáticos de 1712 que perteneció a Maximilian von Welsch, el ingeniero responsable de las obras de fortificación de la ciudad. (Uno de los tres cajones de von Welsch. 1712. Landesmuseum- Maguncia) La caja, más bien se trata de una pequeña maleta, tiene tres niveles. En el fondo se almacenan los instrumentos topográficos, la zona intermedia se dedica al dibujo y coloreado, y la parte superior a los compases, transportador, pantómetras, cuadrantes, escuadra, brújula, reglas, escalas… Los acabados en latón y acero son esmerados y de gran calidad. Los talleres alemanes venían mostrando desde el siglo XVI su destreza en la fabricación de instrumentos de precisión. Los cofres de instrumentos del Tesoro de Munich La Cámara del Tesoro del Palacio Real de Munich, Residenz, conserva dos lujosos cofres de instrumentos. Especialmente el arca de los hermanos Lencker, realizado en Núremberg hacia 1580. Se trata de un bello contenedor esmaltado ornado con alegorías de las distintas disciplinas. Reproducimos las representaciones de la Aritmética y la Geometría. (Cofrecillo de Lencker. 1580. Residenz. Munich) Johannes Lencker fue orfebre y artista gráfico. Junto con Wenzel Jamnitzer y Lorenz Stöer, es uno de los tres maestros de Núremberg que se ocupan de la perspectiva matemática en profundidad. La ciudad fue la primera en pagar un profesor de matemáticas desde la finanzas locales. El erote de la Aritmética tiene la correspondiente tablilla de números y el de la Geometría utiliza el compás sobre el globo. La caja está delicadamente esmaltada y ha perdido gran parte de su contenido. El único objeto matemático que permanece es una regla. El otro baúl es muy posterior, perteneció a María Luisa de Austria y fue fabricado en París en 1810. Se trata de una maleta de equipaje muy bien equipada, con utensilios muy diversos que van desde el aseo personal a las matemáticas. Resulta curioso encontrar un compartimiento con reglas (nácar y latón) y compases junto a jabones, cubiertos y cepillos. No olvidemos portar instrumentos geométricos, pues como decía Don Quijote de las matemáticas: siempre podemos tener necesidad de ellas. Instrumentos del “Historisches” en Fráncfort (Maleta de instrumentos astronómicos y topográficos. 1620. Historisches museum. Fráncfort) El laberíntico Historisches museum de Fráncfort del Meno ha reconstruido la historia de la ciudad imperial usando las colecciones de sus ciudadanos y las herramientas de sus artesanos. No podían faltar instrumentos científicos, medida y patrones que pertenecieron a Wilhelm Dilich (1571-1650), maestro de obras de la ciudad (Transportador de la colección Dilich. 1620. Historisches museum. Fráncfort) La calidad de los fabricantes de instrumentos se pone de manifiesto al final de la visita con los astrolabios, transportadores y otros artificios geométricos. La caja completa con astrolabio que mostramos es un buen ejemplo de la maestría alcanzada. Los estuches del Museo Galileo El Instituto y Museo de Historia de la Ciencia cambió su nombre por Museo Galileo en el año 2010. El Galileo de Florencia es uno de los mejores museos de instrumentos matemáticos históricos del mundo. Astrolabios, relojes de sol, esferas armilares, cuadrantes, cajas de instrumentos, telescopios, calculadoras mecánicas primitivas y un sinfín de objetos hacen que el museo sea el justo complemento de la cercana Galería de los Uffizi. Son las dos caras del esplendor de la ciudad renacentista: arte y ciencia. Los estuches son múltiples y muestran la evolución desde el siglo XVI al XVIII. (Estuche matemático. Siglo XVIII . Museo Galileo. Florencia) Las cajas de uso común (Estuche matemático. Siglo XVIII . Palacio de la Orangerie. Kassel) En contraste con los lujosos, reproducimos una caja más modesta y tardía que también se encuentra en el  museo de Kassel. Este tipo compacto fue el modelo práctico más usado hasta el siglo XIX por militares, marinos e ingenieros. Incluye la pantómetra como calculadora.

Miércoles, 01 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico

255. Agosto 2021: Matemáticas con una baraja corriente (II)

1. Introducción. En la primera parte de este artículo ya se expuso cuál era su principal objetivo: mostrar una serie de juegos matemáticos para repasar el cálculo numérico de una forma lúdica. Todo el que esté interesado un poco en los materiales didácticos para el aula de matemáticas, sabe que se pueden encontrar multitud de juegos y barajas creadas especialmente para trabajar conceptos matemáticos en el aula. Este tipo de material suele estar indicado para practicar contenidos que ya se hayan asimilado, con lo que se pueden utilizar para afianzar esos contenidos, tras haberlos visto en clase o en cursos posteriores, se pueden usar como repaso e introducción a la profundización en esos conceptos. Las posibilidades que nos brindan hoy en día las tecnologías nos permiten crear con relativa facilidad cualquier tipo de cartas que necesitemos, si es que nos queremos tomar la molestia de adaptarlas a nuestra situación concreta. En caso contrario, podemos encontrar en internet docenas de barajas de cartas para todos los ítems que nos ofrecen sus autores, y que sólo tenemos que copiar y utilizar. Pero el objetivo de los juegos presentados para el epígrafe de baraja corriente va un poco más allá, y presenta juegos que se pueden practicar utilizando una baraja de las que se utilizan para los juegos tradicionales como el póker o el tute. Son juegos en los que lo que nos interesan son las cantidades que aparecen en las cartas y que nos permiten hacer con ellas operaciones. Lo que le da una dimensión diferente es usar un material que no se asocia normalmente a la escuela, y que la propia aleatoriedad que lleva el extraer cartas de una baraja nos permite plantear el mismo problema con valores muy diversos. En la primera parte se agruparon una serie de juegos que trabajaban las operaciones básicas de sumas, restas y productos. En este segundo bloque vamos a trabajar conceptos más elevados como fracciones, redondeo, múltiplos, potencias, etc… Vamos a comenzar con algo que debería haber entrado en el anterior, pero que por extensión lo hemos pasado a éste. Me refiero la ordenación de resultados, aunque en todo juego en el que se realiza una operación, y al final gana el que tenga el mayor o menor resultado, se está trabajando de alguna manera, la ordenación. En cierta forma, se puede considerar que la primera parte, junto con la ordenación, iba más dirigida a infantil y primaria y esta segunda parte se ajustaría más a secundaria o último ciclo de primaria. Pero esta división no es estricta. Hay juegos del artículo anterior que se pueden trabajar en secundaria, por ejemplo como repaso o en curso con alumnos con dificultades como en compensatoria o similares, y varios de los que veremos aquí se pueden trabajar en primaria, quizás reduciendo los números con los que vamos a proponerlos. Para los juegos de esta segunda parte he abusado libremente del material de mi amiga Ana García Azcárate. Varios de los juegos son adaptados o directamente copiados de los que ella misma ofrece en su impresionante blog de juegos (ver referencias al final). Aunque algunos de los juegos ya habían aparecido en los libros del Grupo Azarquiel o en los editados por ella misma, yo los he recogido directamente del blog, por lo que sólo pondré esa referencia. De todos modos, en el blog hay información sobre los libros, que es un material que debería haber, al menos, en toda biblioteca del departamento de matemáticas. 2. Los seises. Se juega con una baraja española de 40 cartas (es decir sin 8 y 9) y está pensada para cuatro jugadores. Pueden jugar también 5 ó 3 jugadores. En este último caso, se coloca sobre la mesa el seis de oros y se reparten entre los tres las 39 restantes. Comienza el juego quien tenga el seis de oros que lo coloca sobre la mesa, si hay tres jugadores se considera que quien ha repartido ha comenzado la partida colocando el seis de oros sobre la mesa. El jugador a su derecha tiene que colocar o el 5 o el 7 de oros al lado correspondiente del seis ya colocado. Si no tiene ninguno de los dos puede colocar otro seis. En caso contrario para el turno. A partir de ahí, cada jugador en su turno puede colocar una carta ordenada a la izquierda o derecha de las filas, que se irán formando para cada palo. Gana el primer jugador que coloca todas sus cartas sobre la mesa. Imagen 1: Partida parcial de los seises. Este juego es quizás más conocido como El Cinquillo, en el que proceso es igual con la variación de que cada palo se comienza colocando el 5 en lugar del 6. El objetivo del juego es básicamente practicar el orden de los números naturales. Podemos ampliar a la baraja completa de 48 cartas, en cuyo caso se puede empezar cada fila por el seis o el siete. O incluso trabajar con los palos de la baraja francesa para tener trece números que ordenar. En este caso se suele salir con el 7 de corazones. Una vez dominado el juego, y según el nivel donde estemos trabajando, se pueden plantear investigaciones a partir de problemas planteados. Por ejemplo, se muestra la imagen 1 anterior y se pregunta: ¿si yo he colocado la sota de copas, qué cartas puede haber colocado el jugador anterior? Otro problema es, ¿qué posibilidades tengo de poder colocar una carta a continuación de las que ya están puestas sobre la mesa? En este caso hay que contar las que faltan por colocar y en cuántas de ellas puede colocarse según la distribución ya colocada. Otro problema más complicado es mostrar una distribución como la de la imagen 1 y preguntar de cuántas formas diferentes hemos podido llegar a esa colocación final. En este tipo de problema conviene comenzar con un planteamiento con menos cartas. 3. Cartas ordenadas. Es un juego pensado para tres o cuatro jugadores y se puede jugar tanto con la baraja española como la francesa. Se reparten cinco cartas a cada jugador y se echa una carta del mazo sobre la mesa. Comenzando por el jugador a la derecha del que ha repartido y siempre en sentido antihorario, cada jugador, en su turno, tiene que lanzar una carta que supere a la última carta sobre la mesa. Si no puede hacerlo toma una carta del mazo, si puede la coloca, y si no se queda con ella y pasa el turno. Con idea de hacer más dinámico el juego, cuando se llega al rey, se cambia el orden de las cartas y entonces hay que colocar una carta menor que la última sobre la mesa, hasta llegar al uno, en cuyo caso se vuelve a cambiar al orden ascendente y así sucesivamente. El juego acaba cuando el mazo se ha acabado y nadie puede poner carta, por ejemplo, se está colocando una carta superior y sobre la mesa ha quedado el 10, y nadie tiene en las manos una carta superior al 10. En ese caso gana el que tenga menos cartas en la mano. También acaba el juego si durante el proceso algún jugador consigue colocar todas sus cartas. 4. Mi valor es más grande. Se reparten todas las cartas de una baraja entre los jugadores, que suelen ser cuatro. En cada ronda, todos los jugadores muestran una de sus cartas colocándola boca arriba sobre la mesa. Quién tenga la carta mayor se lleva todas las de la ronda. Si en un momento hay un empate, los jugadores que han empatado recogen sus cartas y vuelven a echar de nuevo, y el ganador se lleva las cartas. Hay veces, que los que han empatado, echan cartas menores y es posible que alguno de los que antes perdía al final queda ganador. Siempre el que tenga mayor valor se lleva las cuatro cartas mostradas. Al final gana quien haya recogido más cartas. Una posibilidad es variar la regla y considerar que gana quien tenga menos puntuación. También se puede trabajar el orden después de haber realizado una operación. Se coloca el mazo sobre la mesa y cada jugador toma dos cartas del montón, las suma y el que obtenga el mayor valor se queda con las cartas de todos. En este caso la operación se puede modificar y trabajar la resta o el producto, con el fin de practicar esas operaciones. De la misma manera se puede considerar que gana el que tenga la menor puntuación, lo que es interesante si trabajamos la resta y admitimos números negativos, pues ya sabemos que el orden en negativos siempre cuesta más trabajo. 5. Jerarquía de operaciones. Todos los que ya hemos cumplido algunas décadas recordaremos seguramente un exitoso programa televisivo de la década de los 90 y los 2000. Me refiero al programa, inicialmente de la TVE, conocido como Cifras y Letras. Este programa estaba basado en el titulado Des chiffres et des lettres, programa francés creado en 1972, aunque desde 1965 existía uno similar pero solo con la parte de letras. El programa en su momento causó bastante expectación hasta el punto de que no era raro que en las semanas culturales de los centros educativos, dentro de las actividades complementarias, se organizaran concursos entre alumnos con la misma estructura. La parte de cifras consistía en que se daban seis números menores que 100 y otro número de tres cifras, y utilizando las cuatro operaciones aritméticas básicas y todos o alguno de esos seis números, había que conseguir el de tres cifras. Esta idea puede estar basada en el juego que se conoce como 24, que según la Wikipedia, fue un juego que se jugaba en la década de los 60 en Shanghai. En él se utiliza una baraja de cartas normal, a la que se le han extraído las figuras. Se entregan cuatro cartas a un jugador y con esos números y las operaciones básicas, hay que conseguir el 24. Como hay gente muy lista, en 1988 Robert Sun patentó y comercializó este juego en forma de cartas, con la característica de que cada carta del juego tiene cuatro números ya fijados, y el jugador sólo toma una carta y ya tiene los valores con los que trabajar. Ana García Azcárate tiene una adaptación de este juego con las reglas y las cartas con que trabajari. Con lo anterior, he pretendido dejar claro que lo que propongo a continuación no es original sino adaptado de un tipo de actividad muy corriente. Sólo es cambiar la forma de plantearlo y, como hemos dicho antes, utilizar una baraja normal de cartas sin necesidad de imprimir o plastificar nada. Mi propuesta se juega con las cartas del 1 al 9 de una baraja, sea francesa o española. Se barajan las cartas y cada jugador coloca cinco cartas boca arriba sobre la mesa. A continuación, extrae otras dos cartas de la baraja y con ellas forma un número de dos cifras que será el objetivo a alcanzar. Selecciona las cartas que están sobre la mesa y con las que puede conseguir el número objetivo utilizando las operaciones básicas. El alumno debe escribir la operación respetando la jerarquía de operaciones y utilizando paréntesis si fuese necesario. Si el jugador consigue el valor buscado, recoge de la mesa las cartas que haya utilizado y las coloca en un montó propio aparte. Si no lo consigue pasa el turno. En ambos casos, las dos cartas que se han utilizado para crear el número objetivo se devuelven al mazo introduciéndolas entre las cartas que quedan en él. Si el jugador no resuelve el problema y otro jugador encuentra la solución, éste jugador, aunque no sea su turno, puede mostrar el cálculo y recoger las cartas que hay sobre la mesa. A veces, se contempla la posibilidad de que si un jugador consigue, por ejemplo, con tres cartas la solución y otro jugador observa que se pueden utilizar cuatro o cinco de las cartas a la vista para hallar el valor objetivo del juego, entonces éste segundo jugador es el que se lleva el premio de recoger las cartas. Con esta regla obligamos a que se utilice la mayor cantidad de cartas, aunque lógicamente, mientras más cartas se utilicen más puntos se consiguen. Una vez que ha pasado el turno al siguiente jugador, lo primero que debe hacer es completar con cartas del mazo las cinco que deben estar a la vista sobre la mesa, si en el turno anterior se hubiese retirado alguna carta. Después saca dos cartas para formar el número que debe conseguir y se repite el proceso. Cuando se acaba el mazo, gana la partida quien tenga más cartas en su poder. Una regla restrictiva que se puede añadir es que la primera carta que se saca del mazo sea la de las decenas del valor a conseguir, y la segunda la de las unidades. Si no se exige esto, el jugador tiene opciones de formar dos números diferentes, por lo que puede decidir, a la vista de las cartas que están sobre la mesa, cuál es el número que le interesa como objetivo a conseguir. Si se juega de esta forma, puede ser que el jugador tarde mucho tiempo en buscar la solución, por lo que los contrarios pueden llegar a aburrirse esperando. Por ello, es conveniente fijar un tiempo máximo para encontrar la solución y si se termina se considera que el jugador no ha resuelto el problema y pasa el turno. La modalidad anterior es una propuestaii de Ana García Azcárate, pero hay otra modalidad que trata de paliar el problema anterior y es que todos jueguen a la vez. En este caso, se reparten cinco cartas a cada jugador y se extraen dos, primero decenas y después unidades, del número a conseguir y se colocan en medio de la mesa. Cada jugador intenta conseguir ese valor con la mayor cantidad de cartas posibles. Si uno, o varios, lo logran, igual que en la modalidad anterior, apartan todas las cartas que han utilizado para lograrlo. Si nadie consigue el valor exacto se suele considerar ganador aquel jugador que se ha acercado más al valor objetivo. Una vez acabado el turno se recoge las dos cartas que han fijado el valor, se mezclan dentro del mazo, se reponen las cartas que cada jugador haya apartado, de forma que vuelvan a tener cinco cartas en la mano y se vuelve a plantear un nuevo reto a alcanzar. Es conveniente que los jugadores dejen escrito, de forma adecuada, la operación que ha hecho, para así poder confirmar que el resultado es correcto. Si otro jugador descubre que una operación, realizada por un jugador, no es válida se anula el resultado de ese jugador. Ahora vamos a ver unos juegos donde trabajar los números enteros. Para utilizar números positivos y negativos se puede trabajar de dos maneras. Una es utilizar las cartas para obtener el número y complementarlo con una moneda o un dado para asignarle el valor positivo o negativo. El otro modo, que a mí me gusta más, es trabajar con las cartas de la baraja francesa considerando que las cartas negras son positivas y las rojas negativas. Así, el 7 de tréboles correspondería a +7 y el tres de corazones a -3. No debe ser una mala idea cuando he encontrado, buscando información para estos artículos, otras páginas donde se reproduce ese esquema. En concreto en la página de Denise Gaskiniii donde existen muchos juegos para trabajar con una baraja de cartas de póker. En esa página plantea una serie de enfrentamientos, que ella llama Guerra matemática, título que me parece horroroso, y entre ellos aparece el siguiente. 6. Competición de enteros. Es un juego para dos jugadores y se utilizan las cartas de una baraja francesa, sin las figuras, y considerando positivos los números de los palos de cartas negras y negativos los de cartas rojas. Cada jugador toma dos cartas del mazo, que se habrá barajado previamente y colocado boca abajo en mitad de la mesa. Los jugadores suman los valores de las dos cartas y gana el que obtenga el mayor valor de las cartas. El que gana se lleva las cuatro cartas que se han utilizado en la jugada y las almacena en un montón propio de descartes. Al final gana quien haya conseguido más cartas. En la página anterior plantea el mismo enfrentamiento pero realizando el producto en lugar de la suma. Es conveniente que los alumnos anoten en una hoja la operación y el resultado obtenido, pues pueden aparecer errores corrientes en las operaciones con enteros. Por supuesto, si el contrario del jugador que se proclama ganador observa que ese jugador se ha confundido al hacer la operación, entonces pierde la jugada y se la lleva el contrario. Esto último se puede considerar, aunque el supuesto ganador al equivocarse haya dicho menos valor del que realmente tiene. Es decir, jugador que se equivoca en la operación pierde la jugada. Retorciendo más aún el tema, si los dos jugadores se han equivocado, las cartas se devuelven al mazo y hay que barajar de nuevo. Esta regla obliga a que cada jugador compruebe no sólo su cálculo sino el del contrario. En ambos casos propuestos, se puede plantear que gana el que obtiene el menor valor. Lo curioso es que no plantea la que me parece la opción más interesante y que es restar los dos números, pues ahí es donde aparecen las mayores dificultades de las operaciones con enteros. Se puede jugar de dos maneras. La primera carta que se extrae es el minuendo y la segunda el sustraendo, o bien, se sacan dos números enteros aleatoriamente, y el jugador decide cuál de los dos es el minuendo y cuál es el que se resta de él. De esta manera puede realizar dos operaciones distintas y elegir la que se acerque más a su objetivo, conseguir el mayor o el menor valor posible. Si se considera la segunda opción es conveniente que el contrario no vea nuestras cartas hasta que hayamos elegido el resultado que más nos conviene. En cualquiera de las otras modalidades da igual que las cartas extraídas de la baraja estén o no a la vista. En todos los casos, al decir el resultado hay que mostrar las cartas e indicar qué operación hemos realizado para llegar a ese valor. Este juego, que también plantea una versión Ana García Azcárate en su blog, se puede jugar con hasta cuatro jugadores y repartiéndose las cartas entre los jugadores. Como ella plantea usar sólo hasta el 9, se puede repartir todo el mazo entre los dos, tres o cuatro jugadores. Cada jugador toma entonces las dos cartas de su propio mazo. A mí me gusta más tomarlo del mazo central, aunque haya varios jugadores. 7. Jerarquía de operaciones con enteros. Este juego también lo encontré inicialmente en el blog de Ana García Azcárateiv, aunque allí lo plantea con unas cartas especiales que van desde el -12 hasta el 12, yo prefiero hacerlo con las cartas francesas tal como hemos dicho anteriormente. Y he adaptado algunos aspectos. Es un juego que se puede hacer en grupos de dos a seis jugadores o incluso se puede plantear para todo el curso clase. Trabajamos con las 40 cartas del 1 al 10 de la baraja francesa, siendo las negras positivas y las rojas negativas. Se mezclan las cartas del mazo y se extraen seis cartas. Con ellas, se colocan en las casillas de la siguiente operación y se realizan las operaciones correspondientes. Imagen 2: Orden para el juego de cartas con enteros. Gana el jugador que obtiene el valor más grande como resultado y se anota un punto. Si los restantes jugadores observan que la operación es incorrecta (sobre todo hay que ser muy cuidadosos con la jerarquía de operaciones) el alumno se anota un punto negativo y gana el jugador que le siga en orden. Es importante que la jerarquía de operaciones se respete. Si hay dificultades para hallar la división última, se puede permitir el uso de calculadora para la operación final. A veces, se juega haciendo un alumno de juez que con una calculadora científica comprueba que el resultado es el indicado. Hay alumnos que tardan mucho en encontrar una posible solución, por lo que a veces es conveniente fijar un tiempo límite para hallar la solución. Lo normal es que se dé un tiempo prudencial y los jugadores puedan encontrar distintas cadenas Se puede poner la restricción de que el número que se obtenga debe ser el mayor entero que se pueda obtener, es decir, no se puede obtener decimales en el resultado. Se puede cambiar el objetivo para obtener el menor valor posible. Si el profesor juega con toda la clase, puede en cada jugada modificar el orden en que se deben hacer las operaciones. También se pueden proponer distintas distribuciones de operaciones, como la de la imagen 2, y se realizan distintas jugadas utilizando en cada ocasión un tablero distinto. Después del número de partidas que se estimen oportunas, según el tiempo que se tarde en el juego, gana quien tenga más puntos. En el planteamiento de Ana García hay distintas variaciones. Se separan las cartas negras y las cartas rojas en dos mazos diferentes, se barajan y se extraen tres cartas de cada uno de ellos. De esa forma trabajamos con tres números positivos y tres negativos. Para animar a conseguir puntos se deja un tiempo prudencial para que los alumnos construyan todas las cadenas que puedan, variando el orden como colocan los enteros, y entonces se puntúa 2 puntos por obtener el mayor valor, otros dos por obtener el menos valor y un punto por cada una de las cadenas rellenas que sean correctas, es decir, que se obtenga el resultado que se indica. 8. Redondeando mi número. Este es un juego muy simple para practicar el redondeo. Se trabaja con las cartas del 1 al 9, sean de la baraja francesa o española ampliada, y un dado. Pueden jugar hasta seis jugadores. Se reparten todas las cartas del mazo mientras sea posible. Es decir, si hay cinco jugadores reciben siete cartas cada uno y se desprecia la última del mazo. Es conveniente que jueguen varios jugadores, es decir, con dos o tres jugadores no tiene mucho sentido pues se tienen muchas cartas en la mano y casi todo serán empates. Se lanza el dado y se multiplica el resultado obtenido por 10. Cada jugador busca entre sus cartas y escoge dos con las que obtener un número cuyo redondeo sea el valor obtenido. Por ejemplo, si sale un 3 y por tanto el valor buscado es 30, los jugadores pueden construir desde el 25 hasta el 34, salvo el propio 30, claro está. Gana el jugador que presenta el número más cercano al buscado. Cuando decimos más cercano nos referimos a aquel que tenga menor diferencia con el valor buscado. El que lo consiga se anota un punto. Puede haber varios jugadores que presenten números con esa característica, por ejemplo, para llegar a 30 un jugador puede presentar el 29 y otro el 31. En ese caso ambos se anota un punto. Se vuelven a guardar las cartas utilizadas en el mazo que tienen los jugadores en la mano y se vuelve a lanzar el dado para repetir el proceso. Después de diez jugadas gana el jugador que ha obtenido más puntos. Este juego tiene el inconveniente de que si en el reparto inicial a un jugador no le entra ningún nueve ni ningún uno, lo tiene difícil para conseguir ganar el juego. Por ello, lo que se suele hacer es, después de tres jugadas, se recogen las cartas, se vuelven a barajar y a repartir. En ese situación gana el que tiene más puntos después de doce jugadas. Con idea de animar el juego, se pueden añadir reglas que permitan conseguir más puntos. Una sería que quien consiga el número más cercano al buscado recibe dos puntos y el que escriba el más alejado, siempre dentro de que su redondeo es el valor buscado, se anota un punto. De esta forma un jugador debe estimar si le interesa ir al valor más grande o más pequeño dependiendo de las cartas que tenga. Otra forma, para que no sean siempre los mismos los que consigan puntos, es darle un punto a todo el que presente un número cuyo redondeo sea el número buscado y dos puntos extra al que tenga el más cercano. Si lo mezclamos con lo anterior, daríamos un punto extra al que presenta el más alejado del objetivo. Si se tiene disponibilidad se debe jugar con dados, en lugar de cúbicos, con ocho o diez caras de los que se utilizan en los juegos de rol. En caso contrario siempre se puede construir una ruleta artesanal con la cantidad de números que se quiera. 9. Múltiplos y divisores. También podemos trabajar con múltiplos y divisores utilizando las cartas. Jugarían dos o tres jugadores con la baraja del 1 al 9. Se barajan las cartas y se muestra aleatoriamente un valor que debe ser mayor que 3. Si sale un número menor que cuatro se extrae otra carta. Una vez que se tiene el objetivo a conseguir, se vuelve a introducir la carta en medio del mazo y se reparten todas las cartas. Entonces cada jugador tiene que ver cuántos múltiplos del número fijado puede conseguir uniendo dos cartas, es decir tienen que ser siempre múltiplos de dos cifras. Muestra los múltiplos y se anota un punto por cada múltiplo que ha obtenido. Si los contrarios observan que uno de los supuestos múltiplos es un camelo, ese valor se retira de las soluciones. Para la siguiente jugada se recogen todas las cartas y se vuelve a repetir el proceso. Gana quien tenga más puntuación después de cinco jugadas. En el blog de Ana García Azcárate existe un juego similarv, pero donde se trabaja con una baraja especial. En ese juego el valor del que hay que calcular el múltiplo se obtiene asignando un valor a las caras de un dado, del 1 al 6 hay que conseguir los múltiplos de 4, 5, 6, 7, 9 y 11. Se puede construir una ruleta casera donde se coloquen los números de los que queremos hallar sus múltiplos, pues incluir el 11 ya añade un valor de dos cifras y además limita mucho el encontrar múltiplos. Para trabajar los divisores se debe disponer de dos dados cúbicos, o uno que se lanza dos veces. En cada jugada, quien se encargue de repartir las cartas, lanza los dos dados y forma un número que no sea primo. Si no hay posibilidad se vuelven a lanzan los dos dados. Esto se puede obviar haciendo como antes extrayendo, previo al reparto, dos cartas de la baraja y formando el número objetivo. Una vez fijado el objetivo, se reparten todas las cartas y cada jugador se descarta de todas las cartas que sean divisores del número propuesto. Se pueden considerar divisores de una sola carta o formada por dos. Por ejemplo, hemos formado el número 38 con las dos cartas, entonces un jugador se puede descartas del 1, del 2 y del 19. Las cartas descartadas se van acumulando en un montón personal de descartes. Al acabar la jugada se cuentan cuantos puntos – cartas se han obtenido en el descarte. Igual que en el caso anterior, al acabar la jugada se recogen todas las cartas, pasa el mazo al jugador a la derecha del que repartió antes y se repite el proceso. 10. Y seguimos en el juego. Cuando comencé a escribir sobre este tema, ya tenía mucho material descartado del libro de juegos que habíamos escrito el Grupo Alquerque. Como a mí me tocó la parte de cartas, había recogido mucho material que no entró en esa publicación, aparte de los juegos que ya había trabajado en clase. Cuando me puse a escribir amplié el banco de juegos y de pronto me encontré con que no cabían los juegos que me gustaban en un solo artículo, por lo que lo amplié, como en otras ocasiones, a dos. Pero al enrollarme con distintas opciones me encontré con que el tema daba más de sí de lo previsto y por eso he tenido que dejar una serie de juegos en los que vamos a trabajar con fracciones, potencias y raíces para el tercer, y prometo que último, artículo de esta serie de juegos. Allí nos volvemos a encontrar. 11. Referencias. Aparte de las direcciones que aparecen al final del capítulo, las referencias generales serían las siguientes. Página “Pasatiempos y juegos en clase de matemáticas” de Ana García Azcárate. Revisada el 10 de mayo de 2020. https://anagarciaazcarate.wordpress.com/ Página “Juguemos a las matemáticas” de Denise Gaskins. Revisada el 10 de mayo de 2020. https://denisegaskins.com/   Notas: [i] https://anagarciaazcarate.wordpress.com/2017/11/28/juego-conseguir-24-jerarquia-de-las-operaciones/ [ii] https://anagarciaazcarate.wordpress.com/2018/03/27/baraja-para-jerarquia-de-operaciones/ [iii] https://denisegaskins.com/2006/12/29/the-game-that-is-worth-1000-worksheets/ [iv] https://anagarciaazcarate.wordpress.com/2018/10/09/calculos-con-numeros-enteros-competicion/ [v] https://anagarciaazcarate.wordpress.com/2017/01/10/multiplos-y-dados-baraja/

Domingo, 01 de Agosto de 2021 | Imprimir | PDF |  Correo electrónico

256. Brian Weaver presenta sus reverspectivas

Una reverspectiva es una ilusión óptica sobre una superficie 3D, en la que las partes de la imagen que parecen más lejanas son de hecho las que físicamente están más cerca del observador. http://www.thisiscolossal.com/wp-content/uploads/2014/07/reverse.gif En el video de debajo se ve una reverspectiva del artista Brian Weaver, que forma parte de la exposición 3D Art: An Exhibition of Reverse Perspective by Brian Weavers. http://www.thegalleryatice.co.uk/exhibitions/ El artista británico Patrick Hughes –ver ‘Reverspectivas’ de Patrick Hughes en ::ZTFNews, en la que se explica esta técnica– es el ‘padre’ de esta forma de arte ilusorio. En este video de Brian Weaver se muestra otra de sus obras que utiliza esta perspectiva invertida. Visto en Neatorama. Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Lunes, 19 de Julio de 2021 | Imprimir | PDF |  Correo electrónico

257. ‘Reverspectivas’ de Patrick Hughes

El artista Patrick Hughes (1939-) crea imágenes con la técnica de la reverspectiva, una ilusión óptica sobre una superficie 3D, en la que las partes de la imagen que parecen más lejanas son de hecho las que físicamente están más cerca del observador. Patrick Hughes, “Tea Shop”, 2013 http://www.patrickhughes.co.uk/ Cuando la pintura se ve de frente, se percibe una superficie plana; pero al mover la cabeza la superficie 3D aparece, se acentúa la profundidad de la imagen… Patrick Hughes, “Vanishing Venice” http://en.wikipedia.org/wiki/File:Vanishing_Venice_-_Patrick_Hughes.jpg La figura de arriba se titula Vanishing Venice: en realidad es una figura 3D, formada por dos pirámides que sobresalen hacia el espectador y con  ‘los picos’ eliminados (es decir, dos troncos de pirámide): las bases de las pirámides están más alejadas (contra la pared). Los dos rectángulos más claros, que parecen estar muy alejados, al fondo de la imagen, son en realidad la parte más cercana al observador. Estructura física de “Vanishing Venice” http://en.wikipedia.org/wiki/File:Hughes-Venice-diagram2.jpg —oOo— Diferentes trabajos sobre la psicología de la percepción tratan sobre la reverspectiva: Nicholas Wade, Fooling the eyes: trompe l’oeil and reverse perspective“, Perception 28, 1115-1119, 1999 Thomas V. Papathomas, Experiments on the role of painted cues in Hughes’s reverspectives, Perception 31, 521-530, 2002 Thomas V. Papathomas & Lisa Bono Lisa, Experiments with a hollow mask and a reverspective: Top-down influences in the inversion effect for 3-D stimuli, Perception 33, 1129-1138, 2004 Thomas V. Papathomas, Art pieces that ‘move’ in our minds – An explanation of illusory motion based on depth reversal, Spatial Vision 21, 79-95, 2007 M. Wagner, WH Ehrenstein, Thomas V. Papathomas, Vergence in reverspective: Percept-driven versus data-driven eye movement control, Neurosci Lett. 449(2), 2009 Rebecca Achtman & Duje Tadin, Reverse Perspective —oOo— Muchas y muchos artistas se dedican ahora a crear ilusiones con esta técnica de la ‘perspectiva invertida‘. Os dejo unos cuantos videos de Patrick Hughes para disfrutar: —oOo— Visto en Futility Closet e información obtenida en Wikipedia. Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Lunes, 19 de Julio de 2021 | Imprimir | PDF |  Correo electrónico

258. ¡Quédate en tu cola!

La teoría de colas es el estudio matemático de las colas o líneas de espera en un sistema: analiza factores como el tiempo de espera medio o la capacidad de trabajo del sistema sin que llegue a colapsarse. Captura de pantalla de “Stay in Queue” de Ferdinand Lutz La teoría de colas podría haber enseñado a este pobre oso que era mejor no cambiar de fila… Ya lo decía Harper… No importa en qué cola se sitúe: La otra siempre avanzará más rápido. Primera Ley de Harper Y si se cambia de cola, aquélla en la que estaba al principio empezará a ir más deprisa. Segunda Ley de Harper Nota 1: El corto Stay in Queue de Ferdinand Lutz ganó el primer puesto en el festival Kurz.film.spiele en 2008 Nota 2: Visto en Neatorama Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Martes, 13 de Julio de 2021 | Imprimir | PDF |  Correo electrónico

259. El problema de Freudenthal

El problema de Freudenthal apareció publicado por primera vez en 1969, en la revista Nieuw Archief voor Wiskunde, en la que el matemático Hans Freudenthal (1905-1990) era el redactor de la sección de ‘problemas’. Copia de la publicación original, problema No. 223, en [1]. El problema –con la redacción adaptada, pero sin cambiar la parte matemática– dice lo siguiente: Jesús, María y José son tres amigos. Jesús elige dos números enteros x e y, donde 1 < x < y, y x + y ≤ 100. Jesús dice a María el resultado del producto P = xy y a José le informa del valor de la suma S = x+y. A continuación tiene lugar el siguiente diálogo: María: Desconozco los valores de x e y. José: Ya sabía que te era imposible saber los valores de x e y. María: Bien, ahora, ya conozco x e y. José:  Bien, ahora yo también sé sus valores. ¿Quiénes son x e y? Hans Freudenthal En [2], se discuten varias de las soluciones propuestas –muchas de ellas de conocidas personas del ámbito matemático– y se da el resultado: x = 4 e y = 13. ¿Cómo se ha llegado a ello? Reproduzco el argumento utilizado (extraído de [3]) para su resolución, aunque es preciso realizar algunos cálculos (sencillos, pero largos) para llegar a ello. A priori, hay muchos pares de números enteros que cumplen las condiciones dadas en el enunciado. Pero la frase 1. de María permite eliminar algunos (los que sólo pueden escribirse de una única manera como un producto xy). Las frases 2., 3. y 4. permiten eliminar sucesivamente todos los demás pares posibles, excepto uno de ellos. Vamos a ir razonando poco a poco. (i) María conoce el producto P = xy, pero no sabe los valores de x y de y. Eso significa que el número P pose varias posibles descomposiciones. Este es el caso, por ejemplo de 12 = 2×6 = 3×4, 18 = 2×9 = 3×6, y tantos otros. Si se pasa revista a todos los posibles productos, existen 574 productos ambiguos, es decir, que pueden descomponerse de al menos dos maneras diferentes. Llamemos P1 al conjunto de estos números ambiguos: el primero es 12 y el último es 2400 (2400 = 40×60 = 48×50): P1 = . (ii) José conoce la suma S = x+y. Como José dice: ‘Ya sabía que te era imposible saber los valores de x e y’, eso significa que, para todas las maneras de descomponer S como suma de dos enteros, S = 2+(S-2) = 3+(S-3),… todas dan un producto ambiguo, que es por lo tanto un elemento de P1 . Ese es el caso, por ejemplo de 11 = 2+9 que tiene como producto 18, 11 = 3+8 de producto 24, 11 = 4+7 de producto 28, 11 = 5+6 de producto 30. Estas sumas dan lugar al conjunto S1 = . (iii) María dice que, con esa información, reconoce los valores de x e y. Eso significa que entre las muchas descomposiciones de P = xy que son un producto ambiguo, sólo una da una suma S = x+y que pertenece a S1. Por ejemplo, si María piensa en el producto 18 = 2×9 = 3×6, constata que sólo el par (2,9) tiene una suma perteneciente a S1. Los productos ambiguos para los que sólo una descomposición pertenece a S1 describen un conjunto P2 que se reduce a 86 elementos en vez de los 574 que contenía P1: P2 = . (iv) José dice que también conoce los valores de los números elegidos por Jesús. Eso significa que entre las descomposiciones de la suma S = x+y, sólo una da como producto un elemento de P2. Por ejemplo, 11 = 2+9 = 3+8 = 4+7 = 5+6, da como posibles productos 18, 24, 28 y 30, y dos de esos productos pertenecen a P2. En este caso, María no podría dar x e y. Las sumas tales que una única descomposición da un producto perteneciente a P2 se reducen al número 17; en efecto: 17 = 2+15 = 3+14 = 4+13 = 5+12 = 6+11 = 7+10 = 8+9, cuyos productos son 30, 42, 52, 60, 66, 70 y 72, y sólo 52 está en P2 . Por lo tanto, María (y nosotras y nosotros) sabe que x+y= 17 y que xy = 52, y por lo tanto, x = 4 e y = 13. Visto en Le Blog d’ABC Maths Más información: [1] H. Freudenthal, Nieuw Archief Voor Wiskunde, Ser 3, 17 (1969) 152 (planteamiento del problema) [2] H. Freudenthal, Nieuw Archief Voor Wiskunde, Ser 3, 18 (1970) 102-106 (solucón del problema) [3] Hans Freudenthal, Wikipedia (en francés) [4] Sum and Product Puzzle, Wikipedia [5] Jean-Paul Delahaye, L’incroyable problème de Freudenthal, Interstices, 2008 [6] Hans van Ditmarsch, Jan van Eijck, and L.C. Verbrugge, Publieke Werken Freudenthal’s Som-en-productraadsel, NAW 5/10 nr. 2 juni 2009, 126-131 Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Martes, 13 de Julio de 2021 | Imprimir | PDF |  Correo electrónico

260. Cómo nace un teorema

Autor: Cédric Villani Editorial: Catarata Año de Publicación: 2021 Nº de Hojas: 240 ISBN: 978-84-1352-258-6

Miércoles, 07 de Julio de 2021 | Imprimir | PDF |  Correo electrónico | Leer más