271. Recomendaciones matemáticas para el verano

ABC, 28 de Junio de 2021 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 28 de Junio de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

272. Sí, las matemáticas resuelven problemas reales y estos son algunos ejemplos

ABC, 21 de Junio de 2021 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 21 de Junio de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

273. Junio 2021: La ratonera, una investigación en matemáticas con cartas

1. Los juegos como creación de matemáticas. Los que llevamos mucho tiempo, algunos más de treinta años, utilizando los juegos en nuestras clases de matemáticas, nos hemos encontrado en ocasiones con compañeros que han despreciado la utilización de dicho recurso, por considerar que no estaban en consonancia con la “seriedad” que requiere la investigación y la enseñanza de dicha disciplina. Como si lo lúdico no tuviese cabida en las matemáticas. Posiblemente, esas personas no sepan la estrecha relación que ha habido, a lo largo de la historia, entre el juego y las matemáticas. En varios casos, las matemáticas han surgido o han evolucionado al calor de los juegos, y normalmente esos juegos han iluminado las mentes más brillantes de esa historia. Por citar sólo unos breves ejemplos de cómo los aspectos lúdicos han estado siempre relacionados con las matemáticas, basta citar el problema de los bueyes atribuido a Arquímedes, pero también Leonardo de Pisa, más conocido como Fibonacci, planteó muchos problemas numéricos como juegos para animar a su resolución. El científico universal Gotfried W. Leibniz no pudo ser más claro con el comentario en una de sus cartas “Nunca son los hombres más ingeniosos que en la invención de los juegos... Sería deseable que se hiciese un curso entero de juegos, tratados matemáticamente". El, quizás no tan conocido, matemático italiano Leon Battista Alberti publicó en 1542 el libro Juegos matemáticos, donde planteaba problemas geométricos y físicos en forma de juegos y situaciones recreativas. Pero además, hay partes de las matemáticas que han surgido a partir de juegos. Por ejemplo, el genial matemático Leonhard Euler puso los cimientos de la teoría de grafos al estudiar el paseo que realizaban los habitantes de Köninsberg (actual Kaliningrado). La Teoría de Juegos fue desarrollada por el matemático húngaro-estadounidense John Von Neumann, junto al economista alemán Oskar Morgenstern. Esta teoría y su aplicación a la economía le valieron al matemático estadounidense John Nash el Premio Nobel de Economía en 1994. Pero si hay una parte de las matemáticas que deja clara evidencia de cómo el juego puede servir para, tras su investigación, dar pie a un desarrollo matemático, esa es la probabilidad y el azar. Ya el matemático italiano Gerolamo Cardano (1501 – 1576) escribió el libro Liber de ludo aleae, que no fue publicado hasta 1663, donde hacía un estudio de los juegos de azar. Ese estudio se adelantó casi un siglo a la consulta que hizo el Caballero de Meré a los matemáticos Pierre de Fermat y Blaise Pascal, de cuya correspondencia saldrían las bases para la fundamentación teórica de la probabilidad. Aunque sería el matemático neerlandes Christiaan Huygens el primero en publicar en 1656 un libro sobre probabilidad con el título De Ratiociniis in Ludo Aleae. Otros muchos matemáticos estudiaron los juegos de azar, como el francés Pierre Rémond de Montmort, que publicó en 1708 la primera edición de Essai de Analyse sur les jeux de hazards, en el que dedicaba su segunda parte a los juegos de cartas y la tercera a los juegos de dados. También el suizo Jakob Bernouilli escribió Ars Conjectandi, que no se publicó hasta 1713, ocho años después de su muerte. Y en 1812 se publicó Théorie analytique des probabilités de Pierre Simón Laplace con un estudio analítico de los juegos. Hay muchos más nombres famosos de las matemáticas que han tenido relación con los juegos. Se dice que el alemán Carl Friedrich Gauss (1777 – 1855) era un gran aficionado a los juegos de cartas, e incluso anotaba cuidadosamente las jugadas en que participaba para estudiarlas posteriormente. Con esto hemos querido dejar de manifiesto que los grandes nombres de las matemáticas siempre han estado fascinados por las matemáticas que regían los juegos. Pero es que esa fascinación sigue vigente y matemáticos más recientes no sólo han estudiado los juegos, sino que han inventado algunos muy interesantes. Como el que queremos presentar hoy, un curioso solitario con cartas que permite investigar con números. 2. El prolífico Arthur Cayley. Lo primero es hablar un poco del inventor del juego, ya que no es uno de los nombres que suele sonar a los aficionados matemáticos. El británico Arthur Cayley (1821 – 1895) está considerado como uno de los fundadores de la escuela de matemáticas puras en su país. Se educó en el conocido Trinity College de Cambridge, donde estudió y fue profesor Isaac Newton, estudiando derecho y matemáticas. Aunque inicialmente ejerció como abogado, desde 1863 fue profesor de matemáticas puras en la Universidad de Cambridge en la cátedra sadleiriana. Cayley es uno de los matemáticos más prolíficos de la historia, sólo por detrás de Euler y Cauchy, ya que escribió casi mil artículos, lo que equivale a trece volúmenes con toda su obrai. Se puede ver que sólo la lista de artículos incluidos en la colección ocupa 68 páginas. Aunque desarrolló sus estudios en muchas partes de la matemática, es conocido por sus avances en el álgebra lineal. Fue el introductor del concepto de matriz, estudiando sus propiedades y también desarrolló las características y propiedades de los determinantes, siendo quien creó la actual notación. Pero también estudió los invariantes algebraicos o la geometría n-dimensional, o introdujo la noción de grupo abstracto. Además, llegó a la conclusión de que la geometría métrica estaba incluida en la proyectiva, lo que fijó el rumbo para que años más tarde Felix Klein abordara las geometrías no euclídeas. Descubrió muchos otros elementos, por ejemplo, los octoniones, que son una extensión no asociativa de los cuaterniones y que suelen recibir el nombre de números de Cayley. Aunque hay otros elementos que llevan su nombre como el Grafo de Cayley, un grafo que nuestra la estructura de un grupo. Y muchos teoremas que llevan su nombre en colaboración con otros matemáticos. Comentar para acabar, que recibió muchos méritos en su país, por ejemplo la Medalla de la Reina, la Medalla de Morgan o la Medalla Copley, de la Royal Society a la que pertenecía, y que en la Luna existe un cráter nombrado en su honor. En 1857 publicó un pequeño artículo en la revista Quarterly Journal of pure and Applied Mathematics con el título “A problem in permutations” donde proponía, en la página 79 del volumen 1 de la revista, el juego La Ratonera (Mousetrap) que presentamos en este artículo. 3. La ratonera. El juego inventado por Cayley es un solitario que es muy interesante para trabajar el concepto de permutación. Aunque se puede trabajar directamente con números, es mucho más atractivo afrontarlo utilizando cartas tal como lo propuso el creador. Vamos a proponerlo como nos gusta presentarlo y después veremos sus variaciones. Tomamos las trece cartas de un palo de la baraja, en el que suponemos que la J tiene el valor de 11, la reina (la Q) valdría 12 y el rey (la K) equivaldría al 13. Se mezclan las 13 cartas obteniendo una permutación de las treces cartas, y se comienza el juego. Aunque mi amigo Raúl Ibáñez, en el artículo de donde he sacado este juego, plantea jugar con las cartas boca abajo, a mí me gusta más tener la cara de las cartas a la vista. La dinámica del juego es muy simple. Se comienza a contar por 1 hasta 13, si la carta que tenemos delante no coincide con el número que acabamos de decir, se coloca esa carta detrás del mazo. Si la carta coincide con el número que decimos en ese momento, se deja sobre la mesa y comenzamos a contar de nuevo desde uno con el mazo tal como nos ha quedado. Si en algún momento llegamos a contar 13 y ninguna de las cartas que nos queda en la mano ha coincidido en su momento con el orden que hemos ido contando, la partida se pierde. Solo se gana si se consigue colocar todas las cartas sobre la mesa. En el planteamiento original de Cayler, las cartas se colocaban formando un círculo. Lo que nosotros hemos propuesto es equivalente pues al colocar las cartas, que no se pueden apartar, detrás del mazo en realidad estamos jugando como si las cartas estuviesen en círculo. El juego se puede plantear para una serie menor de cartas, basta que tengamos n cartas numeradas del 1 al n y realicemos con ellas una permutación. Veamos un ejemplo utilizando sólo seis cartas. Partimos de la distribución de la imagen siguiente. Imagen 1: Permutación de 6 perdedora. El primer en salir sería el 3, pues al contar 3 nos encontraríamos con esa carta. Nos quedarían las cartas ordenadas como 5 6 1 4 2. Al empezar a contar de nuevo desde uno, el 4 estaría en su lugar correspondiente, luego sería la siguiente carta en salir y la distribución que nos quedaría sería 2 5 6 1 y si de forma cíclica contamos desde 1 hasta 6 ya no podríamos sacar ninguna otra carta, luego hemos acabado la partida y perdido. Veamos otro ejemplo, ahora con la siguiente distribución de cartas. Imagen 2: Permutación de 6 ganadora. Vamos a colocar una tabla donde veamos las cartas como van saliendo y como queda el orden en el mazo. Cartas que salen Orden resultante en el mazo   2 4 3 1 6 5 3 1 6 5 2 4 3 1 6 5 2 4 3 1 4 6 5 2 3 1 4 5 2 6 3 1 4 5 6 2 3 1 4 5 6 2   Por lo que con esta distribución ganamos la partida. El planteamiento del juego puede ser, como hemos dicho, como solitario. Tomamos las treces cartas, las barajamos aleatoriamente y comprobamos si el resultado obtenido es ganador o no. Incluso si jugamos varias partidas, ya que son muy rápidas, estudiar en qué proporción ganamos o, por ejemplo, en qué proporción de juegos no podemos separar ni una carta siquiera. Pero vamos a ver que el estudio da para algo más profundo. 4. Investigación combinatoria. En el artículo que hemos comentado, en apenas 25 líneas Cayley plantea su juego de cartas, da algunas soluciones y deja una última frase indicando que el juego requiere una teoría general. A Cayley lo que le interesaba era el estudio de qué permutaciones eran ganadoras y cómo encontrar el número de casos en que se descartaban una determinada cantidad de cartas. Por ejemplo, si partimos del mazo con 13 cartas, en cuantas de las 6.227.020.800 permutaciones posibles se consiguen separar 3 cartas. Dado el número de permutaciones posibles podemos suponer que no es un problema fácilmente resoluble sin herramientas matemáticas muy potentes. Muchos matemáticos han recogido el reto de Cayley y han investigado el juego. El primero el propio Cayley. En la misma revista en que presentó el juego, pero en el volumen 15 de 1878, apareció un nuevo artículo con el título “On the game of Mousetrap” en el que estudiaba todas las opciones para un caso particular de cuatro cartas. Lo curioso de esta revista, que puede consultarse en internetii, es que incluía un total de 16 artículos del propio Cayley, tratando temas tan diversos como problemas goniométricos, determinantes, superficies cuárticas, función arcoseno de números complejos, etc.. En la misma revista aparecía un artículo del político y matemático Adolph Steen (1816 – 1886) con el título “Some formulae respecting the game of mousetrap” en el que, como indicaba su título, mostraba algunas fórmulas relacionadas con el juego. En ellas estudiaba cuántas permutaciones de n cartas cumplían que la primera carta en salir era una determinada de antemano, por ejemplo la j, siendo 1 ≤ j ≤ n, y otras fórmulas similares. En este artículo había algunos errores que se corrigieron en 1993 en el artículo “Mousetrap”iii publicado en el volumen 1 de la revista Combinatorics, Paul Erdős is Eighty por el británico Richard Guy y el canadiense Richard Nowakowsky. También en el artículo de 1994 publicado por Daniel Mundfrom, de la Universidad de Kentucky Oriental, con el título “A problema in permutations: the game of Mousetrap”iv y aparecido en la revista European Journal of Combinatorics. Pero el juego ha seguido interesando a los matemáticos. En 2009 el informático británico Michael Spivey publicó, en la última revista anterior, el artículo “Staircase rook polynomials and Cayley's game of Mousetrap”v, en el que estudia polinomios que calculan la cantidad de permutaciones en que se elimina una carta determinada o una pareja de cartas determinadas. El estudio de las permutaciones que son ganadoras, o que permiten separar alguna carta, es fácil para pocos valores. En el segundo artículo de Cayley sobre La Ratonera, del que hemos hablado en este epígrafe, el propio creador del juego hace un estudio de completo de las soluciones que podemos obtener con cuatro cartas, podemos verlo en la siguiente imagen extraída de la revista Quarterly Journal of pure and Applied Mathematics. Imagen 3: página del artículo de Cayley. En él puede apreciarse que hay 6 permutaciones ganadoras, 3 donde pueden extraerse dos caras, otras 3 donde se extrae sólo una carta y 9 en la que no se puede extraer ningún carta. 5. La sucesión A007709. En 1964 el matemático británico-estadounidense Neil Solane creó la base de datos OEISvi, iniciales en inglés de la Enciclopedia On-line de Secuencias de números Enteros. Aunque no sé el dato actualizado, hace dos años el número de sucesiones y series incluidas en la base de datos sobrepasaba las 300.000. Cualquier persona puede incluir una secuencia numérica de enteros que no esté incluida, si es que la encuentra. En esa base de datos existen un total de 27 resultados relacionados con el juego Mousetrap. Entre ellas, podemos citar la sucesión A007709, incluida por el propio Sloane, que nos da el número de combinaciones ganadoras en el juego según el número de cartas. Esa sucesión es: 1, 1, 2, 6, 15, 84, 330, 1812, 9978, 65503, 449719, 3674670, 28886593, 266242729, 2527701273, 25749021720 Los primeros números son fáciles de comprobar. Si tenemos una sola carta, hay una sola permutación, el 1, que es ganadora. Si tenemos dos cartas, tenemos dos posibles permutaciones 1 2 ó 2 1, de la que la primera sería la solución. Si tenemos tres cartas, las soluciones ganadoras posibles son 1 3 2 y 3 2 1. Para cuatro cartas, tenemos la solución en el artículo de Cayley que vimos en la imagen 3. Para cinco cartas, las permutaciones que separan todas las cartas son las siguientes: 1, 2, 5, 3, 4 1, 3, 2, 5, 4 1, 5, 2, 4, 3 1, 5, 4, 2, 3 1, 5, 4, 3, 2 2, 1, 3, 5, 4 2, 1, 5, 4, 3 2, 5, 1, 4, 3 2, 5, 3, 1, 4 3, 2, 1, 5, 4 4, 1, 3, 5, 2 4, 2, 3, 5, 1 4, 2, 5, 1, 3 5, 2, 1, 4, 3 5, 4, 3, 1, 2 La serie A002467, también de Sloane, nos da el número de permutaciones que permiten separar al menos una carta. Él la plantea colocando n cartas y n sobre numerados y da el número de soluciones en el que, al menos 1 de las cartas está en el sobre con su número. Esta sucesión comienza por los números. 1, 1, 4, 15, 76, 455, 3186, 25487, 229384, 2293839, 25232230, 302786759, 3936227868, 55107190151, 826607852266 Si restamos esos valores del número de permutaciones posibles según el número n: 1, 2, 6, 24, 120, 720, etc… nos daría el número de permutaciones en donde no se separa ninguna carta. Esto ocurre, lógicamente, en aquellos casos en que en la permutación de partida no hay ninguna carta en su lugar correspondiente. Para terminar, citar la serie A028305, también de Sloane, en el que aparece un triángulo numérico en el que aparecen el número de permutaciones en las que se pueden sacar desde 0, 1, 2,… hasta n cartas. Por ejemplo, en la cuarta fila del triángulo nos encontramos con los valores 9, 6, 3, 0, 6 que corresponden a los que vimos en el segundo artículo de Cayley. 6. La permutación ganadora óptima. Dentro de las permutaciones ganadoras, aquellas que permiten separar todas las cartas, ha habido una que siempre ha interesado a los matemáticos y es aquella en que las cartas salen en su orden lógico, es decir, la primera carta en salir es el 1, la segunda el 2, la tercera el 3 y así hasta la última que sería la n, si estamos jugando con n cartas. El propio Arthur Cayley, en el artículo donde presentaba el juego en 1857, incluía las permutaciones ganadoras óptimas desde una hasta ocho cartas. Eran las siguientes: 1 1 2 1 3 2 1 4 2 3 1 3 2 5 4 1 4 2 5 6 3 1 5 2 7 4 3 6 1 6 2 4 5 3 7 8 Para conseguir encontrar de qué permutación debemos partir para obtener al final las cartas ordenadas no es necesario estudiar todos los casos si no que es más fácil utilizar métodos de resolución de problemas para lograrlo. En concreto, podemos hacer el camino contrario suponiendo el problema resuelto hasta llegar al punto de partida. Vamos a verlo para encontrar cuál sería la permutación de nueve cartas que daría el orden natural en la extracción de cartas. 9 La última carta a sacar debe ser la 9, pero no hay problemas pues basta contar hasta nueve para que se obtenga. 9 8 La anterior debe ser la 8. Como habrá dos cartas sólo, tendremos una en la posición impar y otra en la par. Como debe salir la carta 8, ésta debe comenzar en el lugar par 7 9 8 Cuando nos quede también la 7, tendremos tres cartas, luego deberemos contar cíclicamente dos veces las tres cartas y en la siguiente cuenta, el puesto 7, debe estar la carta a salir. Luego ésta debe ir en la primera posición. 8 6 7 9 Al añadir la 6 y tener, por tanto, cuatro cartas, deberemos dar una vuelta completa y en la siguiente en la segunda posición debe encontrarse el 6. Como al extraer esa carta debe quedar la posición del paso anterior, la carta que debe ir delante del 6 es la que quedará después en último lugar. 8 6 7 9 5 Al incluir el 5 y tener cinco cartas, el 5 va precisamente en la posición 5, sin afectar al orden de las demás. 7 9 5 4 8 6 El 4 debe ir en la posición cuarta para salir y debe llevar delante tres cartas que, al aplicar el juego, deben ir al final del mazo para quedar la disposición del paso anterior. 8 6 3 7 9 5 4 Lo que se ha hecho con el 4 se repite con el 3, que debe ir en la tercera posición y llevar delante las dos cartas que quedarán al final al retirarse. 4 2 8 6 3 7 9 5 Hacemos lo mismo con el 2, en este caso sólo la última carta del paso anterior debe ir delante. 1 4 2 8 6 3 7 9 5 Y el último paso es el más simple, pues la carta 1, yendo en la primera posición será la primera en salir y dejar la distribución que vimos antes. Luego, para nueve cartas, la permutación que permite obtener todas las cartas en orden sería 1 4 2 8 6 3 7 9 5. Pero hay otro método que permite hallar cuál es la permutación ganadora óptima de la que debemos partir. Para ello, suponemos que partimos de la permutación genérica dada por a b c d e f g h i y vemos en qué orden deben salir las cartas y a qué letra corresponden. En la siguiente tabla tenemos el proceso. Valor que sale Orden que queda a = 1 b c d e f g h i c = 2 d e f g h i b f = 3 g h i b d e b = 4 d e g h i i = 5 d e g h e = 6 g h d g = 7 h d d = 8 h h = 9   Por tanto, para ganar ordenadamente, la permutación inicial es: 1 4 2 8 6 3 7 9 5 como vimos antes. Si se encuentra con ganas, nuestro lector puede utilizar uno de los dos métodos para hallar la permutación inicial deseada y puede comprobarla con las siguientes soluciones para 10, 11, 12 y 13 cartas 1 9 2 9 7 3 10 5 6 4 1 10 2 9 6 3 5 8 7 4 11 1 6 2 7 5 3 11 12 8 4 9 10 1 8 2 5 10 2 12 11 9 4 7 6 13 7. Y algo más con lo que jugar. Una vez practicado el juego y visto en qué casos se gana y en cuáles no, hay una serie de cuestiones que se pueden plantear y que cualquier alumno, que haya entendido el juego, está en disposición de investigar. Veamos algunas de ellas. a)    ¿Qué ocurre con el juego si partimos con n cartas y conseguimos sacar n – 1 cartas? La respuesta es evidente, que se ha ganado en el juego pues al quedar una sola carta, basta contar hasta su número para que también podamos descartarla. Por eso, en la serie A028305 de la que hablamos antes, en todas las filas del triángulo el penúltimo número siempre es cero. Es decir no puede haber ninguna permutación de n cartas en las que sólo podamos extraer n – 1 cartas. b)    Dado que en todos los casos de n cartas podemos encontrar en qué permutación se obtiene que las cartas extraídas siguen el orden natural, ¿es posible encontrar una permutación que al extraer las cartas queden en orden inverso al natural, es decir que queden en el orden n, n – 1, n – 2, ….., 2, 1? La respuesta también es fácil de deducir. No es posible conseguir el orden inverso pues si la primera carta que se extrae es la que tiene el valor n quiere decir que hemos tenido que llegar hasta el lugar n para extraer la primera carta y, por ello, las anteriores no está ninguna en su lugar adecuado y como ese orden no cambia al extraer la última, ya no podríamos extraer ninguna más. Podemos comprobarlo en la imagen 3 con las soluciones de Cayley, aquellas permutaciones en las que el primero en salir es el 4, ya no se puede sacar ninguna carta más. c)    Una vez que hemos visto cómo conseguir una permutación a partir de una solución, como hemos hecho en el epígrafe anterior, se pueden plantear retos en esa línea. Por ejemplo, encontrar la permutación original que al extraer las cartas nos da el orden de extracción el siguiente: 5 2 6 1 3 4. Siguiendo el razonamiento del epígrafe anterior obtendríamos la permutación inicial 2 4 6 1 5 3. Se podría plantear como juego inverso a la ratonera. Elegir una permutación aleatoria de n números y buscar la permutación de partida. El problema es que no toda permutación de n elementos se puede conseguir en el juego de La Ratonera. Por ejemplo, si en lugar de partir de la permutación anterior planteamos la distribución 5 2 6 1 4 3 nos encontramos con que no hay solución pues el último en salir debe ser el 3, si el siguiente en salir debe ser el 4, la distribución, en ese momento, sería 3 4, pero en esa distribución sale primero el 3 y luego el 4, no al revés. d)    Una vez visto el juego y su desarrollo tanto en la forma normal como en la inversa, podemos trabajar con números más grandes de 13 pues ya no trabajaríamos con cartas y así podríamos trabajar con permutaciones de 20 números naturales. e)    Otra investigación sería trabajar con números que no sean consecutivos. Por ejemplo, con los números impares de una cifra y deberíamos buscar permutaciones que sea ganadoras, por ejemplo, la 5 7 3 1 9 cuya solución es 3 1 5 7 9. Los matemáticos, antes citados, Richard Guy y Richard Nowakowski plantearon en, el libro de Guy, Unsolved Problems in Number Theory de 1981 un versión que llamaron ratonera modularvii, en la que, una vez terminado de contar hasta n sin conseguir extraer ninguna carta más, se vuelve a comenzar desde 1 hasta que se consigan eliminar todas las cartas o se llegue a un bucle infinito. Con esta versión, si repasamos los casos que estudió Cayley en su segundo artículo y en los que se extraía alguna carta, pero no se conseguía ganar, tendríamos, con este método, los siguientes resultados. Original Método Cayley Ratonera modular Como es lógico, aquellas permutaciones en las que en una primera vuelta no se ha podido sacar ninguna carta, no sufren variación aunque se aplique el método modular. En los cálculos anteriores (donde puede haber algún error, como en todo lo anterior cuando a uno ya le varían los números) se ha utilizado la fórmula modular contando siempre de 1 a 4, incluso en los casos en que ya ha salido el 4. En el libro Guy y Nowakowski estudiaron diversas posibilidades y demostraron que si n es un número primo entonces solo hay dos tipos de permutaciones, ganadoras o desarreglos, es decir que no podemos quitar ninguna. Si consideramos la ratonera modular para tres cartas obtenemos los siguientes resultados. Inicial Resultado [1, 2, 3] [1, 2, 3] [3, 1, 2] [–] [–] [2, 1, 3] En el artículo de Raúl Ibáñez donde encontré el juego, se cita otro modo de jugar de forma modular. El reto es jugar con varias copas de las 13 cartas, por ejemplo, con dos palos completos o con las 52 cartas de la baraja de póker. Por si alguien tiene interés en dedicarle tiempo, yo ahí lo dejo. Para acabar sólo comentar que en el planteamiento del juego inicial siempre se ha propuesto trabajar con una baraja francesa, pero como lo suyo es estudiar permutaciones de números, es perfectamente posible trabajar con una baraja española, a ser posible de 48 cartas, es decir, con 8 y 9. La mayoría de lo presentado en este artículo funciona exactamente igual con ella. Sí quiero dejar un último consejo. Aunque se puede trabajar directamente con las permutaciones de números, es aconsejable comprobar los resultados obtenidos utilizando las cartas, ya que por experiencia sé que no es raro que algún número baile sin darnos cuenta. 8. Referencias bibliográficas. Creo que no dispongo de ningún libro donde se cite el juego, por lo que toda la información está extraída de internet y algunos de los resultados son de elaboración propia. Aparte de los artículos originales cuya referencia están en las notas finales, el artículo donde encontré el juego y la principal información, repetida en el resto de artículos en español que he encontrado, es: Ibáñez, Raúl (2017): La ratonera, el juego de Cayley. Consultado el 06/04/2020 https://culturacientifica.com/2017/01/25/la-ratonera-juego-cayley/ Aunque he utilizado poco de ese material, la biografía más extensa y detallada sobre Arthur Cayley la he encontrado en la página de biografías de la Universidad de St. Andrews. http://mathshistory.st-andrews.ac.uk/Biographies/Cayley.html   Notas: [i] En la página de Internet Archive se pueden consultar los 13 volúmenes de “The collected mathematical papers of Arthur Cayley”. Por ejemplo, en la siguiente dirección accedemos a la lista de artículos incluidos en la compilación https://archive.org/details/collectedmathem17caylgoog/page/n3/mode/2up/search/cayley+mousetrap?q=cayley+mousetrap . En Internet se pueden encontrar también, en otros lugares, ejemplos en pdf de algunos de sus artículos. Por ejemplo, en la página de la Universidad de Michigan hay en pdf 100 artículos publicados entre 1841 y 1851. La lista de páginas está en https://quod.lib.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ABS3153.0001.001. En otra página hay un volumen entero de la colección el VIII. Incluye unas abundantes notas biográficas del autor. Se puede consultar en: https://geographiclib.sourceforge.io/geodesic-papers/cayley-V8.pdf. No he conseguido localizar en la misma página más volúmenes salvo el VII para el que basta sustituir en la dirección al final V8 por V7. [ii] En la página de la Universidad de Göttingen puede consultarse la revista y, teóricamente, descargarse en pdf sin otros requerimientos, pero al intentarlo suele dar error. https://gdz.sub.uni-goettingen.de/id/PPN600494829_0015?tify= [iii] El artículo está en pdf en la dirección: https://oeis.org/A002467/a002467_1.pdf. [iv] Abstract en la dirección https://www.sciencedirect.com/science/article/pii/S0195669884710572?via%3Dihub [v] Se puede descargar desde la dirección http://www.math.ups.edu/~mspivey/MousetrapFinal2.pdf. [vi] https://oeis.org/?language=spanish [vii] En la siguiente dirección se da información sobre opciones de la ratonera modular y, aunque no está muy actualizado, podemos encontrar información interesante. http://www.dmmm.uniroma1.it/~alberto.bersani/mousetrap.html

Lunes, 28 de Junio de 2021 | Imprimir | PDF |  Correo electrónico

274. 162. CONCURSO DEL VERANO DE 2021

Volviendo poco a poco a la “normalidad”, lo que no nos va a faltar un verano más es nuestra cita con el cine, la cultura y las matemáticas. A ver qué tal esta vez. ¡¡Mucha Suerte!! Como sabéis, se trata de, a partir de las pistas que se dan, tratar de averiguar el título de una película oculta, y de paso, responder unas preguntillas (las de tipo matemático en color rojo; las culturales, en azul). Quien o quienes mayor puntuación alcancen serán los ganadores, a los que la dirección de DivulgaMAT les hará llegar algún obsequio. Se intenta (no siempre se logra) plantear cuestiones de todos los niveles (sencillas, medias, difíciles pocas), pero como nadie sabe a qué categoría pertenece cada una (además de que la dificultad es un concepto subjetivo), ninguna a priori debería evitarse. Como en la edición anterior, creo que ninguna excede el nivel de 2º de Bachillerato, es decir, matemáticas elementales (lo que no quiere decir triviales). Tampoco debería dejarse de enviar las respuestas, aunque sólo se sepa una (quien sabe, a lo mejor, nadie ha acertado más, cosas más raras se ven diariamente). Y por supuesto, descubrir (o revisar) títulos, quizá olvidados, de la Historia del Cine. No hay un orden establecido ni a la hora de describir escenas de la película, ni a la hora de descifrar el contenido de las cuestiones. Puede que sepamos responder antes a la pregunta quinta que a las anteriores. Pero todas pueden ayudar en averiguar el título de la película. Los fotogramas que se incluyen son todos de la película en cuestión. XVII  CONCURSO Los que hayan ido siguiendo la dinámica de estos pasados dieciséis concursos se habrán percatado que pocas veces he propuesto comedias como películas a descubrir. No es casualidad: rara es la comedia que me hace una mínima gracia. Además, encuentro algunos momentos en ellas bastante absurdos, incluso estúpidos. Eso no quita para que, a lo largo de la historia del cine, haya habido obras maestras que son comedias. Este año voy a intentar corregir esa tendencia, aunque, también en ella encuentro alguna secuencia verdaderamente ridícula. Por supuesto, en versión original es más soportable. Nada más terminar los títulos de crédito, vemos esta idílica estampa con el loro de la imagen saludándonos. Podría decir Es conocido en qué consiste un criptograma como éste: suma en la que a letras distintas corresponden dígitos distintos. ¿Cuál es el valor de esas letras? (M – 1) (C – 1). A continuación, un camarero nos muestra el cheque que vemos en la imagen, de un buen cliente que pide cierta cantidad en efectivo. No se puede ver la cantidad, pero a tenor de la reacción del encargado, debe ser alta, aunque al comprobar quien la pide, no pone objeción alguna en proporcionársela. Después, el cliente empieza a distribuir cantidades del fajo de billetes a amigos y conocidos que se acercan a saludarlo o a los que él llama que andan por allí. Ese fajo es de billetes de 5000 cruzeiros. Vemos que el reparto se hace a cuatro personas, y que todas reciben distinto número de billetes. A uno le entrega la décima parte del que más recibe. Los otros reciben cantidades pares de billetes cuya suma es el total de uno de ellos. Al generoso personaje le sobran al final tantos billetes como la suma de dos de sus agraciados amigos (M – 2) (C – 2) (C – 3). Mientras esto sucedía, la cámara ha ido mostrándonos a las personas que había en el restaurante, que parecen disfrutar de lo lindo, con orquesta de fondo en directo incluida. En una de las mesas, seis personas esperan ser servidas. Ron está sentado a la izquierda de la chica que está sentada a la izquierda del hombre que está sentado a la izquierda de Joan, y Ann está sentada a la izquierda del hombre que está sentado a la izquierda de la chica que se sienta a la izquierda del marido de Pam, mientras que Steve está sentado a la derecha de la chica que está sentada a la derecha de Harry. Pam no está sentada al lado de su marido. ¿Cuál de los tres caballeros es su marido? (M – 3). En la película se citan bastantes cifras y cantidades. Una de las más relevantes en el argumento es el 100. Y también vemos en esa escena inicial mesas circulares. Así que podemos combinar ambas ideas y plantear lo siguiente: Escribimos cien números enteros alrededor de una mesa circular. Su suma es 100. La suma de seis números consecutivos cualesquiera no excede de 6 (otra cifra que se cita en la película, por cierto). Si el primer número en que nos fijamos es precisamente un 6, determinar los números restantes (M – 4). El protagonista de la película se define a sí mismo como un ser ignorado entre los miles que pululan diariamente por la ciudad. Está considerado por sus jefes como un empleado ejemplar (de hecho, comentan de él que no merece la pena dársele una oportunidad en la vida porque su mayor y única virtud es la honradez), una buena persona. Suele leer por las tardes un libro a la casera donde vive que tiene alquiladas varias estancias de su casa. En el momento en que transcurre la acción era una novela de crímenes de título un tanto siniestro, la verdad (C – 4). Cuando lo compraron se rebajaba una tercera parte de lo que marcaba la etiqueta redondeándose al penique más cercano. Curiosamente al hacer esta oferta, los valores de libras y peniques se intercambiaban. Es decir, si el precio original era 43.21 libras, el precio a pagar final sería 21.43 libras (en este ejemplo no se ha tenido en cuenta la condición de la tercera parte, obviamente). 1.- ¿Cuál era el precio del libro? 2.- Si hiciéramos el cálculo en la época de la película, ¿tendría el mismo valor? Si la respuesta fuera negativa, ¿podríamos saber cuánto valdría entonces utilizando las mismas condiciones del enunciado? (M – 5). Prácticamente en cada escena de la película puede plantearse alguna cuestión o ejercicio relacionado con las matemáticas o la física. También hay muchos objetos que tienen especial relevancia. De uno de ellos, hay cien copias, y se dice (en la versión original de la película, no en la doblada) que todas juntas pesan 495987 libras (M – 6) (C – 5). Teniendo en cuenta la forma y dimensiones que suelen tener esos objetos (hay mucha información sobre los mismos en internet), ¿cuáles serían las dimensiones para que cada uno de ellos pesara aproximadamente un kilogramo, si damos un ángulo de inclinación de 5º? (M – 7) Otro objeto importante en el argumento son unos souvenirs de esos que compramos cuando visitamos un lugar turístico. En este caso, aparecen unos pisapapeles que reproducen un monumento a escala. El original tiene 300 metros de altura y pesa unas 7300 toneladas. Si el pisapapeles estuviera construido con el mismo material que el monumento original, pero querríamos que sólo pesara medio kilo, ¿qué altura debería tener? ¿Y si quisiéramos que pesara un kilo para que fuera un pisapapeles consistente? ¿Sería el doble? (M – 8 ). Sin embargo, en la película esas réplicas no están construidas con el material original, sino con otro. ¿Cómo serían los pisapapeles con ese material de la película? ¿Cuántas serían necesarias para lograr el propósito de los protagonistas? ¿Qué se deduce de ello? (M – 9). A la hora de construir las réplicas, los protagonistas tuvieron que hacer un molde. Para ello, tomaron las coordenadas de algunos puntos a partir de una fotografía. Algunos de esos valores fueron los siguientes: . Con esos valores (y un poco de ingenio) es posible obtener el alzado completo aproximado del monumento (M – 10). Esos pisapapeles ocultan algo importante. Para que no dé demasiado de ojo, deberían estar formados por una mezcla de metales (en la película no se dice nada de ello, pero así debería ser). Suponiendo que cada pisapapel pesara 750 gramos, y que al sumergirlo en el agua perdiera 50 gramos de peso, ¿cuál sería la cantidad de cada metal que tendría la aleación sabiendo que la densidad de uno fuera 19,50 gr/cm3 y la del otro 10,50 gr/cm3? (M – 11) Posteriormente, por culpa de un malentendido, se extravían algunos de esos pisapapeles (C – 6). En la película se dice que reportarían 25000 libras. También se dice que el material con el que están formadas está valorado en 240 chelines la onza. Con esos datos, ¿cuánto debe pesar cada una de esas piezas? (M – 12) (C – 7). En su afán por recuperar los pisapapeles, dos de los protagonistas tienen que desplazarse a otra ciudad. Localizan que un grupo de personas los tiene. Tratan de alcanzar a dicho grupo, pero les llevan cierta delantera, ya que han logrado tomar un ascensor antes que ellos. Sin perder un segundo, deciden bajar por las escaleras. El problema es que la escalera que toman es de caracol: 300 metros, el ascensor bajando a 2 metros/segundo (M – 13) (C – 8). Finalmente, los protagonistas no llegan a tiempo (y con un mareo monumental). Mientras se recuperan, levantan la vista y ven algo parecido a lo que aparece en la imagen (M – 14) (C – 8). En un momento dado, los protagonistas deben entrar en un colegio de niñas a tratar de recuperar seis objetos muy importantes para ellos. La directora del centro no duda en colaborar, y proponen a las chicas un cambio ventajoso. Sin embargo, sólo cinco de ellas, de edades 6, 7, 8, 9 y 10 años, acceden al cambio. Si eligiéramos a dos de ellas aleatoriamente, ¿cuál sería la probabilidad de que al menos se diferenciaran en dos años? (M – 15) Una de las pistas que suele ayudar bastante al lector a localizar (o al menos acotar un poco) la película incógnita, es su año de estreno. En este caso con muy pocas indicaciones se puede encontrar: la suma de los dígitos del año es un cuadrado perfecto además de ser un número primo, aunque si se revierten los dígitos, el número resultante no es primo (M – 16). Quizá también pueda ayudar una palabra relacionada con la película codificada del siguiente modo: tenemos un cuadrado mágico de orden cuatro con todos los números del 1 al 16. Además de las propiedades habituales de los cuadrados mágicos, las casillas con el borde verde y las casillas con el borde rojo también suman la constante mágica para estos cuadrados. Teniendo esto en cuenta, las casillas marcadas con fondo naranja (seis de ellas; una ya se da, la del número 14), encubren esa palabra que puede ser una pista definitiva para desvelar la película en cuestión (M – 17). Seguramente alguno de los lectores piense que este último ejercicio es igual (similar, mejor dicho) al criptograma inicial. Y tiene toda la razón, pero es que la película, acaba también en el mismo sitio donde empezó, cerrándose el círculo, aunque ahora las cosas se ven de distinta manera que al inicio (M – 18). CUESTIONES MATEMÁTICAS M – 1.- Determinar la suma que esconde el criptograma. M – 2.- ¿Cuántos billetes recibe cada uno? ¿Cuánto dinero pidió sabiendo que es la mínima cantidad posible que cumple con todas las condiciones descritas? M – 3.- ¿Cómo se llama el marido de Pam? M – 4.- Distribución de los números en la mesa. M – 5.- Responder a las dos preguntas planteadas. M – 6.- ¿Es esto posible? Argumentar la respuesta. M – 7.- Forma y dimensiones del objeto. M – 8.- Responder a las cuestiones, justificando las respuestas. M – 9.- ¿Qué se deduce del resultado obtenido? M – 10.- Encontrar como máximo tres funciones que describan aproximadamente el alzado de dicho monumento a partir de las coordenadas descritas. M – 11.- ¿Cuál sería la cantidad de cada metal? M – 12.- ¿Cuánto debe pesar cada una de esas piezas? M – 13.- ¿Cuántos escalones deberían bajar? (Si necesitas añadir algún dato, hazlo, pero que sea lo más consistente posible con la realidad, no inventado). ¿Cuántos escalones deberían bajar por minuto para llegar a la vez que el ascensor? M – 14.- Determinar justificadamente la superficie encerrada por esa gráfica. M – 15.- ¿Cuál es dicha probabilidad? M – 16.- ¿En qué año se estrenó la película? M – 17.- Completar el cuadrado mágico que se indica. M – 18.- ¿Cuál es la película enigma de este concurso? CUESTIONES CULTURALES C – 1.- ¿Por qué repite esa frase el loro? C – 2.- En el cheque vemos escrito “Banco Lowndes”. ¿Existe o existió? ¿Por qué se llama así? C – 3.- La persona que más billetes recibe es la primera vez que aparece en el cine, y con el tiempo se convertiría en todo un icono popular, al punto de que en la actualidad seguimos viendo su imagen en posters, tiendas, etc. ¿A quién nos referimos y cuál es su nombre en la película (en la ficción)? C – 4.- ¿Cuál es el título del libro? ¿Es real? C – 5.- ¿Qué peso se indica en la versión doblada al castellano? C – 6.- ¿Cómo se extraviaron? C – 7.- En el doblaje de la película al castellano hay un error relacionado con cifras que no está en la versión original. Trata de dar con él. C – 8.- A estas alturas es posible que hayas averiguado el monumento del que se habla. Las matemáticas están presentes en él en varios aspectos. Indica al menos dos diferentes. C – 9.- Ha habido muchas películas en las que aparece el monumento en el que se desarrollan estas escenas. Indica otras películas en las que lo veamos como en ésta, desde su interior (no sirven aquellas en las que aparece de lejos, o de fondo; sólo aquellas en las que veamos con detalle imágenes desde dentro). Indicar una (aparte de la que nos ocupa) será valorado con 5 puntos; dos, 7 puntos; y más de dos, 10 puntos. C – 10.- El polifacético George Lucas era un niño cuando se estrenó esta película, pero existen al menos dos detalles en ella que tiene relación con él. ¿Cuáles? C – 11.- En la película hay un momento en que los personajes asisten a una exposición. ¿De qué trataba esa exposición? ¿Tiene alguna relación con el argumento de la película? ¿Qué relevancia tiene el personaje al que se dedica? ¿Aparece previamente en algún momento de la película algo relacionado con esta exposición? C – 12.- Opinión sobre la película. ¿Te ha gustado? ¿La conocías? ¿Te ha llamado la atención algún aspecto de ella? Baremo: Todas las cuestiones tanto las rojas (las matemáticas) como las azules (cine y demás) se valorarán con 10 puntos como máximo. En total, 300 puntos en juego, si las cuentas no me fallan. Todo comentario, sugerencia, queja, etc., será bien recibido. Si no salen algunas cosas, no importa; lo que cuenta es tratar de pasar un buen rato, disfrutar de la película (que el verano da para mucho), y mantener las neuronas un poco activas. Confío que no haya demasiados errores en las cuestiones. Se han repasado varias veces, pero algunas, al ser inventadas o retocadas de otros enunciados, podrían tener alguna errata. Sed benévolos con vuestros calificativos si tal cosa sucediera. El plazo para enviar las respuestas, es como en años precedentes, hasta las 00:00 del miércoles 1 de Septiembre de 2021, a la dirección apoblacion@uva.es, indicando en el asunto Verano 2021. ¡¡¡¡Buen Verano Cine-matemático!!!

Miércoles, 23 de Junio de 2021 | Imprimir | PDF |  Correo electrónico

275. Historia de las matemáticas: del cero al infinito

Categoría: Historia de las Matemáticas Autor: Sergio Castro Editorial: The Galobart Books Año de publicación:  2021 Nº de hojas: 288 ISBN: 978-84-12264-98-2

Martes, 09 de Febrero de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

276. Muere Narasimhan, el matemático indio que unió la geometría con la física teórica

ABC, 10 de Junio de 2021 CIENCIA Alfonso Jesús Población Sáez

Jueves, 10 de Junio de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

277. El profesor de matemáticas bilbaíno que hacía bailar a los números

ABC, 14 de Junio de 2021 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 14 de Junio de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

278. Madera, acero, piedra: geometría

Lee Jae-Hyo es un artista coreano, un verdadero mago de la geometría. Fijaos por ejemplo en estos dos toros enlazados, su escultura 0121-1110=105021 (madera,  800 x 150 x 230 cm, 2005): Lee Jae-Hyo, “0121-1110=105021”, http://www.leeart.name/Gallery/Wood/ Mirad también esta esfera titulada 0121-1110=102071 (hierro, 180 x 180 x 180 cm, 2002): Lee Jae-Hyo, “0121-1110=102071”, http://www.leeart.name/Gallery/Still ¿Y qué os parece 0121-1110=1080620 (piedra, 151 x 410 x 280cm , 2006)? Lee Jae-Hyo, “0121-1110=1080620”, http://www.leeart.name/Gallery/stone Es pura geometría. Pero sobran las palabras; lo mejor es entrar en la página de Lee Jae-Hyo, y entretenerse durante un buen rato mirando sus magníficas obras. Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Miércoles, 26 de Mayo de 2021 | Imprimir | PDF |  Correo electrónico

279. Nilakantha Somayaji, de la Escuela de Kerala

El matemático y astrónomo Nilakantha Somayaji (1444-1544) nació un 14 de junio. Formaba parte de la Escuela de Kerala de astronomía y matemáticas. Una de sus obras más influyentes fue el tratado astronómico Tantrasamgraha, completado en 1501. En este texto, revisó el modelo del matemático y astronómica Aryabhata para los planetas Mercurio y Venus. Su ecuación del centro de estos planetas se mantuvo como la más precisa hasta la época de Johannes Kepler (1571-1630). También realizó un elaborado comentario del tratado astronómico Aryabhatiya, el Aryabhatiya Bhasya, en el que hablaba sobre desarrollos en series infinitas de funciones trigonométricas, problemas de álgebra y geometría esférica. En este  texto desarrolló un sistema computacional para un modelo planetario parcialmente heliocéntrico, en el que Mercurio, Venus, Marte, Júpiter y Saturno giran alrededor del Sol, que a su vez gira alrededor de la Tierra. Su Grahapareeksakrama es un manual sobre la realización de observaciones astronómicas basadas en instrumentos de la época. Más información: K.V. Sarma (editor); V.S. Narasimhan (translator), Tantrasamgraha with English translation (in Sanskrit and English),  Indian National Academy of Science A.K. Bag, Indian literature on mathematics during 1400 – 1800 AD, Indian Journal of History of Science 15 (1) (1980) 79–93 K. Ramasubramanian, M. D. Srinivas, M. S. Sriram, Modification of the earlier Indian planetary theory by the Kerala astronomers (c. 1500 AD) and the implied heliocentric picture of planetary motion, Current Science 66 (1994) 784-790 M. S. Sriram, 500 years of Tantrasamgraha. A landmark in the history of astronomy, Indian Journal of the History of Science 35 (2) (2000) 161-168 Cómo encontrar el número Pi en el triángulo de Pascal, Gaussianos, 2014 Wikipedia Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Lunes, 14 de Junio de 2021 | Imprimir | PDF |  Correo electrónico

280. 135. (Junio 2021) El ritual de los Musgrave, de Arthur Conan Doyle

El ritual de los Musgrave –que aparece en Memorias de Sherlock Holmes – es un relato corto de Arthur Conan Doyle en el que el famoso detective ayuda a resolver un enigma que afecta a la familia Musgrave, una de más antiguas de Inglaterra. En este relato corto, Reginald Musgrave –un compañero de colegio de Sherlock Holmes– contrata al detective para que investigue la desaparición de Richard Brunton –el mayordomo– y de Rachel Howells –la segunda doncella–. Musgrave había encontrado unos días antes al mayordomo fisgando unos papeles en la biblioteca y le había despedido, dándole el plazo de una semana para irse de la casa. Pero Brunton desaparece y poco más tarde la doncella enamorada del mayordomo, que la ha abandonado por otra. El papel que el mayordomo leía en la biblioteca era el conocido como Ritual de los Musgrave, que decía lo siguiente: – ¿De quién era? – Del que se ha marchado. – ¿Quién la tendrá? – El que vendrá. – ¿Dónde estaba el sol? – Sobre el roble. – ¿Dónde estaba la sombra? – Bajo el olmo. – ¿Con qué pasos se medía? – Al norte por diez y por diez, al este por cinco y por cinco, al sur por dos y por dos, al oeste por uno y por uno, y por debajo. – ¿Qué daremos por ella? – Todo lo que poseemos. – ¿Por qué deberíamos darlo? – Para responder a la confianza. El detective –con gran acierto– piensa que en el ritual debe estar la clave del misterio, y que Brunton –un hombre inteligente– debía haberse empeñado en encontrar el secreto escondido entre aquellas extrañas palabras: Fue perfectamente obvio para mí, al leer el Ritual de los Musgrave, que las medidas habían de referirse sin duda a algún punto al que aludía el resto del documento, y que si podíamos encontrar ese punto estaríamos en buen camino para saber cuál era aquel secreto que los antiguos Musgrave habían juzgado necesario enmascarar de un modo tan curioso y peculiar. Para comenzar se nos daban dos guías: un roble y un olmo. En cuanto al roble, no podía haber la menor duda. Directamente ante la casa, a la izquierda del camino que llevaba a la misma, se alzaba un patriarca entre los robles, uno de los árboles más magníficos que yo haya visto jamás. – ¿Ya estaba aquí cuando se redactó vuestro Ritual? –pregunté al pasar delante de él. – Según todas las probabilidades, ya lo estaba cuando se produjo la conquista normanda –me respondió–. Tiene una circunferencia de veintitrés pies. Así quedaba asegurado uno de mis puntos de partida. – ¿Tenéis algún olmo viejo? –inquirí. – Antes había uno muy viejo, pero hace diez años cayó sobre él un rayo y sólo quedó el tocón. – ¿Puedes enseñarme dónde estaba? – Ya lo creo. – ¿Y no hay más olmos? – Viejos no, pero abundan las hayas. – Me gustaría ver dónde crecía. Habíamos llegado en un dog-cart, y mi cliente me condujo en seguida, sin entrar en la casa, a una cicatriz en la hierba que marcaba donde se había alzado el olmo. Estaba casi a mitad de camino entre el roble y la casa. Mi investigación parecía progresar. – Supongo que es imposible averiguar qué altura tenía el olmo –quise saber. – Puedo decírtelo en seguida. Medía sesenta y cuatro pies. – ¿Cómo lo sabes? –pregunté sorprendido. – Cuando mi viejo profesor me planteaba un problema de trigonometría, siempre consistía en una medición de alturas. Cuando era un mozalbete calculé las de todos los árboles y edificios de la propiedad. Había sido un inesperado golpe de suerte y mis datos acudían a mí con mayor rapidez de la que yo hubiera podido esperar razonablemente. ¿Un olmo que ya no existe, pero del que Holmes –y también el mayordomo– conoce su altura, además de las indicaciones dadas por el ritual? Las deducciones continúan: Miré el sol. Estaba bajo en el cielo, y calculé que en menos de una hora se situaría exactamente sobre las ramas más altas del viejo roble, y se cumpliría entonces una condición mencionada en el Ritual. Y la sombra del olmo había de referirse al extremo distante de la sombra, pues de lo contrario se habría elegido como guía el tronco. Por consiguiente, había de averiguar dónde se encontraba el extremo distante de la sombra cuando el sol estuviera exactamente fuera del árbol. – Esto debió de ser difícil, Holmes, dado que el olmo ya no estaba allí – Pero al menos sabía que, si Brunton pudo hacerlo, yo también podría. 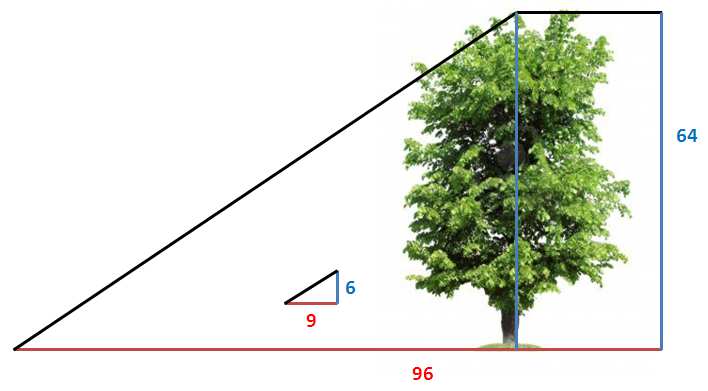Además, de hecho, no había dificultad. Fui con Musgrave a su estudio y me confeccioné esta clavija, a la que até este largo cordel, con un nudo en cada yarda. Cogí después dos tramos de caña de pescar, que representaban exactamente seis pies, y volví con mi cliente allí donde había estado el olmo. El sol rozaba ya la copa del roble. Aseguré la caña de pescar en el suelo, marqué la dirección de la sombra y la medí. Su longitud era de nueve pies. Desde luego, el cálculo era ahora de lo más sencillo. Si una caña de seis pies proyectaba una sombra de nueve, un árbol de sesenta y cuatro pies proyectaría una de noventa y seis, y ambas tendrían la misma dirección. Medí la distancia, lo que me llevó casi hasta la pared de la casa, y fijé una clavija en aquel punto. Imagen realizada por Marta Macho Stadler. Tras encontrar el punto definido por la sombra –gracias al teorema de proporcionalidad de triángulos de Tales, perfectamente descrito por Holmes–queda por utilizar la última parte del ritual: Al norte por diez y por diez, al este por cinco y por cinco, al sur por dos y por dos, al oeste por uno y por uno, y por debajo. Siguiendo estas instrucciones, Holmes y Musgrave descubren una cava bajo la casa… y allí el cadáver del mayordomo –probablemente asesinado por la agraviada sirvienta, celosa de la nueva amante de Brunton– y la corona de los reyes de Inglaterra confiada a la custodia de la familia, y que por alguna razón el heredero del trono no había recuperado… – ¿De quién era? – Del que se ha marchado. – ¿Quién la tendrá? – El que vendrá. Nota Una primera versión de este artículo se publicó el 15 de mayo de 2013 en el Cuaderno de Cultura Científica bajo el título de Thales.

Miércoles, 09 de Junio de 2021 | Imprimir | PDF |  Correo electrónico