31. 174. Los Oscars® de las matemáticas (I)

Repasamos en esta reseña y en la del próximo mes, ejemplos, ambos en películas de animación, en los que las matemáticas han sido las responsables de merecer y conseguir el más preciado de los galardones del mundo cinematográfico: el Oscar® de Hollywood. Si preguntáramos, a modo de curiosidad, a personas elegidas al azar, qué le sugiere la palabra PIXAR, seguramente sólo acertarían a decirnos algo coherente algunos aficionados al cine, padres de niños menores de diez años y algún amante de los dibujos animados, menor de cuarenta años, probablemente. Sonsacando lo más aprovechable, nos dirían que se trata de un estudio cinematográfico de animación por ordenador subsidiario de Walt Disney Studios y propiedad de The Walt Disney Company, con sede en Emeryville, California, Estados Unidos. Seguramente también nos dirían que fueron los que sacaron las películas Disney de la ñoñería con que los sucesivos responsables de la empresa fueron encorsetándolas, tras la muerte de su fundador (ñoñería en algunos aspectos, como los insufribles números musicales, porque en otros no se cortaban un pelo si tenían que mostrar los más bajos instintos; en definitiva, la doble moral yanki de la que ya se ha hablado muchas veces). Lo cierto es que la aparición de estos estudios de animación, con técnicas distintas a las clásicas (No se le puede negar a Walt Disney sus innovaciones y avances en animación; invirtió mucho tiempo y dinero en su mejora, lo que no hicieron los herederos de su emporio) y argumentos más atractivos, revolucionaron este tipo de películas, además de atraer no sólo a públicos infantiles. Una de sus señas de identidad fue el diseño realista de personajes y fenómenos naturales por ordenador. Y para lograrlo necesitaron muchas matemáticas y muy novedosas. Así lo indican los responsables de efectos visuales en las numerosas charlas y conferencias que han impartido por todo el mundo. Pero no solo montando un par de presentaciones llamativas y epatantes, sino poniendo por delante artículos serios de investigación que además coloca la empresa a disposición libre de todo aquel que quiera acercarse a ellos en su página web. Si echáis un vistazo a alguno de ellos, como curiosidad simplemente, comprobareis que no los puede leer cualquiera, sino que hay matemáticas muy avanzadas detrás de ellos. Cuesta, al menos para el que esto escribe, tratar de explicar de manera sencilla lo que hay detrás de muchos de ellos. Lo intentaré con un par de conceptos que han desarrollado, simplificando mucho las cosas. Paralelamente, describiré la trayectoria del científico que logró con su primer trabajo para PIXAR la preciada estatuilla con un cortometraje: Tony DeRose. Tony DeRose es actualmente científico sénior y director del grupo de investigación de Pixar Animation Studios. Se licenció en Física en la Universidad de California, Davis, y se doctoró en Informática de la Universidad de California, Berkeley. Entre 1986 a 1995, DeRose fue profesor de informática e ingeniería en la Universidad de Washington, y trabajando en un grupo de investigación centrado en la representación de superficies y otros problemas geométricos motivados por gráficos por ordenador. En varias entrevistas y en las charlas que imparte, remarca que siempre le fascinó la parte aplicada de las matemáticas. Desde niño le apasionaba la capacidad de cálculo de las matemáticas, lo que podía saber y averiguar sin necesidad de medir físicamente las magnitudes o esperar a que se produjeran los experimentos. Al acabar sus estudios universitarios e iniciar los de posgrado comenta que se le presentaban dos opciones: tratar de mejorar 400 años de físicos brillantes, o quedarse esencialmente en la planta baja de los gráficos por ordenador, ya que prácticamente no se sabía nada del tema en aquel momento. Eligió esta segunda opción, trasladándose a Berkeley, incorporándose al equipo de Brian Barsky, que estaba trabajando en representaciones de superficies, splines, y cosas de ese estilo. Ahí fue donde encontró la belleza de hacer matemáticas constructivas, y los gráficos por ordenador fueron una forma de hacerlas visuales, tangibles. En aquel momento, muy cerca, literalmente en frente a su puesto de trabajo, George Lucas había contratado a Edwin Catmull para iniciar The Graphics Group, la división computacional de Lucasfilm que tras ser adquirido en 1986 por el co-fundador de Apple Computer, Steve Jobs, pasó a ser Pixar Animation Studios. Catmull se había graduado en la Universidad de Utah, doctorándose posteriormente en Ciencias de la Computación. Creó en 1972 el primer dibujo en animación 3D, una recreación de su propia mano izquierda. Quedó tan realista que fue aprovechada para la película Mundo futuro (Futureworld, Richard T. Heffron, EE. UU., 1976) (la secuela de la célebre Almas de metal (Westworld, Michael Crichton, EE. UU., 1973)). Catmull formaría parte del comité asesor en la tesis doctoral de DeRose. Catmull ha ganado cuatro Premios de la Academia por sus proezas técnicas y ha colaborado en crear algunos de los principales softwares de imágenes generadas por computadora en los que confían los animadores en la actualidad. Diez años después, ya siendo profesor en la Universidad de Washington, Ed Catmull propone a DeRose trabajar más estrechamente en gráficos después del enorme éxito obtenido por la película Toy Story (Toy Story, John Lasseter, EE. UU., 1995), primera producción en la historia de la animación totalmente realizada con CGI (Computer Generated Images). Catmull fue el diseñador del software de renderización de imágenes de la película, además de productor. Además del público y la crítica, técnicos y especialistas de todo tipo valoraron muy positivamente muchos aspectos de Toy Story. La historia enganchó al público, los personajes de juguete eran creíbles, convincentes, pero observaron que, cada vez que aparecía un ser humano en la pantalla, la cosa no cuadraba tan bien; de hecho, se apreciaban discordancias. Decidieron que uno de los objetivos en futuros trabajos debería ser mejorar la presencia de personas, tanto gráfica como argumentalmente. Y aquí es donde entró DeRose junto a un completo equipo de informáticos, ingenieros y matemáticos. Matemáticas pioneras En sus conferencias divulgativas, DeRose suele remarcar la importancia de las matemáticas en la concepción de este tipo de películas. "No debería sorprender en absoluto que las matemáticas desempeñen un papel relevante", comenta. “Las imágenes resultantes son todas digitales. Tres números definen cada píxel, uno para la cantidad de rojo, verde y azul. Todo lo que tenemos básicamente son números que representan posiciones de geometría y valores de grados de libertad, por lo que tiene que haber un gran cálculo en el camino". Hablemos de tres ideas, utilizadas en otros tantos apartados de animación de gráficos. La iluminación global de una escena implica simular cómo la luz rebota en un entorno: "Matemáticamente, dados dos puntos cualesquiera, pongamos y, z, es necesario calcular cuánta luz viaja desde y hacia z. Uno de los instrumentos utilizados para modelizar esta situación es la función de distribución de reflectancia bidireccional, fr (wi, wr) (BRDF, siglas en inglés). Fue definida hacia 1965 por el físico Fred Nicodemus, del siguiente modo fr (wi, wr) = En la imagen, tenemos sobre un punto situado en una superficie opaca, tres direcciones: wi indica la luz entrante desde la fuente de luz, wr es la luz reflejada y apunta hacia la cámara (o al espectador, en general) que recoge la luz percibida, y n indica la superficie normal. La función está definida como el cociente entre la variación de la radiancia L (potencia por unidad de ángulo sólido en la dirección de un rayo por unidad de área proyectada perpendicular al rayo) y la variación de la irradiancia E (potencia por unidad de superficie). Ese cálculo de la cantidad de luz entre dos puntos, hay que hacerlo para cada par de puntos en el entorno, que, al ser un espacio continuo, se convierte en una integral: la denominada ecuación de renderizado. En el enlace se accede a un artículo sobre esta ecuación de James T. Kajiya de 1986 en el que la aplica en la computación gráfica. Se trata de una ecuación integral que describe la cantidad total de luz emitida desde un punto a lo largo de una dirección de visualización particular, dada una función para la luz entrante y una función de distribución de reflectancia bidireccional. Básicamente, la luz saliente de cada punto es la suma de la luz emitida y la luz reflejada. Ésta última, la luz reflejada, es la suma de todas las direcciones de la luz entrante multiplicada por la reflexión superficial y el coseno del ángulo incidente. Lo que los ordenadores hacen es aproximar esa la ecuación integral mediante un conjunto de ecuaciones lineales. Hay una ecuación para cada punto de cada objeto que aparece en cada secuencia. De media, entre un millón y diez millones de puntos por cada cuadro de película. Estimen el número de ecuaciones total. Existen diferentes técnicas de representación realista para resolver este tipo de ecuaciones. Resolver la ecuación de renderizado para cualquier escena dada es el principal desafío en el renderizado realista. Un enfoque para hacerlo se basa en métodos de elementos finitos. Otro enfoque diferente utiliza los métodos Monte Carlo, dando lugar a muchos algoritmos diferentes. Por otra parte, aunque la ecuación de renderizado es muy general, no es capaz de contemplar todos los aspectos del reflejo de la luz. Entre sus limitaciones se encuentran los efectos no lineales, el efecto Doppler, la polarización, la fosforescencia, las interferencias, entre otras. Subdivisión de superficies Otro aspecto presente en la animación de gráficos por ordenador es la representación de superficies tridimensionales complejas de manera eficiente en un ordenador, preservando en la medida de lo posible la ilusión de suavidad. El modo más extendido ha sido la utilización de NURBS (B-splines racionales no uniformes). Pero un gran inconveniente de utilizar NURBS es el requisito de que las redes de control (el conjunto de puntos de control) tenga que ser una cuadrícula rectangular regular. Esa elección limita mucho el tipo de objetos que pueden representarse porque no existen procedimientos de refinado local de la superficie, dando lugar a abombamientos u otros defectos del dibujo final. Una alternativa es la técnica de las superficies de subdivisión, definidas como límite de un proceso de refinamiento infinito. Este método mejora muchas de las deficiencias de los NURBS. Por ejemplo, las imágenes que se muestran a continuación, a partir de una malla de control inicial, se pasa a un proceso de refinamiento mediante iteraciones. Las imágenes muestran el resultado con una etapa, dos y la final con un refinamiento infinito, respectivamente. Las superficies de subdivisión son fáciles de implementar, pueden modelar superficies de tipo topológico arbitrario y, como se ha indicado, la continuidad de la superficie se puede controlar localmente. Aunque las superficies de subdivisión se conocen desde hace quince años, su uso se ha visto obstaculizado por la falta de una forma cerrada: se definen solo como límite de un procedimiento infinito. La técnica de subdivisión de superficies se utilizó por primera vez en animación para crear el personaje de Geri en el cortometraje El juego de Geri (Geri's Game, Jan Pinkava, EE. UU., 1997), que le valió a Tony DeRose un Oscarâ de la Academia a los efectos visuales. En el enlace pueden contemplar el cortometraje al completo. Observen el realismo de los cambios de expresión del rostro del personaje. Como explica el propio DeRose, se trata de un proceso similar al control de los movimientos mediante cuerdas en las marionetas, sólo que aquí las cuerdas son digitales. Las cuerdas digitales sirven como controles de la animación, que permiten a los animadores definir todos los movimientos de los personajes, desde doblar un codo hasta levantar una ceja. En una marioneta física tenemos media docena, una docena de cuerdas a lo sumo; aquí se pueden controlar hasta 700, lo que da unos grados de libertad de movimientos impresionante. Imagínense una marioneta controlada por 700 cuerdas. Con eso es con lo que se trabaja gracias al ordenador y las matemáticas. Coordenadas armónicas Un tercer aspecto novedoso en las técnicas de animación mediante ordenador es la creación y el control de las deformaciones de volumen utilizadas para articular personajes. Para ello, los ingenieros de Pixar han recurrido a las coordenadas armónicas. Las coordenadas armónicas son una generalización de las coordenadas baricéntricas que se pueden extender a cualquier dimensión; describen cómo se mueven los puntos interiores dentro de polígonos en el plano o poliedros en el espacio. Las coordenadas baricéntricas son ternas de números (t1, t2, t3) que responden a masas situadas en los vértices de un triángulo de referencia. En la imagen tenemos las coordenadas baricéntricas (0.41, 0.3, 0.29). Una característica es que la suma de esos tres valores es la unidad, y que esas masas determinan entonces un punto P, que es el baricentro geométrico de las tres masas (de ahí su nombre). Las coordenadas baricéntricas fueron descubiertas por Möebius en 1827, y tiene muchas aplicaciones que el lector interesado puede consultar en cualquier texto de geometría afín. Sobre las coordenadas armónicas y su utilización en el modelo gráfico por ordenador puede verse este video de apenas seis minutos de duración (en inglés). Gracias a este tipo de coordenadas, los animadores reducen considerablemente el tiempo y el esfuerzo que dedican a mover los objetos. Una visita a Pixar in a box En un loable intento por promocionar las materias STEM relacionadas con el trabajo de los estudios Pixar, han incorporado a su página web, con la colaboración de un centro educativo, unas unidades básicas (con vídeos explicativos, ejercicios, animaciones, etc.) que explican lo que se necesita en la realización de una película. A esta sección la han llamado Pixar in a box. Entre el material desarrollado hay algunas unidades de matemáticas, muy elementales (es una sección dirigida a un público más bien joven), pero no triviales (el cálculo de curvas de Bézier, por ejemplo, muy útil en la animación por ordenador, no puede decirse que sea evidente).

Jueves, 13 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

32. 11/10/1887: se patenta el primer comptómetro

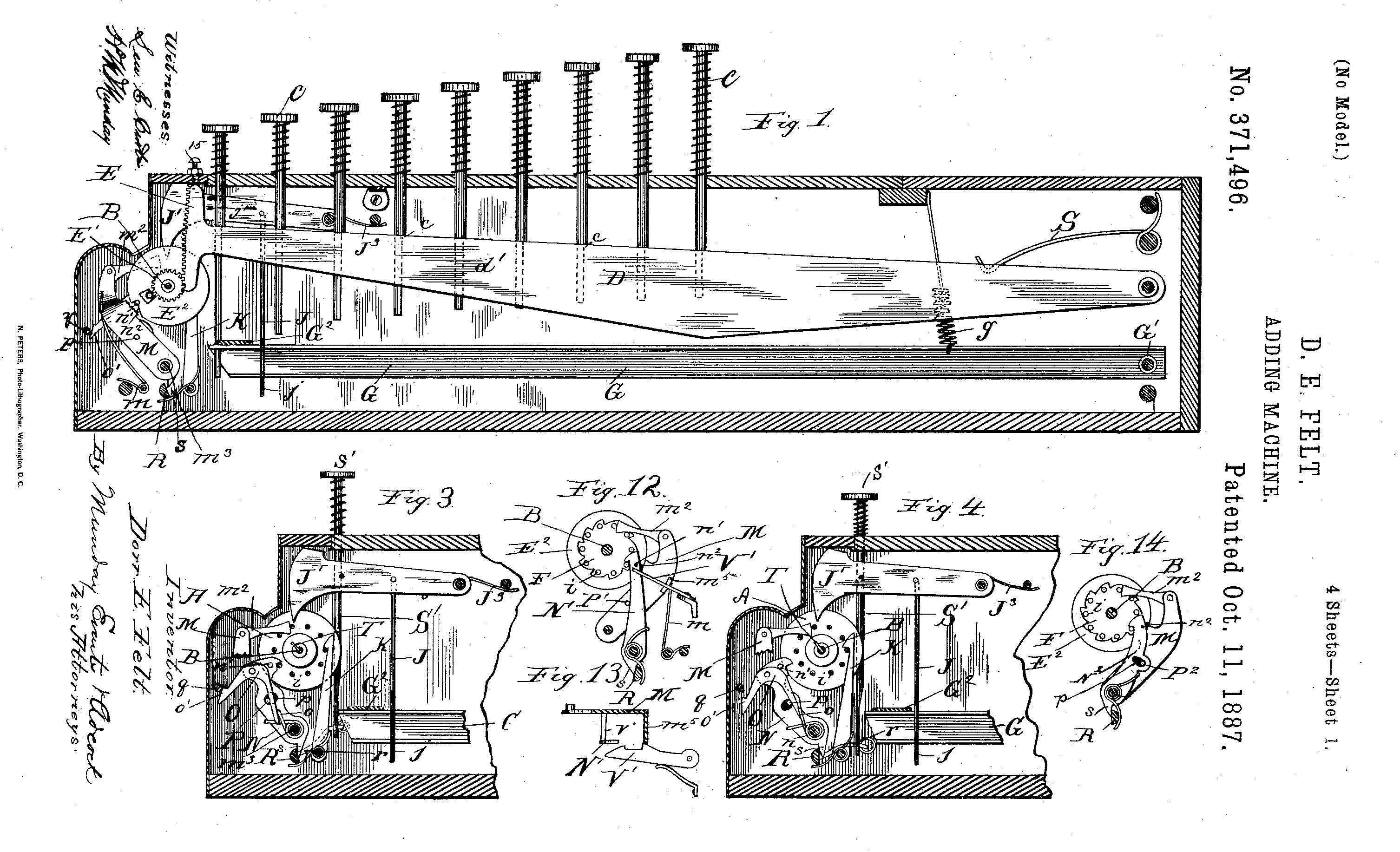
El inventor Dorr Eugene Felt (1862-1930) patentó en 11 de octubre de 1887 una máquina de sumar, el comptómetro. Primera página de la patente #371,496 de la Adding Machine de D.E. Felt. Dorr Felt comenzó su primer prototipo de comptómetro durante las vacaciones de Acción de Gracias (EE.UU.) de 1884. Segunda página de la patente #371,496 de la Adding Machine de D.E. Felt. Para construirlo utilizó una caja de macarrones para la armadura exterior, y pinchos de carne, grapas y gomas elásticas (que funcionaban como muelles) para el mecanismo interior: este primer prototipo se llamó la caja de macarrones (en la referencia 5 puede encontrarse una fotografía de este primer prototipo conservado en el  National Museum of American History de la Smithsonian Institution). Fue la primera calculadora que funcionaba sólo presionando teclas (en vez de girar ruedas, por ejemplo), con suficiente velocidad, fiabilidad y economía. The macaroni box (1885) Felt fundó en enero de 1889 –junto con Robert Tarrant– la compañía Felt & Tarrant Manufacturing Company, una compañía importante en la industria de las calculadoras hasta mediados de 1970. Visto en Today in Science Más información: Patente #371,496 de la Adding Machine de D.E. Felt Comptometer, Wikipedia Shoebox Comptometers – The Models, Comptometer Web Site Comptometer Web Site Key-Driven Calculating Machines, Early Office Museum Comptometer Model A, National Museum of American History, Smithsonian Institution Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Martes, 11 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

33. Cahit Arf, el mayor matemático turco del siglo XX

El matemático Cahit Arf (1910-1997) nació un 11 de octubre. Doodle con motivo del centenario del nacimiento de Cahit Arf (2010) Realizó su tesis doctoral bajo la dirección de Helmut Hasse (1898-1979) en la Universidad de Gotinga. Es conocido por: el invariante de Arf de una forma cuadrática en característica 2, usado en teoría de nudos y en cirugía topológica, el teorema de Hasse-Arf en teoría de ramificaciones, y los semigrupos de Arf y los anillos de Arf. Billete de 10 liras turcas con Cahit Arf y su invariante como protagonistas Más información: Cahit Arf, MacTutor Archive, University of St Andrews Pınar Süngü, Cahit Arf: The Man Who Popularized Mathematics in Turkey, Kurious Cahit Arf, METU Falko Lorenz and Peter Roquette, Cahit Arf and his invariant, Preprint, 2011 Ali Sinan Sertoz, A Scientific Biography of Cahit Arf (1910-1997), arXiv:1301.3699, 2013 Francisco R. Villatoro, Demostrada la conjetura de Arf-Kervaire sobre hiperesferas exóticas tras 45 años de intentos fallidos, La ciencia de la Mula Francis, 2008 Wikipedia Anverso moneda (2001): 7.500.000 liras Reverso moneda (2001): 7.500.000 liras Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Martes, 11 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

34. Una ilusión óptica en tu salón

El diseñador Charles Kalpakian es el creador de Rocky, una estantería realmente singular. Rocky Kalpakian ha creado una variación 3D  de un patrón clásico usado por los carpinteros para fabricar aparadores. Su aspecto cambia dependiendo del punto de vista del observador, provocando curiosos cambios en la percepción de los volúmenes. No es el único de sus trabajos que provoca ambigüedad en nuestra visión… fijaos en su Ciné-tisme, un armario de pared en el que se produce la ilusión óptica del cubo de Necker. Ciné-tisme Visto en El Safari Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Lunes, 10 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

35. 86. (Octubre 2022) Alegorías de la Perspectiva

(La Perspectiva y Especularia de Euclides. Madrid, 1585) El renacimiento medieval europeo del siglo XIII y la revalorización de la matemática deben mucho al redescubrimiento de la óptica geométrica. El conocimiento de la óptica de Euclides por Robert Grosseteste, y la de Alhacén por Roger Bacon, John Pecham y Witelo prepararon el camino que nos condujo hasta Galileo, Kepler, Descartes y Newton. La matemática se fue construyendo sobre técnicas aplicadas desde la antigüedad. La agrimensura, la construcción, la canalización, la contabilidad o el calendario van desde las primeras civilizaciones sentando las bases de una ciencia abstracta cada vez más compleja.  Hay dos disciplinas que empiezan a destacar hasta el punto de hacerse parte de la matemática: la Astronomía y la Perspectiva (nombre antiguo de la Óptica). El mismo Aristóteles ya incluyó la Perspectiva como matemática aplicada. A Euclides no solo se deben los XIII libros de Los Elementos también conservamos de su mano un tratado sistemático titulado en castellano Perspectiva y Especularia (1585), traducido por Pedro Ambrosio Ondériz de la Academia de Matemáticas creada por Juan de Herrera en Madrid al amparo de Felipe II. A la sistematización de la óptica geométrica de Euclides siguen en Alejandría la formalización del principio del camino mínimo por Herón  y los estudios de Ptolomeo con espejos curvos (catóptrica) y de la refracción (dióptrica). La ciencia árabe superó el nivel griego con el descubrimiento de la hoy llamada ley de Snell de la refracción por Ibn Sahl y sobre todo con la deslumbrante Perspectiva de Alhacen, el Arquímedes árabe. El renacimiento de los estudios matemáticos de Oxford en el siglo XIII se deben a la Perspectiva. Algo parecido ocurre con el arte del Renacimiento italiano, se redescubre la Perspectiva a hombros de Euclides. Así un Leonardo podía decir no lea mis escritos quien no sea matemático. La Perspectiva se va convirtiendo durante el siglo XVII en Óptica aupándose en gigantes como Kepler, Descartes, Huygens y Newton. La importancia es tal que nueva ciencia amplia los límites de lo observado: el telescopio e Galileo y la Micrographia.de Hooke extienden el mundo en varios ordenes de magnitud. Los artistas no solo usaron la Perspectiva, también la representaron. Pasamos a ver algunas muestras de alegorías. La Perspectiva en el Mausoleo de Sixto IV Como Papa renacentista, Sixto IV tiene esculpidas en bronce las artes liberales en su panteón funerario. Antonio Pallaiolo fue el ejecutor de esta soberbia obra, que fue terminada en 1493. Las imágenes hablan por si mismas del esplendor de la tumba. Cisneros encargo algo parecido, y un precedente se encuentra en la tumba de Roberto de Anjou en Nápoles. La Capilla Sixtina debe su nombre a Sixto IV. Para ver la tumba hay que localizar el Museo del Tesoro de San Pedro, cuya entrada está en el lateral izquierdo de la basílica. (Alegoría de la Perspectiva. Mausoleo de Sixto IV. Vaticano) La Perspectiva usa un circulo graduado con una alidada, similar a los astrolabios marinos, y que servia para medir ángulos. El libro es un elemento que también caracteriza la alegoría. Gnomónica catóptrica y Perspectiva en el Palazzo Spada de Roma Una curiosa aplicación de la catóptrica, teoría de la reflexión de la luz en un espejo, nos la ofrecen los espectaculares relojes solares astronómicos “de techo”, de los que se han conservado tres soberbios ejemplares en funcionamiento, dos en Roma y uno en Grenoble. Los dos romanos son obra del padre Emmanuel Maignan de la orden de los Mínimos: uno se localiza en el convento de la Trinitá dei Monti (parte superior de la escalinata de la Plaza de España) y otro en la Galería del Palazzo Spada. La luz reflejada en un pequeño espejo horizontal tiene la ventaja de verse en los techos interiores de los pórticos lo que facilita mucho la lectura. Se considera que el primer constructor de un reloj solar catóptrico fue Copérnico en el castillo de Olsztyn, recientemente restaurado, y se extendieron con el diseñado para el Palacio de los Papas en Avignon por el jesuita Atanasius Kircher, hoy desaparecido. Las alegorías de la Geometría, la Aritmética y la Astronomía colaborando con la Perspectiva expresan muy bien como la construcción de un reloj especular requiere el uso de las cuatro disciplinas. El arte termina de darle belleza a la representación. En el lomo del libro se lee Witellionis, el autor de la Perspectiva que divulga la de Alhacen. (Alegorías de la Perspectiva, la Geometría, la Astronomía y la Aritmética. Palazzo Spada. Roma) La alegoría de la Perspectiva en la Villa del Príncipe en Génova El palacio de Andrea Doria, la Villa del Príncipe, es uno de los mejores ejemplos de la concepción renacentista de los saberes, de cuando las disciplinas recogen distintas tradiciones y toman nombres que hoy nos resultan chocantes. La sala que cuenta la historia de Aracne, la mítica tejedora de las Metamorfosis de Ovidio, tiene incrustadas doce artes, tres por lado, en lugar de las siete de Marciano Capella. Las alegorías femeninas de la Astronomía, la Aritmética y la Geometría están en el mismo lado en ese orden. La Astronomía porta una esfera sólida, la Geometría lleva un compás en una mano y una estrella hexagonal en la otra y la Aritmética sujeta una tablilla con operaciones y un triángulo. La decoración del palacio fue encargada a los pintores il Beccafumi, il Pordenone o Girolamo da Treviso, todos del siglo XVI. Las otras artes matemáticas que se representan son la Estereografía y la Perspectiva, ambas emparentadas y fundamentales para la pintura. Lo que resulta más llamativo es la presencia de la Mágica: la Magia Natural es nuestra Física. El estado de conservación de los frescos no es bueno. (Alegorías de la Estereografía y la Perspectiva. Villa del Príncipe. Génova) La Perspectiva según Wentzel Jamnitzer El orfebre geómetra Jamnitzer escribió Perspectiva corporum regularium (1568) y en su portada diseñó un esquema de lo que iba a ser su placa mortuoria. Un marco de espejo en plata que se exhibe en Nueva York reproduce fielmente la portada pero el diseño en fundición de la lápida es algo diferente. En ambas la alegoría de la Geometría y la Aritmética se encuentra en la parte superior mientras la Arquitectura y la Perspectiva ocupan la inferior. La Perspectiva observa a través de un circulo con alidada extendida y su otra mano reposa sobre un globo celeste. En el Germanisches Nacional Museum se expone la placa original pero es más agradable ver la copia en su lugar original, en el cementerio histórico de San Juan (Johannisfriedhof) (Alegorías de la Perspectiva, la Geometría, la Arquitectura  y la Aritmética. Núremberg) La Perspectiva en la Iconología de Ripa y en los grabados La extensión de las artes decorativas y la imprenta dieron lugar a tratados de iconología siendo el más célebre el de Cesare Ripa (1560-1622). Artistas y artesanos encuentran en los tratados o en grabados sus fuentes de inspiración. (Perspectiva. Iconología Cesare Ripa) Los accesorios para la Perspectiva de Ripa son la escuadra, el compás, la plomada y el espejo sujetos con la mano derecha y los libros con la izquierda. Un colgante con un ojo completa la alegoría femenina. Los grabados de Étienne Delaune (1518-1595) nos muestran a la alegoría mirando por una barra de nivel (el catalejo no se había inventado) mientras en la otra mano sujeta un compás y una vara de medir. (Perspectiva. 1572. Étienne Dalaune) De la Perspectiva a la Óptica en Alcora La Reial Fàbrica de Pisa i Porcellana que fundó el ilustrado Conde de Aranda en l´Alcora tuvo una larga aunque azarosa existencia entre 1727 y 1944. Una época brillante fue la de sus inicios, cuando fueron contratados artistas y ceramistas franceses para la fabricación de productos de alta calidad. La nueva monarquía borbónica trajo consigo los gustos versallescos que la nobleza terminó adoptando. En 1666 se funda la Academia de Ciencias francesa y un año después se construye el Observatorio Astronómico de París. La pintura y la imprenta dan cuenta de que la revolución científica es imparable: la realeza y la aristocracia no pueden permanecer al margen. Así, en la producción de l´Alcora nos encontramos con  imágenes de los acontecimientos que se están produciendo en la ciencia y la industria. (Alegoría de la Óptica. 1740. Museu de l´Alcora) El Museu de Ceràmica de l´Alcora exhibe en depósito una salvilla que representa alegóricamente a la Óptica y que reproduce un grabado francés de Corneille y Simonneau (1740) que proviene de Bernard Picart. Al fondo aparece el Observatorio de París todavía en obras. La salvilla forma parte de una serie de reproducciones de los avances científicos de los dan testimonio incluso las mesas de los nobles ilustrados españoles. Es destacable ya la presencia del telescopio o el catalejo. La Perspectiva de Bayeu en el Palacio de El Pardo El fresco de Francisco Bayeu (1734 –1795) en el Palacio de El Pardo es posterior a la salvilla de cerámica pero el pintor utiliza la iconología tradicional, nada de telescopio, un espejo, escuadra, plomada, y compás. Los libros son los tratados de Ptolomeo y Witelo. El pintor de Corte de Carlos III reproduce modelos que ignoran la revolución científica moderna: se queda en la ciencia antigua y medieval.

Lunes, 03 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

36. Xuanji Tu

En el siglo IV, la poeta y palindromista china Su Hui perdió ‘el favor’ de su marido por una concubina. Su Hui con un palíndromo. http://en.wikipedia.org/wiki/File:Su_Hui_with_a_palindrome.jpg Para consolar su pena e intentar atraer a su esposo de nuevo, compuso un ingenioso conjunto de 841 caracteres -un tablero de 29 por 29 casillas- que pueden leerse en cualquier dirección -vertical, horizontal o diagonal- y sentido. Es el poema Xuanji Tu. El poema «Xuanji Tu». http://en.wikipedia.org/wiki/File:Xuanjitu.GIF Esta estructura genera 2.848 posibles poemas. Se dice que el esposo de Su Hui ‘se conmovió’, y abandonó a la concubina por su Su Hui… ¡cuánta nobleza por parte del marido! Visto en Futility Closet Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Lunes, 03 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

37. René Gâteaux (1889-1914)

El matemático René Eugène Gâteaux (1889-1914) falleció un 3 de octubre, en la entrada del pueblo de Rouvroy (Francia), durante la guerra. René Gateaux (encuadrado en verde) con sus colegas de la promoción de 1907 en l’École normale supérieure. ©Le journal du CNRS Es principalmente conocido por su definición de una derivada direccional utilizada en el cálculo de variaciones y en teoría de control óptimo. En agosto de 1915, Jacques Hadamard (1865-1963) comienza las gestiones para la concesión póstuma de uno de los premios de la Académie des sciences a Gâteaux: en 1916 se le concede el prix Francœur. En 1918, Hadamard habla a Paul Lévy, encargado de impartir un curso de Análisis Funcional en el Collège de France, sobre los borradores dejados por Gâteaux antes de partir al frente: le propone editarlos para el Bulletin de la Société mathématique de France, labor que se realizará en dos tiempos (ver las referencias debajo). El mayor descubrimiento que Lévy extrae de los papeles de Gâteaux es un esbozo de una teoría para la integración de funciones en dimensión infinita; la importancia de este trabajo será considerable para Lévy, porque le animará a escribir su texto Leçons d’analyse fonctionnelle (1922). Cuando Lévy comenta con Norbert Wiener el trabajo de Gâteaux, el matemático americano percibe inmediatamente que puede utilizar la definición de Gâteaux para poner en forma su concepto de ‘espacio diferencial’ y construir la medida del movimiento browniano, llamada a partir de entonces medida de Wiener. En su artículo fundador Differential space (J. Math, and Phys. 2 (1923), 131-174), Wiener rinde homenaje a Gâteaux y Lévy, citándolos como aquellos que han realizado los estudios más profundos sobre la integración en dimensión infinita. Extracto de ‘Differential space’ con el reconocimiento a Gâteaux y Lévy, entre otros Más información: Gâteaux, R., Sur la notion d’intégrale dans le domaine fonctionnel et sur la théorie du potentiel, Bulletin de la Société Mathématique de France 47(1919) 47-70 Gâteaux, R., Fonctions d’une infinité de variables indépendantes, Bulletin de la Société Mathématique de France 47(1919) 70-96 René Eugène Gâteaux, MacTutor History of Mathematics archive, University of  St. Andrews Paul Levy and René Gateaux, MacTutor History of Mathematics archive, University of St. Andrews Laurent Mazliak, The ghosts of the Ecole Normale. Life, death and legacy of René Gateaux, 2011 Laurent Mazliak, René Gateaux, jeune savant fauché par la guerre, Le journal du CNRS, 2014 Wikipedia (en francés) Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Lunes, 03 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

38. ¿Qué es una rosquilla?: explicación topológica

Aquí puedes ver varias rosquillas: http://commons.wikimedia.org/wiki/File:Rosquillas.JPG Pero éstas también son –topológicamente equivalentes a– rosquillas: http://themetapicture.com/madness-has-never-looked-so-delicious/ Nota: ¿A que pensabas que iba a poner una taza de café? Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Lunes, 26 de Septiembre de 2022 | Imprimir | PDF |  Correo electrónico

39. Anneli Cahn Lax, matemática

La matemática Anneli Cahn Lax (1922-1999) falleció un 24 de septiembre. Su tesis doctoral Cauchy’s Problem for a Partial Differential Equation with Real Multiple Characteristics (1955) fue dirigida por Richard Courant. Se le conoce fundamentalmente por sus contribuciones para hacer las matemáticas accesibles a estudiantes y público en general, sobre todo como editora de la New Mathematical Library Series de la Mathematical Association of America. Su marido es el matemático Peter Lax (1926-). Más información: Anneli Cahn Lax,  MacTutor History of Mathematics archive, University of  St. Andrews Mark Saul, Anneli Cahn Lax (1922–1999), Notices of the AMS 47 (7) (2000) 766–769 Photos by Paul Halmos Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Sábado, 24 de Septiembre de 2022 | Imprimir | PDF |  Correo electrónico

40. Raoul Bott (1923-2005)

El matemático Raoul Bott (1923-2005) nació un 24 de septiembre. Es conocido por sus numerosas contribuciones en geometría, en particular por el teorema de periodicidad de Bott aplicado en K-teoría, por las funciones de Morse-Bott utilizadas en teoría de Morse y por el teorema de Borel-Bott-Weil sobre representaciones de grupos de Lie… aunque trabajó en la teoría de circuitos eléctricos (teorema Bott-Duffin, 1949) antes de pasar a las matemáticas puras. Bott dirigió 20 tesis doctorales, entre otros a Stephen Smale, Lawrence Conlon, Daniel Quillen, Robert MacPherson o Eric Weinstein. Recibió varios premios, entre ellos el premio Wolf en 2000. Recuerdo con especial cariño el libro Differential Forms in Algebraic Topology de Raoul Bott y Loring W. Tu, en el que conseguí entender las formas diferenciales en la época de mi tesis doctoral. Más información: Raoul Bott, 1923-2005, Universidad de Harvard. Contiene diversos enlaces con entrevistas, biografías, obituarios, etc. Loring Tu,The life and works of Raoul Bott, 2002 Wikipedia Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Sábado, 24 de Septiembre de 2022 | Imprimir | PDF |  Correo electrónico