321. Webinar CASIO: La mancha de café

En esta sesión se resolverá un problema de un sistema no lineal con ayuda de la calculadora grafica utilizando diferentes menús. Recomendado par los niveles de 4º ESO y 1º Bachillerato. Profesor: Lluís Bonet Juan Calculadora: fx-CG50 Descarga el emulador gratuito de la calculadora: https://www.edu-casio.es/emulador/​ Actividades webinar (PDF): https://www.edu-casio.es/wp-content/uploads/2021/03/2.3.21-La-mancha-de-cafe%CC%81-y-chocolate-Llui%CC%81s-Bonet-v4-1.pdf Lluís Bonet Juan Lluís BONET JUAN, licenciado en CC Matemáticas por la Universidad de Valencia es profesor de secundaria en el IES Mare Nostrum de Alicante y profesor-tutor en la UNED de Denia-Benidorm. Ha recibido el Premio EDUCA al mejor docente de España 2019 de secundaria y bachillerato. Es miembro de la SEMCV y colaborador con la FESPM y CASIO en el grupo de trabajo sobre implementación de la calculadora en el aula como recurso didáctico.

Martes, 02 de Marzo de 2021 | Imprimir | PDF |  Correo electrónico

322. Webinar CASIO: Área de un cuadrilátero dentro de un rectángulo

En esta sesión se resolverá un problema de optimización con ayuda de la calculadora científica. Se utilizarán diferentes menús de la calculadora para resolverlo. Profesor: Ricard Peiró Calculadora: ClassWiz. Modelos fx-570/991SP X II Descarga el emulador gratuito de la calculadora: https://www.edu-casio.es/emulador/​ Material webinar (PDF): https://www.edu-casio.es/wp-content/uploads/2021/02/A%CC%81rea-de-un-cuadrila%CC%81tero-dentro-de-un-recta%CC%81ngulo.pdf RICARD PEIRÓ I ESTRUCH Licenciado en Matemáticas por la Universitat de València. Docente de matemáticas en la Comunidad Valenciana, actualmente en el IES “Abastos” de València. Ha impartido como ponente diversos cursos de TIC en el CEFIRE de la Comunidad de Valencia y ha sido premiado dos veces por estos materiales en concursos de la Conselleria de Educació de València. Colaborador en el Grupo de Calculadora de la FESPM y CASIO.

Martes, 23 de Febrero de 2021 | Imprimir | PDF |  Correo electrónico

323. Webinar CASIO: Representación gráfica de una función

Representación gráfica de una función En esta sesión se enseñarán todas las posibilidades que ofrece el menú gráfico: ajuste de la ventana de visualización, zoom, características de la función. Representación de funciones a trozos, de la función derivada…. Dual screen. Cálculo de áreas entre funciones. Cálculo de la función inversa. Profesora: Isabel Goñi Calculadora: fx-CG50 Descarga emulador CG50: https://www.edu-casio.es/emulador/ Curso FESPM Aplicaciones didácticas en el aula con la calculadora gráfica: https://fespm.es/index.php/2021/01/15... Material webinar (PDF): https://www.edu-casio.es/wp-content/uploads/2021/02/Representacio%CC%81n-gra%CC%81fica-de-una-funcio%CC%81n-ISABEL-GON%CC%83I-16-de-febrero.pdf Isabel Goñi Profesora de Matemáticas de Nacional y IB PD en el Colegio San Patricio, el Soto.Tutora de Bachillerato.Responsable de taller presencial y en línea. Miembro de delegaciones visitantes, examinadora y lectora de esquemas de asignaturas de IB. Licenciada en Ciencias Matemáticas. Especialidad en Estadística e Investigación Operativa. Master Europeo en Dirección de Centros Educativos.

Martes, 16 de Febrero de 2021 | Imprimir | PDF |  Correo electrónico

324. Webinar CASIO: Estadística con la calculadora científica ClassWiz

Estadística unidimensional y bidimensional. Se verán todas las posibilidades de la calculadora ClassWiz para afrontar problemas de estadística. Realizar fácilmente los cálculos, permite dedicar más tiempo a la interpretación de los datos estadísticos. Aplicaciones para Secundaria y Bachillerato. Profesor: José Mª Chacón Calculadora: ClassWiz. Modelos fx-82/85SP X II y fx-570/991SP X II Descarga el emulador gratuito de la calculadora: https://www.edu-casio.es/emulador/​ Material webinar (PDF): https://www.edu-casio.es/wp-content/uploads/2021/02/Estadi%CC%81stica-con-calculadora-cienti%CC%81fica-ClassWiz.pdf José Mª Chacón Licenciado en Matemáticas. Ha desarrollado su labor docente como profesor de Educación Secundaria en Sevilla. Colaborador del la División Educativa de CASIO y tutor en los cursos a distancia sobre uso de calculadoras realizados en la SAEM Thales.

Martes, 09 de Febrero de 2021 | Imprimir | PDF |  Correo electrónico

325. Webinar CASIO: Las fases de la luna

En esta sesión se resolverá un problema de funciones con ayuda de la calculadora gráfica. La representación y visualización de la gráfica de una función permite dar respuesta a cuestiones de un problema contextualizado. Profesor: Ricard Peiró Calculadora: fx-CG50 Descarga el emulador gratuito de la calculadora: https://www.edu-casio.es/emulador/​ Material webinar (PDF): https://www.edu-casio.es/wp-content/uploads/2021/02/FASES-DE-LA-LUNA-PRESENTACIO%CC%81N-RICARD-2.pdf RICARD PEIRÓ I ESTRUCH Licenciado en Matemáticas por la Universitat de València. Docente de matemáticas en la Comunidad Valenciana, actualmente en el IES “Abastos” de València. Ha impartido como ponente diversos cursos de TIC en el CEFIRE de la Comunidad de Valencia y ha sido premiado dos veces por estos materiales en concursos de la Conselleria de Educació de València. Colaborador en el Grupo de Calculadora de la FESPM y CASIO.

Martes, 02 de Febrero de 2021 | Imprimir | PDF |  Correo electrónico

326. Los científicos que demostraron la cuadratura del cuadrado

ABC, 12 de Abril de 2021 CIENCIA - El ABCdario de las matemáticas Pedro Alegría

Lunes, 12 de Abril de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

327. 115. (Abril 2021) Herramientas de MIR en MatLab

1. Tecnología Musical y Musicología Computacional Hoy en día la música se investiga desde muchos puntos de vista, tal es su complejidad por un lado y tal es la variedad y potencia de los métodos de investigación modernos por otro lado. Las siglas de MIR, Music Information Retrieval, vienen del inglés y es el nombre que se le da actualmente al campo de la Computación Musical en un sentido muy amplio. Originalmente, el campo del MIR empezó en los años 60 con un pequeño grupo de ingenieros y músicos intentando resolver problemas prácticos de tratamiento musical, entre los cuales se contaba el de la recuperación de la información. Poco a poco se fueron juntando investigadores y profesionales de este incipiente campo y tras no mucho tiempo explotó como disciplina científica. Aunque los objetivos y métodos pronto engulleron a los problemas de tratamiento de la información musical de los primeros tiempos, por razones que aun hoy en día no alcanzo a comprender, se mantuvo el nombre de MIR. Creo que un nombre más adecuado sería el de Computación Musical (que uso en mis columnas aquí y en otros trabajos). Sea como fuere, el nombre se ha quedado por razones históricas y es el más usado para referirse a esta disciplina. Actualmente, la Computación Musical (MIR) es un campo multidisciplinar que se nutre de la propia Música, la Musicología, Computación —en particular, de la Inteligencia Artificial y la Ciencia de Datos —, Cognición y Psicología, diversas disciplinas de humanidades tales como la Lingüística, la Sociología. Entre los problemas que aborda la Computación Musical están el análisis musical (problemas tales como la similitud melódica, la detección del pulso, el reconocimiento de la estructura musical, las medidas de complejidad rítmica, melódica, armónica, solo por nombrar unos pocos); y a estos se añade, la clasificación de la música, los sistemas de recomendación, la generación automática de música, el estudio de la conexión entre música y emoción por métodos computacionales, la transcripción automática de la música, la separación de fuentes en una señal de audio musical, entre otros. En esta columna se han tratado de manera divulgativa muchos de estos problemas; véanse las siguientes columnas y las referencias que tienen: [Góm12a, Góm11a, Góm12b, Góm13, Góm11b, Góm14, Góm16, Góm18, Góm20b]. Dentro del MIR hay una rama evidentemente tecnológica e industrial y, de hecho, empresas importantes tales como Yamaha, Pandora, Sony, Spotify, por ejemplo, trabajan en las aplicaciones de los conceptos y métodos del MIR (quizás sea el problema de la recomendación musical el más arquetípico). Otra disciplina distinta de la Computación Musical es la Musicología Computacional. Este último campo consiste en el estudio musicológico a través de métodos computacionales. Esta rama de la musicología, de origen moderno cuando se compara con la musicología histórica, por ejemplo, se suele considerar como una parte de la Musicología Sistemática. La Musicología Computacional no llegó sin rechazo e incomprensión en un principio; y, por otra parte, algunos de sus practicantes cometieron excesos que alimentaron tal rechazo. Para un resumen de este debate, véase el artículo de esta columna Alcance y extralimitaciones de las matemáticas y la computación en la música [Góm20a]. Por otra parte, la Computacional Musical ha prestado apoyo metodológico e inspirado varios problemas a la Musicología Computacional. 2. La herramienta MIRtoolbox En la columna de este mes nos vamos a centrar en algo más práctico. Es algo que me han pedido algunos lectores, músicos principalmente, y es que describa y comente herramientas de computación musical. En particular, voy a describir la herramienta MIRtoolbox, diseñada y construida por los investigadores Lartillot y Toiviainen (con la intervención de Tuomas en la primera parte) [LT07a, LTE07]. MIRtoolbox es una herramienta escrita en MATLAB y está concebida para la extracción de características musicales de bajo y medio nivel de música dada en formato de audio (y no en formato simbólico como pueda ser el MIDI). Una de sus ventajas es que MIRtoolbox ha sido diseñado con un usuario no experto en programación en mente y, como consecuencia de ello, la sintaxis y la interfaz son muy fáciles de usar. 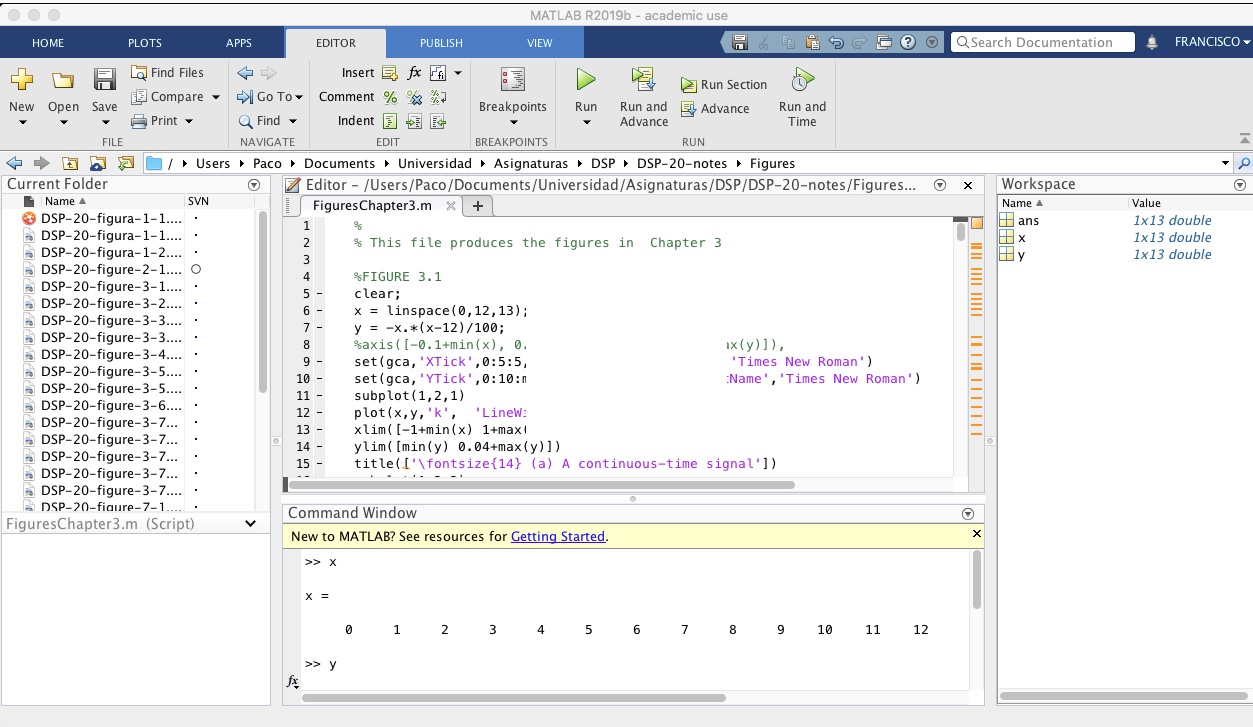MATLAB es el acrónimo de MATrix LABoratory. Inicialmente, este paquete de cálculo se especializó en el cálculo de matrices. Posteriormente, se convirtió en un paquete de cálculo multi-propósito y hoy en día es el estándar en ingeniería y en buena parte de las matemáticas. MATLAB es multi-plataforma y existen versiones para Windows, macOS, Unix y GNU/Linux. Tiene tanto cálculo simbólico como cálculo numérico y a través de sus toolboxes, módulos especializados, se pueden ampliar sus capacidades de cómputo a campos concretos tales como el procesamiento de la señal, la simulación, la biología computacional, la estadística avanzada, entre otros. La web de este paquete se puede encontrar en [Mat21]. En la figura de abajo se puede ver el interfaz gráfico de MATLAB. Figura 1: Interfaz gráfica de MATLAB MIRtoolbox es una herramienta gratuita y se puede descargar en [LT07b]. Sirve tanto para la investigación como para la docencia. A continuación vamos a describir las principales características de interés para el musicólogo computacional y/o sistemático. 3. Extracción de caracerísticas musicales en MIRtoolbox En la figura 1, tomada del propio artículo [LT07a] de presentación de la herramienta, muestra los distintos niveles de extracción. Todos los procesos empiezan por considerar la señal (a la izquierda) y se van aplicando diversas operaciones según se va hacia la izquierda. Leída de izquierda a derecha, las características musicales van de bajo nivel a medio nivel. Leída en de arriba abajo la figura 1 nos devuelve las principales operaciones del MIRtoolbox en orden creciente de complejidad computacional. Figura 2: Características musicales extraíbles con el MIRtoolbox (figura tomada de [LT07a] He aquí una lista con sucintas explicaciones de las principales características extraíbles desde MIRtoolbox: La tasa de cambios de signo (zero-crossing rate), que se usa en procesamiento musical y del habla y que sirve para identificar sonidos percusivos (por ejemplo, en problemas de separación de fuentes). La energía de la señal, medida como el valor cuadrático medio (RMS). El contorno de una señal, que da importante información sobre su comportamiento desde un punto de vista musical, por ejemplo, sobre el timbre o la finalidad melódica. El espectro de la señal, obtenido a través de la transformada de Fourier, del cual se obtienen medidas relevantes para la identificación de la señal así como la detección de patrones dentro de la misma. Entre esas medidas, encontramos las básicas tales como el centroide, la curtosis o el coeficiente de asimetría; y luego más complejas, el flujo espectral, la disonancia textural (roughness), la escala Mel. A partir de estas medidas se pueden obtener los descriptores de medio nivel tales como tempo, claridad del pulso, altura o fluctuación. Como muestra de la sencillez de uso de MIRtoolbox, en la figura 2 se pueden ver los comandos para obtener algunas de las medidas anteriores. Empezamos por cargar un fichero de audio (1); lo descomponemos en secuencias (2); extraemos el espectro (3); convertimos el espectro del dominio de la frecuencia al dominio de la escala de Mel (4); por último, obtenemos los coeficientes MFCC. Figura 3: Sintaxis de MIRtoolbox (figura tomada de [LT07a] El proceso anterior se puede resumir más gráficamente como se muestra en la figura 4: Figura 4: Cálculo de los coeficientes MCC en MIRtoolbox (figura tomada de [LT07a] Por último, ilustramos el proceso de estimación de la fuerza tonal; véase la figura 4. Esta medida cuantifica cuán predominante es una tonalidad en una pieza de música. El método sigue las ideas de Krumhansl y Kessler; véanse [KK82, Kru90]. En primer lugar, se pasa del dominio de la frecuencia al de las alturas mediante una transformación logarítmica de aquellas. Esta representación es el cromagrama. Este cromagrama se consolida y se ponen en las mismas clases las alturas que están a distancia de un múltiplo de una octava entre sí. Esto da una representación en forma de histograma de las clases de alturas. Se aplica entonces correlación cruzada entre el histograma obtenido y los histogramas de las 12 tonalidades posibles dados en [KK82], los cuales provienen de experimentos hechos con oyentes. Figura 5: Cálculo de los coeficientes MCC en MIRtoolbox (figura tomada de [LT07a] 4. Conclusiones El MIRtoolbox permite muchos más análisis y procesos de computación musical que los brevemente glosados aquí. Por ejemplo, el análisis rítmico, la segmentación a varios niveles, el análisis de grandes volúmenes de datos, el análisis de secuencias. Remitimos al lector al manual de la herramienta, que se puede encontrar en [LT07a]. En este artículo se encontrarán también detalles técnicos de la arquitectura y la representación de datos de la herramienta.   Bibliografía [Góm11a] Paco Gómez. Distancia y similitud musical, mayo de 2011. [Góm11b] Paco Gómez. Distancia y similitud musical (I), mayo de 2011. [Góm12a] Paco Gómez. El teorema del hexacordo (I), Octubre de 2012. [Góm12b] Paco Gómez. Medidas matemática de síncopa (I), Octubre de 2012. [Góm13] Paco Gómez. COFLA: la música flamenca y su estudio computacional, agosto de 2013. [Góm14] Paco Gómez. Teoría generativa de la música (I), junio de 2014. [Góm16] Paco Gómez. Composición algorítmica (I), junio de 2016. [Góm18] Paco Gómez. Ritmos euclídeos y ritmos equilibrados, marzo de 2018. [Góm20a] Paco Gómez. Alcance y extralimitaciones de las matemáticas y la computación en la música, julio de 2020. [Góm20b] Paco Gómez. Música y entropía - I, julio de 2020. [KK82] C. L. Krumhansl and E. J. Kessler. Tracing the dynamic changes in perceived tonal organization in a spatial representation of musical keys. Psychological Review, 89:334–368, 1982. [Kru90] C. L. Krumhansl. Cognitive Foundations of Musical Pitch. Oxford University Press, New York, 1990. [LT07a] Olivier Lartillot and Petri Toiviainen. Mir in matlab (ii): A toolbox for musical feature extraction from audio. pages 127–130, 01 2007. [LT07b] Olivier Lartillot and Petri Toiviainen. MIRtoolbox, 2007. [LTE07] Olivier Lartillot, Petri Toiviainen, and Tuomas Eerola. A matlab toolbox for music information retrieval. volume 4, pages 261–268, 01 2007. [Mat21] Mathworks. MATLAB, 1994–2021.

Lunes, 12 de Abril de 2021 | Imprimir | PDF |  Correo electrónico

328. Webinar CASIO: Primer contacto con la calculadora gráfica

Esta sesión está destinada a familiarizarse con la calculadora gráfica fx-CG50. Se explicará brevemente para qué sirve cada menú y se realizarán operaciones básicas para conocer mejor la calculadora, su configuración, el modo examen… Un taller para descubrir poco a poco y desde el inicio la calculadora gráfica. Profesora: Isabel Goñi Calculadora: fx-CG50 Descarga emulador CG50: http://edu.casio.com/softwarelicense/... Curso FESPM Aplicaciones didácticas en el aula con la calculadora gráfica: https://fespm.es/index.php/2021/01/15... Material webinar (PDF): https://www.edu-casio.es/wp-content/uploads/2021/01/CASIO... Isabel Goñi Profesora de Matemáticas de Nacional y IB PD en el Colegio San Patricio, el Soto. Tutora de Bachillerato. Responsable de taller presencial y en línea. Miembro de delegaciones visitantes, examinadora y lectora de esquemas de asignaturas de IB. Licenciada en Ciencias Matemáticas. Especialidad en Estadística e Investigación Operativa. Master Europeo en Dirección de Centros Educativos.

Martes, 19 de Enero de 2021 | Imprimir | PDF |  Correo electrónico

329. Webinar CASIO: Acabo de tener la gripe

En esta sesión se resolverá una actividad para trabajar funciones cuadráticas, sus propiedades, analizar tablas de valores y representar las parábolas gracias al código QR. La aplicación CASIO EDU+ convertirá esta actividad en colaborativa y se compartirán los resultados obtenidos entre todos los participantes. Profesor: Lluís Bonet Juan Calculadora: ClassWiz. Modelos fx-570/991SP X II La App CASIO EDU+ está disponible aquí: https://wes.casio.com/es-es/​ Descarga el emulador gratuito de la calculadora: https://www.edu-casio.es/emulador/​ Todos los materiales de esta sesión: https://www.edu-casio.es/portfolio-it... Actividades webinar (PDF): https://www.edu-casio.es/wp-content/uploads/2021/01/CASIO-webinar-Acabo-de-tener-la-gripe.pdf Lluís Bonet Juan Lluís BONET JUAN, licenciado en CC Matemáticas por la Universidad de Valencia es profesor de secundaria en el IES Mare Nostrum de Alicante y profesor-tutor en la UNED de Denia-Benidorm. Ha recibido el Premio EDUCA al mejor docente de España 2019 de secundaria y bachillerato. Es miembro de la SEMCV y colaborador con la FESPM y CASIO en el grupo de trabajo sobre implementación de la calculadora en el aula como recurso didáctico.

Martes, 12 de Enero de 2021 | Imprimir | PDF |  Correo electrónico

330. Webinar CASIO: Conociendo la calculadora científica

Durante este taller se mostrarán las múltiples posibilidades que ofrece la calculadora científica dependiendo de su configuración, se realizarán actividades interesantes para la divisibilidad y se descubrirá la ayuda que ofrece en los procesos de cálculo el menú “Verificar”. Profesor: Lorenzo Sevilla Calculadora: ClassWiz. Modelos fx-82/85SP X II y fx-570/991SP X II Descarga el emulador gratuito de la calculadora: https://www.edu-casio.es/emulador/​ Material webinar (PDF): https://www.edu-casio.es/wp-content/uploads/2021/01/Conociendo-la-calculadora-cienti%CC%81fica-FINAL.pdf Lorenzo Sevilla Lorenzo Sevilla, licenciado en CC Matemáticas por la Universidad Autónoma de Madrid es profesor de educación secundaria en el IES Las Musas (Madrid). Ha participado en congresos y talleres para la integración de las TIC en la clase de matemáticas, es colaborador de la división Educativa de CASIO e imparte talleres de calculadoras científicas y gráficas. Participa con su centro en proyectos de investigación y ha sido premiado con “Experiencias en el aula con Geogebra”.

Martes, 26 de Enero de 2021 | Imprimir | PDF |  Correo electrónico