331. 192. (Abril 2021) Magia en el aula

Al amparo de este rincón, en muchas ocasiones hemos destacado las propiedades didácticas de los juegos de magia matemática. También hemos querido señalar aquellos autores que han publicado material pedagógico con el que potenciar la enseñanza de las matemáticas a través de la magia (como, por ejemplo, en el número 179 de febrero de 2020 y en el número 144 de diciembre de 2016). Parece que esta tendencia es imparable y ya es constante el flujo de información relacionada con este tema y la gran diversidad de enfoques que los profesionales de la educación están desarrollando para aprovechar las bondades de la magia en la didáctica de las matemáticas. Esta vez quiero comentar dos de los últimos trabajos que he encontrado y me han parecido interesantes. El primero de ellos se titula "Mathematical Explorations of Card Tricks", su autor es Timothy Weeks de la Universidad John Carroll en Ohio (EEUU) y se ha publicado en el número 73 de Senior Honors Projects en la primavera de 2015. En la introducción, el autor recoge una famosa sentencia de Martin Gardner: «La magia matemática combina el aspecto académico de las matemáticas con el valor de entretenimiento de la magia». A lo largo de su trabajo, el autor recorre algunos juegos basados en ciertas propiedades combinatorias en las que se basa un determinado reparto de las cartas de una baraja, así como aplicaciones del principio del palomar o de la teoría de códigos correctores de errores. Los juegos seleccionados son adaptaciones de otros contenidos en el libro "Mathematical Card Magic", escrito por Colm Mulcahy y publicado por CRC Press el año 2013 pero proporciona las demostraciones matemáticas de los resultados obtenidos. El segundo artículo que quiero citar es el trabajo de Morgan Mitchell y Jay Cummings (aquí en la foto) titulado "When and how to use math based card tricks in the classroom", publicado en McNair Scholars Journal el año 2017. Con el fin de mejorar la percepción de los estudiantes sobre su propia habilidad en la comprensión de las matemáticas, su respuesta emocional hacia los retos que plantean y la ansiedad que produce su propia inseguridad, los autores desarrollan una colección de juegos de magia con cartas así como las explicaciones matemáticas en las que se apoyan. Pretenden así ofrecer a los educadores algunas herramientas con las que "reenganchar" a los estudiantes y mostrarles los aspectos lúdicos a la vez que formativos de la magia matemática. En este trabajo se cita el estudio titulado "Using Illusions in the Classroom: Principles, Best Practices, and Measurement" de Kevin Elder, David Deviney, Ronald MacKinnon y John Dyer (2012), quienes apuntaron cuatro principios básicos sobre el uso de la magia en el aula: No dejar que la ilusión sobrepase a la lección. Practicar antes de ejecutar. Nunca repetir un truco ante la misma audiencia. No explicar el truco porque no dejaría apreciar la ilusión y el misterio. No entraré a discutir la idoneidad de estas reglas básicas así que pasaré directamente a comentar algún juego de los que allí se proponen. Algunas versiones de la mayoría de los juegos que se incluyen en los dos artículos anteriores están tratados en este rincón así que he optado por mostrar algunas variantes del primer juego que enseñan Morgan Mitchell y Jay Cummings en su trabajo, que es básicamente el que apareció sin explicación en el número 7 nada menos que en julio de 2004. En el libro «The very best of Dai Vernon», de Richard Vollmer (escrito en francés), aparece esta versión titulada "Las cartas calculadoras". A grandes rasgos, este es el juego: Busca una baraja, comprueba que está completa (tiene las 52 cartas) y mézclala. Recoge la baraja con las caras hacia ti y reparte sobre la mesa, caras hacia abajo, varios montones de cartas, de la siguiente forma: Pasa de una mano a otra la carta superior y mira su valor. Pasa a continuación tantas cartas como hace falta para llegar a 13, una encima de otra formando un montón. Por ejemplo, si la carta superior es un 6, pasa a la otra mano siete cartas más; si es una dama, pasa una carta más (la dama cuenta como 12); si es un as, pasa 12 cartas más. La forma más sencilla es contar de una en una las cartas mientras las vas pasando de una mano a otra, empezando por el número de la primera carta y terminando en 13. Deja el montón así formado sobre la mesa, caras hacia abajo. Una vez que haya sobre la mesa unos seis o siete montones, selecciona tres de ellos. Retira los montones eliminados añadiéndolos al resto de cartas que te quedan en la mano. De los tres montones seleccionados, gira cara arriba la carta superior de dos de ellos. Suma sus valores y reparte, del paquete que tienes en la mano, tantas cartas como el valor de dicha suma. Reparte luego diez cartas más, porque me da la gana, y cuenta el número de cartas que quedan sin repartir. Dicho valor coincidirá con el de la carta superior del tercer montón que quedaba. Como indican los autores del trabajo citado, es una buena tarea para el estudiante hacer las operaciones necesarias con el fin de averiguar el funcionamiento del truco. Veamos: si las cartas superiores de los tres montones elegidos tienen valores desconocidos X, Y y Z, dichos montones contienen 14 - X, 14 - Y y 14 - Z cartas, respectivamente. En la mano tienes entonces 52 - (14 - X) - (14 - Y) - (14 - Z) = 10 + X + Y + Z cartas. Supongamos que el montón elegido es que tiene el valor X como carta superior. Al girar las cartas superiores de los otros dos montones, aparecerán los valores Y y Z. Se retiran entonces Y + Z cartas y, por último 10 cartas. Evidentemente, quedan únicamente X cartas. Otra versión, algo diferente, es la siguiente: Busca una baraja francesa (también completa) y selecciona nueve cartas. Deja el resto sobre la mesa. Elige una de esas nueve cartas, dejando las demás en un montón caras abajo sobre la mesa. Después de mirar y recordar la carta elegida, déjala sobre el montón de las ocho cartas no elegidas. Coloca el resto de la baraja sobre este montón. Recoge de nuevo la baraja completa y reparte la carta superior sobre la mesa, girándola cara arriba, diciendo "diez". Sobre ella reparte la segunda diciendo "nueve", y así sucesivamente hasta que aparezca una carta cuyo valor coincida con el número nombrado en ese momento. Esas cartas formarán el primer montón. Si has repartido la décima carta diciendo "uno" y no ha habido ninguna coincidencia, reparte una carta más cara abajo tapando dicho montón. En cualquiera de los casos, repite el mismo procedimiento tres veces más hasta que haya sobre la mesa cuatro montones. Suma entonces los valores de las cartas superiores de cada montón (si están cara arriba) y, con las cartas que tienes todavía en la mano, reparte tantas cartas como indica dicha suma. La última carta repartida será la que habías elegido inicialmente. Vayamos con la justificación del juego. Observemos en primer lugar que la carta elegida está en la posición 44 de la baraja (tiene sólo 8 cartas bajo ella). Al repartir cuatro montones, si no ha habido ninguna coincidencia, cada montón tiene 11 cartas, lo que hace un total de 44. La última carta es precisamente la elegida. Si el montón i-ésimo tiene ni cartas, el valor de la carta superior es 11 - ni. En total se han repartido n1 + n2 + n3 + n4 cartas. Al sumar los valores de las cartas superiores, se reparten 11 - n1 + 11 - n2 + 11 - n3 + 11 - n4 cartas, precisamente las que faltan para llegar a 44 cartas. Por cierto, si el paquete no está completo, basta restar de 9 el número de cartas que faltan para que funcione el juego. El mismo principio permite diversas adaptaciones como la siguiente (que es una variante del juego "Afinidades" publicado en el segundo volumen de "The Vernon Chronicles" por Stephen Minch). Busca una baraja completa (de 52 cartas) y mézclala. Teniendo las cartas con las caras hacia arriba, forma sobre la mesa varios montones de cartas, de la siguiente forma: pela la primera carta y fíjate en su valor (en lo sucesivo, las figuras cuentan como 10); empieza una cuenta mental con el valor de dicha carta; sigue pelando cartas, formando un paquete en la otra mano (dejando cada carta sobre la anterior), y siguiendo la cuenta mental, hasta que hayas pasado tantas cartas como sea necesario para llegar a doce. Un ejemplo: si la carta de cara es un siete, pásala a la otra mano empezando la cuenta por siete; al pasar la siguiente carta, cuenta "ocho"; pasa otra más contando "nueve"; otra más a la cuenta de "diez", una más a la cuenta de "once" y la última para llegar a "doce". Deja sobre la mesa, con las caras hacia abajo, el montón de cartas que has formado. Repite el proceso hasta dejar en la mesa un grupo de más de seis montones. No hace falta utilizar todas las cartas pero sí la mayoría de ellas. Selecciona cuatro montones volviendo cara arriba la carta superior de cada montón elegido. Retira los montones no elegidos y forma un paquete con todos ellos y con las cartas no utilizadas anteriormente. Recuerda que los valores de las cartas vueltas son completamente aleatorios ya que has mezclado la baraja y has elegido esos montones y no otros. Suma los valores de dichas cartas (recuerda que las figuras valen 10) y comprueba que las cartas tienen la habilidad de adelantarse a los acontecimientos. Resulta que la suma de los valores de las cuatro cartas elegidas coincide con el número de cartas que forman el paquete desechado. Comentarios finales: El principio utilizado en estos juegos es el llamado «principio del complemento a 13» o, por su nombre en inglés «10, 9, 8, ... Count», pero también podría llamarse el del complemento a doce o a cualquier otro número. Su origen es desconocido aunque apareció publicado el año 1593 en el libro "Giochi di carte bellissimi di regola e di memoria" de Horatio Galasso (en la imagen), tan antiguo que se puede disfrutar digitalizado en el Archivo de Internet (en este caso, se aplica el principio del complemento a 15, con una baraja de 48 cartas). En el libro "La pasión de un cartómago aficionado" de Pablo Nagata se detalla el gran recorrido y desarrollo que ha tenido esta simple propiedad matemática a lo largo de la historia de la magia. Este principio y otros similares han dado lugar a sucesivos refinamientos e ingeniosas adaptaciones. Quiero destacar las aportadas en los maravillosos libros "La magia pensada" y "Más magia pensada" del maestro Ramón Riobóo, cuya reciente pérdida seguimos lamentando. ¡Que tengas buen viaje, Ramón! Aunque ya sabemos que las casualidades no existen, cuando estaba a punto de dejar terminada esta reseña, la editorial Cossetània me hizo llegar un nuevo libro dedicado a las aplicaciones didácticas de la magia matemática. Se trata del titulado "100 jocs automàtics de matemàgia" escrito por Enric Ramiro y Pilar Gandía, que han dedicado toda su carrrera a la docencia. Como su título indica, recoge de manera estructurada una gran selección de juegos que podrán ser utilizados en el aula como material complementario a todos los niveles de educación básica. Seguro que un docente encontrará más de un juego con el que salir de la rutina diaria y motivar a sus estudiantes para interesarse en las matemáticas. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Martes, 06 de Abril de 2021 | Imprimir | PDF |  Correo electrónico

332. 160. Matemáticas Alternativas

Para variar, en esta ocasión la reseña propuesta será inusualmente corta (y no porque traigamos a escena un cortometraje), pero no por ello menos jugosa respecto a su mensaje, que va más allá de las propias matemáticas. Es una reflexión sobre todo el sistema educativo. Ficha Técnica: Título Original: Alternative Math. Nacionalidad: EE. UU, 2017. Dirección: David Maddox. Guion: David Maddox y  Malcolm Morrison. Fotografía: David Blood, en Color. Montaje: David Maddox. Música: Damon Criswell. Producción: Liz Cardenas y David Maddox. Duración: 9 min. Ficha artística: Intérpretes: Allyn Carrell (Mrs. Wells), Hope Whitaker (Danny), Mykle McCoslin (madre de Danny), Bryan Massey (padre de Danny), Paul T. Taylor (Director del colegio), Sean McGraw (Superintendente), Wilbur Penn (Alcalde), La'Netia D. Taylor     (madre enfadada), Gabriel Horn (padre loco), Augustine Frizzell (madre psicópata), Malcolm Morrison (guarda de seguridad), Steffanie Blackmon (periodista local),      Eric Hanson (experto orgulloso), Liz Cardenas (experta enfadada), Michael Clemmons (experto diplomático). Argumento Una maestra de escuela se enfrenta a graves problemas por el tremendo delito de llevar la contraria a un alumno. Comentario, análisis y curiosidades Lo primero de todo: vean el cortometraje. Pueden hacerlo en esta dirección. No se olviden activar los subtitulos (están en castellano). Una vez visto (si no lo han hecho, perderá toda la gracia si leen lo que sigue), da pie a una interesante reflexión por parte de los diferentes estamentos de la comunidad educativa (extensible a todo lo que nos ha dejado la era Trump, y la actual política internacional, de la que la de nuestro país no se libra, sino más bien, representa un alumno bastante aventajado del inclíto yanqui mencionado). Para ello propondría algunas cuestiones sobre las que reflexionar y dialogar, a tres bandas: docentes, padres y responsables educativos. Seguramente, como en el corto (que puede parecer una exageración, pero les puedo asegurar que no; habiendo estado más de diez años en la asociación de madres y padres del colegio público de mis hijos, constato que, es muy real; obviamente no con la cuestión planteada, que se pone como muestra de algo entendible por todos y jocoso, como una sátira). El cuestionario seria: 1.- Como primera aproximación, ¿qué opinión te ha merecido el cortometraje? 2.- ¿Está el maestro/profesor/docente de nuestras escuelas e institutos presionado en diferentes modos respecto a las enseñanzas/métodos que intenta aplicar? Si existe tal presión, ¿por parte de quién? ¿Está justificada? 3.- ¿Estamos convencidos de que el temario, las asignaturas, los métodos docentes, vigentes en nuestro sistema son los apropiados para nuestros alumnos? ¿Qué capacitación tenemos para opinar sobre ello? Porque basarse en lo que me conviene, o lo que yo creo, no es precisamente el argumento más adecuado, ¿saben? (y conste que esta pregunta no va para padres exclusivamente; también para responsables educativos al dictado del partido político de turno, y para docentes apoltronados (los que lo estén) en su cómodo puesto por los siglos de los siglos, bien por la oposición aprobada años ha, o por el amigable dedo que lo colocó allí). 4.- ¿Es ciencia ficción el argumento que aparece en el corto de “aplastar la creatividad”, “acallar la opinión discrepante”, o “imponer el pensamiento único”? 5.- ¿Es adecuada la actitud del jovencito cuando le llevan la contraria? ¿Sucede o es una invención con niños mega-hiper-consentidos? ¿Qué genera este tipo de educación al ser adulto? 6.- ¿Está el sistema educativo más interesado en apaciguar a los padres enojados que en asegurarse de que los estudiantes estén aprendiendo? ¿Es más importante la política que la verdad? 7.- La actitud beligerante y aparentemente exagerada de los padres que aparecen en el corto, ¿no se parece demasiado a la forma de comportarse la gente en internet, en redes sociales, escudada en el anonimato? 8.- ¿Importan algo los profesores? ¿Se valora su saber, su profesionalidad, su dedicación, o sólo cuenta que sea amable, sea simpático, ponga buenas notas y haga la pelota a los padres aún engañandolos respecto a la capacidad y/o actitud de sus hijos? Mira a tu alrededor Probablemente haya personas que sigan pensando: “bueno, esto es un corto, una broma bien hilada para hacernos sonreir, pero esto no se da. Es una retorcida, falsa e incluso destructiva exageración”. Bien, quizá tengan razón, pero entonces tendrán respuesta a argumentos del tipo de que la Tierra no es esférica, que las evidencias son una conspiración de la NASA, o aquellos que afirman que el cambio climático no es provocado por el hombre y lo acomodan a las conspiraciones de la izquierda, o, incluso más apropiadamente, aquellos que piensan que la teoría de la evolución de Darwin tiene el mismo derecho a ser discutida en una clase de ciencias que el Génesis en la Biblia, como si el Génesis pudiera ser probado en un laboratorio. O que no existe el COVID-19. Son argumentos que provienen de la ignorancia o del interés propio y se apoyan en el privilegio, al igual que en la película. Es un privilegio - de dinero, poder, etc. - lo que permite a ciertas personas engañar a la gente buscando incluso supuestos expertos que relinchan sus cinco minutos en televisión. Esto es lo que muestra el cortometraje, cómo el privilegio intimida la razón y la verdad. Un par de apuntes matemáticos Desde un punto de vista estrictamente matemático, es interesante porque ayuda a diferenciar algo tan básico y elemental como es la diferencia entre 2 y 2 (2 AND 2, como operador lógico, cuya respuesta es 22) y  2 + 2, que no es lo mismo. La unión no es igual a la suma. Y en contextos un poco más elaborados, muchas personas las confunden. Finalmente, cuando todos estamos satisfechos con la conclusión del corto, y nos regocijamos de que en realidad la maestra deberá percibir 22000 dólares, vuelve la matemática real (o la lógica, como ustedes prefieran) a decirnos: “De eso nada”. Si admitimos que 2 + 2 = 22, entonces lo que corresponde a la maestra con 2000 + 2000 es 20002000. En definitiva, mucho más (¡¡y mejor!!). Las matemáticas siguen molando, y siempre superan la ficción. El Director David Maddox es uno de los cineastas norteamericanos más destacados de la zona de Dallas-Fort Worth. Lleva más de dos décadas trabajando como escritor, director, productor y editor de películas. Es propietario de IdeaMan Studios, empresa que ha producido cine comercial, corporativo (anuncios publicitarios) e independiente. Además de ayudar a otros a hacer realidad sus proyectos, incluida la producción del éxito de Sundance A Ghost Story (David Lowery, EE. UU., 2017), el presente cortometraje Alternative Math estuvo seleccionado para los Oscars de la Academia en 2019. Con millones de visitas, docenas de premios y traducciones a varios idiomas, sigue dando que pensar a los espectadores de todo el mundo. Su última película, Baby Proof, está previsto que se estrene a finales de este año.   Alfonso Jesús Población Sáez

Martes, 06 de Abril de 2021 | Imprimir | PDF |  Correo electrónico

333. 72. (Abril 2021) El encanto del poliedro de Durero

(Alberto Durero. Melancolía I. 1514) El enigmático grabado Melancolia I (1514) de Alberto Durero es una de las expresiones más acabadas de la cultura del Renacimiento y fundamental para su estudio. Belleza aparte. La obra es de extrema complejidad: en ella conviven referencias astronómicas, astrológicas, alquímicas, mágicas...y matemáticas, además de las estrictamente pictóricas. Durero, Piero della Francesca y Leonardo, grandes de la pintura de todos los tiempos, escribieron tratados de matemáticas. Los tres se relacionaron con el matemático Luca Pacioli. No solo la perspectiva les llevaba al estudio de la geometría. El artista del Renacimiento solía trabajar varias artes: la arquitectura y la mecánica también exigían saber matemáticas. De ahí la famosa advertencia de Leonardo: no lea mis escritos quien no sea matemático. Tres centros de atención matemática en Melancolía I: el compás, el cuadrado mágico 4x4 y el raro poliedro de ocho caras, seis pentagonales y dos triangulares. El humor melancólico es el de los sabios, por ello el compás, que debía compensarse con la mensula jovis, el Sello de Júpiter, el cuadrado mágico de 4x4, con número mágico 34. Todas las filas, las columnas y las diagonales suman 34. Incluso los cuatro subcudrados 2x2 de las esquinas y el central suman 34. Las cifras inferiores del centro, 1514, señalan la fecha de ejecución. Tanto el cuadrado como el poliedro han sido reproducidos profusamente. Nos dedicamos al poliedro. El enigma del poliedro ¿Qué poliedro es? No se trata de uno de los más conocidos: ni de los regulares sólidos platónicos, ni los de caras regulares arquimedianos, ni  los de Catalan, sus duales. En un primer estudio parece un cubo con dos vértices opuestos truncados. Así salen las seis caras pentagonales iguales y las dos caras triangulares equiláteras. En dicho caso tres ángulos del pentágonos serían rectos. No parece que sea así. La hipótesis más generalizada es que se trata de un romboedro, un hexaedro rómbico semirregular, una ligera deformación del cubo. Francesca Folicaldi, en la presentación de la bella exposición Il Numero e le sue Forme (2005) que tuvo lugar en el Instituto e Museo di Storia della Scienza de Florencia, considera que el ángulo agudo del rombo está comprendido entre 80º y 83º, y en consecuencia el obtuso entre 100º y 97º. José María Valero Navarro, catedrático de dibujo del instituto Bachiller Sabuco de Albacete ha realizado un detallo estudio en su breve artículo El enigmático poliedro “La Melancolía I”(1989). La única truncación doble posible del romboedro que conserve las caras pentagonales iguales, y los triángulos equiláteros, son los dos vértices en diagonal que son triedros de caras agudas Jesús Martínez Frias (El enigmático poliedro de Dureo“La Melancolía I”, 2007) del Centro de Astrobiología del CSIC/INTA ha estudiado el posible origen de la forma: se trataría de una recreación de los cristales de alunita, un sulfato hidratado de potasio y aluminio. Cristaliza en sistema trigonal. La alunita es un alumbre usado en la pintura y su producción en los Estados Pontificios era muy conocida. Se trata de una hipótesis razonable que Durero no nos puede confirmar. (Cristal de alunita) El poliedro en el Panta Rhei de Hans Erni Lucerna tiene un museo espléndido para la pintura matemática, él del pintor suizo Hans Erni. Nos lo encontraremos dentro del Museo del Transporte, pero con un edificio independiente. No tan conocido en ambientes matemáticos como el holandés Escher, Hans Erni utiliza la matemática -especialmente las superficies regladas- con profusión. Sus pinturas más conocidas son las series de deportes encargadas por el Comité Olímpico, en ellas el cuerpo humano y su movimiento se encuentran matemáticamente definidos. (Hans Erni. Panta Rhei. 1980. Lucerna) Pero la joya de Lucerna no está en el Museo en sí, sino en su Auditorio, allí admiraremos el Panta Rhei, el origen de todas las cosas. En dos soberbios murales que decoran las paredes nos encontramos con la historia de la humanidad, desde Prometeo, y donde no faltan Tales, Pitágoras, Copérnico, Galileo, Descartes, Pascal, Newton, Leibniz o Einstein. La ciencia, la filosofía y la matemática son el hilo conductor de la humanidad desde que Prometeo roba el fuego de los dioses y lo pone al servicio de los hombres para su liberación. El final no es optimista: Pandora abre su caja: ¿acaso lo que empezó como liberación puede terminar como amenaza? Es significativo que el poliedro de Durero sea representado en este gráfico y sintético resumen de la historia de la humanidad. Durero en la Sagrada Familia Las matemáticas de Gaudí y en particular de la sagrada Familia son un tema de magníficos estudios. El cuadrado mágico de Dalí deriva del de Durero, corregido para sumar 33 y aparece tanto en el Beso de Judas como en el Portal de la Pasión. En las puertas de bronce (Puerta de la Oración en el Huerto de Getsemaní ) podemos ver el sólido de Durero del mismo grabado, el romboedro con dos vértices truncados (seis pentágonos y dos triángulos como caras) y debajo leeremos la palabra Melancolía. (Portal de la Pasión. Detalle. Templo de la Sagrada Familia. Barcelona) En la otra hoja de la puerta se ha reproducido un compás y varias figuras geométricas que insisten en el contenido simbólico matemático. La pasión de Cristo parece querer reflejar esa tristeza del aparta de mí ese cáliz. En las culturas tradicionales el cuadrado mágico se emplea como talismán protector, el de Gaudí también refleja la edad de la Pasión. (Puerta de la Oración en el Huerto. Templo de la Sagrada Familia. Barcelona) El  Antidudero de Anatoli Fomenko Anatoli Timoféyevich Fomenko (nadido en 1945) es un conocido matemático ruso de la Universidad de Moscu, trabaja fundamentalmente en  geometría diferencial y topología, así como en métodos numéricos en su campo. Fomenko no elude la creación artística basada en la matemática. Así, la American Mathematical Society publico en 1990 un compendio titulado Mathematical Impressions. La versión personal de Melancolia I no podía faltar, pero ahora es un Antidurero. El cuadrado aumenta a 11x11 y el sólido se agrieta. (Anatoli Fomenko. Antidudero. 1975) En Girgio de Chirico Giorgio de Chirico (1888-1978) fue un importante artista italiano creador del movimiento artístico scuola metafísica. En su metafísica no falta el poliedro de Durero en una versión muysingular de la moderna melancolía. (Giorgio de Chirico. Melancolía. 1912) En Carlos Colombino (Carlos Colombino. Poliedros enlazados de Durero) Carlos Colombino (1937 – 2013) fue un artista plástico, arquitecto, escritor y animador cultural del Paraguay. Quizá su figura internacionalmente mas destacada. Dedicó toda una serie a Durero con varias versiones de su poliedro. (Carlos Colombino. El ángel  de la Melancolía) En Miguel Rothschild Miguel Rothschild, un joven artista argentino asentado en Alemania, ha realizado la representación espacial más exagerada y multicolor en base a paralelogramos rigidizados por una diagonal para mantener la integridad tensional. (Miguel Rothschild. Melancolía) En la Estación de Hamburgo En la Estación de Ferrocarril de Hamburgo se localiza el poliedro de Durero, en vidrio que es casi un buzón de sugerencias. Se atribuye a Anna Blume pero quizá solo sea la fotografía. (Estación de Ferrocarril de Hamburgo) Plaza de Brujas en Valencia La plaza de Brujas, no dedicada a las perseguidas hechiceras sino a la ciudad flamenca, está en un lugar muy emblemático de la ciudad de Valencia con el Mercado Central y la Iglesia de los Juanes. Recibe el nombre por ser el lugar de fallecimiento del humanista valenciano Luís Vives. El busto de Vives se colocó en la plaza y los arquitectos municipales Román Jiménez Iranzo y Pedro Soler García tuvieron el acierto de dedicar una fuente a la Melancolía y colocar un poliedro de Durero. La escultura estaba próxima a la iglesia y al busto. (Fuente de Jiménez-Soler. Valencia) La plaza se esta remodelando en el 2020 y en el proyecto está la reubicación de la fuente. (Proyecto de remodelación. Plaza de Brujas. Valencia)

Jueves, 01 de Abril de 2021 | Imprimir | PDF |  Correo electrónico

334. El juego del jazz

Para promocionar el festival de jazz ELBJAZZ 2013 en Hamburgo, la organización ideó este Jazzgame: Captura de pantalla del video que aparece debajo. Se colocaron en plena calle 10 sillas que debían ocupar la vocalista y los músicos, y frente a ellas, otras 10 sillas vacías esperaban a que alguien se sentara… Si una persona ocupaba un asiento, el o la intérprete sentada en el lugar simétrico se levantaba para interpretar Summertime de George Gerswhing –al menos en el caso de este video–. ¿Cuántas posibles melodías pueden interpretarse? Es decir, ¿cuántas combinaciones de instrumentos son posibles? Si hubiera sólo una persona sentada, podría estarlo en 10 lugares diferentes.  Así que hay 10 posibles melodías con un único instrumento. ¿Y con dos? Si dos personas se sientan en alguna de las 10 sillas, pueden hacerlo –da lo mismo el orden en el que se sienten, lo importante es que asientos se ocupan, no las personas que lo hacen– de 45 maneras diferentes: son las combinaciones de 10 elementos tomadas de dos en dos C(10,2)=10! / 2! 8!. Si continuamos de este modo, está claro que hay C(10,n) maneras de conseguir que toquen n de los intérpretes: C(10,n) = 10! / n! (10-n)! Así, hay 1023 posibles melodías a escuchar, ya que –no cuento el momento en que no tocan, es decir, en el que las sillas están vacías; recordar las propiedades de los números combinatorios– sería la suma: C(10,1)+C(10,2)+C(10,3)+C(10,4)+C(10,5)+C(10,6)+C(10,7)+C(10,8)+C(10,9)+C(10,10)= 10+45+120+210+252+210+120+45+10+1 = 210– 1 =1023 Triángulo de Pascal. ¡Una bonita iniciativa! Se parece a la propuesta Madera a la deriva de Jorge Drexler. Visto en Froot Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 25 de Marzo de 2021 | Imprimir | PDF |  Correo electrónico

335. 114. (Marzo 2021) Escalas multioctavas

Las escalas multi-octavas La música es un fenómeno altamente estructurado que depende de una serie de principios organizativos. Con estos principios, que posibilitan su existencia, están familiarizados tanto músico como oyentes, si bien a menudo de forma inconsciente. Entre esos principios se cuenta la organización rítmica y melódica, y dentro de esta última destacan las escalas. El concepto de escala está presente en la mayoría de tradiciones musicales. La escala, en su papel estructural, constituye una forma de determinar el contenido tonal de una pieza. Aunque existe una gran variedad de escalas en el mundo, diferentes en muchos sentidos, la mayoría tiene ciertos elementos en común. Como señala Patel [Pa08] en Music, Language and the Brain, las escalas generalmente contienen de 5 a 7 notas por octava, progresan por grados continuos de entre 1 y 3 semitonos y normalmente no son simétricas. Una característica muy extendida, y que suele ser parte de la propia definición de escala en la mayoría de los casos, es que la escala consta de una serie de notas que se repite en cada octava. Esto no es sorprendente teniendo en cuenta que está demostrado que los seres humanos percibimos las notas a distancia de octava como equivalentes, seguramente uno de los pocos universales de la música; véase [BJ11] para más información sobre los universales musicales. Lo anterior nos lleva a preguntarnos: ¿es la repetición en la octava un requisito indispensable de toda escala? ¿Es posible una escala en que no repitiese en la octava? ¿Tendría sentido musical? Aunque para la mayoría sea un fenómeno seguramente desconocido, la realidad es que sí existen escalas que no se repiten en la octava. De hecho, hay culturas musicales centenarias en las que el contenido tonal es determinado por escalas que no se repiten en la octava o escalas multi-octava. La escala del Znamenny Rospev –el canto litúrgico de la iglesia ortodoxa rusa, probablemente de origen bizantino [Sw40]– es un claro ejemplo. Como se puede observar en la figura 1, consta de una serie de tetracordios mayores consecutivos, repitiendo así en la cuarta, en vez de en la octava. Mientras que la primera octava contiene la nota si natural, la segunda contiene un si bemol y si se prolongara la estructura a lo largo de más octavas, irían apareciendo cada vez más notas diferentes en cada octava. Este tipo de escala es común en la música folclórica rusa, así como de países de la región tales como Albania, Georgia, Azerbaiyán o Bulgaria [N16]. Figura 1: Construcción de escalas – La escala Znamenny Las escalas multi-octavas, aunque poco comunes, fueron utilizadas y estudiadas a mediados de la primera mitad del siglo XX por músicos y musicólogos como Nicolás Slonimsky, Joseph Shillinger, Elliot Carter, Alfred Schnittke; también por músicos de jazz como David Liebman, David Baker o Dennis Sandole; así como por compositores actuales como Joel Hoffman, Gao Weijie o Ramón Paús. Estas escalas suelen estar construidas de una de las siguientes maneras: Escalas simétricas a partir de un intervalo que divide un determinado número de octavas de manera equidistante; véanse [Sl47], [Sh46] y [Ym13]. Por una sucesión de tetracordios diferentes; véanse [P61], [Ba90] y [Li91]. Por una sucesión de tetracordios similares; véase [P61]. Por la combinación de dos escalas de una octava con una misma tónica; véanse [P61] y  [Ym13]. La gran variedad de música que ha brindado este concepto justifica la validez del mismo, pero, por ahora, pocos investigadores se han dedicado a estudiar las características y propiedades estructurales de estas escalas. Por razones evidentes, la escala que más ha sido estudiada en este sentido ha sido probablemente la escala mayor. Estudios de investigadores como Carlton Gamer [Ga67], Clough y Douthett [CD91], Clough y Myerson [CM85], o Carey y Clampitt [CM89], han conseguido desvelar propiedades auténticamente sorprendentes y fascinantes de esta colección tan determinante en la historia de la música. A continuación, vamos a describir brevemente algunas de estas características con la siguiente pregunta en mente: ¿Es posible construir una escala multi-octava que comparta algunas de estas características? Propiedades de la escala mayor La escala diatónica, así como la escala pentatónica, son sin duda de las escalas más relevantes en la historia de la música. Han definido y estructurado el contenido tonal en múltiples culturas musicales y épocas. Lo cierto es que están íntimamente relacionadas y sus propiedades han sido estudiadas por numerosos investigadores de lo que se denomina la teoría diatónica. Para un excelente resumen de la teoría diatónica, véase el primer capítulo de la tesis de Carey [Ca98]. Tomemos un momento para pensar en el teclado del piano, que consta de 7 teclas blancas y 5 teclas negras por octava. Las teclas blancas corresponden a la escala mayor (en concreto a la escala de Do mayor) y las teclas negras corresponden a la escala pentatónica (en concreto a la escala pentatónica de Sol bemol mayor). Por lo que, si tomamos las doce notas de la colección cromática y omitimos las siete notas de la escala mayor, quedan las cinco notas de la escala pentatónica. Muchos investigadores se refieren a este hecho como el complemento de la escala mayor. Es llamativo que la cardinalidad de estas escalas –esto es, el número de notas de la escala–, cinco y siete, sean primos relativos con 12, el número de semitonos en que se divide la octava (primos relativos significa que no tienen divisores comunes). Con estas cardinalidades es imposible la formación de escalas simétricas1. Además, ambas escalas comparten el mismo intervalo generador, la quinta, ya que sus notas pueden ser obtenidas recorriendo el ciclo de quintas siete y cinco pasos, respectivamente. Como muestra la figura 2, si recorremos siete pasos desde la nota fa, obtenemos las notas de la escala de do mayor, mientras que, si recorremos solo cinco, obtenemos las notas de la pentatónica de fa mayor. Si repitiéramos esto desde cada una de las 12 notas en el ciclo de quintas, obtendríamos los 12 tonos de la escala mayor y pentatónica, respectivamente. Figura 2: Intervalo generador En las siguientes secciones estudiaremos algunas propiedades estructurales de la escala diatónica. Escalas de regularidad máxima o escalas euclídeas Para definir este tipo de escalas, supondremos que tenemos una colección de notas, llamada el universo cromático o la colección cromática, de la cual elegiremos un subconjunto de notas que formará la escala. En las escalas occidentales, el universo cromático suele estar formado por 12 semitonos y el número de notas de las escalas más comunes suele ser 5 o 7. La propiedad de regularidad máxima fue definida por Clough y Douthett [CD91] y consiste en exigir que las notas de la escala estén distribuidas de la manera más regular posible entre las notas del universo cromático. Una analogía común para explicar este fenómeno es el de una mesa redonda en la que hay 12 sillas distribuidas de manera uniforme, fijadas de manera que no se pueden cambiar, y hay que distribuir a los invitados de la manera más regular posible. En el caso de seis invitados, solo hay una solución correcta, como muestra la figura 3. En el caso de, por ejemplo, siete invitados, como en la escala mayor, la solución no es tan evidente. No es posible distribuir siete en doce de una manera totalmente uniforme, por lo que hay que buscar la manera más uniforme posible o de máxima regularidad (maximally even). Las escalas con regularidad máxima se llamarán ME (por sus siglas en inglés). Figura 3: Distribución uniforme de 6 en 12 En lo que sigue, vamos a referirnos al artículo de esta misma columna de marzo del 18 Ritmos euclídeos y ritmos equilibrados [Go18]. Ilustraremos el proceso con un ejemplo de escalas. Supongamos que tenemos 17 semitonos y queremos distribuir de forma regular 7 notas entre los 17 semitonos. Estas 7 notas formarán la escala heptatónica en un universo cromático de 17 semitonos. Sigamos los pasos dados en la figura 4. Primero, alineamos las notas de la escala y añadimos notas que no son de la escala hasta completar las 17 notas totales. Esto se representa por siete unos (la escala) y diez ceros (el resto); véase la figura 4-paso (1). A continuación, formamos grupos de 7, los cuales corresponden a efectuar la división de 17 entre 7; obtenemos, pues, 7 grupos formados por [1 0] (en columnas en el paso (2) de la figura 4). Sobran tres ceros, lo cual indica que en el paso siguiente formaremos grupos de 3. Tras formar el primer grupo —véase el paso (3) de la figura 4— nos quedamos sin ceros. Continuamos agrupando de 3 en 3 tomando los grupos de la otra caja, en la que quedan 4 columnas (figura 4-paso (4)). Procedemos así que queden uno o cero grupos; de nuevo, esto es equivalente a efectuar la división de 7 entre 3. En nuestro caso, queda un solo grupo y hemos terminado (paso (5)). Finalmente, la escala se obtiene leyendo por columnas y de izquierda a derecha la agrupación obtenida (paso (6)). Figura 4: Escalas regulares Tras este proceso hemos obtenido una escala microtonal de 7 notas en un universo cromático de 17 notas. Para más información sobre distribuciones regulares en ritmos y escalas, véanse [DGMM+09], [GTT09a] y [GTT09b]. Por último, querríamos incluir la observación de que, si una escala es de regularidad máxima (ME), entonces su complementario también lo es. El complementario de una escala se construye intercambiando notas de la escala por notas que no lo son y viceversa. En términos de la notación de ceros y unos de arriba, el complementario consiste en intercambiar ceros y unos. La idea que hay detrás de este hecho es que toda distribución regular de notas en un universo cromático implica también una distribución regular de las notas que no están en la escala. Las escalas profundas o de multiplicidad única Esta propiedad fue definida por Carlton Gamer [Ga67] en 1967. Las escalas con la propiedad de profundidad (deep scale property) muestran una propiedad denominada multiplicidad única de distancias (unique multiplicity property). Esta propiedad significa que cada intervalo se repite un número único de veces, donde se cuentan todos los intervalos posibles entre las notas de la escala. La escala mayor contiene, por ejemplo, dos intervalos de segunda menor (o séptima mayor), cinco intervalos de segunda mayor (o séptima menor), cuatro intervalos de tercera menor (o sexta mayor), tres intervalos de tercera mayor (o sexta menor), seis intervalos de cuarta justa (o quinta justa) y un intervalo de cuarta aumentada (o quinta disminuida). Esta relación se refleja en las notas en común en las diferentes transposiciones de la escala; dos escalas mayores a distancia de semitono tendrán dos notas en común, dos escalas a distancia de tono tendrán cinco notas en común, etc. Para que una escala tenga la propiedad de la profundidad tiene que generarse mediante un intervalo primo relativo con el número de semitonos de la colección cromática completa. Además, el número de notas de la escala corresponderá a la mitad o la mitad más uno de la colección cromática. Si el número de notas es d y la colección cromática completa es n, el número de notas de una escala profunda será d = [n/2] o d = [n/2] + 1. En el caso de la escala mayor, su intervalo generador es la quinta– que abarca siete semitonos, siendo así relativamente primo a la colección cromática de 12– y su número de notas sería 7= 12/2 + 1. Las escalas bien formadas Esta propiedad la definieron Carey y Clampitt [CC89] en un conocido artículo de 1989. En esencia, implica que la simetría de su intervalo generador se mantiene al reordenar las notas dentro de una octava por grados conjuntos para formar la escala. Esto se entiende mejor de una manera gráfica. La figura 5 muestra las notas de la escala de do mayor en un ciclo de quintas. A la izquierda, las notas han sido unidas siguiendo el ciclo de quintas; a la derecha por grados conjuntos (do-re-mi-fa-sol-la-si-do). Como se puede observar, ambas opciones resultan en polígonos con simetría rotacional. Figura 5: Simetría en la escala mayor (figura tomada de [CC89]) También es el caso de la escala pentatónica, como podemos observar en la figura 6: Figura 6: Simetría en la escala pentatónica (figura tomada de [CC89]) Pero no es así si recorremos, por ejemplo, seis pasos en el ciclo de quintas para formar una escala hexátona, como en la figura 7: Figura 7: Ejemplo de escala en la que simetría del intervalo generador no se mantiene en la escala (figura tomada de [CC89]) En busca de escalas multi-octava con buenas propiedades estructurales Posiblemente, en parte, gracias a las sorprendentes propiedades estructurales descritas en la sección anterior, la colección diatónica es sin lugar a duda la más utilizada de las 462 posibilidades teóricas de escalas heptatónicas de una octava. La pregunta que nos hacemos en este artículo es bastante natural: ¿es posible encontrar las mismas propiedades en una escala multi-octava? Las propiedades de escala profunda y de ser bien formada parecen, a priori, imposibles de aplicar en un contexto de escala multi-octava. En primer lugar, si las notas de la escala deben poder obtenerse por un intervalo generador ¿cómo se ordenan luego para formar una escala? En el caso de una escala de una octava la solución es evidente (se ordenan por grado conjunto de grave a agudo dentro de una octava), pero, al abarcar la escala más octavas, ¿cómo se disponen las notas a lo largo del registro completo sino es de manera arbitraria? Este problema se amplifica cuando consideramos que una escala multi-octava puede contener potencialmente los 12 tonos a lo largo de su registro total. ¿De qué nos sirve el concepto de intervalo generador para obtener las notas de la escala si finalmente las vamos a incluir todas? No obstante, en esta sección nos vamos a armar de valor y embarcar en la búsqueda de una escala multi-octava que muestre las tres propiedades descritas anteriormente en relación a la escala mayor. Escalas de regularidad máxima La cantidad de escalas multi-octava posibles es prácticamente infinita, por lo que es importante delimitar nuestra búsqueda. Nos restringiremos a las escalas de dos octavas. Vamos a empezar por la propiedad de regularidad máxima, que es relativamente sencilla de aplicar a este tipo de escalas. Cualquier número de notas d pueden ser distribuidas de la manera más uniforme a lo largo de un rango total de c semitonos, en el caso de dos octavas, 24. Evidentemente, no todas las opciones tienen sentido como escala. Si elegimos un número demasiado grande para d, tendremos que agrupar las notas demasiado para lo que solemos entender como escala; por ejemplo, si d = 23, la escala será prácticamente cromática. Por lo contrario, si d es un número demasiado pequeño, los espacios entre las notas serán demasiado grandes para funcionar como escala; imaginemos, por ejemplo, las posibles agrupaciones de d = 2. Por esta razón, vamos a imponer tres restricciones en cuanto a la sucesión de intervalos dentro de las escalas, comunes a la mayoría de escalas utilizadas en la música occidental2 (véanse [Ty04] y [Pr78]): No consideraremos escalas en las que existan intervalos de dos semitonos consecutivos. No consideraremos escalas en las que existan intervalos mayores a tres semitonos. No consideraremos escalas en las que existen dos intervalos de tres semitonos consecutivos. Con estas tres restricciones garantizaremos que nuestras escalas tengan una construcción interválica equivalente a la mayoría de las escalas que utilizamos. En dos octavas, consideraremos, por lo tanto, escalas en las que d sea un número entre 10 y 15. En d ≤ 9 e inferior no podremos cumplir con las condiciones b) y/o c). Si d ≥ 17, no podremos cumplir con la condición a). Considerando d =16 solo hay dos opciones que cumplen las tres condiciones, siendo la secuencia interválica de estas, respectivamente: 1-2-1-2-1-2-1-2-1-2-1-2-1-2-1-2 2-1-2-1-2-1-2-1-2-1-2-1-2-1-2-1 Estas dos secuencias son rotaciones de la misma escala y corresponden al segundo modo de transposición limitada de Messiaen [Me44], también conocido como escala disminuida u octotónica. Esta escala repite en la octava, por lo que no nos interesa para nuestros propósitos. Con lo cual, nos quedan seis opciones para formar escalas de dos octavas bien formadas, que detallaremos a continuación: ME d = 10 Secuencia interválica: 3-2-2-3-2-3-2-2-3-2 ME d = 11 Secuencia interválica: 3-2-2-2-2-2-3-2-2-2-2 ME d = 12 Secuencia interválica: 2-2-2-2-2-2-2-2-2-2-2-2 ME d =13 Secuencia interválica: 2-1-2-2-2-2-2-2-1-2-2-2-2 ME d = 14 Secuencia interválica: 2-2-1-2-2-2-1-2-2-1-2-2-2-1 ME d = 15 Secuencia interválica: 2-1-2-2-1-2-1-2-2-1-2-1-2-2-1 De estas descartaremos, naturalmente, d = 10 (escala pentatónica en dos octavas), d = 12 (escala simétrica de tonos enteros en dos octavas) y d =14 (escala mayor en dos octavas) al ser en realidad escalas que repiten a la octava. De las escalas bien formadas que quedan, d = 15 tiene máximo común divisor (mcd a partir de ahora) mcd(24, 15)=3. Esto hace que la escala presente simetrías (para más información sobre por qué ocurre esto, véase [GTT09a]). Al ser el mcd(24, 15)=3, la escala divide el rango de dos octavas en tres partes iguales, siendo cada uno de los tres tramos de escala interválicamente idénticos. Nicolas Slonimsky recoge una gran cantidad de escalas de este tipo en su Thesaurus of scales and melodic patterns [Sl47]. La escala regular con d = 15 corresponde a la escala nº 707 del Thesaurus. Las escalas regulares con d = 11 y d =13 cumplen que mcd(24, d)=1 y parecen estar relacionadas, ya que d =13 contiene la totalidad de d =9, donde la diferencia entre ambas escalas es únicamente dos notas. Escalas profundas y bien formadas Para poder empezar a hablar de las siguientes dos propiedades, es necesario solucionar el problema del intervalo generador. ¿Cómo se disponen las notas generadas por un intervalo generador i a lo largo del registro completo c si no se hace de manera arbitraria? Si mi escala puede incluir potencialmente las 12 notas ¿qué sentido tiene un intervalo generador? La solución puede ser más sencilla de lo que parece. El pensar un rango modular de 12 notas es lógico, ya que, como indicábamos antes, los seres humanos percibimos notas a distancia de octava como equivalentes (dos notas se piensan equivalentes si están a una distancia de una octava). Pensar en las clases de equivalencias de las alturas (pitch-class equivalence) de esta manera tiene sentido incluso en escalas multi-octava, puesto que aporta información valiosa sobre la sonoridad de las mismas; cuantas más notas de la colección cromática contenga, más densa será su sonoridad, por ejemplo. Pero, por otro lado, las escalas que estamos estudiando transcurren en un rango modular de 24 semitonos, no de 12. Entonces, para poder entender mejor sus propiedades estructurales ¿no sería más revelador pensar en una equivalencia dentro de módulo 24 en vez de módulo 12? De esta manera do1 sería equivalente a do3, do2 equivalente a do4, etc.  La figura 8 muestra un ciclo de 24 semitonos que abarca 2 octavas. Figura 8: Ciclo de 24 semitonos Ahora vamos a comenzar nuestra búsqueda de una escala de dos octavas con la propiedad de la profundidad. Trasladando el caso de la escala mayor, una escala profunda cumple , a dos octavas, estaríamos buscando una escala de 13 notas. Ahora nos falta un intervalo generador i, relativamente primo con el rango cromático n, del que obtener las notas de nuestra escala. Como podemos observar en la escala mayor, el número de semitonos que abarca el intervalo generador i corresponde al número de notas d de la escala, es decir i = d. Por ejemplo, la escala mayor contiene siete notas y el intervalo generador de la escala mayor, la 5ª, abarca siete semitonos. El que d = i sea una propiedad de la colección diatónica fue demostrado definitivamente por Clough y Dhoutett [CD91]. Siguiendo esta lógica, nuestro intervalo generador en dos octavas debería abarcar 13 semitonos. La figura 9 muestra un ciclo de 13 semitonos dentro de un rango modular de 24 semitonos; al ser ambos números i y n relativamente primos, esto es, mcd(i,n)=1, el ciclo abarca los 24 tonos. Figura 9: Ciclo de 13 semitonos dentro de un rango modular de 24 semitonos Ahora podemos reparar en un hecho asombroso. Si recorremos 13 pasos en el sentido de las agujas del reloj desde la nota Eb1, obtenemos la colección de la escala regular con d =13; si recorremos 11 pasos, obtenemos la colección de la escala regular d =11. Tenemos dos escalas regulares con mcd(d,n)=1, que se diferencian en tan solo dos notas y tienen un mismo intervalo generador. ¿Nos resulta familiar? Efectivamente, guardan la misma relación entre sí que la pentatónica y la escala mayor. De hecho, la escala regular d =11 es el complementario de la escala regular d =13. Si omitimos las 13 notas de la escala d =13 de la colección completa n, nos quedamos con las 11 notas de la escala d =11. Es más, si nos fijamos en el número total de intervalos de la escala regular d =13, veremos que la escala es profunda, puesto que contiene cada tipo de intervalo un número limitado de veces. Para observar esto es necesario considerar los intervalos en un rango modular de 24 semitonos como en el cuadro 1. Si recorremos un paso en un sentido, es necesario recorrer 23 en el sentido contrario para llegar al mismo punto, no 11 como en un rango modular de 12. Por lo que las equivalencias interválicas, en vez de ser 1-11, 2-10, 3-9, 4-8, 5-7, 6-6, como de costumbre en un rango modular de 12, serán 1-23, 2-22, 3-21, etc. La siguiente tabla muestra el vector interválico (las ocurrencias de las distancias interválicas) de la escala regular de 13 notas, evidenciando que se trata de una escala profunda. Vector interválico módulo 24 de la escala regular con d = 13 Clase de intervalo 1 2 3 4 5 6 7 8 9 10 11 12 Número de ocurrencias 2 11 4 9 6 7 8 5 10 3 12 1 Cuadro 1: Vector interválico módulo 24 Considerar el vector interválico en un rango modular de 24 semitonos es esencial para poder apreciar esta propiedad, ya que en el vector interválico en un rango modular de 12 semitonos no se aprecia la propiedad de multiplicidad única. En cambio, el vector interválico en un rango modular de 12 semitonos sí es útil para evidenciar el alto contenido cromático de esta escala (cuadro 2). Vector interválico módulo 12 de la escala regular con d = 13 Clase de intervalo 1 2 3 4 5 6 Número de ocurrencias 14 14 14 14 14 7 Cuadro 2: Vector interválico módulo 12 Ahora únicamente queda por comprobar que esta escala está bien formada. Para ello, comprobamos si la simetría del intervalo generador (como en la figura 7) se mantiene al agrupar las notas por grados conjuntos para formar la escala. Como muestra la Figura10, definitivamente es el caso: Figura 10: Simetría en las escalas regulares con d =13 y d =11 Conclusión Aunque no es un hecho conocido y pueda parecer sorprendente, gracias a una idea tan sencilla como considerar las propiedades estructurales de una escala de dos octavas dentro de un rango modular de 24 semitonos, es posible encontrar escalas que comparten propiedades importantes con la escala diatónica y su complementario, la escala pentatónica. En el caso de escalas de dos octavas, estas son la escala regular d = 13 y su complementario, la escala regular con d = 11. Un dato a considerar es que la escala regular con d = 13 contiene las 12 notas de la colección cromática, lo cual permitiría a un compositor crear música en un contexto cromático que a la vez muestra propiedades importantes en común con la escala diatónica. Será interesante descubrir cómo este dato tan contundente a nivel teórico se traduce en la práctica musical.   Bibliografía [Ba90] Baker, D. (1990). Modern concepts in jazz improvisation. Alfred Music Publishing Co., Inc. [BJ11] S. Brown and J. Jordania. Music evokes vicarious emotions in listeners. Psychology of Music, 41(2):229–248, 2011. [Ca98] Carey, N. (1998) Distribution Modulo 1 and Musical Scales. PhD. Dissertation, University of Rochester [CC89] N. Carey y D. Clampitt (1989). Aspects of well-formed scales. Music Theory Spectrum, páginas 187–206. [CD91] J. Clough y J. Douthett (1991). Maximally even sets. Journal of Music Theory, páginas 93–173, 1991. [CM85] J. Clough y G. Myerson (1985). Variety and multiplicity in diatonic systems. Journal of Music Theory, 29(2):249–270, 1985. [DGMM+09] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, and David R. Wood. The distance geometry of music. Computational Geometry: Theory and Application, 42(5):429–454, 2009. [Ga67] C. Gamer (1967). Deep scales and difference sets in equal-tempered systems. In Proceedings of the 2nd Annual Conference of the American Society of University Composers, páginas 113–122. [GTT09a] F. Gomez-Martin, P. Taslakian, and G. T. Toussaint. Interlocking and euclidean rhythms. Journal of Mathematics and Music, 3(1), 2009. [GTT09b] F. Gomez-Martin, P. Taslakian, and G. T. Toussaint. Structural properties of euclidean rhythms. Journal of Mathematics and Music, 3(1), 2009. [Li91] Liebman, D. (1991). A chromatic approach to jazz harmony and melody. Advance Music. [Me44] Messiaen, O. (1944). Technique de mon langage musical (No. v. 1). Alphonse Leduc. [N16] Nikolsky, A. (2016). Evolution of tonal organization in music optimized neural mechanisms in symbolic encoding of perceptual reality. Part-2: Ancient to seventeenth century. Frontiers in Psychology, 7, 211. [Pa08] Patel, A., Patel, P., & Press, O. U. (2008). Music, language, and the brain. Oxford University Press, USA. Retrieved from https://books.google.es/books?id=EkItxyZqNecC [P61] Persichetti, V. (1961). Twentieth century harmony: Creative aspects and practice. W. W. Norton & Company, Inc. [Pr78] Pressing, Jeff. 1978. “Towards an Understanding of Scales in Jazz.” Jazz Research 9:25-35. [Sl47] Slonimsky, N. (1947). Thesaurus of scales and melodic patterns. Shirmer Books. [Sh46] Shillinger, J. (1946). The Schillinger System of Musical Composition. C. Fischer, Incorporated. [SW40] Swan, A. J. (1940). The Znamenny chant of the Russian church: part I. The Musical Quarterly, 26 (2). [Ty04] Tymoczko, D. (2004). Scale Networks and Debussy. Journal of Music Theory, vol. 48, nº2. Duke University Press. [Ym13] Ymaguchi, M. (2013). Synthetic Scales for Jazz Improvisation: Two-Octave and Multi-Octave Scales. Masaya Music Services. Notas: [1] Es cierto que el número once también muestra esta característica, pero en vista de que contiene prácticamente la colección cromática completa, no es una opción muy viable para una escala de una octava. [2] Este hecho ha sido observado por investigadores como Tymoczco o Pressing.

Lunes, 15 de Marzo de 2021 | Imprimir | PDF |  Correo electrónico

336. Los cuatro elementos

Investigations: The Four Elements es una serie de cuatro libros del artista Daniel E. Kelm, realizados en colaboración con Timothy Ely, que nacen de su interés por la alquimia y la geometría sagrada. Los cuatro elementos de Daniel E. Kelm http://danielkelm.com/ Cada libro consta de un número determinado de paneles entrelazados, que pueden ensamblarse para formar uno o varios de los sólidos platónicos. 1. Aire (1994) Libro cerrado http://danielkelm.com/core/galleryfullsize/75/1 Un primer vistazo dentro de la caja muestra paneles y un tubo de metal con un papel enroscado http://danielkelm.com/core/galleryfullsize/75/3 Una ranura sostiene los paneles cuadrados y otra los paneles triangulares http://danielkelm.com/core/galleryfullsize/75/4 Las páginas se pueden ensamblar para crear dos de los sólidos platónicos: un cubo y un octaedro http://danielkelm.com/core/galleryfullsize/75/06 El cubo-octaedro parcialmente montado http://danielkelm.com/core/galleryfullsize/75/11 Aquí puede ver todas las páginas combinadas para formar un cubo-octaedro http://danielkelm.com/core/galleryfullsize/75/10 2. Tierra (1989–2007) El libro cerrado http://danielkelm.com/core/galleryfullsize/106/1 Un primer vistazo dentro de la caja muestra paneles y un tubo de metal con un papel enroscado http://danielkelm.com/core/galleryfullsize/106/2 El rollo de papel desplegado http://danielkelm.com/core/galleryfullsize/106/4 El tubo de metal contiene alfileres que se utilizarán para mantener el conjunto unido http://danielkelm.com/core/galleryfullsize/106/3 Las páginas combinadas para formar un cubo-octaedro http://danielkelm.com/core/galleryfullsize/106/5 Detalle de la pintura y la articulación http://danielkelm.com/core/galleryfullsize/106/6 3. Fuego (1989) La caja en forma triangular http://danielkelm.com/core/galleryfullsize/97/1 Primera vista de los paneles http://danielkelm.com/core/galleryfullsize/97/2 Los diversos componentes del libro http://danielkelm.com/core/galleryfullsize/97/3 Los paneles pueden formar diversos sólidos platónicos http://danielkelm.com/core/galleryfullsize/97/4 4. Agua (1989) La caja en forma triangular http://danielkelm.com/core/galleryfullsize/99/1 Los veinte paneles crean un icosaedro http://danielkelm.com/core/galleryfullsize/99/4 Detalle http://danielkelm.com/core/galleryfullsize/99/5 Detalle http://danielkelm.com/core/galleryfullsize/99/9 Nota: Ya habíamos hablado de otro de los libros de Daniel E. Kelm en Neo emblemata nova: alquimia en una banda de Möbius Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Viernes, 12 de Marzo de 2021 | Imprimir | PDF |  Correo electrónico

337. Neo emblemata nova: alquimia en una banda de Möbius

Gran parte del trabajo del artista Daniel E. Kelm busca ampliar el concepto de libro, y sorprende con innovadoras estructuras. De formación química, muchos de los estudios y proyectos de Kelm tienen que ver con la alquimia. Daniel E. Kelm, “Neo emblemata nova” (2005) http://danielkelm.com/core/galleryfullsize/1/1/2 Su Neo emblemata nova es un libro construido imitando una banda de Möbius… Daniel E. Kelm, “Neo emblemata nova” (2005) http://danielkelm.com/core/galleryfullsize/1/2 … de este modo, la o el lector puede ver todas las ilustraciones, en ambos lados, sencillamente pasando las imágenes a lo largo de sus manos, una a una, sin necesidad de dar la vuelta a las páginas. Daniel E. Kelm, “Neo emblemata nova” (2005) http://danielkelm.com/core/galleryfullsize/1/3 En Neo emblemata nova, se muestran 50 imágenes de Emblemata Nova o Atalanta fugiens del alquimista y médico Michael Maier (1568–1622), representando procesos alquímicos. En la imagen de arriba, aparece representada la apertura del huevo filosofal, un recipiente herméticamente sellado, en el que tienen lugar toda serie de transformaciones… Portada de “Atalanta Fugiens” de Michael Maier, 1617 En la imagen de debajo, se observa el retorcido que genera la estructura de banda de Möbius. Daniel E. Kelm, “Neo emblemata nova” (2005) http://danielkelm.com/core/galleryfullsize/1/4 Daniel E. Kelm, “Neo emblemata nova” (2005) http://danielkelm.com/core/galleryfullsize/1/5 Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Viernes, 12 de Marzo de 2021 | Imprimir | PDF |  Correo electrónico

338. Videos topológicos de Jos Leys

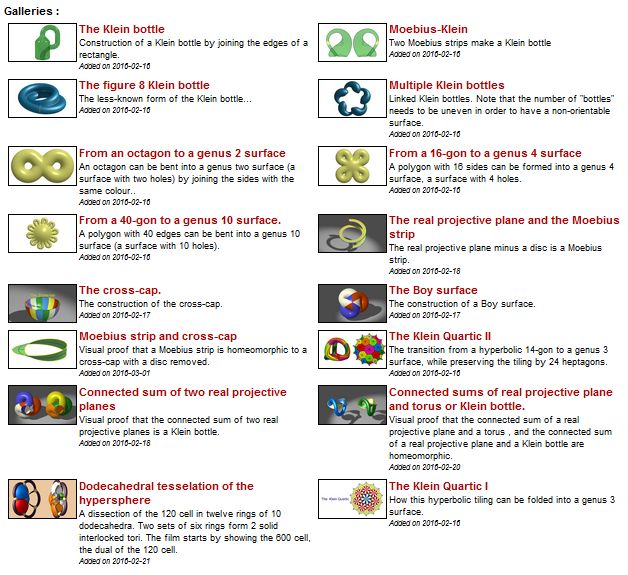
No es la primera vez que hablamos en ::ZTFNews del ingeniero y artista Jos Leys. Sus extraordinarias animaciones de diferentes nociones matemáticas son una delicia: bellas y técnicamente perfectas. Recordemos las de Dimensions, Caos, sus fractales (y más fractales), sus teselaciones o la banda de Möbius en relación con un canon retrógrado de Bach. Galería de videos de topología de Jos Leys. Esta vez traemos al blog su nueva galería de conceptos topológicos, gracias a la cual se pueden comprender mucho mejor algunos de los objetos topológicos más conocidos, y la manera de generarlos. Desde sumas conexas, pasando por la superficie de Boy, la botella de Klein obtenida de diferentes maneras (cociente de un cuadrado o suma conexa de dos bandas de Möbius), la banda de Möbius, el bonete cruzado… Os dejo dos de ellas, el resto se pueden encontrar aquí… y ¡habrá que estar atentas y atentos a las nuevas incorporaciones! Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 11 de Marzo de 2021 | Imprimir | PDF |  Correo electrónico

339. Real Sociedad Matemática Española

Divulgamat es un portal de la Real Sociedad Matemática Española que se mantiene gracias a los ingresos de la propia sociedad (como por ejemplo las cuotas de sus socios). Si quieres contribuir a su mantenimiento puedes hacerlo haciéndote socio (para hacerte socio de la RSME pincha aquí).

Jueves, 05 de Diciembre de 2013 | Imprimir | PDF |  Correo electrónico

340. Arranca “Marzo, mes de las matemáticas”

Este mes han arrancado las actividades y eventos incluidos en el proyecto “Marzo, mes de las matemáticas”, considerada la mayor iniciativa de divulgación de las matemáticas hasta la fecha en España.

Viernes, 05 de Marzo de 2021 | Imprimir | PDF |  Correo electrónico | Leer más