351. Muerte de un matemático napolitano

El matemático Renato Caccioppoli (1904-1959) nació un 20 de enero. Trabajó en análisis funcional, cálculo de variaciones y ecuaciones en derivadas parciales, y publicó más de 80 artículos de investigación en estos y otros temas. La película Morte di un matematico napoletano –Muerte de un matemático napolitano– (1992) de Mario Martone narra los últimos días de la vida del genio inconformista Caccioppoli, que terminó en suicidio. Más información: Morte di un matematico napoletano: el suicidio, Matemáticas de cine, 2011 Renato Caccioppoli, un genio desventurado y comprometido, Matemolivares, 2012 Carlo Sbordone,  Renato Caccioppoli, nel centenario della nascita, Bollettino della Unione Matematica Italiana, Sezione A, La Matematica nella Società e nella Cultura 7 (2), 193–214, 2004 Piero Antonio Toma, Renato Caccioppoli, l’enigma, Edizioni Scientifiche Italiane, 1992 Angelo Guerraggio, Renato Caccioppoli. Naples: Fascism and the Post-War Period, Springer Robert Nowlan, Renato Caccioppoli, A Chronicle of Mathematical People Renato Caccioppoli, Physics Light Fotografías de Renato Caccioppoli Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Miércoles, 20 de Enero de 2021 | Imprimir | PDF |  Correo electrónico

352. Arquímedes y la medida del círculo

ABC, 11 de Enero de 2021 CIENCIA - El ABCdario de las matemáticas Urtzi Buijs y Miriam González

Lunes, 11 de Enero de 2021 | Imprimir | PDF |  Correo electrónico | Leer más

353. 112. (Enero 2021) La Tabla Periódica Musical (2/2)

1. Introducción En la primera parte de este trabajo hemos visto la forma interválica y el vector de clases de intervalos o ICV, que indica el contenido de un conjunto de notas en cuanto a intervalos, es decir, clases de cardinalidad c = 2. En esta segunda parte introduciremos unas versiones avanzadas del mismo, que son el “Vector de Tipos de Tricordos” y el “Vector de Clases de Tricordos”, los cuales indican el contenido de un conjunto de notas en cuanto a tricordos, es decir, tipos y clases de cardinalidad c = 3. Estos tres vectores han sido claves para elaborar la Tabla Periódica vista anteriormente, cuyo estudio completaremos ahora con la información relativa a los tipos de conjuntos y a los pares de clases Z-relacionadas. Por último, veremos también las formas primas de Forte y de Rahn, ampliamente utilizadas para representar las clases de conjuntos y que pueden obtenerse muy fácilmente a partir de la forma interválica introducida aquí, lo que constituye otra de sus interesantes propiedades. 2. Vector de Tipos de Tricordos: TTV Para c = 3, hay 12 clases de conjuntos, los tricordos, cuyas formas interválicas primas, ordenadas por ICV decreciente, pueden verse en la Tabla Periódica (Tabla 1). Todas ellas tienen s = 1 salvo la 3-12, la tríada aumentada, que tiene s = 3. Cinco de ellas son inversionalmente simétricas, concretamente 3-1, 3-6, 3-9, 3-10 y 3-12. Y cada una de las otras 7 está formada por dos tipos de conjuntos, relacionados entre sí por inversión. Los dos tipos que forman una clase tienen el mismo ICV, pero una sonoridad diferente, así como una forma interválica también diferente. Un claro ejemplo es la clase 3-11, formada por las tríadas mayor y menor, cuyas formas interválicas normales son, respectivamente, y . En estos casos, al tipo de conjunto que tenga la menor de ellas le llamaremos “tipo a” y al otro “tipo b”. Por tanto, la tríada menor será de tipo a y la tríada mayor de tipo b (ya que 345 es menor que 354). En total, para c = 3 tenemos 5 + 2x7 = 19 tipos de tricordos. Tabla 1. Tabla Periódica de las Clases de Conjuntos. Para los conjuntos de más de 3 notas, podemos determinar cuántos tricordos de cada tipo se pueden formar con sus notas. El resultado son 19 números que forman el “Vector de Tipos de Tricordos” o TTV. Por claridad, este vector lo escribiremos como dos grupos de 9 y 10 números separados por un guion, el primero de los cuales corresponde a los tricordos 3-1, 3-2a, 3-2b, 3-3a, 3-3b, 3-4a, 3-4b, 3-5a y 3-5b (los cuales contienen al menos un semitono) y el segundo a 3-6, 3-7a, 3-7b, 3-8a, 3-8b, 3-9, 3-10, 3-11a, 3-11b y 3-12 (los cuales no contienen ningún semitono). Por ejemplo, el TTV de la clase 4-28 (acorde de séptima disminuida) es (000000000-0000004000), ya que solo contiene 4 tricordos del tipo 3-10, que es la tríada disminuida. El TTV de la clase 5-35 (escala pentatónica) es (000000000-1220030110), donde el primer grupo de números son todos ceros porque esta clase no contiene semitonos, y el TTV de la clase 7-35 (escala mayor) es (022002211-3441151330), donde los últimos cuatro elementos indican que hay 1 tríada disminuida, 3 menores, 3 mayores y ninguna aumentada. Se ha comprobado que solo hay dos tipos de conjuntos con el mismo TTV, que son los pertenecientes a la clase 6-14, el cual es (111222200-1110010221). Todos los demás tipos tienen TTV diferentes, por lo que este vector caracteriza completamente su sonoridad. En las clases de conjuntos de más de 3 notas que tienen dos tipos, la asignación de los tipos a y b ya no se hace según su forma interválica normal, sino que se asigna el tipo a al que tenga mayor TTV, siendo el otro de tipo b. De esta forma, se demuestra que el complementario de un tipo a es siempre un tipo b y viceversa [1]. La única excepción son los dos tipos de la clase 6-14, ya que tienen el mismo TTV, lo cual se indica en la Tabla Periódica mediante un superíndice con el símbolo “=”. Además, ambos son autocomplementarios, es decir, cada uno es el complementario de sí mismo. Entonces, en este caso, sí asignamos el tipo a al de menor forma interválica normal, es decir, al que tiene la forma interválica prima. Con estos criterios, la mayoría de las formas interválicas primas resultan ser de tipo a. Hay, sin embargo, excepciones, en donde la forma interválica prima es de tipo b, que son 6-10, 6-18, 7-11, 7-26, 7-28, 8-12, 8-14, todas las cuales ocurren para c ≥ 6 y se indican en la Tabla Periódica mediante un asterisco (*). Por otra parte, los TTV de los tipos a y b de una misma clase de conjunto están relacionados entre sí de una forma muy sencilla, de manera que podemos obtener el TTV de uno de ellos a partir del del otro. Para ello solo hay que intercambiar los elementos que corresponden a dos tipos de la misma clase de tricordo, tal como se muestra en la Figura 2. Por ejemplo, para la clase , considerada en la Sección 2 del artículo anterior, si conocemos el TTV de su tipo a, que es (010001211-0001010110), podemos obtener el del tipo b, que es (001002111-0000110110). Figura 2. Relación ente los TTV de los tipos a y b de una misma clase de conjunto. 3. Vector de Clases de Tricordos: TCV De forma alternativa al TTV, podemos definir también un “Vector de Clases de Tricordos” o TCV, que indique cuántos tricordos de cada clase contiene un conjunto dado de más de 3 notas. Este vector constará de 12 elementos, los cuales se pueden obtener fácilmente del TTV, simplemente sumando los elementos que corresponden a dos tipos de la misma clase de tricordo. Esta operación se muestra en la Figura 3, donde t1 … t19 son los elementos del TTV (cualquiera de los dos tipos, a o b) y f1 … f12 los elementos del TCV. Así, por ejemplo, el TCV de la clase 4-28 (acorde de séptima disminuida) es (00000-0000400), el de la clase 5-35 (escala pentatónica) es (00000-1403020), el de la clase 7-35 (escala mayor) es (04042-3825160) y el de la clase es (01032-0011020). Figura 3. Relación entre la TTV y la TCV de una misma clase de conjunto. Se puede comprobar que cada clase de conjunto tiene un TCV diferente, por lo que este vector caracteriza completamente su sonoridad. Esto no ocurre con el ICV ya que, como hemos visto, hay pares de clases con el mismo ICV o Z-relacionadas. En estos casos, la que tiene mayor TCV diremos que es “dura”, ya que siempre tiene los intervalos menores más juntos, y la otra “blanda”. Además, se demuestra que la complementaria de una clase dura siempre es blanda y viceversa [1]. En el caso particular de los hexacordos (c = 6) esto implica que, si dos clases están Z-relacionadas, cada una es la complementaria de la otra. En la Tabla Periódica, los pares de clases Z-relacionadas, como ya se ha indicado, están en la misma celda, ya que tienen el mismo ICV. Entonces, para identificarlas, la dura se ha colocado en la parte superior. Como ejemplo, consideremos las clases 5-Z12 y 5-Z36, cuyo ICV común es (222121). Sus TCV son, respectivamente, (02022-1200100) y (11102-1101110), por lo que la primera es blanda (parte inferior de la celda) y la segunda dura (parte superior de la celda). Sus formas interválicas primas son, respectivamente, y , donde podemos comprobar que la segunda tiene, efectivamente, los intervalos menores más juntos (dos “1” seguidos frente a dos “1” separados cuatro semitonos). Sus clases complementarias son, respectivamente, 7-Z12 (dura) y 7-Z36 (blanda), pudiéndose comprobar que la primera tiene los intervalos menores más juntos. Además, la clase 5-Z36 está formada por dos tipos, 5-Z36a y 5-Z36b, por los que sus complementarios son, respectivamente, 7-Z36b y 7-Z36a. Una última característica de la Tabla Periódica es que, en cada período, las clases que tienen el mismo número de semitonos (número de “1” en la forma interválica o el primer elemento del ICV) se han representado con un mismo color de fondo. Y este color se ha asignado también a sus clases complementarias. De esta manera, dada una forma interválica prima, es más fácil localizarla en la tabla. Por ejemplo, la forma interválica prima , considerada en la Sección 2 del artículo anterior, tiene 5 notas y 2 semitonos, por lo que está en el período 5, en las celdas de color azul, y es la clase 5-20. Conviene señalar que este grupo de celdas es uno de los más numerosos, por lo que en otros casos esta búsqueda resulta mucho más sencilla. En la Tabla 2 se muestra, para cada período, el número de clases de conjuntos que tienen el mismo número de semitonos, es decir, el mismo color de fondo en la Tabla 1 (se ha seguido una disposición similar en ambas tablas). Así mismo, para cada período se muestra el número total de clases, tipos y conjuntos de notas. Dado que también se ha incluido la clase 0-1 (silencio), el número total de conjuntos de notas es, lógicamente, 212 = 4096, que pueden agruparse en 352 tipos o 224 clases. Nótense las simetrías que hay entre los períodos complementarios. Tabla 2. Número de Clases, Tipos y Conjuntos de Notas. Período Clases de conjuntos con el mismo número de Semitonos Clases Tipos Conj. Notas 12 11 10 9 8 7 6 5 4 3 2 1 0 0- 1 1 1 1 1- 1 1 1 12 2- 1 5 6 6 66 3- 1 4 7 12 19 220 4- 1 8 12 8 29 43 495 5- 1 6 18 10 3 38 66 792 6- 1 9 19 17 3 1 50 80 924 7- 1 6 18 10 3 38 66 792 8- 1 8 12 8 29 43 495 9- 1 4 7 12 19 220 10- 1 5 6 6 66 11- 1 1 1 12 12- 1 1 1 1 Total 1 0 1 1 6 5 16 19 36 36 47 30 26 224 352 4096 4. Formas Primas de Forte y de Rahn Como hemos visto en la primera parte de este trabajo, la forma interválica que hemos introducido aquí es realmente útil para representar los tipos de conjuntos, dadas sus importantes propiedades. Sin embargo, en los listados proporcionados por Forte [2] y Rahn [3] solo se incluyen las clases de conjuntos y se representan mediante sus propias “formas primas”, que en la mayoría de los casos son iguales, pero no siempre. Lo mismo ocurre en los listados de Straus [4], quien utiliza las formas primas de Rahn. Por otra parte, estas formas primas no están basadas en intervalos, sino en notas y empiezan siempre por el Do. Por ejemplo, la forma prima, tanto de Forte como de Rahn, de la clase 3-11 (tríadas mayores y menores) es [037], es decir, las notas Do, Mib, Sol, que corresponden al acorde de Do menor. Y la forma prima de la clase 3-12 (tríada aumentada) es [048] (Do, Mi, Sol#). En otros casos, sin embargo, la forma prima no es tan fácil de reconocer. Por ejemplo, la forma prima, tanto de Forte como de Rahn, de la clase 7-35 (escala mayor) es [013568A], que corresponde a la escala de Reb mayor. Esto es consecuencia de los procedimientos utilizados por Forte y Rahn para obtener sus formas primas, que por cierto son bastante laboriosos. Sin embargo, ambas pueden obtenerse fácilmente a partir de la forma interválica vista aquí. A continuación, veremos cómo y lo ilustraremos con el conjunto de notas [59A24], visto en la Sección 2 del artículo anterior, cuya forma interválica es . Forma Normal de Rahn: tomamos la permutación circular que corresponda al número mayor, pero visto de derecha a izquierda (es decir, en “orden colexicográfico”), que es . Y ahora, empezando por “0”, escribimos las demás notas separadas por los intervalos indicados en esa forma interválica (salvo el último), es decir, [02378]. Forma Normal de Forte: tomamos la permutación circular que tenga el mayor intervalo a la derecha y, si hay varias opciones (como ocurre aquí, ya que hay dos “4”), la que corresponda al número menor (visto de izquierda a derecha), que es . Y ahora, empezando por “0”, escribimos las demás notas separadas por los intervalos indicados en esa forma interválica (salvo el último), es decir, [01578]. Aunque en este caso las formas normales de Forte y de Rahn son distintas, en la mayoría de los casos son iguales. Forma Prima de Rahn: hay que hallar las formas normales del conjunto dado y de su inverso, y tomar la menor de ellas. La forma interválica del conjunto inverso es , que es también su forma interválica prima. Su permutación circular que corresponde al número mayor visto de derecha a izquierda es , que da lugar al conjunto de notas empezando por “0”: [01568]. Esta es también la forma prima de Rahn, ya que es menor que [02378]. Forma Prima de Forte: también hay que hallar las formas normales del conjunto dado y de su inverso, y tomar la menor de ellas. Para el conjunto inverso, la forma interválica que tiene el mayor intervalo a la derecha y corresponde al número menor es precisamente , que da lugar al conjunto de notas empezando por “0”: [01378]. Esta es también la forma prima de Forte, ya que es menor que [01578]. De nuevo, en este caso las formas normales de Forte y de Rahn para el conjunto inverso son distintas, aunque en la mayoría de los casos son iguales. No obstante, siempre coinciden en si la forma prima corresponde al conjunto dado o a su inverso. En este sentido, la forma interválica prima también suele coincidir con ellas, como ocurre en este ejemplo, pero no siempre es así. La mayoría de las formas primas de Forte y de Rahn son de tipo a, pero algunas son de tipo b, las cuales se indican en la Tabla Periódica mediante el superíndice “+”. Sorprendentemente, son justo las complementarias de las marcadas con “*” más la 6-14, por lo que todas ellas ocurren para c ≤ 6. Como se puede observar, dada la forma normal de Forte o de Rahn de un conjunto de notas, no es nada obvio obtener, a partir de ella y sin usar la forma interválica, la correspondiente forma normal de su inverso o su complementario. Y tampoco permite determinar fácilmente sus simetrías, ni inversional ni transposicional. Por tanto, lo más práctico y sencillo es usar siempre la forma interválica introducida aquí y, a partir de ella, obtener las formas de Forte y de Rahn que sean necesarias. 5. Conclusiones e Información Adicional En la segunda parte de este trabajo se han realizado dos generalizaciones del vector de clases de intervalos o ICV: el vector de clases de tricordos o TCV y el vector de tipos de tricordos o TTV. El TCV permite distinguir entre dos clases Z-relacionadas, por lo que caracteriza la sonoridad de las clases de conjuntos. Y el TTV permite distinguir entre los dos tipos de una misma clase, por lo que caracteriza la sonoridad de los tipos de conjuntos, salvo el 6-14a y el 6-14b, que son los únicos que tienen un mismo TTV. Además, hemos visto una nueva utilidad de la forma interválica, que es la obtención de las formas normales y primas de Forte y de Rahn. Como resumen final diremos que, en la Tabla Periódica que se ha desarrollado, aparecen ordenadas todas las clases de conjuntos y permite ver, de un simple vistazo, sus principales características y las relaciones entre ellas. En particular, proporciona la siguiente información: los nombres de Forte, los tipos de simetría inversional y transposicional, las relaciones Z y las clases complementarias, las formas interválicas primas y la indicación de su tipo (a o b), lo cual permite obtener las formas normales de todos los tipos de conjuntos y, a partir de ellas, las correspondientes formas de Forte y de Rahn. Además, dada una forma interválica prima, es fácil localizarla en la tabla. Los tres vectores ICV, TCV y TTV han sido claves para elaborar esta tabla. En la publicación [1], además de la Tabla Periódica, se incluye un apéndice matemático donde se obtienen las fórmulas que relacionan los ICV y los TTV de un conjunto y su complementario, mediante las cuales se demuestran las afirmaciones que se han dado aquí sin demostración. Además, se incluye un segundo apéndice que es un listado pormenorizado de las clases y tipos de conjuntos, donde se da, para cada uno de ellos, la forma interválica normal, la forma normal de Rahn (y la de Forte cuando es diferente de ella), el nombre de Forte “extendido” (incluyendo el tipo, a o b, y su Z-relacionado si lo tiene), el ICV y el TTV. La inclusión de este último vector representa una diferencia significativa con respecto a los listados publicados con anterioridad en la bibliografía. Puede encontrarse más información sobre esta y otras materias similares en la página Web www.ruedaarmonica.com o www.harmonicwheel.com. 6. Referencias [1] Nuño, Luis. (2020). A Detailed List and a Periodic Table of Set Classes. Journal of Mathematics and Music, DOI: 10.1080/17459737.2020.1775902. [2] Forte, A. (1973). The Structure of Atonal Music. New Haven: Yale University Press. [3] Rahn, J. (1980). Basic Atonal Theory. New York: Schirmer Books. [4] Straus, J. N. (2016). Introduction to Post-Tonal Theory, 4th Edition. New York: W. W. Norton.

Martes, 12 de Enero de 2021 | Imprimir | PDF |  Correo electrónico

354. 189. (Enero 2021) Sobre ciclos y espejos

En nuestra última aparición por este rincón —que fue el año pasado aunque sólo haya pasado un mes—, comentamos algunos tipos de mezclas, que son en realidad permutaciones del conjunto de cartas, sobre las que podemos predecir el orden final de las cartas o, al menos, la posición relativa entre ellas. En esta ocasión, nos dedicaremos a estudiar con más detalle algunas de estas propiedades. Entre la gran cantidad de maneras de ordenar un conjunto de cartas, hay dos que gustan o deben gustar a los amantes de las simetrías: el orden cíclico y el orden especular. Veamos en qué consisten con un caso sencillo: si tenemos dos conjuntos idénticos de 5 números, digamos y , formamos cualquier permutación del primer conjunto y colocamos a continuación la misma permutación del segundo conjunto, el resultado  es un conjunto de 10 números en orden cíclico. Sin embargo, si invertimos el orden de la segunda permutación, el conjunto total tendrá orden especular. Por ejemplo, el conjunto tiene orden cíclico pero el conjunto  tiene orden especular. La primera ordenación se llama cíclica porque el ciclo 13254 se repite y tiene la propiedad de que, al cortar por cualquier lugar y completar el corte, el conjunto sigue estando compuesto por dos grupos iguales con la misma permutación. La segunda ordenación se llama especular porque se comporta como si se colocara un espejo entre ambos. Ahora ya no se puede cortar por cualquier lugar pues se perdería dicha propiedad. Es relativamente sencillo descubrir diversas propiedades de invariancia entre estas dos ordenaciones cuando se realizan ciertas mezclas pero, antes de señalar algunas de ellas, prefiero que las descubras a partir del juego que proponemos a continuación. Ya hemos mencionado en este rincón al prolífico mago canadiense Stewart James (por ejemplo, en el número 99 de noviembre de 2012). En uno de sus recordados artículos para la revista «Scientific American», Martin Gardner se refirió a él como «un mago que ha inventado más juegos de magia matemática con cartas de alta calidad que cualquier otro». Alrededor de 1928, ideó un juego que tituló "Murder By Suggestion", que fue publicado casi inmediatamente, en marzo de 1980, en la revista New Pentagram (en la imagen adjunta se muestra la portada de dicho número), que fue seleccionado posteriormente en la monumental recopilación The James File (2000), así como en la posterior selección The Essential Stewart James (2007), ambos escritos por Allan Slaight, y que ha sido adaptado por varios autores, como Werner Miller (también asiduo a este rincón) y Shane Causer. Describiremos aquí esta última versión que el autor titula "Finding a Mate", como aparece en su libro «Automata: beyond self-working magic» (2005). Antes de empezar con el juego, busca una baraja y aparta las cartas del as al siete de dos palos cualesquiera. Puedes descartar el resto pues no las usaremos más. Miento, busca también un comodín o la dama de corazones o cualquier otra carta que se distinga de las catorce elegidas. Ordena las cartas del modo indicado en la imagen: Forma con ellas un paquete, colócalas con las caras hacia abajo y corta por cualquier lugar. Completa el corte para no saber el orden en que han quedado. Intercala el comodín por cualquier lugar, cara arriba para no perderlo de vista durante el siguiente proceso. Reparte las cartas sobre la mesa, una a una y forma con ellas dos montones: la primera a la izquierda, la segunda a la derecha, la tercera a la izquierda, y así sucesivamente. El primer montón tendrá una carta más pero no es importante. Recoge las cartas colocando uno de los montones sobre el otro; no importa si colocas el de la izquierda sobre el de la derecha o viceversa. Repite el reparto del paso 4 y la recogida del paso 5. Extiende las cartas en abanico y retira el comodín junto con las dos cartas adyacentes a él, la que está encima y la que está debajo. Vuelve a cerrar el abanico con las cartas restantes. ¡Sorpresa! Si giras las cartas del paquete por parejas, ninguna de ellas contiene dos cartas del mismo valor pero las dos cartas que estaban junto al comodín sí tienen el mismo valor. Parece que el comodín ha interpretado el papel de Cupido. COMENTARIOS FINALES: El orden indicado en la descripción no es importante: basta que el segundo grupo esté en el mismo orden que el primero. Un método habitual para conseguir que un grupo de cartas quede en orden cíclico es romper todas las cartas por la mitad en bloque y colocar una mitad sobre la otra. Ya hemos aplicado esta drástica solución en algún lugar, como en el número 84 de junio de 2011, con el juego "Las cartas rotas" y puede ser una opción para este juego lo que ahorraría la ordenación de los dos grupos de cartas. Esto significa que tampoco tienen que estar separadas las rojas y las negras, lo importante son los valores de las cartas. En el juego original, Stewart James utilizaba dos grupos de 14 cartas en orden cíclico de manera que la suma de los valores de las dos cartas adyacentes al comodín fuera el resultado de una predicción inicial. Para conseguirlo, basta observar qué cartas son las que se colocan junto al comodín cada vez que se realizan los repartos indicados en la descripción del juego. Como había prometido al principio, plantearé algunas características invariantes del orden especular y el orden cíclico respecto a ciertas mezclas. Estas mezclas son la mezcla Klondike y Monge (de las que ya hablamos el mes pasado) y la mezcla antifaro (que consiste simplemente en repartir las cartas sobre la mesa en dos montones —como en el juego anterior— y recoger uno sobre el otro). Te dejo como tarea la interpretación y comprobación de estas propiedades y la aplicación en algún juego de magia que se te ocurra con ellas: + CORTE ANTIFARO KLONDIKE MONGE CÍCLICO cíclico especular ESPECULAR especular cartas en parejas cíclico Las secuencias cíclicas son también fuente de juegos matemáticos sorprendentes (como, por ejemplo, en el número 30 de este rincón correspondiente a julio de 2006) y aparecen con mucha frecuencia; sin ir más lejos, la representación decimal de las fracciones es siempre cíclica, desde los números enteros cuya parte decimal contiene un ciclo infinito de ceros hasta ejemplos más complejos como los primos generadores, que forman la sucesión A001913 como aparece en la On-line Encyclopedia of Integer Sequences. ¿Te imaginas encontrar la parte cíclica del número 1/223? Tiene 222 cifras. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Martes, 05 de Enero de 2021 | Imprimir | PDF |  Correo electrónico

355. 69. (Enero 2021) Meridianas de cámara oscura en España

(Meridiana de la Antecámara Real. Monasterio de San Lorenzo de El Escorial) España no ha destacado por la construcción de líneas meridianas de uso astronómico u horario. Ninguna de sus grandes catedrales ha visto su pavimento atravesado por esa lujosa línea ni sus edificios públicos muestran su meridiana con analema como en Italia o Francia. Habría que esperar hasta el siglo XVIII para que tres palacios reales construyeran meridianas. Un modesto franciscano diseñó una en su convento de Benissa en los inicios del siglo XX y nada más hasta nuestros días, cuando en la restauración de San Pedro de Becerril de Campos se incluye su implantación. Meridianas: un sencillo y útil instrumento astronómico La inclinación del eje de rotación de la Tierra respecto al plano de su traslación es la causa de la diferente duración de los días y del aumento o disminución de las sombras al mediodía a lo largo de las Estaciones. La consecuencia de la diferente insolación e intensidad son los cambios climáticos de temporada o que en el interior de los círculos árticos se tenga Sol de medianoche. La elevación solar del mediodía puede cambiar hasta 47º (el arco entre los dos Trópicos), lo que hace que en lugares como San Lorenzo de El Escorial la sombra de una vara de 1 metro supere los 2 metros al mediodía en el solsticio de invierno y alcance solo 31 centímetros en el solsticio de verano. Estos cambios permiten tener tanto un calendario de las Estaciones como un ajuste de la hora. Una meridiana no es más que una línea trazada en un plano horizontal (incluso en vertical o curvo) que lleva la dirección sur-norte del meridiano del lugar y que recibe una pequeña elipse de luz de un orificio gnomónico (meridianas de cámara oscura) o la sombra de un gnomon (meridianas exteriores). Sobre la línea se suelen marcar los solsticios, equinoccios y el resto de los puntos del zodiaco. Las meridianas mayores suelen incluir hasta los días. Y cuando el sistema horario era diferente marcaba las horas del mediodía solar. Las grandes meridianas pueden ser buenos instrumentos para fijar ajustar fechas y horas, además de otras verificaciones astronómicas. Cuánto más alto está el orificio más precisión se obtiene. Durante el Renacimiento empezaron a proliferar meridianas en los grandes edificios: no es de extrañar que la Catedral de Florencia tenga en la linterna de Brunelleschi un orificio marcado. La meridiana es la más antigua conservada y la más alta: fue construida en 1475 por el astrónomo Paolo del Pozzo Toscanelli, quien aprovechó los 90 metros de altura de la cúpula. La elipse de luz solo llega al suelo en los días próximos al solsticio de verano. (Diseño de la Meridiana. Duomo de Florencia) La meridiana de referencia que sirvió como verdadero laboratorio de investigación fue la de San Petronio en Bolonia con sus 66 metros de larga. La meridiana de la colosal iglesia vio la coronación de Carlos V como emperador. Muchas catedrales como la de Milán o Palermo cuentan con sus lujosas y largas meridiana. El analema Analema es un término que ha ido evolucionando. En su etimología griega y el uso que hace Vitruvio se refiere al pedestal de un reloj de gnomon vertical. Hoy un reloj solar analemático es aquel cuyas horas están marcadas en una elipse y que usa la sombra de una persona que se debe situar en distintas posiciones del eje menor según la fecha marcada. (Analema. Posición del Sol al mediodía civil en un año) La palabra analema ha quedado reservada para la curva lemniscata que diferencia la hora solar de la hora civil, diferencia que en ejes cartesianos se llama ecuación del tiempo. El analema permite compensar la hora marcada por el reloj solar sobre la meridiana, tiempo solar aparente, del tiempo solar medio que es el tiempo civil. La diferencia se debe tanto a la órbita elíptica como la inclinación del eje de rotación. La ecuación del tiempo es suma de las dos sinusoides, una de periodicidad anual (la elipse) y otra de periodo semestral (la inclinación). La máxima diferencia se produce en Noviembre y no alcanza los 17 minutos. Las meridianas del Padre Wendlingén El jesuita Juan Wendlingén (Praga, 1715 – 1790) llegó a España como profesor de Matemáticas de los Estudios Reales del Colegio Imperial (Reales Estudios de San Isidro) y del Real Seminario de Nobles, ambos regentados por la Compañía de Jesús. Alcanzó el puesto de Cosmógrafo Real, del Supremo Consejo de Indias, y además fue profesor del futuro Carlos IV. El matemático abandona el Reino tras la Pragmática Sanción de 1766 que decreta la expulsión de la Orden. El padre Wendlingén construye cuatro meridianas en Palacios Reales, dos en San Lorenzo de El Escorial (1755), una en el Buen Retiro (1756) y otra en el Despacho del Rey en Aranjuez. Todas fueron encargadas por Fernando VI. La del Buen Retiro ha desaparecido y la de Aranjuez fue cegada ignorándose su estado por estar cubierta por moqueta. Un libro da cuenta detallada de la construcción y funcionamiento de la Meridiana del Buen Retiro. El libro describe una meridiana con Analema. Si las de San Lorenzo lo tuvieron no se ha conservado. (Portada del libro de padre Wendlingén) En dos salas colindantes de la zona palaciega del Monasterio de El Escorial, Antecámara Real y Sala del Paseo, destacan sobre el rojo pavimento dos líneas de piedra negra con incrustaciones de latón dorado que incluyen marcas de los signos del zodiaco. Una de ella va firmada por el Padre Wendlingén en 1755. Las dos   miden unos cinco metros y su orificio se localiza encima de las ventanas a algo más de dos metros. Las meridianas no funcionan por estar permanentemente cerrado el ventanuco con un postigo de hierro. La recuperación del orificio gnomónico solo requiere sensibilidad y respeto por la cultura científica. No se debería esperar ni un día más para dejarlas que funcionen. No necesitan mantenimiento: el Sol lo hace todo. (Atribución al padre Wendlingén. San Lorenzo de El Escorial) La cornisa mordida del jardín de los frailes Un paseo por los jardines de los frailes, vertiente sur del Monasterio de San Lorenzo de El Escorial, permite apreciar dos postigos metálicos situados encima de dos ventanas. Son las protecciones de los orificios de las meridianas. (Orificios gnomónicos. San Lorenzo de El Escorial) Lo que no resulta fácil de apreciar si no hemos sido advertidos es que la cornisa tuvo que ser recortada para que en el solsticio de verano, el Sol a solo 17º de la vertical no fuera ocultado por el saliente. Los postigos no dejan ver como los gruesos muros de piedra tiene una hendidura inclinada para que los rayos de luz penetren sin obstáculo. La meridiana de Fray Pacífico en Benissa (Detalle del trazado de la meridiana. Benissa) El modesto convento franciscano de la Purísima Concepción de la Madre de Díos de Benissa fue fundado en 1611 con buena traza y fachada de sillería. Un patio muy agradable con arcadas de medio punto, a modo de claustro, no desmerece de la sencilla construcción. Este pequeño monasterio de Benissa goza del honor de tener todavía dibujado en el suelo una línea meridiana con analema. El orificio gnómonico desapareció con las obras de la fachada sur pero el azulejo rayado con la meridiana se conserva. El monje valenciano Fray Pacífico Albero Estany estuvo en Benissa antes de trasladarse a Argentina, donde falleció. Fray Pacífico construyó la meridiana, a principios del siglo XX, en lo que fue la biblioteca. El muro sur tuvo que ser demolido y su balcón cambió de lugar. La biblioteca fue dividida y hoy son el despacho y el dormitorio del Padre Superior. Solo ha quedado la huella de la línea meridiana, unos 4 metros de trazo sencillo, y de su analema, con trazada múltiple, apenas unos arañazos sobre una bella baldosa hidráulica de simetría p4m (celda base obtenida juntado cuatro baldosas). La meridiana de San Pedro en Becerril de Campos Desde el 19 de marzo de 2015 se puede visitar una meridiana de cámara oscura funcionando en España. La reconversión de una iglesia en ruinas en un espacio cultural astronómico ha rellenado ese lamentable vacío. En Italia están catalogadas más de setenta meridianas en funcionamiento. En España no había ninguna visitable hasta que Becerril de Campos, al lado de Palencia, ha construido la suya. (Meridiana de San Pedro. Becerril de Campos) La Iglesia de San Pedro se ha convertido en una referencia obligada. Además la meridiana no está sola; un Péndulo de Foucault, y dos estenopes (orificios pequeños) más para estudiar el movimiento de precesión y el solsticio de invierno completan el conjunto del interior. Los frescos con el cielo estrellado y los planetas crean el ambiente propicio. Fuera se han instalado dos pequeños relojes solares Becerril ya era lugar de visita obligada por las maravillosos tablas de Berruguete, por el Canal de Castilla y por su mudéjar: con la meridiana han mostrado que patrimonio histórico, arte y ciencia combinan muy bien. El estenope gnomónico está en una ventana lo suficientemente alta para que la línea meridiana se quiebre y continúe en el muro opuesto: la elipse luminosa en invierno supera el ancho de la nave. La meridiana debe visitarse en días soleados pasada la una en horario de invierno y pasadas las dos en el de verano para poder ver la transición Se habla de poner la analema, ecuación del tiempo, pero ahora no la tiene. (Panorámica de San Pedro. Becerril de Campos) Meridiana virtual de Ceballos en San Lorenzo de El Escorial Las dos meridianas del Padre Juan Wendlingen de 1755 no son las únicas que se pueden contemplar en el Real Monasterio de San Lorenzo de El Escorial. Luís Ceballos Medrano, ingeniero de Montes y catedrático de Geodesia, utiliza en 1905  como práctica de la asignatura una línea casi diagonal del atrio principal (poniente) que utilizó como referencia de la meridiana geográfica del lugar. El Monasterio se diseño con una declinación de más de 12º al nordeste. Se han aportado distintas razones para la rotación del edificio: conseguir mayor insolación invernal en la fachada de mediodía, error de medición, orientación oeste a la festividad de San Lorenzo, eje orientado a los Santos Lugares, o un criterio escenográfico para realzar la visión del monumento. Ceballos aporta otra sin mucho sentido: orientada según la brújula en el momento de su diseño. El polo norte magnético en 1550 estaba al noroeste y no al nordeste. El resto de las razones son especulativas: ni Juan Bautista de Toledo ni el propio Monarca expresaron su razón. (Placa en el pavimento del atrio principal. San Lorenzo de El Escorial) En 1995 el Patrimonio Nacional tuvo el acierto de colocar dos nuevas placas metálicas conmemorativas que marcaban la dirección de la meridiana de Ceballos. En los dos extremos del atrio principal. Son una buena referencia para apreciar la declinación de la obra. Meridiana exterior del Parque de las Ciencias de Granada La parte al Este de la esquina Sur del Parque de las Ciencias de Granada está dedicada a los relojes solares y las meridianas. Se trata de un conjunto didáctico de gran interés y encanto por dar relevancia a una materia que debería ser de conocimiento general. Encontraremos relojes de todo tipo pero sencillos, orientados al sur y al este/oeste, ecuatoriales y de gnomón vertical, con correcciones de la ecuación del tiempo y sin ella. La meridiana de agujero es quizá la única en funcionamiento en España con analema pero queda ridícula y paupérrima, por pequeña y carecer de las habituales marcas del zodiaco.  Las explicaciones brillan por su ausencia. (Meridiana exterior con analema. Granada)

Martes, 05 de Enero de 2021 | Imprimir | PDF |  Correo electrónico

356. Enero 2021: Matgram algebraico

1. ¿Qué es un matgram? Entre los recursos manipulables que se pueden utilizar en clase de matemáticas, quizás los más atractivos para los alumnos sean los puzles y rompecabezas. Dado que uno de los juegos básicos que la mayoría de tiernos infantes disfrutan en su casa son los puzles más o menos figurativos, cuando en el aula se utiliza este tipo de material, suele ser bien acogido por el alumnado, aunque los que se presenten estén adaptados para trabajar conceptos matemáticos. 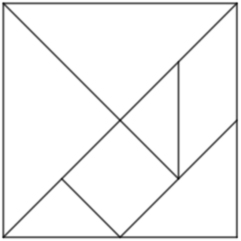En clase de matemáticas se pueden utilizar muchos tipos de puzles, por ejemplo, las teselas para estudiar posibles recubrimientos del plano; pero uno de los más interesantes es el tangram. Un tangram es una figura geométrica dividida en trozos cuya propuesta va más allá de reconstruir la figura original con las divisiones realizadas, siendo posible realizar una gran cantidad de construcciones, no solo geométricas sino también figurativas. Este aspecto es el que da pie a desarrollar la creatividad y originalidad de los jugadores. Existen muchos tipos de tangram: pitagórico, F, corazón, circular, triangular, de Brugner, etc. Aunque seguramente el más conocido es el Tangram Chino. Este tangram presenta la disección de un cuadrado en siete piezas, que son cinco triángulos, de distinto tamaño, un cuadrado y un romboide. En la imagen 1 podemos ver las divisiones del cuadrado en las siete partes. Imagen 1: Tangram chino Aunque suelen encontrarse referencias a este juego como muy antiguo en la cultura china, los especialistas aseguran que la historia fue una invención del creador estadounidense de pasatiempos y juegos del siglo XIX Sam Loyd. Además, no se encuentran referencias bibliográficas al juego anteriores a ese siglo. Hay autores que han publicado libros con cientos de figuras utilizando todas o parte de las piezas del tangram, por ejemplo, los libros de Joost Elffers de 1976 o de Innocent de Marchi de 2012 (aunque este último está dedicado a varios tipos de tangram). La versatilidad del tangram chino permite utilizarlo como recurso educativo en muchos bloques de las matemáticas. No solamente para componer polígonos convexos, de los que solo se pueden construir 13 utilizando todas las piezas, también se puede trabajar ángulos, pues todos los ángulos de sus piezas son múltiplos de 45º; estudiar el área de las piezas respecto del cuadrado original, con lo que surgirán fracciones, y si analizamos los perímetros, trabajaremos con números irracionales. Y muchas más cosas se pueden abordar con sus piezas y sus construcciones, como simetrías, giros, homotecias, etc. Pero, además de trabajar con los elementos del tangram chino, podemos adaptar el puzle para realizar actividades de cualquier concepto matemático, incluso de otras materias. Y ahí es donde aparece el matgram. Un matgram es básicamente un tangram chino de forma que en los lados de las piezas se colocan elementos matemáticos que debemos unir con sus correspondientes parejas. Al conectar los lados que tienen relación se obtiene una figura de las que se pueden construir con el tangram. Ya en el artículo que publicamos en el número 67 de la revista Suma (Grupo Alquerque, 2011) mostramos algunos de esos elementos; en aquel momento relacionados con el trabajo con medidas. Como comentábamos en el artículo, la primera referencia que conocemos de este material se remonta al año 1996 en que la editorial Editex presentó una serie de cuadernillos de material complementario para el aula de matemáticas. Entre esos cuadernillos, dirigido a la E.S.O., se encontraban matemáticas de la vida cotidiana o en la prensa. En particular, se editaron cuatro cuadernillos de matgram, uno para cada curso, creados por la profesora Lucía Puchalt Guillem. En cada uno de ellos aparecía un gran número de matgrams, cubriendo casi todo el temario del curso, y listo para fotocopiar y resolver en el aula. Imagen 2: Cuadernillo de actividades sobre matgrams Como hemos comentado en otros artículos de esta sección, participamos todos los años en la Feria de la Ciencia que se celebra en Sevilla a principios del mes de mayo. En 2019 hemos desarrollado un proyecto sobre juegos y actividades para trabajar el álgebra y, entre el material creado para la ocasión, hemos construido varios matgrams sobre distintos apartados del bloque de álgebra. Vamos a presentar aquí algunos de ellos. 2. Matgram de pre-algebra. Dado que el último de los días de la Feria de la Ciencia es sábado y suelen asistir familias completas con sus hijos, solemos preparar actividades que puedan hacer los más pequeños. Aunque este año el tema algebraico se nos iba un poco elevado para esos chavales, pensamos en crear una serie de matgrams utilizando lo que se denomina pre-algebra, es decir, operaciones en las que se conoce uno de los operadores y el resultado y hay que encontrar el operador que falta. En los ejemplos que adjuntamos en este apartado los alumnos deben encontrar qué número debe ir en el recuadro para que se cumpla la igualdad. Por ejemplo, si tenemos la operación □ – 4 = 9, el jugador debe unir a ese lado el trozo de pieza que tenga el valor 13. En las siguientes imágenes aparecen un par de ejemplos de esta idea. Imagen 3: Matgram de preálgebra, sumas y restas Dependiendo de lo complicado que se desee hacer, se pueden añadir más o menos operaciones. En el siguiente ejemplo, utilizamos productos y cocientes. Imagen 4: Matgram de preálgebra, productos y divisiones 3. Matgram de operaciones con monomios. Dado que en el proyecto, los divulgadores están elegidos entre alumnos de secundaria y hay entre ellos algunos de 1º de ESO, las operaciones que planteábamos debían ser, en su mayoría, cálculos que pudiesen hacer esos alumnos. Por ello, otro bloque de construcción se refería a operaciones básicas con monomios. En este caso cada operación debía asociarse con su resultado correspondiente. En el primer ejemplo (imagen 5) tenemos, igual que en el epígrafe anterior, operaciones de sumas y restas pero de monomios. Imagen 5: Matgram de sumas y restas de monomios Y en el segundo (imagen 6) aparecen productos y divisiones. Imagen 6: Matgram de productos y divisiones de monomios 4. Matgram de ecuaciones Como es evidente, la dificultad puede ser la que queramos. Otro de los bloques utilizando matgrams fue el de ecuaciones, donde incluimos el siguiente ejemplo en el que había que unir cada ecuación de segundo grado con sus soluciones (por una cuestión de espacio, en el diseño solo aparecen la expresión polinómica -sin igualar a cero- y las soluciones). Imagen 7: Matgram de ecuaciones 5. Matgram de sucesiones Para terminar vamos a añadir un matgram un poco más complicado correspondiente a sucesiones. La dificultad estriba en que los emparejamientos no relacionan siempre los mismos conceptos, como ocurre en los anteriores. El primer elemento de la pareja es siempre el comienzo de una sucesión, pero su complemento son unas veces los elementos de la sucesión que siguen; otras su término general, y, a veces, cuando es una progresión aritmética aparece la diferencia, o la razón si es geométrica. Imagen 8: Matgram de sucesiones 6. Soluciones y construcción A la hora de corregir esta actividad se tiene la ventaja de que el profesor o profesora puede conocer qué imagen resulta al unir correctamente las piezas (imagen 9 y siguientes para los ejemplos mostrados). Por lo que, de un solo vistazo, puede saber si el alumnado ha cometido algún error al resolver las relaciones planteadas. De todos modos, es conveniente pedir que se escriban las operaciones realizadas aunque la figura sea correcta, para protegernos de la picaresca del alumnado de copiarla de otro compañero sin hacer los cálculos adecuados. La solución debe ser siempre una figura, a poder ser, geométrica reconocible, pues si colocamos un dibujo figurativo (un barco, una damisela, un chino moviéndose, etc.) es mucho más difícil engarzar correctamente las piezas. En las siguientes imágenes vemos las soluciones que deben quedar en los matgrams que hemos propuesto. Imagen 9: Solución de pre-algebra de sumas y restas Imagen 10: Solución de pre-algebra de productos y divisiones Imagen 11: Solución de sumas y restas de monomios Imagen 12: Solución de productos y divisiones de monomios Imagen 13: Solución del matgram de ecuaciones Imagen 14: Solución del matgram de sucesiones A lo hora de crear un matgram que nos interese el proceso se hace justo al revés del de su resolución. Primero seleccionamos una figura que queramos obtener, construimos su solución tangram (todavía no han aparecido términos matemáticos en los lados) y después elegimos parejas de valores que correspondan a los segmentos de los polígonos que están en contacto. Como ejemplo tenemos una figura en la siguiente imagen, en la que hemos colocado los mismos valores (en este caso la misma letra) en los lugares donde deben ir los elementos que queremos emparejar. Imagen 15: Ejemplo de diseño de un tangram A la hora de trabajar con el alumnado el comienzo puede ser resolver el matgram propuesto por el profesor o profesora, pero es mucho más enriquecedor, una vez que se conoce el proceso, que sean los propios alumnos quienes diseñen sus propios matgrams y que sean sus compañeros quienes tengan que resolverlos. De esa manera se puede comprobar quién maneja conceptos más fáciles y quién plantea relaciones más rebuscadas, algo que le encanta hacer al alumnado. 7. Referencias bibliográficas Grupo Alquerque (2011): ¡Medidas, las justas! SUMA, nº 64, pp. 59-63. Hay versión digital en la página de Divulgamat, en la siguiente dirección: http://www.divulgamat.net/index.php?option=com_content&view=article&id=15399&directory=67 Puchalt Gillem, L. (1996): Matgrams. 4 niveles. Editorial Editex, Madrid.

Martes, 05 de Enero de 2021 | Imprimir | PDF |  Correo electrónico

357. 157. ¿Matemáticas o B.B.? Esa es la cuestión

Si recuerdan la anterior reseña, acabábamos el año hablando de ñoñerías. Como seguimos de fiestas navideñas, empezamos el año nuevo con más de lo mismo (esta peli se estrenó un 8 de enero de 1965), una comedia familiar con las que los yanquis hacían soñar al mundo con su idílica way of life (que luego descubrimos/descubrieron que era más falsa que una gaseosa sin azúcar). Si leemos el cartel anunciador de la película, nos dice (traduzco a mi aire): “¿Qué es toda esa escandalera? Son carcajadas, ... ¡¡por la película más divertida del año!! Y debajo nos relata prácticamente todo el argumento de la película: Un profesor de poesía descubre que su hijo de ocho años es: 1.- Un genio matemático 2.- Un músico con un oído pésimo 3.- Un artista daltónico 4.- Un espabilado por una gatita sexy de 36 – 24 – 36 llamada “Querida Brigitte”. Añada apuestas de caballos, adolescentes conspiradores, y te troncharás a cada minuto. Como es mi costumbre, empezamos conociendo sus datos técnicos y artísticos: Ficha Técnica: Título: Querida Brigitte. Título Original: Dear Brigitte. Nacionalidad: EE. UU, 1965. Dirección: Henry Koster. Guion: Hal Kanter, basado en la novela Erasmus with Freckles de John Haase. Fotografía: Lucien Ballard, en Color De Luxe. Montaje: Marjorie Fowler. Música: George Duning. Producción: Fred Kohlmar y Henry Koster. Duración: 100 min. Ficha artística: Intérpretes: James Stewart  (Profesor Robert Leaf), Fabian (Kenneth “Kenny” Taylor), Glynis Johns (Vina Leaf), Cindy Carol (Pandora “Panny” Leaf), Bill Mumy (Erasmus “Ras” Leaf), John Williams (Peregrine Upjohn), Jack Kruschen (Doctor Volker), Charles Robinson (George), Howard Freeman (Rector Sawyer), Jane Wald (Terry, la esposa de George), Alice Pearce (Empleada de la Oficina de empleo), Jesse White (Cliff Argyle, el corredor de apuestas), Gene O'Donnell (Teniente de Policía Rink), Ed Wynn (El Capitán), y por supuesto, aunque no aparezca en los títulos de crédito, Brigitte Bardot, haciendo de ella misma. Argumento Aunque ya está bien resumido en la traducción del cartel publicitario hecho anteriormente, digamos que James Stewart interpreta a un profesor despistado que vive en su mundo, esta vez poeta, convencido del desastre mundial que va a suponer el auge de las ciencias en detrimento de las humanidades. Y descubre con estupor y resignación que su hijo es un negado total para todo lo artístico (música, pintura, literatura) salvo para las matemáticas para las que es un auténtico genio. Conocidas las altas capacidades del niño, todos los que le rodean intentan sacar beneficio de las mismas, aunque el único deseo de éste es conocer a Brigitte Bardot, a la que todas las noches escribe una carta. Y mientras, su padre, intentando que nadie se aproveche del chico, aunque las penurias económicas familiares quizá le hagan cambiar de opinión... Comentario, análisis y curiosidades Se describen y resuelven varias cuentas y ejercicios de matemáticas a lo largo de la película, todos de tipo aritmético, completamente rutinarios (sí, sí, ya sé que desgraciadamente así son las clases de muchos profesores, así que en ese sentido esta película de hace 56 años, sigue describiendo muchos aspectos actuales), sin demasiado interés matemático. Pero es un entretenimiento (malevolo, pero divertido, si los hay) comprobar y localizar errores en las resoluciones. Uno de los enfrentamientos que aparecen en la película es el de Quico (el niño en la versión original se llama Erasmus, aunque por comodidad lo llaman Ras, pero era una moda, o quizá era norma del régimen, el “españolizar” todo lo posible en el doblaje, para que no nos familiarizaramos excesivamente con lo foráneo; así nos va hoy con los idiomas) con una “moderna computadora” (un panel de plástico lleno de lucecitas, como vemos en la imagen), que acabará sucumbiendo ante el chaval. Esta misma máquina-decorado fue la utilizada en otra película de la misma productora que comentamos hace tiempo, Su otra esposa (Desk Set, Walter Lang, EE. UU., 1957; ver la reseña 65) y en el clásico de terror La mosca (The Fly, Kurt Neumann, EE. UU., 1958). Había que rentabilizar inversiones. También los títulos de crédito emulan los pixels de las máquinas de aquellos años. Además de los nombres de los actores principales (que se repiten con letras “normales” por si el espectador no se entera de lo que pone), aparecen algunas expresiones matemáticas y el juego del tres en raya (tic-tac-toe, en inglés, recordemos), como vemos en las imágenes siguientes: Vayamos por orden, según transcurre la película. Empieza con los improperios del padre ante todo lo que suene a científico. Sale discutiendo de la universidad, gritandole al rector: – ¡¡Estoy harto ya de vosotros y de vuestra maldita ciencia!! Al parecer la universidad ha instalado una central nuclear de uranio en su campus, y desconfia de que “cualquier mañana se presenta uno de esos sabiondos con una borrachera de éxitos y de vino, aprieta un botón que no corresponde, o echa demasiado uranio al plutonio, y ¡¡wham!!”. Ya sabemos, los años en que todo lo nuclear tenía en la opinión pública un efecto muy negativo, en parte por la mala propaganda precisamente de los medios de comunicación (y el desconocimiento, claro, y que la gente sólo veía ensayos de bombazos, y tenían reciente lo de Hiroshima y Nagasaki, y bueno, había miedo, era entendible). Ahora, ¡¡una central nuclear en un campus universitario!! Un tanto excesivo. Seguramente fuera un simple laboratorio. Un poco más adelante vuelve a la carga (a sus alumnos): – Anoten mis palabras: Dentro de cinco años nos veremos aplastados por los científicos. No habrá más que científicos donde quiera que se detenga nuestra vista, por mucho alcance que esta tenga. Y la base de la verdadera civilización, como es la literatura, la filosofía y las artes, ¡olvidada! ¡Olvidada! Tan muerta como el minué. Y en lugar de estudiar al ser humano, y la poesía de sus sueños, todo el mundo trabajará en una máquina de ahumar jamones de Virginia por un, por un sistema electrónico, o hará de las gallinas una ametralladora, pthump, pthump, pthump, ¡venga a poner huevos! ¡La gran evolución de la tecnología! Máquinas de tal perfección y tan rápidas, que automaticamente dejarán sin trabajo a un millón de obreros de la noche a la mañana. ¡Un gran adelanto! Personalmente, no quiero hacer el vuelo de San Francisco a Nueva York en menos de una hora, vaciando mi estómago sobre cualquier lugar de Denver. Le tengo delicado. Me niego a ser cómplice de ello.  En fin, menos mal que sólo es un estereotipo cómico (¿o no?). Presentado el personaje, que algunos profesores compañeros califican de medieval (¡¡qué mania de oponer siempre la materialización de la sociedad y la desaparición del humanismo frente al avance científico!! Si en realidad, las limitaciones del ser humano ante la Naturaleza y los avisos de su progresiva destrucción han venido advertidas por los científicos y desde luego el mayor materialismo lo han traido los políticos. En fin, se ve que el discurso calumniador y tendencioso, no es exclusivo de la era Trump, aunque en todas partes cuecen habas, sin duda, y tampoco deberiamos generalizar respecto a unos y otros), el primer gran golpe a su ideal lo recibe cuando la profesora relata a los padres que su hijo es capaz de realizar operaciones grandes mentalmente:  9 x 12, 17 x 142 y 2765 x 127976. El padre le ruega que no diga nada, que es necesario pensarlo bien. La maestra sentencia: – Ante todo debemos pensar en el muchacho, no en el matemático. No obstante, el padre habla a solas con el niño, preguntándole si tiene algún truco, porque es imposible que realice esas operaciones mentalmente con tanta rapidez. Y le pregunta por 1726 x 8726. Quico le responde en el acto: 15061076. – ¿Es eso?, pregunta a su esposa con cara de incredulidad. Voy a decirte una cosa: no quiero que vuelvas a hacerlo más. Porque si alguien llegara a descubrirlo, ¿sabes lo que dirían de ti? Fíjate, ahí va Quico Leaf, ¡¡un matemático!!Y nosotros no queremos que digan eso, ¿verdad? Pero la cosa no será fácil de ocultar. Sobre todo cuando, en un banco (ver imagen), mirando la pizarra del balance anual, el chico dice a su madre en voz alta que está mal, que han puesto 1012 dólares más de los reales. El director de la entidad pasa en ese momento por allí (ver imagen), y pide a un empleado que compruebe con una máquina si es verdad lo que dice el chico, que encima les vacila diciendo que “El error está en la última columna”. Y comprueban que está en lo cierto. Al día siguiente es noticia en todos los periódicos locales: “Niño de ocho años hacer quedar como un mono a un computador de banco”. Desde ese momento, periodistas, profesores de la universidad, medios de comunicación etc., lo acosan. “¡Pobre hijo! Mi niño esclavo del cálculo”, indica su padre, desesperado. Pero no sólo la amenaza vendrá del exterior. Su hermana mayor, por la noche entra en su cuarto, pidiendole que le haga sus deberes. Claro, el niño no sabe de qué le habla: Quico: ¿Qué es la raíz cuadrada? Panny: Es el número que multiplicas por si mismo para obtener otro número. Por ejemplo, 2 x 2, 4, 2 es la raíz cuadrada de 4. ¿Entiendes? Tienes que sacar la raíz cuadrada de 221 con tres cifras decimales. Quico: 14 con 866 milésimas. Panny: ¡Eres un genio, hermanito! No sólo la hermana, también el novio de la hermana, Kenny, se “aprovecha” del genio. En una cafetería, le pide que le resuelva sus deberes: Kenny: Un ascensor de un edificio de 60 pisos hace los siguientes viajes: empieza por el primer piso hasta el piso 20, baja 4, sube 8, baja 3, baja 17, sube 10, baja 1, sube 5, sube 11, baja 22. ¿Dónde se encuentra el ascensor? Quico: Séptimo piso. Efectivamente, no hay más que hacer 20 – 4 + 8 – 3 – 17 + 10 – 1 + 5 + 11 – 22. Lo que cuesta creer es que el novio de la hermana, talludito y bastante “suelto” en otras lides, no sepa resolver tamaña gilipollez (con perdón). El siguiente ejercicio dice: Kenny: Si un pionero hubiese llevado una acción de un dólar el día que embarcó en Plymouth Rock, y esta acción venciera un interés compuesto de un 5% anual, ¿cuánto valdría dicha acción en el día de la fecha? Panny: Le falta la fecha de embarque. Kenny: El 16 de diciembre de 1620. Quico: 18 millones 532 mil 311 dólares y 52 centavos. En la versión original son 42 centavos en lugar de 52 pero bueno, no nos pondremos demasiado exigentes. En el fotograma que ilustra esta escena, vemos a un joven con gafas, detrás de Quico que no pierde detalle. Éste (Orville de nombre) y Kenny se valdrán de Quico para apostar (y ganar) en las carreras de caballos (no serán los únicos posteriormente). La última referencia que pudiera considerarse matemática, vuelve a tener que ver con efectuar operaciones aritméticas complicadas mentalmente. Tiene lugar en la universidad en la que trabaja el profesor Leaf, que a regañadientes acepta que hagan al niño una prueba para ver si tiene capacidades realmente o es un fraude. Le plantean dos cuestiones: 1.- La estrella más cercana a nuestro plantea es Próxima Centauri. La luz de la estrella tarda 4 años y 3 meses en llegar a nosotros, y la velocidad de la luz es de 300000 kilómetros por segundo. ¿Cuánto tiempo tardaría un cohete viajando a la velocidad de 22000 millas por hora en llegar a la estrella? Por supuesto, apenas han acabado de formular la cuestión, Quico ya está dando la solución: 129650 años 199 días 2 horas 10 minutos y 54 segundos. Bastante tiempo después, el enorme computador que vimos anteriormente en una de las imágenes suministra una hoja con la misma respuesta. Los asistentes no dan crédito. Seguramente al lector atento le habrá llamado la atención la diferencia de unidades en un mismo enunciado. La velocidad de la luz en kilómetros por segundo, mientras que la del cohete en millas por hora. No se trata de una complicación más para Quico, sino como antes, una sunto de doblaje. En la versión original de la película, la velocidad de la luz se indica como 186000 millas por segundo. La equivalencia es que 1 milla son 1,60934 kilómetros, pero en España estamos más familiarizados con los 300000 kilómetros por segundo. Lo que deberían haber doblado también son esas 22000 millas por hora (que serían 35405 kilómetros), aunque la cantidad, al no salir un nímero más “redondo”, optarían por dejarla en millas. ¿Y quien iba a atender o percatarse de la diferencia de unidades, en una película con “otros alicientes”? En cualquier caso, veamos si los cálculos de Quico y la máquina son correctos: utilizando los datos de la versión original, esto es, con la velocidad de la luz 186000 millas por segundo, caculemos la distancia entre Próxima Centauri y La Tierra. El espacio, como sabemos, es la velocidad por el tiempo. Pasemos los 4 años y 3 meses a segundos: 1 dia = 24 * 3600 segundos = 86400 segundos 3 meses = 3* 30 * 86400 segundos = 7776000 segundos 4 años = 4 * 365 * 86400 segundos = 126144000 segundos 4 años y 3 meses = 126144000 + 7776000 segundos = 133920000 segundos Por tanto, la distancia será de 186000 * 133920000 = 24909120000000 millas. El cohete, desplazandose a una velocidad de 22000 millas por hora, recorrera esa distancia en 24909120000000/22000 = 1.1322327272727272727 * 10^9 horas Esas horas son (1 año tiene aproximadamente 8760 horas) 129250,3113 años. ¡¡Vaya, parece que no cuadran los datos!! Pero es que en la versión original de la película, Quico dice “129354 years, 199 days, 2 hours, 10 minutes, and 54 seconds”. La discrepancia proviene de utilizar 365 dias por año. Cuando yo estudié la EGB, en la escuela nos decían que se tomaban 360 días por año y 30 días por mes. Rehaciendo las cuentas de antes con 360 dias, salen 129354,545454.... Por tanto, los años cuadran en la versión original (no en la doblada al castellano, que se han confundido, como suele ser norma). Terminemos comprobando los dias, horas, minutos, segundos, a ver si cuadran con los decimales que se obtienen. Para pasar 0.545454 .... años a dias, basta con multiplicar por 360 como hemos dicho. Salen 196.363636.... días. Pero sí tomamos 365, tenemos 199.0909.... días. ¿En qué quedamos? ¿Tomamos 360  o 365 dias? Después para los días, multiplicamos 0.09090909...* 24 = 2.18181818... horas; para los minutos, 0.18181818.... *60 = 10.909090... minutos; y finalmente para los segundos, 0.90909090...* 60 = 54.545454... segundos. Por tanto, todos los datos son correctos, en la versión original, salvo que cuando quieren toman el año con 360 o con 365 días. 2.-  Dividir 17 trillones 590 billones 38 millones 552568 entre 680. Quico anuncia que la máquina no podrá hacerlo, porque no sale una cantidad exacta, porque los únicos divisores son 8191 y 2147483647. Esto es claramente un error de guión, porque al multiplicar esas dos cifras, obtenemos 17590038552577, esto es, una unidad menos que el número que mandan dividir. En cualquier caso, una división no exacta nunca provocará el colapso de un computador, por muy antiguo que sea. Hay algunas referencias sobre la necesidad de utilizar el cálculo de probabilidades y las estadísticas para poder tener un mínimo éxito en las apuestas. Lo comenta la hermana, Panny, a sus padres, pero como ven, los guionistas redujeron las matemáticas a la aritmética (quizá para que el público general no se pierda demasiado). Si alguien desea saber cómo sigue la película, no es difícil localizarla en la red (tampoco imaginarse qué va a suceder). La película tiene un aire a producción Disney, y no por casualidad ya que en su momento se barajó esa posibilidad con Bing Crosby como protagonista. Sin embargo, la remodelada 20th Century Fox se hizo finalmente con los derechos. No estuvo claro que Brigitte Bardot quisiera aparecer. La actriz francesa exigió para ello no figurar en los títulos de crédito ni en la publicidad de la película. Los productores idearon entonces un ardid como reclamo: cambiaron el título previsto inicialmente para la película (el homónimo de la novela) sólo para que apareciera la palabra “Brigitte”, y así dar pistas sobre la posible presencia de la popular actriz. Por otra parte, el elenco contaba con el cantante juvenil Fabian Forte, idolo adolescente de los cincuenta y los sesenta de los muchos que surgen a como sucedáneos de Elvis Presley. Apareció en varias películas cantando, pero ya en la época de ésta, de cantar nada: sólo poner la cara bonita y rodearse de chicas. Si ven la película, observen que aparece inmediatamente después de James Stewart en los títulos de crédito, cuando su papel en la película es bastante menor que el de otros actores. Otro aspecto que pretende actualizar este tipo de comedias, y alejarse de la blandenguería Disney, es la presencia de chicas en traje de baño y gags de cierta malicia, por supuesto simples sugerencias, como la de la vecina que posa desnuda para que su marido la retrate, el deseo de todo el mundo (el taxista francés en particular) de conocer en persona a B.B., o el orgullo de James Stewart por su hijo, no por ser un genio matemático, sino por haber puesto el ojo en la mencionada B.B. (por cierto, la permisividad con la hija mayor, roza, para la época, el completo desinterés; desde luego la lectura actual, con los parámetros actuales, sería bastante crítica con los roles masculino/femenino que se muestran). Alfonso Jesús Población Sáez

Martes, 05 de Enero de 2021 | Imprimir | PDF |  Correo electrónico

358. Alicia en el país de las matemáticas

ABC, 21 de Diciembre de 2020 CIENCIA - El ABCdario de las matemáticas Víctor M. Manero

Lunes, 21 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

359. La geometría que sostenía al telescopio de Arecibo hasta que se derrumbó

ABC, 14 de Diciembre de 2020 CIENCIA - El ABCdario de las matemáticas Pedro Alegría

Lunes, 14 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

360. El enigma de los números primos: Del hueso de Ishango al problema del Milenio

ABC, 7 de Diciembre de 2020 CIENCIA - El ABCdario de las matemáticas Iván Blanco Chacón

Lunes, 07 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más