361. Mariano Mataix: el desconocido autor de «Droga matemática» que mostró la diversión tras los números

ABC, 30 de Noviembre de 2020 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 30 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

362. Demostraciones con encanto. Un viaje por las matemáticas elegantes

Categoría: Divulgación matemática Autores: Claudi Alsina y Roger B. Nelsen Editorial: RSME y Ediciones SM. Colección Biblioteca estímulos matemáticos Año de publicación:  2020 Nº de hojas: 292 ISBN: 978-84-1318-779-2

Miércoles, 23 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

363. Dios se fue de viaje (Mapa de las lenguas)

Autora: Beatriz Rivas Texto: Es él quien, desobedeciendo las reglas, le da acceso a los manuscritos de Voltaire y, de paso, a los de Gabrielle-Émilie le Tonnelier de Breteuil, marquise du Châtelet, a quien Gerta no conocía. Una tarde, cuando el área de estudio se ha vaciado, Serge Saumon se sienta a su lado, llevando un ejemplar de los Elementos de la filosofia de Neuton (sí, con u) traducido por Mme. la Mse. Du Châtelet. Era talentosa: desde pequeña hablaba latín, griego y alemán. El italiano y el inglés los aprendió más tarde. Y si no aprendió español fue porque alguien le dijo que la única obra reconocida, la de un tal Cervantes, era demasiado fantasiosa y no valía la pena. ¿Te imaginas? Fue alumna del matemático y físico Maupertuis y de Clairaut. Amiga del poeta y filósofo Jean-Baptiste Rousseau. Un texto suyo fue el primero escrito por una mujer que publicó la Academia de las Ciencias; estamos hablando del ano 1738. Esa publicación la proyectó como la gran científica que era. Serge está exaltado platicando (¿monologando, más bien?), y contagia su entusiasmo a la delgada joven de ojos que quieren saberlo todo. Gerta sigue interesada en Voltaire, pero ahora es Émilie quien acapara su atención. Desde que ella recuerda, se ha sentido atraída por las mujeres que van más allá de cualquier expectativa, que se salen del canon. Mujeres inteligentes, luchadoras, independientes, que ansían el conocimiento y contribuyen a cambiar al mundo. Inasibles. Cuando estudiantes e investigadores se han ido, Serge y la alemana revisan los manuscritos con mucho cuidado, tratando de descifrar la letra y las ecuaciones matemáticas. Él le explica, por ejemplo, los dibujos del glóbulo ocular con los que madame Du Châtelet ha ilustrado su Ensayo sobre la óptica, así como los espejos planos y convexos. Le muestra las más de treinta páginas sobre la planos y convexos. Le muestra las más de treinta páginas sobre la formación de los colores. Trata de que comprenda las fórmulas, tachonadas varias veces, con problemas de geometría y aritmética. Ejemplos de cuatro reglas de números enteros, de la formación de los poderes y de la extracción de las raíces de números enteros... Mein Gott, dice Gerta riendo, creo que entendería mejor si estuviera escrito en cirílico. La letra es pequeña, muy bien trazada, con tinta negra que se distingue fácil en las hojas amarillentas. Aunque no hay rayas que dirijan el trazo, las líneas son rectas y los espacios entre ellas, como medidos con regla. Fuente: Alfaguara, 2015.

Miércoles, 16 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico

364. 111. (Diciembre 2020) La Tabla Periódica Musical (1/2)

1. Introducción Recientemente se ha publicado la Tabla Periódica Musical en la prestigiosa revista internacional Journal of Mathematics and Music [1] y ha recibido una calurosa acogida por parte de varios medios de comunicación. En el presente trabajo se desarrollan las principales ideas contenidas en dicha publicación y, con el objetivo de darle una mayor difusión, se ha hecho de manera que solo sean necesarios por parte del lector unos conocimientos musicales básicos. Para ello se ha simplificado la parte matemática y se han dado más detalles de la parte musical, realizando todas las explicaciones en lenguaje corriente y por medio de ejemplos, pero sin perder por ello rigurosidad. La denominada “Teoría de Conjuntos” o, modernamente, la “Teoría Post-Tonal”, se ha consolidado durante la segunda mitad del s. XX y ha demostrado ser una potente herramienta para el análisis y composición de la música atonal, siendo también aplicable a la música tonal. En esta teoría, los conjuntos de notas relacionados entre sí por “transposición” o “inversión” se agrupan en una “clase de conjunto”, cada una de las cuales tiene asignado un “nombre de Forte” y una “forma prima” [2, 3]. Así mismo, cada una de ellas contiene un cierto número de las distintas clases de intervalos, y estos números forman el correspondiente “Vector de Clases de Intervalos”, el cual caracteriza en gran medida la sonoridad de una clase, aunque no completamente. Los listados de las diferentes clases y sus vectores de clases de intervalos son parte esencial de esta teoría y pueden encontrarse en muchos textos, así como en [1]. Aparte de las referencias mencionadas [2, 3], cabe destacar en esta materia el artículo introductorio [4] y el libro de texto [5]. A diferencia de las referencias anteriores, para analizar los conjuntos de notas usaremos aquí la denominada “forma interválica”, y las clases no “inversionalmente simétricas” las desdoblaremos en dos “tipos de conjuntos” relacionados entre sí por inversión, lo que permite distinguir, por ejemplo, entre los acordes mayor y menor, los cuales forman una misma clase. Además, se han desarrollado unas versiones avanzadas del “Vector de Clases de Intervalos”, que son el “Vector de Tipos de Tricordos” y el “Vector de Clases de Tricordos”. Utilizando estos tres vectores se ha elaborado la mencionada Tabla Periódica, que muestra ordenadamente todas las clases de conjuntos y permite ver sus principales características y las relaciones entre ellas de un vistazo. Este trabajo consta de dos partes, en la primera de las cuales se ha incluido la explicación de los conceptos fundamentales propios de esta teoría (muchos de los cuales ya se han utilizado en esta introducción), de manera que el trabajo global sea autocontenido. 2. Conjuntos de Notas Utilizaremos el habitual sistema temperado de afinación de 12 notas, que representaremos mediante los números 0 al 11, donde el 0 corresponde al Do y el 11 al Si. Podemos imaginarnos estas notas en la carátula de un reloj donde el Do está en la posición de las 12, el Do# en la 1 y así sucesivamente hasta el Si, que está en las 11. Dado que a veces escribiremos varios números seguidos, para evitar confusiones representaremos los números 10 y 11 por las letras A y B, respectivamente. Los conjuntos de notas los escribiremos entre corchetes. Así, por ejemplo, las notas del acorde de Do mayor (Do, Mi, Sol) formarán el conjunto [047], las del acorde de La menor (La, Do, Mi) el conjunto [904] y las de la escala de Do mayor (Do, Re, Mi, Fa, Sol, La, Si) el conjunto [024579B]. Nótese que las notas de un conjunto pueden referirse a sonidos que se tocan simultánea o sucesivamente, y además en cualquier orden, por lo que también pueden, en principio, escribirse en cualquier orden. Sin embargo, lo normal será escribir las notas de un conjunto ordenadas en sentido ascendente dentro de una octava (teniendo en cuenta que después de la B viene de nuevo el 0). Por ejemplo, el conjunto [95A24], formado por las notas La, Fa, Sib, Re, Mi, lo escribiremos normalmente como [59A24], [2459A] o análogamente empezando por cualquier otra nota de ese conjunto. Diremos que dos conjuntos de notas son del mismo “tipo” si están relacionados por “transposición”, es decir, si un conjunto se obtiene a partir del otro transportando todas sus notas un mismo número de semitonos. Esto significa que, por ejemplo, los 12 acordes mayores forman un solo tipo de conjunto, al igual que ocurre con los 12 acordes menores o con las 12 escalas mayores. En el caso del conjunto [59A24], si elevamos todas sus notas 3 semitonos resulta [80157], siendo ambos conjuntos del mismo tipo. Para representar de una forma sencilla todos los conjuntos de un mismo tipo, tomamos uno cualquiera de ellos, ordenamos sus notas en sentido ascendente dentro de una octava y escribimos la secuencia de intervalos, en semitonos, entre cada dos notas consecutivas, incluyendo el intervalo entre la última nota y la primera. Al resultado obtenido, o cualquiera de sus “permutaciones circulares”, le llamaremos “forma interválica” y la escribiremos entre llaves. Por ejemplo, todos los acordes mayores, como es el caso de Do mayor, tienen la forma interválica , ya que los intervalos entre dos notas consecutivas (Do, Mi, Sol) son 4, 3 y 5 semitonos (donde el 5 corresponde al intervalo entre Sol y Do). Sus permutaciones circulares son y , que también corresponden al acorde mayor, pero empezando por diferentes notas. Análogamente, todos los acordes menores tienen la forma interválica y todas las escalas mayores , o cualquiera de sus permutaciones circulares. Para el conjunto [59A24] (u [80157]), su forma interválica es . Y, si hubiéramos escrito ese conjunto como [2459A], habríamos obtenido , que es una permutación circular de la forma interválica anterior y, por tanto, equivalente a ella. Lógicamente, la suma de todos los elementos de una forma interválica es siempre igual a 12, que es el número de semitonos que hay en una octava. Cuando comparemos formas interválicas entre sí (o “vectores”, que veremos más adelante), la “mayor” y la “menor” de ellas se determinarán a partir del número formado por sus elementos (es decir, según el “orden lexicográfico”). Así, diremos que la forma interválica es menor que (ya que el número 21414 es menor que 41421). A la menor de todas las posibles permutaciones circulares de una forma interválica le llamaremos “forma interválica normal”. En este último ejemplo, será . 3. Conjuntos Inverso y Complementario Se entiende por “inversión” de un conjunto de notas el resultado de invertir el sentido de sus intervalos. Por ejemplo, dado el conjunto [59A24], su inversión es [51086], ya que, en el primer conjunto, se pasa de 5 a 9 subiendo 4 semitonos, mientras que en el segundo conjunto se pasa de 5 a 1 bajando 4 semitonos; y análogamente para el resto de las notas. Nótese que las notas de este último conjunto están ordenadas en sentido descendente dentro de una octava. Si las escribimos en sentido ascendente, por ejemplo, [56801], podemos obtener su forma interválica, que es , la cual representa a todos los conjuntos de este tipo. Esta es, además, su forma interválica normal. Como podemos ver, las formas interválicas de un conjunto y su inversión son las mismas pero escribiendo los números en sentido inverso. En el caso del acorde mayor, cuya forma interválica es , su inversión es , que es equivalente a (por permutación circular), es decir, el acorde menor. Diremos que dos conjuntos de notas son de la misma “clase” si están relacionados por transposición, inversión o una combinación de ambas. Es decir, si sus formas interválicas son las mismas o inversas entre sí (o permutaciones cíclicas equivalentes a ellas). Por tanto, los 12 acordes mayores más los 12 acordes menores forman una sola clase de conjunto. Dadas las formas interválicas normales de un conjunto y su inversión, a la menor de ellas le llamaremos “forma interválica prima” y será la que se utilice para representar a todos los conjuntos de la misma clase. Así, la clase formada por todos los acordes mayores y menores tendrá como forma interválica prima . Y, para el conjunto de notas [59A24], la forma interválica prima será la menor de y , es decir, esta última. En general, una clase de conjunto está formada por dos tipos de conjuntos relacionados entre sí por inversión. Sin embargo, algunas formas interválicas son iguales a sus inversiones, como ocurre por ejemplo con la escala mayor, , por lo que esta clase está formada por un solo tipo y se dice entonces que es “inversionalmente simétrica”. Por su parte, un tipo de conjunto está formado, en general, por 12 conjuntos de notas, que son sus 12 posibles transposiciones, pero esto no siempre es así. Por ejemplo, un acorde como Do aumentado (cuyas notas son Do, Mi, Sol#) tiene la forma interválica ; y, debido a su estructura “periódica” (el número “4” está escrito 3 veces), solo existen cuatro acordes aumentados diferentes (es decir, 12/3). Este tipo de conjuntos se dice que son “transposicionalmente simétricos” y al número de períodos que hay en su forma interválica se le llama “grado de simetría transposicional”, el cual representaremos por la letra “s”. Así, en los acordes aumentados, s = 3. Si un tipo de conjunto no presenta simetría transposicional, diremos que s = 1 (toda la forma interválica es un único período), por lo que el número de conjuntos de notas correspondientes a un tipo de conjunto dado es siempre 12/s. Otro ejemplo es la escala disminuida, formada por 8 notas en sucesión de tono-semitono o semitono-tono. Su forma interválica es , que consta de 4 períodos (“12” o “21” escrito 4 veces), es decir, s = 4, por lo que solo hay 12/4 = 3 conjuntos de notas de ese tipo. Lógicamente, el valor de s para un conjunto y su inverso es el mismo. Por tanto, una clase que sea inversionalmente simétrica tendrá 12/s conjuntos de notas y una que no lo sea tendrá 24/s. 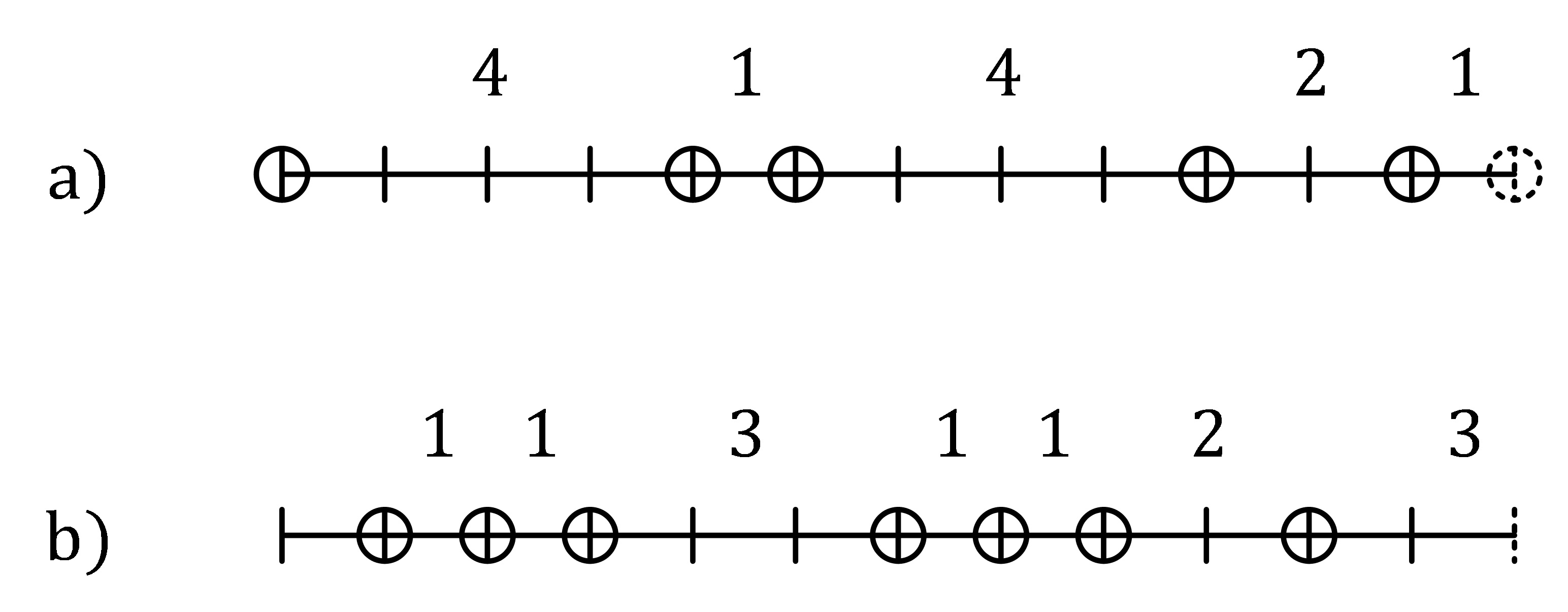Dado un conjunto de notas, su “complementario” es el conjunto formado por las demás notas. Por ejemplo, el complementario del conjunto [59A24] es [013678B]. Si conocemos la forma interválica de un conjunto dado, es fácil obtener mentalmente la del complementario. Para ello, nos imaginamos la forma interválica inicial, en este caso , como en la Figura 1.a), es decir, sobre una línea con 13 marcas, donde la última es equivalente a la primera y los círculos representan las notas de ese conjunto. Puesto que su complementario tiene los círculos en las demás marcas, como se observa en la Figura 1.b), su forma interválica será , o cualquiera de sus permutaciones circulares. Como otro ejemplo, la escala mayor tiene la forma interválica , por lo que la de su complementario será , que corresponde a la escala pentatónica (mayor o menor). Es fácil comprobar que un conjunto y su complementario tienen el mismo tipo de simetría, tanto inversional como transposicional. Por ejemplo, la forma interválica del acorde aumentado es , por lo que la de su complementario es , siendo ambas inversionalmente simétricas y transposicionalmente simétricas de grado s = 3. Y la forma interválica de la escala disminuida es , por lo que la de su complementario es , el acorde de séptima disminuida, siendo ambas inversionalmente simétricas y transposicionalmente simétricas de grado s = 4. Figura 1. Formas interválicas de un conjunto de notas y su complementario. 4. Vector de Clases de Intervalos: ICV El número de notas de un conjunto es su “cardinalidad”, que la representaremos por la letra “c” y podrá tomar los valores desde 0 hasta 12. Para c = 2, hay 6 clases de conjuntos, llamadas díadas, que son simplemente los intervalos de 1 a 6 semitonos. Sus formas interválicas primas, ordenadas de menor a mayor, son: , , , , y . Todas ellas son inversionalmente simétricas y tienen s = 1, salvo la clase , el tritono, que tiene s = 2. Los intervalos de más de 6 semitonos se reducen por inversión a una de las clases anteriores. Para los conjuntos de más de 2 notas, podemos determinar cuántos intervalos de cada clase se pueden formar con sus notas. El resultado son 6 números que forman el “Vector de Clases de Intervalos” o ICV (por sus siglas en inglés) y los escribiremos entre paréntesis. Por ejemplo, en un acorde aumentado sus notas forman 3 intervalos de cuatro semitonos, por lo que su ICV es (000300). Y, en un acorde mayor (como Do mayor), sus notas forman un intervalo de tres semitonos (Mi – Sol), uno de cuatro (Do – Mi) y uno de cinco (Sol – Do), por lo que su ICV es (001110). Un acorde menor tiene ese mismo ICV, ya que un conjunto y su inversión siempre tienen el mismo ICV. Así mismo, se puede comprobar que el ICV de la escala mayor es (254361), ya que tiene 2 intervalos de semitono, 5 de tono, 4 de tercera menor, 3 de tercera mayor, 6 de cuarta justa y 1 de tritono. De este modo, cada clase de conjunto tiene un ICV, el cual determina en buena parte su sonoridad, pero no completamente, ya que hay algunas clases que, siendo diferentes, tienen el mismo ICV. En ese caso se dice que esas clases guardan una “relación Z” o que están “Z-relacionadas” y se ha comprobado que el número de clases con el mismo ICV nunca es superior a dos. Una propiedad importante es que, si tomamos todas las clases de una cierta cardinalidad y las ordenamos según sus ICV, bien por valores crecientes o decrecientes, se puede demostrar que sus complementarios quedan ordenados del mismo modo [1]. De hecho, a cada clase se le asigna un “nombre de Forte” [2], que consta de dos números separados por un guion, el primero de los cuales es su cardinalidad y el segundo un ordinal. Y los ordinales se asignan según su ICV en sentido decreciente. Por ejemplo, la clase formada por los acordes mayores y menores es la 3-11, cuyo ICV es (001110); y la clase siguiente, 3-12, son los acordes aumentados, cuyo ICV es (000300), que es menor que el anterior (el número 000300 es menor que 001110). De esta manera, cada clase y su complementaria tienen el mismo ordinal. Por ejemplo, la escala mayor es la clase 7-35, y su clase complementaria, que es la escala pentatónica, es la 5-35. En el caso de dos clases Z-relacionadas, a una de ellas se le asigna el último ordinal del correspondiente grupo y en ambas se incluye una “Z” delante del ordinal. Por ejemplo, 4-Z15 y 4-Z29. La Tabla 1 es la Tabla Periódica aquí desarrollada, donde cada “periodo” corresponde a un valor de c y se representa mediante ese valor seguido de un guion, como en la parte inicial del nombre de Forte (columna izquierda de la tabla). Para hacer la tabla más compacta, los períodos 0, 1 y 2 se han colocado en la misma fila, al igual que se ha hecho con los períodos 12, 11 y 10. Dentro de cada período se han colocado las correspondientes clases ordenadas por ICV decreciente (el ICV no aparece en la tabla) y se les ha asignado el mismo ordinal que en su nombre de Forte (número grande en cada celda de la tabla). Así, cada celda tiene asignado un ICV diferente y, en el caso de dos clases Z-relacionadas, ambas están en la misma celda. Este es el caso de las clases 4-Z15 y 4-Z29, cuyo ICV común es (111111). A pesar de que 29 es el último ordinal del período 4, la clase que está en la última celda del mismo es la 4-28, el acorde de séptima disminuida, ya que su ICV, (004002), es el menor de este período. Por otra parte, cada clase y su complementaria, al tener el mismo ordinal, están en la misma columna. Por ejemplo, 5-35 y 7-35, o 3-11 y 9-11. Las clases que son inversionalmente simétricas tienen el ordinal subrayado y las que son transposicionalmente simétricas llevan en el ordinal un superíndice, que es su grado s. Por ejemplo, 3-123 o 6-302. Debajo de cada ordinal está la forma interválica prima, escrita sin llaves por simplicidad. Además, cuando en ella aparecen varios “1” seguidos se escriben “en forma de potencia”. Por ejemplo, 1119 se escribe 13 9 (clase 4-1). Como puede observarse, cada período comienza con la clase que tiene sus notas lo más juntas posible (es decir, en secuencia cromática) y termina con la clase que tiene sus notas separadas lo más uniformemente posible. Así, el período 4 empieza con la clase o (las 4 notas en secuencia cromática) y termina con la clase , que es el acorde de séptima disminuida (en el que dos notas consecutivas siempre están separadas la misma distancia, 3 semitonos). Tabla 1. Tabla Periódica de las Clases de Conjuntos. 5. Conclusiones Los conjuntos de notas relacionados entre sí por transposición forman un tipo de conjunto, que representamos por su forma interválica o su forma interválica normal. Si a estos conjuntos les añadimos sus inversos obtenemos una clase de conjunto, que representamos por su forma interválica prima. La forma interválica que hemos introducido aquí ha resultado ser tremendamente útil y versátil, ya que permite obtener de manera sencilla las formas interválicas de los conjuntos inverso y complementario; y, obviamente, también la del inverso del complementario (que es igual a la del complementario del inverso). Y, además, permite determinar fácilmente sus simetrías, tanto inversional como transposicional. Como hemos visto, un conjunto y su complementario (y, obviamente, su inverso) tienen siempre el mismo tipo de simetría, tanto inversional como transposicional. En la Tabla Periódica que se ha desarrollado aparecen todas las clases de conjuntos ordenadas por ICV decreciente y se incluye la siguiente información: nombres de Forte, tipos de simetría inversional y transposicional, relaciones Z y clases complementarias, así como las formas interválicas primas. No obstante, esta tabla contiene aún más información relevante, que se explicará en la segunda parte de este trabajo. 6. Referencias [1] Nuño, Luis. (2020). A Detailed List and a Periodic Table of Set Classes. Journal of Mathematics and Music, DOI: 10.1080/17459737.2020.1775902. [2] Forte, A. (1973). The Structure of Atonal Music. New Haven: Yale University Press. [3] Rahn, J. (1980). Basic Atonal Theory. New York: Schirmer Books. [4] Straus, J. N. (1991). A Primer for Atonal Set Theory. College Music Symposium, 31, 1-26. [5] Straus, J. N. (2016). Introduction to Post-Tonal Theory, 4th Edition. New York: W. W. Norton.

Martes, 15 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico

365. 156. ¿Está acotada la ñoñez de las películas infanto-juveniles?

Aunque las Navidades de este año van a ser muy diferentes de las habituales, habrá cosas que serán como siempre (quizá hasta lo agradezcamos en esta ocasión). Entre ellas, las infumables películas norteamericanas ambientadas en estas fechas. Bien, pues para ir haciendo boca, hoy, una de esas pelis, pero alemana. ¿Será tan ñoña? No hagamos ningún spoiler y veamos, que algo de interés siempre podemos encontrarnos. Ficha Técnica: Título: Socorro, he encogido a la profe. Título Original: Hilfe, ich hab meine Lehrerin geschrumpft. Nacionalidad: Alemania/Austria, 2015. Dirección: Sven Unterwaldt. Guion: Gerrit Hermans, basado en la novela de Sabine Ludwig. Fotografía: Stephan Schuh, en Color. Montaje: Stefan Essl. Música: Leland Cox y Karim Sebastian Elias. Producción: Corinna Mehner y Hans Eddy Schreiber. Duración: 90 min. Ficha artística: Intérpretes: Anja Kling (Directora Schmitt-Gössenwein), Oskar Keymer (Felix Vorndran), Axel Stein (Peter Vorndran), Justus von Dohnányi (Schulrat Henning), Lina Hüesker (Ella Borsig), Georg Sulzer (Mario Henning), Maximilian Ehrenreich (Chris), Eloi Christ (Robert), Johannes Zeiler (Conserje Michalsky), Michael Ostrowski (Señor Coldegol). Argumento Tenemos a un niño, Félix, de 11 años, que sueña con ser piloto. Vive con su padre, que es un auténtico desastre, porque su madre se ha ido a los EE. UU. por un trabajo (¿alguien sabe porque la mayor parte de los padres, y en general personajes masculinos, de series de televisión, películas familiares, dibujos animados, etc., se presentan desde hace algún tiempo como imbéciles profundos? Y no vale decir que porque son así, porque aunque algunos lo seamos, no creo que lo sean todos). El caso es que este chico no es demasiado buen estudiante y lo han expulsado de un colegio. Bien, pues el nuevo centro, el único que queda en la localidad donde viven, en el que debe pasar tres meses para ver si lo aceptan, es un tanto, digamos, siniestro. Y sus responsables no se quedan atrás, desde el conserje, al inspector, y no digamos su directora, Frau Dr. Schmitt-Gössenwein (en la imagen, el colegio y la susodicha, un trasunto de señorita Rottenmeier; se van haciendo a la idea, ¿verdad? Pues sospecho que no, aunque el cartel de la película es ya bastante diáfano también, incluyendo ese 3 x 3 = 6). Al entrar en la clase que le han asignado, Félix observa cómo los alumnos son más o menos “normales”, aunque, para no variar en este tipo de películas, el grupito de bravucones enseguida se mete con él. Afortunadamente entra en escena la directora que, al verlo de pie, lo manda directamente al encerado: Directora: Félix, ven a la pizarra. Recuerda que es tu periodo de prueba. (A la clase) ¡¡Los cuadernos!! (Todos los sacan de debajo del pupitre). ¡Apunta! Longitud del lado A, 40 centímetros. (Es un encerado con cuadrícula; Félix ha apuntado el dato donde le ha parecido). ¿Te importa utilizar la cuadrícula? No está ahí de adorno. Félix: Ya la estoy usando. Directora: ¡¡Empieza otra vez!! (El chico, intimidado, borra lo escrito con la mano). ¡¡Tenemos un borrador!! (Resignado, lo coge y lo vuelve a borrar). Ahora, dibuja una pirámide cuadrangular con triángulos equiláteros. Félix: ¿Esos son los que tiene todos sus lados iguales? Directora: ¡¡Félix!! Félix: ¿No son esos? Directora: ¡¡Dibújalos con la escuadra!! (El resto de la clase se ha reído ya varias veces). Después dibuja otra con la base en forma de octaedro y dime su altura ¡¡Rápido!! Félix: ¿Y lo primero? Directora: Dime, ¿qué te enseñaron en el colegio del que vienes? ¿Tienes la menor idea de cómo hacer lo que te he dicho? Félix: Las mates no son lo mío. Directora: ¿Conque no son lo tuyo, eh? ¿Qué quieres decir? Félix: Que las mates no se me dan bien. Directora: Eso ya lo hemos visto. Ella no estará sentada a tu lado mucho tiempo. ¿Podrías ayudarnos? (Ella es una alumna destacada, obviamente, aunque no nos muestran cómo lo resuelve). Comentario matemático Sin entrar en lo estereotípico de todo en general, pasemos a lo nuestro. Dibujar una pirámide cuadrangular con caras triángulos equiláteros es posible, aunque en la versión original la profesora pedía triángulos isósceles. Pero lo que desde luego es imposible es construir una con base un octaedro. Yo no sé en España que pasa con los doblajes y los aspectos científicos, que siempre “se lucen”. En la versión original en alemán (y en la inglesa), la profesora dice Directora: Después de eso con dos haces un octaedro, y me dices su altura H. Es sobradamente conocido, al menos cuando se estudiaba geometría elemental (en los sucesivos planes de estudio españoles ya saben que, de tener excesiva geometría allá por los inicios del siglo XX, se ha pasado a no tener prácticamente nada, simplemente unas cosillas de geometría analítica), que uniendo dos pirámides cuadrangulares por su base se obtiene un octaedro regular (ver imagen). Por este motivo, al octaedro, uno de los sólidos platónicos, también se le conoce como bipirámide cuadrada. A partir de esta escena, aunque sea tan mediocre, podemos proponer descubrir o repasar algunas propiedades de estos sólidos. Por ejemplo, que la pirámide cuadrangular, como todas las pirámides, es autodual, ya que tiene el mismo número de vértices que de caras (5). Además en el caso particular de caras triángulos equiláteros, entonces la pirámide es uno de los conocidos como sólidos de Johnson. Y en este caso, todas las aristas tienen la misma longitud​. Respecto a la pregunta de la profesora sobre el valor de la altura del octaedro, la podemos completar con el resto de magnitudes, esto es, el volumen y su superficie total. En función de la arista a, el volumen es V = a3 Para calcular la superficie de todas sus caras, por simetría, basta calcular el área de una de ellas, /4 a2, y multiplicarla por ocho, con lo que S = 2a2. Finalmente la altura, entendiendo como tal la diagonal de mayor longitud es H = a. Por tanto la altura pedida por la profesora de la película es 40. Por supuesto podemos también ejercitarnos en las simetrías, verificar que su orden de simetría es 72, obtener su poliedro dual (el cubo), deducir cuáles son las secciones que podemos encontrar en él, que otros tipos de octaedros podemos construir, dónde aparece en la naturaleza o nuestra vida cotidiana, aplicaciones que puede tener, etc. En suma, construir una práctica curiosa en la que no sólo haya cuestiones descriptivas sino también aspectos constructivos, manipulativos, etc. Continuemos con la película. Como no deseo “estropearles” el visionado, digamos a grandes rasgos que, como consecuencia de una serie de sucesos, como suele ser costumbre en estas películas (¡¡que poca imaginación!!), el grupo conocido de chavales deben tomar las riendas del argumento para poder salvar el colegio de las inmisericordes garras de la especulación de uno de los personajes (pretende cerrar el colegio por falta de alumnado para poder reabrirlo como un colegio elitista de familias adineradas, y que el negocio fluya por todas partes; pero claro con las pocas luces del personaje, la cosa, no va a ser demasiado complicada. Y si encima tiene en su contra las fuerzas del más allá, pues para que les voy a decir más, ¿verdad? Vamos que, como para no perder más el tiempo, salvo por otra referencia matemática que puede utilizarse como motivación para experimentar en el aula). El colegio esconde en sus sus sótanos un circuito de salas nombradas como las asignaturas de los planes de estudio (geografia, historia, matemáticas, etc.). Para pasar de una sala a otra la pandilla protagonista debe resolver los enigmas que se les presentan en cada sala (que están relacionados con el nombre de dicha sala). La resolución de los enigmas les abre la puerta que da acceso a la siguiente sala. En la de matemáticas, encontramos decoración relacionada con la asignatura, figuras geométricas de colores colgando del techo a cierta altura, y un suelo que se hunde a los pies del que lo pisa (en realidad es un suelo elástico). Enfrente una puerta cerrada, con el hueco de un cubo a un lado. Vean la imagen, y ya me dirán si no adivinan cuál es la prueba a resolver. Félix lo deduce a la primera (por una felina razón que no les voy a desvelar, tienen que tratar de pasar las pruebas lo más rápido posible). En efecto, las figuras que cuelgan del techo no son superficies geométricas sino diversos policubos. Recordemos que un poliminó o poliominó es un objeto geométrico que se obtiene al unir varios cuadrados del mismo tamaño de manera que cada par de cuadrados vecinos compartan un lado. El nombre, originado en una conferencia de Solomon W. Golomb en 1953, generaliza el conocido dominó, que sería el poliominó de 2 piezas (dos cuadrados iguales unidos por un lado). Los siete tetrominós de la imagen (sólo cinco si consideramos iguales los obtenidos por reflexión) son las piezas del popular tetris. Si en lugar de tomar cuadrados planos, utilizamos cubos tridimensionales, obtenemos policubos. El mostrado en la película es el conjunto de seis policubos de orden cuatro y uno de orden tres, es decir, las siete piezas con las que podemos construir el Cubo Soma 3 x 3 x 3, ya que una sencilla cuenta, 3 + (6 x 4) nos garantiza los 27 cúbitos de que se compone el cubo 3 x 3 x 3. Para construir el Cubo Soma con estas piezas hay 240 soluciones distintas excluyendo rotaciones (giros) y reflexiones (simetrías). Martin Gardner y John Horton Conway analizaron a conciencia las posibilidades de este rompecabezas en diferentes libros y artículos. El Cubo Soma es un rompecabezas de disección inventado por Piet Hein en 1934 durante una conferencia sobre mecánica cuántica impartida por Werner Heisenberg. Suele utilizarse como prueba para medir el rendimiento y el esfuerzo de las personas en experimentos de psicología. En estos experimentos, se pide resolver un Cubo Soma tantas veces como sea posible en un plazo determinado de tiempo. Existen muchos juegos de disección similares al Cubo Soma. Por ejemplo, el rompecabezas pentominó en 3D, en el que hay que construir prismas de tamaños 2 x 3 x 10, 2 x 5 x 6 y 3 x 4 x 5 unidades; El Cubo diabólico célebre en la Inglaterra victoriana construido a partir de seis piezas; El cubo de Mikusinski; El cubo de Bedlam, rompecabezas de caras de cubo de 4 × 4 × 4 que consta de doce pentacubos y un tetracubo; el cubo de Pandora, rompecabezas de seis policubos que pueden ensamblarse entre sí para formar un solo cubo de 3 × 3 × 3); entre otros. Una completa descripción de estas disecciones pueden encontrala aquí. Asimismo hay muchas variantes con los poliominós en el plano (animense a intentar deducir una fórmula para conocer el número total de poliominós de n piezas; hasta el momento sólo se conocen hasta el valor de n = 12, que son 63600 poliominós diferentes). Casi todos los libros de Martin Gardner incluyen algún capítulo de poliominós o policubos. Yo les recomiendo para los primeros el volumen de Festival mágico-matemático (Alianza Editorial), y para los policubos, Rosquillas anudadas y otras amenidades matemáticas (Editorial Labor). En otra escena de la película, Félix es capaz de deducir él solito que si el lado de una habitación en un plano mide 9 centímetros, a una escala 1:50 se convierten en 4 centímetros y medio. Sin comentarios. Tampoco faltan típicas frases de la directora como “Este examen es tan fácil que hasta un bobo como tú debería poder hacerlo solo”, o “Si piensas que el estudio y el juego tienen algo que ver, estás totalmente equivocado”. Si desean “disfrutarla” en su integridad, pueden hacerlo en este enlace. Que ustedes pasen unas muy felices fiestas. A ver si el nuevo año es algo mejor que el que dejamos. Alfonso Jesús Población Sáez

Jueves, 10 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico

366. Casamayor de la Coma, María Andresa (1720-1780)

María Andresa Casamayor de la Coma (Zaragoza 30 de noviembre de 1720, Zaragoza 24 de octubre de 1780) María Juana Rosa Andresa Casamayor de la Coma nació un día de San Andres, 30 de noviembre en el seno de una familia de comerciantes de telas de ascendencia francesa, siendo la séptima de nueve hermanos/as. La casa familiar estaba situada en la Calle del Pilar, junto a la iglesia del mismo nombre. María Andresa recibió su educación en el hogar familiar muy probablemente de un maestro escolapio, orden religiosa que acababa de establecerse en Zaragoza y fundado un centro de enseñanza para varones. En 1738, a los 17 años,  publicó el que a día de hoy es el primer libro de matemáticas escrito por una mujer en español, que ha llegado a nuestros días. El único ejemplar existente de su Tyrocinio Arithmetico se encuentra en la Biblioteca Nacional. El libro está dedicado a las Escuelas Pías a las que agradece en la dedicatoria la formación recibida. El Tyronicio (palabra cuyo significado según el Diccionario de la RAE de 1739 era “el primer ensayo del que aprende cualquier arte”) es un texto de matemática elemental que enseña las cuatro reglas llanas de suma, resta, multiplicación, división con una clara orientación hacia el comercio. María Andresa Casamayor presenta los principales cambios de unidades de monedas, pesas y medidas aragonesas para a continuación practicar las cuatro operaciones mencionadas en un contexto aplicado al comercio. Como ejemplo, multiplica el peso de una cierta mercancía de 648 arrobas 22 libras y 4 onzas por su precio por unidad de 253 sueldos y 4 dineros. Todavía no existe el sistema métrico decimal y las dependencias entre las distintas unidades de moneda, peso y medidas hacen que las operaciones necesiten de un buen número de “trucos aritméticos” que faciliten el cálculo. Además, María Andresa explica que “su fin, en esta Obrilla solo es, faciIitar esta instruccion a muchos, que no pueden lograrla de otro modo”. Muestra así una manera de pensar que en decadas posteriores será implantada por los Ilustrados de hacer llegar la educación a todas las clases sociales. El Parasi  solo(1738) es el título del segundo texto que escribió, un manuscrito hoy perdido. El título es una locución latina de significado (aproximado) Prepara tu suelo. La noticia de la existencia de este manuscrito aparece en la Biblioteca de autores aragoneses de Félix Latassa y, según este autor, el texto contiene «… uso de las tablas de raices y reglas generales para responder a algunas demandas, que con dichas tablas se resuelven sin la Álgebra». Es decir, María Andresa proporciona tablas de raíces para realizar cálculos de manera rápida sin necesidad de utilizar el método tradicional (y más lento) algebráico. Por el significado del título, podemos  conjeturar que estarían aplicadas a la agrimensura o al cálculo de superficies o volúmenes. Las “calculadoras” de la época, las tablas de logarítmos, eran utilizadas en el cálculo por comerciantes, marineros, ingenieros… para realizar pesadas multiplicaciones mediante su transformación en sumas, más sencillas de operar. El mismo método servía para calcular raíces. En El Parasi solo, María Andresa propone el calculo rápido y directo de raíces con ayuda de sus tablas (sin necesidad incluso de pasar por las tablas de logaritmos). María Andresa tuvo que firmar sus libros con nombre de varón. Lo hizo mediante un anagrama (mismas letras en distinto orden) de su verdadero nombre. A partir de entonces, trágicos acontecimientos marcarán su futuro con el fallecimiento de su padre en 1738, de la persona con la que mantuvo una cercana relación intelectual, el dominico Pedro Martínez en 1739, así como la ruina de su familia materna más cercana en 1740. Todos los apoyos que había tenido la joven María Andresa desaparecieron en pocos tiempo. A diferencia de lo habitual en la época, ni se casará ni entrará en la iglesia, con lo que trabajará para ganarse la vida. María Andresa Casamayor fue maestra de niñas. Conocemos la localización de la casa que habitó y que la ciudad le proporcionó como, parte al menos, de su retribución. Sorprendentemente, la casa sigue todavía en pie en el barrio zaragozano de la Magdalena.

Lunes, 07 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico

367. 188. (Diciembre 2020) Sopa de mezclas

Un concepto muy importante en Matemáticas es el de invariancia. De hecho, existe toda una teoría matemática de invariantes, mejor dicho, al menos dos: la teoría de invariantes algebraicos y la de invariantes geométricos. Como es un campo demasiado especializado para darle cabida en este rincón, nos conformaremos con la idea elemental que sustenta dicho concepto y que todos entendemos: un objeto o estructura es invariante bajo cierta operación o transformación matemática cuando no cambia después de dicha operación. Por ejemplo, el círculo es un invariante bajo la operación de giro alrededor de su centro, independientemente del ángulo de giro. Se comprende también que el concepto es un poco más general que el de punto fijo (que citamos en el número 175 de octubre de 2019) porque, salvo el centro, todos los puntos del círculo han cambiado de posición pero, visto el círculo en su conjunto, ha quedado inalterado. La teoría de invariantes proporciona también un gran campo de experimentación en la magia. Desde conceptos tan comunes y ampliamente conocidos, como el hecho de que la suma de las caras opuestas de un dado es siempre igual a siete o que la diferencia entre cualquier número natural y la suma de sus cifras es siempre múltiplo de nueve, hasta ideas mucho más sutiles y elaboradas, como las presentes en los principios de Rusduck, de Hummer, de Gilbreath, de Kruskal, ..., todos ellos aplicados a las mezclas de cartas, podemos encontrar multitud de juegos que se basan en propiedades de invariancia, el éxito de los cuales se fundamenta en la habilidad del mago para ocultar la presencia de dichas propiedades. Como ya empieza a ser habitual, el descubrimiento de nuevas ideas por parte del mundo de las matemáticas junto con la aplicación y desarrollo de dichas ideas por parte del mundo de la magia permite convertir teoremas en juegos de magia y, en esta ocasión, ofreceremos una nueva muestra de ello con un ejemplo de invariantes relacionados con mezclas de cartas. Podemos señalar como punto de partida el artículo académico titulado «The Mathematics of the Flip and Horseshoe Shuffles», firmado por Steve Butler, Persi Diaconis y el recientemente fallecido Ronald Graham, y publicado en la revista The American Mathematical Monthly el año 2016. En ese trabajo ya aparece la primera descripción de un juego de magia basado en la bautizada mezcla herradura, y una versión más elaborada se encuentra en el artículo de Steve Butler titulado «A card trick inspired by perfect shuffling», presentado en la décimotercera edición del Gathering for Gardner de 2018 que, como cualquier aficionado debe saber, constituye el encuentro bianual más importante de aficionados a la magia y a la matemática reunidos para homenajear la figura de Martin Gardner. Para realizar el juego que proponen los autores se necesitan ocho cartas, del as al ocho de cualquier palo. Con las cartas en la mano, sigue las instrucciones que daremos a continuación. Ordena las cartas del modo indicado en la imagen: Aunque parezca extraña esta disposición, en realidad están ordenadas si pensamos el ocho como si fuera el cero, no sólo porque se escribe con dos ceritos, sino por su representación en el sistema binario: Decimal Binario 8 1 2 3 4 5 6 7 1000 001 010 011 100 101 110 111 De ahora en adelante nos olvidaremos de la primera cifra del ocho y lo representaremos como 000. Forma un paquete con las cartas así ordenadas y realiza sucesivamente —en el orden que quieras y las veces que te apetezca— las siguientes mezclas: Mezcla herradura: repartir las cartas sobre la mesa, de una en una y formando dos montones, uno a la izquierda y otro a la derecha. Al terminar, girar en bloque las cartas de uno de los montones y colocarlo sobre el otro montón. Mezcla Monge (explicada en el número 43 de este rincón, en octubre de 2007): con las cartas en una mano, ir pasándolas a la otra mano, una por una, intercambiando el orden de cada carta, es decir, la segunda carta se coloca sobre la primera, la tercera bajo las dos primeras, la cuarta sobre las tres primeras, la siguiente debajo, la siguiente encima, hasta haber pasado todas las cartas. Mezcla lechera, también llamada Klondike o Alfa (explicada en el número 122 de este rincón, en diciembre de 2014): arrastrar juntas las cartas superior e inferior del paquete y dejarlas sobre la mesa, repetir la operación con el paquete restante y dejar las dos cartas sobre las anteriores hasta que queden en la mano dos cartas, las cuales se dejan sobre las demás. Como la primera de las mezclas hace que algunas cartas queden giradas, en las siguientes no importa que las cartas estén cara arriba o cara abajo. Lo único importante es que las mezclas se realicen correctamente. Intercaladas entre las mezclas, puedes realizar —las veces que quieras y en el orden que te apetezca— cualquiera de las siguientes acciones relacionadas con los posibles divisores de ocho: Repartir sobre la mesa todas las cartas, una a una, y recoger todo el paquete. Repartir sobre la mesa todas las cartas, de dos en dos, y recoger todo el paquete. Repartir sobre la mesa todas las cartas, de cuatro en cuatro, y recoger todo el paquete. Repartir sobre la mesa todas las cartas, de ocho en ocho, y recoger todo el paquete. En realidad, esto no será necesario: echar las ocho cartas y recogerlas sólo alarga el proceso pero no produce cambios. Hemos incluido esta opción porque el ocho también es divisor de sí mismo. Una vez que las cartas están bien mezcladas (observa que el número de posibles configuraciones de las ocho cartas es igual a 8! = 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1 = 40320), repártelas sobre la mesa formando una estructura de cuatro filas y dos columnas, en este orden (orden al que nos referiremos en lo sucesivo): Si alguna de las cartas ha quedado cara arriba (que es lo más probable), vuélvela cara abajo para que yo no pueda saber la posición de ninguna de ellas. Como comprenderás, es imposible saber qué lugar ocupa cada carta así que necesitaré algo de información. Por ejemplo, vuelve cara arriba la primera carta (sí, la superior izquierda). Su valor me indicará el valor de la sexta carta, mediante esta tabla: PRIMERA SEXTA 1 2 3 4 5 6 7 8 4 7 6 1 8 3 2 5 Necesitaré una pista más para determinar la posición del resto de cartas. Gira la segunda carta: su valor indicará el valor de la carta en la quinta posición a partir de la misma tabla anterior. Pero también puedo saber las cuatro cartas restantes. Para ello, busca en la siguiente tabla la combinación de la primera y segunda cartas para determinar los valores de la tercera y cuarta cartas pero también, a partir de la combinación de la quinta y sexta cartas, adivinaré los valores de la séptima y octava cartas. Como hay varias combinaciones posibles, la tabla es un poco más larga (aunque se podría reducir a la mitad teniendo en cuenta las simetrías): 1ª - 2ª 3ª - 4ª 1 - 3 1 - 5 1 - 6 1 - 8 2 - 3 2 - 5 2 - 6 2 - 8 3 - 1 3 - 2 3 - 4 3 - 7 4 - 3 4 - 5 4 - 6 4 - 8 5 - 1 5 - 2 5 - 4 5 - 7 6 - 1 6 - 2 6 - 4 6 - 7 7 - 3 7 - 5 7 - 6 7 - 8 8 - 1 8 - 2 8 - 4 8 - 7 5 - 7 6 - 2 8 - 7 3 - 2 8 - 1 3 - 4 5 - 1 6 - 4 7 - 5 1 - 8 2 - 5 4 - 8 5 - 2 6 - 7 8 - 2 3 - 7 2 - 6 4 - 3 7 - 6 1 - 3 7 - 8 1 - 5 2 - 8 4 - 5 8 - 4 3 - 1 5 - 4 6 - 1 2 - 3 4 - 6 7 - 3 1 - 6 ¿He acertado todas las cartas? Pues no he sido yo, sino la magia de las matemáticas. Es más, si no he acertado, ha tenido que haber una equivocación en alguna de las mezclas realizadas. EXPLICACIONES: Como apunta Steve Butler en su artículo «A card trick inspired by perfect shuffling», de las 40320 posibles ordenaciones de las ocho cartas, las mezclas y manipulaciones anteriores sólo conducen a 32 posibilidades. Todas ellas tienen un par de propiedades invariantes que permiten realizar el juego con éxito, precisamente las propiedades que se resumen en las dos tablas anteriores. En el paso 5 de la descripción del juego se puede girar cualquier carta de las ocho que están sobre la mesa. Su valor indicará, utilizando la misma tabla de antes, el valor de la carta que ocupa la posición simétrica dada por los siguientes emparejamientos: primera con sexta, segunda con quinta, tercera con octava, cuarta con séptima. Para descubrir la razón, volvamos a representar las parejas de números en el sistema binario. Decimal Binario 1 4 001 100 2 7 010 111 3 6 011 110 5 8 101 000 Resulta que la segunda cifra en ambos números es la misma y las otras dos cifras son distintas. Por tanto, adivinar una de ellas conocida la otra consiste en representar en base dos la carta, cambiar la primera y tercera cifras y pasar al sistema decimal el número obtenido. Un método más sencillo sería: si la carta descubierta es impar, su pareja será tres unidades mayor (si es un siete, se usa la aritmética de congruencias módulo 8: 7 + 3 = 10, que corresponde al 2); si es par, su pareja es tres unidades menor (con la misma salvedad para el 2 pues 2 - 3 = -1, que corresponde al 7). En el paso 6 no es necesario tampoco que se vuelva la carta de la posición número 2. Basta con cualquiera de las dos cartas que quedan cara abajo en el cuadrado formado por las dos cartas que ya estaban giradas. Con el razonamiento anterior se conoce la cuarta carta de dicho cuadrado. Para determinar el resto, se utiliza la misma tabla anterior, donde cada pareja de la misma fila determina la otra pareja de su misma fila en el orden indicado por la tabla. La correspondencia que se establece entre dichas parejas también se debe a una relación entre sus representaciones en base dos, la cual está explicada en el artículo citado de Steve Butler. OBSERVACIONES FINALES: Parece un poco sorprendente el nombre de mezcla herradura aplicado al proceso antes descrito. Los autores apuntan a que se trata de la versión discreta del llamado mapa de herradura, que consiste en "estirar" el cuadrado unidad y "doblarlo" sobre sí mismo. Este tipo de mapas forma una familia de cuyo estudio se ocupa la teoría matemática del caos. Esta nueva mezcla tiene algunas propiedades interesantes, estudiadas por Jeremy Rayner en su artículo «Flipping perfect shuffles», publicado en el primer número de la revista Metagrobologist Magazine (octubre de 2014). Por ejemplo, cuatro mezclas idénticas con las ocho cartas utilizadas en el juego hacen que el paquete recupere el orden inicial. Esta propiedad es más general, con 2n cartas sólo hacen falta n + 1 mezclas herradura para reordenar de nuevo todas las cartas. Los valores son más caóticos para otros valores: por ejemplo, con seis cartas se necesitan 10 mezclas para volver al orden inicial. Seguramente, esto se deba precisamente a la relación entre la representación binaria de los números y su evolución a lo largo de las mezclas. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Martes, 01 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico

368. 68. (Diciembre 2020) Europa geómetra

(Alegoría de Europa. Museo Episcopal de Textiles y Orfebrería. Toledo) Ve a Europa, la más noble, excelsa y clara En saber, policía y fortaleza. Os Lusiadas. Canto X. Luiz Vaz de Camöes. Europa es superior a las otras partes del mundo en las armas las letras y todas las artes liberales. Iconología de Cesare Ripa Con la circunvalación portuguesa de África para llegar a Oriente y la travesía oceánica de Colón se inicia el colonialismo europeo que se mantendrá con altibajos más de cuatro siglos. Toda dominación requiere un relato que justifique moralmente lo que es injustificable, algo que pusieron de manifiesto los defensores de la dignidad humana como Fray Bartolomé de las Casas. La ciencia, y su expresión matemática, será uno de los argumentos para mostrar la superioridad del llamado viejo continente. Una Europa que se representará con los atributos de la religión, las armas, las letras y también de una ciencia geométrica en pleno despegue. La corona y el cetro de las alegorías dan cuenta de su papel dominante. La Iconología de Ripa ya muestra la Alegoría de Europa con los instrumentos geométricos y esa representación se mantendrá hasta el siglo XX. El encuentro con América tuvo un enorme impacto cultural y económico en Europa. Los continentes no solo se representaban en fachadas, grabados, pinturas y esculturas, también desfilaban por las calles con motivo de ciertos acontecimientos festivos. Los esponsales, el nacimiento de una princesa o la visita de un rey a una población fueron durante siglos motivo de grandes fiestas, desfiles, torneos y de adornos monumentales de las ciudades. Se trata de arquitecturas y manifestaciones artísticas efímeras pero muy impactantes. En circunstancias excepcionales se intenta perpetuar ese efímero esfuerzo con deliciosos libros ilustrados que dan cuenta de lo especial del acontecimiento: estamos ante el caso de las festividades con motivo del bautismo de la Princesa Isabel de Hesse de 1596. La Biblioteca Estatal de Baviera (BSB) conserva dos bellos manuscritos profusamente ilustrados que describen las ocho festividades que organizó el landgrave Mauricio de Hesse (1572–1632) para celebrar el bautismo de su hija, Isabel de Hesse-Kassel (1596–1625), con cuatro días de fastuosos juegos, torneos y fuegos artificiales. Los deliciosos manuscritos nos sirven de introducción de la imagen de Europa coronada como fusión de la ciencia griega y el derecho romano. (Desfile por el bautismo de la Princesa Isabel de Hesse – 1596) Europa geómetra de plata en Toledo En el año 2015 la Catedral Primada de Toledo abrió un nuevo espacio en el Antiguo Colegio Nuestra Señora de los Infantes. Se trata del Museo de Textiles y Orfebrería. Se localiza bajando desde la Puerta de los Leones hacia el Tajo. La joya del museo es el Tapiz del Astrolabio que había estado cedido al Museo de Santa Cruz. Nada más entrar en el recinto nos encontraremos con las espléndidas esculturas de  Las cuatro partes del mundo (1695), fundidas en plata por el napolitano Lorenzo Vaccaro. Sobre cuatro grandes esferas geográficas emergen las estatuas alegóricas de los cuatro continentes (Oceanía y Antártida no se consideraban entonces). Los globos muestran la calidad de la cartografía de la época tras casi dos siglos de exploración del planeta. La navegación hacía amplio uso de la matemática para poder orientarse. La Alegoría de Europa ya ha dejado de representarse como esa princesa robada por Zeus en forma de toro, ahora el discurso iconográfico trata de justificar el dominio colonial: verdadera religión, hegemonía militar y triunfo en las artes y las ciencias. Europa se representa con corona y cetro como reina del mundo. Los símbolos de la geometría no pueden faltar: escuadra y compás. A su lado se muestran los pinceles y una partitura para complementar las artes. Europa geómetra en Palermo Resulta curioso encontrar en Palermo un monumento dedicado a Felipe V, y ubicado además en un lugar tan destacado como los jardines delanteros del Palazzo dei Normanni. El Tratado de Utrecht puso fin a la Guerra de Sucesión Española pero obligaba a los borbones a ceder Sicilia a la Casa de Saboya. Después fue recuperada como reino independiente junto a Nápoles para Carlos III. Los países coloniales hacen muestra de su poder incorporando la iconografía de los cuatro continentes. Europa aparece coronada y con cetro. La matemática es uno de los atributos de esa Europa y una de las bases de su poder. Un compás muy borrado y un cuadrante astronómico aparecen a los pies de Europa. (Alegoría de Europa. Monumento a Felipe V. Palermo) Los Globos de Vincenzo Coronelli en París Dos grandes globos, uno terráqueo y otro celeste, se exhiben en el Hall Oeste de la Biblioteca François Mitterrand, el más grande y moderno emplazamiento de la Biblioteca Nacional de Francia. Los Globos del Rey Sol, miden cuatro metros de diámetro y pesan más de dos toneladas, fueron encargados para ser los más grandes y lujosos jamás construidos al Padre Vincenzo Maria Coronelli (1650 – 1718), cartógrafo veneciano. Los globos tenían que ir a Versalles pero se instalaron en la Biblioteca Real de Marly, y tras varios desplazamientos han terminado enclavados en el Hall des Globes. La decoración pictórica es de gran calidad, cada globo tiene una superficie de 50 metros cuadrados, y se tiene constancia de la participación del pintor Jean-Baptiste Corneille, entre otros. Las pinturas de las constelaciones celestes son azules mientras que el globo terrestre es polícromo. (Alegorías de los Continentes. Globos de Coronelli. París) La cartografía y la navegación eran disciplinas matemáticas como queda patente en una bella inscripción sobre los meridianos con aureola de instrumentos geométricos. El texto da cuenta de la antigüedad del Meridiano de Cádiz (Gades) y del de Toledo (por las Tablas Alfonsíes). Las pinturas también muestran la unión de las Artes y las Ciencias, así como las habituales Alegorías de los Continentes. Una figura femenina con pizarra es alegórica de la Geometría. Europa aparece con esfera armilar y un astrolabio. Europa geómetra en una celda monacal de Valencia Hay un rico patrimonio escondido en lugares dispersos que merece ser conocido y disfrutado. El caso de los azulejos valencianos es uno de ellos. El conjunto de las Azulejerías del Hospital de Pobres Sacerdotes de Valencia ya puede admirarse en forma de libro: edición de Inocencio Vicente Pérez Guillén,  Universidad de Valencia. (Alegoría de Europa. Hospital de pobres sacerdotes. Valencia) Los pavimentos, arrimaderos y murales ocupan diversos lugares pero la obra cumbre es la celda del dominico San Luis Beltrán. El santo valenciano fue evangelizador de Nueva Granada y volvió a su tierra para morir en ella en 1581. Con motivo del segundo centenario se encargó a la fábrica Faure la cubrición del pavimento y los arrimaderos de la celda con una azulejería alegórica a los dos mundos, Europa y América. El contenido simbólico es de gran complejidad. Nos fijamos en la alegoría de Europa por el uso de la geometría como atributo: figura femenina coronada y con cetro, vestido lujoso, dominio de las artes y las ciencias. América es representada como figura masculina desnuda con arco. Lo habitual es que el nuevo continente sea una mujer, pero una señora voluptuosa no debió parecer apropiado para la celda de un monje. Muy significativo resulta que el cetro se junte con el folio de la geometría. Los globos con la eclíptica y el zodiaco, el compás y las figuras geométricas son las referencias matemáticas. La lucha por la hegemonía en Europa Europa justifica su dominio colonial pero a su vez está sumida en frenética lucha por la hegemonía dentro del continente. Primer fue el imperio español, después tomaron el relevo los holandeses para cederlo a continuación rápidamente  a Inglaterra. Las alegorías ponen de manifiesto la visión interesada de cada uno. Empezando por Hispania como cabeza coronada. (Alegoría de Europa. Lámina del Strahov. Praga) Alegorías del Palacio del Dam en Ámsterdam El Palacio de la Plaza del Dam fue concebido en 1648 como Ayuntamiento y convertido en Palacio Real por Luís Napoleón en 1810, uso que se mantiene desde entonces. (Alegoría de Ámsterdam. Rijksmuseum) Nos fijaremos en las alegorías de la fachada posterior, la que da a la Raadhuisstraat, por ser la que mejor refleja la Edad de Oro de las Provincias Unidas de Holanda tras el reconocimiento de su soberanía en la Paz de Westfalia. El tímpano que corona la fachada muestra una dama majestuosa, alegoría de la ciudad de Ámsterdam, servida por los cuatro continentes que le aportan su riqueza. La base de su fortaleza reside en la navegación (velas plegadas y palo mayor) y en los instrumentos matemáticos que están a sus pies: astrolabio y ballestilla. Suele ser Europa la representada con los atributos de las nuevas ciencias y de las artes para mostrar su superioridad sobre los otros continentes y, así, justificar sus objetivos colonialistas, pero en Ámsterdam es la propia ciudad la que domina: Europa, con su cuerno de la abundancia, también se somete al poder de Ámsterdam. La estructurada está coronada por Atlas soportando el universo, figura que se repite en el gran salón de los mapas del interior. L a iconografía del tímpano fue esculpida en 1655 en el taller de Artus Quellinus. Donde mejor se aprecia la obra es en la sala del Rijksmuseum donde se encuentra expuesto un modelo de terracota: la gran maqueta está allí acompañada de detalladas explicaciones. Alegorías matemáticas en la “City” de Londres El escultor Ernest Gillick (1874 – 1951) instaló un interesante conjunto en 1932 para la nueva sede del National Provincial Bank (hoy National Westminster Bank) situado en el 1 de Princes Street de Londres. (Alegoría de Britannia. Princes Street. Londres) En los años 30 el imperio británico todavía era una realidad determinante en la cultura inglesa. El imponente edificio de piedra culmina su chaflán con un grupo alegórico de una dominante Britannia flanqueada por Mercurio (el comercio) y por la Ilustración que porta la luz a los pueblos. Lo que el propio autor destaca son las dos figuras femeninas: Higher Mathematics con el cuadrado mágico de la Melancolia I de Durero y Lower Mathematics con un compás mutilado y varios libros. Una vez más encontramos la matemática como justificación y base del imperio colonial. La figura alegórica de Europa suele aparecer coronada y con instrumentos matemáticos, musicales y religiosos, pero esta Britannia de la City se limita a las dos enigmáticas matemáticas, superior e inferior, que parecen la aritmética y la geometría pero representadas con cierto misticismo. El conjunto releva a la representación de la ciudad de Ámsterdam en el tímpano del edificio del Dam y tiene su misma función simbólica: justificar la hegemonía imperial.

Martes, 01 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico

369. El «secreto» matemático que une a los planetas con los conciertos de rock

ABC, 23 de Noviembre de 2020 CIENCIA - El ABCdario de las matemáticas Ernesto Estrada

Lunes, 23 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

370. El griego Eratóstenes contra los terraplanistas

ABC, 9 de Noviembre de 2020 CIENCIA - El ABCdario de las matemáticas Víctor M. Manero

Lunes, 09 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más