371. Los números de Friedman, cuando los números están dentro de los números

ABC, 2 de Noviembre de 2020 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 02 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

372. James Randi y otros genios de la magia y las matemáticas

ABC, 26 de Octubre de 2020 CIENCIA - El ABCdario de las matemáticas Fernando Blasco Estos días se celebra el aniversario del nacimiento de Martin Gardner, uno de los mayores divulgadores de las matemáticas, que suele reunir a grandes figuras de este campo. Muchos nos han dejado recientemente, pero la vasta obra de Gardner sigue estimulando el pensamiento crítico El matemático James Randi, en 2014, recientemente fallecido Como cada año, se está celebrando el aniversario del nacimiento de Martin Gardner, un prolífico periodista y filósofo, que fue, a juicio de muchos matemáticos, el mejor divulgador de esta disciplina del s.XX. Gardner falleció en 2010 y desde entonces se le recuerda cada año en una fiesta de no cumpleaños. Hace un año ya hablábamos de ello en este ABCdario de las matemáticas. Este año 2020 está siendo un año muy triste y hay muchos de los grandes que nos están dejando. Van ya unos cuantos de los habituales a los encuentros Gathering for Gardner que no van a poder ir nunca más. Esperemos que se sigan celebrando esos encuentros, porque el previsto para abril de 2020 hubo que cancelarlo. Como también estamos cerca de la festividad del 1 de noviembre, no es mala fecha para recordar la obra de muchos de los que trabajaron conjuntamente con Martin Gardner y honrar así su memoria. De John Conway no vamos a hablar mucho en este artículo puesto que ya lo hicimos en su día. En ese artículo hablábamos del matemático Richard Guy pero hoy mencionaremos aquí un poco más sobre sus contribuciones matemáticas. ¿Han pensado los lectores en la existencia de algún poliedro que sea inestable cuando lo apoyamos sobre una cualquiera de sus caras? No pueden dar con ello porque eso es imposible: ya que implicaría la existencia del movimiento continuo. Pero si rebajamos una condición y solo buscamos estabilidad en una de las caras sí que es posible conseguirlo y los interesados pueden consultar cómo es posible en este enlace. Richard Guy (derecha) y John Conway (izquierda) Tiene muchas contribuciones en teoría de números, teoría de grafos y otras ramas de la matemática. Pero nos ha dejado muchas aportaciones en el campo de la matemática recreativa. Es uno de los editores del libro «The lighter side of mathematics» en el que también escribe un artículo. Las cuestiones que proponemos a continuación están tomadas precisamente del artículo «la ley fuerte de los pequeños números». Los lectores que hayan estudiado estadística recordarán la ley fuerte de los grandes números; aquí lo que Guy propone es verificar si algunas propiedades que se cumplen para unos cuantos números son ciertas o no en general. Por ejemplo: 1.- Los números 31, 331, 331, 33331, 333331, 3333331 son primos ¿lo serán todos los de esta forma? 2.- Las identidades de la imagen se verifican para los números 3, 5 y 7. ¿Se verificarán para todos los impares mayores que 7? 3.- Los cinco círculos de la figura tienen 1, 2, 3, 4 o 5 puntos sobre la circunferencia que los limita. Están en posición general, de modo que nunca se cortan 3 cuerdas en un mismo punto. Cuenta en cuántas regiones queda dividido cada círculo. ¿Sigue un patrón? ¿Será siempre así? Es simplemente una muestra del ingenio de Richard Guy y queremos mostrárselo hoy a todos los lectores. En este enlace aparece hablando de Martin Gardner y de alguno de sus problemas. Siempre es bueno poder ver a los personajes de los que escribimos. Otro querido personaje, habitual de los encuentros Gathering for Gardner, era Ron Graham, que también nos ha dejado este año. Además de ser un matemático de primera línea, Graham era el encargado de recibir la correspondencia del excéntrico matemático Paul Erdös. Graham también era alguien especial: un gran gimnasta, malabarista que además ha participado en alguna gira del mundialmente famoso Cirque du Soleil. Graham ostenta un record Guinness, el del número más grande que aparece en una prueba real de matemáticas. En 1980 apareció su número en ese libro. El problema es que no podemos reproducir el número: si lo escribiésemos con dígitos, su representación no cabría en todo el universo observable. A pesar de no poder escribirlo en el sistema decimal, sí que podemos representarlo utilizando la notación de Donald Knuth (otro de los matemáticos a los que hacía referencia Gardner en muchas de sus obras; otro día dedicaremos a él esta sección). Ron Graham izquierda, Persi Diaconis derecha y sujeta el libro Colm Mulcahy, Vicepresidente de Gathering for Gardner Ron Graham es coautor, junto a Persi Diaconis, de una maravilla de libro para los aficionados al ilusionismo y a las matemáticas: Magical Mathematics. El primer libro dedicado íntegramente a la relación de estas dos disciplinas fue precisamente el escrito por Martin Gardner en 1956: Mathematics, Magic and Mystery. Desde entonces unos cuantos autores hemos escrito libros en esa misma dirección. En su libro hablan de Martin Gardner y muestran uno de sus «problemas de desaparición»: en los dos cuadrados de la figura aparecen los mismos elementos: se puede verificar a simple vista. ¿Cómo es posible que, en esas circunstancias, disponiéndolas de otro modo, desaparezca un cuadrado en el centro del dibujo? Hay otras versiones del mismo rompecabezas, pero todas acaban dejando un hueco mucho más pequeño. Esta versión es realmente buena. El otro personaje, habitual en los encuentros sobre Martin Gardner, es James Randi, The Amazing Randi. Nos ha dejado hace muy poquito: justo cuando estábamos celebrando el 106 aniversario del nacimiento de Gardner. Fue un miembro destacado y fundador del Comité para la Investigación Escéptica (CSICOP) al que también pertenecieron Martin Gardner, Isaac Asimov y Carl Sagan, entre otros. Randi fue uno de los responsables de desvelar los trucos que utilizaba el popular Uri Geller. La ciencia, y las matemáticas en particular, nos pueden prevenir de las estafas. Una mayor educación y un mayor conocimiento científico nos ayuda a darnos cuenta de qué cosas tienen sentido y qué cosas tienen fundamento. Es cierto que la ciencia no tiene todas las respuestas, pero sí que tiene el ánimo de buscarlas. Por ello la adquisición de pensamiento crítico es fundamental y creemos también importante tratar esas ideas en esta columna. Premio por demostrar lo paranormal La obra de Gardner, además de muchos libros sobre matemática recreativa, comprende obras importantes para el pensamiento crítico, siendo ya clásicos los libros Modas y falacias en el nombre de la ciencia o La ciencia: lo bueno, lo malo y lo falso. Randi también es el autor de un bestseller sobre este tema: ¡Decir algo! Psíquicos, ESP, unicornios, y otros engaños. La Fundación Randi otorga un premio muy importante a la primera persona que pueda ofrecer una prueba objetiva de actividad paranormal. El premio comenzó siendo de 1.000 dólares pero con el paso de los años ha crecido hasta 1.000.000 de dólares y también se han escrito con mucha más claridad las reglas del desafío. Como requisito para participar en el desafío Randi acordaba con el solicitante qué resultados finales se consideran como «éxito» y cuáles como «fracaso». También determinaba en qué condiciones se iba a hacer el experimento. Él era capaz de reproducir (con técnicas de mago mentalista) muchos de los supuestos fenómenos paranormales que otros también decían ser capaces de experimentar. James Randi vino a España en 2011 y participó en un encuentro de Escépticos en el pub en Madrid, antes de acudir a un encuentro con neurocientíficos en la Isla de San Simón, en Pontevedra. James Randi (izquierda) y Martin Gardner En 2014, con 86 años, Randi hablaba sobre la obra de Martin Gardner en el año de su centenario. Ahora hablamos nosotros de él y seguiremos haciéndolo. En un momento como este en el que se falsean muchos datos y muchas pruebas es necesario estimular el pensamiento crítico como protección frente a los que no tienen argumentos. La ciencia nos hace mucho más libres. La obra de Martin Gardner es muy extensa en muchos ámbitos. Mi opinión particular es que es así porque se rodeaba de los mejores: matemáticos de primera línea, científicos de primera línea y magos de primera línea. Esa es otra de las enseñanzas que debemos aprender de él: saber beber de las buenas fuentes y compartir ese conocimiento. Dentro de poco se celebrará la Semana de la Ciencia en toda España. Animo a los lectores a que acudan (quizás este año tenga que ser a través de una pantalla) a las actividades que sean de su interés. Con la ciencia se disfruta. Fernando Blasco es profesor de Matemática Aplicada de la Universidad Politécnica de Madrid, miembro de la Comisión de Educación de la Real Sociedad Matemática Española (RSME) y miembro del Comité de Sensibilización Pública de la Sociedad Matemática Europea. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME)

Lunes, 26 de Octubre de 2020 | Imprimir | PDF |  Correo electrónico

373. La demostración matemática o cómo llegar a la verdad invariable y eterna de los teoremas

ABC, 19 de Octubre de 2020 CIENCIA - El ABCdario de las matemáticas Víctor M. Manero

Lunes, 19 de Octubre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

374. Matemáticas para la privacidad en un mundo post-cuántico

ABC, 11 de Octubre de 2020 CIENCIA - El ABCdario de las matemáticas Iván Blanco Chacón

Domingo, 11 de Octubre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

375. La primera gran crisis de los matemáticos: las magnitudes inconmensurables

ABC, 5 de Octubre de 2020 CIENCIA - El ABCdario de las matemáticas Urtzi Buijs y Miriam González

Lunes, 05 de Octubre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

376. Noviembre 2020: Kono, un juego simple de estrategia

1. Introducción. Comenzando la segunda semana de confinamiento casero por el coronavirus, he pensado que lo mejor para esta entrega es presentar un juego de tablero. El motivo es la información que llega a través de redes y de medios de comunicación de la dificultad de los padres para tener entretenidos a sus hijos sin que puedan salir de casa. Yo recuerdo que en mi tierna infancia, cuando no podíamos salir a la calle o al parque a jugar, y no teniendo las tecnologías de la comunicación actuales,  lo normal era  que dedicáramos las tardes a jugar a todo tipo de juegos de mesa: parchís, oca, dominós, en general los Juegos Reunidos. Por eso, me voy a ocupar en esta entrega de un juego de tablero que pienso que no es muy conocido, pero que es muy fácil de organizar en casa o en el propio aula y resulta muy atractivo para jugar. Como hemos comentado en otras entregas, en esta sección solemos agrupar los juegos siguiendo la clasificación indicada por Fernando Corbalán, uno de nuestros maestros. Según esa clasificación, agrupamos los juegos en: juegos de procedimiento conocido, juegos de conocimiento y juegos de estrategia. Los primeros son aquellos que se basan en juegos que se conocen fuera del aula, como dominós, rompecabezas, cartas, etc… Los segundos son creados para tratar elementos de los contenidos que debemos trabajar en el aula. Y por último, los juegos de estrategia son aquellos que, aunque a simple vista no parecen tener relación con las matemáticas, lo cierto es que desarrollan un apartado fundamental al que muchas veces no se le tiene en cuenta en la enseñanza de las matemáticas. Desde mediados del siglo XX está reconocido que la resolución de problemas debe ser el hilo conductor de la enseñanza de las matemáticas. Para resolver problemas son necesarios una serie de heurísticos o procedimientos que, aunque algún profesor piense lo contrario, no son innatos al ser humano. Son necesarios aprender a aplicarlos y una buena manera, bastante atractiva y lúdica, es trabajar los juegos de estrategia. Teniendo claro que, como se ha dicho en muchas ocasiones, no basta con jugar sino que es imprescindible el estudio posterior del juego, el recuento de posibilidades, la búsqueda de estrategias que permitan ganar o predispongan a ese resultado. Para ello se suelen utilizar estrategias típicas de la resolución de problemas: buscar juegos similares, comenzar estudiando casos más simples, utilizar el procedimiento de considerar el problema resuelto y comenzar desde el final, y muchos más. Ya en anteriores entregas de esta sección nos  hemos referido a juegos de estrategia. Más concretamente, la segunda entrega la dedicamos al Juego de la L. En esta ocasión vamos a hablar de dos juegos coreanos que tienen el mismo nombre y su estructura es similar, pero la metodología del juego es radicalmente distinta. 2. Los juegos de tipo KONO. El KONO es un juego coreano del que no se tiene claro su origen. La escritora Sally Wilkins lo recoge en su libro “Deportes y juegos de la cultura medieval” editado en 2002, pero no hay ninguna prueba que corrobore que dicho juego fuese conocido en la Edad Media. La primera vez que se cita dicho juego es en una publicación de 1985 del etnógrafo norteamericano Stewart Cullin, quien en su libro “Korean games with notes on the corresponding games China and Japan” habla de este juego en sus distintas versiones. En la siguiente dirección se puede consultar la obra original de Cullin: https://archive.org/details/cu31924023272424 También, uno de los principales especialistas en juegos, el canadiense Robert Charles Bell, autor de referencia sobre juegos de mesa en el mundo, publicó una magna obra sobre juegos de mesa llamada “Board And Table Games From Many Civilizations”. Inicialmente apareció un volumen en 1960 y otro en 1969 que después se reeditaron en un solo libro. En él menciona al Kono, asegurando que en la segunda mitad del siglo XX aunque era un juego habitual. En el libro de Cullin se citan dos juegos similares en su estructura pero totalmente diferentes en su metodología de juego. Ambos se juegan con una cuadrícula sobre la que se mueven una serie de fichas con distinto movimiento en cada uno de ellos. Según el autor, en Corea reciben el nombre de Kono los juegos que se desarrollan sobre un diagrama formado por líneas rectas, normalmente horizontales y verticales. Lo curioso es que, en la forma más usual, las fichas no se colocan en las cuadrículas sino en las intersecciones que forman dichas líneas. Aunque pueden encontrarse comercializados colocando fichas dentro de las cuadrículas Veámoslos más detenidamente. 3. El Kono de campo de cuatro. Este juego, llamado en coreano Nei–pat–ko–no, es un juego del tipo que se conoce como juego de soldados o más corrientemente como juegos de captura. Se juega sobre una cuadrícula de 3x3, y las fichas, ocho por cada jugador, de color distinto, se colocan en las intersecciones de las cuatro líneas horizontales y las cuatro verticales. En la siguiente imagen podemos ver un tablero casero con las fichas ya colocadas. Como vemos basta dibujar una cuadrícula y utilizar fichas o tapones de bebidas para tener nuestro juego listo. Imagen 1: Tablero del Kono de cuatro con las fichas colocadas. En el kono de cuatro hay dos movimientos permitidos: a) Movimiento de captura. Para capturar una ficha del contrario es necesario que una de nuestras fichas salte sobre otra ficha propia cayendo sobre una ficha del contrario que es capturada. Las tres fichas (la que se mueve, sobre la que se mueve y la del contrario) deben de estar en línea recta. El movimiento siempre es en horizontal o vertical, nunca en diagonal. Imagen 2: Movimiento de captura. b) Movimiento de deslizamiento. Una vez que haya intersecciones libres, una ficha puede moverse a un punto contiguo en horizontal o en vertical, nunca en diagonal. Imagen 3: Movimiento de desplazamiento. A diferencia de otros juegos similares, en el Kono no se pueden hacer saltos múltiples, capturando en la misma jugada más de una ficha del contrario como se hace, por ejemplo, en las damas. Como es lógico, vista la distribución de las fichas en la imagen 1, el primer movimiento siempre tiene que ser de captura. Por regla general, si juegan blancas y negras suelen salir las negras, aunque puede sortearse el turno de comienzo. El objetivo de juego es capturar las fichas del contrario y acaba cuando uno de los jugadores tiene una sola ficha, pues con ella no puede capturar ninguna del contrario, o bien si las fichas de un jugador quedan bloqueadas y no puede hacer ningún movimiento. En ambos casos ese jugador pierde la partida. El juego del Kono suele ser bastante rápido pues, salvo que los dos jugadores comiencen a repetir movimientos llegando a alargarse el proceso, lo normal es que en 10 ó 15 minutos de termine la partida, o a veces en menos tiempo. Como en cualquier juego de estrategia, tras unas partidas, lo suyo es buscar los mejores movimientos para ganar e incluso, si lo hubiese, una estrategia ganadora. En todos los casos debemos estudiar movimientos posibles investigando todas las posibilidades. El hecho de comenzar con una distribución simétrica en el tablero hace que el comienzo sea muy previsible. Sólo existen dos posibles formas de comenzar la partida, capturando partiendo de una de las dos columnas exteriores de las fichas o una de las dos centrales. Y a partir de ahí sí que se disparan las posibilidades de movimiento sobretodo porque al no ser obligatorio capturar la ficha del contrario, si es posible, es muy complicado investigar todas las posibilidades. Pero para aquellos con ánimo, ahí dejamos el reto. En YouTube podemos encontrar explicaciones sobre el juego e incluso ver una partida. En el vídeo se van indicando, a la vez que se juega, las reglas del juego. Para verla consultar la siguiente dirección: https://www.youtube.com/watch?v=APc_iPZtrqM En la siguiente dirección se puede jugar en línea al Four Field Kono, nombre en inglés del juego. http://www.lutanho.net/play/fourfieldkono.html En la siguiente dirección tenemos un pdf con las instrucciones del juego en inglés. Si el enlace da algún problema basta copiarlo y colocarlo en el navegador. http://www.cyningstan.com/data-download/239/four-field-kono-leaflet 4. Variaciones en el Kono de cuatro. En algunos lugares he encontrado la regla de que no es obligatorio capturar una ficha contraria si es posible, mientras que en otros lugares se impone que la captura es obligatoria como ocurre en otros juegos. Como la compro, la vendo. Por ejemplo, en el vídeo anterior se impone la obligación de comer ficha, pero después no se cumple en una de las jugadas. En el libro “El gran libro de los juegos” publicado por Paramón Ediciones en 1998, con autoría de Josep M. Aullé, se añade una nueva regla al juego, que también he encontrado en un artículo publicado en la página Cuaderno de Cultura Científica por el gran Raúl Ibáñez. Esa regla extra sería que si una ficha de un jugador queda bloqueada por el contrario también es capturada. Imagen 4: Ficha bloqueada. Aunque no es una regla original, su incorporación hace que el juego sea mucho más rápido, pues se eliminan fichas del tablero con mucha mayor velocidad. Existe una versión ampliada de este juego, citado por Cullin en su obra sobre juegos coreanos. En él cita el juego Ryouk–pat–ko–no que sería algo así como Kono de campo de seis. Se juega en una cuadrícula de 5x5, con seis líneas horizontales y seis verticales. Cada jugador dispone de 18 fichas, de distintos color por jugador. En el libro sobre juegos coreanos se dice que el informante del autor le habla del juego pero no conoce  su  método. Dado que se parte de una estructura similar a la de cuatro, debemos suponer que las reglas deben ser similares. 5. Kono en campo de cinco. La siguiente versión de Kono es bastante curiosa. Tiene el mismo nombre genérico, se juega sobre un tablero similar, aunque mayor, y con fichas de distintos color por jugador, pero menos, aunque el mismo número de fichas. Sin embargo, la forma de jugar es totalmente distinta. El Kono en campo de cinco o en su nombre coreano O–pat–ko–no (Five Field Kono en inglés) se juega sobre una cuadrícula de4 x4 formada por cinco líneas horizontales y cinco verticales. Como en el anterior, las fichas se colocan sobre los puntos intersección de las líneas. Cada jugador dispone de siete fichas, de colores diferentes por jugador, y se colocan en cada uno de los extremos del tablero como se puede ver en la imagen siguiente. Imagen 5: Tablero de Kono en campo de cinco. En esta versión de juego no se capturan fichas del contrario. Es un juego de los que se llaman Juego de intercambio, en él debemos colocar nuestras fichas en el lugar que estaban las del contrario al comenzar el juego. El primero que lo consiga es el ganador. Las reglas son diferentes al otro juego y serían las siguientes: a) Los movimientos siempre son en diagonal. Se puede desplazar una ficha a un punto adyacente vacío. b) Los movimientos pueden ser en cualquier dirección del tablero, tanto hacia adelante como hacia atrás. c) No se puede saltar sobre una ficha sea propia o del contrario. d) En cada intersección sólo puede haber una ficha. Para no alargar el juego demasiado, si ninguno de los jugadores puede pasar al otro, algo realmente raro, se puede considerar el juego en tablas. Para impedir que un jugador pueda dejar una serie de fichas en su lugar original y así impedir que el contrario coloque sus fichas en el lugar del oponente, se suele añadir la regla de que un jugador gana si ocupa todos los lugares dejados libres por su oponente. Si en algún momento debemos mover una ficha y no puede avanzar, es necesario que retroceda. En la siguiente imagen vemos los movimientos posibles de una de las fichas. Imagen 6: Movimientos posibles. En la siguiente dirección de YouTube se puede observar una partida completa al Kono de cinco. https://www.youtube.com/watch?v=T1lBtF1Pilk No he conseguido encontrar ninguna página en la que se pueda jugar en línea al juego, pero en la página de Zillions of games se puede descargar un archivo para instalarlo en el ordenador. Se pueden ver las instrucciones y la descarga en esta dirección. http://www.zillions-of-games.com/cgi-bin/zilligames/submissions.cgi/94592?do=show;id=412 Igual que en caso de cuatro, se pueden descargar en pdf unas instrucciones simples del juego desde la siguiente dirección. http://www.cyningstan.com/data-download/355/five-field-kono-leaflet 6. Y para acabar, algo más. Como se puede observar en los vídeos que hemos incluido en los enlaces, las partidas al kono son rápidas y fáciles en muchos aspectos, pues las instrucciones son simples de entender para comenzar a jugar y también es posible conseguir el tablero y las fichas de una manera fácil. Aparte de las direcciones incluidas en el texto, la más completa sobre el juego del Kono de cuatro es la siguiente: https://arescronida.wordpress.com/tag/kono-campo-de-cuatro/ En ella, se habla en general sobre los llamados juegos de soldados, que serían aquellos en que todas las fichas tienen la misma validez, es decir, no hay distintos estamentos como en el Ajedrez, los jugadores tienen la misma cantidad de fichas y el objetivo es capturar las del contrario. La explicación sobre el kono se complementa con juegos similares en China o en Vietnam. Pero además se explican muchos otros juegos del mismo tipo de soldados o de captura como solemos clasificarlos nosotros. De esa manera, se citan el antiguo juego egipcio del Seega, los juegos Dablot (tablero) de Laponia, el de Dieciséis soldados del sur de la India con algunas de sus variantes, los Ne – jul – gone también coreanos y que se juega sobre el mismo tablero del kono de cuatro, pero con solo cuatro fichas por jugador, el Surakarta tradicional de la isla de Java y varios juegos más de otras partes del mundo, por lo que es una dirección de consulta obligada para los amantes de los juegos de estrategia de tablero.

Miércoles, 18 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico

377. 110. (Noviembre 2020) Reseña del libro de Godfried Toussaint "The geometry of musical rhythm: what makes a “good” rhythm good?"

1. Introducción Este artículo es una reseña del libro de Godfried Toussaint The geometry of musical rhythm: what makes a “good” rhythm good? [Tou17a]. Godfried (en este artículo no lo llamaré Toussaint) fue mi director de tesis y amigo personal. Desgraciadamente, nos dejó en julio de 2019. Estaba dando una charla en una conferencia en Japón y cayó fulminado por causas todavía desconocidas pero que apuntan a un ataque al corazón. Figura 1: Godfried Toussaint Godfried era una persona apasionada de la vida en muchos aspectos. En los intelectuales y académicos, destaca su pasión por la geometría y la música. Empezó su carrera por la geometría, en particular la geometría computacional. Está considerado el padre de la Geometría Computacional. Estudió a fondo los aspectos teóricos de la geometría computacional así como sus aplicaciones a múltiples campos: reconocimiento de patrones (los algoritmos para encontrar los k vecinos más cercanos, análisis de agrupaciones), planificación de movimiento, visualización, teoría de nudos, configuraciones de articulados, los problemas de la galería de arte, triangulaciones, el problema del círculo vacío más grande, entre otros. Y fue productivo, como lo atestiguan sus cerca de 300 artículos en 50 años de carrera académica (su primer artículo data de 1969). Su otra gran pasión fue la música, en especial el ritmo y la percusión. Fue percusionista de música africana, afro-cubana y además tocaba la batería en un grupo de rock y pop formado por profesores de la universidad McGill (la universidad donde desarrolló su carrera) que tenía el significativo nombre de The Algorithmics. Godfried era un investigador de raza. Prefería con mucho inventar nuevos problemas, con perspectivas originales, que supusiese un cambio de perspectiva y metodología, antes que centrarse en problemas de investigación técnicos o de carácter demasiado concreto. Le gustaba pensar en abstracto, conectar varios campos con ideas insólitas; le gustaba ejercer la creatividad desde una cumbre de abstracción. Sin embargo, donde creo que Godfried brilló más fue en las relaciones personales. Godfried trataba bien a la gente con la que colaboraba. Les contagiaba la pasión que tenía por la geometría y la música, en general por la investigación y aun más por la vida misma. En los famosos talleres que organizaba en Barbados (asistí a diez de ellos) la risa pero también el trabajo duro eran constantes. Reconocía genuinamente el talento en otros, calmaba de forma magistral los atisbos de ego y sabía crear un ambiente de seguridad emocional que era altamente productivo y generaba un gran disfrute. 2. La reseña En la página de Amazon, encontramos las siguientes reseñas breves de varios especialistas en el campo del [Tou17b]. Por Marc Chemillier dice del libro: The late Godfried Toussaint studied the rhythms of the world like a gold panner, collecting with meticulousness and passion all the motifs that different cultures have given birth to. Thanks to his skill as a mathematician, he extracted fascinating properties from them. There is no doubt that this unique book will survive for a very long time. El eminente etnomusicólogo francés Simha Arom: Through the original use of distance geometry for analyzing musical rhythm and the visualization of rhythms as cyclic polygons, Godfried Tousssaint?s fascinating book will be extremely valuable to any researcher involved in in the field of rhythm. Y finalmente, los comentarios de Justin London: The new edition of The Geometry of Musical Rhythm takes us further along Godfried Toussaint?s journey through the world?s rhythms. There are new discussions of metric complexity, rhythm visualization, rhythmic performance, and the evolution of rhythmic patterns. Almost every chapter has been expanded and informed by the latest scholarship in music theory, music psychology, ethnomusicology, and music informatics. Specialists and lay readers alike will find this edition even more engaging and valuable than the first, giving us even more reasons to delight in what makes a “good” rhythm good. El libro está compuesto por 38 capítulos en los que el autor ofrece una descripción del ritmo desde sus predilecciones musicales y matemáticas; se trata además de un libro conceptual, donde no hay ejercicios ni está orientado a ser un libro de texto. Como dice el propio Godfried en los prolegómenos, “quería hacer un libro que fuera accesible a un público de músicos y gente del mundo universitaria, con diversas formaciones académicas y actividad musical, y a la vez con un nivel mínimo de prerrequisitos”. En su libro solo se examina música en formato simbólico. En el capítulo 1, titulado ¿qué es el ritmo?, pasa revista a diferentes definiciones dadas en el pasado y por diversos autores de este término. El concepto de ritmo adoptado por Godfried es simple y consiste en considerar una sucesión de k ataques distribuidos sobre un conjunto de n pulsos. Sigue, en el capítulo 2, con un distinción conceptual entre ritmo y pulso, y se adentra en cuestiones cognitivas para precisar tal distinción. Ya en el capítulo 3, se centra en un tipo de ritmo, los ritmos de clave u ostinatos, que será el grupo de ritmos que estudiará extensiva y profundamente en el resto del libro. Un ritmo de clave es un ritmo que se repite a lo largo de una pieza y que sirve como referente y estabilizador rítmico. Típicos ritmos de clave son los ritmos del son, la rumba, o la bossa-nova. En este capítulo encontramos una interesante historia del tresillo cubano (dos negras con puntillo seguidas de una negra en notación 2/2), la cual ilustra con alta erudición musical. Esta erudición musical es una de las características notables del libro de Godfried. En los capítulos 4 y 5 describe más a fondo los ritmos de clave, en especial su función rítmica, y además describe los instrumentos en los que se suelen tocar, esencialmente claves y campanas. En el capítulo 6, presenta la clave son, que en notación de caja es [×⋅ ⋅×⋅ ⋅×⋅ ⋅ ⋅×⋅ ×⋅ ⋅ ⋅ ]. En este punto encontramos una interesante discusión sobre por qué los ritmos más interesantes aparecen cuando k es menor que n∕2. También se discute algunos valores del número de pulsos en términos de su aparición en la práctica musical de diversas tradiciones. Termina este capítulo con un análisis matemático que justifica la particularidad rítmica de la clave son. En el capítulo 7 presenta los seis ritmos binarios objeto de estudio en buena parte del resto del libro. Son estos: Figura 2: Los seis ritmos de clave binarios Explica los orígenes de estos ritmos, su nomenclatura y su aparición en diversos contextos musicales. En los capítulos 8 y 9 presenta su método de visualización de los ritmos de clave a través de su representación geométrica en círculos. Figura 3: La geometría de los ritmos de clave Además, define varios conceptos que se usarán a lo largo del libro tales como contenido del intervalo, distancia entre notas (ataques), distancia geodésica, vector de intervalos, histogramas de distancias e histogramas de distancias adyacentes. También define los ritmos aksak (a partir del trabajo de Simha Arom [Aro91]). En el capítulo 10 se analizan los ritmos binarios y ternarios y se presentan las claves binarias de 5 y 7 notas más importantes, la clave fume-fume y el bembé (ritmos descritos con su terminología). Godfried hace una comparación entre ambos y estudia su contorno rítmico. El capítulo 11 es un capítulo aparte, pues realiza una comparación entre ritmo y alturas de sonido (escalas más bien). El capítulo 12 es una revisión de la obra de Rolando Pérez La binarización de los ritmos ternarios africanos en América Latina [PF86]. En esta obra Pérez propone una teoría de cómo los ritmos binarios que se oyen en América Latina provendrían de una binarización de ritmos ternarios de los esclavos africanos. Godfried hace un análisis de esta hipótesis con una perspectiva computacional y matemática. El capítulo 13 está dedicado a uno de los temas que más le gustaban en la teoría del ritmo: la síncopa. Examina y discute las varias definiciones de síncopa que encuentran en la literatura (como la de Jackendoff y Lerdahl [LJ83] o la de Keith [Kei91]). Gran parte de este capítulo es material de la tesis de maestría que dirigió a Eric Thul [Thu08]; véase también [Góm11]. En el capítulo 14 se zambulle en el fascinante mundo de las operaciones sobre ritmos, en particular, en los collares y las pulseras (necklaces y bracelets). Aplica toda esta teoría combinatoria al estudio de ritmos de clave y destila maneras de clasificar ritmos en base a si existe alguna operación que pase un ritmo a otro. Aquí es otro capítulo donde ilustra sus teorías con abundantes ejemplos de las tradiciones musicales más diversas. En el capítulo 15 estudia el índice de asimetría rítmica, propuesto inicialmente por Simha Arom, y lo aplica al análisis de la música de los pigmeos aka así como a los ritmos de clave seleccionados. Esta parte del libro es fuertemente algorítmica y se disfruta mucho la generación de ritmos en base a propiedades pre-establecidas. El capítulo 16 se especializa en el estudio de índice de contratiempo, que es una medida de complejidad rítmica con inspiración en la teoría de números. Y finalmente, en el capítulo 17 aborda el problema de la complejidad rítmica a través de conceptos tan potentes como puede ser la entropía. 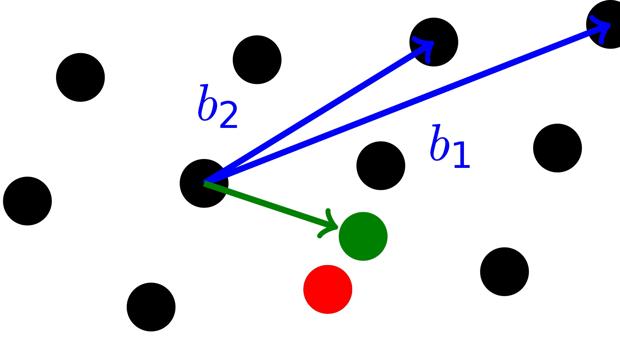Los capítulos 18 a 22 están dedicados a los ritmos euclídeos o ritmos cuyas notas están distribuidas lo más regularmente posible. En el capítulo 18 argumenta muy elocuentemente porque la distancia geodésica en el círculo no es una buena medida de la dispersión de las notas en el ritmo. A continuación, propone la distancia intercordal como una medida de la regularidad de un ritmo y prueba que funciona. Figura 4: Distancias entre las notas de un ritmo En el capítulo 19 expone los aspectos algorítmicos de la generación de los ritmos euclídeos; en concreto, muestra de una manera muy instructiva la conexión entre el algoritmo de Euclides de cálculo del máximo común divisor y los ritmos euclídeos. Variando el número de notas y de pulsos, genera varios ritmos que aparecen en diversas músicas del mundo (el tresillo cubano, el bembé, la clave bossa-nova, ritmos de los pigmeos aka, entre otros). Los ritmos euclídeos o de regularidad máxima tienden a crear tensión rítmica, sobre todo si el número de notas y el número de pulsos son primos entre sí (no tienen divisores comunes salvo el 1). En este caso las notas “contradicen” las notas que se esperan a partir del número total de pulsos. Consideremos, por ejemplo, el ritmo [×⋅ ⋅×⋅ ⋅×⋅ ]. Tiene 8 pulsos y 3 notas y observamos que 3 y 8 son primos entre sí. Por ser 8 divisible por 2 y 4, las notas sobre múltiplos de 2 y 4 se perciben como estables. Sin embargo, este ritmo tiene notas en 0,3 y 7. Al tocar ese ritmo se percibe una superposición de un ritmo ternario, las tres notas del ritmo, sobre un ritmo binario, la estructura binaria de los pulsos. Todo ello, ciertamente, crea tensión rítmica. Demain y otros colegas, autores del trabajo The Distance Geometry of Music [DGM+05], investigaron la relación entre la distribución de regularidad máxima de patrones y otras disciplinas, con especial énfasis en el ritmo musical. ¿Cómo se transforma el cálculo del máximo común divisor en un método para generar patrones distribuidos con regularidad máxima? Ilustraremos el proceso con un ejemplo de ritmos. Supongamos que tenemos 17 pulsos y queremos distribuir de forma regular 7 notas en los 17 pulsos. Sigamos los pasos dados en la figura 5. Primero, alineamos el número de notas y el número de silencios (siete unos y diez ceros); véase la figura 5–paso (1). A continuación, formamos grupos de 7, los cuales corresponden a efectuar la división de 17 entre 7; obtenemos, pues, 7 grupos formados por [10] (en columnas en el paso (2) de la figura). Sobran tres ceros, lo cual indica que en el paso siguiente formaremos grupos de 3. Tras formar el primer grupo –véase el paso (3) de la figura– nos quedamos sin ceros. Continuamos agrupando de 3 en 3 tomando los grupos de la otra caja, en la que quedan 4 columnas (figura 5– paso (4)). Procedemos así que queden uno o cero grupos; de nuevo, esto es equivalente a efectuar la división de 7 entre 3. En nuestro caso, queda un solo grupo y hemos terminado (paso (5)). Finalmente, el ritmo se obtiene leyendo por columnas y de izquierda a derecha la agrupación obtenida (paso (6)). Figura 5: Generación de ritmos euclídeos. Aquí cada 1 representa una nota [×] y cada 0, un silencio [ ⋅ ]. El ritmo que hemos generado con nuestra notación se escribe entonces como [×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ] Los ritmos generados por este método se llaman ritmos euclídeos. El ritmo euclídeo de k notas y n pulsos se designa por E(k,n). Otra manera útil de designar un ritmo es mediante las duraciones de las notas en términos de pulsos. Así, por ejemplo, el ritmo de la sevillana [×⋅ ⋅×⋅ ⋅×⋅ ⋅×⋅ ⋅ ] se puede escribir como (3333), donde cada 3 indica que dura tres pulsos. El ritmo euclídeo que acabamos de obtener con esta notación se escribe E(7,17) = [×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ] = (3232322). Demain y sus coautores [DGM+05] probaron formalmente que este algoritmo proporciona, salvo rotaciones, la única manera de distribuir k objetos entre n del modo más regular posible. Aún más, había varios algoritmos propuestos de manera independiente y ellos probaron que, en realidad, eran todos equivalentes al viejo algoritmo de Euclides. Damos a continuación una pequeñísima muestra de ritmos euclídeos que se encuentran en las músicas tradicionales del mundo y que aparecen en el libro de Godfried. E(5,8) = [×⋅××⋅××⋅ ] = (21212) es el cinquillo cubano, así como el malfuf de Egipto, o el ritmo coreano para tambor mong P’yŏn. Si el ritmo se empieza a tocar desde la segunda nota aparece un popular ritmo típico de Oriente Próximo, así como el timini de Senegal. Si se empieza en la tercera nota tenemos el ritmo del tango. E(5,12) = [×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ] = (32322) es un ritmo muy común en África central que tocan los pigmeos aka. Cuando se toca desde la segunda nota es, entre otros, la clave columbia de la música cubana y el ritmo de la danza chakacha de Kenya. E(5,16) =[×⋅ ⋅×⋅ ⋅×⋅ ⋅×⋅ ⋅×⋅ ⋅ ⋅ ] = (33334) es el ritmo de la bosa-nova de Brasil. Este ritmo se toca a partir de la tercera nota. Existen cerca de dos centenares de ritmos de músicas del mundo documentados que son generados por el algoritmo de Euclides. Para más información sobre ritmos euclídeos, recomendamos los artículos [GTT09b] y [GTT09a] El capítulo 20 trata de la aplicación de los ritmos euclídeos al cálculo de los años bisiestos. Proporciona una fascinante historia del problema de definir los años bisiestos y cómo se han resuelto en diversas culturas (desde la islámica a la cristiana). En el siguiente capítulo, el 21, se estudian los ritmos aproximadamente regulares, que son aquellos que difieren en un ritmo euclídeo por una nota; véase la figura de abajo. Figura 6: Ritmos aproximadamente regulares Para cerrar esta serie de capítulos sobre los ritmos euclídeos, Godfried estudia las conexiones entre estos ritmos y la cristalografía. El capítulo 23 está dedicado a los ritmos complementarios, esto es, a los ritmos obtenidos al intercambiar notas por silencios y viceversa. Estudia Godfried las propiedades que se conservan por la toma de complementarios y en particular analiza el teorema del hexacordo; véase [BBOG09]. El capítulo 24 es una conexión entre los ritmos y la radio astronomía que usa resultados del capítulo anterior. En el capítulo 25 se presentan los ritmos profundos, que son ritmos en que las distancias entre todas las notas ocurren de manera única. Si hacemos el histograma de un ritmo profundo, entonces es posible ordenar sus distancias de tal manera que el histograma sea creciente o decreciente estrictamente. La figura de abajo ilustra un ritmo profundo, en este caso, el bembé. Figura 7: Ritmos profundos El capítulo 26 versa sobre los ritmos cáscara. Dada una propiedad P de un ritmo (ser euclídeo, por ejemplo), se dice que es un ritmo cáscara con respecto a P si existe una sucesión de inserciones o borrados que mantiene la propiedad todo el tiempo. En el capítulo 27 Godfried estudia los ritmos fantasma, que son los ritmos resultantes de considerar como ritmos los silencios de un ritmo dado. En particular, discute las implicaciones cognitivas de estos ritmos. El capítulo 28 consiste en un examen de los cánones rítmicos y también de las simetrías axiales que se pueden encontrar en los ritmos. En el capítulo 29 el tema principal es los ritmos definidos por acentuación. Estos ritmos consisten en tocar todas las notas de los pulsos y acentuar unas cuantas de ellas, lo cual da lugar a un ritmo que destaca sobre la alfombra de pulsos. Este tipo de ritmos aparece, por ejemplo, en el flamenco. El capítulo 30 investiga varios tipos de simetría en los ritmos (simetría axial, palindrómica, etc.), ampliando así el capítulo 28. El capítulo 31 se adentra en los ritmos que tienen un número inusual de pulsos; se trata más bien de un examen musicológico de dichos ritmos más que un análisis matemático del mismo. En el capítulo 32 se discuten y analizan diversas representaciones de los ritmos, desde la notación de caja hasta las duraciones inter-notas. Ya en el capítulo 32 Godfried nos muestra uno de los temas más interesantes en la teoría del ritmo: la similitud rítmica. Examina diversas distancias de similitud, desde la distancia Hamming hasta la distancia de permutación dirigida (cuyo inventor fue él). En el capítulo 33 el autor se enfrenta a definir el concepto de regularidad e irregularidad para ritmos y cómo establecer una gradación entre ambos extremos. El capítulo 35 describe las aplicaciones de los árboles filogenéticos a la teoría del ritmo. Aquí expone buena parte de sus resultados [?] con esta técnica así como sus aplicaciones al análisis del flamenco. El capítulo 36 está consagrado al estudio combinatorio del ritmo. Finalmente, el capítulo 37 consiste en una defensa ardiente del ritmo de la clave son como el ritmo más popular y mejor construido (argumenta para ello su nivel de regularidad, su índice de asimetría, su índice de contratiempo, su complejidad métrica, entre otras). En el último capítulo del libro traza una historia y un recorrido musicológico de este ritmo. El libro cierra con un epílogo en que Godfried hace un resumen de su perspectiva e ideario sobre la teoría del ritmo y justifica una vez más la pertinencia del análisis matemático y computacional del ritmo.   Bibliografía [Aro91] Simha Arom. African Polyphony and Polyrhythm. Cambridge University Press, Cambridge, England, 1991. [BBOG09] B. Ballinger, F. Benbernou, N. Gomez, J. O’Rourke, and Toussaint G. The continuous hexachordal theorem. In E. Chew, A. Childs, and C-H. Chuan, editors, Mathematics and Computation in Music, pages 63–77. Springer, Berlin, 2009. [DGM+05] Erik Demaine, Francisco Gomez, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried Toussaint, Terry Winograd, and David Wood. The distance geometry of deep rhythms and scales. In Proceedings of the 17h Canadian Conference on Computational Geometry, pages 160–163, University of Windsor, Windsor, Ontario, Canada, August 10-12, 2005. [GTT09a] F. Gómez, P. Talaskian, and G.T. Toussaint. Interlocking and euclidean rhythms. Journal of Mathematics and Music, 3(1):15–30, 2009. [GTT09b] F. Gómez, P. Talaskian, and G.T. Toussaint. Structural properties of euclidean rhythms. Journal of Mathematics and Music, 3(1):1–14, 2009. [Góm11] Paco Gómez. Medidas matemática de síncopa (I), 2011. [Kei91] Michael Keith. From Polychords to Pólya: Adventures in Musical Combinatorics. Vinculum Press, Princeton, 1991. [LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983. [PF86] Rolando Antonio Pérez Fernández. La binarización de los ritmos ternarios africanos en América Latina. Casa de las Américas, Havana, 1986. [Thu08] Eric Thul. Measuring the complexity of musical rhythm. Master’s thesis, McGill University, Canada, 2008. [Tou17a] Godfried Toussaint. The geometry of musical rhythm: what makes a “good” rhythm good? CRC Press, Boca Raton, Florida, 2017. [Tou17b] Godfried Toussaint. The geometry of musical rhythm: what makes a “good” rhythm good?, 2017.

Lunes, 16 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico

378. Las matemáticas de la pandemia

Categoría: Divulgación matemática Autores: Manuel de León y Antonio Gómez Corral Editorial: Catarata. Colección ¿Qué sabemos de? Año de publicación:  2020 Nº de hojas: 144 ISBN: 978-84-1352-102-2

Jueves, 12 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

379. Cónicas. Historia de su independencia del cono

Categoría: Divulgación matemática Autores: Agustín Carrillo de Albornoz Torres y Manuel de León Editorial: Catarata. Colección Miradas Matemáticas Año de publicación:  2020 Nº de hojas: 160 ISBN: 978-84-1352-059-9

Jueves, 12 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

380. La geometría de las ciudades

Categoría: Divulgación matemática Autor: José María Sorando Muzás Editorial: Catarata. Colección Miradas Matemáticas Año de publicación:  2020 Nº de hojas: 160 ISBN: 978-84-1352-022-3

Jueves, 12 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más