391. El truco detrás del «misterioso» número 37 y otras fórmulas matemáticas virales

ABC, 28 de Septiembre de 2020 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 28 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

392. 18. (Octubre 2020) Los rectángulos de Mark Rothko

1. Mark Rothko, expresionista abstracto Mark Rothko (2017). Olesya Alexandrovna Denisova El pintor y grabador Marcus Rothkowitz (1903 – 1970), conocido como Mark Rothko, nació en Letonia y vivió en los Estados Unidos. Perteneciente al minimalismo y al expresionismo abstracto, incluyó «manchas» rectangulares en muchas de sus obras de gran formato. Sin temor a equivocarnos podríamos decir que con Rothko el rectángulo es elevado a la categoría de objeto artístico. En lo que sigue ofrecemos una selección del extenso catálogo de sus pinturas rectangulares. 2. Rectángulos artísticos Magenta, Black, Green on Orange (1949) Violet, Black, Orange, Yellow on White and Red (1949) Untitled (1952) Yellow over Purple (1956) Orange and Yellow (1956) White, Red on Yellow (1958) Untitled (Blue divided by Blue, 1966) 3. Arte rectangular Las siete obras anteriores, seleccionadas entre las «pinturas rectangulares» del artista letón Mark Rothko, son suficientes para poner de manifiesto la presencia de los cuadriláteros equiángulos en algunas obras de arte. En ellas, las manchas rectangulares (armónicamente dispuestas) crean una atmósfera cromática que introduce al espectador en un mundo abstracto-conceptual con múltiples interpretaciones. Desde una óptica didáctica creemos que este «arte geométrico minimalista» debe introducirse en las aulas de cualquier nivel educativo. De este modo, los alumnos podrán percibir algunos objetos geométricos 2D como unos seres más atractivos que sus parientes confinados en los manuales consagrados a la enseñanza-aprendizaje de las Matemáticas elementales.   Referencias bibliográficas MEAVILLA SEGUÍ, V. (2007). Las matemáticas del arte. Inspiración ma(r)temática. Córdoba: Editorial Almuzara, S. L.

Jueves, 01 de Octubre de 2020 | Imprimir | PDF |  Correo electrónico

393. 66. (Octubre 2020) Astrolabios universales de rejilla

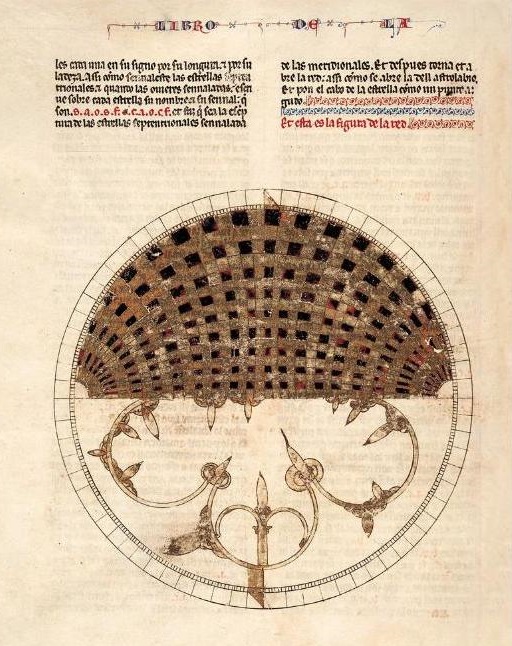
(Araña reticulada. Libro de la lámina. Universidad Complutense. Madrid) La taifa de Toledo fue en el siglo XI un importante centro de actividad matemática. El Libro de las categorías de las naciones del cadí Sa´id al-Andalusí ha dado buena cuenta de ello. Entre los muros de la ciudad se desarrollaron tres instrumentos que simplificaban el astrolabio plano evitando una lámina por cada latitud: la lámina [univeral] de Ali ben Jalaf y los dos tipos de azafea de Azarquiel. Ambas basadas en el cambio del centro y el plano de la proyección estereográfica. En el astrolabio plano (llano le llaman los libros alfonsíes) el centro de proyección es el polo sur mientras que en la lámina y las azafeas es el punto vernal (punto de la eclíptica en el equinoccio de marzo). El plano de proyección pasa a ser el coluro de los solsticios. El cambio de proyección permite un uso universal reduciendo el astrolabio a una sola lámina que queda grabada en la misma madre. La lámina de Jalaf mantiene una red singular: una retícula semicircular y reserva el otro semicírculo como localizador de estrellas. Las azafeas eliminan la red y solo mantienen regletas móviles. Se ha planteado que el tipo de proyección podía haber sido desarrollada por el astrónomo oriental al-Biruní (973-1048) pero no hay certeza y menos que tuviera lugar la transmisión. El uso de una red reticular es muy útil pero hay muy pocas muestras conservadas, quizá por su fragilidad, dificultad constructiva y de lectura. Dado su interés haremos un recorrido por esas láminas universales reticuladas que aparecen por primera vez en Toledo. La lámina de Ali ben Jalaf El descripción detallada que nos ha llegado es El libro de la lámina, que forma parte de los Libros del saber de astronomía alfonsíes, entre el Libro del astrolabio llano y el Libro de la azafea. A diferencia de los demás libros, del de la lámina no existe original árabe, lo que hace el judío redactor Rabiçag es una reconstrucción. En la introducción se atribuye a Jalaf la autoría de la proyección. La realidad parece diferente. La azafea es anterior (sobre el 950) mientras que Jalaf regala el astrolabio al-mamuní al emir (al-Mamun) sobre el año 970. Tenemos constancia, pues, de que la lamina universal fue construida pero ha sufrido la misma suerte que todas las azafeas que salieron de la mano de Azarquiel: no se ha conservado ninguna. (Madre. Libro de la lámina. Universidad Complutense. Madrid) Existen varias copias de los libros alfonsíes, quizá el más bello y antiguo es el de la Universidad Complutense. El de la Biblioteca Nacional reproduce el contenido y las figuras con menos calidad. (Detalle de la retícula. Libro de la lámina. Biblioteca Nacional. Madrid) Una singularidad que no presenta la retícula de los otros astrolabios es que el semicírculo reproduce completos los meridianos y la mitad de los paralelos (o almicantaretes). En los tres conservados de los que vamos a hablar se hace al revés. Astrolabio universal de al-Sarraj El astrolabio conservado más antiguo con rejilla es el fabricado por al-Sarraj (1328): la hermosa araña muestra un semicírculo “enrejado” y el otro con la posición de las estrellas más localizables. Se sabe que al-Sarraj trabajó en Alepo en el siglo XIV y se conserva parte de su obra matemática. Además, el astrolabio tiene grabados los nombres de algunos de sus anteriores propietarios. Probablemente la adquisición de Museo Benaki de Atenas se realizó en El Cairo. El singular y bellísimo astrolabio es un objeto de culto hasta el punto que se comercializan caras reproducciones y que se haya incluido en una esfera de reloj. El astrolabio se exhibió en Sevilla (2006) en la exposición dedicada a Ibn Jaldún. La fina retícula forma una red de 15 x 15 en cada cuadrante (cada 6º). La finura de los arcos de latón hace su lectura muy cómoda. (Faz del astrolabio universal de al-Sarraj . Museo Benaki. Atenas) El astrolabio de al-Sarraj es el único arábigo. Se desconoce si se inspiró en Jalaf o si tuvo noticias de su predecesor. Astrolabio universal de Petrus ab Aggere La Universidad de Lovaina fue durante el siglo XVI un centro destacado en astronomía y geografía. Gemma Frisius (1508-1555) fue la figura impulsora del florecimiento matemático de Flandes. Frisius reinventa el astrolabio universal en   De astrolabio catholico (1556), con un diseño similar al de Azarqiel. Católico significa universal, sin resonancias religiosas. El libro se dedica a Felipe II, soberano de los Países Bajos desde el año anterior. Se puede hablar de una Escuela de Lovaina a la que pertenecerían Gerad Mercator,  Petrus ab Aggere, Hugo Helt, Juan de Rojas y el instrumentista Gualterus Arsenius. Rojas ha dado nombre a una proyección con mucho éxito que sustituyó la estereográfica por la ortogonal sobre el plano meridiano. Es probable que la autoría sea la de Hugo Helt. Tanto Helt como Aggere trabajaron en España. Quizá Aggere tuvo en sus manos alguna copia de los libros alfonsíes. (Astrolabio universal de Aggere. MNCYT. Alcobendas) El Museo Nacional de Ciencia y Tecnología conserva en su sede de Alcobendas (Madrid) un astrolabio universal de rejilla de buena factura. La retícula es de 18 x 9 (cada 5º para los paralelos y 10º para los meridianos). El astrolabio pertenecería a la colección del Instituto San Isidro, heredero del Colegio Imperial. El Museo del Observatorio Adler de Chicago conserva un cuadrante similar que también se atribuye Aggere. La cuadrícula es similar pero con retícula 30 x 18 (cada 3º para los paralelos y 5º para los meridianos). (Cuadrante universal de Aggere. Planetario Adler. Chicago) La construcción de los instrumentos se estima entre 1560 y 1580. Astrolabio universal de Charles Whitwell Charles Whitwell (1568 – 1611) fue un instrumentista inglés asentado en Italia que fabricó para Fernando II de Médici el astrolabio universal que se encuentra en el Museo Galileo de Florencia. La fecha de fabricación es 1595. Whitwell había aprendido en los talleres de Augustine Ryther en Londres. La retícula es de 30 x 6 por cuadrante, 3º entre paralelos y 15º (una hora) entre meridianos). Tras el periodo de esplendor de la segunda mitad del XVI se inicia el declive del astrolabio en Occidente sustituido por nuevos instrumentos. En el mundo islámico pervivirá. (Astrolabio universal de Whitwell . Museo Galileo. Florencia) Un astrolabio escolar El astrolabio de retícula ha sido una rareza en el pasado, su historia ha sido muy corta. La dificultad y fragilidad de la araña anulaba sus ventajas. En cambio hoy puede tener nueva vida. La red puede sustituirse con ventaja por un acetato (una transparencia) imprimible. El astrolabio con retícula explica muy bien la distinta duración de los días según las estaciones y las diferentes elevaciones del sol. Reproducimos un diseño inspirado en el reloj universal del libro de navegación de Rodrigo Zamorano (Compendio de la arte de navegar. Sevilla, 1581). La proyección es ortográfica, tipo Rojas: los paralelos (y almicantaretes) son rectas y los meridianos elipses. Con los actuales programas de diseño gráfico su construcción es inmediata. La retícula ayuda la lectura de forma que su uso en la enseñanza puede ser más que una curiosidad para los talleres de astronomía. Lo que realmente hace el astrolabio (o reloj universal) es un cambio mecánico de coordenadas ecuatoriales a horizontales: se pasa de ángulo horario y declinación solar a acimut y elevación. (Astrolabio universal de uso escolar . Recreación del Reloj de Rodrigo Zamorano)

Jueves, 01 de Octubre de 2020 | Imprimir | PDF |  Correo electrónico

394. Grandes matemáticos y matemáticas en imágenes (2): Hipatia de Alejandría

1. Hipatia, la mujer y la obra Hipatia, hija de Teón (ca. 335 – ca. 405), admirada por su belleza y modestia, nació en Alejandría sobre el año 370 y fue la primera mujer en formar parte de la lista de matemáticas famosas. También destacó en Medicina y Filosofía. A los treinta años de edad se convirtió en la directora de la escuela neoplatónica de Alejandría y en dicha institución se dedicó a la enseñanza de las Matemáticas y la Filosofía. Al parecer, fue una profesora muy carismática. Siguiendo a L. Figuier (1866), las lecciones de Hipatia empezaban por la enseñanza de las Matemáticas; acto seguido, pasaba a las aplicaciones de las Matemáticas y a las diferentes ciencias que configuraban la filosofía antigua. Escribió una obra titulada Canon astronómico y colaboró con su padre en la redacción de algunos comentarios sobre el Almagesto de Ptolomeo (ca. 85 – ca. 165) y en una versión de los Elementos de Euclides. También escribió comentarios sobre la Aritmética de Diofanto (ca. 200 – ca. 284), las Cónicas de Apolonio (ca.262 a.C. – ca. 190 a.C.) y los trabajos astronómicos de Ptolomeo. Desgraciadamente, todas sus obras se han perdido. Hipatia fue una excelente compiladora, editora y conservadora de los textos matemáticos antiguos. De su correspondencia con el filósofo cristiano Sinesio de Cirene (ca. 370 – 413) se desprende que diseñó algunos instrumentos científicos como el astrolabio y el hidroscopio. Siendo un fiel exponente de la «cultura pagana», Hipatia se ganó la enemistad de la comunidad cristiana de Alejandría, algunos de cuyos miembros la asesinaron en plena calle el mes de marzo de 415. Louis Figuier describe este episodio detestable en los siguientes términos: La multitud se amotinó contra la filósofa, se dirigió tumultuosamente hacia su casa y la esperó en la puerta, sabiendo que pronto debía volver del Museo. Hipatia, en efecto, no tardó en aparecer montada en su carro. Uno se precipitó sobre ella, la obligó a descender y la arrastró hacia una iglesia. Allí, aquellos exaltados, después de despojarla de sus vestiduras, la lapidaron con trozos de tejas y jarrones rotos. 2. Pinturas y dibujos La escuela de Atenas (1510 – 1511). Pintura al fresco (500 770 cm). Rafael Sanzio (1483 – 1520). Museos Vaticanos. La escuela de Atenas (detalle). Hipatia entre Parménides (derecha) y Pitágoras (izquierda) En el célebre cuadro La escuela de Atenas, Rafael Sanzio representó a Hipatia con el rostro de su amante Margherita Luti «la fornarina». Hipatia (1885). Óleo sobre tela (244,5 152,5 cm) Charles William Mirchell (1854 – 1903) Hipatia (1889). Óleo. Julius Kronberg (1850 – 1921) Muerte de la filósofa Hipatia en Alejandría Ilustración del libro Vies des Savants de l’Antiquité (1866) Hipatia (1897). Edmund H. Garret (1853 – 1929) Hipatia (1908). Jules Maurice Gaspard (1862 – 1919) 3. Esculturas Hypathia Attacked by the Monks (1873-77) Howard Roberts (1843 – 1900) Pensilvania. Academia de Bellas Artes Hipatia (1874). Odoardo Tabacchi (1831 – 1905) Hipatia. Richard Claude Belt (1851 – 192) 4. Grafiti Grafiti científico https://www.madrimasd.org/blogs/matematicas/2010/06/09/131858 Hipatia El 12 y 13 de noviembre de 2009, una decena de estudiantes no universitarios dieron forma a un grafiti de contenido científico. Esta iniciativa había sido organizada por el ICMAT (Instituto de Ciencias Matemáticas), el CSIC (Consejo Superior de Investigaciones Científicas), UAM (Universidad Autónoma de Madrid), UC3M (Universidad Carlos III de Madrid), UCM (Universidad Complutense de Madrid), el IES «Ramiro de Maeztu de Madrid», y el IES «Beatriz Galindo» de Madrid. El proyecto fue dirigido por el artista digo.aRt y se materializó en las proximidades del IES «Ramiro de Maeztu», la Residencia de Estudiantes y el campus del CSIC. Además del retrato de Einstein, el grafiti incluye un grupo de poliminósi, la identidad de Eulerii, las matemáticas de los paneles hexagonales, el sistema solar de Johannes Kepler, la palabra «mates», y el retrato de Hipatia. 5. Hipatia en la literatura Las tres portadas anteriores corresponden a distintas ediciones de la novela Hypatia, or New Foes with and Old Face escrita por Charles Kingsley (1819 – 1875). La ilustración anterior, creada por John D. Batten (1860 – 1932), corresponde a una obra de teatro en cuatro actos escrita por G. Stuart Ogilvie y basada en la novela de Charles Kingsley. 6. Fotografías Hipatia (1867). Fotografía de Julia Margaret Cameron (1815 – 1879) Modelo: Marie Spartali Stillman (1844 – 1927) La actriz Julia Neilson (1868 – 1957) caracterizada como Hipatia (ca. 1890) La actriz Mary Anderson (1859 – 1940) caracterizada como Hipatia (1900) 7. Hipatia en el cine La figura de Hipatia que, hasta hace bien poco, sólo era conocida por los estudiosos se ha convertido en un personaje popular gracias a la película Ágora dirigida por el español Alejandro Amenábar. En ella, la actriz y modelo británica Rachel Weisz da vida a la matemática de Alejandría.   Referencias bibliográficas CAJORI, F. (1980). A history of Mathematics (tercera edición). New York: Chelsea Publishing Company. EVES, H. (1983). An introduction to the history of Mathematics (quinta edición). New York: Saunders College Publishing. FIGUIER, L. (1866). Vies des Savants de l’Antiquité. Paris: Librairie Internationale. SMITH, D. E. (1958). History of Mathematics (dos volúmenes). New York: Dover.   Referencias online https://mujeresconciencia.com/2015/06/15/hipatia/ https://mathshistory.st-andrews.ac.uk/Biographies/Hypatia/   NOTAS i Se llama poliminó a la figura geométrica obtenida al juntar cuadrados lado a lado. ii eπi+1=0.

Viernes, 25 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

395. Hermann von Reichenau (1013-1054)

Hermann der Lahme, Mönch des Klosters Reichenau El erudito, compositor, matemático y astrónomo Hermann von Reichenau (1013-1054) –Hermannus Contractus debido a algún defecto físico que padecía– falleció un 24 de septiembre. Desarrolló su propia notación musical y parece que compuso el Alma Redemptoris Mater, el Salve Regina y quizás el Ave Regina. Trabajó en astronomía –sobre todo en la descripción de astrolabios, sus escritos incluyen De Mensura Astrolabii, una revisón de los escritos de Gerbert d’Aurillac, y De Utilitatibus Astrolabii– e hizo algunas aportaciones en gnomónica. Más información: Hermann of Reichenau, University of  St. Andrews Hermann der Lahme, Mönch des Klosters Reichenau Wikipedia Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 24 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

396. 16. (Septiembre 2020) Dick Termes: su obra artística al margen de las esferas

En otro artículoi hemos prestado atención a las pinturas acrílicas de Dick Termes sobre lienzos esféricos. Dick Termes con una de sus TERMESferas En esta ocasión presentamos una colección de obras del artista estadounidense realizadas sobre otro tipo de soportes y relacionadas con objetos matemáticos. 1.  TERMESpoliedros 1.1. Rombododecaedro El rombododecaedro es uno de los trece sólidos de Catalan cuyas doce caras son rombos congruentes. Tiene veinticuatro aristas y catorce vértices. Es el poliedro conjugado del cuboctaedroii. Rombododecaedro Cuboctaedro Rombododecaedro y cuboctaedro conjugados La escena de Flat Sphere está construida sobre un rombododecaedro Flat Sphere (1988) 1.2. Dodecaedro En esta obra, Termes se sirve de una perspectiva con seis puntos de fuga situados en los puntos medios de algunas aristas del dodecaedro. En los árboles se adivinan varios rostros humanos. Dodecperspective (1989) 1.3. Icosaedro Como en la pintura anterior, el artista afincado en Dakota del Sur utiliza una perspectiva con seis puntos de fuga ubicados en los puntos medios de ciertas aristas de un icosaedro Icosa Painting (1991) 1.4. Pirámides En las dos obras siguientes, Dick Termes se sirve de las pirámides. En la primera, Cluster of Tetra Homes presenta una cadena de tetraedros, cada uno de los cuales representa una habitación. Cuando dichos poliedros se acoplan (cara con cara), el objeto resultante sigue siendo una habitación cada vez más grande. En la segunda, Lakota Headmen, dos pirámides hexagonales, unidas por sus bases, recrean un «tipi» en cuyo interior están reunidos los jefes del pueblo Lakotaiii. Cluster of Tetra Homes (1996) Lakota Headmen (1999) 2. Semiesferas Concavex Room (2019) Además de sus famosas termesferas, el artista norteamericano también representa sus pinturas en  soportes semiesféricos Así, por ejemplo, en su Concavex Room, utiliza las superficies cóncava y convexa de media esfera para mostrar una habitación completa. En otras palabras, una mitad de la habitación se ve desde el interior y la otra mitad desde el exterior. En ocasiones, cuando miras la semiesfera, es difícil saber si lo que ves es la parte cóncava o la convexa. 3. TERMESdibujos Además de sus pinturas tridimensionales, el artista afincado en Spearfish (Dakota del Sur) tiene un surtido catálogo de dibujos 2D. Veamos algunos de ellos. 3.1. Figuras imposibles Los dibujos anteriores pertenecen a la misma categoría de figuras imposibles que el famoso y popular elefante del psicólogo californiano Roger Shepard (1929). 3.2. Laberintos con rostro Dentro del fascinante mundo de los laberintos[iv], los más simples son los llamados univiarios. En ellos, una vez que se cruza la puerta de entrada, es preciso recorrer todo el circuito para llegar al centro. En otras palabras: en este tipo de dédalos no se ofrece la posibilidad de tomar caminos alternativos, no hay encrucijadas, y la puerta por la que se sale es la misma por la que se entra. En consecuencia, en estos recorridos es imposible perderse. En los dos dibujos siguientes, Dick Termes nos ofrece un par de laberintos univiarios con rostro. 3.3. Bocetos para termesferas Los dibujos precedentes son dos ejemplos de bocetos 2D para creaciones tridimensionales. 4. Inspiración matemática Este artículo que acaba de concluir, junto con el que dedicamos a las termesferas, ofrece suficientes ejemplos para concluir que el pintor Dick Termes recurre a las Matemáticas para estructurar algunas de sus obras. Esta inspiración ma(r)temática, presente en las producciones artísticas de muchos creadores, justifica, a nuestro modesto entender, la inclusión del arte-matemático (Arte para matemáticos) y de la matemática-artística (Matemática para artistas) en los planes de estudio de los artistas y matemáticos.   Referencias bibliográficas LUCAS, E. (1891). Récréations Mathématiques (Segunda edición, cuatro tomos). Paris: Gauthier-Villars et Fils, Imprimeurs-Libraires MEAVILLA SEGUÍ, V. (2007). Las matemáticas del arte. Inspiración ma(r)temática. Córdoba: Editorial Almuzara, S. L.   Referencias online https://culturacientifica.com/2014/02/26/el-rombododecaedro-estrellado-arte-abejas-y-puzzles-primera-parte/   NOTAS i Las TERMESferas: pinturas singulares sobre lienzos esféricos, publicado en Divulgamat ii Poliedro arquimediano con ocho caras triangulares y seis cuadradas. Tiene doce vértices y veinticuatro aristas. iii Los lakota son un pueblo perteneciente a la tribu sioux. Vivían en las márgenes del norte del río Misuri. iv El lector interesado puede consultar la tercera recreación (Le Jeu des labyrinthes) del primer tomo de las Récréations Mathématiques (1891) de Édouard Lucas.

Jueves, 24 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

397. 17. (Septiembre 2020) Las TERMESferas: pinturas singulares sobre lienzos esféricos

Conocí la obra de Dick Termes cuando, allá por el 2006, estaba ocupado en la redacción de un libro sobre las Matemáticas del Artei. Recuerdo que me llamó mucho la atención el soporte sobre el que el artista norteamericano pintaba sus acrílicos: la esfera. De ahí que las creaciones de Termes son conocidas universalmente con el nombre de Termespheres. En las líneas que siguen ofrecemos una muestra de su producción esférica y algunos comentarios relativos a su contenido. 1. ¿Qué son las termesferas? Dick Termes en su Termesphere Gallery de Spearfish (Dakota del Sur) Para entender el concepto de termesfera nada mejor que recurrir a algunas explicaciones y comentarios de su autor: Imagina que estás de pie en el interior de una esfera transparente suspendida a cincuenta pies de altura sobre el suelo del Gran Cañón. Tú estás más arriba que algunas paredes del cañón y más abajo que otras. Tienes pintura y un pincel, y empiezas a pintar lo que ves en la superficie interior de la esfera. Pintas la cara norte, después la este, la sur y la oeste. Finalmente, pintas todo lo que ves encima y debajo de ti. Pones la esfera en lugar seguro, sales de ella y observas lo que has pintado. Entra en una esfera transparente. Con la cabeza en el centro copia en la superficie   interior todo lo que veas fuera de ella. Cuando lo hayas copiado todo, sal de la esfera y mira lo que has pintado. Lo que ves cuando miras una Termesfera es una ilusión óptica. Para ilustrar la información precedente presentamos dos fotografías del Panteón de Agripa (Roma) y sus «imágenes asociadas» en The Pantheon (1998), una de las termesferas favoritas de Dick. 2. Galería de imágenes comentadas 2.1. Relación platónica Platonic Relationship (1993) En la web oficial de D. Termes leemos: Esta esfera estudia las relaciones entre los cinco poliedros regulares. A veces son los vértices, otras las aristas y, en ocasiones, las caras las que se relacionan unas con otras. Tomé los triángulos del octaedro, tetraedro e icosaedro y los convertí en una forma toroidal. Los pentágonos del dodecaedro y los cuadrados del cubo también se convirtieron en formas toroidales. Cuanto más pequeño era el número de lados más grueso hice el toro. Cada poliedro fue identificado con  un color diferente para que se pudiera ver cuando la esfera giraii. Se entrelazan entre sí por dentro y por fuera de modo que todos tienen la oportunidad de estar al frente parte del tiempo. A partir del párrafo anterior somos incapaces de decidir cuál es la «relación platónica» que da nombre a la termesfera.  Quizás, el artista afincado en Dakota del Sur se refiere a la relación de conjugacióniii que liga el cubo con el octaedro, el dodecaedro con el icosaedro y el tetraedro consigo mismo. 2.2. Esfera angélica Order of the Angels (2000) En esta termesfera las cabezas de los ángeles están en los vértices de un icosidodecaedro (dodecaedro truncado). Este poliedro arquimediano tiene veinte caras triangulares, doce caras pentagonales, treinta vértices y sesenta aristas. Icosidodecaedro 2.3. Sinfonía de rombos Which Way (2003) El «universo» recreado en esta obra es el esqueletoiv de un triacontaedro rómbicov. Triacontaedro rómbico 2.4. Cubos, cuadrados y espirales Square Dance (2018) Sea ABCD un cuadro. Si sobre sus lados se eligen cuatro puntos A´, B´, C´ y  D´ tales que AA´= BB´= CC´ = DD´ = k, entonces el cuadrilátero A´B´C´D´ también es un cuadrado. Si sobre los lados de A´B´C´D´ se eligen cuatro puntos A´´, B´´, C´´ y  D´´ tales que A´A´´ = B´B´´ = C´C´´ = D´D´´ = k, entonces el cuadrilátero A´´B´´C´´D´´ también es un cuadrado. Si se repite este mismo procedimiento ocho veces más se obtiene una figura (véase el dibujo siguiente) en la que aparecen cuatro poligonales formadas por segmentos rectilíneos de la misma longitud cuyos extremos son los vértices del cuadrado original y los vértices del cuadrado más pequeño. Resulta claro que cuanto menor sea k dichas poligonales se aproximan más a espirales. Vicente Meavilla. Triangles and squares (2020) Pues bien, si en las seis caras de un cubo se aplica la misma técnica, entonces se generan veinticuatro «espirales». Estas curvas son las que representa Dick Termes en su Square Dance. 2.5. Pitagorismo y puntillismo Pitágoras (s. VI a. C.) y sus discípulos, los pitagóricos, utilizaron como señal de identificación el pentágono regular estrellado, llamado «pentalfa», obtenido al trazar todas las diagonales de un pentágono regular. Dichas diagonales se cortan en cinco puntos que determinan otro pentágono regular a partir del cual se genera una nueva estrella de cinco puntas. Este proceso se puede prolongar ad infinitum. Estas sucesiones de pentágonos regulares estrellados son las protagonistas de la siguiente termesfera. Seurat’s Stars (2018) Si a las consideraciones precedentes añadimos que, en esta ocasión, Termes utiliza la técnica del puntillismovi para pintar su esfera, no debe extrañarnos el título de esta obra tridimensional. 3. Esferas, geometría, y reflexiones de carácter En las líneas precedentes hemos prestado atención a algunas obras de contenido geométrico creadas por el artista norteamericano Dick Termes. Dichos acrílicos, pintados sobre esferas, nos han permitido conectar el Arte con diversos objetos de la geometría 2D y 3D (pentágonos regulares estrellados, espirales poligonales, poliedros conjugados, poliedros arquimedianos, sólidos de Catalan). Esta conexión, nos anima a proponer que en la formación académica de los artistas se debería incluir alguna asignatura en la que se estudiasen (desde una óptica puramente descriptiva) algunos tópicos matemáticos. Por otro lado, no sería desdeñable que en la formación de los futuros docentes se incluyesen algunos contenidos transversales que mostrasen la presencia de ciertos  objetos matemáticos en las obras artísticas.   Referencias bibliográficas GARCÍA FERNÁNDEZ, L. (1981). Poliedros regulares y arquimedianos. Sociedad Canaria de Profesores de Matemáticas. MEAVILLA SEGUÍ, V. (2007). Las matemáticas del arte. Inspiración ma(r)temática. Córdoba: Editorial Almuzara, S. L.   Referencias online Dick Termes (web oficial) https://termespheres.com/   AGRADECIMIENTO Agradecemos a nuestro buen amigo y colega Alfinio Flores (profesor jubilado de la University of Delaware) su ayuda a la hora de traducir los textos originales.   NOTAS i En aquella ocasion, Dick nos facilitó un CD y dos diapositivas con muchas fotografías de sus termesferas. Al mismo tiempo, nos remitió información sobre su Galería en Spearfish (Dakota del Sur). ii En un video que acompaña  a la información de la web oficial se declara que el color rojo corresponde al icosaedro, el verde, al tetraedro y el amarillo, al dodecaedro. Sin embargo, debido a deficiencias en el sonido, no hemos podido descubrir los colores que corresponden al octaedro y al cubo. iii Dos poliedros regulares se llaman conjugados cuando los vértices de uno de ellos coinciden con los centros de las caras del otro. El tetraedro regular es conjugado de sí mismo. El cubo y el octaedro regular son conjugados. El dodecaedro regular y el icosaedro regular son conjugados. iv Estructura formada por las aristas de un poliedro. v El triacontaedro rómbico es un sólido de Catalan cuyas treinta caras son rombos congruentes. Tiene sesenta aristas y treinta y dos vértices. Es el poliedro conjugado del icosidodecaedro. vi Técnica pictórica creada por el impresionista francés Georges-Pierre Seurat (1859 – 1891).

Jueves, 24 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

398. Dénes Kőnig y la teoría de grafos

El matemático Dénes Kőnig (1884-1944) nació un 21 de septiembre. Su padre fue el también matemático Gyula Kőnig. Se doctoró en 1907 en la –hoy en día, antes Instituto Técnico de Budapest– Universidad de Tecnología y Economía de Budapest, con una tesis supervisada por József Kürschák y Hermann Minkowski. En 1936, publicó el libro Theorie de endlichen und unendlichen Graphen –Teoría de grafos finitos e infinitos–, que contribuyó al crecimiento del interés por la teoría de grafos en todo el mundo. Se publicó en inglés en 1990 –Theory of finite and infinite graphs–, traducido por Richard McCoart y comentado por William Thomas Tutte. En el prefacio del libro, argumenta que su planteamiento es puramente combinatorio, no topológico (cita extraída de [2]): … mainly because we attribute to the elements of a graph –vertices and edges– no geometrical content at all: the vertices are arbitrary distinguishable elements, and an edge is nothing other than a unification of its two endpoints. This abstract point of view –which Sylvester emphasized in 1873– will be strictly maintained in our representation, with the exception of some examples and applications. Se le debe teorema de König (1931) sobre grafos bipartitos –probado independientemente, en 1931, por Jenő Egerváry– y el lema de König (1936) sobre la existencia de caminos infinitos sobre un grafo. Escribió dos textos sobre matemática recreativa Mathematikai mulatságok –Entretenimientos matemáticos– en 1902 y 1905, en los que parece (ver [3]) que ya tenía en mente la teoría de grafos. Más información: [1] Índice de Theorie der endlichen und unendlichen Graphen [2] Dénes Kőnig, MacTutor History of Mathematics archive, University of St. Andrews [3]  Mitsuk Wate Mizuno, The works of König Dénes (1884-1944) in the domain of mathematical recreations and his treatment of recreational problems in his works of graph theory, Université de Paris VII, 2010 Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Lunes, 21 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

399. Grandes matemáticos y matemáticas en imágenes (1): Luca Pacioli

Con este artículo iniciamos una serie (Grandes matemáticos y matemáticas en imágenes) de monografías en las que ofreceremos imágenes (cuadros, esculturas, fotografías, sellos de correos, etc.) concernientes a la vida y la obra de algunos matemáticos y matemáticas famosos, acompañadas, cuando sea pertinente, de breves comentarios aclaratorios. En cualquier caso, el catálogo de imágenes irá precedido de una biográfica del científico al que se dedique el estudio. 1. Luca Pacioli, el hombre y la obra Luca Pacioli nació en Borgo de Sansepolcro (Italia) en 1445 y posiblemente recibió sus primeras lecciones de Geometría en el taller de su paisano el matemático y Pintor Piero della Francesca (1412 – 1492). A los veinte años abandonó su ciudad natal y se trasladó a Venecia donde fue preceptor de los dos hijos del comerciante Antonio Rompiasi y prosiguió sus estudios de Matemáticas en una escuela pública dependiente de la universidad veneciana. En 1470, tras la muerte de Antonio, dejó Venecia y pasó a Roma invitado por el arquitecto León Battista Alberti (1404 – 1472), uno de los primeros investigadores de la perspectiva geométrica. Dos años más tarde ingresó en la orden de San Francisco de Asís. En 1475 fue lector de Matemáticas en Perugia y entre 1477 y 1480 dio clases de aritmética en la universidad de dicha ciudad. En 1481 se trasladó a Zara (actual Croacia) donde escribió un manual de aritmética. Después de una corta estancia en Florencia volvió a Perugia, obtuvo el título de Magister y explicó Matemáticas desde 1486 hasta 1487. Debido al agotamiento y a su frágil salud dejó la docencia y se instaló en Roma. En 1490 enseñó Teología y Matemáticas en Nápoles y realizó una colección de poliedros regulares que regaló a Guidobaldo de Montefeltro, duque de Urbino. Desde 1490 a 1493 permaneció en su pueblo natal preparando la publicación de su obra Summa de arithmetica geometria proportioni et proportionalità. En 1493 dio lecciones de Matemáticas en Padua. En 1494, una vez acabada la redacción de la Summa, marchó a Venecia para supervisar los trabajos de impresión. En 1496 Pacioli viajó a Milán para enseñar Matemáticas en la corte del duque Ludovico Sforza «il Moro» (1452 – 1508). Allí conoció a Leonardo da Vinci (1452 – 1519) que realizó los dibujos de los sesenta cuerpos geométricos que aparecen en su libro De divina proportione, redactado durante esta etapa milanesa. En 1499 Milán fue ocupada por las tropas francesas y Ludovico el Moro fue hecho prisionero. Por este motivo, Luca y Leonardo abandonaron la ciudad pasando primero a Mantua, luego a Venecia y finalmente a Florencia. En 1500 Pacioli se convirtió en profesor de la universidad de Pisa, cuya sede se había trasladado a Florencia desde las revueltas ciudadanas de 1494. Allí continuó su labor docente hasta 1505. No obstante, entre 1501 y 1502 dio clases de Matemáticas en la universidad de Bolonia donde coincidió con Scipione del Ferro (1465 – 1526), uno de los grandes algebristas italianos que intervino en la resolución por radicales de la ecuación de tercer grado con una incógnita. En 1505 regresó a Roma y en 1508 viajó a Venecia. En dicha ciudad vio la luz la primera edición impresa de De divina proportione. En 1510, debido a su delicada salud, volvió a su ciudad natal. Sin embargo, a instancias del Papa León X, en 1514 volvió a Roma y fue profesor de la Sapienza, la universidad de la «ciudad eterna». Luca Pacioli murió en Borgo de Sansepolcro en torno al 1517. 2. Los cuadros y el fresco Sacra Conversazione (Palla de Brera) (1472 – 74). Temple sobre tabla (248 x 150 cm) Piero della Francesca. Pinacoteca de Brera En dicho cuadro el fraile que aparece en segundo plano tiene los rasgos de Luca Pacioli. Retrato de Luca Pacioli (1495). Témpera sobre panel (98 x 108 cm). Atribuido a Jacopo de Barbari (1450 – 1516). Museo Capodimonte (Nápoles) La mayor parte de la superficie del cuadro está ocupada por dos personajes. Uno de ellos, el fraile franciscano Luca Pacioli, parece estar explicando al otro (posiblemente Guidobaldo de Montefeltro, duque de Urbino) algún teorema geométrico contenido en un tratado matemático. En la pizarra que se apoya sobre la mesa puede leerse la palabra EUCLIDES. Además, sobre el libro cerrado de tapas rojas descansa un dodecaedro regular y a la derecha de Luca, colgado del techo, puede verse un poliedro arquimediano transparente (el rombicuboctaedro) compuesto por dieciocho caras cuadradas y ocho caras triangulares. Leonardo da Vinci con Luca Pacioli y Ludovico Sforza (ca. 1841). Fresco. Nicola Ciafaneli (1793 – 1848). Tribuna de Galileo (Florencia) Luca Pacioli acabó de redactar su De divina proportione en diciembre de 1498 y mandó realizar tres manuscritos. Regaló uno de ellos a Ludovico Sforza «il Moro». En el fresco anterior Leonardo sostiene un rollo que bien podría contener algún boceto de sus ilustraciones. Piero della Francesca dicta las reglas de la Geometría a Luca Pacioli. Óleo sobre tela. Angelo Tricca (1817 – 1884). Museo Civico di Sansepolcro En su juventud, Luca Pacioli posiblemente recibió lecciones de Geometría de Piero della Francesca. Por aquel entonces Luca no había ingresado en la orden de San Francisco de Asís. Por consiguiente, el óleo de Tricca no se ajusta a la biografía del matemático del Borgo de Sansepolcro. 3. Las miniaturas Retrato-miniatura de Luca Pacioli El grabado anterior, en el que se reproduce la figura de Luca Pacioli, se encuentra en distintas ediciones de la Summa de arithmetica geometria proportioni et proportionalità. En la de 1523, que hemos consultado, aparece en el prefacio de la obra. Luca Pacioli presenta a Ludovico Sforza su De divina proportione La miniatura anterior está contenida en el manuscrito de De divina proportione que Pacioli regaló a Ludovico Sforzai. Sobre la imagen se lee la siguiente inscripción: EX[cellentissi]MO P[rincipi] LUDOVICO M[ariae] SF[ortiae] AN[gliae] MEDIOLANE[nsi] DUCI INCLITO PACIS ET BELLI ORNAMENTO FR[atris] LECE EX BURGO S[ancti] SEPULCRI OR[dinis] MI[norum] SACRAE THEOL[ogiae] PROFES[soris] DE DIVINA PROPORT[ione] EPISTOLA. 4. Las esculturas Homenaje a Luca Pacioli. Eduardo Chillida (1986) Busto de Luca Pacioli. Juan Rosillo Busto de Luca Pacioli. Karen Blakeman (2014) Luca Pacioli en la Plaza de San Francisco (Sansepolcro). Franco Alessandrini (1994) En el pedestal y la base de la escultura de la Plaza San Francisco leemos: LVCA PACIOLI SVMMA 1494        1994 I CONCITTADINI E LE SCUOLE DI RAGIONERIA IN GIAPPONE AL PATRIARCA DELLA COMPUTISTERIA SUI LAUDE ET CLORIAii 5. Placa conmemorativa en Sansepolcro A LUCA PACIOLI CHE EBBERO AMICO E CONSULTORE LEONARDO DA VINCI E LEON BATTISTA ALBERTI CHE PRIMO DIE ALL ALGEBRA LINGUAGGIO E STRUTTURA DI SCIENZA AVVIO IL GRAN TROVATO DI APPLICARLA ALLA GEOMETRIA INVENTO LA SCRITTURA DOPPIA COMMERCIALE DETTO OPERE DI MATEMATICA BASE E NORMA INVARIATE ALLE POSTERE LUCUBRAZIONI ______________ IL POPOLO DI SANSEPOLCRO AD INIZIATIVA DELLA SUA SOCIETA OPERARIA VERGOGNANDO 370 ANNI DI OBLIO AL GRAN CONCITTADINO PONEVA 1878 6. Medallas, moneda y sellos Medalla de Luca Pacioli. Henry Lagriffoul (1907 – 1981) Medalla de Luca Pacioliiii Moneda de 500 liras, conmemorativa de los 500 años de la publicación de la Summa de arithmetica geometria proportioni et proportionalità   Referencias bibliográficas PACIOLI, L. (1523). Summa de arithmetica geometria proportioni et proportionalità. Venecia: Paganino de Paganini. PACIOLI, L. (1991). La divina proporción (Introducción de Antonio M. González. Traducción de Juan Calatrava). Madrid: Ediciones Akal, S. A.   Referencias online https://it.wikipedia.org/wiki/Luca_Pacioli https://mathshistory.st-andrews.ac.uk/Biographies/Pacioli/ http://jeff560.tripod.com/stamps.html   NOTAS i Dicho manuscrito se conserva en la Biblioteca Pública de Ginebra. ii Debajo del texto en italiano aparecen unos caracteres japoneses. iii El año de fallecimiento es incorrecto.

Jueves, 17 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

400. Septiembre 2020: El cálculo se domina con el juego

Introducción. De los múltiples recursos didácticos que pueden usarse en el aula de matemáticas, uno de los más interesantes es el juego. Al llevar a clase un juego se crea un ambiente lúdico que resulta atractivo para el alumnado, creando una expectativa que hace que, de entrada, todo el mundo quiera participar y que anima a implicarse en él, especialmente si podemos quedar por encima de los contrincantes. La implicación en esos juegos es mayor si es un juego conocido fuera del ambiente escolar y del que se conoce la dinámica de juego por haberlo practicado en otras situaciones. Esto ocurre con los puzles, los juegos de cartas, los de dados y, dado que es uno de los más versátiles, el dominó. Aunque ahora priman los regalos tecnológicos, hasta hace muy poco no era raro que los pequeños recibieran como regalo navideño un dominó, que no tenía que ser necesariamente el tradicional con puntos. Muchos hemos jugado con dominós de colores, con figuras o con personajes de mayor o menor actualidad. Por ello, la dinámica del juego es relativamente conocida por todos. El dominó tiene la ventaja de que no requiere unas reglas complicadas y que inmediatamente todo el mundo puede comenzar a jugar. Su facilidad para ser adaptado lo convierte en un recurso muy potente para practicar matemáticas, pues podemos crear dominós con conceptos de todas las áreas matemáticas de las que se imparten en los niveles no universitarios. Con dominós adaptados es posible trabajar casi cualquier ítem didáctico, pero con el dominó clásico de 28 fichas con los valores desde el cero hasta el seis, también se pueden trabajar aspectos matemáticos. Aunque la manera usual de jugar al dominó no requiere ningún tipo de cálculo, pues basta unir unas distribuciones de puntos con las mismas distribuciones, el hecho de que en cada cara de una ficha haya una puntuación permite realizar cálculos de una manera entretenida y fácil, con lo que se pueden repasar las bases del cálculo de una forma atractiva. La numeración anterior permite que existan multitud de retos en los que aparecen dominós. No es raro revisar cualquier documentación importante sobre matemática recreativa, y encontrar pasatiempos y rompecabezas en las que se utilizan las fichas de este juego. Ya en la sección de juegos de la revista SUMA se publicó en 2012 un artículo donde se planteaban desafíos para resolver con las fichas típicas del dominó, desde operaciones de sumas y productos hasta puzles y cuadrados mágicos conseguidos con ese material1. En este caso vamos a presentar una serie de juegos de cálculo en los que se trabaja también con las fichas del dominó clásico del doble seis, es decir, las 28 fichas que van desde la blanca doble hasta el seis doble. Estos juegos nos servirán para repasar operaciones aritméticas o trabajar con fracciones. La ventaja de usar el dominó es que los alumnos van a tener, de forma aleatoria, una serie de valores con los que realizar cálculos, por lo que si se juegan diferentes partidas, pues todas ellas suelen ser rápidas, en cada caso van a tener que operar con números diferentes. Voy a partir del supuesto de que el alumnado conoce la dinámica del juego básico, aunque mi experiencia es en que los últimos años cada vez hay más alumnos que no conocen el juego. 1. Sumar seis. Este juego tiene el objetivo de repasar, utilizando el cálculo mental, las sumas con números hasta el seis. Se juega sin dobles, es decir, con las 21 fichas del dominó donde no se repiten valores en las mismas fichas. Está previsto para que jueguen tres jugadores, repartiéndose todas las fichas. También pueden jugar dos o cuatro jugadores, en ese caso se aparta una ficha al azar, que se colocará como comienzo de la cadena, y las restantes se reparten proporcionalmente. Hay que formar una cadena de fichas, igual que en el dominó normal, pero en lugar de emparejar una parte de la ficha de uno de los extremos con otra ficha que tenga la misma distribución, hay que unirla a otra ficha de forma que los dos trozos que se unan sumen seis. Imagen 1: Partida de sumar seis. La dinámica es la misma que en el original y gana el primero que se queda sin fichas. Si en un momento se bloquea la partida gana el jugador que tengan menos puntos en la mano. Hay una variedad que consiste en usar también los dobles, pero en ese caso se colocan en la misma dirección que le resto de las fichas, no cruzados como es habitual. Imagen 2: Sumar seis con dobles. Se puede modificar el valor que se quiere obtener al sumar, pero para ello es imprescindible eliminar fichas del juego. Por ejemplo, si queremos que al unir dos fichas los trozos que se unen sumen cinco, debemos quitar las siete fichas que tienen seis. Si queremos que el valor a obtener sea siete debemos quitar las blancas. En estos casos se juega con 21 fichas como en el caso primero. Si se dispone de la posibilidad de jugar con un dominó doble 9, el que dispone de 55 fichas, se puede jugar quitando las blancas, lo que reduce el número a 45 y entonces pueden jugar más alumnos, pudiendo dejar varias de las fichas en un montón para robar cuando no se tenga ficha que poner. En este caso se puede plantear que las dos fichas que se unan sumen 10 con lo que se amplían las posibilidades. 2. Matador. Aunque el juego del dominó está muy extendido por el mundo, la forma de jugar varía de unos países a otros, encontrándose opciones en las que no es necesario solamente repetir los elementos que se unen, sino también hacer alguna pequeña operación. Similar al que hemos propuesto antes es el juego conocido como Matador, que creo que es de origen ruso. En él, hay que colocar una ficha junto a una de los extremos de la cadena de forma que sumen siete. Se juegan con todas las fichas y, como es de suponer, cuando se coloca una ficha que termina en blanca, el juego se bloquea por esa parte pues ya no se puede sumar siete con ninguna ficha. Entonces se pueden utilizar las fichas que se llaman matadores que son las que tienen como valores 1 – 6, 2 – 5 y 3 – 4, considerándose también a la blanca doble como matador. Las fichas llamadas matadores se pueden colocar en cualquier momento y se colocan de forma perpendicular a la cadena formada (como un doble en el juego clásico) mientras que el resto de dobles se colocan de forma lineal con las restantes fichas no dobles. Cuando se coloca un matador, el jugador que continúa la jugada debe colocar una ficha cuya parte sume siete con cualquiera de las dos cifras que forman parte de la ficha matador que se ha colocado. Gana el jugador que se quede o sin fichas o el que tenga menor puntuación en la mano una vez que la partida quede bloqueada, que suele ser lo más habitual. Lo usual es que el primer jugador comience con un doble o una ficha cualquiera, y a partir de él se imponga la necesidad de conseguir siete. Imagen 3: Partida de matador en proceso. 3. Muggins. Este es un juego muy extendido en el mundo anglosajón. Se juega con el dominó clásico de 28 piezas. Vamos a suponer que juegan cuatro jugadores que se reparten, de forma aleatoria, todas las fichas. En caso contrario se suelen tomar siete fichas por jugador y el resto se deja en un montón aparte para robar en caso de necesidad. La forma de jugar esta modalidad es la clásica, pero durante el desarrollo cada jugador va consiguiendo puntos de la siguiente manera. Cuando un jugador coloca una ficha en la cadena, si ambos extremos de la cadena suman un múltiplo de 5, el jugador se anota el valor de ese múltiplo. Si uno de los extremos es un doble, se cuenta los dos valores del doble. Por ejemplo, en la siguiente jugada, el jugador que ha colocado la ficha 2 – 3 se cuenta 15 puntos que es la suma de los dos seis más el tres de su ficha. Imagen 4: Múltiplo de 5 en Muggins. El ganador es quien se queda sin fichas o el que, al cerrarse la partida, tenga menos puntos en la mano. Según el acuerdo inicial, a veces se cuentan todos los puntos que quedan en la mano de los jugadores y el ganador se anota el mayor múltiplo de 5 que es menor que la suma de esos tantos. La partida se juega a varias manos y gana el jugador que antes alcance un valor prefijado al comenzar a jugar, que pueden ser 100 ó 200 puntos o lo que se estime adecuado según el tiempo que se le vaya a dedicar al juego. Si se consulta este juego, se pueden encontrar formas de jugar muy diferentes, pero existe una variedad en la cual se pueden colocar fichas en cualquiera de los extremos del doble por el que se ha comenzado a jugar, formando una cruz y pudiendo jugar en cuatro lugares diferentes. La cruz sólo se puede hacer en el doble inicial y conseguir múltiplo de 5 bien sólo en las líneas perpendiculares que forman la cruz, o bien con todos los extremos de los cuatro brazos de la cruz. Esta modalidad suele conocerse como spinner, aunque en alguna referencia lo hemos encontrado con el nombre de Belga y referenciándolo como juego típico de Portugal. Si se quiere aprovechar el trabajar los múltiplos y divisores se puede jugar con una pequeña variación. Cuando se consigue un múltiplo de 5, el jugador se anota el valor correspondiente a dividir entre cinco lo obtenido. Así, su suma 5 se anota un punto, si suma 10, se anota dos, con 15 consigue 3 puntos. Y el juego se gana, por ejemplo, al conseguir 25 puntos. Pero en cada jugada se modifica el múltiplo que debemos conseguir. Por ejemplo, en la primera jugada hay que conseguir múltiplos de tres, en la segunda de cuatro y así sucesivamente. En cada jugada se divide el valor obtenido entre el valor del que queremos hallar el múltiplo, como hemos hecho con el cinco. 4. Conseguir primo. Mezclando un poco los juegos que hemos visto hasta el momento se puede trabajar el concepto de número primo. Para ello, se puede trabajar sin los dobles o bien considerar los dobles como una ficha normal, colocándola longitudinalmente y no perpendicularmente como se acostumbra. Si se juega con los dobles no es necesario comenzar la partida por un doble, se puede comenzar por cualquier ficha. Las fichas hay que colocarlas de forma que los dos cuadrados que se toquen, al unir una ficha con una de los extremos de la cadena, sumen un número que sea primo. El resto del proceso es igual, gana quien se queda sin fichas o quien tiene menor valor en su mano cuando el juego queda bloqueado. Imagen 5: Parcial en partida de conseguir primo. 5. Uno más o uno menos. Este juego lo he visto referenciado con el nombre de Turco pero no he conseguido más información sobre él. Se juega de la manera tradicional, aunque se suele comenzar con el doble blanca en lugar del doble seis. En cada jugada, la pieza que se une al extremo no es igual, sino que debe tener una unidad más o una unidad menos que el cuadrado que formaba el extremo. Como tenemos la opción de unir con una unidad más o menos, realmente podemos comenzar con el doble que se quiera o con cualquier pieza aunque no sea doble. Un ejemplo de partida parcial la tenemos en la siguiente imagen. Imagen 6: Partida de Turco. 6. La cadena que aumenta. Basado en el caso anterior existen diversos pasatiempos recreativos que consiste en hacer cadenas con unas determinadas condiciones. Uno de ellos aparece en la enciclopedia de acertijos y juegos llamada Amusements in mathematics (1917) escrita por el matemático inglés Henry Dudeney (1857 – 1930), uno de los principales creadores de acertijos del siglo XIX. Se pide al jugador que elija una serie de fichas para crear una cadena, uniéndolas con las condiciones clásicas, de forma que cada ficha tenga una cantidad de valores fija superior a la ficha anterior. Por ejemplo, si consideramos que cada ficha debe tener tres unidades más que la anterior, podemos considerar la siguiente cadena. Imagen 7: Cadena con tres más. Al final gana el jugador que consigue crear la cadena más larga posible. Lógicamente, mientras mayor sea el número a añadir más corta será la cadena. Se pueden jugar varias partidas cambiando el valor que debe aumentar de una ficha a la siguiente. Se puede complementar el pasatiempo utilizando un dado, que al lanzarlo nos indicará cuánto tendremos que añadir a cada ficha para obtener la siguiente. Hasta el momento hemos jugado más o menos de la manera clásica a ir colocando en una cadena las fichas según determinadas condiciones. En los siguientes juegos vamos a trabajar con las fichas independientemente aprovechando su valor. 7. El mayor gana. Pueden jugar desde dos a cinco jugadores. Se mezclan bien todas las fichas, boca abajo, y se dejan en un montón en medio de la mesa. Los jugadores van tomando, en su turno, una ficha del montón y jugando según la dinámica siguiente. Cada jugador toma una ficha del montón y suma los dos valores que tiene esa ficha. El que consigue mayor puntuación gana y se queda con las fichas que tienen en ese momento todos los jugadores. Si dos o más jugadores tuviesen la misma suma, esos jugadores toman una nueva ficha para desempatar. El juego termina cuando no quedan fichas en el montón o no hay bastantes para que todos tomen una. Gana el jugador que ha acumulado más fichas. El juego permite fácilmente modificar las condiciones que se usan, así podemos considerar que gana el que tiene menor puntuación. También podemos cambiar la operación y considerar que se restan, se multiplican o se dividen los valores, en este último caso gana quien tenga la fracción más grande. Podemos incluso trabajar con potencias, elevando un valor al otro. 8. La fracción más cercana. Como hemos indicado en el juego anterior, se puede trabajar con fracciones utilizando las fichas.  Es interesante, previo al juego,  estudiar todas las fracciones diferentes que se pueden obtener, eliminando la doble blanca. Debemos tener en cuenta que las fichas, salvo que sean las blancas que todas dan lugar al cero, o los dobles, que todas dan lugar al uno, pueden dar lugar a dos fracciones diferentes, por ejemplo la ficha con 1 y 2 nos da la fracción 2/1 y la ½. Para este juego se suelen utilizar solamente los valores que no son dobles. Se separa una ficha y las restantes 20 se reparten aleatoriamente entre los cuatro jugadores. Una vez repartidas se da la vuelta a la ficha separada y se convierte en fracción. Gana el jugador que entre sus fichas tiene la fracción más cercana a la girada. Si hay varios jugares con la misma condición, cada uno se anota un punto. Como una ficha, por ejemplo la 3 – 4, puede lugar a dos fracciones la ¾ y 4/3, se anotan un punto tanto el jugador que esté más cerca de una de las fracciones como de la otra. Gana el jugador que después de diez partidas tiene más puntos. 9. Operaciones con fracciones. Vamos a suponer que juegan cuatro jugadores y se establece, como se estime oportuno, el orden da salida. Se separa la doble blanca y se mezclan bien las fichas restantes dejándolas boca abajo en el medio de la mesa. Cada jugador, por turno, elige dos fichas del montón y cuando todos han cogido, se vuelven las fichas que quedan en el montón central, quedando a la vista las restantes fichas. Ahora cada jugador, en su turno, toma las dos fichas que tomó al principio y construye con ellas dos fracciones, las suma y tiene que buscar, entre las que quedan sobre la mesa, una ficha cuyo valor coincida con el resultante de la operación. Si la encuentra, recoge la ficha del montón y se apunta, en su cuenta personal, el valor de esa ficha retirada. Si no encuentra la solución, pasa su turno. Si los restantes jugadores ven que el jugador en activo ha realizado mal la operación entonces pierde su turno. Una vez que los cuatro jugadores han realizado sus cálculos, se vuelven a mezclar todas las fichas, boca abajo sobre la mesa, y se juega otra partida comenzando ahora el segundo jugador. Después de cuatro u ocho partidas los jugadores suman las fracciones que se han anotado y quién obtenga mayor resultado resulta el ganador. Se puede plantear repasar cualquier otra operación que no sea la suma, por ejemplo, la resta, producto o división de las dos fracciones. En cada caso, el jugador, antes de tomar la ficha resultado del montón debe indicar qué fracciones va a utilizar, pues las fracciones pueden ser propias o impropias (siempre que no sean una blanca). 10. Conseguir un valor fijado. Hay otra forma de trabajar con fracciones. Se reparten todas las fichas de la forma tradicional, suponiendo que juegan cuatro jugadores. Si juegan sólo tres, se separa la doble blanca y se reparten las demás entre los tres jugadores. Cada jugador debe convertir sus fichas en fracciones y conseguir sumar, con algunas de ellas, para conseguir el valor 2. El jugador que lo consiga se anota tres puntos. Si un jugador consigue agrupar varias de sus fichas de forma que consiga varias veces el valor 2, por ejemplo, con dos de sus fichas suma 2 y con tres de las restantes también lo consigue, se anota tres puntos por cada una de ellos. El valor que se puede conseguir se puede cambiar dentro de la misma partida, por ejemplo, en la primera jugada hay que conseguir 2 y en la segunda 3/2. Basta reordenar las fichas para conseguir una cosa u otra. Otra opción es permitir utilizar cualquier operación. Es decir, el alumno debe conseguir, por ejemplo, el valor 2 como resultado de operar con las fracciones y el jugador puede tomar unas fichas cuya suma sea ese valor, pero también cuyo producto lo sea, o la resta o la división. Por cada agrupación, aunque sea con distinta operación, en la que consiga obtener 2 se anota los puntos correspondientes. Se pueden jugar varias partidas con las mismas fichas cambiando el objetivo o volviendo a mezclar y cogiendo fichas de nuevo. Gana quien tiene mayor puntuación después de las partidas jugadas. 11. De fracción impropia a número mixto. Este juego está pensado para tres jugadores que juegan con las 21 fichas que quedan en el dominó al retirar las blancas. Se reparten aleatoriamente las fichas a los jugadores y cada uno comienza, de entrada, un juego individual. El objetivo es tomar una ficha cualquiera que no sea un doble ni dé lugar a un número entero al simplificar la fracción, convertirla en una fracción impropia y buscar entre sus fichas las necesarias para convertirla en número mixto, es decir, buscar dos fichas que correspondan, una a la parte entera y otra a la fracción propia resultante. Vemos un ejemplo en la siguiente imagen. Imagen 8: De impropia a número mixto. Todos aquellos que lo consigan colocan delante suya, y a la vista de los demás jugadores, las igualdades conseguidas. Una vez terminado se pasa a la segunda fase. El primer jugador, que se habrá designado al principio antes de coger las fichas, toma una ficha del jugador de su izquierda y comprueba si con esa ficha puede crear otra igualdad, si lo consigue la hace visible y si no pasa su turno. A continuación de él, los otros jugadores hacen la misma operación y se da un par de vueltas completas hasta terminar la partida. Cada jugador se anota tres puntos por las igualdades conseguidas. Después de tres manos gana el jugador que tenga más puntos. Si algún jugador consigue en el primer turno relacionar dos grupos de fichas y, por lo tanto, sólo le queda una ficha, entonces se acaba la jugada y no se pasa a la segunda fase. A la hora de relacionar las fichas se puede considerar como válido, si así lo aceptan los jugadores, que en lugar de dos fichas se utilicen tres para conseguir la fracción impropia, dos correspondientes a parte entera y otra correspondiente a la fracción propia resultante. En este caso sólo se anotan dos puntos por la relación conseguida. Imagen 9: Utilizando tres fichas.   Bibliografía. IES MARRATXÍ (2016): Videomat 2016: Quines operacions podem fer amb les fraccions d’un dómino? https://www.youtube.com/watch?v=AIaYL-WYBmI enlace revisado el 30/12/2019. Pol i Llompart, J.L. (2015): “Jugando con las fracciones del dominó”. Capítulo del libro Gardner para aficionados, coordinado por Fernando Blasco. Biblioteca Estímulos matemáticos. SM y FESPM, Madrid. UBEDA SÁNCHEZ. J. (1981): Juegos de dominó españoles y exóticos. Normas y preceptos. Edición del autor, Almería.   Nota: 1 Se puede consultar en la dirección http://www.divulgamat.net/index.php?option=com_content&view=article&id=15892&directory=67  

Viernes, 11 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico