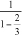41. Maurice d’Ocagne y la nomografía

El matemático e ingeniero Maurice d’Ocagne (1862-1938) falleció un 23 de septiembre. D’Ocagne trabajó durante toda su vida en las ayudas mecánicas para la realización de cálculos matemáticos complicados, campo en el que fue un reconocido especialista. Sus aportaciones más innovadoras se centraron en los métodos gráficos, en especial en el ámbito de la nomografía –él mismo le dió este nombre en 1981 en [2]–, es decir, el cálculo mediante nomogramas, cuya exposición metódica publicó en 1899 (ver [4]) en una obra que sigue siendo la fundamental hoy en día. http://sajri.astronomy.cz/astronavigace/on.pdf Otra de sus obras (ver [3]) es el catálogo más completo de todo tipo de recursos aplicados a la dotación de cálculos matemáticos hasta finales del primer cuarto del siglo XX: en ese momento comenzó la gran revolución que iban a suponer las grandes máquinas calculadoras mecánicas y electrónicas. Fue condecorado dos veces por la Académie des sciences: en 1892 con el prix Leconte por su Nomographie y en 1894 con el prix Dalmont por el conjunto de sus trabajos matemáticos, que incluyen estudios sobre invariantes algebraicos, sucesiones recurrentes, probabilidad de errores, nuevos sistemas de coordenadas y geometría infinitesimal. Más información: M. D’Ocagne, Coordonnées parallèles & axiales: méthode de transformation géométrique et procédé nouveau de calcul graphique déduits de la considération des coordonnées parallèles, Gauthier-Villars. París, 1885 M. D’Ocagne, Nomographie. Les calculs usuels effectués au moyen des abaques. Essai d’une théorie générale, Gauthier-Villars. París, 1891 M. D’Ocagne, Le calcul simplifié par les procédés mécaniques et graphiques, Gauthier-Villars. París, 1894 M. D’Ocagne, Traité de nomographie, Gauthier-Villars. París, 1899 Wikipedia Modern Nomographs Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Viernes, 23 de Septiembre de 2022 | Imprimir | PDF |  Correo electrónico

42. Las nueve campanas de Tom Johnson

Compuesta en 1979 por Tom Johnson, Nine Bells explora los posibles caminos que unen nueve campañas de diferentes tamaños –la música que puede componerse dependiendo del orden y la intensidad con que se toquen– suspendidas en una cuadrícula de 3×3, cada una de ellas situada a distancia de 6 pies de las campañas contiguas. http://continuo.files.wordpress.com/2011/01/bells-front.jpg La música se produce al hacer repicar las campanas siguiendo caminos precisos alrededor de la instalación. Los recorridos se realizan a mayor o menor velocidad, y el sonido de estos pasos –raudos o más pausados– forma parte de la pieza (recordar también Quad de Samuel Beckett). En la contraportada del vinilo pueden apreciarse algunos de los caminos recorridos http://continuo.files.wordpress.com/2011/01/bells-back.jpg En el LP grabado por India Navigation (IN-3023, New York, 1982) dura 57:30 minutos (puede descargarse en este enlace). 01 First Bell (8:06) 02 Second Bell (6:44) 03 Third Bell (7:22) 04 Fourth Bell (7:31) 05 Fifth Bell (8:30) 06 Sixth Bell (6:40) 07 Seventh Bell (3:58) 08 Eighth Bell (5:05) 09 Ninth Bell (3:40) El propio compositor se encargaba de tocar su obra, hasta llegar a la edad de 55 años, momento en el que Johnson tuvo que dejar de representarla –se requiere una excelente forma física para poder realizar los trayectos requeridos durante la hora que dura la obra–. Otros artistas han interpretado Nine Bells, cambiando en algunos casos, la colocación de las campanas. En I want to find the music, not to compose it (ver [1]),  Johnson explica: […] Nine Bells was a similar case, though here, as I walked around my bells, the logic was more geometric than arithmetic. It is often easier to see logic than to hear it, easier to visualize the rotations around a circle than to calculate a note sequence, and I managed to find a strict and audible logic for each of the nine movements. Later, when performing this piece, I sometimes had a very strange sensation. As I played the first note, stepped off on my left foot, and began the first cycle, the experience was very different from that of playing any other kind of music. It was the feeling of beginning something completely inevitable, something I could not stop, and it was clear that my feet were going to carry me on through the sequence, even if my memory failed, or if fatigue set in, or if the audience all walked out. I was a kind of puppet being driven by some inevitable geometric- musical logic that had little to do with my own will power. One could say that I had become merely a machine, but it was a very agreeable experience. […] Más información: Tom Johnson, I want to find the music, not to compose it, Editions 75 Tom Johnson – Nine Bells, Continuo’s weblog Quad, pura geometría, Cuaderno de Cultura Científica Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Viernes, 22 de Septiembre de 2017 | Imprimir | PDF |  Correo electrónico

43. SOLUCIÓN CONCURSO DEL VERANO 2022

Ya está disponible la solución al Concurso del Verano en la sección de Cine y matemáticas.

Miércoles, 14 de Septiembre de 2022 | Imprimir | PDF |  Correo electrónico

44. La paradoja de Condorcet

El filósofo, matemático y politólogo Nicolas de Condorcet (1743-1794) nació un 17 de septiembre. Para él, las matemáticas debían servir también a las ciencias morales cuyo objetivo es la felicidad del ser humano. Entre sus numerosas obras destaca su Essai sur l’application de l’analyse à la probabilité des décisions rendues à la pluralité des voix en el que, por ejemplo, se encuentra el problema de la formación de tribunales. Se interesó en el problema de la representatividad en los sistemas de voto y puso en evidencia la conocida como paradoja de Condorcet, que puede enunciarse de manera sencilla: tres votantes V1, V2 y V3 eligen entre tres alternativas A (Alicia), B (Benito), C (Cecilia), como sigue: V1 = , V2 = , V2 = , es decir, A es preferida a B por dos a uno, B preferido a C por dos a uno y C a A por dos a uno también. Una simple comprobación por pares no determina una alternativa preferida entre las tres. Se trata de una situación de ausencia de ganador, al existir una mayoría cíclica. El procedimiento de elección más usual es la regla de la mayoría simple en el que cada votante elige una o un candidato, y el candidato que reciba más de la mitad de los votos es el ganador. Esta regla es válida cuando sólo hay dos candidatos, ya que gana el que tiene más votos. Cuando hay más de dos, puede ser que el candidato con mayor número de votos no tenga la mayoría absoluta de los votos emitidos. La solución más frecuente es recurrir a la regla de la pluralidad o mayoría relativa, por la que se elige al candidato que queda situado en primer lugar por el mayor número de votantes. Otra solución es aplicar el criterio de Condorcet o de comparación por parejas, por el que se elige el candidato que derrota a todos los demás en elecciones entre pares de candidatos, usando la regla de mayoría. Por este método se puede producir una relación no transitiva, la paradoja de Condorcet, indicada arriba: se puede probar que la probabilidad de tener una mayoría cíclica se incrementa cuando el número de opciones aumenta, y decrece cuando el número de votantes aumenta. Condorcet fue un gran defensor de la igualdad, como lo atestigua, por ejemplo, su texto de 1790  Sur l’admission des femmes au droit de cité (en francés y en inglés): … o bien ningún individuo de la especie humana tiene verdaderos derechos o todos tienen los mismos; y el que vota contra el derecho de otro, cualquiera que sea su religión, color o sexo, ha abjurado de los suyos a partir de ese momento. Marqués de Condorcet, 1790 Más información (sobre Condorcet matemático): Pierre Crépel, Marqués de Condorcet (1743-1794), DivulgaMAT Jacqueline Feldman, Condorcet et la mathématique sociale. Enthousiasmes et bémols, Mathématiques et Sciences humaines no. 172 (4), 7-41, 2005. Nicolas de Condorcet, Du problème des trois corps, Didot, 1767 Nicolas de Condorcet, Essais d’analyse , Didot, 1768 Nicolas de Condorcet, Essai sur l’application de l’analyse à la probabilité des décisions rendues à la pluralité des voix, Imprimerie royale, 1785 Nicolas de Condorcet, Traité du calcul intégral, Imprimerie royale, 1786 Nicolas de Condorcet, Moyens d’apprendre à compter sûrement et avec facilité, 1799 Wikipedia Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Sábado, 17 de Septiembre de 2022 | Imprimir | PDF |  Correo electrónico

45. Esponja de Menger… con post-it

Nicholas Rougeux es un diseñador fascinado por los conjuntos fractales. Esponja de Menger, Nicholas-Rougeux Esta preciosa esponja de Menger está construida con mini post-it… Pueden verse las etapas de la construcción en este enlace. Como el propio artista explica, se ha inspirado en la escultura original de Jeannine Mosely. Jeannine Mosely y su esponja de Menger ¡Un auténtico ejercicio de paciencia! Visto en kottke.org Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Miércoles, 14 de Septiembre de 2022 | Imprimir | PDF |  Correo electrónico

46. 173. SOLUCIONES DEL XVIII CONCURSO DEL VERANO 2022

CUESTIONES MATEMÁTICAS M – 1.- Existen diferentes estrategias para resolver laberintos de este tipo. Entre todos los concursantes ha habido varias (grafos, ensayo-error, backtracking, etc.). Utilicemos la más difundida a nivel elemental para abordar los laberintos regulares: comenzar desde el final e ir determinando el trayecto desde el inicio (backtracking). Para cada casilla, analizamos desde cuál de alrededor podemos llegar a parar allí. Previamente vamos a definir un sistema de notación y localización. Podríamos utilizar coordenadas después de fijar un origen, pero creo que es más sencillo e inmediato en este caso considerar el cuadro completo como una matriz 5x5 de elementos aij, siendo el primer subíndice, la i, la fila, y el segundo, la j, la columna. De este modo el elemento a11, primera fila primera columna, corresponde al +2. El punto de inicio sería el elemento a53 = +1. Dicho esto, situémonos en la casilla final, a33 = 0. De las casillas que la rodean sólo es válida aquella que tenga un 1, ya que solo podremos alcanzarla después de dar un único paso. Por tanto a ella sólo se puede llegar desde a23 = –1. Y estando en a23, la pregunta es la misma: ¿cómo llegamos allí, desde arriba, abajo, izquierda o derecha? - Desde arriba: imposible, ya que la casilla tiene un 4 (demasiado grande) - Desde abajo: imposible, ya que los pasos a dar son 1 (demasiado pequeño) o 3 (demasiado grande) - Desde la izquierda: imposible, ya que los pasos a dar son en ambos 3 (demasiado grandes). - Desde la derecha: ¡hay un candidato!, a25 = –2, porque al saltar dos casillas a la izquierda desde allí, terminamos en a23. De este modo vamos razonando con esa misma lógica. Si hay más de una posibilidad, podemos hacer dos cosas: o elegir una, o mirar todas ellas. Eligiendo sólo una, resolvemos el laberinto sin tener en cuenta el signo (modalidad sencilla); si examinamos todas, en alguna seguro que aparece la solución de la modalidad experto (teniendo en cuenta el signo y llegar a suma cero). Aunque no se imponían más condiciones, algún participante ha tratado después de dar una solución a cada modalidad, imponerse otros retos, como encontrar soluciones que visiten todas las casillas, o dar recorridos lo más cortos posibles. Agradeciendo y admirando sus iniciativas, la puntuación ha sido la misma para todos: 5 puntos para cada uno de los recorridos válidos, independientemente de su tenacidad, que no obstante elogiamos (y tendremos en cuenta en caso de empate). Exponemos soluciones de cada modalidad (hay más): Recorrido modalidad sencilla (visitando todas las casillas, encontrada por Alejandro Apezteguia Torres): a53 → a52 → a32 → a43 → a55 → a35 → a25 → a14 → a15 → a34 → a54 → a44 → a24 → a45 → a23 → a22 → a12 → a21 → a13 → a11 → a31 → a41 → a42 → a51 → a33 La más corta modalidad sencilla (con dos recorridos simétricos): a53 → a43 → a33 Recorrido modalidad experto: En la que recorre todas las casillas expuesta arriba, la suma es +2. Eliminando una única casilla, la a42 = +2, se tiene suma cero (también de Alejandro): a53 → a52 → a32 → a43 → a55 → a35 → a25 → a14 → a15 → a34 → a54 → a44 → a24 → a45 → a23 → a22 → a12 → a21 → a13 → a11 → a31 → a41 → a51 → a33 El más corto, en sólo seis pasos (de Celso de Frutos): a53 (+1) → a52 (–2) → a41 (–3) → a44 (+2) → a35 (+3) → a23 (–1) → a33 La mejor solución con suma 0 que yo tenía era en 14 pasos: a53 (+1) → a52 (–2) → a32 (–2) → a43 (–2) → a54 (–3) → a51 (+4) → a11 (+2) → a31 (+1) → a41 (–3)  → a44 (+2) → a42 (+2) → a22 (+3) → a25 (–2) → a23 (–1) → a33 M – 2 Si denotamos por an la distancia recorrida por la bola en el segundo n-ésimo, del enunciado se tiene que an = 2/3 an-1, para n ≥ 2  y  a1 = 10 Esas condiciones nos llevan, sin más que ir calculando los términos, a que an = 10 (2/3)n-1, una progresión geométrica, cuya suma se calcula como S = 10 = 30. Por tanto, la bola se detiene a los 30 cm. de haber iniciado su andadura. M – 3 i.- El número 3.816.547.290 tiene la propiedad de que el número formado por los primeros n dígitos es divisible por n, para n = 1, 2, 3, …10. Si los movimientos se llevan a cabo en este orden, entonces el juego puede terminar en empate. ii.- El primer jugador (en este caso Andrew) tiene una estrategia ganadora. Obsérvese que, según las condiciones, Milo debe jugar un dígito par en cada uno de sus movimientos. Por tanto, el objetivo de Andrew es “gastar” tantos números pares como sea posible. Por ejemplo, Andrew puede poner un 6 para empezar. En ese caso, hay tres posibilidades a considerar para el segundo movimiento: (1) Si Milo juega un 4 o un 2, entonces Andrew utiliza el otro en tercer lugar. Milo debe a continuación jugar un número par porque su número ahora tiene que ser divisible por 4, así que, si  utiliza el 8, entonces Andrew pone el 0 y Milo pierde porque en el sexto movimiento, tendría que jugar un número par y no queda ninguno. Si Milo jugara un 0, entonces Andrew pone el 5 y Milo también pierde porque ahora debe jugar un número par en el sexto movimiento, y el único que queda es un 8, pero ni 642.058 ni 624.058 son divisibles por 6. (2) Si Milo juega un 0, entonces Andrew usa el 9. Milo debe entonces jugar el 2 para hacer que el número de cuatro dígitos sea divisible por 4. Entonces Andrew coloca el 5. Milo debe emplear el 8 para hacer que su número sea divisible por 6. Y Andrew puede contrarrestar con el 3, ya que 6.092.583 es ​​divisible por 7. El único número par que Milo puede utilizar ahora es el 4, pero 60.925.834 no es divisible por 8, por lo que pierde. (3) Si Milo juega el 8, entonces Andrew pone el 4. La única opción de Milo es entonces el 0. Entonces Andrew echa mano del 5. Y la única opción de Milo sería el 2, pero 684052 no es divisible por 6, por lo que pierde. Téngase en cuenta que esto cubre todos los casos porque Milo debe jugar un dígito par en el segundo movimiento. Por lo tanto, Andrew siempre puede forzar una victoria. Otra estrategia ganadora: Andrew comienza con el 4. Luego, Milo debe colocar un número par. Si responde con un 2 o un 8, entonces el siguiente movimiento de Andrew es un 0. Si la respuesta de Milo fuera un 0 o un 6, entonces el siguiente movimiento de Andrew es un 2. En el caso de que se haya escrito el número 480, Milo no puede encontrar un dígito para hacer un número de cuatro dígitos divisible por 4, por lo que inmediatamente pierde. En los otros tres casos, hay al menos un dígito que Milo puede elegir para permanecer en el juego. Por lo tanto, después de cuatro movimientos, si el juego durara tanto tiempo, uno de los siguientes números estarán en la mesa: 4028, 4208, 4620 o 4628. Entonces Andrew pondría el 5, y en cada uno de esos cuatro casos, será imposible para Milo hacer un movimiento para que el nuevo número de seis dígitos sea divisible por 6, ya que todos los dígitos que necesita se han utilizado. Por lo tanto, si Andrew sigue esta estrategia, puede siempre forzar una victoria. iii.- Aunque describirlo con detalle nos llevaría mucho espacio, en efecto este juego es más justo ya que el segundo jugador no está tan restringido por los movimientos del primero. Hay cuatro números que pueden colocarse en cualquier momento (1, 2, 5, 0) para cualquiera de los jugadores (salvo que el primer jugador no puede empezar con el 0). Además, si los dos últimos números que quedan por poner son el 9 y el 0, ambos pueden colocarse en cualquier orden con finalización exitosa y empate entre los jugadores. Además, hay un movimiento garantizado: colocar el 6 inmediatamente después de haber puesto el 3, ya para ser divisible entre 6, el número lo ha de ser entre 2 (lo es pues 6 es par) y entre 3 (también lo es pues estaríamos sumando un 6, que es un múltiplo de 3 a otro número que ya era múltiplo de 3). No parece haber estrategia ganadora para ninguno. Alejandro Azpeteguia indica una estrategia “empatadora” para cualquier jugador. Eso convierte este juego en más justo, pero sin interés, si ambos conocen dicha estrategia, obviamente. Debo indicar que esta cuestión fue inventada y por tanto abierta, siendo su orden de complejidad bastante alto por el número enorme de posibilidades (como pasa con estas cosas). Celebro que la mayor parte de los participantes sin embargo, hayan pensado en ella deportivamente, y hayan llegado a mi misma conclusión. M – 4 Es claro que las velocidades de las agujas de las horas y del minutero son diferentes. La primera tarda 12 horas en recorrer toda la esfera, por lo que su velocidad (espacio/tiempo) es La aguja del minutero sin embargo recorre toda la esfera (o sea el espacio 2πt) en una sola hora, por lo que su velocidad es asimismo 2πt. Queremos saber cuándo están ambas agujas formando 90º (un ángulo recto; en radianes π/2) y eso sucede un número impar de veces (porque en un número par la diferencia es π). Por tanto, deseamos conocer los valores de t para los que 2πt - = (2n + 1) Simplificando nos queda que  t = (2n + 1) Dando valores a n, se comprueba que para n = 22, obtenemos un valor que supera 12 (concretamente, 135/11 ≈ 12.272727…), por lo que en una vuelta completa de la aguja de los minutos (12 horas) hay 22 veces en las que se forma un ángulo recto. Al cabo del día, por tanto, que era la pregunta, hay 44 veces en las que las agujas forman un ángulo recto. Calculamos esos 22 valores de una vuelta completa para n entre 0 y 21: Para obtener a qué horas corresponden exactamente, basta con tomar la parte entera como la hora, e ir multiplicando la parte decimal por 60 para saber los minutos (y por 3600 si quisiéramos los segundos. Por ejemplo, = 0.272727… 0.272727 x 60 = 16.363636…. 0.363636 x 60 = 21.818181… Luego serían las 0 horas 16 minutos 21 segundos. Haciendo lo mismo con las demás, tenemos que todas las horas en las que las manecillas forman un ángulo recto son: 1.- 0 horas 16 minutos 21 segundos (00:16:21) 2.- 0 horas 49 minutos 5 segundos (00:49:05) 3.- 01:21:49 4.- 01:54:32 5.- 02:27:16 6.- 03:00:00 7.- 03:32:43 8.- 04:05:27 9.- 04:38:10 10.- 05:10:54 11.- 05:43:38 12.- 06:16:21 13.- 06:49:05 14.- 07:21:49 15.- 07:54:32 16.- 08:27:16 17.- 09:00:00 18.- 09:32:43 19.- 10:05:27 20.- 10:38:10 21.- 11:10:54 22.- 11:43:38 Obsérvese la simetría existente en los minutos y los segundos antes y después de las 6 horas (la mitad del recorrido de la aguja de las horas). Se han señalado en rojo las dos posibilidades existentes entre las 7 y las 8 tal y como se pedía en el enunciado. M – 5 Supongamos que tenemos N cuadrados de cada tipo embaldosando un cuadrado de lado S (en cm2). Entonces, S2 = N × 1 + N × 4 = 5N El S más pequeño que satisface esta ecuación es 5, lo que implica N = 5. Sin embargo, no hay una disposición posible de los mosaicos que satisfaga esto, como se puede ver en la figura, ya que cualquier ficha 2 x 2 colocada en el cuadrado, taparía alguno de los cuadrados coloreados en gris. Por tanto, no se pueden poner fichas 2 x 2 en un cuadrado 5 x 5. El siguiente S posible que satisface la ecuación es 10, lo que implica N = 20. Un posible mosaico se muestra a la derecha. Por tanto, el cuadrado más pequeño que se puede formar con números iguales de cada tipo de baldosas tiene una longitud de lado de 10 cm. M – 6 Si contamos el número de triángulos pequeños de que está compuesto el hexágono, comprobamos que son 96. Sea el área de cada uno de esos triángulos igual a 1. Llamaremos s al lado de cada pequeño triángulo equilátero. Entonces = 1 (no hay más que calcular la altura de cada triángulo equilátero mediante el teorema de Pitágoras, s √3/2, y después utilizar la expresión del área del triángulo). Sea d la longitud del lado de la esmeralda (triángulo equilátero de color verde), cuya superficie queremos calcular. En la imagen se ha representado un triángulo de color rojo, de lados d, 5s y 2s, con un ángulo de 120º opuesto a d. Por el teorema del coseno obtenemos que d2 = (2s)2 + (5s)2 - 2 (2s)(5s) cos 120º = 4s2 + 25s2 + 10s2 = 39s2. Entonces el área de la esmeralda (triángulo equilátero verde) es = 39 M – 7 A primera vista, parece que el segundo lanzamiento es irrelevante: como nuestra habilidad es constante, el segundo lanzamiento no influye de ninguna manera en el tercer lanzamiento. Además, da la impresión de que esta pregunta solo puede responderse en términos de la distancia desde el centro al lugar donde cayó el primer lanzamiento. Si denotamos esa distancia por d, y suponemos que el área del tablero de dardos es 1, la probabilidad de que el tercer lanzamiento sea más lejano que el primero aparentemente sería el área del anillo, dada por 1− π d2. Pero esta aproximación se puede mejorar. Sin embargo, podemos razonar de otro modo. Llamemos di a la distancia del i-ésimo lanzamiento al centro. Los posibles resultados, asumiendo que el segundo lanzamiento es más lejano que el primero, son: d3 < d1 < d2 d1 < d3 < d2 d1 < d2 < d3 Y los que satisfacen la pregunta que se hace son sólo los dos últimos, de modo que la probabilidad buscada sería 2/3. Otro modo de razonar, más “elaborado”. Sean f1(r), f2(r), f3(r) las funciones de densidad de probabilidad de la distancia desde el centro de los tres dardos, respectivamente, y F1(r), F2(r), F3(r) sus funciones de distribución acumulativa. (Estos, por supuesto, serán iguales porque suponemos que los dardos son idénticos, están por tanto idénticamente distribuidos). f1(r) = f2(r) = f3(r) = 2r/R2 F1(r) = F2(r) = F3(r) = r2/R2   p(d1 < d2) = M – 8 El primer jugador tiene una estrategia ganadora. Su primer movimiento es colocar una moneda en el centro de la mesa. A partir de ahí, lo único que debe hacer es ir poniendo monedas en una posición simétrica respecto al centro a las que ponga el segundo jugador. Este argumento sirve igualmente para cualquier mesa que tenga simetría central, obviamente. M – 9 La solución al crucigrama se muestra al final de la página. Está compuesto por 84 palabras. Quien haya resuelto al menos 42 tiene 5 puntos. Hasta 52, 6 puntos; Hasta 62, 7 puntos; Hasta 72, 8 puntos; Hasta 80, 9 puntos; y entre 81 y 84, 10 puntos. M – 10 Aunque lo suyo sería que se pudieran obtener las fechas de ambas películas únicamente con los datos del enunciado, lo cierto es que debe utilizarse información de apartados anteriores; incluso les habrá sucedido a muchos participantes que ya conocieran de qué películas se trataba antes de afrontar esta cuestión, con lo que simplemente les servirá para confirmar sus sospechas. No obstante, veamos que podemos inferir exclusivamente del enunciado de esta cuestión. Sólo se ha valorado con 10 puntos (o una cantidad proporcional) aquellas respuestas con algún razonamiento matemático que ayude a determinar el año. Quienes simplemente hayan puesto el año, sin mayor explicación, la puntuación que se ha dado ha sido 4. Desde luego, el dato más objetivo es el de que el año actual es el 2022. Veamos en que columna estaría colocado. De acuerdo con la disposición en columnas de los números son claras las congruencias dispuestas al pie de cada columna Como 2022 ≡ 6 mod 8, se halla en la columna E. Además, nos dicen que el año de la segunda versión es dentro del siglo XXI (por tanto del 2001 en adelante), que comparte la misma columna que la diferencia entre el año actual con ese año, y que además es un múltiplo de cinco. Eso nos lleva a los años Año:               2017               2012               2007               2002 Diferencia          5                    10                   15                   20 Sólo se encuentran en la misma columna de la tabla 2017 y 5 (columna D) y 2007 y 15 (columna D). Sea la que sea, están en la columna D, por lo que el año de la primera versión, y la diferencia entre 2022 y ese año, no se encuentran en las columnas D ni E (porque dicen que están en columnas diferentes todas salvo la del año del remake y la de diferencia de ésta con el año actual). Entre las imágenes de la película, vemos al guitarrista troglodita con una guitarra eléctrica. Este instrumento data de 1920, pero el modelo de la estatua es como poco de mediados de los años sesenta del siglo pasado, pongamos de 1965 (¡¡gran año!!) en adelante. Otra de las imágenes, la del retrato, corresponde a la actriz Joanne Woodward (véase pregunta C – 7), que nació en 1930, si bien su primer trabajo en el cine es en 1955 (en televisión comenzó en 1952). En el retrato, no obstante, tiene un aspecto que desde luego es posterior a ese 1965 que hemos fijado como extremo del intervalo donde asignar el año de la primera versión. Y es claramente inferior a 1980 si observamos alguna foto de la actriz en ese año, como la de la imagen de la derecha del telefilme La caja oscura (The Shadow Box, Paul Newman, EE. UU., 1980). Eso nos deja como posibles años únicamente 1968, 1969, 1970, 1971, 1972, 1976, 1977, 1978, 1979 y 1980 (ninguno en columnas D o E). Sin embargo, como la diferencia de años con el actual debe ser un múltiplo de 5, en realidad sólo quedan 1972 y 1977 (con 50 y 45 años de diferencia, respectivamente). Pero 45 ≡ 5 mod 8, lo que sitúa este valor en la columna D, por lo que no sirve. La película se estrena por tanto en 1972 (que estaría en la columna C), hace 50 años (columna A). M – 11 Buscando películas rodadas aquel año (1972) que hayan tenido una nueva versión, llegamos con poco esfuerzo a La huella (Sleuth, Joseph L. Mankiewicz, Reino Unido, 1972) y La huella (Sleuth, Kenneth Branagh, EE. UU., 2007). CUESTIONES CULTURALES Algunas tienen pregunta múltiple. Cuando he utilizado alguna baremación para repartir la puntuación, lo indico en color azul oscuro. C – 1 La solución aparece en la imagen adjunta. C – 2 Se pedían tres laberintos reales, y se indicaba que se valorarían aspectos como estar cercano al de la película, estar en España y antigüedad. Lo ideal por tanto es poner uno de cada. Pero quien haya dado tres que cumplan todo a la vez, también es correcto. Los participantes han recopilado un montón de laberintos, con imágenes sugestivas de cada uno. No voy a enumerarlos todos, sino que voy a indicar, uno de cada una de las características pedidas. Más cercano al lugar de rodaje: Laberinto de Longleat Hedge Maze, en Warminster,  Inglaterra. Los exteriores y la casa de la película son visitables y se llama Athelhampton House, construida en 1485, en Dorset, Inglaterra. En España (pongo varios): Jardines del Palacio Real de La Granja de San Ildefondo (Segovia, sobre 1730), El Capricho (Madrid, 1784), Laberinto de Horta (Barcelona, 1808); Laberinto de Villapresente (Cantabria, 2007), Más antiguo: Il Labirinto, Villa Pisani, Venecia (Italia, 1720). Esta página puede resultaros curiosa: https://www.elle.com/es/living/viajes/news/g795538/los-10-laberintos-mas-impresionantes-del-mundo/ C – 3 Es tal la cantidad de objetos que aparecen en la película que hacer una lista de todos los juegos es complicado. Con dar media docena de ellos, he considerado la cuestión resuelta. Los que yo he visto son: laberinto, ajedrez, senet, puzzle, billar, ruleta, diana y dardos, crucigrama, croquet, backgammon, adivinanzas, ... Casi todos los concursantes han incluido también los juguetes que aparecen. Estrictamente no son juegos, pero también se han dado por válidos (son juegos para Andrew Wyke). C – 4 La estatua del guitarrista troglodita aparece en la discoteca de la película Play It Cool! (Michael Winner, Reino Unido, 1962), también aparece en una escena de discoteca en Band of Thieves (Peter Bezencenet, Reino Unido, 1962); en el bar de Rudi en el episodio 6 de la primera temporada de la serie de televisión británica The Human Jungle (1963) titulado A Friend of the Sergeant Major emitido el 4 de mayo de 1963; y en la nuestra, en el laberinto de la casa de Laurence Olivier en La huella (Sleuth, Joseph L. Mankiewicz, Reino Unido, 1972). En la primera de esas películas, se pretendía lanzar un emulo de Elvis Presley en el Reino Unido, el cantante Billy Fury (1940 – 1983). Allí tuvo cierto éxito (igualó el récord de 24 éxitos de los Beatles en la década de 1960, y estuvo 332 semanas en las listas de éxitos del Reino Unido; sólo fue superado por los Beatles, Cliff Richard y Elvis Presley), pero nunca alcanzó un número uno. En España no es demasiado conocido, y esa película nunca se ha estrenado. La actualidad a que se aludía en el enunciado de la cuestión es el reciente estreno de la película Elvis (Baz Luhrmann, EE. UU., 2022). C – 5.- Se comenta que el padre de Milo Tindle (Michael Caine) fue relojero. Además, hacia el final del primer acto, Andrew Wyke (Laurence Olivier) atormenta a Milo con el tiempo que le queda de vida, lo que reproducirá en el tercer acto Milo con él, con el tiempo que le queda para encontrar unos objetos que lo incriminan antes de que llegue la policía. Aparecen también relojes en las muñecas de los protagonistas (marcando su estilo la diferencia de clase social), y por supuesto el reloj de péndulo de la escalera en el que se esconde una de las pruebas incriminatorias, además de ser enfocado numerosas veces a lo largo de la película. C – 6.- Andrew Wyke es escritor de novelas de crímenes y detectives. El busto sobre la repisa de la chimenea de la imagen corresponde al premio Edgar Allan Poe que ganó el autor de la obra teatral, Anthony Shaffer, precisamente por esta obra, Sleuth. Pero lo hizo en 1971, que no se corresponde con ese 1946 de la imagen. El director de la película, Joseph L. Mankiewicz también ganó un Edgar Allan Poe por Operación Cicerón (Five Fingers, EE. UU.,1952). Otros detectives literarios mencionados o referenciados en la película son Lord Peter Whimsey (de la escritora británica Dorothy Leigh Sayers; de hecho, el detective al que Wyke alude en la película como su creación, St. John Lord Merridew, es claramente un homenaje Whimsey, que utiliza monóculos en sus pesquisas); el detective Nero Wolfe (del escritor norteamericano Rex Stout; es un gran amante de las orquídeas, referencia que aparece también en la película); por supuesto Sherlock Holmes (del británico Arthur Conan Doyle; destaca por su inteligencia, su hábil uso de la observación y el razonamiento deductivo, y conocemos muchas de sus aficiones que aparecen de algún u otro modo en la película: es muy habilidoso disfrazándose, fuma en pipa, le gustan las galletas, toca el violín con maestría (un Stradivarius, a menudo a horas poco adecuadas), es un experto apicultor, excelente boxeador, tiene un gran conocimiento científico, en especial en química, y, cuando se aburre por falta de los retos intelectuales que suponen sus casos, consume cocaína en una solución al siete por ciento. Además, viste una gorra típica de las cacerías que también está en la película); el padre Brown (creado por el novelista inglés G. K. Chesterton, es el contrapunto a Sherlock Holmes, ya que resuelve sus casos por intuición y conocimiento de la naturaleza humana más que de la ciencia; su característico sombrero de pala también está presente en la película). Y por supuesto encontramos entre las fotografías de la pared a Agatha Christie, creadora de Hercules Poirot y la Srta. Marple. Y finalmente, se menciona o referencia un par de veces al malvado Fu Manchú, creado por el escritor Sax Rohmer, cuyos malvados planes siempre son desbaratados por Sir Denis Nayland Smith, junto a su acompañante, el doctor Petrie. Indicar el oficio del protagonista: 5 puntos. Los otros cinco autores y sus creaciones: 5 puntos (uno por cabeza). C – 7.- Es un retrato de la actriz norteamericana Joanne Woodward, que interpreta sin aparecer físicamente a la esposa de Andrew y amante de Milo, Marguerite Wyke. Joanne fue una de las actrices que hicieron una prueba para encarnar a Cleopatra en la película homónima de J. L. Mankiewicz (junto a Joan Collins y otras actrices), antes de que finalmente se lo adjudicaran a Elizabeth Taylor. Es la única relación que he encontrado acerca de la utilización de esta actriz para esta película. Además del retrato, aparece en una fotografía junto a Laurence Olivier en otro trabajo que hicieron juntos, justamente la foto a la que Andrew hace un agujero con su revólver. Sobre la presencia del retrato de Joanne Woodward, algunos participantes indican otras posibilidades: ganó el Óscar a la mejor actriz en 1957 por Las tres caras de Eva. En esa película interpreta un personaje que posee personalidad múltiple (hasta 3 diferentes), muy en la línea de engaños y falsos personajes de La huella. Recordemos además que Mankiewicz fue el director de Eva al desnudo. Además siendo niña, acudió a la premiere de Lo que el viento se llevó (1939) en Atlanta, y logró sentarse en el regazo de Laurence Olivier (quien tenía entonces 32 años), que era entonces el compañero sentimental de Vivien Leigh. Otro concursante nos dice que en la biografía del director Mankiewicz, Pictures Will Talk,  se indica que esta presencia no es sino una broma (una más de la película) entre él y sus amigos Joanne Woodward y Paul Newman (ya saben, pareja en la vida real). Se proponen cuatro cuestiones: 2.5 por cada una resuelta. C – 8 En los títulos de crédito aparecen los nombres de seis actores, pero la película sólo tiene dos. Los otros no existen (el del detective, Alec Cawthorne, es casi un anagrama de "O Michael Caine": se invierte la "W" en Cawthorne para obtener la "M" en Michael, y se separan las líneas horizontales y verticales en la letra "T" para obtener las dos "I" necesarias). En 1993, Mankiewicz afirmó en una entrevista que los cuatro restantes eran nombres reales de parientes de su esposa, aunque Eve Channing es claramente una mezcla entre Eve Harrington y Margo Channing, nombres de dos de las protagonistas de Eva al desnudo. Los concursantes han aportado un buen número de películas con uno o dos personajes solamente. En algunas, aunque el peso de toda la película sea sólo de uno o dos, si aparecen más personas, aunque sean de fondo, no se han considerado. He aquí una selección:: Locke (Locke, Steven Knight, Reino Unido/EE. UU., 2013). Un único actor, Tom Hardy, y voces de otros. La Venus de las pieles (La Vénus à la fourrure, Roman Polanski, Francia, 2013). Dos actores solamente, Mathieu Amalric y Emmanuelle Seigner. Gravity (Gravity, Alfonso Cuarón, Reino Unido/EE. UU., 2013). Sólo Sandra Bullock y George Clooney, con voces de otros. Buried (Rodrigo Cortés, España, 2010). Un único actor, Ryan Reynolds, y voces de otros. Vida/perra (Javier Aguirre, España, 1982). Una única actriz, Esperanza Roy Give 'em Hell, Harry! (Steve Binder y Peter H. Hunt, EE. UU., 1975), con James Whitmore como único actor. Infierno en el Pacífico (Hell in the Pacific, John Boorman, EE. UU., 1968). Sólo dos actores, Lee Marvin y Toshirô Mifune. C – 9 Nos referiremos a la primera versión como v1, y a la segunda como v2. Diferencias: 1.- En v1 Milo es propietario de una cadena de salones de belleza, mientras que en v2 es un joven escritor en paro. 2.- En v1 hay diálogos cargados de ironía y sutilidad mientras que en v2 hablan a gritos, insultando y diciendo palabrotas. 3.- En v1 el interior de la casa está decorada con numerosos muñecos, juegos, objetos singulares, muy recargada, mientras que en v2 es todo minimalista y con muchos aparatos tecnológicos. 4.- La duración del metraje de v2 es sensiblemente inferior a la de v1 (50 minutos menos). 5.- En v1 el autor de la obra de teatro, Anthony Shaffer, es quien hace el guion, mientras que en v2, lo hace Harold Pinter, premio nobel de literatura. 6.- En la escena inicial de v1, Milo aparca su coche en solitario, mientras que en v2 lo aparca junto al de Andrew, pudiéndose así apreciar la diferencia de tamaños entre estos, indicador claro del nivel económico de cada uno. 7.- La realización cinematográfica de v1 es más clásica, mientras que en v2 hay una amplia gama de planos. 8.- En v2, las alusiones a la homosexualidad son mucho más explícitas que en v1. 9.- En v1 aparecen en los títulos de crédito actores inexistentes, mientras que en v2 aparecen personajes que no están en los títulos de crédito (salen por televisión). 10.- El sentido del juego y el desenlace son diferentes. 11.- Milo es invitado a la casa en v1, mientras que en v2 aparece por su cuenta. 12.- El carácter de Milo en v1 es respetuoso inicialmente e incluso con cierto complejo de inferioridad, mientras que en v2 es muy agresivo y muy seguro de si mismo. Andrew en v2 es también más perverso. Semejanzas 1.- Michael Caine protagoniza ambas, aunque con diferentes papeles: en la v1 es Milo Tindle, mientras que en la v2 es Andrew Wyke. C – 10 En la versión original de la película en inglés, Andrew indica a Milo (minuto 41, aproximadamente), “If you'll be good enough to follow me, Miss Rebecca”. En la versión española dice “Si es usted tan amable de seguirme, mi querido amigo”. Además en la versión original, Laurence Olivier imita la forma de hablar de la señorita Danvers, personaje de Rebeca (Rebecca, Alfred Hitchcock, EE. UU., 1940), en la que Olivier encarna al marido de la difunta Rebeca. Es claramente, como sucede en toda la película, un nuevo guiño al espectador. En cuanto al actor que rechazó interpretar a Milo (algún concursante ha pensado que la pregunta era sobre Rebeca) fue Alan Bates, que tras los primeros ensayos manifestó que el papel no estaba a su altura. Albert Finney fue descartado previamente por ser un poco regordete. Michael Caine fue la tercera opción. C – 11 Me alegra que la película haya gustado a todos los participantes (menos el remake, que tiene sus virtudes, pero claramente muy por debajo de la original). No es una película sencilla de ver para el público actual, en el que tanto diálogo (junto a las reflexiones que conlleva) puede resultarles agotador (a eso se ha mal acostumbrado a la gente: lo vemos diariamente en entrevistas o debates, en las que enseguida se corta al orador; por supuesto eso conlleva un deficiente estudio de nada. El síndrome Twitter, lo podemos llamar). PUNTUACIONES FINALES Como cada año, el nivel mostrado por todos los participantes ha sido más que sobresaliente. Las diferencias son mínimas y normalmente por cuestiones de detalle. Recordemos que la puntuación máxima que se podía obtener en esta ocasión era de 220 puntos (110 las cuestiones matemáticas, en rojo; y 110 las de tipo cultural, en azul). Así ha quedado al final: 1.- Alejandro Apezteguia Torres  212 (107 + 105) 2.- Francisco Pi Martínez   205 (101 + 104) 3.- Equipo formado por Engracia, María y Javier   205 (96 + 109) 4.- Paz Jiménez Seral     177 (97 + 80) 5.- Celso de Frutos de Nicolás   175 (96 + 79) 6.- Alba Diez Mariño    153 (51 + 102) En el caso del segundo y tercer puesto, he terminado por ponerlos en ese orden primando las preguntas de tipo matemático. Aunque leer y valorar todos los documentos recibidos lleva un tiempo no despreciable, debo agradecer a los participantes su excelente trabajo del que no dejo de aprender cada año (hay razonamientos y resoluciones realmente magníficas), y me he divertido enormemente con sus comentarios tanto sobre las cuestiones matemáticas como las culturales y de cine. Y celebro especialmente que haya habido tantas mujeres como hombres involucradas en el concurso. Ojalá sea la tendencia futura en todo. Espero que todos hayan pasado de verdad un buen rato. En breve recibiréis un mail, algunos para pediros una dirección postal a la que enviaros un pequeño obsequio de DivulgaMAT (ignoro a fecha de hoy el número de obsequios de los que dispone la organización), y a todos para detallaros las puntuaciones de cada cuestión, una vez hayáis leído las soluciones. ¡¡Enhorabuena a todos!!

Jueves, 08 de Septiembre de 2022 | Imprimir | PDF |  Correo electrónico

47. 85. (Septiembre 2022) Demócrito, el matemático risueño

(Rubens. Demócrito, el filósofo que rie, Museo del Prado. Madrid) Demócrito de Abdera (460 a 370 a.C.) dejó escrita amplia e importante obra matemática, tal como nos cuenta Diógenes Laercio en el libro IX de las Vidas de los filósofos más ilustres: De la variedad de la regla o Del contacto del círculo y la esfera, De Geometría, Geométrico, Números, Líneas irracionales, De los sólidos, Extensiones y Tablas astronómicas. Las grandes síntesis alejandrinas, como los Elementos de Euclides, las Cónicas de Apolonio y el Almagesto de Ptolomeo, presentaban de forma coherente y sintética los resultados anteriores: en consecuencia las obras originales no han sobrevivido, y solo nos queda la memoria literaria. Se atribuye a Demócrito el factor del tercio para los volúmenes del cono y la pirámide en relación con sus correspondientes cilindro y prisma. Lo que no sabemos es si su determinación fue empírica o uso algún método exhaustivo como Eudoxo o Arquímedes. El mismo Laercio deja patente la formación universal del sabio abderita y su dominio de múltiples campos del saber. Parece que Domócrito gastó su herencia en viajes de formación: geometría en Egipto, aritmética y astronomía en Caldea y Persia, y matemática con los gimnosofistas de la India. La modernidad de Demócrito reside en la teoría atomista que aprendió de su maestro Leucipo y que fue recogida por Epicuro y su escuela. El propio término átomo fue acuñado por él. Precisamente la tesis doctoral de Karl Marx se dedicó a Demócrito. El sabio que ríe Durante el Renacimiento y sobre todo en el Barroco, Demócrito es representado profusamente por su valor moral, es su autodefensa contra la estupidez humana mediante la risa. El origen de esta visón se encuentra en las fuentes clásicas, reproducimos las de Séneca y  Juvenal. Debemos, pues, rendirnos á no tener por aborrecibles sino por ridículos todos los vicios del vulgo, imitando antes á Demócrito que á Heráclito. Este siempre que salía en público lloraba, y el otro reía. Este juzgaba todas nuestras acciones por miserias, y aquél las tenía por locuras. Súfranse todas las cosas con suavidad de ánimo, siendo más humana acción reírnos de la vida que llorarla. Y añade que en mayor obligación pone al género humano el que se ríe de él, que no el que le llora; porque el primero deja alguna parte de esperanza, y estotro llora neciamente aquello que desconfía poder remediarse. Y bien considerado todo, mayor grandeza de ánimo es no poder enfrenar la risa que el no poder detener las lágrimas. Séneca. Sobre la serenidad del espíritu (De tranquillitate animi). Traducción de Pedro Fernández Navarrete [1564-1632] En todas las tierras que hay desde Cádiz hasta la Aurora y el Ganges pocos saben discernir los verdaderos bienes de aquellos tan opuestos, despejada la niebla del error. También en su época encontró Demócrito materia de risa en todos los encuentros con hombres, y su perspicacia revela que los hombres más ilustres y llamados a dar grandes ejemplos, pueden nacer en la patria de los borregos y bajo un clima pesado, Se burlaba asimismo de las cuitas y alegrías de la gente. Juvenal. Sátiras X Demócrito y los abderitas (Panel de Demócrito e Hipócrates. Monasterio de San Vicente de Fora. Lisboa) La iglesia y monasterio de San Vicente de Fora domina con su impresionante mole el Este de Lisboa. La construcción actual, de finales del XVI e inicios del XVII, puede recordar el manierismo escurialense del que es casi contemporáneo. Los dos grandes patios del monasterio y sus escaleras están totalmente cubiertos en casi sus tres plantas de azulejos del siglo XVIII. Por si esto fuera poco, se exhiben allí además treinta y ocho bellos paneles de Las fábulas de Jean de la Fontaine. El panel numero once está dedicado a Demócrito y los abderitas: la población local considera loco al filósofo matemático hasta que una visita de Hipócrates les hace dudar de la opinión mayoritaria. El panel recoge el encuentro de ambos sabios. La historia puede ser apócrifa, veamos como la cuenta la Histoire critique de la philosophie (1756) de André François Deslandes: "Me gustaría", continuó Demócrito, "que todo el Universo se nos revele de repente. ¿Qué veríamos allí, esos hombres débiles, ligeros, preocupados, apasionados por las bagatelas, por los granos de arena; solo inclinaciones bajas y ridículas, que se enmascara con el nombre de virtud; solo intereses mezquinos, encuentros familiares, negociaciones llenas de engaño, por lo que nos felicitamos en secreto y que no nos atreveríamos a producir a plena luz del día; esos lazos formados por casualidad, semejanzas del gusto que pasan por una serie de reflexiones; ¡esas cosas que nuestra debilidad, nuestra extrema ignorancia nos llevan a considerar bellas, heroicas, brillantes, aunque al final solo son dignas de desprecio! Y después de eso, dejaríamos de reírnos de los hombres, burlándonos de su supuesta sabiduría y de todo lo que presumen tanto. " "Este discurso, que acorté a propósito, llena a Hipócrates de sorpresa y admiración. Se dio cuenta de que, para ser un verdadero filósofo, tenía que convencerse en detalle de que casi hay en el mundo, solo locos y niños. Tontos más dignos de piedad que de ira; niños que deben ser compadecidos y contra quienes nunca se les permite amargarse o enojarse. Tras el examen, Hipócrates declaró a Demócrito "sabio entre los sabios, solo capaz de apaciguar a los hombres". La risa de Demócrito era una risa triste y satírica, una forma de resistencia. Se ríe de la locura, el ridículo y, en general, la estupidez de los hombres. El mundo es cómico para Demócrito, trágico para Heráclito. Demócrito se contenta con el mundo tal como es y prefiere reírse de las fallas de la sociedad en lugar de llorar por ello. Considera que el espectáculo del mundo es inmutable y que la única alternativa a la melancolía es el hedonismo. Demócrito de Velázquez en Ruan Diego Velázquez no fue un gran pintor de filósofos como lo fue José Ribera. Ello hace que este Demócrito de Ruan tenga más valor añadido, si cabe. Demócrito, el filósofo que ríe, es una figura de tal complejidad que desafía los pinceles de cualquier artista: ¿Cuál es la razón de su risa? ¿Cómo expresarla? Ante Demócrito no podemos permanecer indiferentes, le tenemos que rehuir la mirada, esa risa nos desarma, es abisal. Demócrito es conocido como físico por el atomismo y como matemático por el volumen de la pirámide, pero en el barroco es representado una y otra vez con su enigmática sonrisa. El globo terráqueo revela su condición científica. Es probable que una de las fuentes de Diego Velázquez sea un Demócrito de Rubens que forma parte de los fondos del Prado. El tratamiento de uno y otro marca las diferencias: la serenidad de Velázquez concentra todo el impacto en la risa y en la mano que levita detenida a cierta distancia del mundo, mientras que en Rubens la fuerza sobrecogedora queda algo diluida. La colocación del cuadro en Ruan en un lugar destacado y de transición nos facilita verle una y otra vez, como una aproximación que amortigüe el choque. (Velázqez. Demócrito. Museo de Bellas Artes. Ruan) Demócrito de Ribera en El Prado Las pinturas de sabios de Ribera nos muestran a hombres del pueblo pobremente vestidos como si quisieran insistir en la modestia y en la riqueza del espíritu frente a lo mundano, todo ello muy propio de la piedad barroca. La pintura del Españoleto ha sufrido diversas identificaciones del personaje hasta apuntar a Demócrito, la tenue y profunda sonrisa resuelve el problema. Durante mucho tiempo ha sido conocido como Arquímedes pues el compás muestra el carácter matemático del filósofo. (José Ribera. Demócrito. Museo del Prado. Madrid) Los Demócrito de Giordano en Brescia y Hamburgo La herencia del pintor de Xàtiva afincado en Nápoles –José Ribera- se pone de manifiesto en su discípulo Luca Giordano extremando más si cabe su barroquismo. Como muestra: están los impresionantes retrato de Demócrito, el filósofo matemático padre del materialismo, en Brescia y Hamburgo. Como en los retratos de Ribera -y otros que le siguen- la figura del sabio va asociada a la pobreza, el abandono del cuerpo, la concentración mental, el alejamiento y el desprecio del mundo. La característica del atomista es además la risa, Demócrito es el filósofo que ríe. Risa que no sabemos si es ironía, condescendencia o enajenación. (Luca Giordano. Demócrito. Museo Tosio Martinengo. Brescia) Cuerpo semidesnudo con trapos que sirven para portar los escritos que a juzgar por el que lleva en la mano son astrológicos: horóscopos. Los horóscopos se representan mediante tres cuadrados anidados de forma que el vértice de uno se sitúa en la mitad del lado del otro. Compás en la mano o en la faltriquera. Astrónomo, astrólogo y matemático han sido términos casi indistinguibles hasta el siglo XVII, siendo Kepler quizá la culminación y disolución de esa figura múltiple. Las pinturas de Giordano se conserva en las pinacotecas Tosio Martinengo de Brescia y en el Kunsthalle de Hamburgo. El Demócrito de Hamburgo resalta más sus conocimientos matemáticos y astronómicos, conservando el astrológico que como decía Diego Torres Villarroel es lo que da de comer al matemático. (Luca Giordano. Demócrito. Kunsthalle. Hamburgo) Demócrito de Rembrandt Rembrandt fue otro de los grandes que representa a Demócrito, lo hace solo con su risa. Dificilísimo pintar un rostro risueño que no represente un loco o un idiota sino pensamiento profundo. La pintura pertenece a una colección privada. (Rembrandt. Demócrito. Colección privada) El Demócrito de Breslavia Otra representación de Demócrito como matemático la encontramos en el Museo Nacional de Breslavia, hoy Wrocław en Polonia. La pintura se atribuye al suizo Giuseppe Antonio Petrini (1667-1759), un barroco tardío y tenebrista. Sonrisa, esfera y compás son los atributos ya consolidados del sabio abderita. (Perini. Demócrito. Museo Nacional. Breslavia) Las risas exageradas (Hendrik ter Brugghen. Demócrito. Museo Nacional. Breslavia) De lo sublime al ridículo. De la inteligencia a la locura. Algunas representaciones no superan el reto. Los Demócritos de Hendrik ter Brugghen  (1588 – 1629) en el Rijksmuseum y de Johannes Moreelse (1603 – 1634) en el Centraal Museum de Utrecht son muestra del extravío. Ambas representaciones comparten un globo estelar. La dedicación a la ciencia astronómica es puesta de manifiesto. (Johannes Moreelse. Demócrito. Centraal Museum. Utrecht)

Lunes, 05 de Septiembre de 2022 | Imprimir | PDF |  Correo electrónico

48. Gerd Faltings y la conjetura de Mordell

El matemático Gerd Faltings (1954-) cumple hoy años. Es conocido por su trabajo en geometría algebraica aritmética. Se le concedió la Medalla Fields en 1986 por su demostración de la conjetura de Mordell usando métodos de geometría algebraica aritmética. La conjetura de Mordell fue establecida por Louis Mordell en 1922, y Faltings demostró una generalización, que puede enunciarse del siguiente modo: Cualquier curva proyectiva no singular, de género g > 1 definida sobre un cuerpo de números K, contiene sólo un número finito de puntos racionales en K. Además de otros premios, Faltings recibió en 1996 el Premio Gottfried Wilhelm Leibniz de la Deutsche Forschungsgemeinschaft, el máximo honor concedido a la investigación en Alemania. Cartel del congreso con motivo de su 60 cumpleaños Más información: Página en la Universidad de Bonn Página en el Max Planck Institute Gerd Faltings, Mathematics Genealogy Project Gerd Faltings, MacTutor History of Mathematics archive, University of St Andrews King Faisal International Prize 2014 B. Mazur, On Some of the Mathematical Contributions of Gerd Faltings, Proceedings of the International Congress of Mathematicians, 1986 Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 28 de Julio de 2022 | Imprimir | PDF |  Correo electrónico

49. 127. (Agosto 2022) Divulgación científica en el congreso Mathematics and Computation in Music 22

La columna de este agosto caluroso está dividida en tres partes. En la primera, haremos unas cuantas reflexiones sobre la divulgación científica en general; en la segunda parte, aplicaremos esas reflexiones a la divulgación científica en el campo de la Teoría Matemática y Computacional de la Música (TMCM en adelante); y, por último, pondremos ejemplos de acciones de divulgación científica que tuvieron lugar en el reciente congreso Mathematics and Computation in Music 22 (MCM22) celebrado en Atlanta bajo la excelente organización de Mariana Montiel de la Universidad Estatal de Georgia (GSU en sus siglas inglesas). 1. Ciencia y divulgación La ciencia es una aventura intelectual en la que las ideas de progreso y creatividad son esenciales. Además, la ciencia es una parte fundamental de la cultura moderna. El objetivo de la ciencia es construir conocimiento sólido, verificable, y a través de ese conocimiento llegar a la comprensión del mundo. De esa comprensión, surgen aplicaciones asombrosas y ubicuas que transforman nuestra sociedad constantemente. La ciencia, además y como parte de su genésis y praxis, nos plantea dilemas morales y éticos. Los científicos tienen un compromiso con la sociedad en la que trabajan. La sociedad les ha proporcionado formación y medios para desarrollar su tarea. A cambio, deberían explicar los resultados que obtienen, pero no en forma de publicación en una revista de prestigio o en un congreso especializado, sino en un contexto y en unos términos adecuados para que el gran público entienda su relevancia y aplicaciones. Los científicos tenemos la obligación de divulgar y popularizar la ciencia que producimos. Igual que la universidad nos exige ser buenos profesores, buenos investigadores, buenos gestores, debemos ser también buenos divulgadores (de los sistemas de calidad universitaria hay mucho que hablar y nada bien desde luego). Sin embargo, en general, los científicos no hacen tal esfuerzo en divulgar sus resultados y este esfuerzo debe hacerse a todos los niveles de la educación, desde la educación infantil cuando sea posible hasta los adultos y especialmente en la primaria y secundaria. Por su parte, la sociedad debería apreciar la naturaleza y los objetivos de la ciencia. Con frecuencia, la sociedad reacciona con resistencia o incredulidad ante los objetivos y resultados de la ciencia. Los científicos, a nuestra vez, no deberíamos reaccionar a tal resistencia con rechazo e indiferencia, como lamentablemente es el caso con harta frecuencia. Antes al contrario, deberíamos crear una diálogo abierto y libre de condescendencia con el gran público. Mi teoría personal es que parte de esta resistencia reside en lo que el escritor C. P. Snow (1905–1980) llamó la gran división de las dos culturas; aquí por las dos culturas se refiere a las humanidades y a las ciencias, respectivamente. En una famosa conferencia que pronunció en 1959 en el Senate House en Cambridge, hizo una crítica en términos intelectuales y económicos de esa división y sus consecuencias. Desde que tengo uso de razón he presenciado una división inmediata de las personas entre persona de ciencias y persona de letras, división que, por cierto, el propio sistema educativo propicia (aquí en España y en otros muchos países occidentales). La “gente de letras” no conocen los más elementales hechos científicios ni está familiarizada con la más mínima lógica científica. La “gente de ciencia” ignora las grandes obras de la literatura y su capacidad de experiencia emocional y explicación del mundo. En su libro Las dos culturas [Sno77], Snow lo expone con bastante elocuencia. El extracto que reproduzco a continuación se refiere a la actitud de los no científicos ante la ignorancia de los científicos ante la cultura tradicional. En otras partes del libro, se queja amargamente de la situación contraria. Leamos a Snow: Pero ¿qué ocurre del otro lado? También se han empobrecido —quizás más seriamente porque se enorgullecen de ello. Todavía les agrada fingir que la cultura tradicional es toda la “cultura”, como si no existiese el orden natural. Como si la exploración del orden natural no tuviese interés alguno de suyo ni por sus consecuencias. Como si el edificio científico del mundo físico no fuera, en su hondura intelectual, su complejidad y su coherencia, la obra colectiva más bella y maravillosa de la mente humana. Pero los no científicos no tienen ningún conocimiento del edificio. Aunque quieran tenerlo, no pueden. Es como si todo el grupo fuera incapaz de percibir el sonido de la cuerda inmensa de la experiencia intelectual. Solo que esa sordera no se tiene por naturaleza, sino por educación, o más bien por falta de educación. Y como no perciben todos los tonos, no saben lo que se pierden. Hacen una mueca de risa piadosa al saber que hay científicos que no han leído jamás una obra importante de la literatura inglesa. Los descartan como especialistas ignorantes. Y sin embargo su propia ignorancia y su propia especialización son igualmente pasmosas. Muchas veces he estado en reuniones de gentes consideradas muy cultas según las normas de la cultura tradicional, y que con sumo placer expresaban su incredulidad ante la ignorancia de los hombres de ciencia. Una o dos veces me he incomodado y he preguntado a los presentes cuál era la segunda ley de la termodinámica. La respuesta fue fría, y también negativa. Sin embargo, yo estaba preguntando algo que es el equivalente científico de “¿Ha leído usted alguna obra de Shakespeare?” Ahora pienso que si hubiese preguntado algo más simple —como que era la masa, o la aceleración, científicamente equivalente a preguntar ¿Sabe leer?—no más de una entre diez de las personas muy cultas habría sentido que yo hablaba el mismo idioma que ella. Así el gran edificio de la física moderna se va levantando, y la mayoría de la gente más inteligente del mundo occidental tiene de ello más o menos la misma consciencia que habrían tenido sus antepasados neolíticos. Una manera de romper esta división, este muro invisible pero impermeable, es a través de la divulgación científica. La divulgación es narración, es contar historias, es dotar a los resultados científicos de valor emocional y moral. 2. Divulgación científica en la TMCM La Teoría Matemática y Computacional de la música (TMCM) es una disciplina científica de pleno derecho. Analiza un fenómeno muy complejo: la música; con herramientas muy potentes: las matemáticas y la computación. La música está llena de patrones, reglas; está altamente estructurada, es compleja, rica en matices, desafiante desde un punto de vista cognitivo, altamente gratificante desde un punto de vista emocional y con importantes funciones sociales (véase [RB03] para mayor desarrollo de estas cuestiones). Las matemáticas es la ciencia que estudia los patrones en abstracto, desde el rigor, la ciencia que describe la estructura a altos niveles de complejidad; es también una disciplina altamente desafiante desde un punto de vista cognitivo. En la evidente convergencia de estas dos disciplinas nace la TMCM. Y como disciplina, los practicantes de la TMCM tenemos la obligación de hacer divulgación científica. Hay muchas ventajas y facilidades para hacer tal cosa. La música siempre es atractiva para el gran público. Y con frecuencia, conceptos matemáticos simples pueden dar explicación novedosas a fenómenos musicales. Las matemáticas junto con la computación pueden proporcionar maneras muy efectivas y potentes de visualizar la música. Cierto es que el material de divulgación tiene que ser diseñado con creatividad y meticulosidad, además de adaptarlo con precisión al público final. 3. Divulgación científica en el MCM22 En los congresos de nuestro campo, especialmente en los dos últimos, se ha hecho hincapié en la divulgación. En el congreso MCM 22 (https://mcm2022.org/) en particular se realizaron una serie de actividades divulgativas que nos gustaría glosar aquí como muestra del interés y el compromiso de nuestra comunidad con la divulgación científica. En la tarde del 23 de junio de 2022 se llevó a cabo en el Museum of Design Atlanta (MODA; see https://www.museumofdesign.org/) una jornada de divulgación científica y que describimos a continuación. 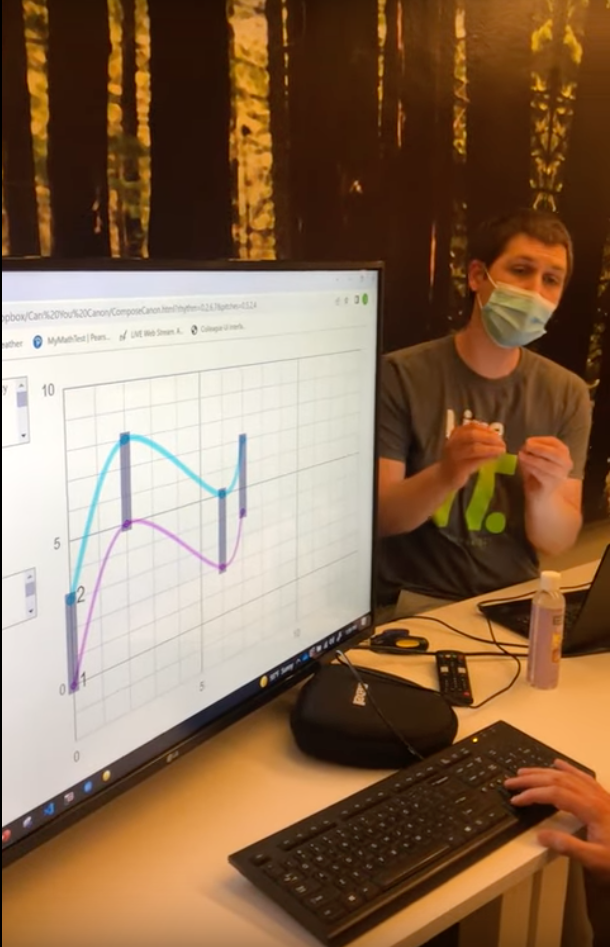3.1. Jeremy Kastine y su actividad Can you canon? Jeremy Kastine, que fue el organizador del evento, presentó una actividad en que los participantes tenían que componer canones monofónicos con ciertas restricciones. Los participantes aprendieron que este problema se puede formular en términos de encontrar los cliques maximales de un grafo. El software con que se construían los cánones fue programado por el propio Kastine. Figura 1: Jeremy Kastine y su actividad Can you canon? 3.2. Thomas Noll y The Collective Public Fourier Performance En esta actividad hay tres participantes que controlan los coeficientes de Fourier de una onda sonora variando la altura de ciertas banderas. Estas alturas son captadas por dispositivos móviles, los cuales las transfieren a un ordenador que sintetiza una onda sonora. Se trata de una representación física de la transformada de Fourier. Desde un punto de vista musical, se hace una performance con los participantes. Figura 2: Thomas Noll and The Collective Public Fourier Performance 3.3. Paco Gómez y los ritmos euclídeos En esta actividad, presenté algunos resultados sencillos de divisibilidad y los conecté con la teoría del ritmo. De ahí pasamos a tocar con los famosos tubos afinados boomwhacker. Es esta una actividad que permite varios niveles de complejidad que se adaptan fácilmente al nivel del público. Figura 3: Paco Gómez y Matherhythm or rhythm is a killer 3.4. Luis Nuño y su rueda armónica Luis Nuño presentó una actividad basada en su rueda armónica, un dispositivo físico que consiste en el tonnetz pasado a coordenadas polares y donde se pueden ver las transformaciones entre distintas escalas. Figura 4: Luis Nuño y su rueda armónica 3.5. Maria Manonne y su CubeHarmonic Maria Mannone presentó su CubeHarmonic, un intrumento musical novedoso que emplea el concepto de triada en el tonnetz representado en el cubo de Rubik. Figura 5: Maria Mannone y su CubeHarmonic   Bibliografía [RB03] R. E. Radocy and D. J. Boyle. Psychological Foundations of Musical Behaviors. Charles C. Thomas, Springfield, Ill., 2003. [Sno77] C. P. Snow. Las dos culturas. Editorial: Alianza, 1977.

Lunes, 01 de Agosto de 2022 | Imprimir | PDF |  Correo electrónico

50. El Sistema Solar, a escala

Un grupo de amigos ha construido una maqueta del Sistema Solar, con órbitas planetarias completas, en el lecho de un lago seco en Nevada… Imagen construida con pantallazos del video. Mirad este maravilloso video. Visto en The Presurfer Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Viernes, 22 de Julio de 2022 | Imprimir | PDF |  Correo electrónico