401. 15. (Septiembre 2020) Cuadrados, círculos y semicírculos en la obra de Frank Stella

1. Frank Stella: octogenario, norteamericano y minimalista Frank Stella (1936). Fotografía de Elena Cué El pintor, escultor y grabador norteamericano Frank Stella, de ascendencia italiana, nació el 12 de mayo de 1936 en Massachusetts. Titulado en Historia por la Universidad de Princenton, pertenece al movimiento minimalista y expresionista abstracto. En la composición de muchas de sus obras pictóricas Stella se sirve de cuadrados concéntricos, círculos y semicírculos. A ellas dedicamos este trabajo. 2. Cuadradosi Fez (1964) Rabat (1964) Gray Scramble Double Square (1964) Block-House of Flowers (1967)ii Wlid (1967) Gray Scramble (1968-69) 3. Círculos y semicírculos Untitled (1965) Harram II (1967) Firuzabad (1970) Firuzabad (variation), 1970 4. Geometría y Arte En las líneas precedentes hemos presentado diez obras del artista norteamericano Frank Stella que son un buen ejemplo, eso creemos, de la presencia de las figuras geométricas en el arte. En ellas también se muestra el potencial de los objetos geométricos 2D para generar auténticas obras de arte. Desde aquí animamos a nuestros colegas, los profesores de Matemáticas, a que (de vez en cuando) muestren a sus alumnos creaciones de este tipo para que puedan apreciar la influencia de la Geometría en el Arte y la existencia de unas «Matemáticas bellas».   NOTAS i En las obras cuadradas que ofrecemos, Stella crea ilusiones ópticas dignas de tenerse en cuenta. ii En esta obra los dos cuadrados contienen sendas espirales generadas por cuadrados concéntricos.

Viernes, 11 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

402. 109. (Septiembre 2020) Música y entropía - III

1. Introducción En la primera entrega de esta serie [Góm20b] estudiamos la relación entre la entropía y la música de una manera general. En la segunda entrega [Góm20a] repasamos los modelos de Markov (ya vistos también en otras entregas([Góm16b], [Góm16a]). En este tercera entrega vamos examinar a fondo el tratamiento que hacen de la entropía los autores Gerardo Febres y Klaus Jaffe en su artículo del año 2017 Music viewed by its entropy content: A novel window for comparative analysis [FJ17]. En su trabajo, los autores estudian cómo aplicar la entropía a la caracterización del estilo musical de una manera más completa y significativa que en estudios previos. El artículo empieza con una larga introducción donde, con erudición pero sin pesadez, revisan a fondo el estado del arte en el problema del estudio de la entropía en música. Evidentemente, empiezan mencionando a Meyer [Mey56] con su teoría de las expectativas y los grandes continuadores de sus ideas (como Huron [Hur06]). Identifican la entropía como una medida de regularidades estadísticas y como tal, cuando se aplica al fenómeno musical, permite extraer características musicales en base a dichas regularidades. Febres y Jaffe evalúan los principales esfuerzos de investigación en este sentido. Examinan, por ejemplo, los métodos basados en cadenas de Markov y apuntan a Mavromatis como uno de sus practicantes más notables [Mav05] (como vimos el mes pasado). Como método alternativo a las cadenas de Markov, los autores mencionan a Rohrmeier [Roh11], quien propone un método basado en reglas gramaticales inspirado en las teorías generativas de Lerdahl y Jackendorf [LJ83]. La entropía necesita como base un alfabeto de símbolos. En el caso de la música ese conjunto sería los símbolos que aparecen en la partitura entera. Sin embargo, para calcular medidas de entropía hace falta codificar la música en un alfabeto adecuado. Muchos investigadores han usado la codificación MIDI, que es una opción bastante natural por su versatilidad y por constituir una aproximación aceptable a la música. Ponce de León e Iñesta [PI07] usaron música en formato MIDI que analizaron a través de la entropía; su análisis incluía varios parámetros musicales tales como altura de las notas, duración de las notas, duración de los silencios, síncopas, entre otros. El corpus que usaron fue de jazz y era polifónico (muchos de los primeros estudios con entropía se limitaban a la música monofónica). Kranenburg y Backer [vKB04] diseñaron un procedimiento para reconocer el estilo a través de la entropía, pero, aunque prometedor, no alcanzaron a construir un sistema que reconociese estilos de manera fiable. Metodológicamente, la mayor parte de los trabajos han usado cadenas de Markov, como el mencionado de Mavromatis. Una excepción notable a esta tendencia es el trabajo de Cox [Cox10], que usa redes neuronales. En un futuro artículo de esta sección, abordaremos las redes neuronales y su aplicación a la música. Por el momento, nos conformaremos con describir el trabajo de Cox desde un punto de vista general. Respecto a la entropía y el significado musical, Cox escribe lo siguiente (nuestra traducción): Sin embargo, las fronteras estructurales son solo una parte del significado musical. Si el significado musical está relacionado con la tensión subjetiva que surge de la incertidumbre —esto es, de la entropía— , entonces debería ser posible correlacionar medidas instantáneas de la entropía (“perfiles de entropía”) con las respuestas afectivas a la música en el momento. Por ejemplo, una cadencia auténtica es un punto de reposo y, por tanto, debería estar correlacionado con una entropía baja. Un clímax dramático debería estar correlacionado con un valor alto de la entropía (un máximo local) porque representa una cantidad alta de tensión. 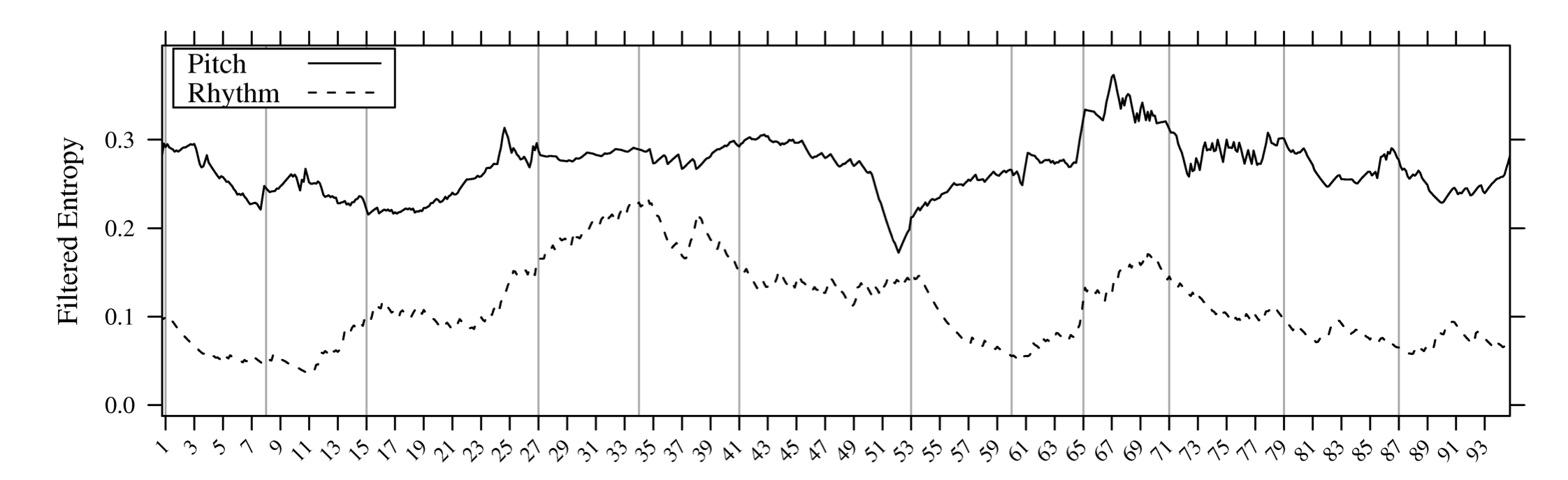El mérito de Cox es que usando redes neuronales fue capaz de producir unos perfiles de entropía que le sirvió para estudiar el estilo musical. En la figura 1 se ve un ejemplo de dichos perfiles. En su artículo analizó el cuarteto para cuerda opus 20, número 3 (los perfiles de abajo pertenecen al primer movimiento). En la figura se ven perfiles de entropía para las alturas y el ritmo; el eje x son los compases del movimiento. Figura 1: Perfiles de entropía (figura tomada de [Cox10]) La hipótesis musicológica aquí es que música que pertenece a un estilo concreto debería tener unos perfiles de entropía característicos, los cuales permitiría distinguir entre estilos. Esfuerzos anteriores en este sentido habían generado perfiles que eran demasiado bastos como para tal distinción. El trabajo de Cox representa un paso adelante en ese sentido, pero el trabajo de Febres y Jaffe constituye un paso mayor aun. Ellos usan tres medidas relacionadas con la entropía (diversidad específica, entropía y entropía de segundo orden) para estudiar el estilo musical. 2. Estilo musical y entropía 2.1. Perfiles de entropía Febres y Jaffe aplican la idea de los perfiles de entropía para analizar el estilo musical y en particular para resolver el problema de distinguir entre estilos musicales. Para ello, tomaron una muestra de 450 piezas en formato MIDI y estudiaron el estilo con la entropía. El alfabeto base para su estudio es el propio alfabeto del formato MIDI. La música está caracterizada por varias variables musicales: altura, duración, melodía, armonía, textura, etc. El propósito de un modelo es identificar la estructura (bloques y sintaxis) de la música en base a los valores de las variables musicales. Esa estructura se manifiesta como regularidades estadísticas en las cadenas de símbolos que representan la música. Esas regularidades representan normas estilísticas. La búsqueda de esas regularidades se llama reconocimiento de patrones. En su modelo se busca minimizar la entropía según está definida por Shannon; véanse [Góm20b],  [Góm20a]. De nuevo, este modelo se basa en el modelo de longitud de descripción mínima de Mavromatis [Mav05]. Se extraen del corpus una serie de símbolos que minimizan la entropía (o se acercan al mínimo dentro de un margen). Dicha extracción va acompañada de una distribución de probabilidad. Véamos más en detalle cómo ocurre esto. Empezaremos por considerar el conjunto B de símbolos MIDI que aparecen en un corpus musical (o en una pieza). A continuación, se extrae un conjunto mínimo de símbolos que minimizan lo más posible la entropía de Shannon [Sha10]. Este conjunto recibe el nombre de símbolos fundamentales y D será el número total de dichos símbolos fundamentales. D es la diversidad del lenguaje. De la observación de las piezas del corpus se obtiene la frecuencia de cada símbolo xi, que será una distribución de probabilidad P(xi). Si N es el número total de símbolos de B, se define la diversidad específica como el cociente d La entropía h viene dada por la fórmula h = -P log D(P). En su artículo, los autores comparan un breve texto en inglés con un segmento de un fichero MIDI para ilustrar cómo opera la entropía. Reproducimos aquí dicha comparación; véase la figura 2 (en el fichero de texto ∅ representa el espacio). Figura 2: Perfiles de entropía (figura tomada de [FJ17]) A continuación, Febres y Jaffe crean los llamados perfiles de frecuencias. Para cada distribución P, los autores asocian un perfil. El perfil está compuesto por una gráfica de los símbolos ordenados por frecuencia relativa decreciente en el eje x contra dichas frecuencias en el eje y; véase la figura 3. El perfil resulta ser una poligonal decreciente (pero no estrictamente decreciente en todos los casos). Distintos perfiles pueden tener distintos número de símbolos en sus descripciones. Eso da un problema a la hora de comparar los perfiles, ya que los perfiles no serán comparables a menos que tengan la misma longitud. Los autores resuelven esta dificultad usando lo que han bautizado como un método de reducción de escala. En este método reducen el número de símbolos mientras que mantienen el vector de frecuencias. El método lleva a cabo fusiones de símbolos y redistribuye adecuadamente las frecuencias entre los nuevos símbolos. En la figura 3 se ilustra este proceso; la condición para la fusión de símbolos está dada en la parte de la izquierda; para más información matemática sobre este procedimiento, consúltense los apéndices del artículo de Febres y Jaffe. Figura 3: Fusión de símbolos (figura tomada de [FJ17]) Para la comparación, se considera que la música tiene el mismo comportamiento que el lenguaje y se aplica la ley de Zipf para comparar perfiles. La ley de Zipf es una ley empírica que establece que en una lengua dada la frecuencia de aparición de las palabras sigue una distribución de tipo potencial, esto es, la frecuencia de la n-ésima palabra más frecuente es proporcional a 1∕na, donde a es un parámetro fijo que depende de la lengua en particular (a suele ser mayor que 1). Otra manera de enunciar la ley de Zipf es decir que una palabra es inversamente proporcional a su rango en la tabla de frecuencias de palabras. Cuando se dibuja la gráfica en escala logarítmica (log-log), la ley de Zipf se manifiesta como una recta decreciente. Es posible comparar los perfiles de frecuencias con el perfil de referencia (perfil de Zipf). En general, se pueden comparar dos perfiles arbitrarios entre sí. En efecto, sean fr,gr las frecuencias de dos perfiles dados para los símbolos que están en la posición r y sea S el número total de símbolos. La distancia E entre los perfiles viene dada por Si se quiere comparar con el perfil de Zipf, basta hacer gr = , donde g1 es el símbolo más frecuente. En la figura 4 se ve la comparación de perfiles musicales con el perfil de Zipf, que es la línea recta en gris. Volveremos a ellos más tarde. Figura 4: Perfiles de frecuencia de los símbolos 2.2. Entropía de orden superior La novedad que presenta Febres y Jaffe es la idea de una entropía de segundo orden. La entropía habitual la llaman entropía de primer orden y está dada por la fórmula h = -P log D(P), como vimos más arriba. Esta entropía se usa para ver cuánto se desvía el perfil de frecuencias de los símbolos del ideal de la ley de Zipf (la línea recta). Sabemos que cuanto más uniformes sean las frecuencias más alta es la entropía (de primer orden). Esto, sin embargo, es insuficiente para discriminar la complejidad de una pieza. La entropía de segundo orden se centra en los huecos entre las frecuencias de los símbolos en orden con respecto a la distribución dada por la ley de Zipf. Por tanto, detecta los cambios de pendiente en el perfil de las probabilidades de los símbolos. Para el cálculo de esta entropía de segundo orden, se definen las probabilidades Zi, donde i varía en el número de símbolos, como Zi = , siendo g la pendiente de la recta de la ley de Zipf y k una constante de modo que la línea recta empiece en la probabilidad p1, la primera probabilidad. La entropía de segundo orden se calcula en base a las diferencias pi - Zi, como se puede ver en la figura 5; para más detalles técnicos, véase el apéndice S2 de [FJ17]. Figura 5: Entropía de segundo orden La tabla de abajo muestra los resultados obtenidos calculando los dos tipos de entropía. El término MusicNet que vemos en la tabla se refiere a la clasificación de los estilos estudiados en el trabajo. Por ejemplo, la música occidental se divide en académica y popular/contemporánea, y cada una de estas categorías se divide en otras subcategorías. Dado que las entropías son esperanzas de variables aleatorias, los autores dan los valores medios junto con las desviaciones típicas para evaluar la dispersión. Figura 6: Medidas de diversidad, entropía y entropía de segundo orden A partir de los datos de la tabla anterior y tomando como referencia la ley de Zipf, es posible calcular la distancia entre piezas musicales, como muestra la siguiente tabla. En este caso vemos incluso la distancia entre dos interpretaciones de la misma pieza, la tocata y fuga en re menor de Back interpretada al órgano y al piano. También vemos la comparación entre distintas interpretaciones de piezas de diversa índole. Figura 7: Distancias entre piezas Una vez que se obtienen las distancias entre las piezas se pueden estudiar aspectos interesantes tales como la agrupación (a través de árboles filogenéticos, por ejemplo) o tendencias. Febres y Jaffe proponen tres medidas de complejidad, la diversidad específica, la entropía y la entropía de segundo orden que, combinadas entre ellas, llegan al estudio del estilo más de lo que trabajos previos habían logrado. En su artículo, usando estas medidas, comparan distintos estilos musicales de los cuales llegan a identificar algunas regularidades estadísticas. La lección que sacamos del trabajo de Febres y Jaffe es que el estilo es un fenómeno complejo y que hay que estudiarlo con un arsenal diverso y profundo de medidas estadísticas. Bibliografía [Cox10] G. Cox. On the relationship between entropy and meaning in music: An exploration with recurrent neural networks. In Proceeding Annual Meeting of the Cognitive Science Society, Portland, USA, August 2010. [FJ17] G. Febres and K. Jaffe. Music viewed by its entropy content: A novel window for comparative analysis. PLoS ONE, 12(10):1–30, 2017. [Góm16a] P. Gómez. Música y Probabilidad (II), diciembre de 2016. [Góm16b] P. Gómez. Música y Probabilidad (I), noviembre de 2016. [Góm20a] P. Gómez. Música y Entropía - II, agosto de 2020. [Góm20b] P. Gómez. Música y Entropía - I, julio de 2020. [Hur06] David Huron. Sweet Anticipation. MIT Press Books, Massachusetts, 2006. [LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983. [Mav05] P. Mavromatis. A hidden markov model of melody production in greek church chant. Computing in Musicology, 14:93–12, 2005. [Mey56] Leonard Meyer. Emotion and Meaning in Music. University of Chicago Press, Chicago, 1956. [PI07] P. J. Ponce de Leon and J. M. Iñesta. Pattern recognition approach for music style identification using shallow statistical descriptors. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 37(2):248–257, 2007. [Roh11] M. Rohrmeier. Towards a generative syntax of tonal harmony. Journal of Mathematics and Computation in Music, 5:35–53, 2011. [Sha10] C. E. Shannon. A Mathematical Theory of Communication. Bell System Technical Journal, 27:379–423, 623–656, julio, octubre 2010. [vKB04] P. van Kranenburg and E. Backer. Musical style recognition–a quantitative approach. In Conference on Interdisciplinary Musicology (CIM04), pages 1–10, Graz, Austria, Abril 2004.

Jueves, 10 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

403. 153. SOLUCIONES CONCURSO DEL VERANO DE 2020

Septiembre de nuevo, aunque en este caso, como medio año ya, diferente, extraño. Pero a pesar de todo con todas las ganas de seguir contando y descubriendo películas en las que las matemáticas aparezcan por algún lado, porque, aunque llevemos ya 153 reseñas (¡¡dieciséis años!!), nos queda mucho de qué hablar. Y como tradición desde los inicios, lo que toca este mes es mostrar las soluciones al concurso propuesto para el verano. Empezamos. CUESTIONES MATEMÁTICAS M – 1. Sabemos que AK = 56. Es obvio que AK = AD + DG + GJ + JK. Por otra parte, nos indican que AD, DG y GJ ≥ 17. Por tanto, AD + DG + GJ ≥ 51, y por ello, JK ≤ 5 para que se cumpla que AK = 56. Además, nos indican que HK ≥ 17, y como JK ≤ 5, entonces HJ ≥ 12. Como también nos dicen que HJ ≤ 12, entonces es claro que HJ = 12. Por otro lado, como HK ≥ 17 y HJ = 12, entonces JK ≥ 5. Luego JK = 5. Razonando de un modo similar, tenemos que AB = 5 y BD = 12. Entonces, DH = AK − AB − BD − HJ – JK = 56 − 5 − 12 − 5 − 12 = 22. Como GJ ≥ 17 pero HJ = 12, entonces, GH ≥ 5. Como DG ≥ 17 y DH = DG + GH = 22, se deduce que DG = 17 y GH = 5. Finalmente, BG = BD + DG = 12 + 17 = 29 kilómetros. Uno de los participantes, Alejandro Apezteguia, nos indica en su solución que las tres únicas posibilidades con las condiciones del enunciado (sin prueba) son 5 – 6 – 6 – 5 – 6 – 6 – 5 – 6 – 6 – 5 5 – 5 – 7 – 5 – 5 – 7 – 5 – 5 – 7 – 5 5 – 7 – 5 – 5 – 7 – 5 – 5 – 7 – 5 – 5 Observo que algunos participantes no han considerado correctamente las condiciones que se describían en el enunciado. El uso del pronombre nos ha jugado en este caso una mala pasada. El enunciado dice, “un viaje a lo largo de dos tramos sucesivos cualesquiera nunca superara los 12 kilómetros, y que uno a lo largo de tres secciones sucesivas fuera de al menos 17 kilómetros”. La situación que se trataba de describir era un (viaje) tal que a lo largo de tres secciones sucesivas cualesquiera fuera de al menos 17 kilómetros. Es decir, cualquier distancia entre tres estaciones consecutivas es de al menos 17 kilómetros. Estos concursantes han interpretado que bastaba con que hubiera un trayecto entre tres estaciones de al menos 17 kilómetros. En ese caso, no se podía calcular con solo esos datos la distancia entre B y G pedida. Entendiendo por tanto que ha sido un problema de enunciado confuso, y que todos han hecho un razonamiento correcto de acuerdo a lo que han entendido, hay dos opciones: anular la cuestión o darla como correcta a todos. Como me parece más justo valorar los razonamientos, se han dado por válidas ambas opciones. Disculpen el desafortunado enunciado. M – 2 El triángulo rectángulo de catetos 3 y 4 es el que configura las distancias entre los sucesivos ojetes del tipo de lazada descrito. En este caso las longitudes entre los ojetes de diferentes hileras son las hipotenusas de esos rectángulos de modo que, empezando por uno de los extremos tenemos las longitudes 10 + 5 + 5 + 5 + 5 + 4 (la base de la lazada) + 5 + 5 + 5 + 5 + 10 = 64 centímetros. M – 3 Los seguidores de este cuestionario estival saben que siempre hay alguna cuestión en la que no todo está perfectamente definido y determinado, buscando un poco motivar la creatividad y ver por dónde sale el concursante. En cualquier caso, esta pregunta tenía en sí tres cuestiones: un cálculo (de acuerdo a las decisiones que haya tomado el concursante) e indicar dos lazadas posibles, una útil y otra inútil (el reparto de los 10 puntos ha sido, respectivamente, 4 – 3 – 3). Si pensamos en el acto habitual en nuestras vidas de atarnos los cordones, lo “usual” es utilizar todos los ojetes (dijimos diez, es decir, dos hileras de cinco), y pasar el cordón una única vez por cada uno (sobre todo porque en la realidad, no nos cabría si lo hiciéramos más veces), dejando cordón suficiente en los extremos para hacer un nudo y que el calzado se fije bien sujeto al pie. Veamos el número de posibilidades con estas especificaciones. Por el primer ojete tenemos dos posibilidades diferentes de introducir el cordón (desde el exterior del ojete, o desde el interior). Ahí tenemos ya 2 ∙ 10 maneras (hay diez ojetes, recordemos). Para el siguiente que elijamos tenemos 2 ∙ 9 maneras, y así sucesivamente. Es decir, 2 ∙ 10 ∙ 2 ∙ 10 ∙ 2 ∙ 10 ∙ 2 ∙ 10 ∙ 2 ∙ 10 ∙ 2 ∙ 10 ∙ 2 ∙ 10 ∙ 2 ∙ 10 ∙ 2 ∙ 10 ∙ 2 ∙ 10 = 210 ∙ 10! Esta cantidad, por cierto, se conoce como doble factorial, y se denota mediante 10!! (un valor en este caso de 3 715 891 200; ¡¡un montón de maneras!!). Ahora bien, se preguntaba por formas diferentes. Y como nos indica con un ejemplo, Alejandro Apezteguia, hay maneras que se repiten a pesar de haberse configurado de modos diferentes (atado inverso). Por ejemplo, denotando los ojetes de la izquierda con la letra i y los de la derecha con la letra d, y poniendo letras minúsculas si el cordón lo atraviesa de abajo hacia arriba y en mayúsculas si lo hace al revés, tenemos que (los numeramos de 1 a 5 por orden de cercanía al tobillo) el esquema de atado i1 - I2 - d1 - i3 - i4 - D3 - D2 - I5 - d5 - D4 es idéntico al esquema d4 - D5 - i5 - d2 - d3 - I4 - I3 - D1 - i2 - I1 De ahí que, a la cantidad total, debemos dividirla por dos, quedando, 29 ∙ 10! Y esta cifra podría verse nuevamente reducida si se consideran iguales esquemas que sean “simétricos”; o si se consideran iguales esquemas que hagan el mismo recorrido, pero con las formas de paso por el ojete contrarias, en vez de abajo hacia arriba, hacerlo de arriba hacia abajo y viceversa. Considerando todas esas restricciones, en realidad hay sólo 1440 formas realmente diferentes, pero deducirlo no es nada sencillo. El lector interesado puede consultar el libro The Shoelace Book (A Mathematical Guide to the Best (and Worst) ways to lace your shoes), de Burkard Polster, y comprobarán que deducirlo excede considerablemente nuestros propósitos de este concurso. De modo que, daremos por válidas las respuestas indicadas anteriormente. Respecto a formas útiles y formas inútiles, deberiamos decidir qué entendemos por útil (que se ajuste bien es lo usual, aunque depende del tipo de pie que tengamos; cuál es la más estética, cuál emplea la menor longitud de cordón, etc.; hay muchas variantes). Lo que es claro es que la más inútil porque ni ajusta el pie ni hace nada es: Al estirar los extremos, acercaría los ojetes en vertical, pero no en horizontal (salvo el par i5 – d5). Entre los prácticos, podemos citar los tres siguientes (con una hilera más): en zig zag, en zig zag con N y en pajarita, respectivamente. M – 4 El procedimiento indicado en la cuestión M – 2 empleaba, como vimos, 64 cm., dejando libres 36 centímetros de los 100 que se indican, quedando por tanto 18 centímetros a cada extremo para hacer el nudo. El procedimiento que utiliza menor cantidad de cordón de todos los indicados por los concursantes es cualquiera de los tres que mostramos en la siguiente imagen (todos con la misma longitud): 4 + 4 ∙ 3 + 4 ∙ 5 = 36 cm. Con cualquiera de ellos nos sobrarían 100 – 36 = 64 cm. El modo de valorar la cuestión ha sido la siguiente: 10 puntos para quien ha indicado el procedimiento con el valor menor, como se pedía, y en orden decreciente, un punto menos con el resto de propuestas que utilizaban más cantidad de cordón (es decir, los siguientes 9 puntos, 8, etc.). M – 5 El único anudado que realmente hace un nudo es el c. Además de haciéndolos, se puede probar uniendo los extremos de las cuerdas e ir aplicando los tres tipos de movimientos de Reidemeister (transforman el diagrama plano del nudo en otro equivalente). Observaríamos así que salvo en el caso c, en los restantes diagramas obtendríamos una circunferencia, lo que se conoce como nudo simple (si no hubiéramos unido los extremos no existiría nudo, solo el cordón alargado). M – 6 En primer lugar deberíamos observar que en el enunciado no se dice nada del lugar en el que colocamos los pesos, porque podríamos colocarlos en uno solo de los platillos (lo que prácticamente todo el mundo contempla), pero también podrían colocarse en ambos. En ese caso, cualquier cantidad de puede pesar, ya que, por ejemplo, 1 gramo lo pesaríamos colocando tres pesos de 5 gramos en uno de los platillos junto al objeto de 1 gramo, y dos de 8 gramos en el otro platillo. Duplicando el número de pesas de esa situación, lograríamos el equilibrio para 2 gramos, y así sucesivamente para cualquier valor de n gramos. También es válido argumentar de acuerdo al teorema de Bezout teniendo en cuenta que mcd(5, 8) = 1. Si solamente permitimos el objeto en uno de los platillos y en el otro los pesos, entonces la solución es distinta. Designemos por P el peso en gramos del objeto. Éste podría pesarse siempre que cumpla que P = 5x + 8y, siendo x e y enteros positivos. A su vez, y puede ser escrito como 5z + r, siendo z ≥ 0 y r = 0, 1, 2, 3, 4. Entonces tenemos cinco situaciones: P = 5(x + 8z) + 8 ∙ 0 = 5(x + 8z) P = 5(x + 8z) + 8 ∙ 1 = 5(x + 8z + 1) + 3 P = 5(x + 8z) + 8 ∙ 2 = 5(x + 8z + 3) + 1 P = 5(x + 8z) + 8 ∙ 3 = 5(x + 8z + 4) + 4 P = 5(x + 8z) + 8 ∙ 4 = 5(x + 8z + 6) + 2 Llamando k = x + 8z, tenemos respectivamente P = 5k P = 5(k + 1) + 3 = 5α + 3 P = 5(k + 3) + 1 = 5β + 1 P = 5(k + 4) + 4 = 5γ + 4 P = 5(k + 6) + 2 = 5δ + 2 En definitiva, si nos fijamos, son múltiplos de 5, múltiplos de 5 módulo 3, múltiplos de 5 módulo 1, múltiplos de 5 módulo 4 y múltiplos de 5 módulo 2. Por otra parte, P puede ponerse de alguna de las formas: 5K, 5K + 1, 5K + 2, 5K + 3, o 5K + 4 (utilizo K mayúscula para denotar “múltiplos” en vez de tanta letra distinta). Comparando éstas con las anteriores, se concluye que (i) si P es de la forma 5K, entonces puede ser pesada (con K pesas de 5 gramos). (ii) si P es de la forma 5K + 1, puede ser pesada si K ≥ 3. (iii) si P es de la forma 5K + 2, puede ser pesada si K ≥ 6. (iv) si P es de la forma 5K + 3; puede ser pesada si K ≥ 1. (v) si P es de la forma 5K + 4, puede ser pesada si K ≥ 4. En consecuencia, los valores de P que NO pueden ser pesados son: 1g, 2g, 3g, 4g, 6g, 7g, 9g, 11g, 12g, 14g, 17g, 19g, 22g y 27g. Los concursantes establecieron una tabla que, visualmente es mucho más ilustrativa. En la que se incluye (debida a Alejandro Apezteguía), se observa que la quinta columna son todos los múltiplos de 5, y en el resto de columnas a partir del primer múltiplo de 8 que aparece todos también son de la forma 5x + 8y. Por tanto, los que quedan en color blanco son los “no pesables”. La puntuación se ha repartido del siguiente modo: 3 puntos para la primera de las situaciones (claramente más sencilla) y 7 puntos para la segunda. M – 7 Después de sacar dos litros de leche, cada litro de la mezcla tiene 3/5 de leche. Si volvemos a sacar dos litros de la mezcla, tendremos que 3 – 3 (3/5) = 9/5 de leche permanecen. Eso nos da una concentración de (9/5):5 x 100% = 36 % M – 8 Empezando en la silla 1, un número par de movimientos siempre va a terminar en las sillas 1, 3 o 5 (un número impar más otro par, resulta siempre un número impar), mientras que un número impar de movimientos acaba en las sillas 2 o 4 (impar más impar es par). Después de 19 o 2733, ambos impares, va a estar en la silla 2 o en la silla 4. En ese momento se retiran las sillas 1 y 5 quedando las sillas 2, 3 y 4. La señora se encuentra en una silla de un extremo (aunque tengan nombre de números pares, atendiendo a su orden, esas sillas corresponden a valores impares: la primera y la tercera). De nuevo, cualquier movimiento impar (se citan 97 o 5931), la llevarán siempre a la silla 3 (que es la que corresponde a la posición par de las que quedan). M – 9 En esta cuestión algunos concursantes no han tenido en cuenta que las entregas anuales también devengan intereses, por lo tanto no hay únicamente que considerar la fórmula del interés compuesto C (1 + r)n, sino también el valor total de esos intereses al cabo de los n años, que será, después de efectuar algunas operaciones siendo a =10655.2 pesetas, lo que se conoce como anualidad. Sustituyendo los datos del enunciado, es decir, 10655.2 = 10000 , se llega a que n = 12.000048 ≈ 12 años. Uno de los concursantes, Pablo Palacio, nos incluye una tabla EXCEL en la que puede verse la amortización año a año (imagen adjunta). M – 10 Si unimos los centros de los semicírculos pequeños con el centro del círculo, se obtiene un triángulo isósceles de lados 6 y 3 + R, como vemos en la imagen. Sea h la altura perpendicular a la base de longitud 6 unidades. Esa altura junto al radio del círculo nos da el radio de la semicircunferencia grande, esto es, h + R = 6. De acuerdo con el teorema de Pitágoras, h2 + 32 = (R + 3)2. A partir de ambas ecuaciones, despejando h de la primera, se obtiene que (6 – R)2 + 32 = (R + 3)2 36 – 12 R + R2 + 9 = R2 + 6R + 9, y de ahí, se sigue que R = 2. De este modo, la superficie que encierra dicho círculo es 4π. Si sumamos el área las dos semicircunferencias tendremos 9π; la semicircunferencia grande ocupa 18π, de modo que la superficie restante es  18π – 9π – 4π = 5π. De acuerdo a la imagen adjunta de uno de los participantes, tenemos entonces que S1 = 18π,   S2 = y   S3 = 4π Nos falta determinar S4 y S5. Sabemos además por pura observación que S4 + 2S5 = S1 – 2S2 – S3 = 5π, de modo que basta calcular S4 o S5 para conocer ambas. El triángulo DFO tiene área 6, ya que DO = 3 y FO = 4. Sean S6 la superficie del sector circular que definen los puntos DXO y S7 la del que definen los puntos FXT. Entonces S4 =2 ∙ (6 – S6 – S7) Por otra parte, como los ángulos del triángulo DFO son complementarios (es un triángulo rectángulo), como la relación de áreas es el cuadrado de la razón de semejanza ∙ S7 = ∙ S2 – S6 Sustituyendo esta expresión en la anterior, tenemos que S4 = 2 (6 – S6 – (π – S6)) = 12 − 2 π − S6 Por tanto, basta con que calculemos el área del sector circular S6. De la conocida fórmula para hacerlo nos falta conocer el ángulo α determinado en FDO, que será arctg(). Con ello S6 = 9 arctg() y, por tanto, S4 = 12 − 2 π – 5 arctg() y S5 = − 6 + arctg(). Por tanto, sí es posible calcular de modo exacto la superficie de cada una de las zonas. M – 11 Denotemos por Ar, Br, Cr la cantidad de rateras que capturaron respectivamente A, B y C, y sean Ac, Bc, Cc la cantidad de cornejas de cada uno, respectivamente. Del enunciado se siguen las siguientes ecuaciones: Ar = 3Br Bc = 4Cc Ar + Ac = Br + Bc = Cr + Cc Ar + Br + Cr = Ac + Bc + Cc Ar + Br + Cr + Ac + Bc + Cc < 200 con n < 100. Se trata de un sistema lineal y compatible con solución . Para que sean números enteros, n deber ser múltiplo de 51, pero menor de 100; por tanto, n = 51 y la solución es (18, 6, 27, 16, 28, 7), que corresponden a que A obtiene 18 rateras y 16 cornejas, B se cobra 6 rateras y 28 cornejas y C a 27 rateras y 7 cornejas. M – 12 Como los triángulos con la misma altura tienen área proporcional a sus respectivas bases, y como los triángulos AOB y COD son semejantes, tenemos que , por lo que área(DOA) = área(AOB). Por otra parte, como las áreas de triángulos semejantes son proporcionales a los cuadrados de los lados correspondientes, , entonces  área(COD) = área(AOB). Finalmente, como los triángulos ABD y ABC tienen la misma base e igual altura, entonces sus áreas son iguales, y como área(ABD) = área(AOB) + área(DOA) área(ABC) = área(AOB) + área(BOC) se deduce que área(DOA) = área(BOC). En consecuencia, área(ABCD) = área(AOB) + área(BOC) + área(COD) + área(DOA) = área(AOB) + 2 área(DOA) + área(COD) Es decir, área(ABCD) = área(AOB). Y, por tanto, M – 13 El número total de disposiciones de las doce letras es . Para contar aquellas que no tienen dos letras A adjuntas, distribuimos primero las otras nueve letras, que serán . Para cada una de esas disposiciones, elegimos tres cualesquiera de los diez “huecos” que hay entre letras consecutives, incluyendo las de los finales. Esto se puede hacer de formas. Después insertamos las tres A en los tres espacios que hemos elegido. Esto responde a un único arreglo sin A’s adyacentes. El número total es entonces Por tanto, la probabilidad pedida es CUESTIONES CULTURALES C – 1 Las palabras que aparecen en el texto, de escasa utilización actualmente (si bien esto es una apreciación subjetiva, porque en determinadas zonas pueden seguir siendo habituales) son, entre otras: Albarca, Ojete, Borceguíes, Zapatranco, Romana, Campero, Difidentes, Alquería, Gañanes, Delfines, Tollos, Rateras, Cornejas, Aguardadero, Corralada, Apaleadores, Bordonear. No hemos incluido su significado por no alargar esta reseña, pero son fácilmente localizables, como han hecho los participantes. C – 2 La romana es un tipo de balanza cuyo funcionamiento está basado en la ley de la palanca (la potencia por su brazo es igual a la resistencia por el suyo). De acuerdo a la imagen, P ∙ x = R ∙ y Según la posición de P y de R respecto al punto de apoyo (también llamado fulcro) tenemos diferentes tipos de palanca. En el caso concreto de las romanas (las primeras se fechan en torno al año 200 a. C.), el punto de apoyo sostiene a la palanca por la parte superior en vez de por la parte inferior y el brazo de la resistencia es mucho más largo que el de la potencia, pudiéndose desplazar la resistencia por dicho brazo, como observamos en la imagen. El material del que estaban construidas solía ser de hierro o latón, y el contrapeso (denominado aequipondium o pilón) solía ser de bronce, y en algunos casos relleno de plomo para alcanzar el peso de un modo más preciso. Este contrapeso se desplaza por el brazo graduado de la romana junto con una anilla llamada registro, para llevar a cabo la pesada. Cuando el sistema queda equilibrado (se sabe gracias a un hierro en forma de pincho llamado fiel que queda alineado con la parte superior en la alcoba y es perpendicular a la barra) la muesca de la barra graduada nos indica el peso del objeto. Las piezas más comunes de la romana son once: alcoba, calamón, gancho, ejes, registro, fiel, cabeza pequeña, cabeza larga, pilón, cadena y plato. La gran ventaja de una balanza romana o de una clásica es que comparan masas y por tanto no dependen de la gravedad del lugar donde se encuentren (miden lo mismo independientemente de que estemos en un valle o en un lugar de alta montaña), lo que no pasa con una báscula electrónica o con un dinamómetro, ya que miden fuerzas. Dependiendo de lo detallado o escueto de la descripción del funcionamiento se han dado a los concursantes valoraciones entre 8 y 10 puntos. C – 3 Existen varias razones por las que muchas personas desconfiaban de la romana, unas de tipo técnico (la exactitud y precisión de la romana depende de la calidad de los materiales con que haya sido fabricada y del calibrado de la barra y el pilón), disculpables en general por los clientes, y las más por la picaresca y “habilidad” del que la manejara ya que existen numerosos trucos y ardides para sisar en la venta (poner un plato en lugar de un gancho y no descontar su peso del del objeto; poner platos en el objeto (brazo corto) y en el pilón (brazo largo), aparentemente iguales pero de diferente peso; o reemplazar alguna pieza de la romana por otras de distinto peso; o sujetar el fiel con un dedo simulando una falsa posición de equilibrio; lijar la barra donde va el pilón; al estar sujeta de la mano, no fija a ningún sitio, moverla ligeramente, etc.). Por todo ello, se prohibió su uso, aunque en algunos lugares (pueblos apartados, mercadillos, etc.) aún pueda alguien encontrar algún paisano que la utilice. C – 4 En efecto, tal y como han descrito los concursantes, nos referíamos a la actriz Ágata Lys (cuyo nombre real es Margarita García San Segundo). Nacida en Valladolid el 3 de diciembre de 1953 se hizo popular como azafata del concurso televisivo Un, Dos, Tres…, Responda Otra Vez. Su físico y la época (segunda mitad de los años 70 del siglo pasado tras la muerte de Franco y la desaparición de la censura) en la que primaba el cine de evasión y de destape, la encasilló en producciones de baja calidad artística. Entre éstas, títulos como Las marginadas (Ignacio Iquino, 1974), El valle de las viudas (F. Windder, 1975), Fango (Silvio F. Balbuena, 1976), Deseo carnal (Manuel Iglesias, 1977), Trauma (León Klimovsky, 1978), hasta un total de treinta y siete entre 1972 a 1979. Harta de estos papeles, reconduce su trabajo hacia el teatro, aunque no desdeña en participar, aunque sea brevemente, en productos de mayor calidad, como Los santos inocentes (Mario Camus, 1984), Familia (Fernando León de Aranoa, 1996), Mala uva (Javier Domingo, 2004), o series de televisión como Amar en tiempos revueltos (2005-2006). Según sus palabras, “no está retirada, solo “en la retaguardia”. “Si me ofrecen algo interesante, que me haga crecer, lo voy hacer, aunque tenga ochenta años”. C – 5 Se pregunta por la edad del señorito Iván. Ni en la película ni en la novela se dice ninguna edad explícita de ningún personaje salvo de Azarías que indica que tiene 61 años. Pero podemos deducir un rango de edades. Tanto en la película como en la novela se indica que “el Ivancito con el rifle o la escopeta, en el monte o los labajos y el año 43, en el ojeo inaugural del Día de la Raza, ante el pasmo general con trece años mal cumplidos, el Ivancito entre los tres primeros”. Claramente entonces el señorito Iván ha nacido en 1930 (1943 – 13 = 1930). Por otra parte, en la fiesta que dan en el cortijo con motivo de la Primera Comunión del hijo mayor de Iván, se comenta de modo jocoso por lo inaudito de la propuesta, que la hija mayor de Paco, el bajo, quería hacer también la Primera Comunión. Entonces, el señorito Iván comenta que “la culpa la tiene ese dichoso Concilio que les malmete”. Evidentemente se refiere al Concilio Vaticano II que se celebró entre 1962 y 1965. Por tanto, el señorito Iván tiene entre 32 y 35 años. C – 6 En la novela se explica perfectamente: “La propia Señora Marquesa, con objeto de erradicar el analfabetismo del cortijo, hizo venir durante tres veranos consecutivos a dos señoritos de la ciudad para que, al terminar las faenas cotidianas, les juntasen a todos en el porche de la corralada, a los pastores, a los porqueros, a los apaleadores, a los muleros, a los gañanes y a los guardas, y allí, a la cruda luz del aladino, con los moscones y polillas bordoneando alrededor, les enseñasen las letras y sus mil misteriosas combinaciones”. C – 7 Milana Bonita. Como anécdota, uno de los participantes, que conoce a una de las hijas del escritor, indica en sus respuestas que cada vez que Dirk Bogarde se cruzaba con Paco Rabal en el Festival de Cannes de 1984 le repetía “milana bonita, milana bonita”. Le agradecemos que nos la de a conocer. C – 8 Azarías sólo sabe contar hasta once; después salta a cuarenta y tres, cuarenta y cuatro, etc. En la novela lo descubrimos al contar los tapones de las válvulas de las ruedas y las mazorcas de maíz. En la película lo hace también con las panochas y con habas. C – 9 En el punto dado, la función alcanza el máximo absoluto. Cuando Miguel Delibes conoció al amor de su vida, Ángeles de Castro, empezó a firmar sus primeras obras con el acrónimo MAX, lo cual era una sencilla y romántica expresión en la que la M representaba a Miguel, la A era por Ángeles y la X era la incógnita que el futuro podía deparar a la joven pareja, tal y como explicó el propio autor. Esa es la relación en la que yo había pensado y la dada como correcta. Sin embargo, los concursantes han ideado además otras relaciones que reproduzco por su originalidad: 1.- Al observar la gráfica, ese punto parece la “cumbre” de una montaña. Por otra parte, entre las muchas novelas de Miguel Delibes más afamadas por público y crítica, Los santos inocentes puede ser la que contenga los personajes "cumbre" de la pluma del autor vallisoletano. Además, la función presenta infinitos puntos donde se alcanza ese valor máximo (es periódica), mientras que Delibes obtuvo una infinidad de premios entre los que destacan el Nacional de Literatura, el premio de la Crítica, el Nacional de las Letras, el Príncipe de Asturias o el Cervantes, entre otros. No pueden ser infinitos, pero la expresión coloquial “una infinidad de premios” se utiliza por abuso de lenguaje en muchas ocasiones. 2.- El valor 4π /3 = 4.1887902.... ≈ 4.189. El valor e + 4/e = 4.1887902.... ≈ 4.189799 ≈ 4.189. El valor del máximo de esa función es ½ (3) = 2.598... ≈ 3e/π. De alguna manera, el punto dado está relacionado con el número e. Precisamente Delibes ocupaba la silla de la Real Academia Española (RAE) correspondiente justamente a la letra e hasta que murió con 89 años (número de Fibonacci). 3.- El valor x = 4π /3 en grados equivale a 240º. Al menos tres novelas de Delibes tienen justamente 240 páginas: Parábola del náufrago. Tapa blanda. Ediciones Destino; Los santos inocentes. Tapa blanda. Austral; Diario de un emigrante. Ediciones Destino. Y finalmente, otro concursante ha detectado que tomando la expresión decimal de ese valor máximo (2.5980....) y la fecha del fallecimiento del escritor, 12/03/2010 escrita en modo decimal mediante 0.1203, se obtiene como suma 2.5980 + 0.1203 = 2.7183 que es un redondeo del número e (2.71828...), y la letra e como se dijo antes es el sillón que Miguel Delibes ocupaba en la Real Academia Española de la Lengua. (¡¡¡Nunca se me hubiera ocurrido!!!) C – 10 Las nueve novelas adaptadas al cine de la obra de Miguel Delibes son: 1.- El Camino publicada en 1950. La adaptación fue dirigida por Ana Mariscal en 1963. 2.- Mi idolatrado hijo Sisí (1953): la película se tituló Retrato de familia (Antonio Giménez Rico, 1976). 3.- El Príncipe Destronado (1973); en cine fue La guerra de papá (Antonio Mercero, 1977). 4.- Los Santos Inocentes (1981); la adaptación cinematográfica la dirigió Mario Camús en 1984. 5.- El disputado voto del señor Cayo (1978); llevada al cine por Antonio Giménez Rico en 1986. 6.- El Tesoro (1985); la dirigió Antonio Mercero en 1988. 7.- La sombra del ciprés es alargada (1948), dirigida por Luis Alcoriza en 1990. 8.- Las ratas (1962), llevada al cine por Antonio Giménez Rico en 1997. 9.- Diario de un jubilado (1995); la versión cinematográfica se tituló Una pareja perfecta (Francesc Betriú, 1998). Francisco Rabal interpretó también al protagonista principal de El disputado voto del señor Cayo, película que mencionamos en el Concurso del Verano del año 2010, en la reseña número 52, en las cuestiones 22 y 23. C – 11 En este año en el que estamos, 2020, se celebra el centenario del nacimiento del autor (17 de octubre de 1920). Casualmente se cumplen también diez años de su fallecimiento, que tuvo lugar el 12 de marzo de 2010, por lo que también se le puede hacer un homenaje, pero las celebraciones son normalmente como referencia de hechos alegres, y no los fallecimientos. C – 12 Las diferencias más evidentes entre película y novela son: 1.- La película elimina algunos personajes de la novela (los seis capítulos de la novela se redujeron a cuatro en el guion de la película). Entre los personajes eliminados podemos destacar a Rogelio, el cuarto hijo de Paco el bajo; o al señorito Lucas, que enseñó los rudimentos de la gramática a Paco el bajo. 2.- En la obra de Delibes no se dice expresamente que los hechos ocurran en un lugar concreto (aunque Azarías menciona al mago del Almendral, municipio de la provincia de Badajoz, cuando está preocupado por la salud de su búho). En la primera escena de la película, sin embargo, aparece el rótulo de la estación ferroviaria de Zafra. 3.- La celebración de la comunión del señorito Carlos Alberto, en el libro se refleja solamente como una reunión en la corralada para comer chocolate con migas, mientras que en la película, hay una gran fiesta con presencia de autoridades, baile y otras escenas festivas. 4.- La “rebelión silenciosa” de la Nieves y el Quirce, que pertenecen a una generación posterior a la de sus padres y deciden tomar caminos distintos a los que se les han asignado (trabajar en una fábrica en la ciudad y como mecánico respectivamente), solo se ve reflejada en la película, no en el libro. Los flashbacks de estos personajes no existen en la novela. 5.- Otra diferencia es que al final de la película, Régula y Paco, vuelven a estar instalados en la raya de Abendújar y esta situación no existe en el argumento literario. 6.- La novela acaba con la muerte del señorito mientras que en la película se representan acontecimientos posteriores, como los descritos con los hijos de Paco y el internado de Azarías en un centro psiquiátrico. Del mismo modo, la Niña Chica no muere en la novela, y en la película si se menciona su destino. Por supuesto la película es una magnífica adaptación de la novela, que agradó al propio escritor. Pocas veces se ha logrado una trasposición al cine tan fiel al original. C – 13 Obviamente hablamos de Los santos inocentes. Casi todos los participantes conocían la película, y algunos menos habían leído la novela. Como otros años, uno de los objetivos del concurso es ahondar un poco en cine, literatura, arte, etc., y descubrir algunas de sus relaciones, lo cual ha agradado un año más (al menos eso manifiestan) a los participantes. Ha habido un montón de sugerencias, indicaciones de cómo habían descubierto la película, etc. Una que me gustaría reseñar (para dejar constancia de cómo hilan de fino los participantes) es que se podía haber hecho alusión al popular concurso 1, 2, 3, …, responda otra vez dado que Ágata Lys fue azafata del concurso (lo comentamos anteriormente) y además el personaje de la señora Marquesa en la película lo interpreta Mary Carrillo (la única actriz que se reconoce en el fotograma que se puso en la propuesta del concurso; la dejé porque pensé que nadie la conocería, pero me equivoqué y fue la “pista” para un par de concursantes para descubrir la película rápidamente), que es la madre de las hermanas Hurtado que relevaron a Don Cicuta en el mencionado concurso en la “parte negativa”.   Puntuaciones Aunque es cierto que las cuestiones matemáticas de esta edición eran un poco más sencillas que en otras ediciones (lo cual no ha animado sin embargo a más lectores a participar), es realmente destacable comprobar el buen nivel de todos los participantes (como el año anterior, me gustaría destacar y agradecer la participación de Alba Diez Mariño, una jovencita de quince años, que ha resuelto, con las herramientas matemáticas que conoce, la mayor parte de las cuestiones). Salvo malentendido de algún enunciado, todos han afrontado perfectamente todas las cuestiones matemáticas. Respecto a las de cine, siempre baja un poquillo, pero internet suele suplir las lagunas. Este año, detallo la puntuación alcanzada y además entre paréntesis la puntuación de la parte matemática (en rojo) y de la parte cultural (en azul), respectivamente. A sugerencia de un concursante, enviaré también la puntuación a cada uno por apartados. 1.- Francisco Pi Martínez.- 259 puntos (129 + 130) 2.-. Alejandro Apezteguía - 250 puntos (130 + 120) 3.- Carlos Marijuán López.- 232 puntos (112 + 120) 4.- Pedro Pablo Palacio.- 222 puntos (107 + 115) 5.- Celso de Frutos de Nicolás.- 196 puntos (81 + 115) 6.-. Alba Diez Mariño - 188 puntos (80 + 108)   Agradezco a todos su buenísima disposición, la aceptación de la propuesta, y sus elogios (inmerecidos). Espero que hayan pasado de verdad un buen rato. En breve recibiréis un mail, algunos para pediros una dirección postal a la que enviaros un pequeño obsequio de DivulgaMAT, y los demás para detallaros las puntuaciones de cada cuestión, una vez hayáis leído las soluciones.

Miércoles, 09 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

404. Fractales, sello a sello

Heraldo de Aragón, 28 de Julio de 2020 SOCIEDAD - Ciencia y filatelia Raquel Villacampa Gutiérrez y Antonio C. Ramo Antón

Viernes, 28 de Agosto de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

405. 133. (Septiembre 2020) Tareas de un matemático loco, de Antón Chéjov

Antón Chéjov publicó en 1882 Tareas de un matemático loco bajo el seudónimo de “Antosha Chejonté”. Se trata de una hilarante parodia del quehacer matemático a través de ocho absurdas cuestiones planteadas por un matemático “loco”. Se reproduce debajo el cuento completo. Antón Pávlovich Chéjov (Wikimedia Commons). Tareas de un matemático loco Me perseguían 30 perros, de los cuales 7 eran blancos, 8 grises y los restantes negros. Se pregunta: ¿en qué pierna me mordieron los perros, en la derecha o en la izquierda? Autolimioi nació en el 223, y murió tras vivir 84 años. Una mitad de la vida la pasó en viajes, un tercio lo gastó en placeres. ¿Cuánto vale una libra de clavos y estuvo acaso casado Autolimio? En el año nuevo, de la mascarada del teatro Bolshói fueron sacados 200 hombres por pelea. Si los que peleaban eran doscientos pues, ¿cuántos eran los injuriosos, los borrachos, los levemente borrachos y los que deseaban, pero no hallaban ocasión de pelear? ¿Qué se obtiene tras la suma de esas cifras? Se compraron 20 cajas de té. En cada caja había 5 pudsii, cada pud tenía 40 libras. De los caballos que cargaban el té, dos se cayeron en el camino, uno de los cocheros se enfermó y 18 libras se derramaron. La libra tiene 96 zolotniksiii de té. Se pregunta, ¿qué diferencia hay entre el pepino en salmuera y la perplejidad? La lengua inglesa tiene 137 856 738 palabras, la francesa 0,7 más. Los ingleses se juntaron con los franceses y unieron ambas lenguas en una. Se pregunta, ¿qué vale el tercer papagayo y cuánto tiempo se necesitó para subyugar a esos pueblos? El miércoles 17 de junio de 1881, a las 3 de la madrugada, debió salir el tren de la estación A por la vía férrea, para llegar a la estación B a las 11 de la noche pero, antes de la misma partida del tren, se recibió la orden de que el tren llegara a la estación В a las 7 de la noche. ¿Quién ama más prolongado, el hombre o la mujer? Mi suegra tiene 75 años y mi esposa 42. ¿Qué hora es? Informó Antosha Chejonté Si alguien conoce la respuesta a alguna de estas cuestiones… ¿sería tan amable de compartirla? Gracias. Referencias [1] Antón Chéjov, Cuentos completos (1880-1885), Edición de Paul Viejo, Titivillus, 2013 Nota Esta breve reseña es parte del artículo Tareas de un matemático loco publicado en Cuaderno de Cultura Científica el 19 de agosto de 2020.   i Autolimio es un nombre inventado por Chéjov. ii El pud es una unidad de masa equivalente 40 libras rusas, unos 16,38 kilogramos. iii El zolotnik es una antigua unidad de masa rusa equivalente a unos 4,26 gramos.

Lunes, 07 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

406. 14. (Septiembre 2020) Josef Albers y su Homenaje al cuadrado

1. Josef Albers: apunte biográfico Josef Albers (1888 – 1976), pintor, artista y diseñador gráfico, nació en Bottrop (Alemania) y estudió arte en Berlín, Essen y Munich. Fue profesor de dibujo de la Bauhaus[i] en Weimar (1923 – 1925), en Dessau (1925 – 1932) y en Berlín (1932 – 1933). Cuando los nazis cerraron la escuela en 1933, Albers se trasladó al Black Mountain College (Carolina del Norte), donde enseñó los principios de la Bauhaus. En 1950 fue nombrado director del Departamento de Diseño de la Universidad de Yale, puesto que ocupó hasta su jubilación en 1958. Entre su obra pictórica destaca la serie Homenaje al cuadrado, iniciada en la década de 1950, en la que utilizó e ilustró su teoría de que los cambios de lugar, forma y luz producen cambios en el color. Dicha obra está integrada por cuadros en los que se representan cuadrados de distintos colores contenidos en otros. Josef Albers. Autorretrato (1918) En las páginas siguientes ofrecemos una selección de obras pertenecientes a la antedicha serie. 2. Homenaje al cuadrado: algunos ejemplos Homage to the Square (1951) Guarded (1952) Ascending (1953) Warm Welcome (1953 – 1955) Homage to the Square (1958) Apparition (1959) Rooted (1961) Embedded (1963) Closing (1964) Study for Homage to the Square (1965) 3. El cuadrado, algo más que un cuadrilátero En el epígrafe anterior hemos presentado algunas obras pertenecientes a la serie Homage to the Square. En ellas, Josef Albers ofrece diversas visiones multicolores de tres o cuatro cuadrados encajados que incluyen a este cuadrilátero regular en el grupo selecto de los actores principales de algunas obras de arte. Esta versión artística del cuadrado debería ponerse al alcance de los estudiantes de todos los niveles educativos para que contemplen a dicho cuadrilátero equilátero y equiángulo no sólo como un objeto geométrico 2D, sino como un elemento indispensable en la composición de ciertas manifestaciones artísticas. Con ello, estarán en condiciones de poder afirmar que el cuadrado es algo más que un cuadrilátero.   Referencias bibliográficas MEAVILLA SEGUÍ, V. (2007). Las matemáticas del arte. Inspiración ma( r)temática. Córdoba: Editorial Almuzara, S. L. Referencias online https://albersfoundation.org/art/josef-albers/paintings/homages-to-the-square/index/ NOTAS [i] El término Bauhaus («Casa de la Construcción») se acuñó para denominar la escuela de diseño, arte y arquitectura fundada en 1919 por Walter Gropius en Weimar (Alemania). La Bauhaus sentó las bases de lo que hoy en día se conoce como diseño industrial y gráfico.

Jueves, 03 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

407. 13. (Septiembre 2020) El poliedro Melancolía en la obra del artista francés Antoine Dorotte

1. Preámbulo En otro trabajo[1] dimos un breve paseo por el grabado Melencolia I (1514) del artista alemán Albrecht Dürer. En dicha excursión pasamos revista a los aspectos aritméticos (cuadrados mágicos normales de orden cuatro), geométricos (poliedro Melancolía) y artísticos de esta obra maestra del arte universal. El poliedro Melancolía o sólido de Durero Conscientes de que en aquella ocasión no incluimos todas las manifestaciones artísticas en las que interviene el famoso poliedro de Durero, en este artículo (a modo de anexo) ampliamos el catálogo de artistas y obras de arte relacionadas con él, presentando la escultura Amalgamma del francés Antoine Dorotte. 2. Antoine Dorotte, breve biografía artística El escultor francés Antoine Dorotte nació en Sens (Borgoña) el año 1976. Vive y trabaja en Pont-l’Abbé, París y La Courneuve y su obra tiene un marcado sabor matemático como puede apreciarse en las dos fotografías adjuntas en las que se representan dos de sus esculturas. Una, dedicada a la esfera y otra al tetraedro regular, sólido platónico que el filósofo griego identificó con el fuego. Antoine Dorotte con una de sus esculturas Simplexe, la mare au feu 3. Dorotte y el sólido de Durero Dentro de su «obra matemática», Antoine diseñó en 2010 un complejo escultórico, Amalgamma, formado por ocho poliedros Melancolía. Cada uno de ellos está construido con planchas de metal cortadas y dobladas manualmente. La elegancia y sencillez de sus formas apela a la componente artística de cada uno. Dejamos, pues, que el lector contemple las bellas fotografías cedidas por A.  Dorotte y se impregne de las sensaciones artístico-matemáticas que emanan de ellas. 4. Palabras finales y agradecimiento En las líneas precedentes hemos contemplado un objeto geométrico 3D, el poliedro Melancolía, con ojos no matemáticos. Creemos que para los profesores de Matemáticas de los niveles no universitarios (y para los de los niveles universitarios también) puede ser saludable tener más de una visión de un mismo objeto matemático; de este modo, pueden ofrecer a sus alumnos distintos enfoques de un mismo tema que, quizás,  puedan motivar a sus estudiantes. En el caso de los cuerpos geométricos esta «multivisión» se puede conseguir fácilmente recurriendo a las obras de muchos creadores (pintores, escultores, arquitectos,. . .) que incluyen las figuras y sólidos geométricos en sus producciones artísticas. Acabamos este modesto trabajo agradeciendo a Antoine Dorotte la deferencia que ha tenido con nosotros al dejarnos incluir en este artículo sus bellas fotografías.   Nota: [1] Paseo meláncolico, matemático y artístico de un grabado alemán del siglo XVI, publicado por Divulgamat.   Referencias online Antoine DOROTTE http://ddab.org/fr/oeuvres/Dorotte/Page19

Jueves, 03 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

408. 185. (Septiembre 2020) Pascal en Technicolor

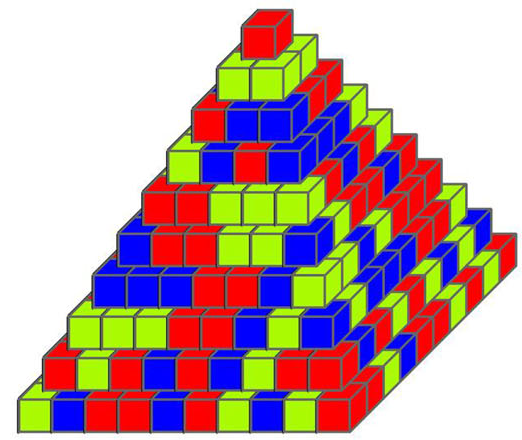
[Imagen extraída del artículo Pyramid Mysteries de Ehrhard Behrends.] Comenzábamos el número anterior de nuestro rincón (julio de 2020) destacando que el triángulo de Pascal oculta muchas propiedades que podemos convertir en juegos de magia. Allí desarrollamos dos juegos que aprovechaban las características especiales del triángulo cuando se escriben sus elementos en base nueve o base diez. Terminábamos dicho artículo proponiendo una versión basada en propiedades de la aritmética binaria. Como se puede suponer, es posible diseñar versiones del juego para cualquier sistema de numeración pues las características se mantienen y el secreto es el mismo en todos ellos. El problema es que no resulta natural en un juego de magia pedir la construcción de un triángulo donde los números utilizados no sean mayores que cierta cantidad, salvo que exista una justificación adecuada. En algunos casos, resulta bastante sencillo plantear alguna excusa; por ejemplo, se puede disimular el uso de la aritmética binaria utilizando los colores de las cartas de una baraja, rojo y negro, si establecemos, por ejemplo, la correspondencia “rojo = 0”, “negro = 1”. De este modo, como la tabla de sumar en la aritmética binaria es simplemente 0 + 0 = 1 + 1 = 0 y 0 + 1 = 1 + 0 = 1, podríamos plantear el siguiente juego, para el que necesitarás solamente una baraja (y una mesa despejada). Coloca sobre la mesa, y formando una fila, un conjunto de cartas, con las caras hacia arriba. Supongamos, por ejemplo, que las cartas colocadas son las siguientes: Construye una segunda fila sobre la anterior, siguiendo estas reglas relativas a dos cartas consecutivas: Sobre dos cartas del mismo color, coloca una carta roja (por aquello de que 0 + 0 = 1 + 1 = 0). Sobre dos cartas de distinto color, coloca una carta negra (representando las sumas 1 + 0 = 0 + 1 = 1). Siguiendo nuestro ejemplo, como las dos primeras cartas son de distinto color, sobre ellas se colocaría una carta negra; como la segunda y tercera cartas son del mismo color, sobre ellas se colocaría una carta roja. Al repetir este proceso con todas las parejas de cartas consecutivas, llegaríamos a una segunda fila que tendría esta pinta: Sigue formando filas de cartas sobre las anteriores obedeciendo las mismas reglas anteriores. Al final llegarás a una fila formada por una sola carta, que podrá ser roja o negra. Pues bien, una simple inspección de la primera fila proporciona información suficiente para saber el color de la última carta colocada. Ahora viene la inevitable cuestión: ¿cómo deducir rápidamente cuál será el color de la última carta? La respuesta se basa nuevamente en interpretar el triángulo de Pascal escrito en el sistema binario y realizar la correspondencia que habíamos establecido entre los colores y los números. Hay que tener en cuenta que la operación puede ser más o menos inmediata según el número inicial de cartas. Por esta razón, es conveniente que el número de cartas que se colocan en la primera fila se corresponda a una fila del triángulo de Pascal que sea fácilmente identificable. Veamos los casos más simples a la vista de este triángulo, donde el color rojo corresponde al cero y el color azul al uno: Si el número inicial de cartas es una potencia de dos (2, 4, 8, 16, etc.), la fila correspondiente del triángulo de Pascal sólo contiene unos. Por tanto, el mago debe contar el número de cartas negras (o rojas) que hay en la primera fila formada por el espectador. Si hay un número par, la carta final será roja; si hay un número impar, la carta final será negra. Este es precisamente el caso que hemos puesto como ejemplo, donde colocamos ocho cartas en la primera fila; como cuatro de ellas son negras, la carta que ocupará la última fila será roja. Si el número inicial de cartas es una unidad mayor de una potencia de dos (3, 5, 9, 17, etc.), la fila que le corresponde en el triángulo de Pascal sólo contiene ceros, salvo los dos unos en los extremos. Basta fijarse en los colores de las cartas en los extremos: si son del mismo color, la carta final será roja; si son de distinto color, la carta final será negra. Si el número inicial de cartas es una unidad menor que una potencia de dos (3, 7, 15, 31, etc.), la fila que le corresponde en el triángulo de Pascal contiene unos y ceros de forma alternada. Así pues, el mago debe contar el número de cartas negras que ocupan los lugares impares. Como en el primer caso, si hay un número par, la carta final será roja; si hay un número impar, la carta final será negra. Así pues, un poco de psicología barata ayudaría en las demás situaciones: si el número de cartas que coloca el espectador no corresponde a uno de estos tres casos, el mago podría pedirle que añadiera algunas cartas más para «complicar» la adivinación. En caso necesario, el mago podría incluso completar él mismo las primeras filas como «ejemplo» de lo que pretende que haga el espectador hasta llegar a un número de cartas donde el cálculo sea sencillo. A pesar del innegable interés didáctico del juego, no parece muy mágico intentar adivinar un color entre dos posibles, pues la probabilidad de acertar es del 50%. De hecho, el objetivo principal de esta entrega es el de presentar una versión más divertida y sorprendente: el caso de la aritmética en base tres. La idea básica es similar a la anterior pero, como no hay cartas de tres colores en las barajas (aunque Colm Mulcahy propone usar tres palos de la baraja o bien distinguir entre cartas rojas, negras o de dorso), lo realizaremos con cartulinas de colores. Para ello, sería interesante disponer de un surtido de tarjetas o cartulinas de tres colores. En condiciones normales, bastará con 25 rojas, 25 azules y 25 verdes. Para una versión simiplificada en papel, necesitarás tener a mano tres rotuladores, uno rojo, uno verde y uno azul. En cualquier caso, para comprender el desarrollo del juego, deberás seguir estas indicaciones: Coloca diez de las cartulinas en una fila, con los colores al azar. En esta imagen mostramos un ejemplo (por el momento, los números no son importantes): Sobre esta fila, coloca otra fila de nueve cartulinas, siguiendo estas reglas: Si dos cartulinas consecutivas son del mismo color, coloca sobre ellas otra del mismo color que ambas. Si dos cartulinas consecutivas son de distinto color, coloca sobre ellas una cartulina del color diferente a ambas. Según el ejemplo anterior, las dos primeras filas serían como las de esta imagen (las dos primeras son rojas, de modo que la fila superior empieza en rojo; la segunda es roja y tercera es verde, de modo que sobre ellas irá una azul; la tercera es verde y la cuarta es azul, con lo que sobre ellas irá una roja; y así sucesivamente): Continúa formando filas con las cartulinas de colores siguiendo las mismas reglas establecidas en el punto anterior hasta llegar a una fila con una sola cartulina. Siguiendo con el ejemplo, el triángulo completo sería el que termina en una cartulina verde como se ilustra a continuación: Sí, has adivinado: una vez colocada la primera fila de cartulinas, puedo saber el color de la cartulina que ocupará el vértice superior del triángulo. La solución es sorprendentemente simple: basta aplicar las reglas anteriores a la primera y última cartulinas de la primera fila. En el ejemplo con el que hemos ilustrado el proceso, como estos colores son rojo y azul, la cartulina que ocupará la última fila deberá ser verde. Por cierto, ¿te has percatado de que las mismas reglas se aplican a los triángulos sombreados que tienen cuatro cartulinas en cada lado? ¿Y que esas mismas propiedades se mantienen al girar 120 grados cualquiera de esos triángulos? Te habrás preguntado también qué interpretación tienen los números asociados a cada color. La respuesta es que las dos reglas de formación del triángulo a partir de los colores corresponden a unas operaciones aritméticas con sus números. Estas operaciones pueden sintetizarse en la siguiente tabla (mostramos las dos versiones, la de colores y la de números): A R V A A V R R V R A V R A V 0 1 2 0 0 2 1 1 2 1 0 2 1 0 2 Como se puede comprobar, no se trata de la suma habitual, ni siquiera en base tres, pero sí conserva las propiedades algebraicas básicas: es conmutativa y asociativa. Esto significa que este juego ya no está basado en el triángulo de Pascal y hay que buscar la solución mediante otros argumentos. Es posible que estas pistas te sugieran la justificación del funcionamiento del juego. Por si acaso, en este enlace propongo mi versión, que no requiere conocimientos matemáticos. OBSERVACIONES FINALES: Los dos juegos que hemos descrito tienen un gran recorrido histórico que me gustaría compartir. Sobre el triángulo de Pascal binario, hace unos años recibí un mensaje de Ricardo Ramírez, músico y seguidor de este rincón. En su comunicación describía este juego sugerido por un problema que le propuso su profesor de Análisis Matemático, el recordado Miguel de Guzmán, precisamente el problema que planteábamos en este rincón al final de la entrega 58 de febrero de 2009. Copio y pego el último párrafo de aquel artículo: Por último, un problema: Escribe una sucesión de ceros y unos. Debajo de cada par consecutivo escribe un cero si los dos números son iguales, y un uno si son distintos. Repite el proceso hasta que te quede un único dígito en la sucesión. ¿Puedes predecir cuál va a ser el dígito final? Si conoces la respuesta, puedes realizar un juego de magia simulando los unos con cartas cara arriba y los ceros con cartas cara abajo (o viceversa). Pues bien, al proceso eliminatorio que parte de una fila de cartas, rojas y negras, y construye sucesivamente filas de cartas hasta llegar a una fila con una sola carta a partir de las reglas ya explicadas en el juego, Ricardo dio el nombre de «cuenta Stendhal» (nombre sugerido por el famoso título "Rojo y negro" de la novela de Stendhal y supongo que también por la belleza y sorpresa final del proceso asociadas al famoso síndrome). Él había estudiado y deducido el resultado final de la cuenta para cualquier cantidad inicial de cartas (hasta 52), incluso diseñó una completa y elaborada rutina con varios juegos de cartas en los que se utilizaba esta y otras cuentas con cartas. Comparto su opinión de que estas ideas pueden ser muy apropiadas para ayudar en la comprensión y motivar el estudio de los números combinatorios y sus aplicaciones. La historia detrás del juego de los tres colores también es interesante y productiva (puedes encontrar los detalles en el artículo del 13 de mayo de 2013 del blog Wordplay escrito por Gary Antonick y titulado Triangle Mysteries). Descubrimos que el inventor del juego es Steve Humble -más conocido por su pseudónimo DrMaths-, profesor en el Departamento de Educación de la Universidad de Newcastle y prolífico autor de material didáctico para la educación primaria. Tras compartir el juego con Ehrhard Behrends, profesor en el Departamento de Matemáticas e Informática de la Universidad Libre de Berlín y autor de un interesante libro de magia y matemáticas, ambos publicaron los resultados y sus generalizaciones en el volumen 35 (año 2013) de la revista The Mathematical Intelligencer. Allí aparece la siguiente foto en la que se ve a Steve Humble supervisando el juego ante un grupo de escolares: Posteriormente, Yutaka Nishiyama, profesor de matemáticas en la Universidad de Economía de Osaka, trató el mismo juego en el artículo The three-color triangle problem (en el que se cuela una errata al considerar que operación correspondiente a las reglas de formación de los colores tiene estructura de grupo abeliano). En su artículo relaciona el problema y su solución con el triángulo de Sierpinski, estructura fractal que aparece en la representación binaria del triángulo de Pascal. En este enlace de Youtube, Nishiyama publica una versión animada del proceso. Es fácil encontrar en internet otras adaptaciones y estudios sobre este interesante juego. Muchas preguntas surgen al querer comprender en profundidad el fundamento del juego de los colores. Me limitaré a plantear tres de ellas: ¿Qué pasa si modificamos las reglas de formación del triángulo de colores? Lo más natural -matemáticamente hablando- sería que, al simbolizar cada color con un número, digamos como antes 0 = azul, 1 = rojo, 2 = verde, aplicáramos la aritmética usual, es decir, azul + azul = azul, rojo + rojo = verde, verde + verde = rojo, azul + rojo = rojo, azul + verde = verde, rojo + verde = azul. Esta situación corresponde precisamente al comportamiento del triángulo de Pascal en base tres, de modo que el número de filas necesarias para que las cartulinas de los extremos sean las únicas que proporcionan la solución será la que contenga todo ceros (salvo los dos unos de los extremos). Observando la imagen adjunta, llegamos a la misma conclusión: si se empieza con una fila formada por 3n + 1 cartulinas, la suma de los valores correspondientes a los colores de las esquinas da como resultado el valor correspondiente al color de la última cartulina colocada. ¿Qué podemos decir si utilizamos cartulinas de cuatro colores y aplicamos alguna regla adecuada? Dejo la cuestión en el aire. ¿Se pueden obtener propiedades similares para juegos en más dimensiones? Pues sí, el propio Ehrhard Behrends se permitió el lujo de proporcionar nuevas versiones de este juego en espacios de tres o más dimensiones. En lugar de empezar con filas de colores, se puede empezar con cuadrados o triángulos y construir pirámides con reglas similares a las utilizadas en el plano de modo que el color de la cúspide de la pirámide se puede deducir solamente a partir de algunos colores de la base. Los detalles de su trabajo están publicados bajo el título “Pyramid Mysteries” en la revista Mathematical Intelligencer, volumen 36, número 3 (2014), artículo en el que aparece la imagen que encabeza este artículo. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Jueves, 03 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

409. 65. (Septiembre 2020) Matemáticas en los órganos

(Alegoría de la Música, 1580. Jan Soens. Museo Cívico de Piacenza) La Música formó parte de la Matemática durante muchos siglos. Desde que Pitágoras (o su escuela) relacionó la escala musical con fracciones simples, la Música fue considerada como Aritmética aplicada. La figura de Pitágoras es representada muchas veces como acompañante de la alegoría de la Música y no con la Aritmética, como en el portal de la Catedral de Chartres o en la Biblioteca del Monasterio de San Lorenzo de El Escorial. Cuando el imperio romano occidental se desmoronaba, algunos pensadores reflejaron la cultura de ese mundo en descomposición, uno de ellos fue Marciano Capella, quien en un latín semibárbaro, en prosa y verso, escribe Las nupcias de Filología y Mercurio. Las siete disciplinas, que constituirían el trivium y el quadrivium, tomaron desde entonces forma alegórica de mujer, y sus cultivadores las acompañarán en un festivo cortejo. Teofrasto, Aristóxeno y Pitágoras son los sabios vinculados a la dama Armonía según Capella. Pero la Música no solo estará vinculada a la Aritmética, también se relaciona con la Astronomía. La música mundana no es sino reflejo de la música de las esferas, de los astros. Las siete estrellas errantes de la antigüedad (Luna, Venus, Mercurio, Sol, Marte, Júpiter y Saturno) nos proporcional las siete notas de la escala musical. Quizá la expresión más acabada de la música de las esferas se encuentra en El sueño de Escipión de Marco Tulio Cicerón del siglo I a.C, uno de los tratados fundamentales de la cultura grecorromana: ¿Qué es esta música tan encantadora y tan dulce que llega a mis oídos? Es –me contestó- aquella que está compuesta por intervalos desiguales que, con todo, se caracterizan por tener una proporción racional; la produce el impulso y el movimiento de las esferas,… No debe sorprendernos que en la decoración de los órganos tanto de palacios como de iglesias aparezcan personajes y alegorías matemáticas. Exponemos algunas de ellas. Alegorías matemático-musicales del Museo Cívico en Piacenza El Museo Cívico de Piacenza, ubicado en el Palazzo Farnese, exhibe en su pinacoteca dos espectaculares dípticos que se usaron como puertas de órganos en palacios de Parma. Presentamos en primer lugar el espléndido díptico pintado por Jan Soens il Fiamingo (1547 – 1611). Se trata de dos alegorías relacionadas con la música según la concepción renacentista: la propia Música y la Astronomía. Al igual que se hablaba del hombre como microcosmos frente al macrocosmos, se consideraban dos tipos de música: la mundana que deleita nuestros oídos y la música de las esferas expresión de la armonía del cosmos. Las siete notas y los siete planetas están en concordancia. (Alegoría de la Astronomía, 1580. Jan Soens. Museo Cívico de Piacenza) La correlación de la música de las estrellas y la instrumental encuentra en las liras de la Oda a Salinas de Fray Luís de León su más deliciosa expresión castellana (cuarta estrofa): Traspasa el aire todo hasta llegar a la más alta esfera, y oye allí otro modo de no perecedera música, que es la fuente y la primera. La Astronomía mira el cielo representado al modo ptolomeico de la época y calcula con un compás. A sus pies un cuadrante y una esfera armilar. (Alegorías de la Astronomía y la Música, 1580. Jan Soens. Museo Cívico de Piacenza) La Música también mide y muestra su vinculación pitagórica con la Aritmética. Pocas veces la armonía matemática del cosmos se ha expuesto tan brillantemente como en este díptico que cerraba un órgano palaciego de 1580. Pitágoras y Euclides en el Palacio Farnesio de Piacenza La pinacoteca del Museo Cívico de Piacenza tiene una segunda puerta que vincula la música y las matemáticas. Girolamo Mazzola Bedoli (1500-1569) es el pintor de Parma que decoró las dos planchas que formando un díptico cierran el órgano de una familia noble de la ciudad y donde fueron representados Euclides y Pitágoras. (Pitágoras y Euclides, 1545. Girolamo Mazzola. Museo Cívico de Piacenza) Pitágoras aparece muy a menudo como creador de la música. Los martillos crean el sonido mientras que la balanza y el compás ponen medida para hacerlo armonioso. Euclides como padre de la geometría y de las proporciones aritméticas completa con su compás el potente conjunto. El dinamismo de los personajes es ya plenamente manierista. El Museo del Prado archiva un dibujo de Bedoli representando a Pitágoras que contiene similares elementos iconográficos: martillo con yunque, una romana y una cítara al fondo. La música era aritmética aplicada. (Pitágoras, 1545. Detalle. Girolamo Mazzola. Museo Cívico de Piacenza) Órgano de las Artes Liberales en Bristow Al norte de Alemania, en la paradisíaca orilla noroeste del lago Malchin, se encuentra la minúscula aldea de Bristow, que hoy forma parte del municipio de Schorssow. El mariscal y administrador del distrito Werner Hahn fundó allí en 1597 tanto la  bonita iglesia como el túmulo funerario. Su hijo Hans Hahn (1558-1633) se encargó de ampliarla magníficamente al estilo renacentista. El altar, el púlpito y el órgano son testigos. La tribuna y soporte en madera del órgano data de 1601 y fue decorado con representaciones alegóricas de las siete artes liberales: Dialéctica, Retórica, Música, Aritmética y Astronomía al frente, y la Geométrica y la Gramática a ambos lados. (Órgano de las Artes Liberales en Bristow, 1601) La Aritmética con tablilla, la Geometría, coronada y con compás, y la Astronomía alada recuerdan mucho a las alegorías de Marten de Vos. El tallista se tomó algunas libertades para encajarlas en su lugar. Las tallas del órgano son menos coloristas que las del púlpito y el altar, pero no tienen porqué ser acordes con las originales tras cuatro siglos. La iglesia de Bristrow es una buena muestra de la extensión de la cultura renacentista por lugares remotos. (Alegoría de la Aritmética. Órgano de las Artes Liberales. Bristow, 1601) Los “mirones” de la Catedral de Viena La Catedral de San Esteban de Viena admite múltiples relatos donde no pueden faltar los matemáticos o numerológicos: proporciones, medidas, relojes o representaciones. Entre todos los posibles nos quedamos en primer lugar con el geómetra mirón, los dos autorretratos del escultor y arquitecto renacentista moravo Anton Pilgram (1460-1516). La mirada que penetra, que va más allá, es la base donde se apoya la razón. ¿Lo veis? es lo que solemos decir a nuestros alumnos en lugar de ¿lo comprendéis? Los vieneses empezaron a llamar mirón a la figura que debajo del púlpito abría una ventana sin soltar su compás: un observador atento de la realidad que le rodea. (Anton Pilgram. Catedral de Viena) Durante mucho tiempo se atribuyó a Pilgram la autoría del púlpito gótico pero hoy se considera anterior. Lo que sí se debe al arquitecto es el gran píe del viejo órgano. Se considera que Pilgram se autorretrató en la base misma de apoyo de dicho píe con los atributos del geómetra, escuadra y compás, y del bonete universitario. La reproducción del bellísimo púlpito es de la misma figura que hay en el órgano. Antón Pilgram mirándolo todo y dispuesto a medirlo y calcularlo. (Pie del viejo órgano. Catedral de Viena)

Miércoles, 02 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

410. 108. (Agosto 2020) Música y entropía - II

1. Modelos musicales Esta es la segunda entrega de la serie Música y entropía. En el primer artículo [Góm20] examinamos de manera general el concepto de entropía y su relación con la música y el análisis musical. Describimos allí el origen moderno de ese interés —el trabajo de Meyer [Mey56]— así como ideas recientes de la aplicación de la entropía al análisis musical. Consideramos tanto el potencial analítico de la entropía como sus limitaciones. En este artículo vamos a examinar la entropía en el contexto más general de los modelos musicales; en particular, vamos a hacer una recensión del artículo Minimum description length modeling of musical structure [Mav08]. Este artículo contiene una profunda reflexión sobre los modelos musicales, la complejidad de estos (aquí es donde entra la entropía), una propuesta de modelo, los modelos de descripción mínima, y una aplicación de estos al canto litúrgico griego. 1.1. Modelos El artículo de Mavromatis abre con una frase contundente: ”el problema de la selección de los modelos es de suma importancia en todos los estudios empíricos”. La primera pregunta que surge aquí es: ¿qué es un modelo? El concepto de modelo aparece al final de un camino de conceptos previos que empiezan con el concepto mismo de fenómeno. Un fenómeno es cualquier suceso que puede ser observado. Por observable entendemos sucesos que pueden ser percibidos por los sentidos. Los fenómenos se pueden clasificar de muchos modos, pero hay dos grandes categorías: los fenómenos cuantificables y los fenómenos no cuantificables. Los primeros admiten una descripción numérica y los segundos, no. En el caso de la entropía, los modelos musicales van a ser con frecuencia cuantificables, esto es, se van a construir en base a los aspectos cuantificables de la música tales como la frecuencia de las notas, su altura, la duración, los grados de la escala, entre otros. Los modelos cuantificables suelen ser modelos matemáticos y computacionales. Un modelo matemático consta de los siguientes componentes: (1) Una entrada, normalmente un conjunto de números, vectores u otras estructuras numéricas; (2) Un conjunto de variables independientes, que están asociadas con la descripción conceptual del fenómeno bajo estudio. Con frecuencia, se relacionan con las causas del fenómeno en cuestión; (3) Un conjunto de parámetros, los cuales sirven para refinar y ajustar el modelo; (4) Un conjunto de variables dependientes, que representan el efecto observado en el fenómeno; (5) Un conjunto de relaciones, que conectan las variables independientes y las variables dependientes. Estas relaciones se suelen dar en forma de funciones, aplicaciones, transformaciones u operadores; (6) Una salida son el resultado de una observación particular. Sin embargo, como dijimos arriba, el modelo matemático es parte de un proceso más general llamado modelización matemática. Los bloques constituyentes de una modelización matemática son: (1) Formulación del problema. Se escoge un fenómeno de interés y se identifica un problema relativo a él. La formulación del problema también recibe el nombre de pregunta de investigación. (2) Sistematización. Mediante un proceso de abstracción se seleccionan aquellos objetos y relaciones del fenómeno que son relevantes para el problema en cuestión. Este proceso se llama abstracción. (3) Creación del modelo matemático. Los objetos y relaciones del apartado anterior se traducen a su vez en objetos y relaciones en el mundo y lenguajes matemáticos. En la creación del modelo matemático se tiene en cuenta el principio de parsimonia. Este establece que un buen modelo minimiza su complejidad y maximiza su poder explicatorio y predictivo. En otras palabras, siempre es preferible la explicación científica más simple que concuerde con la realidad. Este principio se conoce también con el nombre de principio de la navaja de Occam. (4) Resolución del problema matemático. Uso de métodos matemáticos para resolver los problemas derivados de la modelización del fenómeno. (5) Interpretación de los resultados y conclusiones en el contexto del fenómeno y del problema planteado. (6) Evaluación de la validez del modelo por comparación con el comportamiento del fenómeno o bien con la teoría previamente consolidada acerca del mismo. Es de particular importancia la validación del modelo en cuanto a su capacidad de predicción. Para más información sobre modelos, consultése el artículo de la Wikipedia Conceptual model [Wik20]. La figura de abajo resume la discusión anterior. Figura 1: Modelización matemática 1.2. Evaluación de modelos Normalmente, la calidad o bondad de un modelo se evalúa en función de cuán precisas son sus explicaciones y predicciones hechas a partir de los datos observados. Mavromatis da un paso conceptual hacia delante y propone evaluar la calidad de un modelo en base la capacidad explicativa y predictiva del modelo y además en base a la propia complejidad del modelo (a igual capacidad explicativa y predictiva, son más preferibles los modelos simples a los modelos complejos simplemente por pura aplicación del principio de parsimonia). La manera en que Mavromatis evalúa la complejidad de los modelos tomando prestadas ideas de la teoría de la información. En un modelo musical, la estructura musical está caracterizada por variables simbólicas que representan diversos aspectos de la música tales como la altura de sonido, duración, dinámica, armonía, etc. Un modelo trata de identificar esas variables y su aparición. Esto da lugar a su vez a lo que Mavromatis llama restricciones sintácticas, las cuales dependen del estilo musical. Los valores que toman las variables del modelo se presentan en forma de regularidades estadísticas, las cuales dan lugar a patrones de comportamiento musical. Un campo fecundo de investigación musical es la detección de esos patrones. Volviendo al concepto de parsimonia, perseguiremos que nuestro modelo sea tan simple como sea posible y al mismo tiempo tenga una buena capacidad explicativa y predictiva. Un buen ajuste entre un modelo y los datos se llama bondad del ajuste. En la figura de abajo tenemos un ejemplo sencillo. Supongamos que en nuestro fenómeno observamos una variable dependiente y, representada en el eje Oy, como función de una variable independiente x, representada en el eje Ox. Los puntos negros son las observaciones; se trata de pares de puntos (x1,y1),…,(xn,yn), suponiendo n observaciones. La siguiente pregunta es qué tipo de relación hay entre las variables x e y (en nuestro ejemplo ambas son numéricas). Un modelo muy simple es el modelo lineal, que supone que hay una relación lineal del tipo y = ax + b (una recta), donde a,b son parámetros a determinar en función de los datos observados. La recta de color azul es la recta que mejor explica los datos, mientras que la recta roja arroja un peor modelo. La bondad del modelo es un valor que en la figura aparece como SSE; el mejor modelo es el que tiene este valor lo más bajo posible. Este valor mide los errores cometidos por el modelo al aproximar los datos y en la figura está dado por las distancias verticales de los puntos a la recta. La figura 3 muestra las tres situaciones. Figura 2: Bondad del ajuste en modelos Es posible construir modelos que se ajusten muy muy bien a los datos demasiado bien, reflejando idiosincrasias insignificantes, a base de añadir variables extra. Esto se llama sobreajuste. Esto ocurre cuando el modelo no acierta con el nivel adecuado de abstracción. Produce modelos excesivamente complejos. Lo contrario se llama subajuste: el modelo es pobre y se pierde características importantes del fenómeno. En la figura 3 (a) tenemos un caso de subajuste. El conjunto de datos, que claramente sugiere una forma curva, es aproximado por una recta. En la figura 3 (b) vemos una curva que pasa por todos los puntos observado y el ajuste es perfecto (comete error cero), pero este modelo requiere un alto número de variables independientes que no son parte esencial del modelo. Por último, la figura 3 (c) muestra un modelo más razonable, con pocas variables independientes y con un error de ajuste razonable. Figura 3: Subajuste y sobreajuste (figura tomada de [Mav08]) 2. Modelos de longitud de descripción mínima El modelo propuesto por Mavromatis en su trabajo es un modelo de longitud de descripción mínima (LDM, de aquí en adelante). Este modelo es de tipo inductivo, esto es, se construye a partir de la observación de datos asociados al fenómeno bajo estudio. El modelo LDM no solo evalúa el ajuste de los datos, como los modelos clásicos, sino también evalúa la propia complejidad del modelo. Cualquier regularidad detectada en los datos se puede usar para comprimir ese conjunto de datos. Comprimir aquí significa codificar los datos observados de una manera más corta que si los datos se dejan sin comprimir. Cuantas más regularidades se observen en los datos, más se podrán comprimir estos. Por ejemplo, si los datos se pueden codificar a partir de símbolos del alfabeto A = , la cadena C1 = aaaa se puede comprimir como a4, pero la cadena C2 = aabb se puede comprimir como a2b2, cuya compresión es más larga que a4. En este caso, la codificación de C1 tiene longitud 2 (dos símbolos para a2) y la de C2 tiene 4. El LDM mide la bondad de un modelo por la capacidad de comprimir los datos en base a sus regularidades y por la capacidad de comprimirse a sí mismo. Un modelo LDM está constituido por varias piezas. Primero, hay un conjunto de datos D, típicamente obtenidos de la observación del fenómeno. En nuestro caso, consistirán en piezas musicales extraídas de algún corpus musical. A continuación, un modelo M que modeliza el fenómeno, en particular, los datos D. Después, una función de una codificación C, que transforma los datos en un cadena de caracteres tomados de un alfabeto (puede ser un conjunto de números, los bits 1 y 0, caracteres alfanuméricos, etc.). A continuación, una función LC que mide la longitud del código C. Por último, una función de descripción, que está dada por donde C1,C2 son esquemas de codificación, el primero del modelo M y el segundo de los datos. La expresión D∣M significa la codificación de D según el modelo M. Las codificaciones tienen que tener la propiedad de ser únicas, esto es, dos datos distintos no pueden codificarse por la misma cadena. Esto asegura que se recupera correctamente la información cuando se pasa del código a los datos. En particular, para que esta propiedad se cumpla se requiere que ninguna codificación produzca una cadena que sea prefijo de otra; para más cuestiones técnicas de este tipo recomendamos al lector que consulte el apéndice del artículo de Mavromatis [Mav08]. En general, las mejores codificaciones asignan los códigos más cortos a los símbolos más probables o frecuentes. Esto introduce la idea de probabilidad en el modelo, ya que se hace el recuento de las cadenas más frecuentes en la codificación. Se sabe que siempre hay una codificación óptima que minimiza la esperanza de la longitud de la descripción dada por la distribución de probabilidad P(D∣M). Se llama código de Shannon-Fao. Su función de longitud es En este punto interviene el teorema de Shannon, que establece que la esperanza mínima de la longitud de la codificación para la salida de un modelo probabilístico M con distribución P(x∣M) está dado por donde X es el conjunto de símbolos de la codificación. La cantidad HM recibe el nombre de entropía. La idea de Mavromatis es encontrar una función de codificación que se aproxime lo más posible a la cota impuesta por el teorema de Shannon. La función de codificación de Mavromatis se define como sigue. Sea una distribución de probabilidad pi sobre el conjunto de k símbolos y d un parámetro de truncamiento. donde L*(d) está definida por La L*(d) solo se suma sobre los términos positivos y por tanto la suma anterior es finita. 3. Modelos de Markov A continuación hacemos una revisión breve de las cadenas de Markov, que es un tipo de modelos probabilísticos. Este tipo de modelos son muy comunes en música, como ya hemos glosado en otras entregas de esta columna. Mavromatis los usa en conjunción con su modelo LDM. Una cadena de Markov es un modelo de un fenómeno que tiene los siguientes componentes: Un conjunto finito de estados ; Un conjunto de probabilidades constantes pij del estado si al estado sj; estas probabilidades reciben el nombre de probabilidades de transición. Falta de memoria: Se cumple la condición de que la probabilidad de ir del estado si al estado sj solo depende del estado actual. La matriz de transiciones es s1 s2 s3 T = s1 s2 s3 Por ser los números pij probabilidades, las filas de esta matriz siempre suman 1. En la figura de abajo se ve un esquema que refleja la estructura de una cadena de Markov. Este tipo de diagramas, llamados diagramas de estado, son comunes para describir cadenas de Markov. Figura 4: Una cadena de Markov de tres estados La condición de falta de memoria aparece de manera más general en modelos más abstractos. Se puede pedir que la probabilidad de ir a un estado a otro dependa de un cierto número de estados previos. Por ejemplo, en la figura de abajo a la izquierda se tienen las probabilidades de un conjunto de tres notas entre sí (la, do# y mi♭). En este caso, hablamos de matrices de primer orden. A la derecha de la figura aparecen las probabilidades de continuación de las secuencias de dos notas para otro conjunto de notas diferente (la, do , sol). Ahora la matriz es de orden dos (depende de dos estados previos). Figura 5: Cadenas de Markov aplicadas al análisis musical 4. Modelos de Markov de longitud de descripción mínima Mavromatis aplica los modelos de Markov de longitud de descripción mínima al canto litúrgico griego. Se trata de una música en que letra y melodía se asocian por medio de reglas estilística tanto musicales como prosódicas. En un trabajo anterior [Mav05] Mavromatis demostró la importancia estructural de ciertas fórmulas arquetípicas melódicas o arquetipos melódicos en este tipo de canto litúrgico. Dichas fórmulas son patrones melódicos de entre 6 a 9 notas y que se pueden acomodar a diferentes patrones prosódicos, incluyendo la longitud y los patrones de acentuación de las palabras. En la siguiente figura se muestran esos arquetipos melódicos; en este caso son todas fórmulas cadenciales. Figura 6: Fórmulas arquetípicas de la melodía en el canto litúrgico griego (figura tomada de  [Mav08]) En la figura se ha usado la siguiente convención: dos x significa sílaba acentuada y una x sílaba no acentuada. Asociado a este estilo musical tenemos unas cuantas reglas que rigen la formación y la sintaxis de los arquetipos melódicos (las reglas sintácticas de las que hablábamos arriba): R1 El sol final del arquetipo cae en sílaba acentuada. R2 Si la sílaba final está acentuada, entonces se asigna al sol final. Si, por otro lado, la última sílaba acentuada está seguida de sílabas no acentuadas, entonces en general se le asigna al penúltimo fa. En dicho caso, la sílaba no acentuada siguiente se asigna al sol. R3 Como máximo un sílaba acentuada puede intercalarse entre el sol inicial y la última sílaba acentuada del arquetipo. Si existe tal sílaba, el acento se asigna o bien al fa o al mi. R4 Una vez que las sílabas acentuadas se han fijado según las reglas R1-R3, el número de sílabas no acentuadas en el medio se puede acomodar mediante inserciones o borradas de las notas necesarias. El siguiente paso que da Mavromatis es construir la cadena de Markov. Empieza con un único estado s0 y calcula el total de LDM según las fórmulas que vimos antes. A partir de aquí empieza un proceso en que va añadiendo más estados; llega a hacer hasta 14 estados. En cada paso, calcula las probabilidades a partir de las frecuencias que encuentra en el corpus. En la figura siguiente se ve la cadena de Markov para 6 nodos; en la figura xx significa sílaba acentuada y x_ sílaba no acentuada. Figura 7: El modelo MDL En la tabla de abajo se ven los valores de LDM para los datos y el modelo así como el total de la LDM; nS se refiere al número de nodos de la cadena de Markov. El mínimo de la LDM total se alcanza con 10 nodos (marcado con un asterisco en la tabla). Figura 8: El modelo MDL De la ejecución del modelo sobre el corpus de canto litúrgico griego, Mavromatis obtiene las siguientes conclusiones: El modelo de un estado identifica las frecuencias de cada nota. El modelo de dos estados detecta el papel privilegiado de la nota sol como nota de referencia. El modelo de tres estado capta el papel de las notas fa y la como vecinas de sol El modelo de cuatro estados discierne entre el sol final e inicial. El modelo de cinco estados identifica el papel de la nota mi. En este punto cada estado de la cadena de Markov tiene una definición en términos de altura bien definida. El modelo de seis estados implementa la regla R1. El modelo de 7 estados aprende el contorno sol-fa-mi-fa-sol. El resto de los estados hasta el estado de 10 nodos incrementa progresivamente el aprendizaje de las reglas sobre las alturas. Dado que la LDM mínima se alcanza en 10 nodos, se elige este modelo como el óptimo. Usar más nodos daría lugar a sobreajuste y usar menos nodos a subajuste.   Bibliografía [Góm20] P. Gómez. Música y Entropía - I, julio de 2020. [Mav05] Panayotis Mavromatis. A hidden Markov model of melody production in Greek church cant. Computing in Musicology, 14:93–112, 2005. [Mav08] Panayotis Mavromatis. Minimum Description Length Modeling of Musical Structure. Journal of Mathematics and Music, 0:1–21, enero 2008. [Mey56] Leonard Meyer. Emotion and Meaning in Music. University of Chicago Press, Chicago, 1956. [Wik20] Wikipedia. Conceptual model, consultada en 2020.

Sábado, 01 de Agosto de 2020 | Imprimir | PDF |  Correo electrónico