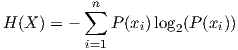411. 12. (Julio 2020) Geometría y arte: El cubo SOMA en las esculturas de David Umemoto

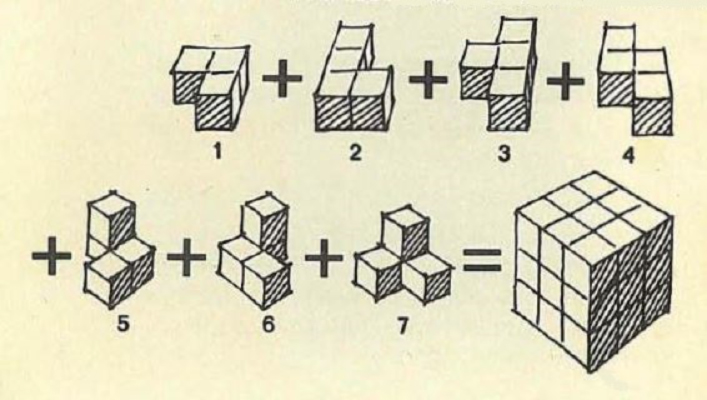
El rompecabezas geométrico SOMA, del que ya hemos hablado en otra ocasión[i], se compone de siete piezas (a las que de ahora en adelante llamaremos somaedros) como las de la figura siguiente. Ilustración de Piet Hein[ii] en el Manual del SOMA[iii] (p. 4) Con ellas, entre otros muchos objetos 3D, se puede construir un cubo 3x3x3 («problema fundamental»). Desde una óptica matemática, la resolución de este problema geométrico y de otros similares, es un reto intelectual que puede mantener ocupada durante un largo tiempo a cualquier persona con la mente despierta. Desde una perspectiva artística, el creador, al margen del «problema fundamental», se dedica a transformar los siete somaedros en estructuras estéticamente atractivas con las cuales (ensamblándolas de forma conveniente) puede generar auténticas obras de arte. En las líneas que siguen, ofrecemos un ejemplo de este enfoque presentando las esculturas SOMÁticas del arquitecto David Umemoto, residente en Montreal (Canadá). Las SOMAesculturas de Diego Umemoto En la página personal de Umemoto (https://davidumemoto.com/info) hemos localizado seis proyectos inspirados en el SOMA. En cada uno de ellos se presentan los siete elementos básicos con algunos resultados obtenidos después de su acoplamiento[iv]. A partir de aquí, dejamos que el lector disfrute de las originales y bellas esculturas del artista canadiense. [1] Soma Cube i (2015) [2] Soma cube ii [3] Soma cube iii [4] Soma cube vi [5] Soma Cube ix [6] Soma Cube xs   Notas: [i] SOMA: antepasados y descendientes (Divulgamat). [ii] Piet Hein (1905 – 1996), poeta, filósofo, matemático y científico danés, creador del SOMA. [iii] Parker Brothers distribuyó el SOMA en Estados Unidos. El manual editado por dicha empresa fue escrito e ilustrado por Piet Hein (Introducing SOMA, 1969). [iv] En algunas esculturas intervienen todos los somaedros y en otras no.

Miércoles, 29 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

412. Julio 2020: Noticias históricas concernientes al uso de material didáctico manipulativo en la enseñanza y aprendizaje de la Geometría

1. Un ejemplo, a modo de introducción En la Arithmetica practica, y speculativa (1562, Lib. IV, cap. II, p. 308), el bachiller Juan Pérez de Moya[1], refiriéndose a las figuras isoperimétricas, nos proporciona un buen ejemplo de la utilización de material didáctico manipulativo (cuatro tablas de cajero de la misma longitud y altura) para demostrar la proposición siguiente: De todas las figuras isoperimétricas, la de mayor área es el círculo. 2. Poliedros didácticos La presencia de representaciones tridimensionales de poliedros se remonta al Neolítico (2000 a. C.). De una época más reciente, siglos II y III d. C., son algunos dados etruscos con la forma de dodecaedro regular e icosaedro regular. Aunque se desconoce la utilidad de dichos objetos 3D, su existencia pone de manifiesto que los poliedros regulares «físicos» convivieron con el hombre desde la más remota antigüedad. Poliedros regulares neolíticos de Escocia (Ashmolean Museum de Oxford) Dodecaedro e icosaedro etruscos (s. II – III d. C.) Así las cosas, dando un gran salto en el tiempo, nos trasladamos al Museo de Capodimonte (Nápoles) donde podemos contemplar el Retrato de Luca Pacioli[2] (1495). Retrato de Luca Pacioli (1495). Atribuido a Jacopo de Barbari. La mayor parte de la superficie del cuadro está ocupada por dos personajes. Uno de ellos, el fraile franciscano Luca Pacioli, parece estar explicando al otro (posiblemente un miembro de la nobleza) algún teorema geométrico contenido en un tratado matemático. Además, en la parte superior izquierda del lienzo, colgado del techo, hay un poliedro arquimediano transparente, hueco y medio lleno de agua. Dicho cuerpo geométrico tiene veintiséis caras (de las cuales dieciocho son cuadrados y ocho son triángulos equiláteros) y recibe el nombre de rombicuboctaedro. Modelo hueco y transparente de rombicuboctaedro Por otro lado, en la parte inferior derecha, apoyado en un libro, se encuentra un dodecaedro regular macizo. Modelo macizo de dodecaedro regular Con esta información, podemos asegurar que, a finales del siglo XV, los profesores italianos ya utilizaron modelos de poliedros en sus clases de Geometría. 3. Leonardo da Vinci y sus esqueletos de poliedros Leonardo da Vinci (1452  - 1519) Entre las ilustraciones creadas por el artista y científico italiano Leonardo da Vinci para la obra De Divina Proportione[3] de Luca Pacioli, destacan aquellas en las que se representan los «esqueletos»[4] de un gran número de poliedros. Esqueleto del icosaedro regular Estos dibujos de Leonardo son probablemente las primeras ilustraciones de los esqueletos de cuerpos geométricos. Nicolas Neufchatel. Retrato de Johannes Neudofer y su hijo (1561) Unos años más tarde, el pintor flamenco Nicolaus Neufchatel (1527 – 1590), en el Retrato de Johannes Neudofer y su hijo, representó al maestro de escritura y cálculo Johannes Neudofer (1497– 1563) impartiendo una clase de Geometría a su hijo. El padre sostiene el «esqueleto» de un dodecaedro regular y el hijo, atento a las explicaciones de su progenitor, sostiene un cuaderno de notas. En la parte superior del cuadro cuelga el «esqueleto» de un cubo. Por tanto, podemos asegurar que, a mediados del siglo XVI, algunos «maestros de cálculo» se sirvieron de los esqueletos de poliedros para explicar determinados objetos geométricos 3D. Actualmente se pueden encontrar en el mercado materiales sofisticados que permiten construir esqueletos de poliedros mediante piezas imantadas (véase la figura  anterior). Sin embargo, desde una óptica económico-didáctica, se recomienda utilizar palillos para las aristas y esferas de plastilina para los vértices. Esqueleto del cubo con palillos y plastilina 4. Alberto Durero y sus «desarrollos» de poliedros Alberto Durero (1471 – 1528) El artista alemán Alberto Durero, en su Underweysung der Messung, mit dem Zirckel und Richtscheyt (1525), fue el primero en publicar los desarrollos planos de algunos poliedros. De esta forma creó una sencilla herramienta bidimensional para construir poliedros 3D. Desarrollo de octaedro truncado[5] Juan Pérez de Moya, en su estudio de los cinco sólidos platónicos (Tratado de Geometria Practica, y Speculativa, 1573), se sirvió de este «instrumental» para construir y describir dichos poliedros regulares. 5. Clairaut y la tarjeta rectangular Alexis Claude Clairaut (1713 – 1765) El matemático francés Alexis Claude Clairaut[6], en la cuarta parte (De la manera de medir los sólidos y sus superficies) de sus Elementos de Geometría, introdujo un sencillo material didáctico, una tarjeta rectangular dividida en dos partes iguales, para explicar los conceptos y procedimientos relativos a la perpendicularidad recta-plano y plano-plano, paralelismo de planos y medida del ángulo determinado por dos planos. Dado su interés pedagógico, reproducimos in extenso la adaptación al castellano del texto original. VI De ello se sigue que la línea AB, perpendicular al plano X, debe ser perpendicular a todas las líneas AC, AD, AE etc. que parten del pie A de esta línea y están contenidas en dicho plano. En efecto, si AB se inclinase sobre una de estas líneas, entonces se inclinaría hacia algún lado del plano, por lo que no sería perpendicular a él. VII Para representar de una forma sensible cómo la línea AB puede ser perpendicular a todas las líneas que parten de su extremo A basta con hacer una figura en relieve de la manera siguiente: Con alguna materia lisa y fácil de plegar, como cartón, se construye un rectángulo FGDE dividido en dos partes iguales por la recta AB perpendicular a los lados ED y FG. A continuación, se pliega este rectángulo a lo largo de la línea AB, y se coloca el rectángulo doblado sobre el plano X. Es evidente que, cualquiera que sea la abertura que se dé a las dos partes FBAE y GBAD del rectángulo plegado EADGBF, estas dos partes siempre permanecerán pegadas al plano X sin que la línea AB cambie de posición en relación a dicho plano. Por tanto, la recta AB será perpendicular a todas las líneas que parten de su pie y están contenidas en el plano X, dado que los lados AE y AD del rectángulo plegado se apoyan sucesivamente sobre cada una de dichas líneas, durante el movimiento que acabamos de describir. VIII De la construcción anterior se deduce un procedimiento muy cómodo para levantar desde un punto dado de un plano una línea perpendicular a dicho plano, o para bajar desde un punto dado exterior a un plano una perpendicular a este plano. Si el punto dado está en el plano, por ejemplo en A, o fuera de él, como en H, siempre se podrá desplazar el rectángulo EFBGDA sobre el plano X, hasta que el pliegue AB toque el punto dado. En los dos casos, AB será la perpendicular pedida. IX También se sigue de ello que una línea AB es perpendicular a un plano X siempre que lo sea a dos líneas AE y AD de dicho plano. Porque entonces AB puede considerarse como el pliegue de un rectángulo, uno de cuyos lados plegados se aplica sobre AE y el otro sobre AD. De modo que este pliegue no puede dejar de ser perpendicular al plano X. X Si se quiere levantar un plano perpendicular a X sobre una línea cualquiera KL, contenida en el plano X, también se puede hacer uso del rectángulo plegado GBFEAD. Para ello basta con poner el lado AD de una de las partes ADGB de este rectángulo plegado sobre la línea KL. Con esto, ADGB es el plano que se pide. XI También se ve fácilmente que si se coloca un tercer plano Y sobre los lados FB y BG del mismo rectángulo plegado, entonces el plano Y es perpendicular a la línea AB y, por consiguiente, paralelo al plano X. Entonces, si en un plano X se levantan tres perpendiculares EF, AB y DG de la misma longitud y que no estén situadas en línea recta, el plano Y, que pasa por los puntos F, B y G es paralelo al plano X. XII Cuando dos planos no son paralelos es fácil determinar el ángulo que forman haciendo uso de nuestro rectángulo plegado. Para ello se aplica una de las dos partes ABGD de este rectángulo sobre el plano X. Es evidente que el ángulo EAD, o el FBG, mide la inclinación del plano EABF sobre el plano DABG. Si se advierte que AB es la intersección de estos planos, y que EA y AD son perpendiculares a AB, se deduce fácilmente la regla siguiente: Si se dan dos planos que no son paralelos es necesario, en primer lugar, determinar su recta de intersección. A continuación, desde un punto cualquiera de esta línea, se trazan dos perpendiculares, cada una en uno de dichos planos. El ángulo que forman las dos rectas mide el ángulo que forman los dos planos dados. 6. A modo de resumen En este artículo que está a punto de concluir hemos ofrecido algunas noticias históricas relativas al uso de material didáctico manipulativo en la enseñanza y aprendizaje de la Geometría. Ordenadas cronológicamente son las siguientes: 1495. En el Retrato de Luca Pacioli se pone de manifiesto que a finales del siglo XV, los profesores italianos ya utilizaron modelos de poliedros en sus clases de Geometría. 1509. En el libro De Divina Proportione de Luca Pacioli, Leonardo da Vinci publica las primeras ilustraciones de los esqueletos de cuerpos geométricos. 1525. Alberto Durero, en su Underweysung der Messung, mit dem Zirckel und Richtscheyt publica, por primera vez, los desarrollos planos de algunos poliedros. 1561. En el Retrato de Johannes Neudofer y su hijo se asegura que, a mediados del siglo XVI, algunos «maestros de cálculo» se sirvieron de los esqueletos de poliedros para explicar determinados objetos geométricos 3D. 1562. En su Arithmetica Practica, y Speculativa, el bachiller Juan Pérez de Moya nos ofrece un material didáctico compuesto por tablas de cajero para demostrar una interesante propiedad de las figuras isoperimétricas. 1573. En su Tratado de Geometria Practica, y Speculativa, Pérez de Moya se sirve de los desarrollos de los sólidos platónicos para construir y describir dichos poliedros regulares. 1775. El matemático francés Alexis Claude Clairaut, en sus Élémens de Géométrie, utiliza una tarjeta rectangular para explicar conceptos y procedimientos relativos a las posiciones relativas de una recta y un plano, y de dos planos. Este reducido catálogo de carácter histórico-didáctico podría ser el principio de una línea de investigación en Educación Matemática en la que, utilizando diversas fuentes (libros, pinturas, etc.) se identifiquen: (i) los creadores de los materiales didácticos para la enseñanza y aprendizaje de las Matemáticas, y (ii) los documentos (gráficos o escritos) en los que, de forma explícita, se certifique la presencia de dichos materiales en la práctica docente. Desde aquí animamos a los enseñantes e investigadores para que se involucren en esta tarea que, sin duda alguna, repercutirá en el aprendizaje de los alumnos de todos los niveles educativos.   Referencias bibliográficas CLAIRAUT, A. C. (1775). Élémens de Géométrie. Paris: Cellot & Jombert. DURERO, A. (1525). Underweysung der Messung, mit dem Zirckel und Richtscheyt. Nürnberg. MEAVILLA SEGUÍ, V. (2017). Aprendiendo matemáticas con los grandes maestros. Córdoba: Editorial Guadalmazán. PACIOLI, L. (1991). La divina proporción (Introducción de Antonio M. González. Traducción de Juan Calatrava). Madrid: Ediciones Akal, S. A. PÉREZ de MOYA. J. (1562). Arithmetica Practica, y Speculativa. Salamanca: Mathias Gast. PÉREZ de MOYA. J. (1573). Tratado de Geometria Practica, y Speculativa. Alcalá: Juan Gracian.   Referencias online MEAVILLA SEGUÍ, V. y VICÉN ANTOLÍN, C. (2008). Los Elementos de geometría de Alexis Claude Clairaut (1713 – 1765).   [1] Los datos disponibles sobre la vida del bachiller Juan Pérez de Moya son escasos e inciertos. Nació antes de 1513, probablemente en 1512, en Santisteban del Puerto (Jaén), tal como se indica en la portada de algunos de sus libros. Estudió en Salamanca y Alcalá de Henares, no fue profesor universitario pero posiblemente se dedicó a la enseñanza de las Matemáticas. En 1536 obtuvo una capellanía en su pueblo natal y, ya muy mayor, fue canónigo de la Catedral de Granada, ciudad en la que murió en 1596. [2] Luca Pacioli (1445 – 1517) nació en Borgo de Sansepolcro (Italia) y posiblemente recibió sus primeras lecciones en el taller de su paisano Piero della Francesca (1412 – 1492). En 1492 ingresó en la orden de San Francisco de Asís. Entre sus obras de carácter matemático destacan Summa de arithmetica geometría proportioni et proportionalità (1494) y De divina proportione (1509). [3] De Divina Proportione se acabó el 14 de diciembre de 1498 y se realizaron tres manuscritos. Se imprimió en 1509. [4] Esqueleto de un poliedro es la estructura 3D formada por todas sus aristas. [5] Poliedro arquimediano con catorce caras (seis triangulares y ocho hexagonales). [6] Alexis Claude Clairaut fue admitido en la Academia de Ciencias francesa cuando aún no tenía dieciocho años, por su trabajo Recherches sur les courbes a doublé courbure que se publicó en 1731. A lo largo de su corta vida también perteneció a la Royal Society of London, a la Academia de Berlín, a la Academia de San Petersburgo, y a las Academias de Bolonia y Upsala. Desde el 20 de abril de 1736 al 20 de agosto de 1737, participó en una expedición a Laponia, liderada por Maupertuis, cuyo objetivo era medir la longitud de un meridiano. En 1743, publicó su famoso trabajo Théorie de la figure de la terre donde confirmó la hipótesis de que la Tierra estaba achatada por los polos, defendida por Newton-Huygens. Además de sus contribuciones a la ciencia en general y a las Matemáticas en particular, Clairaut escribió dos textos dedicados a la enseñanza que alcanzaron varias ediciones: uno de Álgebra y otro de Geometría (Élémens de Géométrie).

Jueves, 23 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

413. Números con arte

Ver detalles del documento

Martes, 21 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

414. 11. (Julio 2020) SOMA: antepasados y descendientes

Las disecciones del cubo proporcionan una rica fuente de inspiración a los diseñadores de rompecabezas tridimensionales. En este artículo ofrecemos una selección de puzles 3D obtenidos a partir del poliedro regular que, en la cosmología platónica, representaba la tierra. 1. El cubo diabólico Profesor Hoffmann En 1893, el profesor Hoffmann[1] publicó en Londres sus Puzzles Old and New en los que introdujo un rompecabezas, el «cubo diabólico», formado por seis piezas con las que se puede construir un cubo 3x3x3. Puzzles Old and New, p. 108 Dichas piezas están formadas por 2, 3, 4, 5, 6 y 7 cubos unitarios, tal como puede verse en la figura adjunta. Las seis piezas del «cubo diabólico» En la páginas 142 y 143 del mismo libro, Angelo John Lewis propuso la siguiente construcción del cubo. Se colocan las piezas c [= 6], a [= 7] y e [= 4] una al lado de otra tal como se indica en la figura anterior. Acto seguido, la pieza f [= 2] se acopla delante de la e. Después, la pieza d [= 3] se sitúa entre a y f, completando una cara del cubo. Por último, en los espacios vacíos que quedan, se coloca la pieza b [= 5]. Para describir la construcción anterior de forma más precisa, utilizaremos tres cuadrados 3x3 que, escritos de izquierda a derecha, representan el primer, segundo, y tercer piso del hexaedro. Además, en cada cuadrícula escribiremos el número de la pieza que se apoya en él. Hay trece formas diferentes de construir un cubo 3  3  3 con las seis piezas del «cubo diabólico». Las presentamos con la ayuda del código que acabamos de describir. Notemos que la segunda de ellas es la propuesta por Hoffmann.     2. El cubo SOMA 2.1. El puzle El rompecabezas tridimensional SOMA fue ideado por el poeta, filósofo, matemático y científico danés Piet Hein. Piet Hein (1905 – 1996) Al parecer, la idea le surgió durante una conferencia sobre Física Cuántica. En la patente inglesa del SOMA, fechada el 19 de marzo de 1934, leemos: Mi invento se ilustra en los dibujos adjuntos, en los que: Las figuras 1-7 son dibujos en perspectiva de las siete piezas. Las figuras 8-13 son ejemplos de cuerpos o figuras geométricas sólidas que se pueden construir con las siete piezas. Cada una de las piezas de las figuras 1-7 se componen de tres o cuatro cubos yuxtapuestos. La pieza 1 está formada por tres cubos, mientras que cada una de las restantes está compuesta por cuatro cubos dispuestos de diferentes formas. El conjunto de todas las piezas equivale a veintisiete cubos. 2.2. El problema fundamental Con las siete piezas del SOMA, se puede generar un sinfín de objetos 3D. Objetos 3D que se pueden construir con el SOMA. Dibujos de Piet Hein (Manual del SOMA, pp. 20-21)[2] Además, se puede construir un cubo 3x3x3 («problema fundamental»). Ilustración del manual del SOMA (p. 4) En 1961, los matemáticos de la Universidad de Cambridge John Horton Conway y Michael J. T. Guy (1942) obtuvieron manualmente las 240 formas distintas de hacerlo. John Horton Conway (1937) En la figura adjunta reproducimos una posible solución del «problema fundamental» Construcción del cubo con las siete piezas del SOMA[3] Utilizando el código descrito en el parágrafo 1, la construcción anterior se convierte en: 2.3. Jugando con el SOMA Con dos juegos SOMA, dos jugadores pueden poner a prueba su habilidad tridimensional en un torneo intelectual que se ajusta a las siguientes reglas: Se determina por sorteo el jugador que inicia el juego. El jugador que inicia el juego elige una de las siete piezas y la posición que debe ocupar. Los dos jugadores, usando la misma pieza y posición de partida, deben construir un cubo 3x3x3 utilizando las restantes piezas del SOMA. Gana el jugador que alcanza el objetivo en menos tiempo. El jugador que pierde, elige la siguiente pieza y posición de partida. Los siguientes dibujos de Piet Hein muestran algunas posiciones teóricas de partida para la pieza 1. Proponemos algunas construcciones del cubo a partir de dichas posiciones. POSICIÓN A POSICIÓN B POSICIÓN C POSICIÓN D POSICIÓN E 3. El cubo de Mikusinski Jan Geniusz Mikusinski (1913 – 1987) El matemático polaco J. G. Mikusinski  obtuvo la siguiente disección del cubo en seis policubos. Las seis piezas del «cubo de Mikusinski» El «cubo de Mikusinski» también se conoce como «cubo de Steinhaus» dado que apareció por primera vez, que sepamos, en el libro Mathematical Snapshots (1950) del matemático y pedagogo polaco Hugo Steinhaus. Hugo Steinhaus (1887 – 1972) La reconstrucción del cubo con dichas piezas sólo admite las dos soluciones que se muestran en la figura siguiente. 4. Disecciones del cubo en piezas idénticas 4.1. El cubo de O’Berine Atendiendo al testimonio de Martin Gardner (Rosquillas anudadas, p. 33), se debe al escocés Thomas H. O’Berine la disección de un cubo en nueve «tricubos» como el de la figura adjunta. Según el divulgador norteamericano: Los intentos de atinar por tanteo a construir un cubo con los nueve tricubos pueden resultar verdaderamente exasperantes, salvo que, por fortuna se haya acertado en un procedimiento sistemático. ¿Cómo descubrir dicho procedimiento sistemático? En primera instancia, notemos que con dos tricubos se puede construir una estructura [= 2TC] como la del diagrama siguiente. Por consiguiente, con seis tricubos se pueden construir tres. Acto seguido, dispongamos los tres tricubos restantes tal como se detalla a continuación. A partir de aquí, añadiendo sucesivamente las tres estructuras 2TC a la «escalera» anterior, se puede completar un cubo 3x3x3 siguiendo las indicaciones de la figura adjunta. 4.2. Un cubo grande: el Gridlock Puzzle El Gridlock Puzzle es un rompecocos 3D compuesto por cincuenta y cuatro piezas como las de la figura adjunta. El objetivo que se persigue es el de construir un cubo 6x6x6 con todos los tetracubos del rompecabezas. Para conseguirlo, basta con construir (utilizando dieciocho piezas) dos capas del cubo superpuestas [= paralelepípedo 6x6x2], tal como se detalla en los diagramas adjuntos. Repitiendo este proceso dos veces más se consigue materializar el cubo con todas las piezas del puzle. 5. El puzle de Slothouber-Graatsma William Graatsma (1925) y Jan Slothouber (1918 – 2007) Se debe a los arquitectos holandeses Jan Slothouber y William Graatsma un puzle formado por seis bloques 1x2x2 y tres bloques 1x1x1 con los que se puede formar un cubo 3x3x3. La solución es única, salvo simetrías y rotaciones, y se comprende fácilmente a partir del esquema siguiente. 6. El cubo de Conway John Horton Conway, del que ya hemos hablado en el parágrafo 2.2., diseñó un puzle compuesto por las dieciocho piezas siguientes: Trece bloques 1x2x4. Tres bloques 1x1x3. Un bloque 2x2x2. Un bloque 1x2x2. Con ellas se debe formar un cubo 5x5x5. Los cuatro tipos de bloques Designando los trece bloques 1x2x4 por A, B, C, D, E, F, G, H, K, L, M, N  y P, los tres bloques 1x1x3 por a, b y c, el bloque 2x2x2 por α, y el bloque 1x2x2 por β, una posible construcción del cubo requerido es: 7. El cubo de Bedlam Acabamos este catálogo de rompecabezas hexaédricos con un puzle compuesto por trece piezas (doce pentacubos y un tetracubo), cuyos bocetos adjuntamos. Su creador es el británico Bruce Bedlam. Bruce Bedlam Con las trece piezas se puede montar un cubo 4x4x4 de 19186 formas diferentes. El reto de conseguir una no es fácil y se necesita una gran dosis de paciencia, organización y constancia. Una solución al cubo de Bedlam 8. Fábrica de rompecabezas cúbicos En las secciones precedentes hemos presentado varios puzles cúbicos sin prestar atención al procedimiento que pudieron seguir sus inventores a la hora de diseñarlos. Desde una óptica formativa, esta fase de creación resulta particularmente interesante. Por este motivo, en este último parágrafo (a modo de anexo), ofrecemos el alumbramiento de un «nuevo» rompecabezas hexaédrico. Un puzle 3x3x3 con seis piezas [1] Empezamos con un pentacubo A, cuatro de cuyos cubos ocupan el primer piso y uno ocupa el segundo. La apariencia tridimensional de A se ajusta al boceto siguiente. [2] Proseguimos con el tetracubo B, dos de cuyos cubos ocupan el primer piso y los dos restantes ocupan el segundo. En la figura siguiente se ofrece una representación en perspectiva de B. [3] En tercer lugar, concebimos el pentacubo C, tres de cuyos cubos ocupan el primer piso y los dos restantes el segundo. En el boceto adjunto se muestra una representación de C. [4] Acto seguido «creamos» el pentacubo D, tres de cuyos cubos están en el segundo piso y los dos restantes en el tercero. En la figura siguiente ofrecemos una representación de D. [5] Incluimos ahora el tetracubo E que tiene un cubo en el segundo piso y tres en el tercero. La representación 3D de dicho policubo se ofrece en el boceto siguiente. [6] Habiendo llegado a este punto, los huecos que quedan por cubrir sólo se pueden llenar con el tetracubo F. La figura adjunta es una representación plana del policubo F. Con esto, acabamos de «inventar» o «reinventar» un rompecabezas cúbico de seis piezas (tres tetracubos y tres pentacubos).   Referencias bibliográficas GARDNER, M. (1987). Rosquillas anudadas y otras amenidades matemáticas. Barcelona: Editorial Labor, S. A. HOFFMANN, P. (1893). Puzzles Old and New. London: Frederick Warne and Co. MEAVILLA SEGUÍ, V. (2011). El lobo, la cabra y la col. Córdoba: Editorial Almuzara, S. L.   Referencias online Cubic Block Puzzles. The 3x3x3 Cube Cubo de Bedlam Gridlock puzzle Cubo de Conway El puzzle de Slothouber-Graatsma Introducing SOMA (Manual del SOMA)   Notas: [1] Pseudónimo del inglés Angelo John Lewis (1839 – 1919). [2] Parker Brothers distribuyó el SOMA en Estados Unidos. El manual editado por dicha empresa fue escrito e ilustrado por Piet Hein (Introducing SOMA, 1969). [3] Manual del SOMA (Parker Brothers), p. 12.

Miércoles, 15 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

415. 107. (Julio 2020) Música y entropía - I

Inauguramos una serie en la que vamos a examinar el concepto de entropía y su aplicación en el análisis musical. A primera vista, no parece que ambos conceptos tengan mucha relación entre sí o si la tienen que sea una relación directa. Además, hay varios conceptos de entropía. En Mecánica Estadística, entropía se refiere al número de configuraciones microscópicas que son consistentes con las cantidades macroscópicas que caracterizan un sistema, tales como el volumen, la presión o la temperatura (véase [Wik]). Esta entropía, llamada entropía termodinámica, está definida de manera que se puede interpretar como una medida del desorden interno del sistema y cuanto mayor es el valor de la entropía, mayor es el desorden del sistema. La segunda ley de la termodinámica establece que en un sistema aislado la entropía nunca decrece y que esta tiende a su máximo valor posible (máximo desorden del sistema). Más tarde, Shannon, en un artículo pionero [Sha10] A Mathematical Theory of Communication, tomó las ideas principales encerradas en el concepto físico de la entropía y las aplicó a la Teoría de la Información. Definió la entropía como la cantidad de información asociada a un mensaje en base a la sorpresa o novedad contenida en los símbolos de ese mensaje. Tal y como pasaba con la entropía termodinámica, la entropía de la teoría de la información está descrita en términos de distribución de probabilidades. Formalmente, la entropía de Shannon se define a partir de un conjunto de símbolos, xi, cada uno con probabilidad de aparición igual a P(xi), donde i = 1,…,n. Las parejas (xi,P(xi)) forman la distribución X de probabilidad de ese conjunto de símbolos. La fórmula matemática de la entropía de Shannon es En la práctica las probabilidades de los símbolos se obtienen observando la transmisión de los mismos. Cuando se aplican estas ideas al análisis musical, en primer lugar se interpreta la propia música como un conjunto de símbolos. Si queremos hallar la entropía de las alturas de sonido, entonces el conjunto de símbolos son las 12 alturas (si se consideran clases de alturas; en otro caso, cada altura es un símbolo distinto). Las probabilidades de dichas alturas (símbolos) se calculan a partir de las frecuencias de aparición en una pieza concreta o en general en un corpus musical. Esta famosa fórmula establece que la máxima cantidad de información contenida en mensajes escritos con los símbolos xi ocurre cuando cada símbolo tiene probabilidad 1∕n. Esta fórmula se puede interpretar como la esperanza de -log 2(X). La variable aleatoria -log 2(X) recibe el nombre de cantidad de información de X. Además, la entropía representa un límite absoluto de la capacidad de codificar un mensaje sin pérdidas en un canal sin ruido, resultado que es importante en teoría de la información. Tras esta breve definición de entropía, surge la pregunta de cómo se relaciona la entropía con la música y su análisis. La música es un fenómeno complejo y altamente estructurado. Desde el principio, músicos y musicólogos buscaron afanosamente conceptualizar, detectar, medir e interpretar esa complejidad. Asociada a la cuestión del estudio de la complejidad musical está una cuestión muy cercana: cómo se genera el significado en la música. De hecho, una cuestión aun más básica, y que todavía está bajo intenso estudio, es la de definir qué es el significado musical (véanse [Mey56, Bro00, Coo01, AaQ17, Chu19] y sus referencias). Muchos investigadores pensaron que la complejidad de la música estaba entroncada con su capacidad para generar significado. Meyer, en su famoso libro del año 56, Emotion and Meaning in Music [Mey56], afirma que el significado musical proviene de la capacidad de que un suceso musical implique otro suceso musical. He aquí sus palabras textuales: Musical meaning arises when an antecedent situation, requiring an estimate as to the probable modes of pattern continuation, produces uncertainty as to the temporal- tonal nature of the expected consequent. (Meyer, 1957, p. 416) Esta teoría supone que los sucesos musicales transcurren en base a un argumento musical cuya lógica encadena dichos sucesos uno tras otro. La mayor o menor sorpresa del argumento musical es proporcional al interés musical que despierta la pieza. Meyer ofrece, pues, una teoría en que explica la emoción musical en base a la creación y satisfacción de expectativas musicales. Obsérvese que Meyer asume una definición de significado musical en que lo extra-musical tiene poca importancia, esto es, el significado se genera a partir de los hechos meramente musicales. Otras teorías acuden, en cambio, a paralelismos con el lenguaje para explicar el significado musical. En un artículo publicado un año después que su libro, Meaning in music and information theory, [Mey57], Meyer ya formula su teoría del significado musical en términos de teoría de la información. En particular, afirma que “dado un antecedente musical, este induce una estimación de la probabilidad de las formas de continuación en el oyente” (página 416). Esta idea pronto atrajo la atención de muchos investigadores, quienes propusieron modelos de todo tipo para explicar la generación de significado musical. Por citar los principales modelos, tenemos Jackendoff y Lerdahl [LJ83] y su teoría generativa de la música tonal, el modelo de implicación-realization de Narmour [Nar90], el modelo de sistema y contraste de Bimbo y sus colaboradores [BDSV12], el modelo de tensión musical de Margulis [Mar05], la teoría de la expectativa de Huron [Hur06] o los modelos probabilísticos de Temperley [Tem10]. La teoría de Meyer contenía varios elementos que apuntaban hacia el uso de la entropía. Por un lado, al hablar de la estimación de la probabilidad de la continuación del discurso musical ya estaba sentando las bases para los modelos probabilísticos. Por otro lado, ¿cómo se estiman esas probabilidades? El oyente de una pieza musical va registrando los eventos musicales que oye y en función de ello y otros factores (familiaridad con el estilo, formación musical, conocimiento de la pieza en concreto) va construyendo un conjunto de probabilidades con que estima el próximo evento musical. Si el siguiente evento musical efectivamente confirma la estimación del oyente, la música producirá significado que si dicho evento rompe drásticamente su estimación. Dicho de otro modo, si la música es muy predecible, no tendrá interés musical para el oyente, mientras que si la música está llena de sorpresas, entonces sí generará mucho interés. A partir del trabajo de Meyer, muchos investigadores examinaron la cuestión de definir formalmente el significado musical a través de la entropía. Por orden cronológico, los esfuerzos más representativos se encuentran en los trabajos de Youngblood [You58], Cohen [Coh62], Knopoff y Hutchinson [KH83], Snyder [Sny90], Margulis [Mar05], Cox [Cox10], Laney y sus colaboradores [LSC15] y Febres y Jaffe [FJ17]. En efecto, la entropía es una medida de la cantidad de información contenida en la distribución de una variable aleatoria (véase [Góm16] para un repaso de estos conceptos). Cuanto más incertidumbre hay sobre los valores que toma la variable aleatoria, mayor es su entropía. Por otro lado, se puede interpretar que una pieza musical es más compleja cuanto más impredecible sea. Y entonces surge la deseada relación entre complejidad musical/significado musical y entropía. Sin embargo, Margulis [MB08], en un trabajo de 2008, llevó a cabo un análisis sistemático de la entropía como herramienta analítica y apunto a tres grandes problemas. El primero es de tipo epistemológico y es cómo hacer preguntas que sean relevantes musicalmente dentro del marco de la teoría de la información. La segunda es cómo recoger datos musicales que necesitan los modelos computacionales de la teoría de la información. La tercera es cómo determinar la unidad básica de análisis (la altura de sonido, el ritmo, las frases, los motivos o una combinación de ellos) que proporcione resultados válidos. Una de las principales virtudes de la entropía es que se puede concebir como una medida de la complejidad con que los elementos de una pieza están integrados entre sí. Sin embargo, no está tan claro cómo relacionar la entropía con la percepción del oyente de los elementos musicales. Varios autores [SJAN99, Mar14] han probado que los humanos pueden tomar propiedades estadísticas complejas cuando están escuchando música. Como Margulis ha escrito con elocuencia, “escuchar música es al mismo tiempo aprender a escuchar música”. Esto puede justificar el uso de la entropía, pero sigue quedando la cuestión de si la entropía se calcula sobre las mismas estadísticas que las que extrae un oyente humano. Otra cuestión fundamental es que la entropía no tiene en cuenta el significado intrínseco de los símbolos musicales, sino únicamente su frecuencia. Tampoco tiene en cuenta el orden en que estos aparecen y es razonable pensar que dicho orden tiene cierta importancia. Como veremos en las siguientes entregas de esta serie, los investigadores han hecho un gran esfuerzo por aplicar la entropía al análisis musical de manera que se superen estos obstáculos y se obtengan resultados que tengan relevancia en la explicación del fenómeno musical. Bibliografía [AaQ17] Pedro Atã and João Queiroz. Semiotic niche construction in musical meaning. Recherches sémiotiques / Semiotic Inquiry, 37(1-2):75–87, 2017. [BDSV12] Frédéric Bimbot, Emmanuel Deruty, Gabriel Sargent, and Emmanuel Vincent. Semiotic structure labeling of music pieces: concepts, methods and annotation conventions. In ISMIR (International Symposium on Music Information Retrieval), Curitiba, Brazil, October 2012. [Bro00] Candace Brower. A cognitive theory of musical meaning. Journal of Music Theory, 44(2):323–379, 2000. [Chu19] Andrew J. Chung. What is musical meaning? theorizing music as performative utterance. Music Theory Online, 25(1), 05 2019. [Coh62] J. E. Cohen. Information theory and music. Behavioral Science, 7(2):137–163, 1962. [Coo01] Nicholas. Cook. Theorizing musical meaning. Music Theory Spectrum, 23(2):170–195, 2001. [Cox10] G. Cox. On the relationship between entropy and meaning in music: An exploration with recurrent neural networks. In Proceeding Annual Meeting of the Cognitive Science Society, Portland, USA, August 2010. [FJ17] G. Febres and K. Jaffe. Music viewed by its entropy content: A novel window for comparative analysis. PLoS ONE, 12(10):1–30, 2017. [Góm16] P. Gómez. Música y Probabilidad (I), noviembre de 2016. [Hur06] David Huron. Sweet Anticipation. MIT Press Books, Massachusetts, 2006. [KH83] L. Knopoff and W. Hutchinson. Entropy as a measure of style: The influence of sample length. Journal of Music Theory, 27(1):75–97, 1983. [LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983. [LSC15] Robin Laney, Robert Samuels, and Emilie Capulet. Cross entropy as a measure of musical contrast. In Tom Collins, David Meredith, and Anja Volk, editors, Mathematics and Computation in Music, volume 9110 of Lecture Notes in Computer Science, pages 193–198. Springer, Cham, Switzerland, 2015. [Mar05] Elizabeth H. Margulis. A model of melodic expectation. Music Perception: An Interdisciplinary Journal, 22(4):663–714, 2005. [Mar14] Elizabeth H. Margulis. On repeat: how the music plays the mind. Oxford University Press, New York, 2014. [MB08] Elizabeth H. Margulis and Andrew P. Beatty. Musical style psychoaesthetics and prospects for entropy as an analytic tool. Computer Music Journal, 32(4):64–78, 2008. [Mey56] Leonard Meyer. Emotion and Meaning in Music. University of Chicago Press, Chicago, 1956. [Mey57] Leonard Meyer. Meaning in music and information theory. Journal of Aesthetics & Art Criticism, 15:412–424, 1957. [Nar90] E. Narmour. The Analysis and Cognition of Basic Melodic Structures: The Implication-Realization Model. University of Chicago Press, Chicago, 1990. [Sha10] C. E. Shannon. A Mathematical Theory of Communication. Bell System Technical Journal, 27:379–423, 623–656, julio, octubre 2010. [SJAN99] J. R. Saffran, E. K. Johnson, R. N. Aslin, and E. L. Newport. Statistical learning of tone sequences by human infants and adults. Cognition, 70:27–52, 1999. [Sny90] J. L. Snyder. Entropy as a measure of musical style: The influence of a priori assumptions. Music Theory Spectrum, 12(1):121–160, 1990. [Tem10] D. Temperley. Music and Probability. MIT Press Ltd, 2010. [Wik] Wikipedia. Entropy. [You58] J. E Youngblood. Style as Information. Journal of Music Theory, 2(1):24–35, 1958.

Martes, 14 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

416. Matemáticas de cine

Categoría: Matemáticas y arte Autor: José María Sorando Muzás Editorial: Guadalmazán. Colección Matemáticas Año de publicación:  2020 Nº de hojas: 256 ISBN: 978-84-17547-17-2

Jueves, 09 de Julio de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

417. Los números de la vida. 7 principios matemáticos que dan forma a nuestra existencia

Categoría: Divulgación matemática Autor: Kit Yates Editorial: Blackie Books Año de publicación:  2020 Nº de hojas: 384 ISBN: 978-84-17552-94-7 Traducción: Francisco J. Ramos Mena

Jueves, 09 de Julio de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

418. Pifias matemáticas. Equivocarse nunca ha sido tan divertido

Categoría: Divulgación matemática Autor: Matt Parker Editorial: Crítica. Colección Drakontos Año de publicación:  2020 Nº de hojas: 352 ISBN: 978-84-91991-91-5 Traducción: Pedro Pacheco González

Jueves, 09 de Julio de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

419. ¡Un matemático ahí, por favor!

Categoría: Divulgación matemática Autor: Adrián Paenza Editorial: Debate Año de publicación:  2020 Nº de hojas: 336 ISBN: 978-84-17636-76-0

Jueves, 09 de Julio de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

420. Jugando con las matemáticas. Los juegos como recurso de enseñanza y aprendizaje matemático

Categoría: Educación matemática Autores: José Muñoz Santoja, Juan Antonio Hans Martín y Antonio Fernández-Aliseda Redondo (Grupo Alquerque) Editorial: Catarata. Colección Miradas Matemáticas Año de publicación:  2020 Nº de hojas: 160 ISBN: 978-84-9097-989-1

Jueves, 09 de Julio de 2020 | Imprimir | PDF |  Correo electrónico | Leer más