421. Una mirada distinta de las matrices. Viajes, retos y magia

Categoría: Educación matemática Autoras: Mireia López Beltran y Pura Fornals Sánchez Editorial: Catarata. Colección Miradas Matemáticas Año de publicación:  2019 Nº de hojas: 128 ISBN: 978-84-9097-732-3

Jueves, 09 de Julio de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

422. Cálculo infinitesimal. El lenguaje matemático de la naturaleza

Categoría: Educación matemática Autor: Antonio J. Durán Editorial: Catarata. Colección Miradas Matemáticas Año de publicación:  2020 Nº de hojas: 112 ISBN: 978-84-9097-926-6

Jueves, 09 de Julio de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

423. 132. (Julio 2020) La Leyenda de Sissa (o el viaje a la luna doblando un papel) de Roberto Muñoz

La Leyenda de Sissa es una reflexión matemática y artística de nuestro compañero y amigo Roberto Muñoz (Universidad Rey Juan Carlos). La ha escrito durante los pasados días de confinamiento debidos a la pandemia provocada por el coronavirus SARS-CoV-2. El título alude a la famosa leyenda de Sissa, la del sirviente del brahmán Rai Bhalit que creó la chaturanga -el ajedrez- para entretener a su caprichoso y aburrido señor. El brahmán dejó elegir a Sissa su recompensa por tan entretenido juego. El inteligente sirviente solicitó como pago algo estrechamente relacionado con el tablero en el que se jugaba la chaturanga: pidió un grano de trigo por el primer cuadrado, dos por el segundo, cuatro en el tercero, dieciséis en el cuarto, etc. El brahmán aceptó lo que pensaba que era una modesta recompensa, hasta que fue consciente de que no había trigo suficiente en el país para pagar semejante petición… Sissa según un dibujo de Thiago Cruz (2007). Imagen: Wikimedia Commons. NOTA: Este texto fue publicado previamente en la revista de educación InkSpace, en su número de junio de 2020 dedicado a la educación y el arte. -OoO- Aplanar una curva, una maldita curva. Una curva que nace exponencial, dos elevado al tiempo que pasa, o quizás tres elevado al número de días, o cuatro. Cada uno contagiando a tantos, dando una mano o un beso, compartiendo un vaso, la saliva, la barandilla del autobús, cama. Diseminando un virus lejano, de pangolines y murciélagos. Un caso en La Rioja, o en Madrid, o en Igualada, qué importa, quién se acuerda, que contagia a dos, estos dos a otros dos y estos a otros: en comidas, en fiestas, en el metro, en el médico. Y sólo así, en veinte unidades de tiempo, dos elevado a la veinte, más de un millón (1.048.576 es el valor exacto de 2^20). En diez unidades de tiempo más, 2^30, esto es 1.073.741.824, imposible, increíble. 2^40= 1.099.511.627.776 2^50= 1.125.899.906.842.624 2^60= 1.152.921.504.606.846.976 Nos habían contado eso de llegar a la luna doblando un papel. Nos habían contado aquella leyenda del premio al creador del juego del ajedrez: granos de arroz que se duplican en cada casilla del tablero y que convertían aquel regalo en impagable pero no, no acabábamos de entender, no, no lo comprendíamos. Y sí. Aunque nosotros no éramos como los chinos -aquí seguro que no, aquí no existe la exponencial, aquí no-, lo somos. Aplanar la curva. Hacer que la segunda derivada sea negativa, que se decelere la función, que crezca más despacio, asfixian los datos, que deje de crecer, cuánto dolor, que deje de crecer, que deje, que empiece a decrecer, sentir alivio. Aplanar la curva para salir a la calle, para respirar árboles y dejar de oler enchufes, para quitarnos el chándal y comprar chisteras. Para producir vitamina D y deseo, para no beber solos, para gritar larga vida al rock and roll. La derivada ya no es un ejercicio académico de rutina, la del cuadrado de x es dos x, la del logaritmo de x es 1/x, ya no es sólo la velocidad, la pendiente de la recta tangente, la tasa de variación instantánea. Es ahora la derivada un deseo y es una expectativa, que la curva deje de ser exponencial y que se convierta en otra cosa, todavía no, todavía no lo ha hecho, unos plazos, no sé qué índice de contagio. Por favor que cambie de signo, que deje de ser positiva y cada vez más grande y empiece por aumentar cada vez más despacio para terminar siendo negativa. Pendiente positiva, crece, pendiente negativa, decrece. Que decrezca. Que decrezca. Un punto de inflexión y luego un máximo y luego para abajo. Si crece a esta velocidad, si la curva tiene esta forma, no podremos atender a todos, no seremos suficientes, no tendremos energía y será peor, nos contagiaremos más; los que cuidan todavía más. Ha de crecer más despacio, todos a casa, todos separados, profilácticos todos, aplausos a las ocho, series y bizcochos. Números en pantallas, números pronunciados, números que no son clases de equivalencia de conjuntos finitos módulo biyección, no. Son cincuentas que duelen, setecientos cincuenta y sietes que te dejan exhausto, o cientos de miles. Millones. Porcentajes. Novecientos cincuenta, dos de abril, 2020. Cero era un punto de equilibrio, las cosas no variaban, cuando no había contagiados nadie se podía contagiar. Se alteró ligeramente el equilibrio -una temperatura media ligeramente superior, unas emisiones que subieron un poco, un mar apenas unas décimas más caliente-, no mucho, epsilon, dos o tres infectados, quizás quince, unos que venían de aquí y de allá, que se movían, y el sistema se activó, se puso a buscar otro punto de equilibrio, ojalá el mismo punto de contagiados cero, en el que detenerse, estabilizarse. Aquella movida del comportamiento asintótico de una función (de un sistema dinámico), aquello de que la exponencial tiende a infinito, pero más rápido que cualquier polinomio, y que 1/x tiende a 0, y que si calcule usted las asíntotas horizontales de la siguiente función, es ahora un horizonte sin metáforas. El de los contagiados que habrá, el de los repuntes, el de las caídas a cero, el de la comparación entre los que podemos y los que debemos cuidar, el de la vida cotidiana que será igual, o no. Una curva que se aplanará, la gráfica de una función: en un eje el tiempo, en el otro los contagiados (o los fallecidos, o los ingresados en unidades especiales, o lo que vayan poniendo). Que se aplanará, al fin y al cabo el conjunto de personas es finito, pero que ni idea, los epidemiólogos algo esperan, pero con prudencia: mesetas, caídas, subidas, periodos. Ciencia. La que destruirá este texto cuando todo se entienda. Y mientras tanto, una cacofonía de enterados, de iluminados, de iracundos, de tontilanes, de toreros de salón. Y muchas dificultades para contar: uno, dos, tres, cuatro, para homogeneizar datos, para comparar, y pocas ganas de hacerlo. O mala intención. Una curva, en unos meses, una curva. -OoO-

Lunes, 06 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

424. Recomendaciones de un matemático para el verano

ABC, 6 de Julio de 2020 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 06 de Julio de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

425. 44. CONCURSO DE VERANO 2020

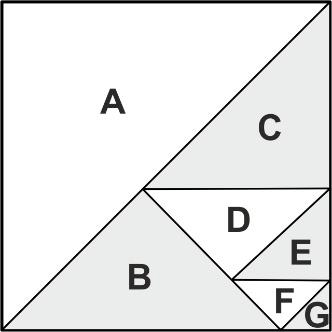
Arthur Stone propuso esta disección del cuadrado en 1940. Un cuadrado se puede diseccionar en siete piezas triángulos rectángulos isósceles de distinto tamaño cumpliéndose que: cateto de G=1; cateto de E=2 y cateto de C=4. (http://www.squaring.net/tritri/twt.html) Existen varias maneras de obtener piezas triángulos rectángulos isósceles doblando un papel cuadrado o doblando un papel rectangular. Dos ejemplos se pueden ver en estos diagramas: RETO: Conseguir las 7 piezas de esta disección doblando los correspondientes papeles cuadrados o rectangulares sin utilizar regla para calcular el tamaño de los papeles utilizados. Para obtener las piezas triangulares se puede usar alguno de los dos métodos propuestos u otro. Podéis enviarnos vuestras soluciones (diagramas y foto del modelo terminado) a la dirección papiroflexiamates@gmail.com hasta el 31 de agosto. Los participantes aceptan que DivulgaMAT pueda publicar las soluciones, independientemente del fallo del concurso. El premio del concurso consiste en un libro de divulgación relacionado con las matemáticas. ¡Feliz verano!

Miércoles, 01 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

426. 9. (Junio 2020) Paseo melancólico, matemático y artístico por un grabado alemán del siglo XVI

1. Introducción Alberto Durero. Melencolia I (1514, 28 x 18,8 cm) Galería Nacional de Arte de Karlsruhe El famoso y popular (entre el público matemático) grabado Melancolía I es obra del artista alemán Alberto Durero. Alberto Durero (1471 – 1528) Firma de A. Durero Junto con los grabados El caballero, la muerte y el diablo y San Jerónimo en su gabinete integra la trilogía Estampas maestras. Contemplada con ojos matemáticos, Melancolía I propone dos ambientes bien diferenciados: el aritmético y el geométrico. En el primero (parte superior derecha del grabado), se representa un cuadrado mágico 4 x 4 con los dieciséis primeros números naturales. En el segundo (parte izquierda) puede verse un poliedro peculiar (el sólido de Durero) y una esfera. Aritmética Geometría Boceto de Durero para el poliedro Melancolía 2. El ambiente aritmético En la parte superior derecha de su Melancolía, debajo de la campana, Durero nos  presenta una distribución numérica, en forma de cuadrado, en la que intervienen los dieciséis primeros números naturales (1, 2, 3, . . ., 14, 15, 16). 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 Notemos que la suma de los cuatro números de cada fila es igual a 34. Lo mismo sucede con la suma de los cuatro números de cada columna y con la suma de los cuatro números de cada diagonal. Además, los números 15 y 14 de la cuarta fila indican el año en que se estampó el grabado. Entre los matemáticos, cualquier distribución numérica similar a la de Durero se llama cuadrado mágico normal de orden 4. En general, se llama cuadrado mágico de orden n a un cuadrado formado por números naturales diferentes tales que los n números de cada fila, columna o diagonal, tienen la misma suma a la que se llama constante mágica [= M] del cuadrado. El cuadrado mágico de orden n se llama normal si los números que lo forman son los primeros números naturales. En el cuadrado mágico de Melancolía I, la suma de los números de las casillas grises en los diagramas siguientes también es igual a 34 [= M]. 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 Estas propiedades se pueden generalizar para cuadrados mágicos 4 x 4 en los siguientes términos: En todo cuadrado mágico de orden 4 la suma de los elementos que ocupan las esquinas es igual a la constante mágica. En todo cuadrado mágico de orden 4 la suma de los elementos que ocupan el cuadrado central de orden 2 es igual a la constante mágica. En todo cuadrado mágico de orden 4 la suma de los elementos que ocupan las esquinas de cualquier rectángulo medio es igual a la constante mágica. 3. El ambiente geométrico Antes de entrar de lleno en el estudio del sólido de Durero vamos a considerar otro poliedro llamado romboedro. El motivo de esta decisión es que, como se verá, aquél se genera a partir de éste. El romboedro es un hexaedro cuyas seis caras son rombos idénticos. Adviértase que el cubo es un caso especial de romboedro en el que las caras son cuadradas. Si se corta el romboedro del diagrama anterior por dos planos π y π´ perpendiculares a una de sus diagonales (por ejemplo, la CE) y tales que sus distancias respectivas a C y E sean iguales, entonces el romboedro se descompone en dos pirámides triangulares idénticas y en un poliedro dos de cuyas caras son triángulos equiláteros iguales y las seis restantes son pentágonos idénticos. Este último cuerpo geométrico es, precisamente, el poliedro Melancolía. Poliedro Melancolía Si el romboedro generador es un cubo, entonces el desarrollo del sólido de Durero toma la apariencia siguiente. 4. El ambiente artístico El poliedro Melancolía y el cuadrado mágico contenido en el grabado Melancolía I están presentes en diversas expresiones artísticas. Sirvan de ejemplo las siguientes. Hans Erni. Panta rhei (1979, detalle)[1]. Auditorio del Museo Hans Erni (Lucerna) Cortesía de la Hans Erni Foundation Giuseppe Modica. Mediterraneo-melanconia (2011). Óleo sobre tela,  20 x 25 cm. Cortesía del autor Giuseppe Modica. Melanconia-frammenti (2011). Óleo sobre tabla, tríptico, 150 x 225 cm. Cortesía del autor John Cornu. Melencolia (2011). 25 x 20 x 16 cm cada escultura. Cortesía del autor John Cornu. Melencolia (2011). 163 x 120 x 120 cm Cortesía del autor Román Jiménez Iranzo y Pedro Soler García. Melancolía (1992)[2] Sello de correos (Angola) Vicente Meavilla. Barcelona[3] (2004) George Widener. Magic Square (2009). 15,5 x 13 x 4 pulgadas Cortesía de la Andrew Edlin Gallery (New York) 5. A modo de epílogo Acabamos de dar un breve paseo por un grabado (Melencolia I) creado por el artista alemán Alberto Durero y estampado en 1514. A lo largo de esta corta excursión hemos pasado revista a los aspectos aritméticos (cuadrado mágico normal de orden cuatro y constante mágica 34), geométricos (poliedro Melancolía)  y artísticos de una obra maestra del arte universal. Con ello, hablando desde una óptica didáctica, hemos pretendido lanzar el siguiente mensaje a los docentes: cuando diseñéis actividades de enseñanza y aprendizaje procurad poner de manifiesto la relación de las Matemáticas con otras facetas de la cultura humana. Que así sea.   Referencias bibliográficas MEAVILLA SEGUÍ, V. (2004). Figuras imposibles. Geometría para heterodoxos. Granada: Proyecto Sur de Ediciones, S. L MEAVILLA SEGUÍ, V. (2016). El arte de las matemáticas. Córdoba: Editorial Guadalmazán. Referencias online Andrew Edlin Gallery (New York) Giuseppe Modica Hans Erni Foundation John Cornu Vicente Meavilla [1] A la izquierda de la imagen aparece Erasmo y a la derecha Lutero [2] La escultura de los arquitectos Jiménez Iranzo y Soler García estaba integrada en una fuente que se ubicó en la Plaza de la Ciudad de Brujas (Valencia). Dicha plaza estuvo en obras y, en la actualidad, desconocemos el paradero del sólido de Durero. [3] La distribución numérica encerrada en la B de Barcelona no es propiamente un cuadrado mágico de orden 4, dado que los números 10 y 14 se repiten dos veces. Este cuadrado cuasi-mágico está presente en la fachada de la Pasión de la Sagrada Familia (Barcelona). Notemos que la constante mágica es igual a 33 (edad de Cristo).

Martes, 23 de Junio de 2020 | Imprimir | PDF |  Correo electrónico

427. Los números también saben mantener la distancia de seguridad

ABC, 29 de Junio de 2020 CIENCIA - El ABCdario de las matemáticas Pedro Alegría

Lunes, 29 de Junio de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

428. 150 enigmas y juegos de historia para viajar en el tiempo

Categoría: Divulgación matemática Autor: Miquel Capó Editorial: Montena Año de publicación:  2020 Nº de hojas: 192 ISBN: 978-84-18038-66-2

Miércoles, 01 de Julio de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

429. Julio 2020: Juego de magia con dados

1. Introducción. Los dados son, sin lugar a dudas, uno de los principales elementos con los que se asocia el azar. Generalmente se piensa que, si están bien construidos, antes de lanzar los dados es imposible saber qué va a obtenerse en ellos. Esa idea lleva a pensar que no es posible predecir algunos resultados que pueden aparecer, y que por tanto, no se puede hacer ninguna predicción. El motivo es que debido a la aleatoriedad que se adjudica a los dados, no se tienen en cuenta propiedades que permiten conocer o predecir alguno de esos resultados. La característica anterior hace que cuando se utilizan dados en un truco de magia, la sorpresa venga aumentada por esa idea de que los dados representan el azar puro y duro. Como hemos comentado en otros artículos de esta sección, la magia tiene el gran atractivo de asombrar al público y atraer su atención. Como además suele crear incredulidad, motiva fácilmente a querer saber cómo ha sido posible algo que, a simple vista, parece imposible. Esta motivación es la que debe interesar al profesorado de matemáticas para utilizar la magia como recurso en el aula. Utilizando juegos de magia cuyo fundamento sea matemático, podemos conseguir que el alumnado investigue con interés las matemáticas que dan consistencia a ese truco mágico. Por ello, en todos los trucos veremos no solamente cómo se pueden hacer sino también los cálculos matemáticos que fundamentan ese truco y que permiten que siempre funcionen sin necesidad de una especial habilidad del mago. En este artículo he pretendido aglutinar todos los casos de trucos mágicos con dados que se pueden encontrar. Aunque algunos son muy conocidos, pues se repiten con asiduidad en la red digital, he preferido incluirlos para acompañarlos de explicaciones que dejen en evidencia las matemáticas que están detrás. Aunque la mayoría los conocía desde hace tiempo, he encontrado algunos nuevos en una de las mejores páginas de magia y matemáticas que existen, la sección “El rincón matemágico” de mi amigo Pedro Alegría, en esta misma página de divulgamat. Sitio de visita obligada para todos los interesados en la magia matemática. Los dados. La forma más cotidiana que conocemos en los dados es la cúbica, aunque no deja de ser curioso que uno de los restos físicos  más antiguos que existen de dados correspondientes al Juego Real de Ur, tienen forma de tetraedro, con una antigüedad de unos 4.500 años. Según los historiadores, los primeros dados que se han encontrado en excavaciones arqueológicas no estaban bien construidos pues, al parecer, se usaban primordialmente de forma esotérica para adivinar el futuro. Como los usuarios pensaban que los resultados dependerían de los dioses, no importaba mucho que la construcción fuese perfecta y que, por lo tanto, los dados fuesen equiprobables. No fue hasta el Renacimiento, tras los estudios probabilísticos de Blaise Pascal y Galileo Galilei cuando se comenzó a cuidar más la forma de construir los dados. Pero lo que a nosotros nos importa es la distribución concreta en que están repartidos los puntos en los dados. Ya en el Libro de axedrez, dados e tablas encargado en el siglo XIII por Alfonso X el Sabio, rey de Castilla, León y Galicia, se dedicaron varios apartados a la construcción correcta de los dados y a la distribución de los puntos en sus caras. Los dados actuales se rigen por lo que se conoce como la distribución de siete, en la cual las caras opuestas suman siete. De esa forma se emparejan el 1 con el 6, el 2 con el 5 y el 3 con 4. Esta distribución es fundamental, pues prácticamente todos los trucos de magia con dados se basan en esa propiedad. Y es importante que confirmemos que se cumple, pues en una ocasión, en que impartía un taller para el profesorado, nos llevamos unos dados de goma grandes de los utilizados en infantil y vimos que no salían los trucos que llevábamos preparados, y era debido a que los dados no seguían esa máxima. Otro aspecto que se suele tomar como norma en los dados es la orientación de las caras. Si tomamos un dado y nos fijamos en el vértice formado por las caras con 1, 2 y 3, vemos que los números están colocados en el sentido antihorario. Aunque esto no siempre se cumple, como podemos ver en la imagen 1. Eso suele ocurrir en los dados chinos que no llevan la misma orientación que los españoles, aunque en nuestro país se suelen encontrar con facilidad dados con orientación horaria. Imagen 1: Orientación antihoraria y horaria. En todo el artículo vamos a suponer que trabajamos con dados que cumplen estas características antihoraria y con la configuración de siete. Voy a comenzar con un juego que no es propiamente de dados, aunque suele aparecer como truco con dados en multitud de páginas. En él no se utilizan las características de la configuración habitual y es un truco que puede encontrarse con cartas, ruletas, dominós, bolas numeradas o simplemente eligiendo un espectador una serie de números.   2. Adivinar tres caras de dados. Se necesitan tres dados y una calculadora por si la persona elegida del público no es muy ducha en cálculos mentales. Si se utiliza una calculadora hay que tener la precaución de que cada vez que se haga una operación se le dé a la tecla de igual, pues como no se suelen utilizar paréntesis, la jerarquía de operaciones puede hacer que el cálculo final de la calculadora no coincida con el que nos interesa. 2.1. Puesta en escena. Se entregan tres dados a un voluntario y, mientras el mago se vuelve de espaldas, se le pide que lance los tres dados y haga una serie de operaciones con los números que le han salido en las caras superiores de los tres dados. Los pasos a seguir son los siguientes: a) Al valor del primer dado le suma 3 y multiplica el resultado por 5. b) A lo obtenido se le suma 2 y se multiplica por 2. c) Al resultado se le suma el valor del segundo dado, se le resta 4 y se multiplica por 2. d) Se suma a lo obtenido 7 y se multiplica por 5. e) Por último, al resultado de las operaciones anteriores se le suma el tercer valor del dado y se le resta 9. f) Basta que el voluntario le indique el valor resultante de todas las operaciones al mago, quien inmediatamente indica cuales han sido los valores que han aparecido en los dados. El mago sólo debe restarle 326 al número que le indica el espectador para obtener un número de tres cifras que son precisamente los valores aparecidos en los dados. 2.2. Explicación del truco. Este es uno de los típicos trucos de magia que se fundamentan en el álgebra para funcionar. Basta escribir la expresión algebraica correspondiente para descubrir el número oculto, que sólo sirve para enmascarar el resultado final. Si suponemos que a, b y c son los tres valores de los dados, veamos el proceso que se sigue: a) (a + 3)·5 b) ((a+3)·5 + 2)·2 c) [((a+3)·5 + 2)·2 + b – 4]·2 d) ·5 e) ·5 + c – 9 Si desarrollamos esta última expresión tenemos: ·5 + c – 9 = ·5 + c – 9 = [(10a +34 + b – 4)·2 + 7]·5 + c – 9 = (20a + 2b + 60 + 7)·5 + c – 9 = 100a +10b + 335 + c – 9 = 100a + 10b + c + 326 Como vemos, si le restamos 326 al número nos queda uno de tres cifras que son a b y c, los números aparecidos en los dados. 2.3. Fundamento matemático. Los números que se suman se pueden cambiar a voluntad, pues lo único importante es que, antes de sumar el segundo valor hayamos multiplicado el primer valor por 10, se puede hacer en una sola multiplicación o en dos, como hemos visto en el ejemplo. Después, antes de sumar el tercer valor, debemos multiplicar el resultado otra vez por 10 en uno o dos pasos. Todos los demás números que se suman o restan, solo sirven para crear lo que se llama el “velo”, es decir, el número que enmascara la solución. Una manera que parece más aleatoria a la hora de poner el truco en escena, consiste en solicitar a nueve espectadores que digan un número entre 2 y 5 inclusive. Raro será que no se repite el 2 dos veces y otras dos el 5. En ese caso, podemos ser nosotros quienes digamos la última cifra según nos convenga. Posteriormente podemos ir sumando o restando a placer, lo único que tenemos que hacer es anotar todas las cifras en un papel, e ir escribiendo el orden en el que le damos al espectador los números, para saber qué “velo” va a quedarnos al final.   3. La columna de dados. Este es un juego que utilizo en clase hace mucho tiempo, pero del que he encontrado una ampliación en la página de Pedro Alegría. Su puede jugar con tres o cuatro dados o los que se quiera, pues el cálculo es equivalente sea cual sea la cantidad de dados. 3.1. Puesta en escena. El mago le entrega a un voluntario del público tres dados y se vuelve de espaldas. Le pide al espectador que lance los tres dados y que coloque uno encima de otro formando una columna. Imagen 2: Columna de dados. Una vez construida, el mago observa la columna y le indica al espectador cuánto vale la suma de las caras que no están a la vista. Las caras que no pueden verse son aquellas en las que un dado se apoya en otro o sobre la mesa. El espectador que está realizando el truco va levantando los dados y sumando las caras, con ayuda del público y se comprueba que el mago ha acertado. Para resolver el truco basta observar el número que está en lo alto de la columna y restarle ese valor al resultado de multiplicar el número de dados que haya por siete. En la columna que aparece en la imagen 2, la suma de las caras ocultas sería 21 – 5 = 16. 3.2. Fundamento matemático. Es uno de los trucos más fáciles de estudiar. Como por la distribución estándar las caras opuestas de un dado suman siete, todas las caras que están ocultas suman siete para cada dado, exceptuando el primer dado una de cuyas caras ya está a la vista. Por ello, todas las caras que están en la vertical de los dados suman siete y sólo hay que multiplicar por siete el número de dados que se ha utilizado en el truco y restarle la cara superior visible. 3.3. Más difícil todavía. Es posible saber cuánto suman las caras ocultas incluso sin necesidad de saber cuánto vale la primera. Para ello, además de utilizar que las caras opuestas de un dado suman siete, debemos tener presente el sentido antihorario de colocación de los valores. Si nos fijamos en la siguiente columna tenemos tapado el valor superior, pero aún así podemos saber no solo cuánto vale la suma de las caras ocultas sino el orden en el que están, lo que puede hacer aún más visible el espectáculo ya que se puede decir que vaya enseñando el voluntario las caras ocultas de los dados y el mago dirá, antes de tomar el dado, cuánto vale la cara que va a salir. Imagen 3: Columna de dados tapada. Fijándonos en el dado verde, como opuesto al seis va el uno, según la orientación estándar, la cara tapada será el dos y, por tanto, en la cara inferior debe ir el cinco. En el rojo, frente al cuatro irá el tres, y frente al cinco el dos, con lo que la cara inferior será un uno, luego la superiores el seis. Por último, en el dado azul, al otro lado del cinco irá el dos, por lo que en la cara superior aparecerá el tres y en la inferior el cuatro. Podemos comprobarlo en la siguiente imagen en la que hemos colocado alineados los dados. Imagen 4: Columna alineada.   4. Tirar y tirar. Se necesitan tres dados y no está de más tener un papel y un lápiz para anotar los puntos que va sumando la persona que hace los cálculos, pues no es raro que haya equivocaciones. 4.1. Puesta en escena. Se entregan tres dados a un espectador y el mago, tras volverse de espaldas, le da las siguientes indicaciones. a) Lanza los tres dados y suma los valores que aparecen en las caras superiores. b) Toma uno cualquier de los dados y añádele al resultado de la suma anterior el valor de la cara inferior, aquella sobre la que estaba apoyada en la mesa. c) Lanza de nuevo ese dado y añade a la suma la cara superior que ha salido tras el nuevo lanzamiento. d) Elige otro dado cualquiera, que puede ser el mismo que en el caso anterior y repite los pasos b y c. Tras seguir esas instrucciones, el mago se gira hacia la mesa donde están los dados y le indica al espectador cuánto ha dado la suma que ha realizado. Para conseguirlo el mago solo tiene que sumar 14 a la suma de los valores que vea en ese momento en los dados sobre la mesa, independientemente de cuál hayan sido los dados que se han vuelto a lanzar. 4.2. Fundamento matemático. Basta recordar que la suma de las dos caras opuestas de un dado siempre vale siete. Si suponemos que los dados han mostrado inicialmente las caras a, b y c, si tomados el primer dado y le sumamos la cara inferior y lo volvemos a lanzar obteniendo d como cara superior tendríamos, hasta el momento, la suma a + b + c + (7 – a) + d = b + c + d + 7. Si tomamos ahora, por ejemplo el segundo dado y le añadimos su cara inferior (7 – b) y lo lanzamos otra vez obteniendo e como resultado, la suma final que hará el espectador será b + c + d + 7 + (7 – b) + e = c + d + e + 14. Los pasos b y c de las instrucciones se puede hacer una sola vez o las veces que estime el mago, sólo debe tener en cuenta que por cada vez que se realicen debe sumar 7 a la suma de los valores que quedan a la vista tras el proceso.   5. Suma y vuelta. De nuevo tenemos tres dados. Para diferenciarlos a la hora de seguir los pasos vamos a suponer que son de tres colores, aunque basta tener claro cuál es el primer dado, cuál el segundo y cuál el tercero. 5.1. Puesta en escena. Se entregan tres dados de colores diferentes a un voluntario junto con una predicción del mago en un papel. Se le pide que realice los siguientes pasos. a) Lanza los tres dados. Toma el rojo y el verde y suma los valores superiores de los dados. b) A continuación coloca el rojo junto al azul, le das a los dos media vuelta y añade a la suma anterior la suma de los valores que quedan ahora en las caras superiores de los dados. c) Por último, toma el verde y al azul, tal como están en ese momento, y de forma conjunta le das media vuelta. De nuevo añade a la suma parcial que llevas hasta el momento los dos valores que han quedado en las caras superiores. d) Ya solo le queda abrir el papel con la predicción del mago y comprobar que la suma le ha dado 21 tal como predijo el mago. 5.2. Fundamento matemático. Vamos a suponer que en la cara de los tres dados han aparecido los números r, v y a. Vamos a seguir los cálculos realizados. a) Sumamos r + v b) Al dar la vuelta al dado rojo y azul, lo que vamos a sumar son sus antiguas caras inferiores: r + v + 7 – r + 7 – a = 14 + v – a. c) Al dar la vuelta a los dados verde y azul tal como estaban nos encontramos con la cara 7 – v y la cara a que añadidos a lo anterior nos da: 14 + v – a + 7 – v + a =21.   6. Cambio de dados. Basado en la idea de los juegos anteriores, imaginé la siguiente versión que yo, al menos, no he encontrado en otro sitio. En este caso se necesitan dos voluntarios que tendrán cada uno de ellos dos dados. Como hay un intercambio de dados que pueden ser cualesquiera, al público le da la impresión de que ese azar puede modificar el resultado final posible. Impresión que es falsa. 6.1. Puesta en escena. Se invitan a dos personas del público a participar. Se entregan cuatro dados, dos a cada uno de los voluntarios del público. Se siguen los siguientes pasos, con el mago vuelto de espaldas. a) Ambos jugadores lanzan los dados y suman los dos valores que han obtenido con sus dados. b) A continuación se intercambian uno de los dos dados. Es decir, el primer jugador entrega uno de sus dados al otro y recibe uno de él, ambos en la misma posición en que han quedado. c) En el siguiente paso, ambos jugadores dan media vuelta conjuntamente a los dos dados de que disponen ahora, y añaden a la suma anterior la suma de las caras que han quedado ahora. d) Por último, el mago pregunta a uno de los jugadores cuánto ha obtenido de suma y puede decir inmediatamente cuánto vale la suma del otro jugador. El mago sólo debe restar de 28 el valor de la suma de uno de los jugadores para obtener lo que tiene el otro. 6.2. Fundamento matemático. El que los jugadores se intercambien un dado sólo trata de enmascarar que realmente lo que se está sumando son las caras opuestas de los cuatro dados, por lo que el resultado de la suma conjunta siempre será 28. Por ello, sabiendo la suma de uno de los jugadores es inmediato saber la del otro. Si queremos dar la impresión de que la suerte modifica los resultados posibles, se puede pedir a otro espectador que indique a cuál de los dos voluntarios le debe preguntar la suma.   7. El producto de las caras. Un espectador recibe dos dados y una predicción del mago sobre el resultado que va a obtener después de hacer una serie de operaciones. 7.1. Puesta en escena. Tras lanzar los dados, el espectador hace las siguientes operaciones. 1) Multiplica los números que quedan en las caras superiores de los dados. 2) Multiplica los números que quedan en las caras inferiores de los dados, aquellas sobre las que han quedado apoyados los dados tras ser lanzados. 3) Multiplica la cara superior del primer dado por la inferior del segundo. 4) Multiplica la cara superior del segundo dado por la inferior del primer dado. 5) Por último suma los cuatro resultados de las operaciones y comprueba que obtiene 49 que es lo mismo que había escrito el mago en el papel. 7.2. Fundamento matemático. Teniendo en cuenta la propiedad fundamental en la distribución de los dados, basta recordar que si el primer dado tiene a en su cara superior, en la inferior tendrá 7 – a, e igual para el otro dado. Si tenemos en cuenta los cuatro productos que debe hacer el espectador y los sumamos tendremos la siguiente expresión: a·b + (7 – a)·(7 – b) + a·(7 – b) + b·(7 – a) = a·b + 49 – 7a – 7b + a·b + 7a – a·b + 7b – a·b = 49. Luego el resultado es siempre 49, independientemente de lo que hubiese salido en los dados al lanzarlos.   8. El número de seis cifras. De nuevo tenemos tres dados y una calculadora para realizar una serie de operaciones. 8.1. Puesta en escena. Tras seleccionar a alguien del público y entregarle los tres dados, el mago se vuelve de espaldas y da las siguientes indicaciones 1) Lanza los tres dados y forma con los tres dados un número de tres cifras uniendo los tres dados, por ejemplo el 253. 2) Ahora le das media vuelta al conjunto de los tres dados sin modificar el orden y esa cantidad la añades detrás del número anterior, obteniendo un número de seis cifras. 3) Por último, divide en una calculadora el número obtenido entre 111 y le indicas el cociente resultante al mago. 4) El mago realiza mentalmente una serie de operaciones y le indica al espectador qué números salieron inicialmente al lanzar los tres dados. El truco consiste en restarle siete al valor que ha indicado el espectador y dividir por 9 el resultado. El mago obtiene un número de tres cifras que son las que salieron aleatoriamente en los dados. 8.2. Fundamento matemático. Vamos a hacer el estudio matemático del fundamento de este truco. Hemos obtenido un número de seis cifras abcdef que desarrollado sería: a·100.000 + b·10.000 + c· 1.000 + d·100 + e·10 + f Ahora bien, como d, e y f eran las caras opuestas en los dados a las caras con a, b y c, resulta que se cumple que d = 7 – a, e = 7 – b y f = 7 – c. Llevando estos resultados a la expresión anterior, operando y reduciendo obtenemos: a·100.000 + b·10.000 + c· 1.000 + (7 – a)·100 + ( 7 – b)·10 + 7 – c = a·99.900 + b·9.990 + c·999 + 777 Tras dividir ese número por 111 nos queda el siguiente valor: a·900 + b·90 + c·9 + 7 Tras restar 7 y dividir el resto por 9 nos quedamos con la expresión a·100 + b·10 + c, es decir el número abc cuyas cifras son los valores aparecidos en los dados tras lanzarlos.   9. Derecha o delante. Vamos a necesitar un dado y aprovechar la orientación para hacer un truco bastante llamativo. Según comenta Pedro Alegría en su página, está creado por el mago americano Karl Fulves, especialista en magia matemática. 9.1. Puesta en escena. Con el mago vuelto de espaldas, el voluntario del público lanza el lado sobre la mesa y ahora evoluciona de la siguiente manera. Si el valor superior es impar gira 90º el dado hacia la derecha, es decir, gira sobre la arista derecha del cuadrado de la base. Si el valor superior es par, gira 90º hacia delante. Este proceso lo repite hasta que aparezca el uno. Lo hace una nueva vez. Si obtiene un número impar, continúa con el proceso hasta que vuelve a conseguir uno y da un último cuarto de vuelta. Tras ese último giro en la cara superior quedará el 4. 9.2. Desarrollo del proceso. Supongamos que el dado ha quedado tal como se presenta en la imagen. Imagen 5: Resultado inicial. Al girar a derecha (impar) o delante (par) el dado anterior vamos obteniendo la siguiente sucesión de valores: 5, 6, 3, 2, 1 y 4. Se puede realizar la prueba varias veces y se puede comprobar que para llegar a la solución siempre se consigue pasando por el 2, después el 1 y por último el 4. El fundamento se basa en la orientación de los dados y en la paridad que vamos a aplicar en el juego siguiente.   10. Par o impar. Para acabar, vamos a ver un juego basado en una idea similar al anterior. 10.1. Puesta en escena. Se entrega un dado a un espectador y se le pide que lo lance. Sobre el dado se le explica al espectador que debe girarlo 90º grados en cualquier dirección. Puede ser girarlo a izquierda o derecha sobre la propia cara que ha quedado sobre la mesa, o girarlo sobre cualquier de las aristas de la cara sobre la que está apoyado el dado. Si obtenemos el siguiente valor del dado: Imagen 6: Resultado inicial. Hay seis posibles maneras de girarlo tal como se ven en la siguiente imagen. Imagen 7: Posibilidades de giro. Una vez hecha la explicación, el mago se gira y le pide a otro espectador que diga un número del uno al seis. Entonces se le pide al voluntario que haga tantos giros como ha dicho el espectador. Los giros se pueden repetir o deshacer un giro anterior. Mientras el espectador lo hace, el mago llama la atención sobre que existen cientos o acaso miles de movimientos posibles pues como había 6 giros posibles cada vez hay una potencia de 6 resultados finales (63=216, 64=1296, 65=7776, 66=46656) según el número de movimientos que haya pedido el espectador. Por último, se le pide al espectador que, sin decirle nada al mago ni hacer ningún ruido, realice o no un nuevo giro del dado. Una vez que el voluntario ha terminado, el mago se vuelve observa el dado e inmediatamente le indica al voluntario si al final ha girado o no el dado. La explicación del truco lo vemos en el siguiente apartado. 10.2. Fundamento matemático. La fundamentación matemática está en el hecho de que si nos fijamos en una esquina determinada del dado y sumamos los tres valores de las caras que determinan ese vértice, al girar 90º en cualquiera de las direcciones indicadas, la nueva distribución que queda en el vértice que ha sustituido al anterior, la suma de sus valores ha cambiado la paridad. Es decir, si al principio era una suma par, al girar 90º la suma que se obtiene es impar. La justificación es evidente. Cuando giramos un dado un cuarto de vuelta, de las tres caras iniciales dos de ellas se mantienen, una en la misma posición y la otra cambiando de lugar, y hay una nueva cara que sustituye a la desaparecida. Pero esa cara es precisamente la opuesta a la que desaparece y como en las caras opuestas una es par y la otra es impar, es lo que hace que cambie la paridad. Esto se puede comprobar comparando las imágenes 6 y 7. Si volvemos ahora al truco. Si nosotros pedimos que se mueva un número par de veces, la paridad del vértice que hemos observado se mantendrá, si se pide un número impar de veces, cambiara la paridad. Por ello, como nos habremos fijado en qué paridad tiene la esquina elegida antes de volvernos y sabemos cuántos movimientos va a realizar el voluntario, sabemos cómo debe quedar la paridad del vértice. Si al volvernos y observar los valores que forman ahora el vértice elegido vemos que la paridad es la esperada, el espectador no ha hecho el último giro, en caso contrario si lo ha realizado.

Miércoles, 01 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

430. 10. (Julio 2020) El cuboctaedro, un poliedro arquimediano con catorce caras

1. Unas palabras introductorias Se llama poliedro semirregular o arquimediano1 a todo poliedro convexo en el que las caras son regulares, pero no iguales, y los ángulos poliedros son iguales y no regulares. Notemos que en un poliedro arquimediano todas las aristas son iguales. El primer documento en el que se alude a los poliedros semirrregulares se debe a Pappus de Alejandría (s. IV d. C.) que, en su Colección matemática, se expresa en los siguientes términos: (…) Es posible, en efecto, imaginar muchas figuras sólidas con superficies de cualquier clase; pero vamos a considerar especialmente aquellas que parecen regulares, las cuales no son solamente las cinco de que habla el divino Platón, a saber: el tetraedro, el hexaedro, el octaedro, el dodecaedro y el icosaedro, sino también las trece2 descubiertas por Arquímedes formadas por polígonos equiláteros y equiángulos, pero no semejantes. 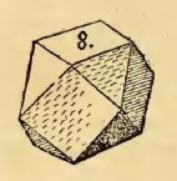A lo largo de este artículo prestaremos nuestra atención al cuboctaedro, formado por ocho caras triangulares y seis cuadradas, dado que se genera fácilmente a partir de un cubo y está presente en múltiples manifestaciones artísticas y cotidianas. Cuboctaedro3 Estas razones justifican la introducción del antedicho poliedro arquimediano en las aulas no universitarias para poner de manifiesto la relación entre las Matemáticas, el Arte y el mundo en que vivimos. 2. Algunos textos y dibujos clásicos [1] Luca Pacioli describe el cuboctaedro en los siguientes términos. El hexaedro despuntado o absciso plano, igualmente sólido o hueco, tiene veinticuatro líneas que originan en él cuarenta y ocho ángulos superficiales, veinticuatro de los cuales son rectos y los demás agudos; tiene doce ángulos sólidos y está contenido por catorce superficies o bases, seis de las cuales son cuadradas y ocho triangulares (…). Y este cuerpo se origina del cubo mediante el corte uniforme en la mitad de sus lados, como demuestra de modo evidente su propia forma material. [De Divina Proportione (1509), cap. XLIX] Luca Pacioli (ca. 1445 – 1517) Leonardo da Vinci (1452 – 1519) Esta descripción se ilustra con dos dibujos de Leonardo da Vinci. Cuboctaedro Esqueleto4 del cuboctaedro [2] Por su parte, el alemán Alberto Durero, en su Underweysung der Messung, mit dem Zirckel und Richtscheyt (1525), ofrece un dibujo en el que se detalla el desarrollo del exacedron abscisus. Alberto Durero (1471 – 1528) Desarrollo del cuboctaedro [3] El holandés Simon Stevin también muestra el desarrollo del poliedro 5 en sus Problematum geometricorum (1583). Simon Stevin (1548 – 1620) Desarrollo del cuboctaedro [4] Juan de Arfe y Villafañe, natural de León, orfebre y autor de la Custodia de la Catedral de Sevilla, en De varia commensuracion para la Esculptura, y Architectura (1585) dibuja el arquimediano y su desarrollo. Juan de Arfe y Villafañe. Dibujos y desarrollo del cuboctaedro 3. El cuboctaedro: ficha técnica El cuboctaedro se obtiene truncando los vértices de un cubo a una distancia igual a  la mitad de la longitud de su arista. Tiene catorce caras (C = 14), doce vértices (V = 12), y veinticuatro aristas (A = 24). Como cualquier poliedro convexo cumple la fórmula de Euler C + V = A + 2. Si 2a es la longitud de la arista del cubo generador, entonces a√2 es la longitud de la arista del hexaedro despuntado. Su volumen V viene dado por la expresión: V = Vc - 8Vp siendo Vc el volumen del cubo generador y Vp el volumen de cada una de las pirámides cortadas. Entonces: Su área A viene dada por: 4. El exacedron abscisus en el dibujo y la pintura 4.1. Un grabado germano El grabador alemán Wenzel Jamnitzer en su Perspectiva Corporum Regularium (1568), nos ofrece una bellísima reproducción del poliedro . Wenzel Jamnitzer (1508 – 1585) Cuboctaedro 4.2. Los dibujos coloreados de Lorenz Stoer (1537 – 1621) A finales del siglo XX se descubrió una carpeta con dibujos coloreados del  alemán Lorenz Stoer (Geometria et Perspectiva: Corpora regulata et irregulata) que se conserva en la Biblioteca de la Universidad de Múnich. Ofrecemos dos de ellos en los que el arquimediano convive con otros cuerpos geométricos (sólidos platónicos, poliedros arquimedianos, poliedros estrellados   y cuerpos redondos). 4.3. Sueño arquimediano En el siguiente dibujo, hace ya unos años, diseñados una composición imposible en la que intervienen diversos poliedros arquimedianos. Vicente Meavilla. Sueño arquimediano (2005) Dejamos que el lector descubra la presencia del cuboctaedro. 4.4. Un cuadro de David Woodcock El artista y profesor británico David Woodcock (1952) dedica una de sus pinturas al hexaedro despuntado. David Woodcock. Cuboctahedron 11,5'' x 11,5'' 4.5. Pasión por el cuboctaedro El norteamericano John Arden Hiigli (1943 – 2017) consagró buena parte de su producción artística al exacedron abscisus. Hemos seleccionado el siguiente grupo de poliedros . 5. El arquimediano  y la marquetería Fray Giovanni de Verona (1433 – 1515), monje y artista italiano, fue el autor de diversas taraceas repartidas por la península italiana. En la Iglesia de Santa María in Organo (Verona) se encuentra una en la que, mirando desde arriba hacia abajo aparecen el exacedron elevatus vacuus6, el cuboctaedroy el duodecedron abscisus elevatus vacuus7. 6. Esculturas hexaédricas despuntadas El artesano carpintero Miguel Ángel Martín es autor de unas bellas esculturas en madera consagradas a los poliedros. En la figura adjunta reproducimos una dedicada al exacedron abscisus. Miguel Ángel Martín. Cuboctaedro Por otro lado, el escultor norteamericano (nacido en Seúl) Laird Hovland también rinde homenaje al poliedro en algunas de sus obras. Laird Hovland 7. Dados arquimedianos El cuboctaedro también forma parte de la nómina de dados poliédricos. Sirvan como ejemplo los dos siguientes cuyas aristas son curvilíneas. 8. Rompecabezas cuboctaédricos Entre los parientes del cubo de Rubik encontramos un puzle en forma de hexaedro despuntado. 9. Cristales La Madre Tierra también es capaz de producir bellísimos reproducciones cristalinas del exacedron abscisus. Cristal cuboctaédrico de galena. Cortesía de Fabre Minerals 10. Consideraciones didácticas En los parágrafos precedentes hemos contemplado un poliedro arquimediano, el cuboctaedro, desde distintos puntos de vista: el geométrico, el artístico, el cotidiano y el geológico. Así, hemos presentado algunos documentos históricos concernientes al exacedron abscisus; hemos efectuado algunos cálculos matemáticos; hemos ofrecido ejemplos concretos de la presencia del poliedro en grabados, pinturas, taraceas y esculturas; hemos mostrado objetos cotidianos (dados y rompecabezas) con formas cuboctaédricas y, por último, hemos admirado un bello cristal con la apariencia de hexaedro despuntado. Por consiguiente, hablando desde una óptica didáctica, podemos decir que en este artículo hemos propuesto un material que, estructurado de forma conveniente, puede ser útil al profesorado de los niveles no universitarios a la hora de diseñar actividades de enseñanza y aprendizaje que pueden involucrar a los departamentos de Matemáticas, Geografía e Historia y Ciencias Naturales.   Referencias bibliográficas ARFE y VILLAFAÑE, J. (1585). De varia commensuracion para la Esculptura, y Architectura. Sevilla: Andrea Pescioni y Iuan de Leon. DURERO, A. (1538)  Underweysung der Messung, mit dem Zirckel und Richtscheyt. Nürnberg. JAMNITZER, W. (1568). Perspectiva Corporum Regularium. Nuremberg: Gotlicher Hulff. KEPLER, J. (1619). Harmonices Mundi Libri V. Lincii Austriae: Sumptibus Godofredi Tampachii. MEAVILLA SEGUÍ, V. (2007). Las matemáticas del arte. Inspiración ma(r)temática. Córdoba: Editorial Almuzara, S. L. PACIOLI, L. (1991). La divina proporción (Introducción de Antonio M. González. Traducción de Juan Calatrava). Madrid: Ediciones Akal, S. A. STEVIN, S. (1583). Problematum geometricorum. Antwerpen: Johannes Bellerus. VERA, F. (1970). Científicos griegos (dos volúmenes). Madrid: Aguilar, S. A. de Ediciones. Referencias online David Woodcock Fabre Minerals John Arden Hiigli Laird Hovland Miguel Ángel Martín Vicente Meavilla Seguí 1 En honor al científico griego Arquímedes (s. III a. C.). 2 Pappus describe los trece poliedros siguientes: tetraedro truncado, cuboctaedro, octaedro truncado, cubo truncado, rombicuboctaedro, cuboctaedro truncado, icosidodecaedro, icosaedro truncado, dodecaedro truncado, cubo achatado, rombicosidodecaedro, icosidodecaedro truncado, y dodecaedro achatado. En esta lista no aparecen los prismas de Arquímedes, poliedros semirregulares cuyas bases son dos polígonos regulares del mismo tipo y cuyas caras laterales son cuadrados, y los antiprismas de Arquímedes o prismatoides regulares, poliedros arquimedianos cuyas bases son dos polígonos regulares del mismo tipo y cuyas caras laterales son triángulos equiláteros. 3 Ilustración contenida en el libro Harmonices mundi (1619. Lib.II, p. 62) de Johannes Kepler (1571 – 1630). 4 Estructura formada por las aristas de un poliedro. 5 El símbolo significa que de las catorce caras del poliedro, ocho son triángulos equiláteros y seis son cuadrados. 6 Poliedro estrellado formado por seis pirámides de base cuadrada, cuyas caras laterales son triángulos equiláteros, que se acoplan exactamente a las seis caras de un cubo. 7 El duodecedron abscisus elevatus vacuus [= icosidodecaedro estrellado] es un poliedro estrellado obtenido a partir de un icosidodecaedro acoplando a sus veinte caras triangulares y a sus doce caras pentagonales las correspondientes pirámides triangulares (cuyas caras laterales son triángulos equiláteros) y pentagonales (cuyas caras laterales son triángulos equiláteros).

Jueves, 02 de Julio de 2020 | Imprimir | PDF |  Correo electrónico