461. La ley Benford: ¿Por qué hay más números que comienzan por uno que por otro dígito?

ABC, 13 de Abril de 2020 CIENCIA - El ABCdario de las matemáticas Víctor M. Manero

Lunes, 13 de Abril de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

462. 150. Sugerencias para un encierro (y para después)

En este periodo singular que nos ha tocado vivir, os presento algunas propuestas para poder disfrutar desde casa. Destaco el recuerdo al grandísimo talento de Emmy Noether, y para acabar el avance de una nueva publicación sobre los que más nos gusta: las matemáticas y el cine. Tras dos semanas y pico de confinamiento domiciliario, seguramente tocaba rebuscar alguna de las muchas películas de catástrofes con las que machacarnos un poco más, pero me ha parecido que no era adecuado ni me apetecía demasiado (aunque al final alguna se menciona), de modo que voy a dedicar la reseña de este mes a enumerar algunas novedades respecto a reseñas anteriores, y adelantaros alguna otra aún por aparecer. Y de paso indicaros donde se pueden ver para amenizar matemáticamente un poco los últimos días (esperemos) de enclaustramiento. El mes pasado traíamos a la sección el microespacio Loco de ReMates, en donde nuestro compañero Enrique Hernando nos recuerda e ilustra sobre las matemáticas de nuestra vida cotidiana. Publicada la reseña, un par de días después, se emitía un nuevo episodio, Mates en la catedral de Burgos, en la que nos muestra algunos aspectos matemáticos de este singular y bello edificio gótico. Sólo algunos porque en 6 minutos tampoco nos puede contar todo, pero puede servir como introducción para los que nunca hayan pensado en admirar la arquitectura desde el punto de vista de las matemáticas y como recordatorio (y deleite, porque siempre es agradable pasear entre sus muros, y más cuando no podemos físicamente) para los que sepan más de ello. El presentador nos ilustra sobre el octógono, el polígono que más predomina a simple vista en la seo, cómo sirve de transición entre el cuadrado y el círculo (y mediante las pechinas alcanzamos en tres dimensiones el círculo, identificado por los antiguos como el cielo como símbolo de perfección; esto sirve para introducir la denominada matemática sagrada y su simbología). Asimismo, nos enseña la diferencia entre un polígono estrellado y una estrella, cómo se forman, hablándonos entre medias del rectángulo de plata y su presencia también en todos los octógonos. De obligado visionado. Y no menos imprescindible son los nuevos episodios de Revoluciones Matemáticas (en el enlace la reseña que ya hicimos hace unos meses), su segunda temporada con tres nuevos episodios a añadir a los cuatro de la primera. En esta ocasión, para ilustrar tres nuevas revoluciones se han elegido otros tantos relevantes personajes, dos mujeres y un hombre. Empezando en orden inverso (ya veréis porqué), el tercer episodio se dedica a la primera programadora de la Historia, que fue una mujer, Ada Lovelace (1815 – 1852), que siempre se la recuerda por ser hija de Lord Byron, a pesar de que su relación con él fue prácticamente inexistente. Junto a Charles Babbage es sin duda el primer ser humano que idea un algoritmo tal y como hoy lo conocemos, puesto en práctica a través de tarjetas perforadas (las órdenes para la máquina), tal y como funcionaban los telares del momento. Pero es que su concepción no se quedó en ejecutar cálculos matemáticos (una simple calculadora), sino que fue capaz de ver que mediante esos algoritmos podría ejecutarse y componerse música, desarrollar ideas matemáticas, jugar, etc. Toda una visionaria que, como en muchos otros casos, no ha sido reconocida su gran valía hasta bien entrado el siglo XX. Sin duda, una gran revolución, y en este caso, no sólo matemática, sino social, cultural, empresarial, … si es que toda nuestra vida actual gira en torno a la programación (vuelvo a recordar el encierro en el que estamos, y cómo sería sin estos aparatitos). El segundo episodio se dedica a otra excelencia, ésta sí, reconocida universalmente, el gran Leonhard Euler (1707 – 1783). Necesitaríamos seguramente días para glosar toda su grandeza y trabajo (no en vano es seguramente el científico más prolífico de la Historia, habiendo dejado escritos más de 70 volúmenes), de modo que resumirlo a dos minutos es difícil, aunque desde luego los hitos elegidos son muy acertados: precursor de nuevos campos cuyo desarrollo han podido aplicarse a muchas otras ramas del saber, además de ser útiles y utilizados hoy en día, el guion se decide por hablarnos de su famosa relación sobre las caras, vértices y aristas de cualquier poliedro convexo. El primer episodio se ha dedicado a Emmy Noether (1882 – 1935), una de las fundadoras del álgebra abstracta. Desgraciadamente, a pesar de que todos quedaban abrumados por la profundidad de sus trabajos, tuvo que luchar durante toda su vida contra la intolerancia académica y social de su entorno solo por el hecho de ser una mujer. Cuando lo logró, los nazis llegaron al poder en el gobierno alemán, y tuvo que emigrar a los Estados Unidos por el hecho de ser judía. Pero continuó su incansable trabajo, siendo la primera mujer en dar una conferencia en el mayor evento matemático que existe, el ICM, en 1932. Sus descubrimientos pusieron en claro desde el punto de vista matemático la teoría de la relatividad de Einstein, al descubrir una intrínseca relación entre la simetría y la conservación de la energía. El teorema por el que se la conoce, es sin duda, uno de los hitos más importantes que haya podido imaginar el ser humano, tanto como el principio de Arquímedes, la ley de la gravedad, o el resto de leyes de Newton: Siempre que haya una invariancia de un sistema físico, entonces existe una ley de conservación. Dejar este capítulo para el final tiene su porqué. Cuando se supo que íbamos a estar varios días confinados en casa, hice acopio de varios capítulos de apuntes de la asignatura (ejercicios resueltos básicamente) para dar clase telemáticamente, me traje también entregas de los alumnos que aún no había corregido, y unos cuantos libros del departamento. Entre ellos, El árbol de Emmy, de Eduardo Sáenz de Cabezón, Plataforma Editorial, Barcelona, 2019. Comencé a leerlo sin demasiada convicción (me pasa con todos los libros; tardo en entrar a ellos, en hacerlos míos, en familiarizarme con el estilo, los personajes, etc. En algunos casos, si no me transmiten algo, los dejo, aunque sea a la mitad; adelanto: éste lo he terminado), porque inicialmente no parecía lo que me había imaginado. Pronto descubres (no hay que ser un lince para verlo rápidamente) que, a pesar de su apariencia de librito breve (165 páginas), en realidad atesora distintos aspectos interesantes. El texto se dispone en forma de tríptico: reflexiones bajo el hilo conductor de algunos sucesos relevantes en la vida de Emmy Noether, paralelismo con la biografía de otras mujeres matemáticas célebres y una selección de hilos de Twitter a cargo de Enrique Borja, Clara Grima y Alberto Márquez, los tres chanchitos. Entre las reflexiones, las hay sobre la vida, sobre las matemáticas, sobre la sociedad, por supuesto sobre la protagonista Emmy Noether, sobre las injusticias que se han cebado con las personas por sexo, raza, cultura, etc. Un libro para reflexionar y, por tanto, con un poso amargo. El poso amargo que también percibimos en este encierro, porque irremediablemente hay muchas similitudes (lo siento, pero es así): intolerancia, egoísmo (lo prioritario es la economía: el mismo que hace pocos meses sacrificaba recursos sanitarios en favor de la privatización de amiguetes que ahora han desaparecido; y no es cuestión de distintas visiones políticas, no: es pura especulación, negocio y provecho propio), … Es cierto que se han cometido equivocaciones, es muy difícil acertar con un improvisto de esta magnitud. Pero bien es cierto que si los recursos hubieran estado donde debían, las cosas no hubieran sido tan lamentables. En todo caso es momento de ir juntos; la repugnante crítica partidista sólo pone de manifiesto la mediocridad de quien la efectúa. Pero no es algo nuevo, desgraciadamente. Hace unos días volví a ver El último hombre… vivo (The Omega Man, Boris Sagal, EE. UU., 1971), segunda adaptación cinematográfica de la novela Soy leyenda (1954) de Richard Matheson. En ella, un médico ha sobrevivido y conseguido una vacuna contra un virus que ha transformado a toda la humanidad en seres albinos fotosensibles. Éstos culpabilizan de su situación a la ciencia, a la tecnología, a los científicos, e intentan establecer un nuevo “orden” en el que nadie se desmande de “sus ideas”. ¿Ciencia Ficción? Enlazo de nuevo con el libro de Eduardo en donde casi al final aparece la referencia a la célebre quema pública de libros en Alemania en 1933 (marzo, por cierto; Cave Idibus Martiis, para dar un poco de vidilla a los conspiranoicos, si se molestan en buscar la traducción, claro), también recreada en otra célebre película Farenheit 451 (François Truffaut, Reino Unido, 1966) sobre el homónimo relato de Ray Bradbury, asunto que parece resurgir en algunos cuando no se actúa del único modo posible, el suyo. Y eso que no es el momento, dicen. Además, el libro me ha hecho releer en paralelo Emmy Noether, matemática ideal, de David Blanco Laserna, publicado por Nivola en 2005, y me ha descubierto algunas mujeres matemáticas que no conocía como Charlotte Scott, Olga Taussky o Ingrid Daubechies. Y no puedo dejar de citar una frase que me ha gustado especialmente, sobre la propia esencia de las matemáticas: “La matemática es abstracta y general, en ello radica su belleza, su poder y su dificultad. Conforme uno se adentra en las matemáticas, encuentra que al principio todo son números, relaciones entre cantidades y medidas concretas, luego resulta que todo son letras, relaciones entre números, y más adelante descubre que todo son diagramas y flechas, relaciones entre conceptos, relaciones entre relaciones. Siempre ha sido así, pero no siempre lo ha sido de igual forma”. Recientemente hemos asistido a la producción de varias películas sobre matemáticos relevantes. Emmy seguro que se merece una que la de a conocer al público en general. De momento tenemos algunos documentales. Referencio un par de ellos, para que, si ahora no disponéis de los libros comentados, al menos podáis aproximaros un poco al genio y la valía de esta mujer. El primero es Noether's Theorem and The Symmetries of Reality, episodio 24 de la cuarta  temporada  de la serie documental PBS Space Time presentado y dirigido por el astrofísico australiano Matthew O'Dowd. Aunque está en inglés, hay una pestañita en la parte inferior desde la que podéis abrir la transcripción al castellano, que está bastante bien hecha (para variar). La serie es de Física, pero en esta ocasión describe bastante bien las ideas matemáticas (a nivel divulgativo) que subyacen en los resultados de Noether. El presentador empieza comentándonos que “Las leyes de conservación se cuentan entre las herramientas más importantes de la Física. Son consideradas las bases más fundamentales que pueden ser establecidas. Y, sin embargo, no son ciertas, o, por lo menos, sólo son ciertas a veces. Estas leyes son derivadas de algo mucho más profundo, de un principio más fundamental, el teorema de Noether.” Antes de explicarlo con más detalle, nos pone en antecedentes de cómo estaba la situación. En 1915, publicada la teoría general de la relatividad de Einstein, surgen un montón de nuevas preguntas de muy difícil respuesta, al menos así lo veían los científicos. La idea del público en general sobre los trabajos de Einstein es que eran incomprensibles, incluso a día de hoy, uno sopla cuando oye hablar de la teoría de la relatividad o de su autor. No es que sea así. Básicamente, esa visión se deriva del hecho del shock que produjo por las múltiples contradicciones aparentes que suscitaba con la mecánica clásica, y de su complejidad. Entre esas contradicciones se encontraba el hecho de que con esa teoría la energía no se conserva siempre. En el documental se da un ejemplo, más o menos entendible de porqué pasa esto: el efecto Doppler, el desplazamiento al rojo del espectro de las galaxias. El presentador lo explica muy bien: “A medida que el universo se expande, la luz que viaja a través de ese espacio en expansión "se estira". Su longitud de onda aumenta, y por lo tanto cae la energía de cada fotón. ¿Adónde va la energía perdida por los fotones desplazados al rojo?” Dos matemáticos, David Hilbert y Felix Klein, trabajaron en la concepción matemática de las teorías de Einstein, tratando de encontrar un marco que diera claridad al asunto, que explicara dicha teoría. Y la clave se logró encontrar gracias a Emmy Noether, una mujer, por mucho que a algunos les fastidiara. Ella descubrió por qué la ley de conservación de la energía no era válida en relatividad general, y lo hizo gracias a la idea de simetría. Tuvo la portentosa genialidad de relacionar dos conceptos que aparentemente no tienen nada que ver, uno geométrico (la simetría) y otro físico (la conservación de la energía). Pocas veces en la historia se ha logrado este tipo de correspondencias (pero sí tenemos otros ejemplos: relacionar la búsqueda de la ecuación de la recta tangente a una función en un punto (algo totalmente geométrico) con la velocidad instantánea de un móvil  (de nuevo algo físico); o relacionar esa misma idea de variación con el cálculo del área encerrada bajo una función (teorema fundamental del cálculo que armoniza derivada con integral); o más recientemente, la relación entre curvas elípticas con las formas modulares que además es clave en la demostración de la no existencia de soluciones para una ecuación algebraica (último teorema de Fermat y lema de Taniyama-Shimura). Encontrar estos nexos de unión entre conceptos tan radicalmente diferentes sólo ha estado en la historia al alcance de verdaderos genios (por supuesto hay más; sólo he recordado los que me viene a la cabeza “a bote pronto”). Es realmente impresionante cuando te encuentras algo así. Y el poso amargo del que hablaba antes, seguido de una rabia infinita, aparece cuando descubres lo mediocre (como hablaba también antes) de los coetáneos ante los que sólo importaba el hecho de haber sido una mujer la que lo descubriera. En fin, continúen viendo el documental que, aunque desde el punto de vista de la puesta en escena es bastante elemental, afortunadamente, y conscientes de ello, sus responsables han puesto el máximo celo en relatarlo de un modo ameno, conciso, pero muy ilustrativo e interesante. Un segundo documental sobre Emmy Noether, más de andar por casa, es el francés Noether et les lois de la physique, dirigido y presentado por Bruce Benamran en 2016 (episodio 8 de la segunda temporada de la serie de divulgación E-penser). De nuevo tienen la transcripción en castellano disponible. En la imagen, el guionista y presentador con su evocadora camiseta de Ghostbusters (Los cazafantasmas, recuerden). Finalmente, el avance de un nuevo libro de nuestro compañero y amigo José María Sorando: Matemáticas de Cine. Aún no lo he podido leer (nos ha pillado en el encierro su distribución), pero conociendo al autor y sus anteriores textos, jugamos sobre seguro: será una delicia. La descripción que nos hace el propio José María en la página oficial de la editorial puede darnos una pista de por dónde van esta vez los tiros:  ejemplos distintos a los ya consignados en los libros anteriores, con un recorrido por la presencia matemática en los diversos elementos de una película: escenarios, imágenes, personajes, guion, diálogos, títulos y mirada del espectador. ¡¡Para no perdérselo!! Como siempre cualquier comentario, aportación, crítica o simplemente saludo, me lo podéis hacer llegar a mi correo electrónico o a las páginas de Facebook o Twitter. Alfonso Jesús Población Sáez

Jueves, 02 de Abril de 2020 | Imprimir | PDF |  Correo electrónico

463. 181. (Abril 2020) Optograma

Muchos juegos de magia basados en principios matemáticos han evolucionado a lo largo del tiempo para convertirse en clásicos, se han adaptado a diferentes niveles y diversos tipos de público y han terminado por convertirse en elementos indispensables del repertorio de magos profesionales. Y, como ya hemos comprobado en multitud de ocasiones, no siempre se trata de principios relacionados con operaciones aritméticas o propiedades numéricas curiosas. Algunas veces interviene la geometría y, en el caso que hoy nos ocupa, las simetrías de figuras geométricas. Por supuesto, el ingenio y creatividad de los primeros que descubrieron las posibilidades mágicas de estas propiedades son los principales ingredientes que convierten la recreación en magia. Vamos a denominar "Principio de la brújula cuadrada" a la propiedad que explota las simetrías de un cuadrado para conseguir algunos efectos que, con una dosis adecuada de disimulo, llegan a ser sorprendentes. Hagamos en primer lugar un recorrido por la historia y desarrollo mágico de este principio: esto permitirá apreciar cómo ha evolucionado y qué detalles creativos consiguen aumentar la sensación mágica que oculta el principio. En 1945, Val Evans comercializó el juego titulado "Optogramma" (figura 1). A juzgar por el número de gente que lo realizaba, parece que el juego tuvo un éxito considerable y no pasó mucho tiempo hasta que aparecieron nuevas versiones y modificaciones: la casa Abbott vendía una versión pirata llamada "Wizzy Dizzy lines", Harry Blackstone hacía el juego con galletitas saladas que tenían líneas dibujadas en ellas pero también las tenía impresas en sus tarjetas de visita. Impartiendo un poco de justicia, Lloyd Jones compró a Val Evans los derechos del juego y publicó su versión en la revista The Bat en abril de 1948. Por otra parte, en 1947, William Lane (Willane) publicó su versión titulada "La brújula china" en el libro "Willane's Wizardry" (figura 2). Un poco más tarde, el juego original fue modificado por Milbourne Christopher (publicado en la revista Hugard’s magic monthly, 1951) con una presentación en forma de una señal de tráfico (figura 3). Otra versión popular fue la de Earle Oakes quien puso a su versión el título "La brújula maestra" (figura 4). Figura 1: Juego original de Val Evans, 1945 Figura 2: Brújula china de Willane, 1947 Figura 3: Señal de tráfico engañosa de Milbourne Christopher, 1951 Figura 4: Folleto con la rutina de Earle Oakes Como se puede comprobar, cada versión utiliza un tipo diferente de figura geométrica, con el fin de aprovechar las simetrías de cada una. La que me parece más apropiada, aunque no sea la que oculta mejor el principio en que se basa, es la del octógono regular pues las líneas que unen vértices opuestos corresponden a los ejes de simetría de un cuadrado. La idea mágica que surgió de este principio consiste en hacer un dibujo en cada cara y observar cómo cambia su orientación según el eje de simetría utilizado. Si tienes buena imaginación, seguro que puedes crear una entretenida historia con la que sustentar los movimientos que describimos a continuación. Recorta un octógono regular y dibuja una flecha azul en la cara delantera y una flecha roja en la cara trasera, de modo que estén orientadas como en la figura (azul apuntando al norte y roja apuntando al este): Muestra la figura con la flecha roja hacia delante y los dedos pulgar y medio en los vértices A y B. Gira la figura con la otra mano para mostrar la cara posterior y explica que, CUANDO LA FLECHA ROJA SEÑALA HACIA EL ESTE, LA FLECHA AZUL SEÑALA HACIA EL NORTE. Puedes girar varias veces el disco mientras recalcas esta situación. Coloca la figura con la flecha roja hacia delante pero sujétala con los dedos pulgar y medio en los vértices C y D. Gira la figura con la otra mano y muestra que, sorprendentemente, la flecha azul señala también hacia el este. Gira varias veces para enfatizar que, CUANDO LA FLECHA ROJA SEÑALA HACIA EL ESTE, LA FLECHA AZUL SEÑALA HACIA EL ESTE. En el momento en que la flecha roja está a la vista, cambia el agarre de los dedos y sujétalos por los vértices E y F. Gira varias veces la figura con la otra mano mientras recuerdas que, CUANDO LA FLECHA ROJA SEÑALA HACIA EL ESTE, LA FLECHA AZUL SEÑALA HACIA EL SUR. Prueba por última vez las propiedades cambiantes de la brújula. Sujétala por los vértices G y H estando la flecha roja a la vista. Al hacer girar el disco sucesivas veces, repite la propiedad, CUANDO LA FLECHA ROJA SEÑALA HACIA EL ESTE, LA FLECHA AZUL SEÑALA HACIA EL OESTE. Si has conseguido que los cambios en el agarre del disco pasen inadvertidos, podrás convencer a tu público de que tu brújula tiene propiedades magnéticas, quizá debido a la fuerza de atracción terrestre. Como habrás podido comprobar, los ejes de simetría del cuadrado -horizontal, vertical y ambas diagonales- hacen que la flecha cambie de orientación sin que la figura cambie de forma. Comentarios finales: Si tu imaginación no es tan fértil como para recrear el juego con alguna situación real, quizá quieras inspirarte en la versión comercializada por Vernet bajo el título WRONG WAY, donde las flechas representan señales de tráfico. Steve Beam publicó un interesante juego basado en este principio en la primera página del primer volumen de la revista The Trapdoor (1983), bajo el título "Upside down". Allí afirma que el juego está basado en el manejo de Bev Bergeron sobre la versión de Milbourne Christopher. Da la impresión de ser un juego al que tenía mucho aprecio para concederle el honor de ser el primero de una colección compuesta por 70 volúmenes publicados entre 1983 y 1998. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Jueves, 02 de Abril de 2020 | Imprimir | PDF |  Correo electrónico

464. 62. (Abril 2020) La prudencia es matemática

(Prudencia. Traité sur les vertus cardinales, Lyon, 1510. François Demoulins) Las artes liberales eran siete, como las virtudes y como los astros. En la Alta Edad Media y en los inicios del Renacimiento era corriente representar las virtudes y las artes liberales conjuntamente. Una persona sabia también era virtuosa. Así vemos rodeado de las artes a San Agustín, Santo Tomás, o a distintos personajes nobles o eclesiásticos. Muy pronto se produce una fusión: las virtudes se empiezan a representar con instrumentos matemáticos. El caso más notable es el de la prudencia que se asocia a la geometría o a la astronomía y se la muestra con un compás o una esfera armilar. Como ejemplo tomamos los bellos miniado del Traité sur les vertus cardinales, Lyon, 1510 de François Demoulins que está firmado en Lyon. En una de las imágenes aparece con un gran compás y en otra con la esfera celeste. (Prudencia. Traité sur les vertus cardinales, Lyon, 1510. François Demoulins) Prudencia matemática en la Santa Croce de Florencia Al fondo del transepto derecho de la Iglesia de la Santa Cruz en Florencia se encuentra la Capilla Baroncelli, con frescos de Taddeo Gaddi del siglo XIV sobre la Vida de la Virgen. Gaddi ejecuta una obra deslumbrante inspirada en la Capilla de los Scrovegni del Giotto, su maestro. La Iglesia de la Santa Cruz viene a ser un panteón de hombres ilustres. Allí se encuentran los mausoleos de Fermi, Marconi, Galileo o Miguel Ángel entre otros. Las alegorías de los dos últimos tienen interés matemático. Gaddi muestra la temprana asociación de las virtudes con las artes: la Prudencia en el medallón del techo aparece con la esfera armilar, el atributo de la Astronomía. La representación de las siete virtudes y las siete artes juntas era habitual, como complemento del bien y el conocimiento, sin embargo, aquí Gaddi dio un paso más y realiza una fusión que proliferará en obras posteriores. (Taddeo Gaddi  Prudencia. Iglesia de la Santa Cruz. Florencia) La Prudencia de la Casa Minerbi de Ferrara La Casa Minerbi es un palacio del siglo XIV con un significativo ciclo de frescos de Stefano da Ferrara en el Salón con las alegorías de las virtudes, los vicios y los meses. La representación de la prudencia se hace con un compás que mide el globo terráqueo con escenas de la vida cotidiana. En otra sala el ciclo de las virtudes se complementa con otro más astronómico, donde se representan los ciclos de los meses y las estaciones. (Stefano de Ferrara.  Prudencia. Casa Minerbi. Ferrra) La Prudencia en la tumba de Francisco II de Bretaña en Nantes La Catedral de Nantes aloja el mausoleo marmóreo del que fue el último duque de Bretaña antes de su incorporación a la corona de Francia. La obra escultórica de Michel Colombe (1507) fue encargada por su hija Ana de Bretaña, que estuvo casada sucesivamente con dos reyes franceses. El conjunto es considerado como la obra maestra de la escultura renacentista en Francia. Francisco II y Margarita de Foix yacen encima de su sarcófago con un lebrel y un león a sus pies. Los laterales tienen hornacinas con apóstoles, santos y reyes. En las esquina se representaron alegóricamente las cuatro virtudes cardinales. Nos fijamos en la Alegoría de la Prudencia por usar el símbolo geométrico del compás en la mano derecha. Midiendo antes de actuar se toman las decisiones acertadas. La representación se completa con el espejo en la mano izquierda (mirarse desde fuera para actuar con objetividad) y una figura bifronte. La prudente joven piensa como el viejo sensato que se ve en la parte trasera. (Michel Colombe.  Prudencia. Catedral de Nantes) La Prudencia de Schaffner en Kassel El Palacio Wilhelmshöhe de Kassel alberga la Galería de Pintura de los Maestros Antiguos del Museo Estatal de Hesse. La rica colección conserva una pintura sobre tablero de mesa realizada por Martín Schaffner en 1533 que es todo un programa iconográfico de la visión medieval del mundo que se extiende por el Renacimiento. Toda una cosmología sobre planetas, metales y ciencias. En el centro de la mesa una luz (divina) se rodea de los siete astros conocidos que extenderán su efecto sobre los asuntos terrestres. Cada astro se asocia a cada una de las siete artes liberales: la Aritmética se vincula con Marte, la Geometría con Júpiter y la Astronomía con Saturno. (Martín Schaffner.  Mesa de las Artes, Virtudes, Planetas y Metales. Kassel) Ya Dante, en el Convivio, había vinculado las siete artes con los siete cielos. Tanto la Geometría como la Astronomía coinciden pero no la Aritmética. Para Dante, la Aritmética es solar y lo razona: El cielo del Sol se puede comparar a la Aritmética por dos propiedades: una es que por su luz todas las estrellas se muestran; la otra es que el ojo no lo puede mirar. Y estas dos propiedades están en la Aritmética: porque por su luz se iluminan todas las ciencias, ya que sus objetos todos se consideran en razón de algún número, y al considerarlos siempre se procede según algún número. Martin Schaffner (1478-1548) fue pintor y medallista, de forma que su obra denota una gran precisión en los detalles. La Geometría es una de las obras más cuidadosas que se han comentado: el compás mide sobre una regla marcada para continuar el sistemático trabajo de cálculo. El sistema del mundo estaba todavía centrado en la Tierra y será precisamente Ptolomeo el sabio que aparece en una de las esquinas de la tabla para completar, por simetría, a ocho las figuras representadas. La representación de la Astronomía es también la de la Prudencia. La serpiente que acecha y el espejo son los símbolos inequívocos de la prudencia y la esfera armilar es la extensión de la virtud a las artes liberales. (Martín Schaffner.  Prudencia/Astronomía/Saturno. Kassel) La Prudencia en el Museo del Renacimiento de Ecouen (París) El Museo del Renacimiento se ha instalado en el Castillo de Ecouen, al norte de París. Los grandes óvalos de cerámica vidriada de Limoges fueron ejecutados por Pierre Courteys sobre 1559. Se conservan nueve placas, seis dioses y héroes, y tres virtudes. Una vez más la Alegoría de la Prudencia se representa con los instrumentos de la Geometría, en este caso reposando a sus pies: una regla y un compás. Las placas reproducen los diseños manieristas de Rosso Florentino, uno de los artistas desplazados a Fontainebleau. La serie encargada sería mayor (quizá con las artes liberales como era normal en los studiolos) pero debió interrumpirse con la muerte de Enrique II en 1559. (Pierre Courteys.  Prudencia. Castillo de Ecouen) Las placas son deslumbrantes y muestran como la cultura de la época ensambla los temas paganos y cristianos en coherente unidad. La belleza es dominante y no olvida la matemática. La “Geometría” de Lorenzo Sabatini en Turín El manierismo renueva la representación de las alegorías con gran libertad y con mensajes que no son fáciles de descifrar. El pintor boloñés Lorenzo Sabatini fue discípulo de Vasari y del Parmigianino, uno de los artistas más inquietos de su época. La pintura atribuida a Sabatini que se puede visitar en la Galería Sabuada de Turín, hoy titulada Alegoría de la Geometría (circa 1560), ha pasado por distintas autorías e interpretaciones. El compás y la esfera celeste podrían hacerla pasar tanto por Urania, Astronomía o Geometría, pero el espejo suele ser acompañante inequívoco de la Prudencia, que también aparece muchas veces con compás aunque no tan desnuda. (Lorenzo Sabatini.  Prudencia/Geometría. Turín) Prudencia barroca en el Palacio Médici-Riccardi de Florencia La representación de las virtudes con las artes matemáticas que se inicia en la Edad Media se mantiene hasta el Barroco. En el Palacio Médici-Riccardi de Florencia veremos un gran fresco de Luca Giordano donde la virtud cardinal se rodea de matemáticos en plena actividad. La Prudencia aparece en el fresco de Luca Giordano de la Galería de los Espejos: La apoteosis de la dinastía de los Médici. El espejo, la serpiente y el ciervo son tres de sus símbolos habituales, mientras debajo, a su lado, dos sabios estudian y contemplan el cielo, uno con cuadrante astronómico y el otro con un compás y una escuadra. Cuando Giordano sigue a Ribera, los sabios son pobres y están retirados del mundo, pero aquí en plana apoteosis medicea no hay lugar para la crítica barroca a la vanidad humana. (Luca Giordano.  Detalle de la Prudencia. Florencia)

Miércoles, 01 de Abril de 2020 | Imprimir | PDF |  Correo electrónico

465. Matemáticas contra una pandemia

ABC, 30 de Marzo de 2020 CIENCIA - El ABCdario de las matemáticas David Gómez-Ullate Oteiza

Lunes, 30 de Marzo de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

466. En busca del «einstein» perdido por los suelos

ABC, 30 de Marzo de 2020 CIENCIA - El ABCdario de las matemáticas Pedro Alegría

Lunes, 30 de Marzo de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

467. Marzo 2020: Colorea que algo sale

1. Pasatiempos para colorear. Como hemos visto en otras entregas de esta sección, es posible encontrar pasatiempos en revistas y periódicos que se pueden utilizar en el aula de matemáticas, convirtiéndolos en actividades atractivas y motivadoras para el alumnado. A veces, se utiliza ese pasatiempo directamente y en otras ocasiones se puede adaptar al contenido o nivel educativo en que estemos trabajando. Vamos a dedicar estas páginas a uno de esos pasatiempos adaptándolos o creando retos similares para la clase. Hoy vamos a adaptar un pasatiempo infantil muy corriente. Partimos de un recuadro dividido en zonas irregulares, algunas de las cuales tienen alguna señal que las diferencia, normalmente un punto, y el jugador debe colorear las zonas que tienen esa señal. Una vez hecho, aparece una imagen que, inicialmente, estaba escondida entre el cruce de líneas. En la siguiente imagen vemos uno de esos pasatiempos. Esta tomado de la sección Rompecocos que desarrolló Antonio G. de Santiago para el País durante la mitad de los años 2000. Lo tradicional era que en las regiones apareciera un punto, pero en esta versión se le da un sesgo algo más educativo. Figura 1: Pequeño País, 11 de septiembre de 2005 2. Adaptando a nuestras necesidades. Tal como está, el pasatiempo tiene poco interés para aplicarlo al curriculum de matemáticas. Por eso, lo interesante es adaptarlo a nuestras necesidades, de forma que nos permita practicar o repasar contenidos propios de nuestra asignatura. A veces, y según el nivel educativo en que vayamos a trabajar, la adaptación es relativamente fácil. Por ejemplo, el pasatiempo de la figura 1 puede modificarse sustituyendo las letras por números, por ejemplo, las vocales por números pares y las consonantes por impares y pedir que se coloreen los números pares, con lo que tenemos una actividad para repasar los pares e impares. Pero también lo podemos hacer para trabajar con primos y compuestos o cualquier otro aspecto que se nos ocurra. Como además podemos encontrar con relativa facilidad este tipo de pasatiempo en las revistas o secciones infantiles, podemos trabajar distintos conceptos variando la imagen final que debe quedar. Este enfoque de la actividad no es algo nuevo, ha habido varios grupos de didáctica que lo han trabajado en sus materiales. Por ejemplo, el grupo Azarquiel de Madrid ya incluía actividades de este tipo en la colección de fichas que se publicaron alrededor del año 2000 por SM con el nombre de Dos Palabras. En concreto, la profesora Ana García Azcárate incluye la siguiente actividad en su última entrega de la colección de Juegos y pasatiempos en clase de matemáticas. Realiza todas las operaciones del dibujo y descubre porqué Iván está tan satisfecho de su obra de bricolaje. Para eso cuando obtengas: Un resultado negativo y par deberás colorear el lugar de beige. Un resultado negativo e impar, deberás colorear el sitio en azul. Un resultado positivo y par, colorearás el sitio de amarillo. Un resultado positivo e impar, colorea el lugar de naranja. Un resultado igual a cero, deberás colorearlo en marrón. La idea principal es tomar un dibujo puzzle como hemos visto antes y adaptarlo al contenido que queremos. Los que suelo utilizar en clase no necesitan tanto colorido como hemos visto en el anterior, más bien son sólo rayar ls regiones para que aparezca el dibujo escondido. En la siguiente actividad vemos un ejemplo que utilizamos desde hace mucho tiempo en nuestro instituto. Lamento no recordar de donde he sacado el dibujo, aunque me imagino que sería de algunos de los materiales didácticos que se difundieron en la década de los años ochenta o noventa, seguramente de algún grupo de didáctica. El puzzle adjunto esconde una figura. Para descubrirla has de colorear o señalar una serie de regiones. Para saber qué regiones resaltar debes resolver las siguientes ecuaciones. Los valores de las soluciones indican esos lugares que debes sombrear. 3. Creando nuestros propios dibujos. El utilizar siempre los mismos dibujos recogidos de distintos lugares, tiene el problema de que se repiten de un año para el siguiente, por lo que los alumnos repetidores pueden tenerlos ya hechos de antes. Además, algunas veces, el puzzle hecho en el dibujo permite intuir qué es lo que tiene que salir, algo que puede pasar en el dibujo misterioso anterior, donde fijándose un poco, enseguida se puede apreciar el cuchillo que va a aparecer al colorear el dibujo. Por esa razón, comenzamos a modificar el puzzle visual inscrito en la actividad, componiendo nuestras propias imágenes. Inicialmente creamos una serie de cuadros geométricos fáciles de construir, basta utilizar un programa de dibujo, aunque con GeoGebra salen muy precisos. A continuación vemos un ejemplo de actividad de álgebra para 3º de ESO. Calcula los valores numéricos de los polinomios en los puntos que aparecen. Raya o colorea las regiones que contengan los números solución de esos valores numéricos. a) P(x)=2x²-3x-5 en x=4, x= -2 y x= ½ b) Q(x)=x3-3x2+2x+4 en x= -1 y x=2 c) R(x)= en x=2 y x= -2 Una vez practicado en clase este tipo de actividad, no hay ningún problema en utilizarlo en un control, como el siguiente ejemplo. El dibujo que queda al final no tiene que ser necesariamente una figura reconocible, basta con que el profesor sepa a simple vista si las regiones rayadas son las que deben quedar visibles. Resuelve Las siguientes cuestiones y las regiones del dibujo donde estén las soluciones coloréalas. a) Valor numérico del polinomio P(x)=2x3-5x2+3 para x = -2 y x= ½. b) Resuelve la ecuación x·(x+3)=(x-1)·(x+2). c) Resuelve la ecuación Otra forma de crearnos nuestras propias plantillas es copiar, con un poco de adaptación, cualquier imagen que nos encontremos y nos pueda parecer interesante. Como ejemplo, tenemos la siguiente imagen que es muy conocida desde hace años y que se puede encontrar dentro de los documentos de matemáticas recreativas. El reto consiste en encontrar, dentro de ese batiburrillo, una estrella de cinco puntas. Figura 2: Encontrar la estrella de cinco puntas Adaptando esa imagen creamos la siguiente actividad para repasar los números en inglés, aprovechando que nuestro centro es bilingüe desde hace muchos años. 1) Colour the gaps with the following numbers   Thirty – one Twelve Eighty – nine Three hundred and five One hundred and seventy – two Thirteen Eighty Eight hundred and seventeen Eighteen Five hundred and eleven Four hundred and sixty   2) When you have coloured the different regions, write the name of thre numbers left in the pictures without stripes. Si no se quiere complicar el dibujo, creando regiones complicadas, se puede hacer incluso un dibujo más simple formado por una simple matriz de números. Esta idea se encontró en un material colgado en Internet correspondiente a un cuadernillo de pasatiempos de matemáticas para 4º de Primaria. El cuadernillo parece extraído de una publicación más extensa, pero no aparece referencia, por lo que colocaremos la dirección directamente. Dentro del cuadernillo aparecen varias actividades de coloreo. Alguna de ellas utiliza una cuadrícula muy fácil de conseguir, en concreto hemos seleccionado una con ítems de multiplicaciones, pero como tiene varios errores la del cuadernillo, hemos adaptado la idea a la siguiente actividad cambiando el repaso de los productos por operaciones combinadas, aunque simples. Sombrea en el recuadro las casillas con los números resultado de las siguientes operaciones. 3x8 – 6 4 + 2x5 5x(8 – 4) 11x5 – 3 3x7 – 5x2 6 – 2x5 + 7 4 – 5 + 6 8 – 2² + 5 (5 – 2)² – 5 4x3 + 3 1 + 3x4 8x(6 + 4) 8x7 + 4 4x5 – 2x6 9 – 6x4 2 – 8x9 8 – 5x9 – 2 4x(9 – 2) – 5 5 – 2²x7 9x7 + 3 8 – 4x(6 – 2) 5 – 3 – 7x6 Como última posibilidad está el pedir la ayuda de expertos. Desde hace muchos años, el departamento de Matemáticas ha colaborado en diversas actividades junto al de Dibujo y en este caso le pedimos que nos creara un dibujo para tener imágenes que no se pudiesen encontrar en otro lugar. Después de probar distintas opciones, Carmen nos presentó el siguiente dibujo que permitía colorear distintas regiones con colores diferentes para obtener una imagen muy colorista. Figura 3: Imagen para colorear Como existían demasiadas regiones para plantear operaciones, lo que hicimos fue modificar el dibujo, adaptándolo a nuestras necesidades y, al final, nos quedó la siguiente actividad. En la siguiente imagen, raya o colorea las regiones donde aparecen números primos. 4. Resumiendo. Esta es un tipo de actividad fácil de construir y que nos permite adaptar a nuestra situación personal el procedimiento a aplicar. De esa manera, podemos atender al nivel exacto de nuestros alumnos. Depende de lo abstracto que se plantee el dibujo puede dar más o menos pistas sobre lo que debe salir, pero si realizamos un dibujo geométrico, como hemos visto anteriormente, nos basta saber qué regiones deben quedar coloreadas para, de un simple vistazo, comprobar si se han obtenido las soluciones buscadas. Además, es posible realizar adaptaciones para alumnos con dificultades o incluso de altas capacidades. Para ello, partiendo del mismo esquema, basta plantear cuestiones con diferentes niveles de dificultad, con lo que toda la clase puede estar trabajando la misma actividad, de forma que cada persona trabaja según su capacidad. En este trabajo hemos recopilado ejemplos que hemos utilizado en clase, algunos de forma repetida. Pero en internet se pueden encontrar multitud de propuestas en este sentido en los que en lugar de rayar o colorear de un solo color las regiones, se les puede dar colores según el resultado, tal como hemos visto en el ejemplo de Ana García Azcárate. Si se quiere disponer de más ejemplos de esto último basta echar un vistazo a la siguiente dirección https://gr.pinterest.com/pin/ARAX1HgPbWxwLzfZ2XeIbUe5Zkbo1I2sTaQVFlmE__-Zvo1nO4C02c4/ Varios de los elementos que aparecen en la página anterior, y otros recursos diversos, pueden encontrarse en la página: https://www.actiludis.com/ 5. Referencias. GARCÍA AZCÁRATE, A. (2015): Pasatiempos y juegos en clase de Matemáticas. Funciones y más sobre números y álgebra. Editorial Aviraneta, Madrid. 4º Primaria: Pasatiempos de matemáticas. Dirección activa el 28/10/2018. https://es.slideshare.net/hiarah/4-pasatiemposmateszeretlekdenkeneshjromo05-30391669

Viernes, 27 de Marzo de 2020 | Imprimir | PDF |  Correo electrónico

468. Piden un banco mundial de datos abiertos para luchar contra el coronavirus

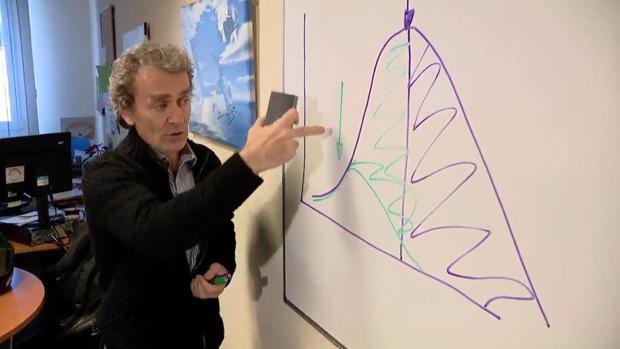
Agencia SINC, 11 de Marzo de 2020 SALUD - Epidemiología SINC

Miércoles, 11 de Marzo de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

469. Un modelo, un teorema y teoría de juegos contra el coronavirus

Agencia SINC, 20 de Marzo de 2020 CIENCIAS Enrique Sacristán

Viernes, 20 de Marzo de 2020 | Imprimir | PDF |  Correo electrónico | Leer más

470. La banda de Möbius, la superficie que solo tiene una sola cara

ABC, 23 de Febrero de 2020 CIENCIA - El ABCdario de las matemáticas Víctor M. Manero

Lunes, 23 de Marzo de 2020 | Imprimir | PDF |  Correo electrónico | Leer más