51. La Tritoniopsis elegans, elegante y fractal

Tritoniopsis elegans un molusco gasterópodo de la especie nudibranquia encontrado en el Indo-Pacífico. Tritoniopsis elegans De la familia Tritoniidae, fue descrita por primera vez en 1826 por el naturalista Jean Victoire Audouin. ¿Habéis visto esas pequeñas ‘papilas’ dorsales? Un precioso ejemplo de fractal en la naturaleza… Más información: W.B. Rudman, Tritoniopsis elegans (Audouin, 1826), Sea Slug Forum Australian Museum, 1999 J.V. Audouin (1826) Explication sommaire des planches de Mollusques de l’Egypte et de Syrie publiees par J.C. Savigny. Description de l’Egypte ou recueil des observations et des recherches qui ont été faites en Egypte pendant l’expedition de l’armée françaises, publie par les ordres de sa majeste l’empereur Napoleon le grand. Histoire Naturelle, Animaux invertebres 1(4): 7–56. Imprimiere imperiale, Paris. Visto en Le blog-notes mathématique du coyote Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Viernes, 22 de Julio de 2022 | Imprimir | PDF |  Correo electrónico

52. En busca de la distancia perdida…

Tenemos cinco puntos dispuestos sobre la recta real: p1 <  p2 <  p3 <  p4 <  p5. Las diez distancias entre esos pares de puntos, enumeradas de menor a mayor, son: 2, 4, 5, 7, 8, k, 13, 15, 17 y 19. Se pide encontrar el valor de k. Antes de leer la respuesta, ¡intenta resolverlo! La distancia entre p1 y p5 es obviamente 19. Eso significa, claramente, que 19 es también la suma de cada uno de los tres pares de distancias intermedias, es decir: (p2 – p1) + (p5 – p2) = 19, (p3 – p1) + (p5 – p3) = 19 y (p4 – p1) + (p5 – p4) = 19. Observando el listado de distancias proporcionado en el enunciado del problema, los únicos pares de distancias que suman 19 son (2,17) y (4,15). Pero debe de haber otro par de tales números sumando esa cantidad. Como 8 < k < 13, ese tercer par debe ser (7,k) u (8,k), lo que implica que k = 12 ó 11, respectivamente. La segunda mayor distancia es de 17, lo que significa que es p5 – p2 = 17 o p4 – p1 = 17. Analicemos cada caso por separado: Si fuera p5 – p2 = 17, al igual que hemos razonado antes, la suma de los pares de distancias intermedias también debería ser de 17. Es decir: (p5 – p3) + (p3 – p2) = 17, (p5 – p4) + (p4 – p2) = 17. Si fuera p4 – p1 = 17, tendríamos: (p4 – p2) + (p2 – p1) = 17, (p4 – p3) + (p3 – p1) = 17. Uno de esos pares de distancias que suman 17 es (4,13) y el otro debe ser (5,k), (7,k) o (8,k). Es decir, k debe ser 12, 10 ó 9. Teniendo en cuenta el razonamiento anterior se concluye que k = 12. Nota Visto en Fixing a Point, Futility Closet, 20 julio 2021 El anterior texto es una adaptación de la respuesta propuesta por el matemático Gustavo Krimker (Buenos Aires). Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 21 de Julio de 2022 | Imprimir | PDF |  Correo electrónico

53. Tres, cuatro… gordo

– ¿Ah, si? ¡Pues yo tengo TRES lados! – ¿Y qué? ¡¡Yo tengo CUATRO lados!! – … – Estás gordo. http://www.loadingartist.com/comic/taking-sides/ El círculo pensaba que iba a ganar tranquilamente al triángulo y al cuadrado… ya que su área se puede pensar como la superficie interior del polígono de infinitos lados: Pero, el concepto de infinito se ha cambiado por el de gordo… en este web cómic del artista Loading Artist (Gregor Czaykowski). Visto en The Meta Picture Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 21 de Julio de 2022 | Imprimir | PDF |  Correo electrónico

54. Figuras imposibles… de montar

La firma IKEA se anuncia con sentido del humor por medio de una campaña de publicidad realizada por la agencia DDB Tribal. ¿A qué no es tan fácil montar ese armario? http://ddb-tribal.com/de/arbeiten/-skit-happens–1830 ¡No consigo que las baldas queden bien colocadas! A través de imágenes de figuras imposibles consiguen, sin duda, llamar la atención sobre sus productos: http://ddb-tribal.com/de/arbeiten/-skit-happens–1830 ¿Cómo has conseguido que la silla quede así montada? http://ddb-tribal.com/de/arbeiten/-skit-happens–1830 ¡La ilusión al servicio de la publicidad! Visto en Le blog-notes mathématique du coyote Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Martes, 12 de Julio de 2022 | Imprimir | PDF |  Correo electrónico

55. 126. (Julio 2022) Modelos computacionales de ritmo y métrica (IV)

1. Introducción Esta es la cuarta entrega de la serie Modelos computacionales de ritmo y métrica. En la columna anterior [Góm22b] estudiamos las palabras de Christoffel y su relación con la teoría del ritmo; en particular, vimos cómo convertir palabras de Christoffel en ritmos y las operaciones que se podían hacer sobre estos ritmos. En la segunda entrega [Góm22a] examinamos los métodos de generación y recuento de ritmos, sobre todo los ritmos aksak. Y, finalmente, en esta columna vamos a estudiar las sucesiones de Farey y su relación con la teoría del ritmo. 2. Sucesiones de Farey Las sucesiones de Farey son representaciones elegantes y útiles de las duraciones relativas en subdivisiones métricas. Una sucesión de Farey de orden n, Fn, es la sucesión de fracciones reducidas que se encuentran en el intervalo [0,1]. En la figura de abajo se ven las sucesiones de Farey desde orden 1 hasta orden 8. Las fracciones se suelen presentar en orden creciente. La primera fracción es siempre y la última . Existen calculadores en línea de las sucesiones de Farey; véase, por ejemplo, Think Calculator [Cal22]. Figura 1: La sucesión de Farey de orden 8 Las sucesiones de Farey presentan una estructura recursiva. En efecto, la sucesión Fn es igual a la sucesión Fn más los dos términos y (este hecho es relativamente fácil de probar). Podemos escribir, pues: Otras propiedades que cumplen las sucesiones de Farey son: Si y son dos términos consecutivos de una sucesión de Farey, entonces se cumple que bc - ad = 1; Si ,, son tres términos consecutivos de una sucesión de Farey, entonces se tiene que = ; la fracción c∕d se dice que es la mediante de las fracciones a∕b y e∕f; Si n > 1, entonces no hay dos términos consecutivos con el mismo denominador. Sea |Fn| el cardinal de la sucesión de Farey de orden n y φ(n) la función de Euler, la cual da el número de primos relativos con n. Entonces, se cumple la bonita relación: En la tabla siguiente se muestras los primeros valores para |Fn|: Figura 2: Primeros valores de |Fn| (tabla tomada de [Ovs17]) Las sucesiones de Farey son simétricas en el sentido en que la subsucesión que de hasta es la imagen especular de la subsucesión que va desde hasta . En la figura siguiente se ilustra este hecho con la sucesión F5 (la sucesión se presenta en orden decreciente esta vez). Figura 3: Simetría de las sucesiones de Farey (figura tomada de [Ovs17]) 3. Ritmo y sucesiones de Farey Dado que las sucesiones de Farey de orden n representan todas las fracciones irreducibles en el intervalo [0,1], basta con identificar dicho intervalo con el pulso y entonces tendremos representadas todas las divisiones del pulso. Por ejemplo, F2 = genera la subdivisión en corcheas de una negra. Por otro lado, los tresillos corresponden al conjunto . F3 es la unión de las corcheas y los tresillos: F3 = . La figura de abajo ilustra estos hechos. Figura 4: Subdivisiones rítmicas asociadas a las sucesiones de Farey (figura tomada de [Boe18]) Se sigue de este razonamiento que las sucesiones de Farey de orden n contiene todos los ataques de los polirritmos en orden creciente para un pulso dado. Sin embargo, es posible librarse de la restricción de tener que considerar un solo pulso. Una sucesión de Farey puede representar las duraciones de una frase rítmica o de una pieza entera de hecho. Para hacer esto es necesario aumentar el orden de la sucesión (en un modo relacionado con la duración mínima de la pieza en cuestión) y quitar aquellas fracciones que no se correspondan con un ataque en la pieza. Boenn [Boe18] llama a estas sucesiones sucesiones de Farey filtradas. Otra restricción que se puede eliminar es la del rango de Fn, que hasta ahora es el intervalo [0,1]. La manera de hacerlo es escalar la sucesión original Fn al nuevo rango. Sea [x,y] un intervalo con x < y. Se designa por Fn[x,y] a la sucesión de Farey en [x,y] obtenida escalando Fn en dicho intervalo. Como ejemplo, consideremos F4, que es: Las sucesiones F4[0,1∕2] y F4[1∕2,1] son entonces: F4[0,1∕2] = F4[1∕2,1] = Es posible ahora considerar la unión de estas dos sucesiones de Farey (el término 1∕2 aparece solo una vez): F4[0,1∕2] ∪ F4[1∕2,1] = ∪ = Nótese que F4[0,1∕2] ∪ F4[1∕2,1 ⊂ F8. Por completitud, F8 es: Este método de generar nuevas sucesiones a partir de sucesiones de Farey se llama concatenación. Las sucesiones de Farey son particularmente adecuadas para estudiar los polirritmos. Boenn [Boe18] en su libro estudia la música de varios compositores a través de estas sucesiones, compositores como de Stravinsky (analiza La consagración de la primavera), Messian o Ockeghem (analiza su famosa misa Missa prolationem). En la tabla de abajo se muestran patrones polirrítmicos (dados en notación SNMR) y sus correspondientes sucesiones de Farey filtradas. Figura 5: Polirritmos y sucesiones de Farey filtradas (figura tomada de [Boe18]) 4. Notación SNMR Cuadro con la notación SNMR: Figura 6: La codificación SNMR (figura tomada de [Boe18])   Bibliografía [Boe18] Georg Boenn. Computational Models of Rhythm and Meter. Springer, New York, Berlín, 2018. [Cal22] Think Calculator. Farey sequences, junio de 2022. [Góm22a] P. Gómez. Modelos computacionales de ritmo y métrica (II), abril de 2022. [Góm22b] P. Gómez. Modelos computacionales de ritmo y métrica (III), junio de 2022. [Ovs17] Valentin Ovsienko. Partitions of unity in SL(2, г), negative continued fractions, and dissections of polygons. Research in the Mathematical Sciences, 5, 10 2017.

Jueves, 07 de Julio de 2022 | Imprimir | PDF |  Correo electrónico

56. Las matemáticas ayudan al CSI

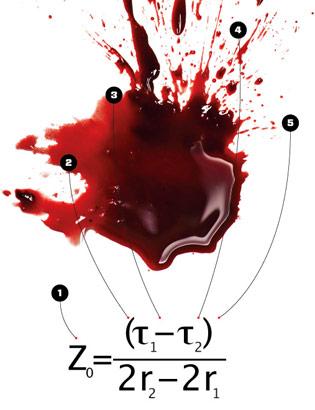
En la entrada Anamorph: el arte de matar hablábamos de un asesino en serie… y seguimos con pesquisas policiales… Foto de Jonathon Kambouris para Wired Science Aunque los investigadores saben definir con precisión la dirección de la que provienen las salpicaduras de sangre tras un asesinato, una pregunta más difícil de responder es la siguiente ¿cómo estaba situada la víctima respecto a su agresor?  Las matemáticas pueden ayudar a saberlo. El problema es que la sangre sale despedida siguiendo una trayectoria parabólica, pero diferentes caminos parabólicos recorridos desde diferentes alturas pueden determinar el mismo ángulo. Una nueva ecuación -que utiliza trigonometría y un poco de física- puede ayudar a descifrar este enigma; la ecuación es la siguiente: Z0 es la altura de la sangre en el comienzo de su arco parabólico, es decir, cuando abandonó el cuerpo de la víctima -este es el dato que se desea averiguar-, t1 es la tangente del ángulo con el que la primera gota de sangre cayó al suelo, t2 es la tangente del ángulo con el que la segunda gota de sangre cayó al suelo, r1 es la distancia horizontal recorrida por la primera gota de sangre, y r2 es la distancia horizontal recorrida por la segunda gota de sangre. Visto en Wired Science Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 07 de Julio de 2022 | Imprimir | PDF |  Correo electrónico

57. La fórmula de la cerveza

Las matemáticas están en todas partes: no nos cansamos de decírlo. Así que la cerveza no podía librarse de ello… Las y los cerveceros utilizan una fórmula matemática que les permite determinar el nivel de amargor de sus productos: es el índice IBU –International Bitterness Unit-, unidad de peso de una parte por millón de isohumulona el ácido que provoca el amargor y que proviene del lúpulo. La fórmula es la siguiente: donde: H es la concentración de lúpulo en gramos por litro, A es la concentración de ácidos α en el lúpulo, en porcentaje, y B es la concentración de ácidos β en el lúpulo, en porcentaje. El amargor aumenta con el IBU. Las cervezas más comerciales tienen un IBU de alrededor de 16. Pero cuanto mayor es la complejidad, mayor el IBU: hay cervezas de alrededor de 60-70 IBU, pero se puede llegar a niveles mucho mayores. Este índice no es siempre una garantía del amargor de la cerveza, que puede verse disminuido por la presencia de malta. Los cerveceros europeos utilizan una fórmula ligeramente diferente, llamada EBU –European Bitterness Unit– de resultados bastante parecidos al IBU. Las cervezas con un índice de amargor considerable -pale ale, IPA, stouts, etc.- llevan la cifra de su IBU impresa en la etiqueta… ¡busca el número que aparece en la que estás tomando! Visto en AlgoRythmes Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Miércoles, 06 de Julio de 2022 | Imprimir | PDF |  Correo electrónico

58. 172. EL CONCURSO DEL VERANO 2022

Nuestro concurso llega a la mayoría de edad. Esperemos que sigáis disfrutando de él como en ediciones pasadas. Aunque el mecanismo es muy sencillo, recordamos las características de este concurso de forma escueta: ■ A partir de las pistas que se dan en el texto, se trata de averiguar el título de una película oculta (clásica normalmente, o al menos con cierta antigüedad), y de paso, responder unas preguntillas (las de tipo matemático en color rojo; las culturales, en azul). Quien o quienes mayor puntuación alcancen serán los ganadores, a los que la dirección de DivulgaMAT les hará llegar algún obsequio, en la medida de sus posibilidades. ■ Se intentan (no siempre se logra) plantear cuestiones de todos los niveles (sencillas, medias, difíciles pocas), pero como nadie sabe a qué categoría pertenece cada una (además de que la dificultad es un concepto subjetivo), ninguna a priori debería evitarse. Trataremos de no exceder el nivel de 2º de Bachillerato, es decir, matemáticas elementales (lo que no quiere decir triviales). Tampoco deberían dejarse de enviar las respuestas, aunque sólo se sepa una (quien sabe, a lo mejor, nadie ha acertado más; cosas más raras se ven diariamente). ■ No hay un orden establecido ni a la hora de describir escenas de la película, ni a la hora de descifrar el contenido de las cuestiones. Puede que sepamos responder antes a la pregunta quinta que a las anteriores. Pero todas pueden ayudar en averiguar el título de la película. Los fotogramas que se incluyen son todos de la película en cuestión. XVIII CONCURSO Es posible que alguna vez hayáis leído que existen procedimientos basados en las matemáticas para escapar de un laberinto. Y es posible que alguna vez hayáis resuelto alguno de los que se proponen en la sección de pasatiempos de las revistas o periódicos. La película de este año es bastante laberíntica por muchos motivos, así que podemos empezar tratando de resolver un par de ellos, uno más matemático (M – 1 , pero que con cierta dosis de paciencia sale), y otro más tradicional (C – 1; C – 2). Otra característica presente en todo el metraje de la película son los juegos (C – 3; M – 2) y los juguetes. Uno de los protagonistas es un amante de los juegos y los enigmas (éstos son parte de su trabajo) (M – 3). Además, hay muchos objetos dispersos en cada escena de la película (C – 4), pero en algún momento los relojes tienen cierta relevancia (C – 5; M – 4). Por otra parte, si observamos el modo en que está embaldosado el suelo en algunos lugares, observamos una disposición con cuadrados y rectángulos de diferentes tamaños que finalmente forman una zona cuadrada perfecta (M – 5). De entre esos muchos objetos que juegan algún papel en la trama de la película hay un joyero que contiene lo que su nombre indica (M – 6). También se encuentra la figura que vemos en la imagen, que quizá pueda ayudar a descubrir el oficio al que se dedica uno de los protagonistas de la historia (C – 6; C – 7). Y también aparece una diana (M – 7). Además de lo comentado, la película es singular por el elenco que muestra (C – 8). Y por el giro que toman los acontecimientos (M – 8). Por cierto, ¿quién no ha ido alguna vez al cuarto de baño con alguna tarea con la que entretenerse? En la película, al lado del retrete, en una pared, podemos observar el enorme crucigrama de la imagen (M – 9). En concursos pasados, los participantes siempre han manifestado que es de cierta ayuda conocer el año de estreno de la película. Normalmente proponemos una cuestión en cuya resolución aparece ese año. En esta ocasión, diremos que se hizo una nueva versión de la película, ya en este siglo, cuya aportación aparte de la estética, es bastante cuestionable, a pesar de que el nuevo guion contara con todo un premio Nobel como responsable. Supongamos que escribimos los números naturales desde el 2, en cinco columnas del siguiente modo Pues bien, el año de la película, el de su remake, el año actual, y la diferencia de años entre el año actual y la primera versión, se encuentran en columnas diferentes. La diferencia entre el año actual y la segunda versión comparte la misma columna que el año de esa segunda versión, y para que no tengáis que contemplar demasiados casos, digamos que esas diferencias entre el año actual y el estreno de ambas versiones son las dos múltiplos de cinco (M – 10; C – 8). Y para acabar (M – 11; C – 9; C – 10; C – 11). CUESTIONES MATEMÁTICAS M – 1.- Imaginemos que nos topamos con el siguiente cuadro Nos situamos en la casilla a la que apunta la flecha (tiene un + 1). Ese valor indica el número de pasos que se pueden dar en cualquiera de las 4 direcciones: arriba, izquierda, derecha, abajo. En este caso, al estar en un borde, no podríamos abajo, ya que una vez en el laberinto, no es posible saltar fuera de la cuadrícula (siempre debemos permanecer dentro de los límites). El objetivo es alcanzar el centro de la cuadrícula, es decir, llegar a la baldosa 0 (donde nos espera nuestro anfitrión). Pero NO se puede repetir nunca una cuadrícula ya visitada. Hay dos modalidades que hay que resolver: la sencilla, que es alcanzar con esas normas la casilla 0, sin tener en cuenta los signos + y – que aparecen; y la del experto, en la que la suma de las casillas visitadas teniendo en cuenta los signos de cada una, debe ser igual a 0 al llegar a la casilla 0. M – 2.- En uno de los juegos aparecen bolas, a las que cada jugador impulsa cuando juega. Una de ellas se desliza por una superficie rugosa. En el primer segundo recorre 10 centímetros, disminuyendo la velocidad a medida que avanza recorriendo en cada segundo 2/3 de la distancia recorrida en el segundo anterior. ¿A qué distancia del inicio se detendrá? M – 3.- No sería difícil pensar que, en su intento de poner en evidencia a otro de los protagonistas, o más bien, demostrar su superioridad sobre él, le propusiera un juego como éste: se trata de formar un número de diez dígitos. Comienza él mismo escribiendo cualquier dígito que no sea cero en el primer lugar sobre un papel. Después su invitado debería escribir un dígito diferente que escribe en segundo lugar, turnándose posteriormente y agregando un dígito al número que va formándose. En cada turno, el dígito seleccionado debe ser diferente de todos los dígitos anteriores, y el número formado por los primeros n dígitos debe ser siempre divisible por n. Por ejemplo, 321 pueden ser los primeros tres movimientos del juego, ya que 3 es divisible por 1, 32 es divisible por 2 y 321 es divisible por 3. Cuando un jugador no pueda escribir un nuevo dígito cumpliendo estas normas, pierde el juego. Si se consigue llegar a los diez movimientos (es decir, se pueden escribir los diez dígitos), se declara un empate. (i) Demostrar que el juego puede terminar en empate. (ii) Demostrar que el anfitrión tiene una estrategia ganadora y describirla. (iii) ¿Sería más justo el juego si cambiamos la segunda condición por la de que el número formado al poner un nuevo dígito sea siempre divisible por el dígito que se añade (considerando el 0 como divisible por 10)? Por ejemplo 3210 sería posible porque 3 es divisible por 3, 32 es divisible por 2, 321 es divisible por 1, 3210 es divisible por 10, etc. M – 4.- ¿Cuántas veces las manecillas de un reloj forman un ángulo recto al cabo del día? ¿A qué horas? (Basta con detallar el cálculo de una de ellas, pongamos, por ejemplo, aquella que está entre las 7 y las 8, aunque se describan todas). M – 5.- Supongamos que tenemos solamente dos tipos de baldosas cuadradas. El primero tiene una longitud de lado 1 cm y el otro tiene una longitud de lado 2 cm. ¿Cuál sería el cuadrado más pequeño que podríamos hacer con el mismo número de baldosas de cada tipo? M – 6.- Además de un collar de rubíes hay otros con perlas, esmeraldas, etc. Este último está formado por una cadena de hexágonos regulares en los que se han incrustado las esmeraldas en forma de triángulos equiláteros como vemos en la imagen. Sabemos que el área de cada hexágono es de 96 unidades. ¿Cuál es entonces la superficie de cada esmeralda? M – 7.- Aunque uno de los protagonistas es un experto lanzador de dardos y acierta en el centro de la diana a la primera, evidentemente eso no es lo normal. Supongamos que somos nosotros los que lanzamos tres dardos (lo usual en el juego, como seguramente sabréis), apuntando al centro. En nuestra imaginaria partida, el segundo dardo cae más lejos del centro que el primero. ¿Cuál es la probabilidad de que el tercer lanzamiento esté más lejos del centro que el primero? Supondremos que nuestra habilidad de lanzamiento es constante. M – 8.- Se proponen nuevos juegos por parte de otros personajes. Imaginemos una mesa circular. Dos jugadores se turnan para colocar monedas en ella sin que se superpongan. El jugador que no pueda hacer un movimiento pierde. ¿Tiene alguno de los jugadores una estrategia ganadora? Si existe, ¿puedes describirla? M – 9.- Para no ser menos, vamos a proponer un crucigrama de contenido matemático. Y por respetar la nacionalidad de la película, las soluciones deben ponerse en inglés. Al final del texto están las definiciones y el crucigrama. M – 10.- Años de estreno de ambas películas. M – 11.- ¿Cuál es la película enigma de este concurso? CUESTIONES CULTURALES C – 1.- Resolver el siguiente laberinto (elige la opción que quieras: o llegar al centro desde la entrada exterior, o desde el centro, salir fuera). C – 2.- Indica al menos tres lugares del mundo en los que haya laberintos reales, describiendo un poco su historia (para qué se diseñaron, por quien, etc.). Se valorarán más aquellos que cumplan las siguientes condiciones: estar en España, estar lo más cerca posible del lugar del rodaje de la película, antigüedad. C – 3.- Haz un listado de todos los juegos que aparecen o se mencionan a lo largo de la película. C – 4.- Uno de ellos es este guitarrista troglodita que aparece además en otras películas. Una de ellas la protagoniza un cantante que trató de emular a otro, de actualidad estos días (¿Quién y por qué?), aunque ese sucedáneo ni triunfó, ni siquiera fue conocido fuera de su país. ¿A qué cantante nos referimos y en qué otras películas aparece el guitarrista troglodita como parte del atrezo? C – 5.- ¿Por qué? C – 6.- ¿Cuál es dicho oficio? ¿Por qué es célebre el protagonista? ¿Qué otros autores y sus creaciones son nombrados y/o representados en fotografías en la película? C – 7.- Repetidas veces vemos el retrato de un personaje importante en el argumento, el de la imagen adjunta, pero que nunca aparece físicamente. ¿Quién es? ¿A qué actriz real corresponde? ¿Por qué aparece precisamente esa actriz? ¿Hay alguna otra imagen suya a lo largo de la película diferente a la de este retrato? C – 8.- ¿Observas alguno “extraño” en los títulos de crédito? ¿A qué se debe? Enumera al menos tres películas más en las que el número de protagonistas sea menos o igual al de ésta. A ser posible de nacionalidades y épocas diferentes. C – 9.- ¿Qué diferencias observas en ambas versiones? Aparte de basarse en la misma obra común, y por tanto tener un argumento “similar”, ¿encuentras alguna cosa súper evidente que coincida en ambas? C – 10.- Para muy cinéfilos: uno de los protagonistas hace una referencia a otra célebre película directamente relacionada con él, aunque de un modo un tanto enigmático. ¿Puedes explicarlo? Y de paso indica algún actor que rechazó participar en esta película. C – 11.- Opinión sobre la película (o películas). ¿Te han gustado? ¿Las conocías? ¿Te han llamado la atención algún aspecto de ellas (algún tema que abordan, por ejemplo)? ¿Cuál te ha gustado más? CRUCIGRAMA PROPUESTO (M – 9) Horizontales: 1.- Conjetura en teoría de números que es una de los siete problemas con premios del Clay Mathematics Institute 11.- Comete esta galleta blanca y negra mientras haces tareas para el hogar 12.- Úsalo para escuchar conferencias de teoría de números 13.- Euclides Alejandría 15.- La fracción continua [1; 1, 1, 1, …] no es The Silver Sum, ni The Copper Product, sino The Golden _____ 17.- Un número con tantos dígitos como su nombre (recordamos que en inglés) 19.- Este símbolo es una función teórica numérica que se define igual a +1 o a -1 21.- Lo que uno espera hacer con una conjetura 24.- Un primo de Sophie Germain es, por definición, un primo p tal que 2p + 1 es 26.- Su último teorema fue garabateado en el margen de una copia de la Aritmética de Diofanto 29.- Función ____ de Riemann 30.- Él originó los símbolos f(x), e, i, p, y Σ 32.- Un ejemplo de un par de números de Ruth-Aaron son (714, 700 + n), donde n = 34.- Probó que M67 = 267 – 1 es compuesto en la 1903 reunión de la American Mathematical Society. 37.- Divisor 42.- Período de tiempo 43.- Cómo ver tu tarea si la electricidad desaparece 44.- La E en John E. Littlewood, quien fue famoso por su asociación con Hardy 45.- Si n se escribe como suma de dos cuadrados, entonces ningún primo de la forma 4k + 3 puede aparecer en una potencia ____ de la descomposición en factores de n 47.- Organización norteamericana fundada en 1888 para motivar la enseñanza y la investigación de las matemáticas 48.- Fue el primero en dar la solución general a las ecuaciones diofánticas lineales 49.- El ganado de Arquímedes pastaba una vez en los campos de esta isla mediterránea (no olvides que hay que escribir la solución en inglés) 50.- Una verificación elemental de la multiplicación que hace uso de la congruencia 10n ≡ 1(mod 9), se denomina en inglés “casting ___ nines” 51.- Fundó, en 1996, la página the Great Internet Mersenne Prime Search 53.- Primera y última letra en la abreviatura de un millón de ciclos por segundo 54.- En 1971, Brillhart y Morrison pudieron factorizar el Número de Fermat Fn, donde n es igual a 60.- Todos los números perfectos pares mayores que 6 tienen una raíz ____ de uno 62.- Tanto él como su padre eran profesores de matemáticas en Oxford, pero se hizo famoso por su relación con la hija del decano de Christ Church, Oxford 65.- Autor del rompecabezas de la Torre de Hanoi 67.- 2 no es una ____ para un triángulo pitagórico (recuerda que está en inglés) 69.- Completó trabajos sobre teoría de números y la curvatura de las superficies antes de morir de cáncer de mama en 1831 70.- Roger Federer, campeón de tenis de Wimbleton en 2004, y Leonhard Euler tienen esto en común 72.- El hermano menor de Littlewood murió a los 8 años al caer en uno de estos 73.- Colección finita o infinita de objetos 74.- Ciudad natal del matemático José Anastacio de Cunha 75.- Según F. R. David, no vienen de manera sencilla Verticales: 1.- La serie de recíprocos de todos los primos gemelos converge a un valor que lleva el nombre de este noruego, Viggo ____ 2.- Abreviatura latina de “eso es” 3.- No es la función floor, sino otra. La misma en la que se encontraba el violinista 4.- Pascal y Fermat usaron las matemáticas para estudiar los juegos y las posibilidades de 5.- Si destacas en teoría de números, puedes estar cualificado para un trabajo en esta organización criptológica 6.- El orden de 12 módulo 13 7.- La forma más obvia de calcular 1210 (mod 23) es multiplicar 12 veces cierto valor calculando el resto al dividir por 23 en cada multiplicación 8.- Robert P. Langlands, quien recibió el Premio Cole en Teoría de Números en 1982 por su trabajo pionero sobre formas automórficas, recibió su doctorado de esta escuela 9.- Debes hacer esto en tu libro de texto de teoría de números 10.- El de 2 (mod 7) es 3 14.- Cualquier número entero positivo se puede expresar como suma de este número de cuadrados 15.- En el popular esquema de encriptación RSA, la letra “R” representa a esta persona 16.- Canción popular de los Beatles “Let” (dos palabras) 18.- A qué velocidad gira un motor (abreviatura) 19.- Si p(n) denota el número de particiones del entero, entonces el _____ cuando n tiende a infinito [p(n)]^(1/n) es 1 20.- El conjunto de enteros positivos de 2 dígitos < 50 que se pueden expresar como suma de dos cuadrados en dos maneras distintas 22.- Si la congruencia x2 ≡ 5 mod 31 tiene solución, entonces 5 es una ____ cuadratica de 31 23.- Si ϕ denota la función phi de Euler, entonces ϕ (n) ≡ c (mód 2), ∀ n > 2; entonces c es igual a esto 24.- Pasa la 25.- El castillo de un célebre personaje de ficción 26.- Estas medallas en matemáticas son los equivalentes de los Premios Nobel 27.- Iniciales de un famoso inventor estadounidense nacido en Ohio 28.- Título que se otorga al completar un doctorado 31.- Los de Galois incluyen una de éstas de los enteros módulo p, con p primo 33.- Una ____ continua es una representación de los números reales en términos de una sucesión de números enteros 35.- Matemático alemán que obtuvo estimaciones asintóticas de cuántos enteros son ≤ x que son expresables como suma de dos cuadrados 36.- Su famoso teorema dice que para cualquier número irracional x existen infinitos p/q racionales tales que 38.- El símbolo “∨” en p ∨ q representa esto 39.- El italiano Maurolico demostró que todo número par perfecto es también numero ____ 40.- Conjeturó que siempre existe un primo entre un número y su doble 41.- Su nombre se asocia a una fórmula de inversión y a una tira de papel. 43.- Los números enteros al cuadrado se pueden escribir como producto de un cuadrado y esto 46.- Pi ___ se celebra el 14 de marzo 49.- El teorema de los cuatro cuadrados afirma que todo número natural es el ____ de 4 cuadrados enteros 52.- Abel, Eisenstein y Ramanujan todos murieron a causa de este (abreviatura) 55.- “Bueno, he hecho una cosa que tú nunca podrías haber hecho, que es haber colaborado con Littlewood y Ramanujan en términos de _____" 56.- Demostró con éxito el último teorema de Fermat 57.- Durante su vida, Gauss produjo todas estas pruebas de la Ley de Reciprocidad Cuadrática 58.- El número de primos menor o igual que cualquier x dado es aproximadamente igual a x dividido por su 59.- El de un conjunto es el menor número ordinal mayor que el rango de cualquier miembro del conjunto 61.- El símbolo del germanio 63.- Este tipo de intervalo no incluye sus extremos 64.- Si completas este rompecabezas, eres un matemático _____ (recuerda, en inglés) 65.- Primera y última letra de la abreviatura de menor múltiplo común 66.- Agencia gubernamental que proporciona al Presidente inteligencia de seguridad nacional (ya que él no suele tener mucha) 68.- Aquí es donde Hardy y Ramanujan encontraron el número 1729 70.- Grado que la mayoría de los estudiantes de licenciatura en matemáticas reciben (abreviatura) 71.- Más vale ___ que arre, dice el dicho borruno popular. Baremo: Todas las cuestiones, tanto las rojas (las matemáticas), como las azules (cine y demás), se valorarán con 10 puntos como máximo. En total, 220 puntos en juego, si las cuentas no me fallan. Todo comentario, sugerencia, queja, etc., será bien recibido. Si no salen algunas cosas, no importa; lo que cuenta es tratar de pasar un buen rato, disfrutar de la película (que el verano da para mucho), y mantener las neuronas un poco activas. Confío que no haya demasiados errores en las cuestiones. Se han repasado varias veces, pero algunas, al ser inventadas o retocadas de otros enunciados, podrían tener alguna errata. Sed benévolos con vuestros calificativos si tal cosa sucediera. El plazo para enviar las respuestas, es como en años precedentes, hasta las 00:00 del jueves 1 de Septiembre de 2022, a la dirección apoblacion@uva.es, indicando en el asunto Verano 2022. ¡¡¡¡Buen Verano Cine-matemático!!!!

Jueves, 30 de Junio de 2022 | Imprimir | PDF |  Correo electrónico

59. El ABCdario de las matemáticas

Tras un acuerdo de la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) con la edición digital del periódico ABC se comenzó a publicar, en marzo de 2017, un artículo semanal y un video quincenal bajo el nombre de “El ABCdario de las matemáticas”. Artículos: "'Salirse por la tangente' o 'buscar el mejor ángulo': los términos matemáticos que adoptó la literatura" por Alfonso Jesús Población Sáez (27/06/2022) "Qué son las coordenadas polares y para qué sirven" por Alfonso Jesús Población Sáez (20/06/2022) "Algún día se nos acabarán los números de las matrículas, ¿cómo lo vamos a solucionar?" por Alfonso Jesús Población Sáez (13/06/2022) "En busca del «sentido matemático» y en qué lugar deja la nueva ley de Educación a las Matemáticas" por Alfonso Jesús Población Sáez (06/06/2022) "¿Seguro que no necesitas las matemáticas?" por Alfonso Jesús Población Sáez (30/05/2022) "El problema del huerto o cómo los matemáticos plantan árboles sin azada" por Alfonso Jesús Población Sáez (23/05/2022) "Los cuatro templos de las matemáticas en España" por Robert Escribano, Mª Carmen Perea, Víctor Manero, Fernando Blasco y Alfonso J. Población (16/05/2022) "¿Qué son los métodos Montecarlo y qué tienen que ver con la bomba atómica?" por Alfonso Jesús Población Sáez (09/05/2022) "El legado perdido de Pappus de Alejandría que dio lugar a unas nuevas matemáticas" por Alfonso Jesús Población Sáez (02/05/2022) "El caso en el que el círculo y el cuadrado son lo mismo" por Alfonso Jesús Población Sáez (25/04/2022) "La solución al problema de los melones y cómo escribir 'amor' con números" por Alfonso Jesús Población Sáez (04/04/2022) "Un recorrido matemático por la primera línea de metro de Madrid''" por María Concepción Romo Santos (28/03/2022) "El 'teorema del suflé' o las matemáticas 'esponjosas''" por Pedro Alegría (21/03/2022) "Un reto para descubrir que no puedes con el número Pi" por Alfonso Jesús Población Sáez (14/03/2022) "Rodríguez Vidal, el matemático humanista que puso en valor a los científicos aragoneses" por Alfonso Jesús Población Sáez (07/03/2022) "La increíble vida de Luis Raluy, el payaso matemático fascinado por la 'Teoría de Números'" por Pedro Alegría (28/02/2022) "Las matemáticas 'ocultas' tras la Catedral de Burgos" por Alfonso Jesús Población Sáez (21/02/2022) "Qué es blockchain y por qué puede llevar a un mundo sin corrupción" por Lierni Ortiz Elorza (14/02/2022) "¿Ha resuelto un profesor de Harvard el antiguo problema de las damas del ajedrez?" por Alfonso Jesús Población Sáez (07/02/2022) "El reto matemático: El crimen de la mujer muerta en su casa de Pirineos, resuelto con grafos" por Víctor M. Manero (31/01/2022) "Ni profecía ni maldición en la Alhambra, solo matemáticas" por Alfonso Jesús Población Sáez (24/01/2022) "¿Pueden las matemáticas resolver un crimen?" por Víctor M. Manero (17/01/2022) "¿Una 'profecía matemática' en la Alhambra?" por Alfonso Jesús Población Sáez (10/01/2022) "Tres ciudades andaluzas, vistas con ojos matemáticos" por Alfonso Jesús Población Sáez (03/01/2022) "Trigonometría, el puente que une todas las matemáticas" por Alfonso Jesús Población Sáez (13/12/2021) "Lo que las matemáticas han cambiado nuestras vidas" por Alfonso Jesús Población Sáez (29/11/2021) "Fractales: las formas que simulan a la naturaleza" por Alfonso Jesús Población Sáez (22/11/2021) "Las ecuaciones matemáticas para adelgazar, ¿son fiables?" por Alfonso Jesús Población Sáez (15/11/2021) "Egmont Colerus y sus matemáticas para todos" por Alfonso Jesús Población Sáez (08/11/2021) "Fórmulas y ecuaciones: cómo perderle el miedo al lenguaje de las matemáticas" por Alfonso Jesús Población Sáez (02/11/2021) "Los límites matemáticos de la amistad, la enemistad y el Big Data" por Ernesto Estrada (25/10/2021) "Investigadores del MIT solucionan un problema matemático de hace 70 años" por Alfonso Jesús Población Sáez (18/10/2021) "¿El portero Buffon es imbatible en 'piedra, papel o tijera'? Una explicación matemática" por Diego Alonso Santamaría (11/10/2021) "La paradoja de Russell o cómo explotar los cimientos de las matemáticas" por Urtzi Buijs y Miriam González (04/10/2021) "Por qué hay más posibilidades en una baraja de cartas que átomos en la Tierra" por Alfonso Jesús Población Sáez (27/09/2021) "Recomendaciones matemáticas para el verano" por Alfonso Jesús Población Sáez (28/06/2021) "Sí, las matemáticas resuelven problemas reales y estos son algunos ejemplos" por Alfonso Jesús Población Sáez (21/06/2021) "El profesor de matemáticas bilbaíno que hacía bailar a los números" por Alfonso Jesús Población Sáez (14/06/2021) "¿Cómo se resuelve el problema de 'los 36 oficiales'?'" por Alfonso Jesús Población Sáez (07/06/2021) "El 'cuadrado mágico de Foz', los 'fozudokus' y las matemáticas llegadas desde Lugo'" por Alfonso Jesús Población Sáez (31/05/2021) "Reglas, compases y papiroflexia para cuadrar círculos y contentar a Apolo" por Iván Blanco Chacón (24/05/2021) "¿A más seguidores, más éxito?: las matemáticas detrás de los 'influencers' y de las redes sociales'" por Ernesto Estrada (17/05/2021) "El italiano que ganó dos premios millonarios en 15 días con un 'rasca y gana'" por Alfonso Jesús Población Sáez (10/05/2021) "Metagrobología o cómo aprender matemáticas jugando con rompezabezas" por Alfonso Jesús Población Sáez (03/05/2021) "Las Cadenas de Markov: las matemáticas que nos enseñó una serie de televisión" por Alfonso Jesús Población Sáez (26/04/2021) "¿Qué son las 'Matemáticas Singapur'?" por Pedro Ramos Alonso (19/04/2021) "Los científicos que demostraron la cuadratura del cuadrado" por Pedro Alegría (12/04/2021) "El truco matemático para organizar las mesas en un banquete de bodas" por Alfonso Jesús Población Sáez (29/03/2021) "¿Son siempre paralelas las ruedas delanteras de un coche? Y otras cosas que aprender en el mes de las matemáticas" por Alfonso Jesús Población Sáez (15/03/2021) "Por qué hoy se celebra el Día del número Pi" por Alfonso Jesús Población Sáez (14/03/2021) "El misterio geométrico resuelto por Desargues" por Víctor M. Manero (08/03/2021) "Un reto muy geométrico" por Víctor M. Manero (01/03/2021) "Y esto, ¿para qué sirve?" por Alfonso Jesús Población Sáez (22/02/2021) "Evariste Galois, la amarga historia del 'enfant terrible' del álgebra" por Iván Blanco Chacón (15/02/2021) "Cómo animar a las niñas a romper la brecha de género y estudiar ciencias" por Mireia López Beltrán (11/02/2021) "Demostrar no es verificar: ¿podrías encontrar la solución a estos problemas matemáticos?" por Alfonso Jesús Población Sáez (01/02/2021) "El misterio del número 77" por Alfonso Jesús Población Sáez (25/01/2021) "La conjetura de Collatz: un problema «sencillo» que desafiará tu intuición" por Víctor M. Manero y Alfonso Jesús Población Sáez (18/01/2021) "Arquímedes y la medida del círculo" por Urtzi Buijs y Miriam González (11/01/2021) "Alicia en el país de las matemáticas", por Víctor M. Manero (21/12/2020) "La geometría que sostenía al telescopio de Arecibo hasta que se derrumbó" por Pedro Alegría (14/12/2020) "El enigma de los números primos: Del hueso de Ishango al problema del Milenio" por Iván Blanco Chacón (07/12/2020) "Mariano Mataix: el desconocido autor de «Droga matemática» que mostró la diversión tras los números" por Alfonso Jesús Población Sáez (30/11/2020) "El «secreto» matemático que une a los planetas con los conciertos de rock" por Ernesto Estrada (23/11/2020) "El ojo de Horus: ¿Qué es eso de la fracción egipcia?" por Pedro Alegría (16/11/2020) "El griego Eratóstenes contra los terraplanistas", por Víctor M. Manero (09/11/2020) "Los números de Friedman, cuando los números están dentro de los números" por Alfonso Jesús Población Sáez (02/11/2020) "James Randi y otros genios de la magia y las matemáticas" por Fernando Blasco (26/10/2020) "La demostración matemática o cómo llegar a la verdad invariable y eterna de los teoremas", por Víctor M. Manero (29/10/2020) "Matemáticas para la privacidad en un mundo post-cuántico" por Iván Blanco Chacón (11/10/2020) "La primera gran crisis de los matemáticos: las magnitudes inconmensurables" por Urtzi Buijs y Miriam González (05/10/2020) "El truco detrás del «misterioso» número 37 y otras fórmulas matemáticas virales" por Alfonso Jesús Población Sáez (28/09/2020) "Recomendaciones de un matemático para el verano" por Alfonso Jesús Población Sáez (06/07/2020) "Los números también saben mantener la distancia de seguridad" por Pedro Alegría (29/06/2020) "El origen matemático del dígito de control «escondido» en tu DNI", por Víctor M. Manero (22/06/2020) "Las probabilidades de tener el covid-19 si hacemos caso a Bayes" por Alfonso Jesús Población Sáez (15/06/2020) "De médicos, porcentajes y falsos positivos" por Alfonso Jesús Población Sáez (08/06/2020) "¿Cuántas personas te pueden besar a la vez?" por Alfonso Jesús Población Sáez (01/06/2020) "¿Qué tienen en común algunos tipos de patatas fritas, las pompas de jabón y las centrales nucleares?", por Víctor M. Manero (25/05/2020) "La «im-posible» cuadratura del círculo" por Pedro Alegría (18/05/2020) "Día Internacional de la Mujer Matemática: Mirzakhani, referentes y estereotipos" por Begoña Barrios Barrera, Rosa Crujeiras Casais, Patricia Contreras Tejada e Irene Epifanio López (11/05/2020) "Matheminecraft: El lugar donde las matemáticas y los videojuegos se encuentran" por Alfonso Jesús Población Sáez (04/05/2020) "El método Moore o cómo aprender matemáticas al estilo tejano" por Pedro Alegría (27/04/2020) "Los acertijos matemáticos que dejó John Conway, fallecido por coronavirus" por Fernando Blasco (20/04/2020) "La ley Benford: ¿Por qué hay más números que comienzan por uno que por otro dígito?", por Víctor M. Manero (13/04/2020) "Matemáticas contra una pandemia" por David Gómez-Ullate Oteiza (30/03/2020) "En busca del «einstein» perdido por los suelos" por Pedro Alegría (30/03/2020) "La banda de Möbius, la superficie que solo tiene una sola cara", por Víctor M. Manero (23/03/2020) "Todo lo que debes saber de Pi, el número que fascina a los matemáticos" por Fernando Blasco (14/03/2020) "Resolver un problema matemático visualmente es posible" por Urtzi Buijs y Miriam González (09/03/2020) "¿Existe la caja perfecta? Así la encuentra un matemático" por Alfonso Jesús Población Sáez (02/03/2020) "El teorema de Fermat: hasta los genios se equivocan" por Pedro Alegría (24/02/2020) "Las matemáticas que revelan el techo de cristal de las mujeres en ciencia" por Rosa Crujeiras Casais, Irene Epifanio López y Teresa Sánchez Rúa (17/02/2020) "¿Por qué 2020 es un año bisiesto? No es tan sencillo como crees" por Víctor M. Manero (10/02/2020) "Las matemáticas que hay detrás de las baldosas" por Alfonso Jesús Población Sáez (03/02/2020) "Los secretos matemáticos del embaldosado" por Alfonso Jesús Población Sáez (27/01/2020) "El paralaje, el cálculo matemático para medir la distancia a las estrellas" por Víctor M. Manero (20/01/2020) "Reflexiones de un matemático al comienzo del año" por Alfonso Jesús Población Sáez (13/01/2020) "¿Quieres regalar juguetes? ¿Por qué no regalar un cubo?" por Fernando Blasco (23/12/2019) "Un matemático explica las probabilidades reales de que te toque el Gordo" por Alfonso Jesús Población Sáez (16/12/2019) "La razón áurea: verdades y mitos del número «mágico»" por Fernando Blasco (09/12/2019) "Cómo ayudan las matemáticas a entender el cambio climático" por Fernando Blasco (02/12/2019) "Para qué sirven los logaritmos: dos retos sin usar la calculadora" por Alfonso Jesús Población Sáez (25/11/2019) "¿Para qué sirven realmente los logaritmos?" por Alfonso Jesús Población Sáez (18/11/2019) "Por qué un matemático no dejaría tirar faltas a Cristiano Ronaldo" por Diego Alonso Santamaría (17/11/2019) "La sociedad secreta de Pitágoras y el «superpoder» de los números figurados" por Urtzi Buijs y Miriam González (04/11/2019) "Matemáticos descubren una nueva forma de multiplicar números grandes" por Alfonso Jesús Población Sáez (28/10/2019) "¿Eres capaz de resolver estos ingeniosos acertijos matemáticos de Martin Gardner?" por Fernando Blasco (21/10/2019) "Las matemáticas detrás del sistema electoral: ¿por qué el voto de un madrileño vale menos?" por Fernando Blasco (14/10/2019) "La «regla del siete» que sí funciona y no te explicaron en la escuela" por Alfonso Jesús Población Sáez (07/10/2019) "Matemáticos encuentran una nueva forma de llegar al número 3" por Alfonso Jesús Población Sáez (30/09/2019) "La serie de Grandi y la «no demostración» de la existencia de Dios" por Maria Pilar Sabariego Arenas (23/09/2019) "Divulgación de las matemáticas: Ellas fueron las primeras" por Alfonso Jesús Población Sáez (16/09/2019) "Cómo averiguar el número de pelos en las cabezas de los madrileños por el principio del palomar" por Alfonso Jesús Población Sáez (01/07/2019) "Curiosidades matemáticas detrás del solsticio de verano" por Fernando Blasco (24/06/2019) "El problema con el que Federico II retó a uno de los matemáticos más asombrosos de la Historia" por Alfonso Jesús Población Sáez (17/06/2019) "Ocho edificios formidables de España con un uso magistral de las matemáticas" por Fernando Blasco (10/06/2019) "El gúgol y otras cantidades matemáticas gigantescas" por Alfonso Jesús Población Sáez (03/06/2019) "Luca Pacioli, el amigo matemático de Da Vinci amante de la divina proporción" por Fernando Blasco (27/05/2019) "Omar Khayyam, el matemático persa al que le debemos que la incógnita sea una X" por Alfonso Jesús Población Sáez (20/05/2019) "Qué es un billón y por qué nos confunde tanto" por Alfonso Jesús Población Sáez (13/05/2019) "El bello mundo de los números imposibles" por Juan Matías Sepulcre Martínez (06/05/2019) "Las asombrosas fórmulas matemáticas desarrolladas por un profesor español" por Alfonso Jesús Población Sáez (29/04/2019) "Solucionan el diabólico acertijo matemático que no ha podido ser resuelto en 64 años" por Alfonso Jesús Población Sáez (08/04/2019) "El hombre que ha propuesto más de 300 problemas de matemáticas" por Alfonso Jesús Población Sáez (01/04/2019) "¿Quién resolverá el teorema de Fermat llevado al cubo?" por Pedro Alegría (25/03/2019) "Los misterios del número Pi aún sin resolver" por Alfonso Jesús Población Sáez (14/03/2019) "Regresa el reto matemático: desvelando lo que las sumas esconden" por Alfonso Jesús Población Sáez (11/03/2019) "Un reto matemático: lo que se esconde en una suma" por Alfonso Jesús Población Sáez (04/03/2019) "Recta o curva: ¿cuál crees que es la forma perfecta de un tobogán?" por Alfonso Jesús Población Sáez (25/02/2019) "¿Es cierto el mito de que la ciencia avanza más rápido en tiempo de guerra?" por Fernando Corbalán (18/02/2019) "El comportamiento secreto de los números primos en espiral" por Pedro Alegría (11/02/2019) "¿De dónde salen los números de la tabla periódica?" por Miquel Duran y Fernando Blasco (04/02/2019) "Siete consejos para que los niños no odien las matemáticas" por David Orden Martín (02/02/2019) "Por qué crees que has visto una película entera pero en realidad te has perdido la mitad" por Alfonso Jesús Población Sáez (20/01/2019) "El problema sin solución al que ha llevado la inteligencia artificial" por Alfonso Jesús Población Sáez (14/01/2019) "Por qué 2019 es un número feliz, según las matemáticas" por Fernando Corbalán (08/01/2019) "La increíble técnica de construción que Da Vinci esbozó en su misterioso «Codex Atlanticus»" por Guido Ramellini y Alfonso Jesús Población Sáez (17/12/2018) "Los secretos de la cultura vaccea, al descubierto gracias a las matemáticas" por Ana María Portillo de la Fuente (10/12/2018) "El algoritmo de Tarry o cómo salir de un laberinto a la primera" por Ángel Martín del Rey (03/12/2018) "La cifra Vigenère: el misterioso código que se tardó tres siglos en descifrar" por Alfonso Jesús Población Sáez (20/11/2018) "Las matemáticas que se esconden detrás de la seguridad del coche autónomo" por Alfonso Jesús Población Sáez (12/11/2018) "La fórmula que predecía quién ganaba un combate aéreo en la Primera Guerra Mundial" por Ángel Martín del Rey (29/10/2018) "¿Eres capaz de resolver estos seis problemas de ingenio?" por Pedro Alegría (22/10/2018) "Los ingenuos mensajes cifrados de los espías españoles en tiempos de los Reyes Católicos" por Alfonso Jesús Población Sáez (16/10/2018) "Te presento al escutoide, la forma geométrica que te da forma" por Clara Grima (30/07/2018) "Cuatro verdades matemáticas que no son como se creía" por Pedro Alegría (24/07/2018) "El matemático que propuso cortar un nudo gordiano (y aprender algo en el camino)" por Alfonso Jesús Población Sáez (16/07/2018) "Otro millón de dólares te espera: ¿Es P = NP?" por Alfonso Jesús Población Sáez (10/07/2018) "Cómo atarte los zapatos, aparcar tu coche y otros problemas cotidianos resueltos por las matemáticas" por Clara Grima (02/07/2018) "¿Cuál es la probabilidad de que España gane el Mundial de Rusia? Un matemático responde" por Alberto Márquez (26/06/2018) "Matemáticas para acertar quién ganará el Mundial de Rusia" por Clara Grima (19/06/2018) "Las matemáticas escondidas en la ciudad de Praga" por Fernando Corbalán (14/06/2018) "Muere el matemático brasileño que pensaba «bonito»" por Isabel Fernández (08/05/2018) "Las matemáticas que descifraron la máquina «Enigma» de los nazis" por Paz Jiménez Seral y Manuel Vázquez Lapuente (30/04/2018) "Por qué no hicieron falta extraterrestres para construir las pirámides" por Alfonso Jesús Población Sáez (23/04/2018) "La aritmética del reloj que practicas cada día sin saberlo" por Urtzi Buijs (16/04/2018) "La curva que logró un gol histórico a 40 metros" por Fernando Corbalán (10/04/2018) "La solución matemática más larga de la Historia" por Pedro Alegría (03/04/2018) "Diez curiosidades sobre el número Pi para celebrar su día" por Fernando Corbalán (14/03/2018) "¿Qué tiene de especial el número 78.557?" por Alfonso Jesús Población Sáez (12/03/2018) "La cicloide, la curva más rápida posible" por Fernando Corbalán (06/03/2018) "Así transforman una cara en otra con matemáticas" por David Orden Martín (26/02/2018) "El puzle que hizo enloquecer a una generación un siglo antes de Rubik" por Pedro Alegría (19/02/2018) "El número de Euler, la otra constante que está en todas partes" por Fernando Corbalán (13/02/2018) "Florence Nightingale, la enfermera que salvó miles de vidas con una rosa" por Clara Grima (05/02/2018) "El teorema más largo de la Historia y otras «monstruosidades» matemáticas" por Alfonso Jesús Población Sáez (29/01/2018) "Sangaku, los problemas matemáticos sagrados de los japoneses" por Fernando Fouz (23/01/2018) "Por qué 2018 es un año pitagórico" por Fernando Corbalán (15/01/2018) "El problema del caballo, el intrincado enigma matemático en el que no se puede repetir" por Pedro Alegría (08/01/2018) "Las matemáticas escondidas detrás de las pinturas de Jackson Pollock" por Fernando Corbalán (18/12/2017) "La peor metedura de pata en el homenaje al matemático del Juego de la vida" por Clara Grima (12/10/2017) "Siempre toca fuera, mejor comprar antes y otras absurdas ideas sobre el Gordo de Navidad" por Fernando Corbalán (04/12/2017) "Shalosh B. Ekhad: El matemático sin alma que resolvió el teorema cosmológico de Conway" por Raúl Ibáñez Torres (29/11/2017) "El genial matemático «tartaja» que lanzó por despecho el gran desafío algebraico de Milán" por Fernando Corbalán (13/11/2017) "Las matemáticas que puede esconder un dónut" por Alfonso Jesús Población Sáez (03/11/2017) "El teorema matemático para que nadie se quede sin pareja" por Pedro Alegría (23/10/2017) "Problemas del Milenio: La conjetura BSD o por qué las matemáticas están reñidas con la charlatanería" por Alfonso Jesús Población Sáez (16/10/2017) "El examen de matemáticas de Cambridge que causaba crisis nerviosas" por Raúl Ibáñez Torres (09/10/2017) "Cuando al 4 de octubre le siguió el día 15 y otros grandes líos del calendario" por Fernando Fouz (02/10/2017) "Los cuadrados mágicos que aún nadie ha podido resolver y se premian con 6.500 euros" por Pedro Alegría (25/07/2017) VIDEO:"El enigma matemático detrás del «problema de Monty Hall»" (23/07/2017) "Tres ¿sencillos? desafíos matemáticos para el verano" por Fernando Corbalán (17/07/2017) VIDEO:"Por qué se venden por docenas y otras curiosidades (matemáticas) de los huevos" (16/07/2017) "Así resuelve un matemático una suma insólita" por Alfonso Jesús Población Sáez (10/07/2017) "¿Eres capaz de resolver estos siete problemas matemáticos? Un chaval de 13 años lo hizo" por Alberto Márquez Pérez (03/07/2017) "La hipótesis de Riemann, el más codiciado de los problemas del milenio" por Alfonso Jesús Población Sáez (27/06/2017) "El problema matemático de la cuerda anudada que dice si te puedes casar" por Fernando Corbalán (19/06/2017) "Este cálculo matemático es una antigualla, ¡pero funciona!" por Luis Rández (12/06/2017) "¿Cuál es el punto sobre la superficie terrestre más cercano al Sol?" por Fernando Fouz (05/06/2017) "El sorteo por apellidos: la gran injusticia de la administración" por Clara Grima (30/05/2017) "La paradoja del cumpleaños, el problema matemático que puedes probar en tu agenda" por Fernando Corbalán (22/05/2017) "El dilema de los cien prisioneros" por Clara Grima (16/05/2017) "De Pitágoras a la conjetura del millón de dólares" por Pedro Alegría (08/05/2017) "Las ecuaciones que nadie ha conseguido resolver y que valen un millón de dólares" por Alfonso Jesús Población Sáez (02/05/2017) "El diagrama de Voronoi, la forma matemática de dividir el mundo" por Clara Grima (24/04/2017) "Eva Miranda: «En España tenemos un importante capital humano en investigación matemática»" por Fernando Corbalán (17/04/2017) VIDEO:"El curioso motivo por el que las tapas de alcantarilla son redondas" (10/04/2017) "El caso de los 14 pentágonos que embaldosan un espacio infinito" por Pedro Alegría (10/04/2017) "El matemático que usa calculadora y otros tópicos sobre los números" por Fernando Corbalán (04/04/2017) "¿Pero qué son las ondículas y por qué han ganado el «nobel» de matemáticas?" por Alfonso Jesús Población Sáez (28/03/2017) VIDEO: "Yo soy Pi, la constante que contiene todos los números del mundo" (27/03/2017) "Matemáticas para ganar un millón de dólares" por Alfonso Jesús Población Sáez (21/03/2017) "Día de Pi: Cuando el número Pi pudo ser 3,2" por Pedro Alegría (14/03/2017) "Los desafíos de Pi, el número de cifras infinitas" por Fernando Corbalán (07/03/2017)

Lunes, 27 de Junio de 2022 | Imprimir | PDF |  Correo electrónico

60. El ABCdario de las matemáticas

Tras un acuerdo de la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) con la edición digital del periódico ABC se comenzó a publicar, en marzo de 2017, un artículo semanal y un video quincenal bajo el nombre de “El ABCdario de las matemáticas”. Artículos: "'Salirse por la tangente' o 'buscar el mejor ángulo': los términos matemáticos que adoptó la literatura" por Alfonso Jesús Población Sáez (27/06/2022) "Qué son las coordenadas polares y para qué sirven" por Alfonso Jesús Población Sáez (20/06/2022) "Algún día se nos acabarán los números de las matrículas, ¿cómo lo vamos a solucionar?" por Alfonso Jesús Población Sáez (13/06/2022) "En busca del «sentido matemático» y en qué lugar deja la nueva ley de Educación a las Matemáticas" por Alfonso Jesús Población Sáez (06/06/2022) "¿Seguro que no necesitas las matemáticas?" por Alfonso Jesús Población Sáez (30/05/2022) "El problema del huerto o cómo los matemáticos plantan árboles sin azada" por Alfonso Jesús Población Sáez (23/05/2022) "Los cuatro templos de las matemáticas en España" por Robert Escribano, Mª Carmen Perea, Víctor Manero, Fernando Blasco y Alfonso J. Población (16/05/2022) "¿Qué son los métodos Montecarlo y qué tienen que ver con la bomba atómica?" por Alfonso Jesús Población Sáez (09/05/2022) "El legado perdido de Pappus de Alejandría que dio lugar a unas nuevas matemáticas" por Alfonso Jesús Población Sáez (02/05/2022) "El caso en el que el círculo y el cuadrado son lo mismo" por Alfonso Jesús Población Sáez (25/04/2022) "La solución al problema de los melones y cómo escribir 'amor' con números" por Alfonso Jesús Población Sáez (04/04/2022) "Un recorrido matemático por la primera línea de metro de Madrid''" por María Concepción Romo Santos (28/03/2022) "El 'teorema del suflé' o las matemáticas 'esponjosas''" por Pedro Alegría (21/03/2022) "Un reto para descubrir que no puedes con el número Pi" por Alfonso Jesús Población Sáez (14/03/2022) "Rodríguez Vidal, el matemático humanista que puso en valor a los científicos aragoneses" por Alfonso Jesús Población Sáez (07/03/2022) "La increíble vida de Luis Raluy, el payaso matemático fascinado por la 'Teoría de Números'" por Pedro Alegría (28/02/2022) "Las matemáticas 'ocultas' tras la Catedral de Burgos" por Alfonso Jesús Población Sáez (21/02/2022) "Qué es blockchain y por qué puede llevar a un mundo sin corrupción" por Lierni Ortiz Elorza (14/02/2022) "¿Ha resuelto un profesor de Harvard el antiguo problema de las damas del ajedrez?" por Alfonso Jesús Población Sáez (07/02/2022) "El reto matemático: El crimen de la mujer muerta en su casa de Pirineos, resuelto con grafos" por Víctor M. Manero (31/01/2022) "Ni profecía ni maldición en la Alhambra, solo matemáticas" por Alfonso Jesús Población Sáez (24/01/2022) "¿Pueden las matemáticas resolver un crimen?" por Víctor M. Manero (17/01/2022) "¿Una 'profecía matemática' en la Alhambra?" por Alfonso Jesús Población Sáez (10/01/2022) "Tres ciudades andaluzas, vistas con ojos matemáticos" por Alfonso Jesús Población Sáez (03/01/2022) "Trigonometría, el puente que une todas las matemáticas" por Alfonso Jesús Población Sáez (13/12/2021) "Lo que las matemáticas han cambiado nuestras vidas" por Alfonso Jesús Población Sáez (29/11/2021) "Fractales: las formas que simulan a la naturaleza" por Alfonso Jesús Población Sáez (22/11/2021) "Las ecuaciones matemáticas para adelgazar, ¿son fiables?" por Alfonso Jesús Población Sáez (15/11/2021) "Egmont Colerus y sus matemáticas para todos" por Alfonso Jesús Población Sáez (08/11/2021) "Fórmulas y ecuaciones: cómo perderle el miedo al lenguaje de las matemáticas" por Alfonso Jesús Población Sáez (02/11/2021) "Los límites matemáticos de la amistad, la enemistad y el Big Data" por Ernesto Estrada (25/10/2021) "Investigadores del MIT solucionan un problema matemático de hace 70 años" por Alfonso Jesús Población Sáez (18/10/2021) "¿El portero Buffon es imbatible en 'piedra, papel o tijera'? Una explicación matemática" por Diego Alonso Santamaría (11/10/2021) "La paradoja de Russell o cómo explotar los cimientos de las matemáticas" por Urtzi Buijs y Miriam González (04/10/2021) "Por qué hay más posibilidades en una baraja de cartas que átomos en la Tierra" por Alfonso Jesús Población Sáez (27/09/2021) "Recomendaciones matemáticas para el verano" por Alfonso Jesús Población Sáez (28/06/2021) "Sí, las matemáticas resuelven problemas reales y estos son algunos ejemplos" por Alfonso Jesús Población Sáez (21/06/2021) "El profesor de matemáticas bilbaíno que hacía bailar a los números" por Alfonso Jesús Población Sáez (14/06/2021) "¿Cómo se resuelve el problema de 'los 36 oficiales'?'" por Alfonso Jesús Población Sáez (07/06/2021) "El 'cuadrado mágico de Foz', los 'fozudokus' y las matemáticas llegadas desde Lugo'" por Alfonso Jesús Población Sáez (31/05/2021) "Reglas, compases y papiroflexia para cuadrar círculos y contentar a Apolo" por Iván Blanco Chacón (24/05/2021) "¿A más seguidores, más éxito?: las matemáticas detrás de los 'influencers' y de las redes sociales'" por Ernesto Estrada (17/05/2021) "El italiano que ganó dos premios millonarios en 15 días con un 'rasca y gana'" por Alfonso Jesús Población Sáez (10/05/2021) "Metagrobología o cómo aprender matemáticas jugando con rompezabezas" por Alfonso Jesús Población Sáez (03/05/2021) "Las Cadenas de Markov: las matemáticas que nos enseñó una serie de televisión" por Alfonso Jesús Población Sáez (26/04/2021) "¿Qué son las 'Matemáticas Singapur'?" por Pedro Ramos Alonso (19/04/2021) "Los científicos que demostraron la cuadratura del cuadrado" por Pedro Alegría (12/04/2021) "El truco matemático para organizar las mesas en un banquete de bodas" por Alfonso Jesús Población Sáez (29/03/2021) "¿Son siempre paralelas las ruedas delanteras de un coche? Y otras cosas que aprender en el mes de las matemáticas" por Alfonso Jesús Población Sáez (15/03/2021) "Por qué hoy se celebra el Día del número Pi" por Alfonso Jesús Población Sáez (14/03/2021) "El misterio geométrico resuelto por Desargues" por Víctor M. Manero (08/03/2021) "Un reto muy geométrico" por Víctor M. Manero (01/03/2021) "Y esto, ¿para qué sirve?" por Alfonso Jesús Población Sáez (22/02/2021) "Evariste Galois, la amarga historia del 'enfant terrible' del álgebra" por Iván Blanco Chacón (15/02/2021) "Cómo animar a las niñas a romper la brecha de género y estudiar ciencias" por Mireia López Beltrán (11/02/2021) "Demostrar no es verificar: ¿podrías encontrar la solución a estos problemas matemáticos?" por Alfonso Jesús Población Sáez (01/02/2021) "El misterio del número 77" por Alfonso Jesús Población Sáez (25/01/2021) "La conjetura de Collatz: un problema «sencillo» que desafiará tu intuición" por Víctor M. Manero y Alfonso Jesús Población Sáez (18/01/2021) "Arquímedes y la medida del círculo" por Urtzi Buijs y Miriam González (11/01/2021) "Alicia en el país de las matemáticas", por Víctor M. Manero (21/12/2020) "La geometría que sostenía al telescopio de Arecibo hasta que se derrumbó" por Pedro Alegría (14/12/2020) "El enigma de los números primos: Del hueso de Ishango al problema del Milenio" por Iván Blanco Chacón (07/12/2020) "Mariano Mataix: el desconocido autor de «Droga matemática» que mostró la diversión tras los números" por Alfonso Jesús Población Sáez (30/11/2020) "El «secreto» matemático que une a los planetas con los conciertos de rock" por Ernesto Estrada (23/11/2020) "El ojo de Horus: ¿Qué es eso de la fracción egipcia?" por Pedro Alegría (16/11/2020) "El griego Eratóstenes contra los terraplanistas", por Víctor M. Manero (09/11/2020) "Los números de Friedman, cuando los números están dentro de los números" por Alfonso Jesús Población Sáez (02/11/2020) "James Randi y otros genios de la magia y las matemáticas" por Fernando Blasco (26/10/2020) "La demostración matemática o cómo llegar a la verdad invariable y eterna de los teoremas", por Víctor M. Manero (29/10/2020) "Matemáticas para la privacidad en un mundo post-cuántico" por Iván Blanco Chacón (11/10/2020) "La primera gran crisis de los matemáticos: las magnitudes inconmensurables" por Urtzi Buijs y Miriam González (05/10/2020) "El truco detrás del «misterioso» número 37 y otras fórmulas matemáticas virales" por Alfonso Jesús Población Sáez (28/09/2020) "Recomendaciones de un matemático para el verano" por Alfonso Jesús Población Sáez (06/07/2020) "Los números también saben mantener la distancia de seguridad" por Pedro Alegría (29/06/2020) "El origen matemático del dígito de control «escondido» en tu DNI", por Víctor M. Manero (22/06/2020) "Las probabilidades de tener el covid-19 si hacemos caso a Bayes" por Alfonso Jesús Población Sáez (15/06/2020) "De médicos, porcentajes y falsos positivos" por Alfonso Jesús Población Sáez (08/06/2020) "¿Cuántas personas te pueden besar a la vez?" por Alfonso Jesús Población Sáez (01/06/2020) "¿Qué tienen en común algunos tipos de patatas fritas, las pompas de jabón y las centrales nucleares?", por Víctor M. Manero (25/05/2020) "La «im-posible» cuadratura del círculo" por Pedro Alegría (18/05/2020) "Día Internacional de la Mujer Matemática: Mirzakhani, referentes y estereotipos" por Begoña Barrios Barrera, Rosa Crujeiras Casais, Patricia Contreras Tejada e Irene Epifanio López (11/05/2020) "Matheminecraft: El lugar donde las matemáticas y los videojuegos se encuentran" por Alfonso Jesús Población Sáez (04/05/2020) "El método Moore o cómo aprender matemáticas al estilo tejano" por Pedro Alegría (27/04/2020) "Los acertijos matemáticos que dejó John Conway, fallecido por coronavirus" por Fernando Blasco (20/04/2020) "La ley Benford: ¿Por qué hay más números que comienzan por uno que por otro dígito?", por Víctor M. Manero (13/04/2020) "Matemáticas contra una pandemia" por David Gómez-Ullate Oteiza (30/03/2020) "En busca del «einstein» perdido por los suelos" por Pedro Alegría (30/03/2020) "La banda de Möbius, la superficie que solo tiene una sola cara", por Víctor M. Manero (23/03/2020) "Todo lo que debes saber de Pi, el número que fascina a los matemáticos" por Fernando Blasco (14/03/2020) "Resolver un problema matemático visualmente es posible" por Urtzi Buijs y Miriam González (09/03/2020) "¿Existe la caja perfecta? Así la encuentra un matemático" por Alfonso Jesús Población Sáez (02/03/2020) "El teorema de Fermat: hasta los genios se equivocan" por Pedro Alegría (24/02/2020) "Las matemáticas que revelan el techo de cristal de las mujeres en ciencia" por Rosa Crujeiras Casais, Irene Epifanio López y Teresa Sánchez Rúa (17/02/2020) "¿Por qué 2020 es un año bisiesto? No es tan sencillo como crees" por Víctor M. Manero (10/02/2020) "Las matemáticas que hay detrás de las baldosas" por Alfonso Jesús Población Sáez (03/02/2020) "Los secretos matemáticos del embaldosado" por Alfonso Jesús Población Sáez (27/01/2020) "El paralaje, el cálculo matemático para medir la distancia a las estrellas" por Víctor M. Manero (20/01/2020) "Reflexiones de un matemático al comienzo del año" por Alfonso Jesús Población Sáez (13/01/2020) "¿Quieres regalar juguetes? ¿Por qué no regalar un cubo?" por Fernando Blasco (23/12/2019) "Un matemático explica las probabilidades reales de que te toque el Gordo" por Alfonso Jesús Población Sáez (16/12/2019) "La razón áurea: verdades y mitos del número «mágico»" por Fernando Blasco (09/12/2019) "Cómo ayudan las matemáticas a entender el cambio climático" por Fernando Blasco (02/12/2019) "Para qué sirven los logaritmos: dos retos sin usar la calculadora" por Alfonso Jesús Población Sáez (25/11/2019) "¿Para qué sirven realmente los logaritmos?" por Alfonso Jesús Población Sáez (18/11/2019) "Por qué un matemático no dejaría tirar faltas a Cristiano Ronaldo" por Diego Alonso Santamaría (17/11/2019) "La sociedad secreta de Pitágoras y el «superpoder» de los números figurados" por Urtzi Buijs y Miriam González (04/11/2019) "Matemáticos descubren una nueva forma de multiplicar números grandes" por Alfonso Jesús Población Sáez (28/10/2019) "¿Eres capaz de resolver estos ingeniosos acertijos matemáticos de Martin Gardner?" por Fernando Blasco (21/10/2019) "Las matemáticas detrás del sistema electoral: ¿por qué el voto de un madrileño vale menos?" por Fernando Blasco (14/10/2019) "La «regla del siete» que sí funciona y no te explicaron en la escuela" por Alfonso Jesús Población Sáez (07/10/2019) "Matemáticos encuentran una nueva forma de llegar al número 3" por Alfonso Jesús Población Sáez (30/09/2019) "La serie de Grandi y la «no demostración» de la existencia de Dios" por Maria Pilar Sabariego Arenas (23/09/2019) "Divulgación de las matemáticas: Ellas fueron las primeras" por Alfonso Jesús Población Sáez (16/09/2019) "Cómo averiguar el número de pelos en las cabezas de los madrileños por el principio del palomar" por Alfonso Jesús Población Sáez (01/07/2019) "Curiosidades matemáticas detrás del solsticio de verano" por Fernando Blasco (24/06/2019) "El problema con el que Federico II retó a uno de los matemáticos más asombrosos de la Historia" por Alfonso Jesús Población Sáez (17/06/2019) "Ocho edificios formidables de España con un uso magistral de las matemáticas" por Fernando Blasco (10/06/2019) "El gúgol y otras cantidades matemáticas gigantescas" por Alfonso Jesús Población Sáez (03/06/2019) "Luca Pacioli, el amigo matemático de Da Vinci amante de la divina proporción" por Fernando Blasco (27/05/2019) "Omar Khayyam, el matemático persa al que le debemos que la incógnita sea una X" por Alfonso Jesús Población Sáez (20/05/2019) "Qué es un billón y por qué nos confunde tanto" por Alfonso Jesús Población Sáez (13/05/2019) "El bello mundo de los números imposibles" por Juan Matías Sepulcre Martínez (06/05/2019) "Las asombrosas fórmulas matemáticas desarrolladas por un profesor español" por Alfonso Jesús Población Sáez (29/04/2019) "Solucionan el diabólico acertijo matemático que no ha podido ser resuelto en 64 años" por Alfonso Jesús Población Sáez (08/04/2019) "El hombre que ha propuesto más de 300 problemas de matemáticas" por Alfonso Jesús Población Sáez (01/04/2019) "¿Quién resolverá el teorema de Fermat llevado al cubo?" por Pedro Alegría (25/03/2019) "Los misterios del número Pi aún sin resolver" por Alfonso Jesús Población Sáez (14/03/2019) "Regresa el reto matemático: desvelando lo que las sumas esconden" por Alfonso Jesús Población Sáez (11/03/2019) "Un reto matemático: lo que se esconde en una suma" por Alfonso Jesús Población Sáez (04/03/2019) "Recta o curva: ¿cuál crees que es la forma perfecta de un tobogán?" por Alfonso Jesús Población Sáez (25/02/2019) "¿Es cierto el mito de que la ciencia avanza más rápido en tiempo de guerra?" por Fernando Corbalán (18/02/2019) "El comportamiento secreto de los números primos en espiral" por Pedro Alegría (11/02/2019) "¿De dónde salen los números de la tabla periódica?" por Miquel Duran y Fernando Blasco (04/02/2019) "Siete consejos para que los niños no odien las matemáticas" por David Orden Martín (02/02/2019) "Por qué crees que has visto una película entera pero en realidad te has perdido la mitad" por Alfonso Jesús Población Sáez (20/01/2019) "El problema sin solución al que ha llevado la inteligencia artificial" por Alfonso Jesús Población Sáez (14/01/2019) "Por qué 2019 es un número feliz, según las matemáticas" por Fernando Corbalán (08/01/2019) "La increíble técnica de construción que Da Vinci esbozó en su misterioso «Codex Atlanticus»" por Guido Ramellini y Alfonso Jesús Población Sáez (17/12/2018) "Los secretos de la cultura vaccea, al descubierto gracias a las matemáticas" por Ana María Portillo de la Fuente (10/12/2018) "El algoritmo de Tarry o cómo salir de un laberinto a la primera" por Ángel Martín del Rey (03/12/2018) "La cifra Vigenère: el misterioso código que se tardó tres siglos en descifrar" por Alfonso Jesús Población Sáez (20/11/2018) "Las matemáticas que se esconden detrás de la seguridad del coche autónomo" por Alfonso Jesús Población Sáez (12/11/2018) "La fórmula que predecía quién ganaba un combate aéreo en la Primera Guerra Mundial" por Ángel Martín del Rey (29/10/2018) "¿Eres capaz de resolver estos seis problemas de ingenio?" por Pedro Alegría (22/10/2018) "Los ingenuos mensajes cifrados de los espías españoles en tiempos de los Reyes Católicos" por Alfonso Jesús Población Sáez (16/10/2018) "Te presento al escutoide, la forma geométrica que te da forma" por Clara Grima (30/07/2018) "Cuatro verdades matemáticas que no son como se creía" por Pedro Alegría (24/07/2018) "El matemático que propuso cortar un nudo gordiano (y aprender algo en el camino)" por Alfonso Jesús Población Sáez (16/07/2018) "Otro millón de dólares te espera: ¿Es P = NP?" por Alfonso Jesús Población Sáez (10/07/2018) "Cómo atarte los zapatos, aparcar tu coche y otros problemas cotidianos resueltos por las matemáticas" por Clara Grima (02/07/2018) "¿Cuál es la probabilidad de que España gane el Mundial de Rusia? Un matemático responde" por Alberto Márquez (26/06/2018) "Matemáticas para acertar quién ganará el Mundial de Rusia" por Clara Grima (19/06/2018) "Las matemáticas escondidas en la ciudad de Praga" por Fernando Corbalán (14/06/2018) "Muere el matemático brasileño que pensaba «bonito»" por Isabel Fernández (08/05/2018) "Las matemáticas que descifraron la máquina «Enigma» de los nazis" por Paz Jiménez Seral y Manuel Vázquez Lapuente (30/04/2018) "Por qué no hicieron falta extraterrestres para construir las pirámides" por Alfonso Jesús Población Sáez (23/04/2018) "La aritmética del reloj que practicas cada día sin saberlo" por Urtzi Buijs (16/04/2018) "La curva que logró un gol histórico a 40 metros" por Fernando Corbalán (10/04/2018) "La solución matemática más larga de la Historia" por Pedro Alegría (03/04/2018) "Diez curiosidades sobre el número Pi para celebrar su día" por Fernando Corbalán (14/03/2018) "¿Qué tiene de especial el número 78.557?" por Alfonso Jesús Población Sáez (12/03/2018) "La cicloide, la curva más rápida posible" por Fernando Corbalán (06/03/2018) "Así transforman una cara en otra con matemáticas" por David Orden Martín (26/02/2018) "El puzle que hizo enloquecer a una generación un siglo antes de Rubik" por Pedro Alegría (19/02/2018) "El número de Euler, la otra constante que está en todas partes" por Fernando Corbalán (13/02/2018) "Florence Nightingale, la enfermera que salvó miles de vidas con una rosa" por Clara Grima (05/02/2018) "El teorema más largo de la Historia y otras «monstruosidades» matemáticas" por Alfonso Jesús Población Sáez (29/01/2018) "Sangaku, los problemas matemáticos sagrados de los japoneses" por Fernando Fouz (23/01/2018) "Por qué 2018 es un año pitagórico" por Fernando Corbalán (15/01/2018) "El problema del caballo, el intrincado enigma matemático en el que no se puede repetir" por Pedro Alegría (08/01/2018) "Las matemáticas escondidas detrás de las pinturas de Jackson Pollock" por Fernando Corbalán (18/12/2017) "La peor metedura de pata en el homenaje al matemático del Juego de la vida" por Clara Grima (12/10/2017) "Siempre toca fuera, mejor comprar antes y otras absurdas ideas sobre el Gordo de Navidad" por Fernando Corbalán (04/12/2017) "Shalosh B. Ekhad: El matemático sin alma que resolvió el teorema cosmológico de Conway" por Raúl Ibáñez Torres (29/11/2017) "El genial matemático «tartaja» que lanzó por despecho el gran desafío algebraico de Milán" por Fernando Corbalán (13/11/2017) "Las matemáticas que puede esconder un dónut" por Alfonso Jesús Población Sáez (03/11/2017) "El teorema matemático para que nadie se quede sin pareja" por Pedro Alegría (23/10/2017) "Problemas del Milenio: La conjetura BSD o por qué las matemáticas están reñidas con la charlatanería" por Alfonso Jesús Población Sáez (16/10/2017) "El examen de matemáticas de Cambridge que causaba crisis nerviosas" por Raúl Ibáñez Torres (09/10/2017) "Cuando al 4 de octubre le siguió el día 15 y otros grandes líos del calendario" por Fernando Fouz (02/10/2017) "Los cuadrados mágicos que aún nadie ha podido resolver y se premian con 6.500 euros" por Pedro Alegría (25/07/2017) VIDEO:"El enigma matemático detrás del «problema de Monty Hall»" (23/07/2017) "Tres ¿sencillos? desafíos matemáticos para el verano" por Fernando Corbalán (17/07/2017) VIDEO:"Por qué se venden por docenas y otras curiosidades (matemáticas) de los huevos" (16/07/2017) "Así resuelve un matemático una suma insólita" por Alfonso Jesús Población Sáez (10/07/2017) "¿Eres capaz de resolver estos siete problemas matemáticos? Un chaval de 13 años lo hizo" por Alberto Márquez Pérez (03/07/2017) "La hipótesis de Riemann, el más codiciado de los problemas del milenio" por Alfonso Jesús Población Sáez (27/06/2017) "El problema matemático de la cuerda anudada que dice si te puedes casar" por Fernando Corbalán (19/06/2017) "Este cálculo matemático es una antigualla, ¡pero funciona!" por Luis Rández (12/06/2017) "¿Cuál es el punto sobre la superficie terrestre más cercano al Sol?" por Fernando Fouz (05/06/2017) "El sorteo por apellidos: la gran injusticia de la administración" por Clara Grima (30/05/2017) "La paradoja del cumpleaños, el problema matemático que puedes probar en tu agenda" por Fernando Corbalán (22/05/2017) "El dilema de los cien prisioneros" por Clara Grima (16/05/2017) "De Pitágoras a la conjetura del millón de dólares" por Pedro Alegría (08/05/2017) "Las ecuaciones que nadie ha conseguido resolver y que valen un millón de dólares" por Alfonso Jesús Población Sáez (02/05/2017) "El diagrama de Voronoi, la forma matemática de dividir el mundo" por Clara Grima (24/04/2017) "Eva Miranda: «En España tenemos un importante capital humano en investigación matemática»" por Fernando Corbalán (17/04/2017) VIDEO:"El curioso motivo por el que las tapas de alcantarilla son redondas" (10/04/2017) "El caso de los 14 pentágonos que embaldosan un espacio infinito" por Pedro Alegría (10/04/2017) "El matemático que usa calculadora y otros tópicos sobre los números" por Fernando Corbalán (04/04/2017) "¿Pero qué son las ondículas y por qué han ganado el «nobel» de matemáticas?" por Alfonso Jesús Población Sáez (28/03/2017) VIDEO: "Yo soy Pi, la constante que contiene todos los números del mundo" (27/03/2017) "Matemáticas para ganar un millón de dólares" por Alfonso Jesús Población Sáez (21/03/2017) "Día de Pi: Cuando el número Pi pudo ser 3,2" por Pedro Alegría (14/03/2017) "Los desafíos de Pi, el número de cifras infinitas" por Fernando Corbalán (07/03/2017)

Lunes, 27 de Junio de 2022 | Imprimir | PDF |  Correo electrónico