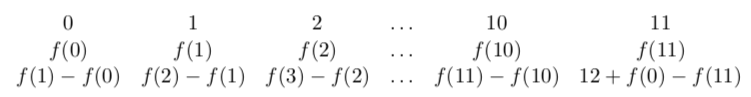531. La aproximación de Padé

El matemático Henri Padé (1863-1953) nació un 17 de diciembre. Es sobre todo conocido por el desarrollo de métodos de aproximación de funciones mediante funciones racionales: es la aproximación de Padé, descrita en su tesis doctoral que realizó bajo la supervisión de Charles Hermite. Esta técnica propuesta por Padé proporciona una mejor aproximación de la función que  la obtenida al truncar su serie de Taylor, y además es válida incluso en los casos en los que la serie de Taylor no es convergente. Más información: H. Padé, Sur la représentation approchée d’une fonction par des fractions rationnelles, Annales scientifiques de l’É.N.S. 3 série, tome 9 (1892), 3-93 H. Padé, Mémoire sur les développements en fractions continues de la fonction exponentielle, pouvant servir d’introduction à la théorie des fractions continues algébriques, Annales scientifiques de l’É.N.S. 3 série, tome 16 (1899), 395-426 H. Padé,  Recherches sur la convergence des développements en fractions continues d’une certaine catégorie de fonctions, Annales scientifiques de l’É.N.S. 3 série, tome 24 (1907),  341-400 La aproximación de Padé La aproximación de Padé de la función exponencial Padé Approximants, Wolfram Demonstrations Project Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Martes, 17 de Diciembre de 2019 | Imprimir | PDF |  Correo electrónico

532. Un matemático explica las probabilidades reales de que te toque el Gordo

ABC, 16 de Diciembre de 2019 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 16 de Diciembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

533. El primer libro impreso de aritmética: L’Arte dell’Abbaco

El primer libro impreso de aritmética se publicó en 10 de diciembre de 1478, en Treviso (Italia). Se titulaba L’arte dell’abaco –el arte del ábaco– y su autor, desconocido, fue probablemente un sacerdote. Arte dell’Abbaco El texto está escrito en dialecto veneciano. Tiene 123 páginas, de 32 líneas cada una, no numeradas, con amplios márgenes, algunos de ellos con notas manuscritas. Incluye información tomada del Liber Abaci de 1202, como la multiplicación de celosía. Más información: L’Arte dell’Abbaco, Calion The First Dated Printed Book on Arithmetic and the Operation of the Abacus, History of information Wikipedia Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Martes, 10 de Diciembre de 2019 | Imprimir | PDF |  Correo electrónico

534. La razón áurea: verdades y mitos del número «mágico»

ABC, 9 de Diciembre de 2019 CIENCIA - El ABCdario de las matemáticas Fernando Blasco

Lunes, 09 de Diciembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

535. 103. (Diciembre 2019) Re-escalando música

Tras la serie de artículos Serialismo y matemática que ha ido de septiembre a noviembre de 2019, Celia Rubio, su autora, me presentó un cuarto texto, Re-escalando música. Este texto constituye la columna de diciembre de 2019. Es de nuevo una inmensa fortuna contar con la colaboración de Celia Rubio. Dejamos al lector con el placer de su escritura y concepto. 1. La visión artística de Schoenberg En julio de 1921, tras haber ideado los fundamentos del dodecafonismo, Schoenberg hizo el siguiente anuncio a su discípulo Josef Rufer [7]: He realizado un descubrimiento que asegurará la supremacía de la música alemana durante los próximos cien años. Durante la mayor parte de su vida, Schoenberg creyó que el público general acabaría aceptando la música dodecafónica del mismo modo que se habían aceptado los distintos sistemas tonales desde hacía siglos. Para él, la naturalidad del sistema dodecafónico residía en que era un paso más en el proceso musical histórico: desde el contrapunto y el desarrollo motívico, practicado por los grandes maestros de la tradición alemana, hasta la disolución de la tonalidad, anticipada por la música postwagneriana e impresionista. Todo era parte de un continuo, del desarrollo de la historia de la música. En palabras de Schoenberg [6]: Yo creo que la composición con doce sonidos, y la que muchos llaman erróneamente “música atonal”, no es el final de un viejo período, sino el comienzo de otro nuevo. Una vez más, como hace dos siglos, hay algo a lo que se llama anticuado; y una vez más, no se trata de ninguna obra en particular, [...] sino que otra vez sucede que es un estilo el condenado al ostracismo. Tras la muerte de Schoenberg en 1951, y durante algunas décadas más, su sistema compositivo fue venerado por los compositores jóvenes más brillantes (véase [4]), pero pronto se desvaneció de las salas de conciertos. El serialismo siempre se consideró una música académica, difícil de entender, apenas musical sino teórica. La complejidad de percibir esta música meramente por su estructura formal impidió, y todavía impide, que se disfrutara más allá de su estudio. Schoenberg intentó eximirse de culpa y a su vez culpó al oyente, quien según él creyó que no se esforzaba lo suficiente [6]: La composición con doce sonidos no tiene otra finalidad que la comprensión. A la vista de ciertos acontecimientos en la historia musical reciente, esto puede causar asombro, ya que las obras escritas en este estilo no han sido entendidas [...] Solo el compositor perfectamente preparado será quien componga para el oyente musical igualmente bien dispuesto. Al contrario de lo que Schoenberg creía, incluso el oyente experto, el que describe T. W. Adorno en su “Introducción a la sociología de la música” [1], tiene grandes dificultades para distinguir auditivamente todos los elementos que caracterizan el serialismo. Somos capaces de retener, a lo sumo, motivos de seis o siete notas, pero no de doce [3]; mucho menos de reconocer si una serie es transformación de otra. ¿En qué medida afectan las reglas dodecafónicas al discurso sonoro de una pieza? El dodecafonismo puede atribuirse el haber prescindido de algunas de las preconcepciones musicales más arraigadas, como la melodía, la consonancia o la tonalidad. Pero precisamente por eso es impopular, porque toma la disonancia y la pone al frente de toda la composición. Para Schoenberg, la aprobación del público no era el objetivo de su arte, y, de hecho, el desagrado colectivo era un signo del alto nivel artístico y espiritual [6]: El valor de mercado es irrelevante para el valor intrínseco (de la música). Un juicio no cualificado puede como máximo decidir el valor de mercado —un valor que puede ser inversamente proporcional al valor intrínseco. Ningún artista, ningún poeta, ningún filósofo y ningún músico, cuyo pensamiento se desenvuelva en la más alta esfera, habrá de descender a la vulgaridad para mostrarse complacientes con un eslogan tal como “Arte para todos”. Porque si es arte no será para todos, y si es para todos no será arte. Sin embargo, el rechazo a no ser rechazado ha dejado de tener cabida en nuestro contexto artístico. El academicismo ya no es excluyente a la divulgación o a la búsqueda de belleza sensorial. De las técnicas serialistas se puede tomar aquello que es interesante intelectualmente e incorporarlo a otras técnicas. Este es el experimento que he querido, con humildad, proponer: despojar al serialismo de uno de los elementos que provoca más rechazo: la disonancia extrema. Ya que esta proviene del cromatismo, el propósito del experimento es utilizar escalas que tengan menos intervalos de semitono para crear con ellas un pseudo-serialismo de menos notas. Se han modificado las notas de varias obras dodecafónicas ya existentes, mientras que el ritmo, la duración, el timbre y las dinámicas, que siguen siendo producto de los compositores originales, se han dejado intactas. El propósito final es intentar conservar la estructura matemática subyacente renovando, en cambio, la percepción colectiva de estas músicas. Para describir el proceso de modificación de las obras debemos definir lo que se entiende por escala y cuáles son las funciones óptimas entre escalas. 2. Escalas y funciones del experimento 2.1. Escalas interválicas, escalas y funciones Una escala interválica es una secuencia ordenada de números naturales – una secuencia de intervalos entre notas – tales que la suma de todos ellos da 12. Así solo consideramos válidas las escalas equivalentes octava a octava. Esto debe ocurrir para poder considerar transformaciones de la escala cromática en escalas menores, aunque es generalizable a cualquier longitud. Diremos entonces que la escala cromática es la súper-escala de las sub-escalas con las que trabajaremos. Por ejemplo, la escala diatónica jónica (o escala mayor) tiene como secuencia de distancias (2, 2, 1, 2, 2, 2, 1) cuando se miden en semitonos. Dada una escala interválica de longitud ℓ y una nota fija inicial, la secuencia de intervalos se convierte en una secuencia de notas de longitud ℓ+1. Se construye comenzando por la nota inicial y sumando cada intervalo para conseguir la nota siguiente. Con la escala mayor y la nota Re se consigue (Re, Mi, Fa#, Sol, La, Si, Do#, Re), ya que es equivalente a (2, 2+2=4, 4+2=6, 6+1=7, 7+2=9, 9+2=11, 11+2=13, 13+1=14). Por construcción, la última nota debe ser equivalente a la primera, ya que en el último paso habremos sumado a la nota inicial todos los términos de la secuencia interválica, y por definición suman 12. De esta forma, se puede definir una escala-k como el conjunto de notas generadas por una escala interválica desde la nota k. Por ejemplo, el conjunto anterior sería la escala-2 mayor; es decir, la escala de Re mayor. Una escala generada por una secuencia de intervalos con longitud ℓ tiene ℓ notas, ya que como la última es repetida no hay por qué considerarla. Su longitud ℓ ≤ 12, ya que una escala-k definida de esta forma siempre es un subconjunto de la escala cromática: Ek ⊆ ℤ∕(12). Al generalizarlo a cualquier súper-escala, habría que considerar las notas distintas según su escala o formular otras definiciones más adecuadas. Una función a una escala-k es una función f que transforma cada nota de la escala cromática a un valor de la escala Ek. Entonces f : ℤ∕(12) → Ek* reduce las notas de una melodía a solamente la escala escogida, donde Ek* está formado por las notas de Ek pero quizás en octavas distintas. Las funciones a escalas se representan de la siguiente manera, con la primera fila representando el dominio de f (la escala cromática); la segunda su imagen (la escala con repeticiones y en distintas octavas, Ek*); y la tercera su secuencia interválica, que es de interés, ya que coincide con la escala interválica de partida salvo en los valores nulos. El proceso verdaderamente interesante está en averiguar, dada una escala E, cuál es la mejor función que transforma melodías cromáticas en melodías en E. Estas son las funciones E-inducidas. ¿Cuáles serán las características de esas funciones óptimas? Deben ser sobreyectivas: si no, la música resultante tendría una escala más reducida de la deseada. Pero además deben conservar la estructura serial y deben conservar el parecido con la melodía original. 2.2. Funciones bien distribuidas La mayor prioridad es conservar la estructura serial de las piezas; por tanto, todas las notas deben aparecer con la menor frecuencia posible, y se debe evitar jerarquías entre las notas en la medida de lo posible. Si |E| < 12, f no puede ser inyectiva, por lo que va a haber elementos repetidos en la imagen. Queremos la f que mejor distribuya esas repeticiones, que distribuya las notas de E a lo largo de la escala cromática. Lo óptimo sería que todas tuvieran la misma frecuencia. Eso solo pasará cuando |E| divida a 12. Por ejemplo, si E = (entonces |E| = 6), existen funciones tales que cada nota de la imagen se repite exactamente 2 veces. La siguiente función E-inducida f cumpliría la condición de buena distribución: En cambio, si |E| no divide a 12 no hay funciones E-inducidas totalmente distribuidas. No existe una sola frecuencia que puedan compartir todas las notas de E. Sin embargo, sí se pueden encontrar dos frecuencias consecutivas, c y c + 1, tales que todos los elementos de E tengan o frecuencia c o frecuencia c + 1. Esto es lo más parecido a que todas tengan la misma frecuencia, y se va a probar a continuación que siempre es posible. La situación es equivalente a que E se pueda dividir en dos subconjuntos disjuntos Q y R, con |Q| = q y |R| = r (entonces q + r = |E|), tales que la frecuencia de las notas en Q es c y la frecuencia de las notas en R es c + 1. En resumen, para probar que Q y R existen, debemos encontrar un c, un q y un r naturales para los que cq + (c + 1)r = 12. En efecto: cq + (c+ 1)r = cq + cr + r = c(q + r)+ r = c|E|+ r = 12 lo cual se cumple por el algoritmo de la división, que asegura que al dividir 12 entre |E| existen su cociente c y su resto r ≥ 0, como queríamos probar. La siguiente tabla describe, para cada posible |E| en cada fila, la frecuencia óptima de sus elementos. Las columnas representan las frecuencias de los elementos, y los números de dentro son cada q y r (cuando es 0 no se escribe: no hay notas con esa frecuencia). Estas funciones forman parte del numeroso conjunto de elementos musicales de máxima regularidad. Un ejemplo importante de ellos son los ritmos euclídeos —para más información ver [2]. 2.3. Funciones E-inducidas Hay que pedir más requisitos a f para que no solo modifique las notas, sino que además las imágenes se parezcan lo máximo posible a sus preimágenes, a las notas originales. En esencia, lo que se busca es una escala a distancia mínima de la escala cromática en cuanto a unos criterios concretos. La manera matemática de formalizar esos criterios es definir una métrica para estas funciones; es decir, una manera de medir la distancia entre ellas para poder compararlas. La distancia d entre dos funciones f y g cualesquiera, d(f,g), debe cumplir estas propiedades básicas: 1. d(f,g) ≥ 0 3. d(f,g) = d(f,g) 2. d(f,g) = 0 ⇔ f = g 4. d(f,g) ≤ d(f,h) + d(h,g) La métrica que he escogido para comparar las funciones consiste en restar sus imágenes una a una, tomar el valor absoluto de esas diferencias y sumarlas: d(f,g) = ∑i=011|f(i) - g(i)|. Esto nos da una idea de cómo de “lejos” se encuentran una de la otra, y cumple los axiomas de una métrica. Nos interesa entonces encontrar la función más cercana a la función identidad, es decir, la que enviaría la escala cromática a sus mismas notas. Así se priorizan las funciones con el mayor número de puntos fijos —ya que el sumando en ese índice sería 0— , o que, al menos, se parezcan en su escala interválica asociada. Puede ocurrir que con esta manera de medir quede más de una función a distancia mínima. Entre ellas, yo he escogido la más grave, y así, dada cualquier escala E, su función E-inducida queda unívocamente determinada. En el enlace https://gitlab.com/dodecafonismo/f-inducida se encuentra el código en Haskell de un programa que, dado una escala, produce su función inducida óptima con las propiedades descritas anteriormente. En el código se puede escoger entre o bien encontrar la mejor función que use solamente las notas de la subescala dada, o bien permitir transposiciones de ésta —que conservan, aun así, la escala interválica asociada— y que es a lo que llamo “inducir la raíz”. También permite cambiar el dominio, o superescala, y que no sea la cromática, aunque en ese caso puede que la métrica definida no devuelva resultados tan intuitivos. 3. Modificación de partituras serialistas 3.1. Escalas utilizadas Las escalas escogidas para este experimento son cuatro escalas de distintos tamaños y sonoridades; desde el sonido oriental hasta el occidental clásico, pasando por el jazz moderno y el impresionismo. Son la escala pentatónica, la escala de tonos enteros, la escala heptafónica de do mayor y la escala octotónica. Estas son las funciones inducidas de dichas escalas según el algoritmo: 3.2. Obras modificadas Ahora se describirán las obras que pasarán por la modificación. Para abarcar distintos estilos compositivos y hacer este estudio más amplio, he escogido obras de los tres principales compositores dodecafónicos: Schoenberg, Berg y Webern. Sin embargo, no se han escogido obras de compositores posteriores ni serialistas integrales. Uno de los motivos es porque interesa en este estudio la relación entre los sonidos: no se modifican más que las alturas de las notas, y por tanto no se tiene en cuenta el resto de elementos musicales. Que estén compuestos serialmente no afecta a las conclusiones de este experimento. Por otro lado, los compositores posteriores a Schoenberg todavía no han pasado al dominio público. Eso impide, por desgracia, que se pueda trabajar libremente con su música. Por último, el hecho de que cada nota tenga su propia dinámica, su propia articulación o su propio timbre hace de las obras serialistas integrales difíciles de manipular. Además, como los audios están hechos mediante ordenador y no con intérpretes reales, la calidad y la intención musical de estas partituras tan complicadas nunca podrían plasmarse a la perfección. La primera obra que pasará por el algoritmo de modificación serial es la Suite para piano, Op. 25 de Schoenberg. Un análisis de esta pieza y de su contexto histórico se puede encontrar en [5]. Su serie principal es: La segunda obra es un arreglo para soprano y piano de una de las arias más destacadas de la segunda ópera de Alban Berg, Lulu. El libreto de la obra está basado en dos tragedias de Frank Wedekind: “El espíritu de la tierra” y “La Caja de Pandora”. El aria, llamada Lied der Lulu, es parte de una dramática disputa entre Lulu y su marido por las infidelidades de ella, que acaba con el homicidio accidental de él. La serie de Lulu es: La tercera, de 1936, es la única obra publicada de Anton Webern para piano solo: Variationen für Klavier, Op. 27, y se compone de tres movimientos: Sehr mässig, Sehr schnell y Ruhig fliessend. Su serie principal es: 3.3. Programa online de modificación de partituras He creado una página web online que transforma cada nota de una partitura a cualquier nota requerida, una a una. Este software sirve para no tener que modificar a mano las partituras del experimento, pero también puede servir para otros propósitos. Por ejemplo, para cambiar una partitura de mayor a menor, o viceversa. El programa solo admite partituras con formato Archivo Musescore sin Comprimir (.mscx) del software libre Musescore. En caso de tener la partitura en otro formato, debe abrirse en Musescore y guardarse en el formato correcto. Está escrita en Elm y el código puede encontrarse aquí. La aplicación web se encuentra en el siguiente enlace: https://modificaciones.netlify.com/. Sus instrucciones de uso se encuentran al final de la página web. 4. Conclusiones Todas las conclusiones que se pueden extraer de este experimento son enteramente subjetivas. El objetivo de realizarlo es poder seguir investigando con las propiedades matemáticas de la música, y analizar el impacto emocional que estas pueden causar. No se puede afirmar que la transformación mejore o empeore ninguna obra. En todo caso podemos interpretar qué transformaciones tienen un determinado sentido musical o estético, dependiendo de la escala utilizada o del estilo con el que estén compuestas. Tampoco debemos olvidar que el cromatismo siempre aportará a las obras una dimensión añadida, un elemento extra que ha impulsado gran parte de la innovación en la historia de la música. Quitarlo por completo es, en realidad, retroceder en la evolución del arte. En general, las transformaciones hexatónica y octotónica siguen conservando mucho del cromatismo que tiene la partitura original. Siguen sonando ajenas al oído tonal del oyente medio. Vamos a comentar algunas de las impresiones que generan las otras dos transformaciones en cada una de las obras, aunque dejaremos al lector que forme su propia opinión. 4.1. Obra de Berg: Lied der Lulu El estilo compositivo de Berg busca, en su mayor parte, acercarse a las formas tonales; maneja la falta de tonalidad serialista sin deshacerse de muchos elementos de la tradición musical. Sus melodías son fluidas y su fraseo inicia a conversar. Así, la transformación pentatónica (5) queda, quizás, algo simplista y repetitiva, y es en cambio la heptatónica (7) la que nos traslada a sonoridades más familiares. https://soundcloud.com/celiarubio/sets/berg-lied-der-lulu 4.2. Obra de Webern: Variationen op. 27 El estilo compositivo de Webern es rompedor y enigmático. Tanto fue así que su música sirvió de inspiración para el serialismo integral de los años 50. Sus melodías suenan fragmentadas y están llenas de intervalos de más de una octava. Es, por tanto, muy difícil que cualquier transformación que conserve similitudes melódicas con la partitura original pueda acercarse a músicas más convencionales. La esencia de esta obra está precisamente en su peculiaridad. https://soundcloud.com/celiarubio/sets/webern-op27-variations 4.3. Obra de Schoenberg: Suite op. 25 El estilo compositivo de Schoenberg en la Suite es tradicional, aunque busca nuevas sonoridades. Su principal objetivo es conservar la estructura formal anterior, y por ello lo único que aleja a la obra es el uso del serialismo en la altura de las notas. La obra es, en general, más armónica que melódica, ya que pretende simular texturas instrumentales del periodo barroco. Además, al centrarse tanto en la formalidad de la pieza aporta una riqueza separada del uso del serialismo. Por ello, la transformación pentatónica (5) no acaba siendo monótona sino muy sugestiva. Por otro lado, la elección concreta de la función transformativa, que hace predominar las notas do y sol —que aparecen en la nueva serie una vez más que el resto de notas— provoca que, en muchos casos, la obra simule estar en do mayor. Como en la partitura original predomina el intervalo de tritono re ♭ – sol, la transformación da peso al intervalo de quinta justa, que es la base de la armonía tradicional. La transformación heptatónica sigue dejando alguna disonancia debido a la existencia de semitonos entre las notas mi – fa y si –  do, y al tritono en fa – si. Al ser una obra ampliamente textural, muchos de estos intervalos aparecen con frecuencia. https://soundcloud.com/celiarubio/sets/schoenberg-op25-1-prelude https://soundcloud.com/celiarubio/sets/schoenberg-op25-2a-gavotte https://soundcloud.com/celiarubio/sets/schoenberg-op25-2b-musette https://soundcloud.com/celiarubio/sets/schoenberg-op25-3-intermezzo https://soundcloud.com/celiarubio/sets/schoenberg-op25-4a-menuet https://soundcloud.com/celiarubio/sets/schoenberg-op25-4b-trio https://soundcloud.com/celiarubio/sets/schoenberg-op25-5-gigue   Bibliografía [1] T.W. Adorno. Disonancias. Introducción a la sociología de la música. Continuum International Publishing Group Ltd., 1973. [2] Paco Gómez. Ritmos euclídeos y ritmos equilibrados, marzo de 2018. Consultado en octubre de 2019. [3] George A. Miller. The Magical Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information. Psychological Review, 63, 1956. [4] Celia Rubio Madrigal. Serialismo y matemáticas - II. Divulgamat, octubre de 2019. [5] Celia Rubio Madrigal. Serialismo y matemáticas - I. Divulgamat, septiembre de 2019. [6] Arnold Schoenberg. Style and Idea, 1950. [7] H. H. Stuckenschmidt. Schoenberg: his life, world, and work. Calder, 1977.

Martes, 03 de Diciembre de 2019 | Imprimir | PDF |  Correo electrónico

536. Mujeres matemáticas, las olvidadas que cambiaron el rumbo de la historia

ABC, 30 de Noviembre de 2019 CIENCIA Patricia Biosca

Sábado, 30 de Noviembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

537. “Para hacer matemáticas no hace falta ser un bicho raro”

El País, 29 de Noviembre de 2019 CIENCIA - ENTREVISTA A ALESSIO FIGALLI Luca Tancredi Barone

Viernes, 29 de Noviembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

538. Cómo ayudan las matemáticas a entender el cambio climático

ABC, 2 de Diciembre de 2019 CIENCIA - El ABCdario de las matemáticas Fernando Blasco

Lunes, 02 de Diciembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

539. 177. (Diciembre 2019) La posada mágica

Uno de los juegos clásicos de magia que casi todos conocemos desde nuestra infancia es el de la posada. ¿Lo recuerdas? Aparecen quince personajes, el cuatro de oros representa el posadero, los cuatro reyes, los cuatro caballeros y las cuatro sotas se representan a sí mismas y los cuatro ases hacen el papel de cuatro amigos. La posada tiene solo cuatro habitaciones así que llegan los cuatro amigos, el posadero les asigna una habitación a cada uno, llegan las cuatro señoritas pero, como no quedan habitaciones libres, cada una se hospeda en una de las habitaciones ya ocupadas, y así sucesivamente van llegando los cuatro caballeros y los cuatro reyes, que también van compartiendo las habitaciones ya ocupadas con el consiguiente enfado de unos y satisfacción de otros. Después del inevitable trasiego de habitaciones, representado por una mezcla de las cartas, al final se impone el orden y cada habitación está ocupada por un solo grupo de visitantes. Por la sencillez en su ejecución y el acompañamiento de una entretenida presentación, este juego ha sido y sigue siendo muy popular entre los principiantes aficionados a la magia. No explicaremos su funcionamiento, basado en propiedades de ordenación de las cartas, así que remitimos al lector interesado a consultar en la web las numerosas versiones del juego, como la que el mago Alfonso V muestra en este video. Como ya hemos adelantado, las matemáticas involucradas en el juego son muy simples: si tenemos un conjunto numérico según la secuencia 1-2-3-4-1-2-3-4-1-2-3-4-1-2-3-4, cualquier corte deja invariable la secuencia que alterna los cuatro números y, al repartirlos en cuatro montones, en cada montón aparecen los cuatro números iguales. Estas sencillas ideas se han utilizado en otros juegos, no menos clásicos ni populares, como el de los tres montones, también llamado el de las 21 cartas, y otros similares, algunos de los cuales han desfilado por este rincón (por ejemplo el de las cartas transpuestas descrito en abril de 2016). También se ha utilizado a modo de elemento didáctico en aulas de primaria, como se muestra en el portal "didáctica mágica". Como es natural, a lo largo del tiempo se han tratado de crear juegos que, a pesar de estar basados en las mismas ideas, oculten de algún modo el principio bajo el cual se apoyan con el fin de acrecentar las dosis de misterio y sorpresa. Uno de estos juegos es el ideado por Werner Miller, mago y matemático habitual en este rincón gracias a su incansable aportación a esta especialidad. El juego, titulado Lure, aparece en el primer libro de la colección Enigmaths, que consta de nueve volúmenes. Aunque el desarrollo de la acción pueda parecer similar al juego de la posada, se adapta más a una situación de punto fijo, como la mostrada en el número de octubre de 2019. Solo necesitaremos las veinte cartas con los valores del as al cinco de cada uno de los cuatro palos. Empieza colocando sobre la mesa y con las caras hacia arriba los cuatro ases en un montón, los cuatro doses en un segundo montón, y así sucesivamente, los cuatro cincos en un quinto montón. La situación será como la siguiente: Gira cara abajo las tres cartas superiores de cada montón, dejándolos en su misma posición. Quedará así: Recoge todas las cartas que están cara abajo, una a una, empezando por las cartas superiores y de izquierda a derecha, formando un paquete de cartas en la mano. Así pues, la primera carta recogida es la superior de la izquierda, luego la carta superior del siguiente montón, luego la superior del montón central, y así sucesivamente, hasta recoger las cinco cartas superiores de todos los montones. A continuación se repite la mismo operación empezando de nuevo por la izquierda y recogiendo las siguientes cinco cartas superiores. Por último se realiza la mismo operación con el resto de cartas cara abajo. Elige ahora un número del uno al cinco y confirma tu elección girando cara abajo la carta de la mesa que corresponde a dicho número. Con las cartas de la mano, pasa de arriba abajo del paquete tantas cartas como el número elegido. Así, por ejemplo, si el número elegido es el tres, sobre la mesa estará cara abajo el tres y cara arriba las otras cuatro cartas y, además, habrás pasado del paquete de la mano las tres cartas superiores a la parte inferior. Con las cartas de la mano, forma sobre la mesa dos montones repartiendo, caras hacia abajo, una a una todas las cartas sucesivamente a izquierda y derecha. Evidentemente, el segundo de los montones tiene una carta menos: coloca este montón sobre el otro para recomponer el paquete. Reparte nuevamente las cartas formando cinco montones: la primera carta sobre el as, la segunda sobre el dos, y así sucesivamente hasta repartir todas las cartas. Por último, gira todas las cartas caras hacia arriba: ¡Solo las cartas que están sobre el número elegido coinciden con dicho número! Comentarios finales: Una original adaptación del juego clásico de la posada que involucra a familias de números, como los números amigos, catalanes, narcisistas y vampiros, aparece en un libro de reciente publicación, del cual comentaremos en una próxima edición de este rincón. Por el momento, si quieres saber más sobre estas y otras familias de números, puedes consultar el libro Momentos entretenidos con los números de Jesús Escudero o la colección completa que aparece en el portal Math Goodies. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Lunes, 02 de Diciembre de 2019 | Imprimir | PDF |  Correo electrónico

540. 146. De noche todos los gatos son pardos

¿Cuál sería el contexto, fuera de las Matemáticas, en el que la gente hablaría de triángulos? Pues de eso va la cosa, de triángulos amorosos y números de Fibonacci. Ficha Técnica: Título: Después de medianoche. Título Original: Dopo mezzanotte. Nacionalidad: Italia, 2004. Dirección: Davide Ferrario. Guion: Davide Ferrario. Fotografía: Dante Cecchin, en Color. Montaje: Claudio Cormio. Música: Fabio Barovero, Banda Ionica y Daniele Sepe. Duración:  92 min. Ficha artística: Intérpretes: Giorgio Pasotti (Martino), Francesca Inaudi (Amanda), Fabio Troiano (Angelo), Francesca Picozza (Bárbara), Silvio Orlando (Narrador), Pietro Eandi (Abuelo de Martino), Andrea Romero (Propietario del Fast Food), Giampiero Perone (Bruno, el vigilante nocturno), Francesco D'Alessio, Andrea Moretti y Gianni Talia (miembros de la banda de la Falchera), Maurizio Vaiana (el primo Maurizio). Sinopsis: Una noche, Martino, un ávido y tímido cinéfilo, vigilante nocturno del museo del cine de Turín, ayuda a Amanda, una joven cocinera de un restaurante de comida rápida que huye de la policía después de rociar a su explotador jefe con aceite caliente. El reino de ensueño de los personajes de películas mudas de Martino se convierte en un santuario para Amanda, mientras espera el rescate de su novio, un ladrón de coches del barrio turinés de la Falchera llamado Angelo. Obnubilada por el museo, Amanda desarrolla una sorprendente conexión romántica con Martino, que hasta ahora solo había encontrado compañía en sus sueños de celuloide. Dividida entre sus nuevos sentimientos por Martino y su problemática relación con el irresistible Ángel, Amanda intenta equilibrar el afecto de sus dos pretendientes. De este modo, se ven envueltos en este improbable triángulo amoroso. Comentario Preparando unos asuntos sobre los orígenes del cine, me encontré hace unos días con esta película, y de pronto, ¡¡matemáticas!! No sé si será conocida por el lector (seguramente no, dado que al cine europeo sólo nos acercamos los muy freakies del cine, o con algunos años ya a las espaldas), pero en cualquier caso se describe cierta (forzada) conexión entre el cine y las matemáticas que aprovecho para comentar. Para empezar, indicar que, siendo una cinta aceptablemente realizada y con ciertos anhelos de originalidad y trascendencia, queda bastante lejos de ser “una nueva Cinema Paradiso” como aparece en el cartel anunciador de la edición española del DVD. El utilizar como recurso antiguas películas mudas, el tener un protagonista convencido de la belleza y el arte del cine, o el disponer como escenario el estupendo y original Museo Nacional del Cine de Turín, no garantiza automáticamente el éxito de la empresa. No obstante, reitero que el resultado es agradable y digno, pero sin más. Comencemos con la parte matemática evidente y reconocible por casi cualquier espectador. El Museo anteriormente citado se encuentra situado en la Mole Antonelliana en el centro histórico de Turín, el edificio más singular de la ciudad, que, obviamente, aparecerá en muchos momentos del metraje de la película. Por la noche, en determinados momentos, aparecen iluminados sobre su torre una serie de tres números. Aunque después nos desvelarán cuáles son, por si no nos percatamos, se trata de distintos términos de la sucesión de Fibonacci. Recordemos que dicha sucesión viene dada por la expresión an = an-1 + an-2,   n ≥ 2 a0 = 0,    a1 = 1 Suponemos al lector suficientemente familiarizado con esta conocida sucesión, ya que, entre los incontables artículos, páginas y blogs de divulgación, e incluso en las aún más innumerables memeces seudo-científico-esotéricas, se han contado muchas de sus particularidades (su supuesto origen como descripción de la descripción de la progenie conejil, sus múltiples presencias en la Naturaleza, que también indica la película, como veremos, etc.). En cualquier caso, tienen montones de sitios a los que acudir como digo, por lo que nos ceñiremos a su estricta aparición en la película que nos ocupa. Hacia el minuto 43, segundo arriba, segundo abajo, Martino ha subido a lo alto de la Mole Antonelliana a Amanda (hasta el año 2017 era el edificio más alto de Turín, pero ese año terminó la construcción del rascacielos Grattacielo della Regione Piemonte; en cualquier caso, como la película es de 2004, en ese momento, la Mole Antonelliana era el edificio más alto de la ciudad). Desde ahí, y de noche, hasta el local de Fast Food en el que mal trabaja Amanda parece hermoso, comenta la joven. A continuación, Amanda pregunta a Martino por esos números iluminados sobre la torre, teniendo lugar el siguiente diálogo: Amanda: ¿Y esos números? Martino: Es la serie de Fibonacci. La serie de Fibonacci. Fibonacci, matemático de Pisa del siglo XI. Es una serie cuya característica más notable es que cada tercer número es la suma de los dos precedentes. Mira: 1, 1, 2, 3, 5, 8, 13, 21, y así hasta el infinito. Prueba a deshojar una margarita, o a contar las escamas de una piña o las semillas de un girasol. El número de pétalos de una flor es casi siempre un número de Fibonacci. Dichos números sugieren que en el Universo hay una especie de orden matemático, lo que nos llevaría a suponer que, probablemente, el mundo tenga algún sentido. Que no es poco. Aunque se entiende lo que quiere decir, digamos que la expresión “cada tercer número” no es demasiado correcta, ni siquiera gramaticalmente, porque el ordinal es único. No hay más que un tercer número. Debería haber dicho cada tres números, u otra expresión. Del mismo modo, aunque también se entiende, la versión original no dice “que el Universo tenga algún sentido”, sino “que tenga algún significado”. La primera sugiere algo con vistas a un futuro, mientras que la que dice en la versión original vendría a indicar que el Universo se ha configurado (pasado) de un modo lógico, matemático, sin la mediación del azar. En efecto, son matices, pero diferentes. La iluminación del edificio con números de Fibonacci no es ningún truco de la película, ni algo circunstancial. En el año 1997, Turín ideó el evento Luci d'Artista (La Luz del Artista), pensado para sacar el arte a la calle y que los ciudadanos pudieran conocer, disfrutar y aprender del trabajo de maestros de renombre internacional. Con el tiempo, las obras luminosas propuestas se han ido convirtiendo en una oportunidad para el diálogo entre el arte contemporáneo y el público en general. Al llevar la colección al tejido urbano, se logra un uso más amplio de las obras de arte y las personas se relacionan con más familiaridad. Aprovechando la redefinición de la iluminación exterior de la Mole Antonelliana y de la edición del año 2000 del evento Luci d'Artista, en el lado sur de la Mole se instaló la creación de Mario Merz (un defensor del uso de luces de neón en sus obras) denominada Il volo dei numeri (El vuelo de los números), que muestra el inicio de la sucesión de Fibonacci elevándose hacia el cielo. Pero no sólo quiso plasmar esa idea de infinitud, sino dejar patente la relación de la cúpula de la construcción de Antonelli con la curva que la delimita (un esquema de utilización matemática frecuente). Un modo estupendo de que el espectador asimile (aunque no tenga ni puñetera idea del significado) que las matemáticas son fundamentales en construcciones artísticas como ésta. Se fusiona así una obra de arte con el pensamiento, que invita cada noche a reflexionar desde el monumento más querido de la ciudad. Al final, las autoridades municipales decidieron dejar la iluminación de modo permanente, desde el anochecer hasta la una de la mañana en verano, y hasta la medianoche en invierno. La ciudad de Turín, propietaria de todas las obras de arte y planes de iluminación anualmente: este es un patrimonio cultural que crece año tras año. La última edición Luci d'Artista ha sido la vigésimo primera, y tuvo lugar entre el 31 de octubre y el 13 de enero de 2019, con 23 obras de arte contemporáneo (13 en el centro de la ciudad y 10 en los otros siete distritos de la ciudad). De ellas, seis obras quedaron permanentes y siempre operativas. Invitamos al lector/espectador a localizar otras apariciones de números de Fibonacci a lo largo de la película. Y como no, a descubrir la original estructura de todo el edificio, en el que se desafió todas las convenciones arquitectónicas, artísticas y técnicas Para lo que se emplearon estructuras geométricas, algunas aparecen en la película (son las matemáticas no explícitas, pero apreciables), de gran mérito e interés. Triángulos Al igual que sucede en ocasiones en la vida real, Amanda no tiene claro con cuál de los dos chicos quedarse, su novio, o Martino, porque cada uno le aporta algo diferente y complementario, y quiere tener ambas posibilidades, dependiendo del momento. Por eso les propone intentar ser tres. Aparece entonces el narrador que va dando explicaciones y haciendo reflexiones durante toda la película: Narrador: ¿Pueden estar enamorados tres? ¿No es bastante complicado con dos? Los seres humanos siempre intentan aplicar reglas matemáticas a las cuestiones del corazón con escaso éxito. Sea cual sea la fórmula escogida, siempre hay un factor por el que no salen las cuentas. Son muchas las composiciones visuales que se plasman en la película utilizando simetrías, reflexiones, transformaciones planas y tridimensionales diversas que aparecen en la película, utilizando elementos del Museo del Cine como espejos, paneles retro iluminados, etc. Cine, cine, cine En el tramo final de la película, el narrador explica la situación de los tres personajes relacionando cine y matemáticas. Para Martino, el cinéfilo por antonomasia, nos cuenta lo siguiente: Narrador: Si, como sugieren los números de Fibonacci, el mundo tiene un sentido, Martino ahora no entiende cuál. Pero las películas no son la vida. Es necesario escoger. A lo que se unen los consejos de su primo Maurizio (lo hace explicándole porque a él no le gusta el cine) y el abuelo de Martino (en ningún caso desvelaré las razones para que vean la película). A Amanda, Fibonacci le vendrá finalmente muy bien, por un motivo que tampoco desvelaré. Y finalmente, para Angelo, que a la vez que descubre los verdaderos sentimientos de Amanda, el guion nos tiene reservados un par de guiños, alguno desgraciadamente cómico (me refiero a algo relativo a Silvio Berlusconi), descrito del siguiente modo: Narrador: En realidad, ha aprendido que la idea de la cliente de Bárbara es la única regla de las historias de amor: para que uno sea feliz, a otro le toca llorar. Es como una matemática de los sentimientos, un más y un menos que suman y sustraen hasta el infinito y que, aunque dejándolo todo igual en términos generales, producen combinaciones especiales y siempre diferentes. Como las películas que cuentan las mismas historias desde hace cien años, pero uno sigue yendo igualmente al cine, porque espera alguna sorpresa. Museo Nacional del Cine de Turín Inaugurado en el año 2000, está dispuesto en torno a cinco pisos con una superficie total de unos 3200 metros cuadrados. Aunque pretende repasar la historia del cine mundial, destaca por el amplio repaso al cine italiano, como no podía ser de otro modo, desde los inicios del cine. Conserva además los fondos de la Fundación María Adriana Prolo, graduada en historia y literatura, pionera en las investigaciones del cine en Turín, entre otros trabajos. En 1941 comienza a recopilar, recuperar y conservar todo tipo de documentos y materiales relacionados con el cine y la fotografía turineses, y ya desde ese momento se tiene en mente establecer un museo para la ciudad. Sin embargo, ella no llegará a disfrutar de esta instalación (fallece en 1991) en una rehabilitada Mole Antonelliana, uno de los edificios históricos de la ciudad y entre los más emblemáticos de Italia. La visita al Museo, independientemente de lo relacionado con el cine, es espectacular y muy recomendable ya que dispone de un ascensor que permite subir hasta la parte más elevada de la torre y disfrutar de una espléndida vista de todos los puntos cardinales de la ciudad. Por supuesto el museo muestra también objetos, documentos, fotografías históricas, carteles, más de 12000 películas, biblioteca, y es la sede principal del Festival de Cine de Turín (Torino Film Festival, TFF), además de organizar ciclos de proyecciones cinematográficas durante todo el año. En la imagen, una escena de la película bajo una frase de un panel del museo de uno de los hermanos Lumiére: El cine es un invento sin futuro. Desde luego, como futurólogo no tuvo precio. La película rinde homenaje tanto a María Adriana Prolo como a Buster Keaton e incorpora al argumento algunos cortometrajes cuyo argumento tiene mucho que ver con lo que les sucede a los protagonistas de la película. Son los siguientes: El fuego (Il fuoco, Giovanni Pastrone, Italia, 1916) (un pintor desconocido está impresionado y obsesionado con conocer a una famosa poetisa, casada, e intentar deslumbrarla, ya que considera que no tiene el talento necesario para poder pintarla; es una película recuperada y restaurada por el Museo Nacional del Cine de Turín).- historia con bastantes puntos en común con la película que nos ocupa: Mario, un pintor desconocido, está obsesionado con conocer a una famosa poetisa a la que no es capaz de pintar. La mujer convencerá al pintor de que abandone a su madre con la que vive y que vaya a vivir con ella en su mansión. Con su amada, encuentra inspiración y alcanza fama con sus obras. Un día, la mujer recibe un telegrama informándole del regreso de su esposo, y decide alejarse de su amante. Una semana (One Week, Edward F. Cline y Buster Keaton, EE. UU., 1920).- Una pareja de recién casados intenta construir una casa con un kit prefabricado, sin saber que un rival saboteó la numeración de los componentes del kit. The Scarecrow (Edward F. Cline y Buster Keaton, EE. UU., 1920).- Dos granjeros inventivos compiten por la mano de la misma chica. En los hipervínculos es posible visualizar las películas íntegramente y en éste, la película de la que hablamos desde el inicio. Que ustedes pasen una estupenda velada y unas maravillosas vacaciones navideñas. Hasta el año que viene. Alfonso Jesús Población Sáez

Lunes, 02 de Diciembre de 2019 | Imprimir | PDF |  Correo electrónico