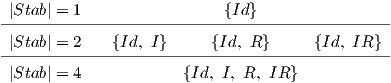541. 58. (Diciembre 2019) Vanidades matemáticas

(Alegoría de la Vanidad. Valdés Leal. Wadsworth Atheneum Museum - Hartford) La matemática es un componente básico de la cultura, un exponente de la humanidad. Cada época tiene una forma de manifestar la presencia y destacar la importancia de la disciplina. Una de las representaciones más genuinas del arte Barroco es el misticismo que reprueba todo aquello que distraiga a las personas de la eternidad: la vida humana es un mero parpadeo en el infinito, dirá Juan de Valdés Leal. Protestantes o católicos, lo mismo da, ambas iglesias, la papista y la reformada, hacen la misma lectura de la sabiduría del Eclesiastés: ¡Vanidad de las vanidades, todo vanidad! ¿Qué saca el hombre de toda fatiga con que se afana bajo el sol? Todo en la vida es pasajero, lo que el hombre anhela le distrae de su ascético fin. El poder, la música, las armas, las dignidades eclesiásticas, las artes y las ciencias son humana vanidad. La calavera, los relojes, la vela apagada y el erote haciendo pompas de jabón suelen ser los recuerdos de que la vida humana dura lo que un suspiro en relación con la eternidad. (Alegoría de la Vanidad. Valdés Leal. Detalle. Hartford) La Alegoría de la Vanidad, Vanitas, será muy representada por muchos artistas del siglo XVII. Para el matemático es una forma de encontrar instrumentos y libros de su ciencia. El ambiente de pesimismo, propiciado por las guerras de religión, fomenta la piedad barroca frente al clima de confianza y apertura del renacimiento. La matemática pasa de ser representada como instrumento de liberación a mera pompa, en clara contradicción con la revolución científica que se estaba produciendo. Las alegorías matemáticas durante el medioevo fueron alabadas por la religión pues eran una forma de conocer la omnipotencia de la divinidad y comprender su diseño del mundo. Las catedrales góticas representaron las Artes Liberales y sus paganos sabios son esculpidos en los edificios cristianos. (Vanitas. Pieter Gerritsz. van Roestraeten - Haarlem, Frans Hals Museum) San Agustín y Santo Tomas, los representantes de la sabiduría cristiana, aparecieron acompañados de la Geometría, la Aritmética, la Astronomía o la Lógica. San Agustín en su estudio parece un escrutador matemático del universo. La matemática durante el Renacimiento es considerada la puerta que hay que franquear hacía la humanidad, aquello que libera de la bestialidad. Ya había dicho el filósofo medieval Roger Bacon que la matemática es puerta y llave. Toda época está llena de contradicciones y bajo la corriente principal coexisten visiones del mundo alternativa. La recuperada Tabla de Cebes marcaba un camino de ascenso místico que ponía la matemática en un desvío de lo verdaderamente importante. La memorable pintura de Los embajadores (1533) de Hans Holbein el Joven con su calavera anamórfica se anticipaba a lo que iban a ser las Vanitas barrocas. (Hans Holbein. Los embajadores (1533). Galería Nacional. Londres) La mayor similitud de las vanitates barrocas y quizá su fuente de inspiración se encuentren en el Omnia vincit Amor de los manieristas. El Caravaggio recuperó la expresión de las Bucólicas de Virgilio: El amor conquista todas las cosas, ríndete al amor. Un adolescente y provocador Eros aparece triunfante con las artes, las ciencias, las pompas militares y religiosas vencidas a sus pies. La Vanitas recoge el mensaje y lo cristianiza.  La comparación de El triunfo del Amor de Caravaggio con la Alegoría de la Vanidad de Antonio de Pereda muestra tanto las similitudes como las abismales diferencias. (El triunfo del Amor de Caravaggio frente a La Alegoría de la Vanidad de Pereda) Eros se transforma en Ángel. La figura mórbida, desnuda y provocativa se cubre castamente. Los objetos del suelo pasan a la mesa. Y sobre todo se incorporan muchas referencias al inexorable paso del tiempo: relojes, velas apagadas, y calaveras. La Vanitas matemática de Von Thum Al pintor sueco Christian von Thum (1625-1696) quizá debemos la alegoría de la Vanidad más matemática. Las vanitates barrocas son un lugar privilegiado para encontrar instrumentos y libros matemáticos. La Vanidad astronómica de Estocolmo nos muestra un bello conjunto de instrumentos: un compás de proporción, una escuadra, un teodolito, un telescopio, un metro, un globo celeste y un transportador de alturas. Las características vela apagada, calavera y reloj mecánico son representados por von Thum en su alegoría. La calavera tiene una corona de laurel. Parecen decirnos: ¿para qué le han servido los mundanos laureles al difunto? El gran compás de proporción era el instrumento privilegiado de cálculo para militares, ingenieros y navegantes. Von Thum representa un modelo de gran formato y por tanto de mayor lujo y precisión. (Christian von Thum. Alegoría de la vanidad. Museo nacional de Estocolmo) La Vanidad de Van Roestraten La localidad holandesa de Haarlem está unida al siglo de oro de la pintura holandesa. La guilda de San Lucas de la ciudad fue un importante foco artístico. Frans Hals realizó allí toda su obra y tiene un museo con su nombre. Pieter Gerritsz van Roestraten aprendió a pintar con Hals y se casó con una de sus hijas. Destacamos una interesante Vanitas que se encuentra precisamente en el Museo Frans Hals. Las Vanidades son muy frecuentes en esta época convulsa, las hallamos tanto en la pintura católica como en la reformada, puede decirse que son muestra de la llamada piedad barroca. En Van Roestraten se pone de manifiesto de la forma más simple la vanidad del saber, el conocimiento y la ciencia. En ellos tenemos la suerte de encontrar instrumentos y detalles de como el espíritu científico estaba impregnando la sociedad. ¡Vana matemática! La “Alegoría de la vanidad” de Valdés Leal El pintor sevillano Juan de Valdés Leal (1622-1690) lleva al límite la llamada piedad barroca, una visión del mundo que hace omnipresente la brevedad de la vida humana y su carácter de mero tránsito hacía la eternidad. Las pinturas de las iglesias sevillanas son obras cumbres del desprecio del mundo. La Alegoría de la vanidad del Wadsworth Atheneum Museum of Art de Hartford, la capital de Connecticut, es más clásica pero de gran interés matemático. Las vanitas son propaganda de las cosas a las que no se debe dar valor precisamente porque pueden tenerlo. El erote haciendo pompas de jabón nos recuerda los amores por los mundos sutiles, ingrávidos y gentiles de Machado (Alegoría de la Vanidad. Valdés Leal. Detalle. Hartford) La matemática está presente en el compás y la escuadra junto al libro abierto de geometría. La esfera armilar y el libro de astronomía completan la alegoría de la ciencia matemática. El reloj mecánico de bolsillo nos hace patente que tempus fugit. La Vanidad tardía de Antonio Cioci Antonio Cioci (1722–1792) es un pintor italiano que trabajó en Florencia para el Opificio de las Piedras Duras. Resulta curioso que los trabajos de taracea en piedra utilicen tanto la matemática como los de madera. Poliedros, instrumentos y perspectivas muestran el interés por la geometría. La Alegoría de la Vanidad de Cioci es una muestra tardía de las representaciones barrocas con fuerte presencia matemática. La esfera armilar, el globo terráqueo, el compás y el libro abierto de geometría conviven con instrumentos musicales, esculturas rotas, pinceles y calaveras. (Alegoría de la Vanidad. Antonio Cioci. Colección privada) El globo terráqueo en las Vanidades Hemos recogido las alegorías de la vanidad más matemáticas. Hay muchas con menos detalles explícitos. El elemento que más aparece es el globo terráqueo con doble valor simbólico: la ciencia y la transitoriedad de todas las actividades terrestres. Terminamos con la Vanidad quizá más terrorífica: el encargo recibido por Valdés Leal del Hospital de la Caridad de Sevilla y que lleva por título: Finis Gloriae Mundi in  ictu oculi (las glorias del mundo duran lo que un parpadeo). (In  ictu oculi. Valdés Leal. Sevilla)

Lunes, 02 de Diciembre de 2019 | Imprimir | PDF |  Correo electrónico

542. La UNESCO declara el 14 de marzo Día Internacional de las Matemáticas

La UNESCO aprobó, el pasado martes 26 de noviembre en su 40.ª Conferencia General, la proclamación de la UNESCO del 14 de marzo (Día Internacional de Pi) como el Día Internacional de las Matemáticas, una propuesta dirigida por la Unión Matemática Internacional. Para la primera edición oficial, que será la del año 2020, el tema será “Las matemáticas están en todas partes”, con el que se pretende mostrar al público la importancia que las matemáticas tienen en nuestra vida diaria. Siguiendo este eje temático tendrán lugar numerosos eventos.

Viernes, 29 de Noviembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

543. La numeración wólof

El idioma wólof es una lengua hablada en Senegal, Gambia y Mauritania, la lengua nativa de la etnia wólof. Es el idioma más hablado en Senegal, no sólo por los wólof -el 40% de la población-, sino por otros senegaleses. Su sistema de numeración es bastante curioso: está basado en el 5 y en el 10. Para expresar números, este sistema de numeración utiliza frases con palabras que involucran la suma y la multiplicación en las bases 5 y 10, que se usan hasta llegar al 100. Se usa el término ak -que significa y o con– para cada número, excepto para los números del 6 al 9 y para los divisibles por 10 -excepto el 10– hasta 100. Número Su expresión en wolóf 0 tus 1 benn 2 ñaar 3 ñett 4 ñeent 5 juróom 6 juróom benn (5 y 1) 7 juróom ñaar (5 y 2) 8 juróom ñett (5 y 3) 9 juróom ñeent (5 y 4) 10 fukk 11 fukk ak benn (10 y 1) 12 fukk ak ñaar (10 y 2) 13 fukk ak ñett (10 y 3) 14 fukk ak ñeent (10 y 4) 15 fukk ak juróom (10 y 5) 16 fukk ak juróom benn (10 y 6) 17 fukk ak juróom ñaar (10 y 7) 18 fukk ak juróom ñett (10 y 8) 19 fukk ak juróom ñeent (10 y 9) 20 ñaar fukk (2×10) 21 ñaar fukk ak benn (2×10 y 1) 22 ñaar fukk ak ñaar (2×10 y 2) 23 ñaar fukk ak ñett (2×10 y 3) 24 ñaar fukk ak ñeent (2×10 y 4) 25 ñaar fukk ak juróom (2×10 y 5) 26 ñaar fukk ak juróom benn (2×10 y 5 y 1) 27 ñaar fukk ak juróom ñaar (2×10 y 5 y 2) 28 ñaar fukk ak juróom ñett (2×10 y 5 y 3) 29 ñaar fukk ak juróom ñeent (2×10 y 5 y 4) 30 ñett fukk (3×10) 40 ñeent fukk (4×10) 50 juróom fukk (5×10) 60 juróom benn fukk (6×10) 61 juróom benn fukk ak benn (6×10 y 1) 62 juróom benn fukk ak ñaar (6×10 y 2) 63 juróom benn fukk ak ñett (6×10 y 3) 64 juróom benn fukk ak ñeent (6×10 y 4) 65 juróom benn fukk ak juróom (6×10 y 5) 66 juróom benn fukk ak juróom benn (6×10 y 5 y 1) 67 juróom benn fukk ak juróom ñaar (6×10 y 5 y 2) 68 juróom benn fukk ak juróom ñett (6×10 y 5 y 3) 69 juróom benn fukk ak juróom ñeent (6×10 y 5 y 4) 70 juróom ñaar fukk (7×10) 80 juróom ñett fukk (8×10) 90 juróom ñeent fukk (9×10) 100 teemeer 1000 junni 1.000.000 fukki teemeeri junni (10x100x1000) A diferencia del sistema de numeración decimal, los números del 6 a 9 se escriben del modo 5 + n. En la página Number Systems of the World se dan diferentes sistemas de numeración, organizados por complejidad decreciente: el más sencillo es el de las Islas Tonga – el que sólo se da la sucesión de las cifras, por ejemplo 327 se dice “tres, dos, siete”- y el más complicado es un sistema de Papua basado en la base 15, pero también con una manera compleja de decir las unidades -por ejemplo, 32 (2 x 15 más 2) se dice “dos por quince y dos unidades del tercer quince”… Interesantes y sorprendentes ejemplos… Visto en Psychologie, mathématiques et choses connexes Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 28 de Noviembre de 2019 | Imprimir | PDF |  Correo electrónico

544. Para qué sirven los logaritmos: dos retos sin usar la calculadora

ABC, 25 de Noviembre de 2019 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 25 de Noviembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

545. ¿Para qué sirven realmente los logaritmos?

ABC, 18 de Noviembre de 2019 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 18 de Noviembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

546. Por qué un matemático no dejaría tirar faltas a Cristiano Ronaldo

ABC, 17 de Noviembre de 2019 CIENCIA - El ABCdario de las matemáticas Diego Alonso Santamaría

Domingo, 17 de Noviembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

547. Noviembre 2019: Más juegos de lápiz y papel II

1. Recordemos. En la primera parte de esta entrega de juegos de lápiz y papel, hablamos de una serie de juegos que han formado parte de nuestra infancia y juventud. Juegos, en ocasiones muy conocidos, que tienen la característica de utilizar unos materiales muy asequibles y que se pueden jugar en cualquier momento y lugar. Para nosotros, como profesores, tienen además el interés de poder estudiar las estrategias que llevan a buscar la solución mejor. Unas estrategias que son similares a las que se utilizan en la resolución de problemas, y que nos permiten aprender y practicar esos heurísticos que después aplicaremos en los problemas matemáticos. En la anterior entrega presentamos juegos que, en algunas ocasiones, eran bastante antiguos, algunos de ellos incluso pueden remontarse al siglo XIX. En esta parte vamos a ver una serie de juegos de creación más reciente. Como veremos existe un gran número de matemáticos que han creado nuevos juegos de lápiz y papel con estudios y estrategias muy interesantes, entre ellos podemos citar a Eric Solomon o John Conway, de los que hablaremos en las siguientes líneas. 2. Brotes. El juego titulado Sprout puede traducirse por brotes o coles, aunque también se conoce en español como Plantón o puntos y líneas. Martín Gardner le da el nombre de “drago” debido al árbol del mismo nombre. Fue creado en 1967 por el profesor, de la Universidad de Cambridge, John Horton Conway, más conocido por ser el creador, entre otros, de “El juego de la vida”, junto al estudiante Michael S. Paterson de la misma universidad. Este juego se considera un juego básicamente topológico. Es un juego pensado para dos jugadores, aunque si hay más de tres es conveniente que se jueguen varias partidas y en cada una de ellas empiece un jugador distinto. Se comienza dibujando una serie de puntos en un papel y cada jugador, en su turno, debe trazar una línea que comience en uno de los puntos y termine en otro, que puede ser el mismo punto. Una vez dibujada la línea, el jugador debe dibujar un punto dentro de la línea que no coincida con ningún otro punto ya dibujado. Los jugadores siguen dibujando líneas con únicamente dos restricciones: Una línea no puede cruzar a otra línea ya dibujada ni a sí misma. En ningún punto pueden converger más de tres líneas. El juego termina cuando un jugador no puede dibujar una nueva línea con las condiciones impuestas. Gana el último jugador que ha dibujado una línea. Existe también una versión llamada Misère en la que gana el primer jugador que no puede dibujar una línea. Veamos una partida partiendo de dos puntos. Posición de partida 1ª jugada 2ª jugada 3ª jugada 4ª jugada   Como vemos en esta partida ha ganado el segundo jugador, pues el primero, al que le toca mover, no puede unir los dos únicos puntos que tienen aún algún grado de libertad sin cruzar otra línea ya existente. En el estudio que realiza Martin Gardner, supone que cada punto tiene inicialmente tres vidas, o tres grados de libertad, cuando un punto tiene tres líneas que parten o confluyen en él, ha perdido sus vidas, luego está muerto. En cada movimiento, se pierden dos vidas al trazar las líneas, una del punto inicial y otra del final y se añade una nueva vida, correspondiente al punto nuevo que se coloca, que ya tiene dos líneas que confluyen en él, pues básicamente ese punto divide a la línea en dos. Por tanto, en cada partida se pierde como mínimo una vida. Pueden ser más si se quedan puntos bloqueados como hemos visto en el ejemplo de partida. Si partimos de n puntos, inicialmente hay 3n vidas y por tanto ninguna puede durar más de 3n – 1 movimientos (pensemos que si queda un único punto para dibujar es imposible seguir). También es posible deducir que cualquier partida puede durar como mínimo 2n movimientos. Al estudiar los primeros casos podemos encontrarnos con las siguientes opciones. Si partimos de un solo punto, el juego es trivial pues sólo es posible hacer dos movimientos y gana el segundo jugador. Si partimos de dos puntos, es fácil comprobar que gana el segundo jugador y que puede forzar ganar en cuatro movimientos, como se ha visto en el ejemplo. Basta estudiar todos los movimientos de comienzo del primer jugador, que sólo hay tres posibles, salvo simetrías, y estudiar como continuar en cada caso. Figura 1: Primeras jugadas posibles con dos puntos El propio Conway demostró que con tres puntos el primer jugador puede ganar siempre. Un estudiante de matemáticas de Cambridge, Denis Mollison, demostró que el primer jugador tiene las de ganar con cuatro y cinco puntos, mientras que con seis gana el segundo. Las partidas más usuales se comienzan con tres puntos. Lógicamente, mientras más puntos se coloquen al principio, más tiempo se tarda en acabar y más complicada es la estrategia para llegar al final. El doctor en matemáticas por la Universidad de Southampton, Eric Solomon, diseñador de juegos y programador de software, ha realizado el siguiente estudio. Cada línea que se dibuja, que en realidad son dos líneas por el punto que se coloca en medio, produce sobre la zona de juegos o bien una nueva región, zona encerrada por una línea, o bien une dos partes separadas, considerando como parte a todo elemento (línea o punto) independiente de otro. Con esas características, se cumple la siguiente regla de Euler: “el número de regiones más el de puntos es igual a la suma del número de partes más el de líneas”. Si nos fijamos en la última jugada de la partida anterior, tenemos una sola parte, ya que está todo conectado, tres regiones, 6 puntos y 8 líneas (recordemos que una línea se considera desde un punto hasta el más próximo, luego en cada jugada un jugador traza dos líneas). Por tanto, 3 + 6 = 1 + 8. Más adelante, Conway realizó una versión que llamó Brussels Sprouts (Coles de Bruselas) cuya variación es que en lugar de puntos se dibujan cruces, y las líneas parten de uno cualquier de los extremos de las cruces. En la línea se dibuja un nuevo trazo como se ve en el dibujo. En esta versión, de cada trazo de la cruz, que se prolonga para conectarlo con otro trazo, sólo puede salir una línea, por lo que ese brazo de la cruz queda invalidado al dibujar una línea. Conway demostró que, partiendo con n cruces, el juego siempre termina después de 5n – 2 movimientos. Si el número de cruces es impar gana el primer jugador, y el segundo con un número par de cruces. 3. Colorear mapas. Veamos ahora un bloque de juegos que se basan en colorear unos determinados mapas. 3.1. El juego de los colores. Este juego aparece en el libro de Luis Ferrero y no he conseguido encontrar más información de la que allí aparece, pero me ha parecido interesante incluirlo. Se basa en el conocido Teorema de los cuatro colores, un resultado típico en la topología Según este teorema, un mapa plano que tiene regiones continuas puede ser coloreado utilizando únicamente cuatro colores, de forma que cada región adyacente tenga distinto color. Se considera región adyacente a la que tiene un poco de frontera común entre las regiones, no se incluye si el contacto se reduce a un solo punto. Para este juego se dispone de cinco colores y está indicado para dos jugadores, aunque se puede jugar también con tres o cuatro. En el caso de ser más de dos jugadores y jugar varias partidas, es conveniente que en cada partida, los jugadores cambien el orden en que están situados. La forma de jugar es la siguiente: El primer jugador dibuja una región cualquiera, y a partir de ese momento, cada jugador en su turno, debe colorear la región que ha dibujado el contrario, con la condición de no poder utilizar un color que se repita en algunas de las regiones adjuntas ya coloreadas. Una vez coloreada la región del oponente, el jugador, aún en su turno, debe añadir una nueva región a las ya existentes. Entonces pasa el turno al siguiente jugador. Pierde el jugador que utilice el quinto color en la región que debe colorear. Veamos el comienzo de una partida con dos jugadores. Suponemos que la jugada del primer jugador ha sido dibujar el recinto que ha coloreado el segundo jugador. Jugador 2º Jugador 1º     Jugador 2º Jugador 2º Se observa, en las dos últimas jugadas, que al abarcar las tres regiones, se obliga a utilizar un cuarto color, pero al encerrar una de las regiones, ese color, en nuestro caso el verde, se puede utilizar para la nueva región sin problemas. Hay una versión que a veces he utilizado y consiste en entregar sólo cuatro colores y un mapa ya dibujado. El primer jugador dibuja una región de un color y, a partir de él, cada jugador debe colorear una región adyacente, al menos a una de las regiones ya coloreadas. Pierde el jugador que debe utilizar el cuarto color. 3.2. Otros juegos con menos colores. Hay toda una colección de juegos basados en el objetivo de colorear mapas, la mayoría de ellos basados en el Teorema de los cuatro colores. Este tipo de juegos se estudian en la “Teoría combinatoria de juegos”. Básicamente se basan en colorear regiones con varios colores, de forma que las regiones que tienen frontera común no lleven el mismo color, aunque hay versiones en que se pide lo contrario. En algunos de estos juegos se aplica una regla vinculante según la cual, cada región que se colorea debe ser vecina de la región coloreada en la jugada anterior. En general, gana el jugador que colorea la última región posible, aunque también se puede jugar al modo contrario, es decir, la versión misère en la que pierde el último que puede colorear. Hay incluso variantes en la que se cuentan las regiones coloreadas con un determinado color, si es que se rellenan todas las posibles según los colores de los jugadores, independientemente del turno que les corresponda. El número de colores puede cambiar según el método de juego. El experto en juegos David L. Silverman, creador entre otros del juego Senderos, que presentamos en el artículo de SUMA de 2002, hace una clasificación de juegos en su libro “Your move: Logic, Math and Word Puzzles for Enthusiasts” de 1976 según el número de colores. Todos ellos se juegan sobre un mapa ya dibujado previamente y son juegos consideramos imparciales, es decir, los dos jugadores tienen las mismas posibilidades de juego en todo momento. Monocromo: se utiliza un solo color, de esa forma cada vez que se colorea una región, tanto ella como todas sus regiones vecinas quedan descartadas para siguientes jugadas. Bicromo: se juegan con dos colores, pero Silverman plantea la posibilidad de que cada jugador, en su turno, elije el color que quiere utilizar en su jugada. Tricromo: a partir de tres colores, se va aumentando el número llegando a una versión similar a la vista en el apartado anterior, aunque como ya hemos dicho, partiendo de un mapa inicial. Silverman también presenta un juego llamado Contact en la que se utiliza un solo color por jugador y se aplica la opción vinculante, es decir, cada región que se colorea debe tener contacto con la región coloreada en la versión anterior. En su libro “Sobre números y juegos” de 1991, John Conway presenta y estudia las dos siguientes versiones de juegos que son considerados partidistas, pues en el desarrollo del juego hay diferentes movimientos disponibles para uno y otro jugador: 3.2.1. COL. Conway atribuye este juego a su colega Colin Vout. Sería una versión simple en la que cada jugador dispone de un color diferente y hay que colorear regiones con la condición de que las regiones no tengan frontera común con otra del mismo color. En la siguiente imagen tenemos una partida terminada en la que el color rojo, que fue el que comenzó la partida, es el que gana. Figura 2: Partida finalizada de Col 3.2.2. SNORT. Atribuido al colega de Conway, Simon Norton. En ella cada jugador tiene un color y se van coloreando regiones con la restricción de que no puede haber dos regiones contiguas con colores diferentes. En las siguientes imágenes puede verse una partida de Snort. Figura 3: Partida de Snort Después de la tercera jugada, el jugador azul no puede mover, queda bloqueado, aunque el jugador rojo aún tiene una jugada posible. Figura 4: Final de la partida de Snort 4. Agresión. Vamos a presentar un juego que, aunque sigue la tónica de los juegos del apartado anterior, se sale un poco del perfil que hemos visto hasta el momento. Básicamente, este juego es de estrategia, más concretamente de lo que se conoce como wargame, es decir, juegos de guerra, y que está inspirado en el conocido juego de batallas llamado Risk. Aunque, como veremos, algunos especialistas hablan de su interés como juego aritmético para Primaria. Ya hemos hablado antes del matemático Eric Solomon, un importante creador británico de juegos. En 1973 publicó un libro con el título de “19 juegos con papel y lápiz” en el que presentaba varios juegos inventados por él, entre ellos éste que llamó simplemente aggression. Es un juego para dos jugadores, cada uno de ellos juega con un lápiz de distinto color. El juego se compone de tres fases diferentes, en cada una de ellas comienza siempre el mismo jugador que en esa partida es el primero. Lo primero es dibujar el mapa donde se va a celebrar el combate. Para ello, el primer jugador dibuja una región cerrada, y a partir de él, cada jugador dibuja una sola región adyacente a alguna de las existentes. En la segunda fase los jugadores deben repartir sus unidades de combate en las regiones que se han dibujado. Por turno, cada uno coloca las unidades que estime en una de las regiones que estén libres, no pudiendo coincidir en una misma región unidades de jugadores distintos. Esta fase termina cuando se han repartido todas las unidades o no quedan regiones libres. La tercera fase es la propia lucha por conseguir regiones del contrario. Cada jugador en su turno “ataca” desde una o varias de sus regiones a una región fronteriza con ellas y que tenga unidades del contrincante. Esta región atacada debe tener menos unidades que la suma de las atacantes. El jugador indica cuál es la región atacada y desde qué regiones. En esa jugada, la región que es atacada pierde todas sus unidades de combate (son tachadas) y es capturada por el atacante, que rallará la región para saber que está inservible. Al final gana el jugador que ha capturado más regiones. Si en algún momento de la partida, un jugador no puede seguir atacando, tiene que pasar en su turno hasta que el contrario termine todos sus posibles ataques. El número de regiones y de unidades de combate varían según se decidan al comienzo de la partida. Solomon propone unas 20 regiones y unas 100 unidades de combate. Lo ideal es comenzar con menos regiones y menos unidades. Veamos un ejemplo. En la siguiente imagen vemos un mapa en el que aparecen 12 regiones donde hay repartidas 30 unidades de cada uno de los jugadores. Se puede considerar que cada jugador sólo puede poner unidades de combate en las regiones que él ha dibujado, o permitir colocarlas en cualquier sitio. He considerado esta segunda opción, por eso no se distinguen colores en el dibujo del mapa. Figura 5: Tablero preparado de Agresión Como hemos indicado en las instrucciones, es posible atacar desde una sola región o desde varias del mismo jugador, en las imágenes siguientes vemos los dos casos. Figura 6: Ataque desde una región Figura 7: Ataque desde varias regiones Es fácil encontrar información sobre este juego en la web. En particular quiero hacer referencia al sitio MathPickle, una página apoyada por el Instituto Americano de Matemáticas. Contiene muchos recursos gratuitos para utilizar en clase. Se pueden encontrar puzles y juegos adaptados a niveles educativos diversos. En esa página, su creador Gordon Hamilton, ha adaptado el juego anterior llamándolo Un poco de agresión, para que no parezca tan violento, y lo plantea para trabajar sumas y restas de números enteros. Comienza con propuestas para trabajar del 1 al 10 y después para trabajar del 1 al 100. En los juegos se propone que, en lugar de crear el mapa los propios jugadores, se utilicen mapas reales. Hamilton propone varios en sus escritos, uno de ellos por cierto el de la península ibérica, donde combaten franceses contra ingleses durante la Guerra de Sucesión del siglo XVIII. En la siguiente dirección se puede encontrar la explicación de cómo realizar el juego. http://mathpickle.com/project/a-little-bit-of-aggression/ Existe también un pdf, aunque en inglés, en el que se describe paso por paso la realización de una partida y otro en el que hay muchos mapas con indicaciones de cuantas unidades de combate utilizar en cada caso. Las direcciones son: https://www.brishtitechnologies.com/uploads/products/14903458901Aggression_-_an_amazing_pen-pencil_and_paper_game_of_Arithmetic.pdf http://mathpickle.com/wp-content/uploads/2016/01/TpT-A-little-bit-of-aggression-2016.pdf 5. El juego de las hojas de hierba. Para terminar, me gustaría incluir un juego diferente, ya que aunque se puede jugar igual que los anteriores, con lápiz y papel, no es propiamente un juego de estrategia sino más bien un juego aleatorio, pues en su resultado interviene el azar. Se dibujan seis líneas verticales paralelas en una hoja. Se dobla la hoja por la mitad y uno de los jugadores, sin que el contrario lo vea, une esas seis líneas en parejas mediante tres arcos. Posteriormente, tapando lo dibujado, el otro jugador une las seis líneas de la parte contraria. Se despliega el papel. Si se ha conseguido un lazo continuo cerrado y único, gana el segundo jugador, en caso contrario gana el primero. Veamos una partida posible. Figura 8: Jugada del primer jugador Figura 9: Jugada del segundo jugador Al abrir la hoja se puede ver la unión completa. En este caso se observa que ha ganado el segundo jugador, pues ha conseguido cerrar un círculo completo, es decir, no hay lazos independientes unidos. Figura 10: Resultado final de la partida Sin más que ver la partida, se puede observar que en el ganar o perder influye poderosamente el azar, ya que el segundo jugador no sabe cómo ha unido sus extremos el primer jugador. Lo interesante es estudiar quién de los dos jugadores tiene mayor probabilidad en ganar en esta partida. En su libro Comunicación extraterrestre, Martin Gardner nos habla de la historia de las muchachas casaderas rusas, que utilizaban un método similar para saber si el futuro les deparaba un buen matrimonio, historia en la que se basa este juego. También hace el estudio probabilístico según el cual, el segundo jugador tiene una probabilidad algo superior al del primer jugador. 6. ¡Llegó la hora de jugar! Como comentábamos al principio de la entrega anterior, existen una gran variedad de juegos de lápiz y papel que son relativamente recientes y que son interesantes para investigar las estrategias que permiten tener más posibilidades de ganar. En los libros de la bibliografía quedan aún muchos más para trabajar conceptos muy diversos. En internet existen multitud de páginas con alguna entrada en que se recogen juegos de lápiz y papel, y en muchos de ellos se puede jugar directamente a esos juegos. Yo no conozco ninguna página en español especializada en estos juegos, pero si existe una página imprescindible en inglés llamada Pencil And Paper Games (www.papg.com) en la que se explican muchos juegos y en varios casos es posible jugar en línea. En concreto los juegos de brotes, col, snort, agresión, toros y vacas y puntos y cajas se tratan en la página, aunque solo se pueden jugar los dos últimos. Varios de estos juegos se presentaron en la primera parte del artículo. Ya solo me queda invitarles a disfrutar con recursos tan fáciles de conseguir, hoy en día, como un lápiz y un papel. 7. Referencias. FERRERO, L. (1991): El juego y la matemática. La Muralla, Madrid. GARDNER, M. (1980): Carnaval matemático. Alianza Editorial, Madrid. GARDNER, M. (1987): Comunicación extraterrestre y otros pasatiempos matemáticos. Catedra, Madrid. Colección Teorema. GRUPO ALQUERQUE (2002): “Juegos de lápiz y papel”. SUMA nº 40, pp. 123-124. SOLOMON, E. (2008): 19 juegos con papel y lápiz. RBA Editores, Barcelona.

Viernes, 15 de Noviembre de 2019 | Imprimir | PDF |  Correo electrónico

548. 102. (Noviembre 2019) Serialismo y matemáticas (III)

1. Introducción Este artículo es el tercero y último de la colección Serialismo y matemáticas. Las músicas serialistas son aquellas que permiten construir castillos con un solo grano de arena: una serie particular, una permutación de notas, dinámicas o timbres. La serie se coloca en la obra secuencialmente, siempre igual o con alguna modificación que la adorne. Y es que para esta música, la serie es el ladrillo y las matemáticas son la pintura con la que decorarlos, ya que las transformaciones que se le puede aplicar a una serie forman preciosas estructuras matemáticas enmarcadas en la Teoría de Grupos. En el primer artículo [7] nos centramos en el dodecafonismo, en sus orígenes y en comentar una de sus obras. En el segundo artículo [6] ampliamos las definiciones dodecafónicas para encontrar el grupo diédrico, y descubrimos la historia de los discípulos de Schoenberg y del serialismo integral. Esta tercera entrega está destinada al lector más ducho en las matemáticas; se notará en el lenguaje y en la exposición de las ideas. En ella proporcionaremos herramientas matemáticas relacionadas con acciones, órbitas y estabilizadores de Teoría de Grupos (sección 2), para después contar de dos maneras distintas el número de espectros seriales, que son el número de órbitas del grupo de transformaciones sobre las series, que un compositor puede utilizar en sus obras (sección 3); en concreto, con las transformaciones (3.1) y (3.2). Y de esta manera habremos hecho un recorrido a fondo por el serialismo y habremos explorado sus posibilidades musicales y matemáticas. 2. Acciones, órbitas y estabilizadores 2.1. Acciones de grupos sobre conjuntos Dado un grupo (G, *) y un conjunto X, una acción de (G, *) sobre X es una función ϕ que asocia un elemento g ∈ G y un elemento x ∈ X – el par (g,x) – a otro elemento g ⋅x que también pertenece a X [1]. ϕ : (g,x) → g ⋅ x Una acción ϕ, expresada mediante la operación (⋅), debe cumplir dos condiciones: 1. Para todo x ∈ X, e ⋅ x = x, siendo e el elemento neutro del grupo. 2. Para todo x ∈ X y para todo par g,h ∈ G, se debe cumplir que (g * h) ⋅ x = g ⋅ (h ⋅ x). La primera operación (*) es la interna del grupo G, y la segunda operación (⋅) es la acción. Como ya se ha visto, las funciones forman el grupo diédrico Dn × Dn, siendo n la longitud de la serie. Se podrá definir entonces la acción ϕ de este grupo sobre el conjunto de permutaciones de orden n, tal que ϕ(Ψ, σ) = Ψ ∘ σ = Ψ(σ) = τ, con Ψ ∈ Dn × Dn y σ,τ ∈ Sn. De igual manera, se puede definir el grupo que forman solamente I y R, que servirá más adelante. Como son dos reflexiones, forman el conocido grupo de Klein —a partir de ahora denotado por Ξ, con elementos Id, I, R e IR. 2.2. Órbitas y estabilizadores Dada una acción de (G, *) sobre X, la órbita de un determinado elemento x0 ∈ X es el subconjunto de elementos x de X que pueden ser alcanzados desde x0 mediante algún g0 ∈ G. Es decir, todos los x para los que existe un g0 que al actuar sobre x0 da x. Trivialmente, x0 ∈ Orb(x0) ya que e ⋅ x0 = x0. Orb(x0) = Por ejemplo, dada una permutación σ, todas las permutaciones a las que se llega desde σ mediante algún Ψ ∈ Dn ×Dn conforman la órbita de σ. Por definición, las series a las que se puede llegar desde una serie original constituyen su espectro serial, por lo que la órbita es en realidad el espectro serial. Para el mismo x0 se define su estabilizador como el conjunto de elementos g ∈ G que fijan x0, es decir, que mandan x0 a sí mismo. Mientras que una órbita es un subconjunto de X, un estabilizador es un subgrupo de G. Trivialmente, e ∈ Stab(x) ∀x ∈ X, porque el elemento identidad fija cualquier otro elemento por definición. Stab(x0) = Si cada g ∈ G llevara a x0 a un x distinto, el número de elementos de Orb(x0) sería igual al número de elementos de G. Sin embargo, si un elemento g0 ∈ G fija x0, entonces no dará nuevos elementos en la órbita de x. Por tanto, intuitivamente el tamaño de la órbita disminuye. De hecho, el teorema de órbita–estabilizador dice que el tamaño de una órbita (|Orb(x0)|) será el tamaño de G (|G|) entre el número de elementos que fijan x0; es decir, el tamaño de su estabilizador (|Stab(x0)|). Además, es cierto para todo x ∈ X. |Orb(x)| = |G| / |Stab(x)|, o lo que es lo mismo, |G| = |Orb (x )||Stab(x)| Para ver una explicación más detallada y una prueba rigurosa del teorema, consúltese [4]. Este teorema implica que los tamaños de cada órbita y cada estabilizador son divisores del tamaño del grupo. Por ejemplo, como el tamaño del grupo Ξ es 4, cualquier estabilizador y cualquier órbita tendrán tamaño 1, 2 o 4. En concreto, como Id está siempre en el estabilizador, para todo σ será de una de estas formas: Una serie σ sin simetrías tendrá una serie distinta para cada una de sus transformaciones. Por tanto, su órbita será y su estabilizador será solamente . Cumple entonces el teorema: 4 ⋅ 1 = 4. 2.3. El lema de Burnside Las órbitas, que son subconjuntos de X, forman una partición de X. Esto significa que son subconjuntos disjuntos: ningún x puede estar en dos órbitas distintas. Interesa entonces saber cuántos subconjuntos hay; es decir, el número de órbitas (#Orb). El lema de Burnside afirma que se pueden calcular así: Se prueba de esta forma: por el teorema de órbita–estabilizador, |Stab(x)| = , por lo que la parte derecha se puede expresar así: Como las órbitas forman una partición de X, la suma sobre todo el conjunto X puede ser dividida en sumas separadas para cada órbita. Además, si por cada elemento de una órbita se suma el inverso del número de elementos de la órbita, esa suma dará uno. Solo queda ahora sumar uno por cada órbita. Este lema permite calcular el número de posibles espectros seriales distintos, ya que el espectro de una serie es igual al espectro de sus series transformadas. Un compositor serialista debe entonces escoger no una serie original, sino el espectro con el que construir la obra. O, más bien, si escoge una serie original está escogiendo el mismo material que si escogiera otra serie de ese mismo espectro. Para más aplicaciones de acciones en el ámbito de la teoría musical, véase [2]. 3. Conteo de espectros seriales 3.1. Espectros de las funciones Es interesante conocer el número de espectros seriales distintos que un compositor puede escoger. Al fin y al cabo, es irrelevante qué serie se escoge como la original dentro de su espectro serial, ya que produce el mismo material compositivo que cualquiera de su mismo espectro. Para calcular el número de espectros seriales se redefinirán las funciones transformativas para una longitud serial arbitraria, n, que será mayor que 2. Para n = 0, 1 y 2 se realizará el cálculo en el apartado 3.3. Además, como las transposiciones siempre son distintas entre sí, siempre pertenecen al mismo espectro. Se tomarán a partir de ahora todas ellas como equivalentes, de manera que solo se necesita hacer el cálculo para el conjunto de funciones . Al calcular con permutaciones se trabajará siempre módulo n. La retrogradación sigue siendo R(σ(m)) = σ(-1 -m). La inversión será I(σ(m)) = -σ(m), omitiendo la transposición habitual, ya que se toman las series transpuestas como equivalentes. De esta forma -σ(m) + 2σ(0) ≡-σ(m). La retrogradación invertida es, por tanto, la composición de ambas: RI(σ(m)) = I∘R(σ(m)) = I(R (σ(m ))) = -σ(-1 -m). La retrogradación, la inversión y la composición de ambas cumplen que al aplicarlas dos veces se vuelve a la serie original. En teoría de grupos se dice que tienen orden 2. Entonces forma el ya mencionado grupo de Klein (Ξ), donde RI ≡ IR, ya que estamos tomando las series transpuestas como equivalentes. En general, un grupo de Klein es el formado por cuatro elementos donde cada elemento es inverso de sí mismo. El grupo de Klein, llamado así en honor al matemático alemán Felix Klein, es el grupo ℤ∕(2) × ℤ∕(2), producto directo de dos grupos cíclicos de orden 2. Por el lema de Burnside: Es decir, se deben calcular para cada posible serie σ ∈ Sn cuántas funciones transformativas lo dejan igual o equivalente bajo transposición. Como los estabilizadores son subgrupos, por el teorema de Lagrange su tamaño debe ser divisor del tamaño del grupo total. Entonces se pueden agrupar los estabilizadores por sus tamaños: 1, 2 o 4, y así calcular ∑ |Stab(σ)| agrupando todas las permutaciones con igual tamaño de estabilizador. Si #σi es el número de permutaciones cuyos estabilizadores tienen tamaño i: Primero, se ha de ver que una permutación nunca va a ser igual ni equivalente mediante transposiciones a su inversa. Así, σ(m) sería constante para todo m ∈ ℤ∕(n), lo cual es imposible. Esto implica que ninguna permutación va a tener a I en su estabilizador, por lo que #σ4 = 0. Queda entonces calcular cuántas permutaciones son equivalentes a su retrogradación y cuántas a su retrogradación inversa. La suma de ambas dará #σ2. 3.1.1. Elementos estables mediante R Las permutaciones que coinciden con alguna transposición de su retrogradación cumplen, para γ constante: γ + σ(m) = R(m) = σ(-1 - m) Aplicándolo a (-1 - m): γ + σ(-1 - m) = σ(m) De ambas ecuaciones: γ = σ(-1 - m) - σ(m) = σ(m) - σ(-1 - m) 2σ(m) ≡ 2σ(-1 - m)=> 2σ(m) - 2σ(-1 - m) ≡ 0 2σ(m) - 2σ(-1 - m) = n => σ(m) - σ(-1 - m) = Entonces n debe ser par. Cuando n es impar este tipo de permutaciones no existe. Además, cumplen que sus elementos simétricos se distancian entre sí un intervalo de unidades: son series con simetría par. -γ = σ(m) - σ(-1 - m) = En una serie de longitud n, existen intervalos que miden . Como no importa por cuál de ellos comience la serie, ya que las transportaciones son equivalentes, se fija el primero de los intervalos. Quedan los otros - 1 intervalos por escoger, así que el número de series con simetría par cuenta las permutaciones de - 1 intervalos y las dos posibles posiciones de cada intervalo —creciente y decreciente [5]—. Por ello, el número de series con simetría par es de: Por definición, si n es par n!! = n(n - 2)(n - 4)…4 ⋅ 2 y si n es impar n!! = n(n - 2)(n - 4)…3 ⋅ 1. 3.1.2. Elementos estables mediante RI Las permutaciones que coinciden con alguna transposición de su retrogradación inversa cumplen, para un γ constante: σ(m) = RI(σ(m)) + γ = - σ(-1-m) +  γ γ = σ(m) + σ(-1-m) Sus elementos simétricos suman una cantidad constante: son series con simetría impar. Tal y como se ha hecho en el apartado anterior, se puede fijar una de las notas, ya que las transportaciones son equivalentes. Si n es impar, la nota central es σ(), que es igual a σ(-1 -). Por tanto, γ = 2 ⋅ σ(). Si se escoge esta nota para ser fijada a 0, entonces γ = 2 ⋅ 0 = 0. Es decir, γ puede ser fijada en 0 sin pérdida de generalidad. Para el resto de notas, σ(m) = -σ(-1 -m). Ya escogida la nota central, permite n-1 posibilidades para σ(0). Ya escogidas la nota central, la primera y su simétrica, permiten n-3 posibilidades para σ(1), y así sucesivamente hasta llegar a la nota anterior a la central, que es . Por ello, para n impar, el número de series con simetría impar es de: = (n - 1)(n - 3)...(n - (n- 5) - 1)(n - (n - 3) - 1) = =  (n - 1)(n - 3)...4⋅2 = (n - 1)!! Si n es par, σ(m) ≠ σ(-1-m) ∀m ∈ ℤ∕(n), ya que no hay elemento central. Sea ahora γ = 2k un número par. Como 2k ≤ n y las permutaciones son suprayectivas, para algún m se cumple que σ(m) = k. Se tiene entonces k + σ(-1 -m) = 2k, lo cual a su vez implica que σ(-1 -m) = k = σ(m). Como esto es una contradicción, γ debe ser impar. Fijando, por ejemplo, σ(0) = 0, se tienen posibilidades para σ(-1 - m), es decir, solamente las posibilidades para las que γ es impar. Para σ(1) hay (n- 2) posibilidades, y ahora su simétrico ya viene determinado por el γ escogido. Para σ(2) hay (n-4), y así sucesivamente [5]. Por tanto, para n par, el número de series con simetría impar es de: = (n - 2)(n - 4) ...(n - (n - 4))(n - (n - 2)) =  2 =  (n - 2)(n - 4)...4⋅2 = (n - 2)!! Suma completa Como ya se ha podido observar, el número de espectros seriales varía según la paridad de la longitud de las series. Una vez se tiene #σ2, solo falta calcular #σ1. Como las permutaciones contadas #σ son todas las de Sn exceptuando las transportaciones, #σ = = = (n - 1)!. Por otro lado, #σ1 + #σ2 = #σ. Entonces #σ1 = (n - 1)! - #σ2. Recuperando la fórmula del apartado 3.1: Para n impar: Para n par: Para n = 12, es decir, para el dodecafonismo, la última fórmula proporciona el dato de 9985920 espectros seriales a escoger por el compositor. Como ejemplo perteneciente al serialismo integral, podemos numerar las dinámicas del 0 al 6: ≡ = ℤ∕(7) Así, con la fórmula para n impar, se obtiene que hay 192 espectros seriales con series de longitud 7. 3.2. Espectros del grupo Dn × Dn Este apartado es una explicación detallada del artículo [3] y aplicada al caso musical. La secuencia de números dada por las fórmulas que obtendremos se encuentra en la OEIS: https://oeis.org/A000940. Ahora calcularemos los espectros formados mediante todas las transformaciones del grupo generado por ; es decir, por Dn ×Dn. Volviendo a la representación mediante diagramas de reloj, el problema es equivalente a averiguar cuántos diagramas distintos, sin números ni flechas, se pueden dibujar. La flecha indica lo transformado por V y C, mientras que los números indican lo transformado por S y T. Un diagrama sin estos dos elementos representa entonces todo un espectro serial. ¿Cuántos diagramas esencialmente distintos hay? De nuevo, por el lema de Burnside: En vez de expresar el sumatorio como “para cada σ, el número de Ψ que fijan σ”, se puede expresar como “para cada Ψ, el número de σ fijados por Ψ” (que llamaremos Fij(Ψ)). La fórmula queda de esta manera: Ahora hay que averiguar para cada elemento de Dn × Dn cuántas series estabiliza. Por ejemplo, trivialmente no hay permutaciones estables mediante C y V solamente. 3.2.1. Elementos estables mediante T Los elementos estables mediante Tk son a los que, tras aplicar una rotación de θk = , para 1 ≤ k ≤ n, quedan igual. Por tanto, los sumandos que aportan a la suma total son ∑ nk=1 Fij(θk). Por otro lado, si 1 ≤ p,q ≤ n y gcd(p,n) = gcd(q,n) entonces Fij(θp) = Fij(θq), ya que por el lema de Bézout lo que genera la rotación θp es igual a lo que genera la rotación θgcd(p,n). Esto permite que se puedan agrupar los sumandos con igual máximo común divisor con respecto a n. Es decir, ∑nk=1 Fij(θk) = ∑d|n , con d divisor de n. Por ejemplo, si n = 6: Fij(θ1) + Fij(θ2) + Fij(θ3) + Fij(θ4) + Fij(θ5) + Fij(θ6) = Fij(θ1) + Fij(θ2) + Fij(θ3) + Fij(θ2) + Fij(θ1) + Fij(θ6) = 2 ⋅ Fij(θ1) + 2 ⋅ Fij(θ2) + 1 ⋅ Fij(θ3) + 1 ⋅ Fij(θ6) Ahora queremos encontrar el coeficiente de Fij(θd), es decir, el número de k ≤ n con igual máximo común divisor d. Pero que k ≤ n y gcd(k,n) = d es equivalente a que ≤ y gcd = 1. Por tanto, el número de k con máximo comun divisor d es φ. La función φ(x) se llama la función phi de Euler, y muestra precisamente la cantidad de números menores que él y coprimos con él. Entonces ∑ k=1nFij(θk) = ∑ d|n. Para calcular Fij(θd) hay que analizar cómo se construyen los diagramas invariantes respecto a una rotación. Estos diagramas deben tener varios ciclos iguales entre sí —para que queden invariantes al rotarlos— pero cada uno desde un punto distinto: desde cada múltiplo de d. El número de ciclos es, por tanto, . Al construir uno de estos diagramas, se escoge la primera nota entre las n. Después se escoge la segunda, pero no se pueden escoger los vértices múltiplos de d (de los que hay ), ya que van a ser el comienzo de los sucesivos ciclos. Hay entonces n- posibilidades. Después se escoge la tercera, pero sin escoger los múltiplos de d ni los múltiplos de d + la segunda posición. Hay n- 2 ⋅ posibilidades, y así sucesivamente hasta terminar el primer ciclo: Por ejemplo, si d = 2 y n = 8, supongamos que escogemos el punto 0(0) como el primero. Después, si cogiéramos alguno de los puntos 0(*) luego no podríamos tener simetría al rotarlo un ángulo de θ2. Entonces hay que escoger alguno de los 1(*). Supongamos que es 1(1). En este ejemplo nuestro ciclo quedaría de la siguiente manera: Para escoger el segundo ciclo, su primera nota debe caer en el conjunto de vértices múltiplos de d —de los que hay . En el ejemplo serían los 0(*). Sin embargo, no podría ser cualquier múltiplo, ya que si se escoge uno con posición no coprima, el polígono se cerraría antes de tiempo sin pasar por todos los vértices. Entonces hay que escoger entre los vértices coprimos, de los que hay φ (). Tras esto el polígono está totalmente determinado, y se puede formar de ∑ d|n maneras. En nuestro ejemplo, si escogemos el siguiente comienzo del ciclo como el 0(2), como 2 no es coprimo con = 4, quedaría de esta manera: Efectivamente, el diagrama se cierra antes de pasar por todos los vértices. En cambio, si escogemos 0(1): Y con 0(3): Sea d = 3 y n = 6. Escogiendo el primer número como 0(0), el segundo como 1(0) y el tercero como 2(1), no queda más remedio que escoger como comienzo del segundo ciclo el 0(1). Pero también podría aparecer este mismo comienzo con la parte final dada la vuelta, simétrica, de esta manera: 0(0), 1(0), 2(1), 2(0), 1(1), 0(1). Esta construcción no está incluida en lo descrito anteriormente, y sin embargo es invariante con respecto a T, V y C a la vez. Y es que con n par, al rotar θn∕2 el diagrama, éste puede llegar con la orientación cambiada. Esto puede ocurrir cuando haya una diagonal; es decir, cuando entre dos notas haya un intervalo de . Se escoge el primer punto de entre posibilidades. No son n ya que saldría la misma figura si se escoge el punto antipodal. Con una rotación de θn∕2, el primer ciclo se escoge igual que antes, de ⋅! = 2 ⋅ ! maneras. Y con esto ya queda la figura determinada. Esto lleva a las ⋅ 2 ⋅ ! formas de dibujar un polígono con las características buscadas. 3.2.2. Elementos estables mediante S Los elementos estables mediante S son aquellos que quedan invariantes mediante reflexiones. De nuevo, en este punto se ha de separar por paridad de n. Para n impar, existen n reflexiones para cada uno de los ejes de simetría que pasan por cada vértice. Después, hay n formas de escoger el primer vértice de la secuencia. Ahora hay parejas de vértices; se escoge los primeros miembros entre ellos de 2 formas, tras lo cual éstos se ordenan de ! formas. Esto da un resultado de n2 ⋅ 2 ⋅! polígonos invariantes. Para n par se tienen dos simetrías: con ejes que pasan por vértices y con ejes que pasan por lados. De manera similar a la anterior, se escoge el eje, el primer vértice, los primeros miembros de las parejas de vértices y se ordenan. Para las simetrías con ejes que pasan por vértices, da un resultado de ⋅ 2 ⋅!. Para las simetrías con ejes que pasan por lados, da un resultado de ⋅ 2-1 ⋅!. Suma completa En resumen, estos a continuación son los numeradores ∑ Fij(Ψ). El resultado final del número de diagramas posibles, o espectros seriales distintos, es dicho numerador entre 4n2, el tamaño del grupo. 3.3. Medefonismo, monofonismo y difonismo Con n = 0 se da el caso de medefonismo. El grupo simétrico de orden 0 tiene 0! = 1 elemento. Por tanto, hay una sola posible serie, σ, que es la que no tiene ninguna nota. El medefonismo es comúnmente llamado silencio; se representará con una tabla vacía. Con n = 1 se da el caso de monofonismo. Con solamente una posible nota, el grupo simétrico de orden 1 tiene 1! = 1 elemento. Por tanto, hay una sola posible serie, σ0, que es igual a su inversa, a su retrogradación y a su retrogradación inversa: Con n = 2 se da el caso de difonismo. Tiene dos posibles notas, así que su grupo simétrico, el de orden 2, tiene 2! = 2 elementos. Por tanto, hay dos series distintas, σ0 y σ1. Se puede observar que ambas pertenecen al mismo espectro serial, dado que σ1 = T1(σ0). Además, al igual que en el monofonismo, ambas coinciden con sus inversas, incumpliendo la regla general para n > 2 probada en el apartado 3.1. Agradecimientos A Ismael Sierra, por dejarme descubrir las matemáticas que aún no había podido alcanzar por mí misma. A Paco Gómez, por permitir que muestre al mundo lo que estudio y ayudarme a que sea de la mejor manera posible. A María Gaspar, por poner la primera piedra. A mis padres, a mis amigos, a todos aquellos cuya ilusión me ha motivado a seguir escribiendo. Bibliografía [1] Mark A. Armstrong. Groups and Symmetry. Undergraduate Texts in Mathematics. Springer New York, 2013. Chapter 6: “Permutations”. Chapter 17: “Actions, Orbits, and Stabilizers”. Chapter 18: “Counting Orbits”. [2] Alissa S. Crans, Thomas M. Fiore, and Ramon Satyendra. Musical Actions of Dihedral Groups. The American Mathematical Monthly, 116:479–495, 06 2009. [3] S. W. Golomb and L. R. Welch. On the enumeration of polygons. The American Mathematical Monthly, 67:349–353, 04 1960. [4] Timothy Gowers. Group actions II: the orbit-stabilizer theorem, 2011. Consultado en octubre de 2019. [5] David L. Reiner. Enumeration in Music Theory. The American Mathematical Monthly, 92:51–54, 01 1985. [6] Celia Rubio Madrigal. Serialismo y matemáticas - II. Divulgamat, octubre de 2019. [7] Celia Rubio Madrigal. Serialismo y matemáticas - I. Divulgamat, septiembre de 2019.

Lunes, 11 de Noviembre de 2019 | Imprimir | PDF |  Correo electrónico

549. 11. (Marzo 2019) Tarjetas Lógicas del libro “Este no es el título de este libro”

Recientemente el País ha lanzado una colección de libros inéditos realizados por reconocidos especialistas y divulgadores de los grandes temas de las matemáticas: “Grandes ideas de las matemáticas”. En Divermates podemos presumir de que nuestro Director y Jefe Creativo, Nelo Maestre, ha participado escribiendo el quinto de los 40 libros que completan la colección. En su libro, “Este no es el título de este libro. Paradojas, axiomas y fundamentos de las matemáticas”, concretamente en el capítulo uno, Nelo nos habla de las llamadas tarjetas lógicas. A lo largo del capítulo Nelo introduce el lenguaje lógico, llegando un momento en que referencia un grupo de tarjetas lógicas ya estudiadas por Martin Gardner en su libro “Máquinas y diagramas lógicos”. Lo sorprendente de estas tarjetas es que pueden facilitarnos notablemente la resolución de problemas sencillos de lógica proposicional. ¿Qué son las tarjetas lógicas? La idea básica de estas tarjetas es automatizar la evaluación de proposiciones lógicas. Dada una proposición nos dirá para que valores de veracidad o falsedad de cada variable A, B y C la proposición evaluada es correcta. Conviene señalar los símbolos lógicos que utilizaremos para referirnos a cada concepto. Conjunciones o (˅) e y (˄). Negación (¬). Equivalencia (≡) e implicación (→). 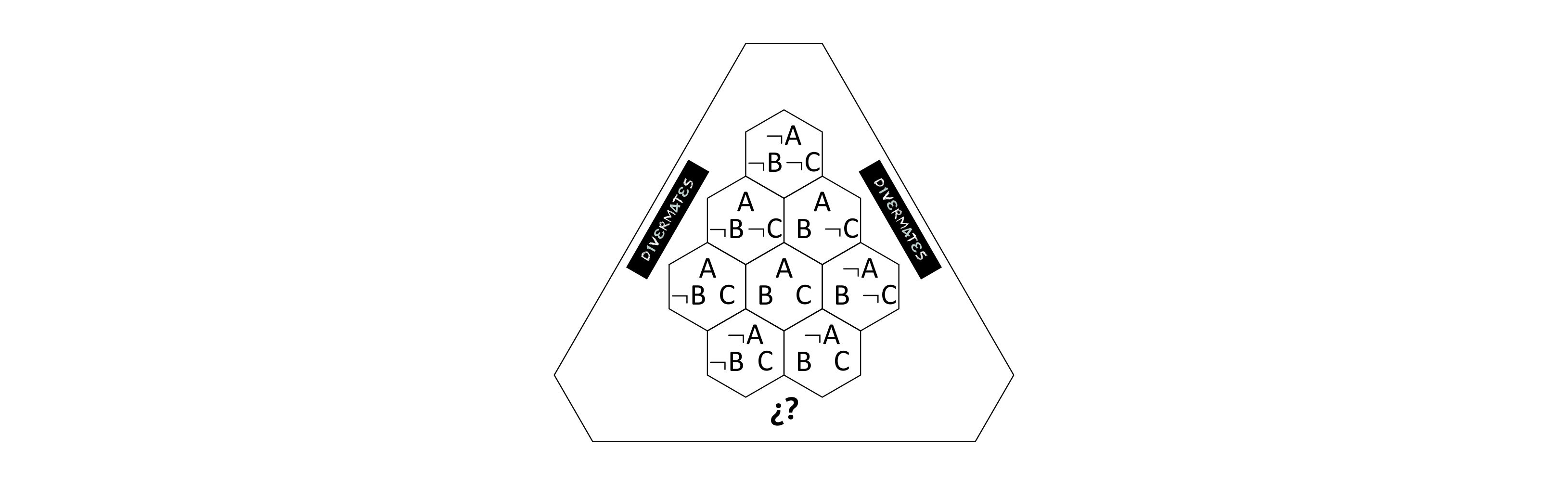Para hacerte con estas tarjetas sólo tendrás que descargártelas aquí: Tarjetas Lógicas Por un lado tenemos la tarjeta base que nos muestra en los hexágonos las combinaciones de las variables A, B y C, en los casos en que cada variable es cierta o lo es su negación. Por otro lado tenemos las tarjetas perforadas, que tendremos que agujerear una vez impresas, recortando las zonas sombreadas. En cada lado de estas tarjetas aparecen distintas premisas, y algunas sentencias equivalentes entre paréntesis. A veces es necesario imprimir varias tarjetas para tener más de una copia. ¿Cómo funcionan las tarjetas lógicas? Cada una de las tarjetas perforadas tiene tres posiciones diferentes. Cuando queramos evaluar una sentencia tendremos que asegurarnos que ponemos la premisa a evaluar sobre el símbolo ¿? de la tarjeta base. Para su uso, sólo tenemos que saber que la conjunción “y”, representada mediante el símbolo ˄, se evalúa simplemente poniendo premisas una sobre otra, y todas ellas sobre la tarjeta base. Hay que tener cuidado de colocar todas las tarjetas en la posición correcta, según la sentencia que queramos evaluar. Para una mejor explicación hemos realizado un video explicativo. Para reproducirlo no dudes en entrar en nuestro blog, al final de la entrada encontrarás un video que resolverá todas tus dudas:    

Martes, 05 de Marzo de 2019 | Imprimir | PDF |  Correo electrónico

550. Aleksandr Gelfond (1906-1968)

El matemático Aleksandr Gelfond (1906-1968) falleció un 7 de noviembre. Es el autor del teorema de Gelfond-Schneider que dice: Si a y b son números algebraicos (con a distinto de 0 y 1), y si b no es un número racional, entonces  ab es un número trascendente. Este teorema da una solución al séptimo problema de Hilbert que trata sobre la irracionalidad y la trascendencia de ciertos números. Por ejemplo, se utiliza para demostrar la trascendencia de la constante de Gelfond, ya que basta con observar que: eπ = (eiπ)-i = (-1)-i Aleksandr Gelfond fue director de tesis de nuestro compañero del Departamento de Matemáticas de la UPV/EHU, Emiliano Aparicio Bernardo (1926-1998). Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 07 de Noviembre de 2019 | Imprimir | PDF |  Correo electrónico