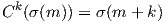571. 101. (Octubre 2019) Serialismo y matemáticas (II)

1. Introducción Este artículo es el segundo de la colección Serialismo y matemáticas. Las músicas serialistas son aquellas que permiten construir castillos con un solo grano de arena: una serie particular, una permutación de notas, dinámicas o timbres. La serie se coloca en la obra secuencialmente, siempre igual o con alguna modificación que la adorne. Y es que para esta música, la serie es el ladrillo y las matemáticas son la pintura con la que decorarlos, ya que las transformaciones que se le puede aplicar a una serie forman preciosas estructuras matemáticas enmarcadas en la Teoría de Grupos. En el primer artículo7 nos centramos en el dodecafonismo, en sus orígenes y en comentar una de sus obras. En este segundo artículo, ampliaremos las definiciones dodecafónicas para descubrir bajo ellas, con ayuda de diagramas, el grupo diédrico (sección 2); y contaremos quiénes fueron los discípulos y sucesores de Schoenberg y cómo provocaron la creación del serialismo integral (sección 3). Más adelante proporcionaremos las herramientas matemáticas para después contar el número de espectros seriales que un compositor puede utilizar. En definitiva, haremos un recorrido a fondo por el serialismo y exploraremos sus posibilidades musicales y matemáticas. 2. El grupo de las transformaciones 2.1. Nuevas definiciones y nuevas transformaciones Como vimos en el anterior artículo7, las fórmulas de las transformaciones dodecafónicas habituales son: I(σ(m)) = -σ(m) + 2σ(0) Tk(σ(m)) = σ(m) + k R(σ(m)) = σ(-1 - m) Sin embargo, la importancia de estas definiciones radica en qué espectro serial forman, y no en cómo se nombra cada serie específica. No importa si la segunda serie que se usa en una obra se llama I6 o RI10, sino cuál es y qué relación tiene con la primera. La nomenclatura no es distinguible a un nivel auditivo, pero es, sin embargo, una útil herramienta para la teoría musical. Es por ello por lo que la forma en la que se nombran las series tiene relevancia y debería ser un reflejo de lo que significan. Aun así, sigue sin haber un convenio predominante y, de hecho, hay al menos dos que se usan a menudo. El primero, el método tradicional, se ha usado desde al menos 1945. El segundo, el método de tonos absolutos, fue concebido por George Perle6 en su libro Twelve-Tone Tonality en 1977. En el método tradicional, T0 se usa para la primera serie que se encuentra en la composición; es decir, es la serie original. En cambio, el método de tonos absolutos nombra las series T basándose solamente en la nota en la que comienzan: T0 se usa para la serie que comienza por un do, T1 para el re, y así sucesivamente. En ambas, las series transpuestas k semitonos de T0 —sea cual sea esta— se nombran como Tk. La composición de esta con otra función Ψ se escribe como Ψk. Estas nomenclaturas no caracterizan adecuadamente el objeto matemático que deben representar, es decir, funciones aplicadas a las series. Son nombres arbitrarios que además producen ambigüedad al añadir otras funciones —por ejemplo, si no conmutan— o al intentar describirlo matemáticamente. Es por ello por lo que en este texto se usa la composición de funciones como convenio de notación. En todo caso, cualquier convenio tendrá fórmulas distintas al resto, pero todas preservan el material compositivo de la obra. Eso quiere decir que se pueden redefinir algunas de las transformaciones siempre que preserven el sentido musical. Por ejemplo, la inversión puede prescindir de ser transportada para que la primera nota coincida con la original. Para distinguirla de la primera definición, ésta se llamará S de simetría: S(σ(m)) = -σ(m). E igual que la inversión es el cambio de signo por fuera, la retrogradación puede convertirse simplemente en el cambio de signo por dentro. Ésta se llamará V de volteo: V (σ(m)) = σ(-m). Así quedan dos transformaciones que se asemejan a reflexiones: una por dentro y otra por fuera; y una adición por fuera. Aquí dentro significa antes de aplicar σ y fuera significa después de aplicar σ, ya que no se debe olvidar que σ, la permutación, es una función en sí misma. Y ahora surge una cuestión natural: ¿cuál sería entonces el resultado de sumar dentro, es decir, antes? Esta nueva transformación, cuya aparición resulta natural tras las otras tres, se llama desplazamiento cíclico. Inventada y usada por Alban Berg2 —de quien se hablará en la sección 3— y en algunas de las primeras obras de Schoenberg, Ck desplaza el comienzo de la serie k posiciones más allá: La serie 4-cíclica sobre la permutación P de la Suite Op. 25 es la siguiente serie C4: Si no se añade la transformación C, entonces V no conserva el espectro serial de ; pero si se añade sí se conserva ya que V es composición de C y R. En resumen, se puede trabajar con un nuevo sistema de definiciones que mantienen el significado musical del serialismo, pero varían la notación con la que se trabaja. Estas son las nuevas fórmulas de las transformaciones: S(σ(m)) = -σ(m) V (σ(m)) = σ(-m) Tk(σ(m)) = σ(m) + k Ck(σ(m)) = σ(m + k) 2.2. Diagramas de reloj Para visualizar mejor cómo actúan las distintas transformaciones, las series se pueden representar mediante diagramas de reloj3: una sucesión de aristas con una orientación establecida que conecta los vértices de un dodecágono en el orden de la serie. Ya que el desplazamiento cíclico actúa como si la serie fuese circular, hay una arista extra que une la última nota a la primera. El comienzo de la serie y su orientación se marcan con una flecha. Arriba se incluye el diagrama de la serie original σ de la Suite Op. 25. Se pueden distinguir las características de la serie, como las tres diagonales, que son los tres intervalos de tritono. A continuación se incluyen los diagramas de las transformaciones dodecafónicas originales: la transposición, la inversión y la retrogradación; así como el nuevo desplazamiento cíclico. La transposición es una rotación en el sentido en el que apunta la flecha; la inversión es una reflexión con el eje de simetría en la diagonal que pasa por la flecha; la retrogradación es un cambio de orientación de la flecha; y el desplazamiento cíclico es el avance interno de la flecha por el recorrido de la serie. La diferencia entre las inversiones I y S es precisamente la transposición de 2σ(0) = 8 semitonos en este ejemplo. Comparando S con T0 se puede además observar que S es una reflexión con el eje de simetría en 0, en vez de que el eje dependa de la propia permutación. Por otro lado, la comparación entre las retrogradaciones R y V muestra que, aunque en principio más arbitraria, V es una transformación más natural, ya que deja fija la flecha. La diferencia entre ellas es en realidad un desplazamiento cíclico de -1. He creado una página interactiva que genera diagramas de reloj de cualquier serie para cualquier longitud serial, además de generar series aleatorias. También se pueden aplicar las transformaciones a la serie, tanto las originales como las del nuevo sistema, para ver cómo se comporta el diagrama. Está escrita en Elm y el código puede encontrarse en https://gitlab.com/dodecafonismo/diagramas. En el enlace https://diagramas.netlify.com se accede a la aplicación web. Sus instrucciones de uso se encuentran al final de la página. Además, he creado un comando en LATEX que dibuja estos diagramas dada su serie, y opcionalmente su nombre y el número que está arriba: y en este caso up=4 no es necesario, ya que por defecto se coloca arriba la primera nota de la serie. El comando se encuentra en el paquete de LATEX ddphonism, disponible en el enlace https://www.ctan.org/pkg/ddphonism. 2.3. El grupo: D12 × D12 El conjunto de transformaciones está compuesto por dos parejas con semejanzas entre sí. S es una reflexión y T una rotación de orden 12 —es decir, que al aplicarla 12 veces se vuelve a la identidad— y ambas se aplican a la figura entera; es como mover el diagrama por el papel. En cambio, V es una reflexión de la flecha en sí, y C una rotación —también de orden 12— de la flecha sobre la línea; ambas aplicadas al interior de la figura. Cada pareja genera un grupo muy conocido: el grupo diédrico o diedral. Se denota por D12 y representa el grupo de simetrías de un polígono regular; en este caso, un dodecágono. En otros ámbitos, Dn también se denota por D2n, ya que 2 * n es el número de elementos que tiene el grupo. Por ejemplo, aquí se muestran todas las simetrías de un octógono, que son los 16 elementos de D8, aplicados a una señal de STOP. De igual manera, el conjunto de series de un espectro serial se consigue aplicando a la serie las distintas funciones transformativas; se obtiene entonces un grupo diédrico para ambas parejas de funciones. Al haber dos parejas distintas que actúan por separado dentro y fuera de la figura, el grupo completo que forman las cuatro transformaciones es el producto directo de dos copias del diédrico: D12 × D12. Podemos observarlo claramente si representamos la serie de una segunda forma: como la correspondencia entre vértices de dos dodecágonos. La serie original, que es en realidad una permutación de 12 elementos, se representa como una función: los vértices del dodecágono interno se envían biyectivamente a los vértices externos. Así, m→σ(m). Este diagrama es similar al matricial pero enroscado en sí mismo, de tal forma que se aprecia la permutación escogida mediante las flechas, que son fijas, y facilita un significado del antes y el después de aplicarla. Las dos primeras figuras describen esto mismo: la representación de la serie original y la representación de la permutación mediante las flechas, que se mantendrán constantes en el resto de figuras. Las cuatro siguientes figuras representan las cuatro funciones transformativas, que son en realidad la reflexión y la rotación del grupo diédrico de cada dodecágono. Aplicarlo al de dentro es aplicarlo antes de las flechas; antes de la permutación. Aplicarlo fuera es transformar después de las flechas; después de la permutación. He creado un comando en LATEX que dibuja estos diagramas diédricos dada su serie original y las funciones aplicadas a ella: t, s, c y v. Se aplican en ese mismo orden, y por defecto están a 0. El comando se encuentra en el paquete de LATEX ddphonism, disponible en el enlace https://www.ctan.org/pkg/ddphonism. 2.4. Conmutatividad entre los elementos del grupo La rotación, r, y la reflexión, s, de un grupo diédrico no conmutan, sino que cumplen la relación r ⋅ s = s ⋅ r-1. Por otro lado, en los productos directos los elementos de un lado conmutan con los del otro. Así, y no conmutan, pero el resto de parejas sí. La verificación de estas afirmaciones, que confirman que el grupo generado es D12 × D12, se encuentran a continuación: Volviendo a las definiciones originales , su estructura interna es bien distinta. El problema de I es que depende de la permutación escogida, por lo que a veces tiene unas propiedades y a veces otras. En cambio, la definición de V con respecto a R es meramente estética: ya que no depende de la permutación, su conmutatividad se mantiene invariante. Viendo cómo conmutan los elementos de este sistema se aprecia la dificultad de I. Curiosamente, la conmutatividad de e se pierde, pero se gana la de . Así, T conmuta con todo en el sistema. Esto muestra una ventaja de la definición de I. Los únicos casos en los que podrían conmutar ocurrirían cuando Es decir, cuando la primera y la última nota de la serie original se distancian en 6 semitonos, como es el caso de la permutación en la Suite Op. 25: Los únicos casos en los que podrían conmutar son cuando Es decir, cuando la primera y la segunda nota de la serie original se distancian en 6 semitonos. Si se echan las cuentas con Ck en vez de con C1, pueden conmutar si σ(k) - σ(0) = 6. Como σ es una permutación, devuelve todos los valores de 0 a 11 y solamente una vez cada uno. Por tanto, también devuelve 6 + σ(0), así que siempre existe un único k para el que I y Ck conmutan. En el caso de la permutación de la Suite Op. 25, como σ(0) = 4 hay que encontrar el k para el que σ(k) = 4 + 6 = 10. En este caso, k = 11, pero depende por completo de la permutación original. 3. El surgimiento del serialismo integral 3.1. Alban Berg y Anton Webern: la Segunda Escuela de Viena Además de Schoenberg, hubo dos compositores más que contribuyeron al desarrollo del dodecafonismo y que demostraron con sus diferentes estilos la versatilidad del sistema. Éstos fueron los discípulos de Schoenberg: Alban Berg y Anton Webern. El maestro y sus dos alumnos formaron la autodenominada Segunda Escuela de Viena, llamada así en honor a los miembros de la Primera: Haydn, Mozart y Beethoven. Aparte del hecho de que Schoenberg, Berg y Webern nacieron y se formaron en Viena, el nombre también simboliza su autoproclamación como herederos legítimos de la tradición musical alemana proveniente del siglo XVIII. La Segunda Escuela de Viena formó parte de las vanguardias artísticas europeas, opuestas a la tendencia neoclásica que seguían Stravinsky o Prokofiev, entre otros, en aquel periodo. Los tres integrantes siguieron carreras compositivas similares en cuanto a estilo y concepción artística: una época tonal, una ruptura atonal y un desarrollo dodecafónico. Con el ascenso del nazismo, Schoenberg, que era judío, se vio obligado a exiliarse a Estados Unidos. Sus discípulos se quedaron en Austria, pero pasaron penurias económicas debido a la censura impuesta por el gobierno: la música dodecafónica se descalificó como Entartete Kunst5 (“arte degenerado”). Figura 1: Alban Berg (1885—1935); figura tomada de Deutsche Welle. Alban Berg se centró en la efusión emocional y el interés por lo humano, utilizando el método dodecafónico libremente y acercándose a formatos tonales. Su etapa atonal fue especialmente relevante, ya que compuso entonces su primera obra dramática, Wozzeck (1925). Es una ópera basada en la pieza teatral de Georg Büchner, en la cual Berg plasmó parte de sus propias experiencias como soldado en la Primera Guerra Mundial. Su segunda ópera, Lulú, quedó inconclusa debido a su muerte por septicemia en 1935, a los 50 años. A continuación el lector podrá escuchar parte de Und ist kein Betrug, la primera escena del tercer acto de Wozzeck: Anton Webern fue un compositor más riguroso en cuanto a las formas, siempre leal al sistema dodecafónico y a su maestro. Se deleitaba en los procedimientos formales más sutiles, aquellos que solo podían ser descubiertos al estudiar detenidamente la obra. Esto quedó reflejado en su dodecafónico Concierto para 9 instrumentos, op. 24 (1934), cuya serie está construida por segmentos derivados de las tres primeras notas de la obra. Además, muestra tendencias a asignar duraciones, timbres y articulaciones a segmentos aislados, lo que más tarde inspiraría el serialismo integral. A continuación el lector podrá escuchar el Concierto op. 24: Durante la ocupación de Viena, Webern salió de su casa una noche tras el toque de queda, y un soldado norteamericano, probablemente en estado de embriaguez, lo mató a tiros. Así, Schoenberg, el maestro y el más mayor de los tres, sobrevivió a sus dos alumnos exiliado en Estados Unidos. 3.2. La escuela de Darmstadt Tras la Segunda Guerra Mundial, el mundo artístico estaba totalmente destruido. La violencia, la censura y la incomunicación habían impedido cualquier posible desarrollo creativo, y los artistas de la generación anterior se habían aislado, exiliado o habían fallecido. Volver a construir los pilares del arte era el cometido de la nueva generación de artistas, quienes compartían la sensación de que el mundo había renacido tras la tragedia. En 1946 se crearon los Cursos de Verano de Darmstadt, fundados por Wolfgang Steinecke y patrocinados por las fuerzas americanas, con el objetivo de retomar la actividad musical en la Alemania de la posguerra. Se centraron en dar a conocer las técnicas compositivas de las generaciones anteriores. Aunque el primer año estuvo enfocado en el movimiento neoclásico, fue en los años posteriores cuando se desarrolló un mayor interés por las técnicas serialistas. Los cursos resultaron en la aparición de una nueva escuela de compositores cuya finalidad artística era crear un lenguaje musical distinto y alejado de la tradición para, de esta forma, obtener una mayor libertad compositiva. Como dijo Karlheinz Stockhausen: Los métodos nuevos cambian la experiencia, y las experiencias nuevas cambian al hombre. Stockhausen en el documental autobiográfico Tuning In4. Esta escuela tomó el nombre de la ciudad donde se realizaban los cursos: se llamó la Escuela de Darmstadt. El término fue acuñado por el compositor Luigi Nono en una de sus clases magistrales en 1957, y con él se describía a sí mismo y a sus compañeros compositores: Pierre Boulez, Karlheinz Stockhausen y Bruno Maderna. Para estos compositores, la tradición artística estaba demasiado relacionada con los fracasos políticos y las penurias sociales pasadas, y precisamente por ello creían necesario romper con todos los vínculos heredados. Sin embargo, para crear aquel nuevo lenguaje no tomaron como referencia el dodecafonismo de Schoenberg, ya que él veía su sistema como parte de la tradición musical, como un elemento más en la evolución de la música. Se centraron, en cambio, en la formalidad y abstracción del serialismo de Anton Webern, y desarrollaron a partir de sus métodos el denominado serialismo integral. Figura 2: Anton Webern (1883—1945); figura tomada de France Musique. Para la Escuela de Viena el estilo compositivo de Webern era tan solo un posible enfoque del amplio abanico que abarcaba el dodecafonismo, pero en Darmstadt se consideró un avance de este. El serialismo integral es un sistema de composición musical que predetermina los materiales compositivos —la melodía, la armonía, el ritmo, el timbre— a partir de la ordenación serial de los diferentes parámetros musicales: alturas, intensidades, duraciones, ataques o instrumentos, entre otros. Es un desarrollo del serialismo dodecafónico de Schoenberg, que serializa solamente las alturas, hacia los demás parámetros sonoros. Tiene, por tanto, un alto grado de planificación pre-composicional: se pretende que la determinación compositiva sea absoluta; y se tiende al automatismo del arte y sus formas, alejándolo de cualquier evocación decimonónica. Desde sus comienzos, el serialismo integral suscitó numerosas críticas, incluso desde el propio colectivo vanguardista. Una de ellas fue la falta de elección del intérprete a la hora de transmitir la obra. El intérprete serialista debe reproducir con total exactitud cada detalle de la partitura, y, por tanto, no puede aportar carácter alguno. Otra de las críticas más extendidas fue la incapacidad para interpretar estas obras correctamente debido a su complejidad técnica. Además, los detalles que precisamente las hacen complejas son, en su mayor parte, inapreciables por parte del oyente. 3.3. Pierre Boulez El compositor que creó y utilizó por primera vez el serialismo integral, además de instruirlo y difundirlo a los demás compositores de Darmstadt, fue el compositor francés Pierre Boulez. Otros músicos habían compuesto obras con tendencias serialistas y elementos predeterminados, como Olivier Messiaen en Mode de valeurs et d’intensités, pero fue Boulez quien sentó sus bases y su técnica. De hecho, los compositores precedentes influyeron prominentemente en la música de Boulez gracias a las clases impartidas en los cursos de Darmstadt. Figura 3: Pierre Boulez (1925—2016); figura tomada de Kultur im Radio. Boulez consideraba necesaria y evidente la extensión de elementos a predeterminar más allá de la melodía, y le parecía incoherente el sistema dodecafónico de Schoenberg, que para él estaba incompleto. En su controvertido ensayo Schoenberg ha muerto1, publicado un año después de la muerte del compositor, comentó: En primer lugar, la exploración del campo serial ha sido conducida unilateralmente: allí falta el plano rítmico, e incluso el plano sonoro propiamente dicho: las intensidades y los ataques. […] Pero la causa esencial de su fracaso reside en el desconocimiento profundo de las FUNCIONES seriales propiamente dichas, las funciones engendradas por el principio mismo de la serie. Es decir, que para ampliar el concepto de serialismo se debía primeramente conocer el fundamento matemático de las series y sus funciones transformativas. Además de ser músico y compositor, Boulez había estudiado matemáticas, lo que le llevó a querer analizar matemáticamente el sistema compositivo y generalizarlo para series de longitudes arbitrarias. Para él, el serialismo no debía ser un mero recurso compositivo, sino la ley que rige todos los elementos de la obra. De hecho, más adelante en su ensayo declaró: […] desde el descubrimiento de la Escuela de Viena, todo compositor alejado de los experimentos seriales ha resultado inútil. Su obra Structures I (1952), para dos pianos, fue compuesta siguiendo las técnicas de serialismo integral: tiene series de doce alturas, doce ataques, doce duraciones y doce tipos dinámicos, aunque más tarde reduciría algunas a diez. A continuación el lector podrá escuchar Structures I: Bibliografía [1] Pierre Boulez. Schoenberg is dead, 1952. Publicado en la revista The Score originalmente; consultado en agosto de 2019. [2] David John Headlam. The Music of Alban Berg. Composers of the twentieth century. Yale University Press, 1996 . [3] David J. Hunter and Paul T. von Hippel. How Rare Is Symmetry in Musical 12-Tone Rows? The American Mathematical Monthly, 110:124–132, 02 2003. [4] Robin Maconie. Tuning In — A Film about Karlheinz Stockhausen, 1981. Producido por Barrie Gavin para la serie de BBC “Horizon”. [5] Vicent Minguet. Las reglas de la música y las leyes del Estado: la “Entartete Musik” y el Tercer Reich. Quodlibet: revista de especialización musical, 69:9–29, 2018. [6] George Perle. Twelve-tone Tonality. University of California Press, 1977. [7] Celia Rubio Madrigal. Serialismo y matemáticas - I, septiembre de 2019 .

Miércoles, 09 de Octubre de 2019 | Imprimir | PDF |  Correo electrónico

572. 144. Hasta Tony Stark ha aprendido matemáticas

Considerada por sus fans la mejor película Marvel hasta la fecha, e incluso para algunos la mejor de la historia, recurre a las matemáticas y la física para justificar su (¿novedoso?) argumento. Adelanto que no soy muy fan del universo Marvel, y en su momento (de más joven) a lo más leí algún tebeo de Spiderman de la editorial Vértice. Eso sí, el tener un chaval de doce años ha provocado que me haya tragado creo que todas las películas estrenadas hasta la fecha (en pantalla pequeña por supuesto; bastante tengo ya con pagarle la entrada a él cuando va con sus amigos al cine para ese tipo de películas). El caso es que fue al cine a ver Vengadores: Endgame el viernes de su estreno mundial (de la que salió encantado, por cierto, y con la ilusión de que yo la viera). Tras algo de resistencia (no mucha la verdad: cuanto antes se pase por lo inevitable, mejor), a finales del verano nos pusimos a verla en DVD. Lamentablemente la tuvimos que ver de tres veces (dura casi tres horas) porque al niño le empieza a molestar que el padre se duerma durante el visionado de “las películas que él elige” (será la edad; a veces también me sucede en las que elijo yo). Bueno pues, mira tú por donde, en una escena, como hace frecuentemente el cine, se recurre a las matemáticas y la física para dar un barniz de verosimilitud a algo completamente descabellado (será por aquello de que como tampoco las entiende nadie, pues cuela). Empecemos con los datos técnicos: Ficha Técnica: Título: Vengadores: Endgame. Título Original: Avengers: Endgame. Nacionalidad: EE.  UU., 2019. Dirección: Anthony Russo y Joe Russo. Guion: Christopher Markus y Stephen McFeely, basado en los comics de Stan Lee, Jack Kirby y Jim Starlin. Fotografía: Trent Opaloch, en Color. Montaje: Jeffrey Ford y Matthew Schmidt. Música: Alan Silvestri. Duración: 181 min. Ficha artística: Intérpretes: Robert Downey Jr. (Tony Stark / Iron Man), Chris Evans (Steve Rogers / Capitán América), Mark Ruffalo (Bruce Banner / Hulk), Chris Hemsworth (Thor), Scarlett Johansson (Natasha Romanoff / Viuda Negra), Jeremy Renner (Clint Barton / Ojo de halcón), Don Cheadle (James Rhodes / Máquina de guerra), Paul Rudd (Scott Lang / Ant-Man), Benedict Cumberbatch           (Doctor Extraño), Chadwick Boseman (T'Challa / Pantera Negra), Brie Larson (Carol Danvers / Capitana Marvel), Tom Holland   (Peter Parker / Spider-Man), Karen Gillan (Nebula), Zoe Saldana (Gamora), Evangeline Lilly (Hope Van Dyne / Avispa), Rene Russo (Frigga), Elizabeth Olsen (Wanda Maximoff / Bruja Escarlata), Natalie Portman (Jane Foster), Marisa Tomei (Tía May), Angela Bassett (Ramonda), Michael Douglas (Hank Pym), Michelle Pfeiffer (Janet Van Dyne), William Hurt (Secretario de Estado Thaddeus Ross), Gwyneth Paltrow (Pepper Potts), Robert Redford (Alexander Pierce), Josh Brolin (Thanos), Chris Pratt (Peter Quill / Star-Lord), Samuel L. Jackson (Nick Fury). Sinopsis: Después de los devastadores sucesos ocurridos en Vengadores: Infinity War, el universo se encuentra en ruina total. Con ayuda de los aliados supervivientes, los Vengadores intentarán revertir el caos provocado por Thanos con la destrucción de las gemas del infinito y así restaurar el orden del Universo. Referencias cinematográficas y literarias Desde luego la solución encontrada para lograrlo no se puede decir que sea demasiado original: viajar en el tiempo, en este caso retroceder en él hasta el momento en que las gemas aún eran una realidad. De ello se encargará el superhéroe correspondiente. Los propios guionistas se percatan de que esto ya está bastante manido en el cine (por supuesto, los jóvenes que van a ver la película no tienen ni idea del asunto y aunque la tuvieran les da lo mismo). Sin embargo, por si hubiera algún despistado por la sala (o algún adulto acompañante que hubiera visto o leído algo del tema), intentan dar una explicación “novedosa y científica”, que comentaremos en el siguiente párrafo. Se permiten el lujo de cachondearse incluso (lo mencionan explícitamente) de películas basadas en los viajes en el tiempo como la saga de Regreso al futuro (Back to the future, Robert Zemeckis, EE. UU. 1985): ¿Me estás diciendo en serio que tu plan para salvar el Universo se basa en Regreso al Futuro? Posteriormente, califican la idea de esta película como “montón de mierda” (textual), y sin embargo cuando Ojo de Halcón prueba la solución que ha puesto en práctica Hulk (no olvidemos que Bruce Banner es un científico), “aterriza” en un granero, lo mismo que Marty McFly precisamente en una de las películas de Regreso al Futuro. Uno de los “escasos” (para mi) alicientes de la película consiste en descubrir las innumerables referencias que se dan a otras películas. Citaré sólo algunas porque hay un montón. Algunas son citadas explícitamente por los Vengadores cuando intentan resolver el problema del viaje en el tiempo mediante la opción de Hulk: La saga Star Trek, el mogollón de referencias cinematográficas al relato La máquina del tiempo de H. G. Wells, de la cual yo me quedo (Ay, ¡qué mayor me estoy haciendo! En realidad, soy de la misma quinta que Tony Stark/Robert Downey Jr.) con El tiempo en sus manos (The Time Machine, George Pal, EE. UU., 1960). Pero es que se citan expresamente (lástima que varias no se han doblado al castellano con sus títulos de las versiones españolas; esto se pierde en el doblaje porque en la versión original, el espectador las reconoce inmediatamente; bueno, el espectador freakie yanqui, porque todas son norteamericanas/anglosajonas) Los pasajeros del tiempo (Time After Time, Nicholas Meyer, EE. UU., 1979), En algún lugar del tiempo (Somewhere in Time, Jeannot Szwarc, EE. UU., 1980), Terminator (The Terminator, James Cameron, EE. UU., 1984), la serie de televisión A través del tiempo (Quantum Leap, creada por Donald P. Bellisario, EE. UU., 1989 – 1993), Las alucinantes aventuras de Bill y Ted (Bill & Ted's Excellent Adventure, Stephen Herek, EE. UU., 1989), Policía en el tiempo (Timecop, Peter Hyams, EE. UU., 1994), Una grieta en el tiempo (A Wrinkle in Time, John Kent Harrison, Canadá, 2003) (reciente versión para cine: Un pliegue en el tiempo (A Wrinkle in Time, Ava DuVernay, EE. UU., 2018), Jacuzzi al pasado (Hot Tub Time Machine, Steve Pink, EE. UU., 2010). Se ve que a los Vengadores les mola el cine un montón. Incluso hay una cita, que no se sabe si es pura equivocación (no creo), o un guiño a que el que lo dice no está muy puesto en esto del cine (idéntico a como hace Woody Allen en Granujas de medio pelo (Small Time Crooks, Woody Allen, EE. UU., 2000) cuando hace a los protagonistas confundir La isla del tesoro con El tesoro de Sierra Madre), citando Jungla de cristal (Die Hard, John McTiernan, EE. UU., 1988) como ejemplo de viaje en el tiempo (todo el mundo que la haya visto sabe que en ella no hay nada de viajes en el tiempo). Sin embargo, Bruce Willis, su popular protagonista, ha participado en varias películas de viajes en el tiempo (Doce monos (Twelve Monkeys, Terry Gilliam, EE. UU., 1995); The Kid (El chico), Jon Turteltaub, EE. UU., 2000; Looper (Rian Johnson, Reino Unido/China, 2012). En definitiva, que ha oído cohetes, pero no sabe dónde. Entre las referencias menos directas (hay montones), señalemos un par de ellas: el momento en el que Ant-Man propone a Tony Stark un viaje en el tiempo empleando la expresión Time Heist (que obviamente no apreciamos sino vemos la versión original en inglés). Time Heist es el título de uno de los episodios de la octava temporada de la serie Dr. Who (de todas las versiones hablamos de la británica creada por Sydney Newman 2005), en la que la actriz Karen Gillan (la que hace aquí del personaje de Nebula) participa en varios episodios. Otra es en la escena de la batalla en Nueva York, con Tony Stark golpeado por la puerta que abre Hulk y las gafas de sol que lleva puestas Thor. Se trata de un homenaje/calco al momento en que Marty McFly trata de recuperar el almanaque deportivo en Regreso al futuro II (Back to the Future Part II, Robert Zemeckis, EE. UU., 1989). Matemáticas, Física, … Pero claro, aunque tengamos dos científicos, el puñetero amo es Tony Stark / Iron Man, así que será él (reticente al principio) el que hallará un procedimiento para regresar al pasado de un modo “muchísimo más sofisticado” que el pedestre de Bruce Banner /Hulk (la película hace bastante guasa a costa del pobre Ant-Man y sus incursiones temporales). La solución está en la mecánica cuántica y …, la banda de Moebius. Vayamos a la escena. Stark está pensando, siendo ayudado por su sofisticado ordenador que le resuelve y presenta en 3D todo lo que le indique. Hacia el minuto 37:29 Tony Stark: He tenido una leve inspiración. Me gustaría confirmarla. A ver. Una última simulación antes de dejarlo por esta noche. Esta vez con la forma de una cinta de Moebius. Invertida, por favor. Máquina: Procesando … Stark: Bien, dame el valor propio de esa partícula factorizando la descomposición espectral. Te ocupará un segundo. Máquina: Un momento … Stark: Y no te preocupes si no sale bien. Sólo intento … Máquina: Modelo renderizado. Y aparece la imagen que vemos a la derecha. Sobre esto debemos hacer varios comentarios. El primero, como tantas otras veces, sobre la traducción al castellano. He puesto en negrita en el diálogo anterior (bueno, monólogo, salvo que consideremos la máquina como ser inteligente) lo que tiene que ver con las matemáticas. En la frase, Bien, dame el valor propio de esa partícula factorizando la descomposición espectral, aunque entendemos lo que significa, en la versión original lo que dice es esto: Give me that eigenvalue. That, particle factoring, and spectral decomp. Disculpen si me equivoco, pero para mí eso quiere decir, Dame ese valor propio. Eso, la factorización de partículas y la descomposición espectral. Entiendo por descomposición espectral (en el contexto de valores propios del álgebra lineal elemental) dar el espectro (el conjunto de los valores propios) de un operador (una transformación, una aplicación lineal, lo que se esté manejando, en este caso, las nano partículas de la mecánica cuántica). Así que lo que dice Tony Stark es que le factorice el conjunto de partículas y le dé la descomposición espectral final del conjunto. Aunque parezca que le está pidiendo dos veces la misma cosa, no es así, ya que los valores propios pueden ser de multiplicidad múltiple, y eso se refleja en la descomposición espectral. Por ejemplo, si un operador está en un espacio de dimensión cuatro (teniendo por tanto asociada una matriz 4 x 4), con tres autovalores λ1, λ2, λ3, su descomposición espectral puede ser (λ1)2λ2λ3, o λ1(λ2)2λ3, o λ1λ2(λ3)2. La traducción al español dice que le dé la factorización (o sea lo que acabamos de explicar), pero lo une al “valor propio de una partícula”, y en conjunto es lo que no es correcto, al dar la impresión de que está trabajando con una única partícula, y obviamente, el viaje en el tiempo no parece cuestión de una única partícula. Por otro lado, está la elección de una banda de Moebius. Como todos deben saber, es la superficie cerrada de una única cara más sencilla que existe no orientable (no voy a volver a repetir como se construye). Tony Stark es un tipo inteligente, un genio tal y como lo pintan los comics originales y la propia saga cinematográfica. En el viaje en el tiempo que plantea la película, la realidad se escinde en varios universos paralelos, cada uno con su propia evolución temporal. Elige entonces la banda de Moebius como analogía a esa situación, ya que en esa banda podemos colocar a dos personas a la vez en un mismo punto, una encima de pie y otra boca abajo, viviendo dos situaciones distintas, pero desde “el mismo lugar”. Igual podríamos imaginarlo en términos temporales, vivir dos situaciones distintas, que ocurren a la vez, en el mismo lugar. Pero como digo, no es más que una analogía. Querer utilizar luego el objeto físico cinta de Moebius para “retroceder” a otro tiempo gracias a las nano partículas de la mecánica cuántica (algo así como los llamados hace años taquiones, partículas imaginarias de la antimateria que podrían volver al pasado a ocupar el lugar de sus homólogos en la materia real), es lo que no parece tener ningún sentido. Es decir, la película trata de dotar de verosimilitud las cosas, uniendo varios conceptos que individualmente son coherentes, pero no en conjunto. Además, Stark indica que quiere una banda de Moebius “invertida” (la que aparece en imagen es la usual). Habría que definir mejor que se entiende por invertida, porque hay diferentes posibilidades. Si lo que se pretende es, pensemos en un vaso lleno de agua, cambiar el interior por el exterior, cayéndose todo el agua fuera, al hacerlo en una banda de Moebius, no pasa gran cosa, ya que se queda como está desde el principio. También se puede pensar en hacer la imagen especular. Al construir una banda de Moebius, se efectúa un medio giro de la cinta, que puede ser en sentido horario o en sentido antihorario. Una tira de Moebius en el sentido de las agujas del reloj y una tira de Moebius en el sentido contrario a las agujas del reloj son imágenes especulares entre sí. Son como un par de guantes, uno es diestro y otro zurdo, iguales, pero no idénticos. Si construyéramos moléculas químicas con forma de banda de Moebius tendríamos moléculas zurdas (L) y diestras (D) con propiedades diferentes. Por ejemplo, el L-aspartamo sabe dulce mientras que el D-aspartamo es insípido. Finalmente podría referirse a un giro al revés. En el caso de la banda de Moebius daríamos con la conocida como cinta de Moebius sudanesa. Como vemos en la imagen, la diferencia con la banda de Moebius usual es que el círculo central que tiene la banda, en ésta se va al borde. ¿Podría ser esta construcción la que quiere Stark? Claramente no, a tenor de lo que muestra su súper-ordenador y lo conforme que él se queda. Además de que cuando dice invertida, simplemente la da la vuelta. Eso no es, amigo Stark, invertir; es un simple giro. Respecto al apartado físico del viaje en el tiempo, desde que Einstein formulara su teoría de la relatividad y Hermann Minkowski propusiera una métrica en la que esto es posible (es decir, hablamos de principios del siglo XX), todo parece posible. Deberíamos hacer la pequeña observación de que teóricamente eso se concibe viajando a la velocidad de la luz. Y en el hipotético caso de hacerlo, el “regreso” es algo más que complicado, incluso teóricamente. Aquí nos topamos, por ejemplo, con la célebre paradoja del abuelo: si retrocediste en el tiempo y mataste a tu abuelo cuando era joven, entonces nunca podrías nacer; pero si no naciste, ¿cómo volviste y lo mataste? Entonces aparece la mecánica cuántica. En mecánica cuántica, las partículas atómicas se parecen más a ondas de probabilidad indistintas. Por ejemplo, nunca se puede saber exactamente dónde está una partícula y en qué dirección se mueve, solo se sabe que hay una cierta probabilidad de que esté en un lugar determinado. El físico británico David Deutsch, que se menciona en la película, combinó esta idea con la teoría de los universos paralelos, demostrando que la paradoja del abuelo puede desaparecer si expresa todo probabilísticamente, porque al igual que las partículas, la persona que retrocede en el tiempo solo tiene una cierta probabilidad de matar a su abuelo, rompiendo el ciclo de causalidad. Aunque suene “raro”, y todo lo que se menciona en la película parece completamente fantasía, en ocasiones, los artículos y trabajos en mecánica cuántica son mucho más extraños (para que luego digan de los matemáticos; nuestra ventaja es que pocas veces descendemos del mundo de las ideas). Aprovechando que el próximo 21 de octubre se celebra el día de Martin Gardner en todo el mundo (nació en ese día de 1914), relacionado con el tema les recomiendo la lectura del primer capítulo de Viajes por el tiempo y otras perplejidades matemáticas (Editorial Labor, Barcelona, 1988). En él descubrirán que esto que plantea Vengadores: Endgame de los universos múltiples es tan moderno como de ¡¡1934!! (concretamente del cuento Branches of Time, de David R. Daniels). Leer a Gardner siempre es una maravilla, pero es que en diez páginas les ilustra sobre todo lo habido (y como se ve, por haber) acerca de los viajes en el tiempo y sus posibilidades.  También les recuerdo que en la reseña 95 de esta misma sección, Geometría para desaparecer, echábamos un vistazo a un cortometraje sobre el viaje a otra dimensión, y también (lo acabo de ver, porque no lo recordaba) recurrí al maestro Gardner (¿hay algo de lo que no hubiera ya hablado Gardner?). Alfonso Jesús Población Sáez

Jueves, 03 de Octubre de 2019 | Imprimir | PDF |  Correo electrónico

573. Una mesa formada por… ¡cubos levitando!

La Float Table –creada por la firma Rock Paper Robot– es una matriz formada por cubos de madera que parecen levitar. Los cubos se mantienen en equilibrio mediante un sistema de cables de acero e imanes incrustados. Fotografía de Marcin J Muchalski, Diamond Shot Studio http://rockpaperrobot.com/ Cada cubo de esta especial mesa parece estar suspendido en el aire. Fotografía de Marcin J Muchalski, Diamond Shot Studio http://rockpaperrobot.com/ El mueble parece robusto y estable, hasta que se mueve siguiendo la presión ejercida por una persona. Nota: Propaganda del producto Visto en Geeks are sexy Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Martes, 01 de Octubre de 2019 | Imprimir | PDF |  Correo electrónico

574. 175. (Octubre 2019) Punto fijo

[Imagen de la portada: carátula del disco Fractal Muzak de Vaporwave, cuyo primer tema es el titulado Banach fixed point theorem.] El teorema del punto fijo es un resultado matemático profundo y muy ubicuo: en su forma más general, establece condiciones para las cuales una determinada transformación deja invariable alguno de sus valores. Por ejemplo, si la transformación consiste en girar un círculo 90 grados alrededor de su centro, el único punto fijo es el centro del círculo (el círculo tiene la misma apariencia pero todos sus puntos -salvo el centro- han cambiado de lugar). Podemos encontrar, según el espacio donde actúa dicha transformación, diversos teoremas del punto fijo: de Banach, de Borsuk-Ulam, de Brouwer, de Kakutani, de Lefschetz, de Ryll-Nardzewski, de Schauder, etc., todos ellos avalados por nombres de personalidades destacadas de las matemáticas. Si tienes una cierta preparación matemática, puedes seguir la interesante presentación de Bernardo Cascales sobre algunos de estos teoremas. Más elemental (al menos la primera parte) es la contenida en el video del canal Archimedes Tube, explicado por nuestro colega Urtzi Buijs. A pesar de su alto contenido teórico, el teorema tiene muchas aplicaciones prácticas (y no tan prácticas). Un ejemplo elemental, consecuencia de este teorema, establece que, si agitamos con una cucharilla un vaso de agua, al final del proceso habrá el menos una molécula de agua que ocupe la misma posición que ocupaba antes de la mezcla. Otra curiosa aplicación establece que, en cualquier momento, siempre habrá dos puntos en la Tierra, diametralmente opuestos, que tienen la misma temperatura y la misma presión atmosférica. Puedes encontrar una explicación elemental y desenfadada en este video. Incluso, al final del video encontramos un juego de adivinación numérica "basado" en este teorema. Un teorema de punto fijo especial tiene el sorprendente nombre de "teorema de la bola peluda", una de cuyas consecuencias afirma que, en algún lugar de la esfera terrestre habrá siempre un fenómeno atmosférico en el que el viento gira sobre sí mismo, como un remolino o tornado. Una forma oportuna de ilustrar el teorema del punto fijo de acuerdo a las características de este rincón sería encontrar un proceso matemático que se pueda convertir en juego de magia. Para ello tendríamos que determinar en primer lugar una transformación que cumpla las premisas del teorema. Si el mago conoce las características del punto fijo, puede plantear un juego y adivinar o prever el resultado final. A lo largo de este rincón hemos presentado gran cantidad de juegos que siguen este esquema, los más significativos son los relativos a los que llamamos "agujeros negros", donde la aplicación reiterada de una determinada transformación conduce a un punto fijo (ver por ejemplo, la secuencia de los números 31, 32 y 33 correspondientes a septiembre, octubre y noviembre de 2006). Curiosamente, hemos encontrado otro ejemplo de estas características en la literatura mágica reciente. Un joven mago autodidacta húngaro, József Kovács (personaje de la figura adjunta), ha recogido en un folleto titulado "Cardopia" algunas de sus contribuciones a la revista de magia The Budget durante el año 2013. Uno de los juegos incluidos en esta recopilación es el que hemos adaptado y describimos a continuación. Separa de la baraja cinco cartas, del as al cinco, de cualquier palo, caras hacia abajo. El orden no importa pero, para recordarlo al final de juego, es mejor ordenarlas de menor a mayor. Digamos que están colocadas así (aunque con las caras hacia abajo): Elige una cualquiera de las cartas; gírala cara arriba manteniendo su posición. A partir de este momento, realizarás una serie de movimientos que tú creerás que son libres pero te llevarán inevitablemente a una situación prevista por mí. Gira cara arriba otra de las cartas, la que quieras. Ahora intercambia la posición de las dos cartas que están cara arriba. Intercambia de posición la carta elegida con cualquiera de las cartas que están cara abajo. Intercambia de posición las dos cartas cara abajo que no han sido movidas aún. Intercambia de posición las dos cartas cara arriba. Gira cara arriba todas las cartas que están cara abajo. Observa la posición final de las cartas. Todas han cambiado de lugar excepto un punto fijo, ¡tu carta elegida! Observaciones finales: Esta secuencia de movimientos puede usarse como juego de adivinación, tal como hace József Kovács en su folleto. Con el mago de espaldas durante toda la secuencia de movimientos, basta una rápida mirada a la posición final para saber cuál ha sido la carta elegida. Es relativamente sencillo elaborar una secuencia de movimientos con las que se consiga el mismo resultado anterior utilizando más de cinco cartas. El inconveniente es que el juego puede hacerse repetitivo y aburrido al alargar innecesariamente el proceso. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Martes, 01 de Octubre de 2019 | Imprimir | PDF |  Correo electrónico

575. Béla Kerékjártó (1898-1946)

El matemático Béla Kerékjártó (1898-1946) nació un 1 de octubre. Kerékjártó obtuvo su título de doctor en la Universidad de Budapest. En 1923 publicó uno de los primeros libros de topología (ver [1]) que fue reseñado por Solomon Lefschetz en 1925. Hermann Weyl comentó que este libro cambió por completo su punto de vista sobre el tema. Kerékjártó demostró que la esfera es la única superficie compacta que admite un grupo topológico 3-transitivo (ver [2]). Más información: B. von Kerékjartó, Vorlesungen über Topologie. I. Flächentopologie, Vol. 8, Courant Series. Berlin, Springer, 1923. B. Kerékjártó, Sur le caractère topologique du groupe homographique de la sphere, Acta Mathematica 74 (1941), 311–341. H. Freudenthal, Béla Kerékjártó, Encyclopedia.com S. Lefschetz, Review: B. von Kerékjártó, Vorlesungen über Topologie. I. Flächentopologie, Bull. Amer. Math. Soc. 31 (3-4) (1925), 176. Obituary of Béla Kerékjártó, Acta Universitatis szegediansis, Acta scientiarum mathematicarum 11 (1946-48), 5-7. Fotografías de Béla Kerékjártó con otros matemáticos, University of St Andrews Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Martes, 01 de Octubre de 2019 | Imprimir | PDF |  Correo electrónico

576. Matemáticos encuentran una nueva forma de llegar al número 3

ABC, 30 de Septiembre de 2019 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 30 de Septiembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

577. 56. (Octubre 2019) Cuadrantes solares andalusíes

(Figura 1. Reloj solar firmado por ibn as-Saffar) La brillantez andalusí en la construcción, diseño e invención de astrolabios, azafeas, lámina universal y lámina general han eclipsado el uso de relojes solares tanto como los relativamente escasos ejemplares encontrados. Solo se conservan ocho cuadrantes solares andalusíes en España y todos parecen del mismo tipo: tres en Medina Azhara, dos en Córdoba, y uno en Granada, Sagunto y Almería. Son pocos si se comparan con los casi treinta ejemplares romanos catalogados. El almuédano necesita conocer la hora de los rezos. Las grandes mezquitas aljamas usarían los astrolabios de latón, producto muy apreciado y de relativo lujo, pero los cuadrantes son más fáciles de usar y de construir. Los tres relojes de Medina Azhara son considerados relojes para ser usados por la guardia. Las características de los cuadrantes son: Horizontales Gnomon vertical (de índice y apenas 5 cm de alto) Con hipérbolas de los solsticios (No solo horas, también calendario) Horas desiguales (planetarias) (Se divide entre doce desde el orto al ocaso) El Mediodía son las seis. Marcan los rezos Algunos incluirían las alturas solares. Este tipo de cuadrantes fue ya usado en la Grecia clásica. Los romanos los conservaron pero los restos arqueológicos en Hispania muestran una clara preferencia por los relojes hemisféricos. Los relojes solares son muy útiles para el aprendizaje práctico de la geometría. Los más pequeños pueden divertirse con el movimiento de la sombra y su cambio a lo largo del día según la inclinación. Conforme avanzan en formación matemática son buena práctica de los conceptos aprendidos. Comprender el cambio de las estaciones y la diferente duración de los días fue en su momento algo vital para la supervivencia en una economía agrícola. Entender el porqué de la hipérbola es una buena introducción de las cónicas. Toda clase orientada más o menos al sur debería tener una línea meridiana. (Figura 2. Reloj solar horizontal andalusí. Museo de de Almería) Los relojes horizontales andalusíes están muy bien documentados: hay un excelente tratado del murciano ibn Raqqan, y referencias de ibn Saffar y Maimónides. Además quedaron recogidos en castellano en los Libros del saber de astronomía, ordenados redactar por Alfonso X, con el hermoso título de Libro del relogio dicho de la piedra de la sombra. Este tipo de cuadrantes fueron muy populares en todo el arco mediterráneo y están totalmente descritos por el sirio al-Battani en el siglo IX. Pronto fueron incorporados a al-Andalus. Sorprende que con la formación astronómica andalusí no se diseñaran otro tipo de relojes. Los astrolabios y azafeas andalusíes suelen ir firmadas, algo que solo ocurre con uno de los cordobeses donde aparece la atribución a Ahmad ibn as-Saffar al-Andalusi (+1035), discípulo de Maslama al-Mayriti y del que se conserva un  tratado sobre uso del astrolabio que fue vertido al latín. Libro del relogio dicho de la piedra de la sombra La última parte de la recopilación alfonsina de los Libros del saber de astrología está dedicada a la construcción de distintos tipos de relojes, el primero y único dedicado a los solares lleva el título de Libro del horologio dicho de la piedra de la sombra. (Figura 3. Libro del relogio. Manuscrito de la Universidad Complutense. Madrid. Siglo XIII) La Universidad Complutense conserva el que quizá sea el manuscrito regio por la calidad y belleza de su composición. Se trata de un manual práctico sin disquisiciones teóricas y que usa tablas astronómicas para la construcción. Los cuadrantes encontrados responden a la descripción alfonsina. Quizá la única mejora apreciable sea la incorporación de los círculos concéntricos de las alturas solares sobre el horizonte, algo que no se ha encontrado en ninguno de los cuadrantes conocidos. La epístola sobre la ciencia de la sombra de ibn as-Raqqam Las recopilaciones alfonsinas no contemplaron el interesante tratado sobre la ciencia de la sombra que estaba escribiendo casi al mismo tiempo el exiliado murciano Muhammad ibn ar-Raqqam al-Andalusí (1245-1315). Resulta curioso que Alfonso X quisiera hacer de Murcia un gran centro científico mientras que sus sabios emigraban a tierras del Islam. La epístola de ar-Raqqam es un precioso tratado que en lugar de utilizar tablas, recurre a la geometría proyectiva resultando muy comprensible y sencillo. Los relogios alfonsíes sólo utilizaban tablas mientras que ar-Raqqam nos permite entender las razones de su construcción con un modelo astronómico completo. (Figura 4. La ciencia de la sombra. Manuscrito de El Escorial. Siglo XIII) El mismo autor indica que ya de joven busqué una proyección sencilla, distinta de la de Ptolomeo, aplicable a los instrumentos de las sombras. La proyección de Ptolomeo es la estereográfica mientras que ar-Raqqam usará la ortogonal con planos abatibles conocida como el analema de Vitruvio por venir descrita someramente en De architectura (libro IX). El tratadista romano no se atribuyó la paternidad y comenta el método sin explicarlo mientras ar-Raqqam revela una comprensión total del procedimiento, quizá por tener que redactarlo dos veces: perdí por préstamo y volví  a escribir sobre algo cuyos fundamentos están olvidados. Un manuscrito del tratado de ar-Raqqam se conserva en la biblioteca del Monasterio de San Lorenzo de El Escorial (manuscrito árabe 918) y ha sido traducido y comentado por Joan Carandell (Universidad de Barcelona, 1988). El cuadrante de Granada De los ocho relojes solares arábigos conservados el de Granada es el único completo, aunque está desubicado (se piensa que es cordobés pero se adquirió ignorando su origen exacto). Se trata de un pequeño reloj de factura singular por utilizar arcos de circunferencia para aproximar las hipérbolas de los solsticios. La recomendación alfonsí es construir con compás el vértice de la hipérbola y con rectas las ramas. El cuadrante de Granada no lo cumple y ambas ramas son graciosos arcos de circunferencia de distinto radio. (Figura 5. Cuadrante solar. Museo de la Alhambra. Granada) El único adorno del cuadrante, aparte de la grafía, es un ingenuo compás. El reloj se muestra en el Museo de la Alhambra que ha acertado iniciando su recorrido con una sala dedicada al cosmos. Los relojes de Medinat al-Zahra Hay ciudades que no sobreviven a sus fundadores y su esplendor desaparece con ellos. La transformación del emirato en califato, proclamado por Abderramán III en el 929, requería una capital acorde con el nuevo poder. La corte se traslada de Córdoba a Medina Azahara en el año 945. En el 1010, en plena la guerra civil, la ciudad palaciega fue prácticamente abandonada. (Figura 6. Cuadrante solar. Museo de Medinat al-Zahra) En el ahora llamado patio de los relojes se localizaron tres cuadrantes; uno de ellos se muestra en el museo del emplazamiento. Se suele considerar el reloj de as-Saffar como el más antiguo pero los relojes de la capital califal muestran que ya en el siglo X se estaban usando. El Museo de Medinat al-Zahrat ha elaborado un panel explicativo detallando las horas y las llamadas a la oración. (Figura 7. Panel explicativo. Museo de Medinat al-Zahra) El gran desarrollo matemático andalusí se produce en el siglo XI durante las taifas, especialmente de Toledo y Zaragoza; por eso es importante ver que los relojes solares de cierta calidad ya se utilizaban en el momento de despegue de la ciencia árabe occidental, impulsada por una figura que dejó escuela: Maslamá al-Mayriti. El reloj de Sagunto De dos relojes se conserva un pequeño fragmento, del encontrado en la alcazaba de Córdoba y del de Sagunto. El de la alcazaba muestra lo suficiente para saber que es del tipo horizontal pero el del Museo Arqueológico de Sagunto puede llevarnos a la duda. El cuadrante saguntino ha usado una piedra romana que puede instalarse verticalmente y es así como lo expone el museo. Lo poco conservado impide conocer cómo se colocaba y si tiene alguna característica singular.  Parece que las líneas horarias son curvas en lugar de rectas que son la aproximación habitual. (Figura 8. Cuadrante andalusí. Museo Arqueológico. Sagunto)

Martes, 01 de Octubre de 2019 | Imprimir | PDF |  Correo electrónico

578. Colorido tornado

Wirbelwerk es una instalación del artista Olafur Eliasson: un espectacular –e inofensivo– tornado formado por vidrios triangulares de colores, barras de metal y una fuente de luz que proyecta patrones cambiantes sobre las paredes del museo Lenbachhaus de Múnich. Wirbelwerk significa vórtice, torbellino… http://www.lenbachhaus.de/uploads/tx_januspresspictures/Eliasson_7_von_unten_gross.jpg Las luces proyectadas parecen las imágenes creadas por un caleidoscopio. http://www.lenbachhaus.de/uploads/tx_januspresspictures/Eliasson_2_dunkel_mit_Menschen_gross.jpg Visto en Thinx Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 26 de Septiembre de 2019 | Imprimir | PDF |  Correo electrónico

579. La serie de Grandi y la «no demostración» de la existencia de Dios

ABC, 23 de Septiembre de 2019 CIENCIA - El ABCdario de las matemáticas Maria Pilar Sabariego Arenas

Lunes, 23 de Septiembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

580. II Concurso de Modelización Matemática del IMI

La RSME colabora con el Instituto de Matemática Interdisciplinar (IMI) en la organización de la 2.ª edición del Concurso de Modelización Matemática (CMM-IMI). Los alumnos de grado de la Universidad de Alcalá, la Universidad Autónoma de Madrid, la Universidad Carlos III, la Universidad Complutense de Madrid, la Universidad Politécnica de Madrid y la Universidad Rey Juan Carlos tienen hasta el 23 de septiembre para resolver el problema: ¿Cuánto podríamos reducir la duración de un viaje tripulado a Marte utilizando una nave propulsada?

Viernes, 20 de Septiembre de 2019 | Imprimir | PDF |  Correo electrónico