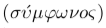581. Divulgación de las matemáticas: Ellas fueron las primeras

ABC, 16 de Septiembre de 2019 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 16 de Septiembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

582. Francesco Maurolico y la inducción

El matemático y astrónomo Francesco Maurolico (1494-1575) nació un 16 de septiembre. Realizó contribuciones en geometría, óptica, mecánica, música y astronomía. Tradujo al latín las obras de Euclides, Arquímedes, Apolonio, Teodosio, Sereno y otros, y también escribió diferentes tratados sobre matemáticas, destacando entre ellos Gnomonica (1553), Arithmeticorum libri duo (1557) –que incluye la primera prueba realizada por el método de inducción– y Opuscola mathematica (1575). Opuscola mathematica Entre sus observaciones astronómicas, se incluye la supernova que apareció en la constelación de Casiopea en 1572 –SN 1572–, también observada por Tycho Brahe cuando era más brillante que Venus. Más información: Francesco Maurolico, MacTutor History of Mathematics, University of St Andrews Il progetto Maurolico Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Lunes, 16 de Septiembre de 2019 | Imprimir | PDF |  Correo electrónico

583. Septiembre 2019: Más juegos de lápiz y papel I

1. Jugando con los materiales más comunes. La historia de los juegos se pierde en el principio de los tiempos. Es posible encontrar juegos de tablero en las antiguas civilizaciones romana, egipcia o mesopotámica. Muchos de ellos han llegado a nuestros días sin modificaciones, mientras que otros han evolucionado adaptándose a los tiempos. Sin embargo, hay otros juegos que son más recientes, y no solo porque en las últimas décadas se haya potenciado la creación de juegos de todo tipo, sino porque hay una serie de juegos que no han surgido hasta disponer de los materiales necesarios para realizarlos. Eso es lo que ocurre con los juegos de lápiz y papel. Está aceptado que la aparición de este tipo de juegos no surge hasta el siglo XIX en que se popularizó el uso de los materiales como lápiz y papel, especialmente en las escuelas. Es decir, se suele considerar que este tipo de juegos comenzaron a aparecer relacionados con las tediosas horas escolares, para aprovechar los huecos existentes entre los ratos de estudio. Vamos a darlo por bueno. Aunque no sabemos si antes de estos materiales, cuando se trabajaba con tiza y pizarrín, ya existirían algunos de ellos. Inicialmente, los juegos de lápiz y papel parecen que están un poco estancados y que no han evolucionado al mismo ritmo que otros tipos de juegos. Pero estudiando un poco la gran variedad de juegos existentes, podemos comprobar cómo en el siglo pasado, algunos matemáticos inventaron una serie de juegos de estrategia, muy interesantes,  donde se aplicaban aspectos matemáticos no especialmente antiguos, como la topología. Lo cierto es que este tipo de juegos son los que requieren materiales más comunes y al alcance de cualquiera. Se puede jugar en cualquier situación, prácticamente en cualquier lugar y son bastante atractivos. Lo interesante, como en la mayoría de juegos aparecidos en esta sección, no es solo el mero placer de jugar y de ganar, si podemos, al contrario, sino el estudiar estrategias que nos permitan, si no ganar seguro, al menos favorecer nuestra posición. Posiblemente pensemos que en este mundo tecnológico, están anticuados este tipo de juegos, pero todos nos hemos encontrado en algún momento sin wifi. Hablando en serio, los juegos de lápiz y papel tienen muchas ventajas: se pueden jugar prácticamente en cualquier sitio y con medios asequibles, suelen ser fáciles de entender, pues tienen reglas sencillas, por lo que todo el mundo puede comenzar a jugar y enseguida suelen enganchar, por lo que desde el principio intentamos encontrar movimientos y estrategias para conseguir vencer a nuestro oponente. Por ello, son interesantes para trabajarlos en el aula. Para los aficionados a las nuevas tecnologías, comentaremos que existen muchas páginas en Internet con información y referencias a este tipo de juegos. Incluso en varias de ellas es posible jugar en línea al propio juego. No es la primera vez que tratamos este tema en este apartado de juegos. Ya en el año 2002, dentro de la sección de Juegos que se publicaba en la revista SUMA, editada por la Federación Española de Sociedades de Profesores de Matemáticas, publicamos una primera entrega1 sobre juegos con lápiz y papel. Con este artículo no pretendemos cerrar el campo, pues aunque no se piense así, este tipo de juegos tiene una variedad mucho mayor de la que se pueda creer. Nuestra intención es simplemente presentar una serie de juegos interesantes y atractivos para entretenernos y, siempre que sea posible, estudiar la lógica que existe detrás de los juegos. 2. Toros y vacas. En el último tercio del siglo pasado se comercializó un juego que se hizo muy popular y al que los aficionados a los juegos dedicamos bastantes horas de entretenimiento. Me refiero al conocido como Mastermind, creado en 1970, un juego de colores en el que había que descubrir la serie de colores que había creado el contrincante preguntando con otras series, conociendo el número de colores que aparecían en la serie oculta y el número de los que estaban bien colocados o no. La versión inicial se modificó después presentando juegos con letras o números. Incluso este tipo de entretenimiento dio el salto a los pasatiempos, encontrándose, con facilidad, retos en los que tenemos la información necesaria para encontrar la solución. Por ejemplo, en la siguiente imagen tenemos un pasatiempo sacado del desaparecido periódico Sol, en concreto, del 17 de junio de 1990. Figura 1: Diario Sol. 17/06/1990 Este juego de colores está basado en un juego mucho más antiguo conocido como “Bulls & Cows” (Toros y vacas) que aunque no he conseguido encontrar información exacta, se estima que puede remontarse al siglo XIX. Básicamente es el juego que aparece en el pasatiempo donde, para encontrar un número de cuatro dígitos desconocidos, se van proponiendo números y se indican cuantos números hay que estén en el número buscado diferenciando si están en el sitio correcto o no. Este juego lo aprendí en la década de los 70 cuando estaba estudiando en la universidad, ya que era un juego con el que nos entreteníamos en los ratos perdidos entre clases, y a veces en las mismas clases. Nosotros lo conocíamos como los numeritos y para nosotros los números que estaban en la misma posición eran muertos, y los que estaban en el número, pero no en la misma posición, eran heridos. La idea del juego, como se ve es muy simple. Se van diciendo números de cuatro cifras y el contrario nos indica cuantos muertos y cuantos heridos hay. El modo en que nosotros jugábamos es que cada jugador esconde un número y el contrario va lanzando una propuesta, por turno, y el otro responde. El primero que consigue descubrir el número del contrario gana. Se juega con las cifras del 0 al 9, aunque el cero no puede ir en primer lugar. Veamos un ejemplo de partida. Vamos a ir diciendo números y entre paréntesis indicaremos cuántos muertos (cifras en la misma posición) y heridos hay (cifras en distinta posición que en el número original). 1234 (2H) 5678 (1M) De lo anterior se deduce que entre el 0 y el 9 hay una cifra del número, luego comenzamos a probar con la información que tenemos. 1239 (1M, 1H) Lo siguiente nos da bastante información. El 9 que acabamos de colocar tiene que ser el muerto, ya que las demás cifras no se han cambiado, y al disminuir en uno el número de heridos nos asegura que el 4, que es la cifra que no hemos puesto, también está en el número inicial. 1249 (1M, 2H) El número 3 no es una de las cifras, conocemos el 4 y 9 y una de las dos que quedan. 1439 (1M, 1H) Con esta propuesta ya hemos encontrado el número. El 2, que no aparece en la propuesta anterior, es la tercera cifra. Como además el 4 ha sido siempre herido, sólo le queda un lugar, el primero. El 2 no puede estar en el segundo lugar, porque es herido, sólo le queda el tercer puesto. Y nos queda una cifra de la segunda propuesta, que como era muerto estaba en su sitio y tiene que ser el 6. Luego el número buscado es el 4629. Este juego se ha utilizado en muchas ocasiones como ejemplo de programación, por lo que es fácil encontrar programas, incluso en el último tercio del siglo pasado, que generan este tipo de propuestas y que permiten jugar en línea. En la página de Math is fun, podemos encontrar este juego pudiendo elegirse versiones con 3, 4 ó 5 números, letras o colores. Es posible jugarlo en la siguiente dirección: https://www.mathsisfun.com/games/bulls-and-cows.html También podemos encontrar sitios donde se hablan de estrategias para ganar en este juego, tanto con lápiz y papel como con ordenador. Incluso es posible jugar. Se pueden consultar las siguientes direcciones: https://divulgadores.com/muertos-heridos-juego-logica-i/ https://divulgadores.com/muertos-heridos-juego-logica-ii/ 3. Sendero solitario. En el artículo que cité anteriormente sobre juegos, aparecido en la revista SUMA, uno de los juegos que presentamos se llama Senderos, aunque el nombre que le dio su autor David Silverman fue Slither. Este es un juego también considerado topológico en el que los dos jugadores deben construir un camino sobre una trama de puntos, cada jugador en su turno debe trazar un segmento horizontal o vertical que una la poligonal dibujada hasta el momento con un nuevo punto adyacente. El jugador que en su jugada tiene que cerrar el camino pierde. En su excelente libro sobre juegos y matemática, Luis Ferrero nos propone una versión de este juego en forma de solitario, llamado rutas solitarias, aunque a mí me gusta más senderos solitarios. En él, sobre una trama de puntos el jugador debe trazar un recorrido que contenga a todos los puntos. Para ello debe trazar segmentos que unan dos puntos adyacentes, en horizontal o vertical con las siguientes restricciones: Un segmento no puede cruzar otro ya trazado. En un punto no pueden coincidir más de dos segmentos. Básicamente se reduce a dibujar, en una trama rectangular de puntos, una poligonal que pase una sola vez por todos los puntos de la trama. Lógicamente, por pocos puntos con los que se comience, suele haber muchas soluciones diferentes. Para cortar la resolución del solitario, ya que pueden existir muchas soluciones posibles, suele ser un buen método considerar iguales los resultados que sean simétricos uno de otro. Esa simetría puede considerarse respecto a un eje vertical, horizontal e incluso diagonal si la trama de puntos es cuadrada, de esa forma se reducen bastantes el número de soluciones. Con esta condición, las soluciones siguientes serían la misma. Figura 2: Soluciones iguales Con la restricción anterior, el número de soluciones se reduce drásticamente, por lo que es posible afrontar la resolución del solitario en un tiempo prudencial, aunque es corriente que al afrontar el proceso resolutivo aparezcan, aun sin quererlo, soluciones que son iguales. En el caso de tener una trama cuadrada de lado tres, las soluciones que a mí me salen quedan reducidas a las siguientes. Figura 3: Soluciones en trama 3x3 La normal es plantear recuadros, no necesariamente cuadrados, y con mayor número de puntos, por ejemplo de 3x4 o 4x4. Este juego se puede convertir con facilidad en un juego para dos o más jugadores. Basta entregar una plantilla con tramas limpias a cada jugador y, ocultando el proceso para que no lo vean los contrarios, cada jugador intenta encontrar todas las soluciones posibles. Gana el jugador que más soluciones encuentre. Lo normal es dar un tiempo, por ejemplo cinco minutos, y al acabar el tiempo se comprueba quien tiene más soluciones. En esta modalidad de juego se puede permitir considerar, al menos en las primeras jugadas, como diferentes soluciones que sean iguales por simetría como hemos visto antes. Si no ponemos esa restricción los jugadores se animan más al encontrar bastantes soluciones en un momento. Si se quiere complicar el solitario se puede ampliar las condiciones permitiendo que dos puntos cercanos se unan con un segmento en diagonal, de esta manera nos podemos encontrar con soluciones como las siguientes. Figura 4: Soluciones con trazos en diagonal 4. Puntos y cajas. Veamos ahora un juego de los que quizás sean más conocidos de lápiz y papel. Aunque cuando he jugado a él yo lo conocía como los cuadraditos, es conocido como Dots and boxes. El primero que lo presentó fue Édouard Lucas, un matemático francés del siglo XIX gran creador de juegos recreativos de matemáticas que lo llamó La Pipopipette. En el año 2001, Ian Stewart publicó en la revista Scientific American un artículo profundizando en este juego. El juego se realiza también sobre una trama de puntos y está pensado para dos jugadores, cada uno de los cuales con un lápiz de distinto color. El proceso del juego es el siguiente: a) Cada jugador, en su turno, dibuja un segmento que una dos puntos adyacentes, siempre en horizontal o vertical. b) Cuando el trazo que dibuja un jugador completa un cuadradito de lado unidad, el jugador escribe su inicial dentro del cuadradito y se lo adjudica. Después de formar el cuadrado puede dibujar un nuevo trazo. Si con ese nuevo trazo se cierra otro cuadradito sigue repitiendo el proceso hasta que al trazar un segmento no cierre ningún cuadrado. c) Cuando toda la trama se ha cuadriculado, se cuentan los cuadraditos obtenidos por cada jugador y gana, lógicamente, quien haya conseguido más. En la siguiente imagen aparece una partida en una trama reducida de 3x3. Las partidas normales se desarrollan en tramas más grandes, tanto cuadradas como rectangulares. Figura 5: Partida de Puntos y Cajas Este juego también es posible encontrarlo en multitud de lugares en Internet para jugar de forma on-line, normalmente contra el propio programa. En la siguiente página podemos encontrar el juego explicado, indicando posibles estrategias y permite jugar contra la máquina en varias dimensiones de la trama. http://www.papg.com/show?1TMU 5. Trazando figuras. Veamos un nuevo juego sobre tramas, inicialmente rectangulares. Este juego también es para dos jugadores que pueden jugar cada uno con un lápiz de distinto color. Se juega sobre una trama cuadrada o rectangular con las siguientes instrucciones. a) Cada jugador, en su turno, debe dibujar un rectángulo, que puede ser cuadrado, cuyos vértices sean los puntos de la trama. De entrada, suponemos que los lados son horizontales y verticales, es decir, excluimos la posibilidad de dibujar rectángulos girados. b) Los lados del rectángulo que se trace pueden cruzarse con lados de otros cuadrados, pero no pueden superponerse, es decir, entre dos puntos adyacentes no pueden coincidir trozos de lados distintos. c) Ningún punto puede ser vértice de más de un rectángulo. d) Cuando un jugador no puede trazar un rectángulo sin incumplir las condiciones anteriores, se acaba la partida y gana el último jugador que ha conseguido dibujar un rectángulo. En la siguiente imagen puede verse una partida, sobre una trama de 5x6 que se ha completado en sólo dos jugadas. Figura 6: Partida de Trazando Figuras Lo normal es que las tramas tengan más puntos. Una variedad del juego sería jugar sobre tramas isométricas dibujando triángulos o hexágonos. Hasta aquí esta primera parte de la entrega sobre juegos de lápiz y papel. En ella hemos visto varios que utilizan una trama de puntos como tablero, de forma que nos guiemos por ellos para trazar las líneas que dan lugar al juego. En la segunda parte vamos a ver algunos juegos más modernos y donde introduciremos conceptos topológicos o juegos de guerra desarrollables con lápiz y papel. 6. Referencias. FERRERO, L. (1991): El juego y la matemática. La Muralla, Madrid. GRUPO ALQUERQUE (2002): “Juegos de lápiz y papel”. SUMA nº 40, pp. 123-124.   Nota: [1] Se puede consultar una versión digital en la página de divulgamat: http://www.divulgamat.net/index.php?option=com_content&view=article&id=10081&directory=67

Jueves, 12 de Septiembre de 2019 | Imprimir | PDF |  Correo electrónico

584. 100. (Septiembre 2019) Serialismo y matemáticas (I)

En las siguientes entregas de Divulgamat tendremos a una autora invitada, Celia Rubio, quien ha escrito una serie sobre el serialismo y matemáticas. Celia Rubio está cursando el doble grado de Matemáticas e Informática en la Universidad Complutense de Madrid y tiene estudios de música en el Conservatorio de Madrid (su instrumento es la flauta de pico, y además ha estudiado canto). Participó muy activamente en el congreso Mathematics and Computation in Music 2019 (véanse las columnas [9, 8]). Su preocupación e interés por la Teoría Matemática de la Música y su divulgación le empujó a mostrarme su texto. Tras leerlo detenidamente y atestiguar su calidad, le propuse enseguida su publicación en esta columna. El lector disfrutará sin duda alguna de la claridad y la fuerza del texto. 1. Introducción Este artículo es el primero de una colección sobre el serialismo musical y las matemáticas que lo fundamentan. Las músicas serialistas son aquellas que permiten construir castillos con un solo grano de arena: una serie particular, una permutación de notas, dinámicas o timbres. La serie se coloca en la obra secuencialmente, siempre igual o con alguna modificación que la adorne. Y es que para esta música, la serie es el ladrillo y las matemáticas son la pintura con la que decorarlos, ya que las transformaciones que se le puede aplicar a una serie forman preciosas estructuras matemáticas enmarcadas en la Teoría de Grupos. En estas estructuras se centrará esta serie de artículos, y más específicamente en el dodecafonismo, el primer sistema compositivo serialista. En este primer artículo hablaremos sobre sus orígenes (sección 2) y sobre los postulados matemáticos que lo definieron (sección 3), y analizaremos una obra como ejemplo (sección 4). Más adelante generalizaremos las definiciones dodecafónicas matemáticamente, descubriremos la historia del serialismo integral y contaremos el número de posibles series distintas —o, más bien, de espectros seriales— que un compositor puede utilizar. En definitiva, haremos un recorrido a fondo por el serialismo y exploraremos sus posibilidades musicales y matemáticas. Los textos irán dirigidos tanto a matemáticos como a músicos; en todas las entregas habrá secciones más matemáticas y secciones más musicales o históricas. Las matemáticas serán avanzadas, pero siempre se definirá todo lo que se utilice y se probará todo lo que se afirme. Algunas de las definiciones matemáticas más comunes se encuentran en la sección 5. ¡Que empiece el viaje! 2. Introducción histórica del dodecafonismo En esta sección describiremos cuál fue el ambiente histórico y musical en el que se cultivó el primer modelo de serialismo musical: el dodecafonismo. A través de su historia analizaremos por qué el serialismo no fue una decisión aleatoria ni espontánea, sino que surgió de una necesidad estética de aquel periodo. Vamos a comenzar con una breve crónica de la disonancia, tras lo cual describiremos las fases por las que el creador del dodecafonismo, Arnold Schoenberg, tuvo que pasar antes de concebirlo. 2.1. La historia de la disonancia La disonancia siempre ha formado parte de la experiencia musical. Con la música ha venido siempre emparejada la disonancia, mano a mano, como instrumento de contraste, confrontación y ruptura, pero también como elemento constructivo del discurso musical. En la Antigua Grecia, la armonía musical se consideraba unida al resto del universo. La rotación de los astros emitía sonidos armónicos, y era la armonía la que apaciguaba el alma. Pero ¿qué era la armonía sino la unión de consonancia y disonancia? Como dijo Aristóteles: El alma es armonía porque la armonía es mezcla y síntesis de contrarios, y de contrarios precisamente está compuesto el cuerpo. (Tomado de [3] J. de Aixquivel, Memorias de Historia Antigua, 1989.) Es bien sabido que la Escuela de Pitágoras, con su estudio sobre proporciones entre notas, buscaba encontrar cuáles eran los intervalos más consonantes: eran aquellos cuya proporción formaba una relación sencilla. El intervalo de octava era consonante porque su ratio era de 2:1, y de igual manera ocurría con los intervalos de quinta (3:2) y cuarta (4:3), a los que Aristóxeno comenzó a llamar sýmphonos [6]. En cambio, a los intervalos no tan sencillos se los llamaba diáphonos , y fue entonces cuando se le dio nombre a la disonancia. Ya en la Edad Media, la polifonía fue forjando normas sobre su uso. La primera regla compositiva de la música occidental —según Knud Jeppesen [11]— fue la regla franconiana, que expresaba que las disonancias debían ocurrir en la parte débil del compás, mientras que las consonancias en la parte fuerte. Es así como los compositores trenzaban consonancia y disonancia al tejer los hilos de la música. Poco a poco la disonancia pasó a ser usada como floritura melódica: en notas de paso, apoyaturas o retardos, entre otras. Esta función melódica fue impregnando el contrapunto hasta llegar a ser pieza clave en la continuidad y el enlace de las voces. Adquirió entonces una nueva función contrapuntística. ¿Quién no se ha deleitado al escuchar una disonancia bachiana? Pero la disonancia estaba aún circunscrita a la tonalidad reinante. No fue hasta la introducción de acordes extraños que la disonancia pasó a ser el centro del interés musical, y fue in crescendo apropiándose del foco de atención hasta llegar a ser más valiosa aún que la consonancia. Para ello hubo que esperar hasta el siglo XIX, que fue testigo de un asombroso desarrollo del sistema armónico que acabó por quebrantar todas las concepciones musicales anteriores. Para más información sobre la disonancia y su fascinante historia, recomendamos al lector el texto de Felipe Aguirre [1]. 2.2. Wagner, Mahler y la emancipación de la disonancia Aunque las posibilidades que prometía la tonalidad parecían inagotables, sus límites comenzaron a percibirse hacia finales del siglo XIX. En palabras de Arnold Schoenberg: El oído se fue familiarizando gradualmente con gran número de disonancias, hasta que llegó a perder el miedo a su efecto perturbador. Mencionado en [13] Composition with twelve tones, de Style and Idea, 1950. Esta época culminó con los dramas musicales de Richard Wagner, en los que todos los elementos de la obra estaban detalladamente estudiados por el compositor. A este concepto lo llamaba Gesamtkunstwerk (“obra de arte total”) —mencionado en [15] Oper und Drama, 1851—, ya que se aseguraba personalmente de que en sus óperas las artes escénicas, musicales, poéticas y visuales se combinaran entre sí a la perfección. Figura 1: Richard Wagner (1813—1883); figura tomada de National Geographic. La idea del Gesamtkunstwerk la desarrolló alrededor de 1850, y la plasmó en su totalidad en su ciclo de cuatro óperas Der Ring des Nibelungen, estrenado en 1876. Wagner controló y creó cada aspecto de la tetralogía, desde la música hasta el libreto, el vestuario y la escenografía. Incluso mandó crear su propia sala de conciertos en Bayreuth, el Festspielhaus, para que el escenario se adecuara a sus ideas sobre el pensamiento y la cultura musical; véase [12] para más detalles. Así, a ojos de compositores posteriores, se habían agotado todas las posibilidades de la música tonal, y quizás ya había comenzado el viraje hacia el predominio de la disonancia con su abundante uso del cromatismo, como en el famoso primer acorde del drama musical Tristan und Isolde (1865). Consta de las notas fa-si-re#-sol#, y sus intervalos desde el fa son una cuarta aumentada, una sexta aumentada y una novena aumentada. Después de Wagner, otros compositores también estuvieron a las puertas de emancipar la disonancia, de desatarla de las ataduras que imponía la tonalidad. Por ejemplo, el gran compositor Gustav Mahler conseguía reflejar en sus sinfonías dos realidades paralelas: tanto la delicada fragilidad de la tradición anterior como la inminencia de su ruptura. El ejemplo más claro es el Adagio de su Décima Sinfonía, que contiene una disonancia con once de las doce notas de la escala cromática. Y es que, sin lugar a dudas, ya se preveía que la tonalidad iba a reemplazarse. Figura 2: Gustav Mahler (1860—1911); figura tomada de Planet Hugill. Siguiendo la concepción del progreso como un camino ascendente, el paso siguiente para la composición musical debía consistir en deshacerse progresivamente de la tonalidad y desarrollar la “emancipación de la disonancia” —mencionado también en [13] Composition with twelve tones—. Así, en el marco expresionista del cambio de siglo, fue como Arnold Schoenberg ideó sus teorías del pensamiento musical, y éstas dieron paso a la creación de la atonalidad. 2.3. Hacia el atonalismo de Schoenberg Fuertemente influido por Wagner y Mahler desde su adolescencia, Schoenberg comenzó componiendo al estilo posromántico de su época, llevando el cromatismo y la orquestación hasta el extremo. Sin embargo, y no espontáneamente, empezó a buscar en sus composiciones que cada sonido tuviera valor por sí mismo, un valor independiente de su funcionalidad tonal. Figura 3: Arnold Schoenberg (1874—1951); figura tomada de Nextews. Para él, la música no estaba intrínsecamente dirigida a una tónica. En las progresiones, lo importante era el paso de un acorde a otro, y no hacia dónde se dirigían estos. Además, él opinaba que se debían poder utilizar las notas de los modos eclesiásticos libremente, por lo que consideraba las notas no diatónicas tan válidas como las diatónicas. Esto hacía imposible distinguir unas de otras, y apenas se podía identificar la tónica. De esta, y de otras muchas formas, Schoenberg conseguía que la jerarquía tonal quedara desestabilizada [12]. De esta época es su primera obra importante, Verklärte Nacht (Noche transfigurada), Op. 4. Compuesto en 1899, este sexteto de cuerdas está inspirado por el poema homónimo de Richard Dehmel. La música, según su autor, expresa el paseo de un hombre y una mujer en medio de la naturaleza. Aunque en la obra aún prevalece la armonía tradicional basada en acordes, Schoenberg sitúa al oyente en un terreno de indefinición tonal, no sólo en el plano armónico sino también en el melódico. Además, hace uso del acorde de novena invertido, inexistente hasta entonces y, por tanto, rechazado por la crítica [5]. Tras pasar por la etapa tonal post-romántica, y debido a su convicción en la inexorabilidad de la evolución de la música hacia el cromatismo total, en 1908 Schoenberg se desligó de la tonalidad completamente con el ciclo de canciones Das Buch der Hängenden Gärten. A partir de entonces se dedicó a componer fragmentos muy breves cuya estructura era definida por motivos y no por la armonía. Era esto lo que solía ocurrir en formas musicales anteriores como la forma sonata. A este periodo en sus composiciones se le llama atonalidad libre, aunque cabe destacar que Schoenberg rechazaba fervientemente este término: La expresión “música atonal” es de lo más desafortunada —es como llamar a volar “el arte de no caer” o a nadar “el arte de no ahogarse”. Mencionado en [14] A. Schoenberg, Hauer’s Theories, en Style and Idea, 1923. A este periodo pertenece también su famoso ciclo de canciones Pierrot Lunaire, Op. 21 (1912). Su nombre completo es Tres veces siete poemas de Pierrot Lunaire de Albert Giraud, ya que está dividida en 3 grupos de 7 canciones cada uno, cuyos textos son una selección de 21 poemas del ciclo homónimo de Albert Giraud. Se encuentran en ella abundantes referencias al número 7. Schoenberg hace un uso extensivo de motivos de 7 notas a lo largo de la obra, mientras que el conjunto musical que la interpreta, incluyendo al director, consta de 7 miembros. De hecho, a este conjunto de instrumentos —flauta, clarinete, violín, violonchelo, piano y voz— se le ha dado el nombre de ensemble Pierrot en su honor. Otros números importantes en la obra son el 3 y el 13. Cada poema consta de 13 líneas, mientras que la primera línea de cada poema aparece 3 veces, en las líneas 1, 7 y 13. En esta obra no sólo hay una ausencia total de relaciones tonales, sino que el tratamiento vocal evita también cualquier relación estética con las técnicas tradicionales: es un Sprechgesang, un canto hablado. De hecho, Schoenberg se refiere a estas piezas no como canciones, sino como melodramas. Véase [5] para más información. 2.4. El surgimiento del sistema dodecafónico Schoenberg no estaba aún satisfecho con su técnica compositiva, ya que admiraba las obras extensas de los músicos románticos y pensaba que su atonalidad no podía sostener una obra de gran envergadura. Es decir, necesitaba un hilo conductor mejor que los motivos para poder componer obras atonales más largas. Por aquella época sufrió crisis en varios aspectos de su vida. En lo personal, su mujer Matilde Zemlinsky acababa de abandonarlo por otro hombre, aunque posteriormente volvería junto al compositor. Y en lo profesional, sus obras no eran del gusto del público, por lo que no contaba con suficiente dinero para mantener a su familia. Todas estas circunstancias, unidas al desarrollo de la Primera Guerra Mundial, no le permitieron componer apenas entre 1914 y 1923. Tras el final de la guerra, en 1919, Schoenberg fundó la Sociedad para Interpretaciones Musicales Privadas junto a sus discípulos y amigos Alban Berg y Anton Webern. Schoenberg, Berg y Webern se autodenominaron la Segunda Escuela de Viena en honor al grupo de compositores del siglo XVIII Haydn, Mozart y Beethoven, quienes formaban la Primera Escuela de Viena. En la Sociedad para Interpretaciones Musicales Privadas se presentaba música contemporánea en circunstancias que favorecieran su adecuada apreciación. Así se evitaba que dichas obras, al no ser entendidas por el público, fueran inmediatamente rechazadas. Las obras de compositores como Mahler, Debussy, Bartók, Ravel, Strauss y Stravinsky se incluyeron en los programas de conciertos organizados por la Sociedad. En este contexto Schoenberg pudo reflexionar sobre sus técnicas compositivas, y al fin publicó en 1923 su ensayo Método de composición con doce sonidos [13], donde se describían por primera vez los axiomas del dodecafonismo. Estos axiomas constituían la solución al problema de la atonalidad libre que tanto le había estado atormentando durante una década. Su primera obra íntegramente dodecafónica, publicada también en 1923, es la Suite para piano Op. 25, que podrán ver a continuación. Es la pieza más temprana en la que Schoenberg usa series dodecafónicas en cada uno de los movimientos. En dos obras anteriores a ella usa series dodecafónicas, pero en movimientos aislados: la Op. 23, 5 Stücke (1920—23), en el movimiento de Waltz final; y su Serenata, Op. 24, en su Soneto central. Las series utilizadas en la Suite Op. 25 servirán de ejemplo en este texto, y su tercer movimiento, Musette, será estudiado y analizado en el apartado 4.3 con el fin de entender una obra dodecafónica en toda su extensión. A continuación el lector podrá escuchar la Suite para piano Op. 25: 3. El sistema dodecafónico de Schoenberg 3.1. Los postulados del dodecafonismo El dodecafonismo es un sistema compositivo que predetermina la melodía y la armonía a partir de una ordenación de las doce notas de la escala cromática, que se llama serie. Esta y algunas de sus transformaciones son los ladrillos con los que se construyen las alturas de las notas; son el único material que se puede utilizar. El resto de elementos de la pieza, como el número de instrumentos, el ritmo, el carácter, la textura o las dinámicas, se deja a discreción del compositor. No serializar todos los conjuntos será la principal crítica al dodecafonismo por parte de los compositores serialistas que sucedieron a su creador, Arnold Schoenberg. Para los serialistas integrales, como Pierre Boulez, aquello restaba cohesión al modelo compositivo; para los dodecafonistas, aportaba libertad [2]. Precisamente la predeterminación dodecafónica, aunque parece limitante, permite realizaciones musicales y estilos de composición muy diferentes: Schoenberg daba un tratamiento tradicional a sus obras, ya que aun admiraba las formas clásicas; Alban Berg iba más allá al utilizar series que recordaban a las tríadas tonales; y, en cambio, Anton Webern evitaba radicalmente cualquier asociación con la tradición. Schoenberg definió su sistema musical a partir de cuatro postulados que, en realidad, se basan en principios matemáticos [4]: 1. La serie (sobre la que se construye la obra dodecafónica) consta de las doce notas de la escala cromática dispuestas en un orden lineal específico. 2. Ninguna nota aparece más de una vez en la serie. Los dos primeros postulados expresan que una obra dodecafónica fundamenta su estructura sobre una permutación de la escala de doce semitonos. Dicha permutación σ es una biyección del conjunto numerado de las doce notas consigo mismo, y se representa de esta forma: La permutación σ(m), con m ∈ ℤ∕(12), pertenece al grupo simétrico de orden 12, S12. Por ejemplo, en la Suite para piano Op. 25 Schoenberg utiliza como serie original en todos los movimientos de la obra la siguiente permutación σ: Los otros dos postulados restantes son: 3. La serie se puede exponer en cualquiera de sus aspectos lineales: serie original, inversión, retrogradación de la original y retrogradación de la inversión. 4. La serie puede usarse en sus cuatro aspectos desde cualquier nota de la escala. Los dos últimos postulados amplían los recursos compositivos al admitir la transformación de la serie original mediante inversión, retrogradación, inversión retrógrada y transposición. El compositor puede utilizar cualquiera de las transformaciones de una serie al componer su obra dodecafónica. El conjunto de series que puede utilizar, que viene dado por la serie original y todas sus posibles transformaciones, se conoce como espectro serial; veáse [4] para más información. 3.2. Las transformaciones de una serie Transformar una serie es matemáticamente equivalente a aplicar una función sobre la serie, y que asocie esa permutación a la permutación transformada. Por tanto, cualquier función Ψ se aplica sobre el conjunto de las permutaciones, S12. 3.2.1. Transposiciones La transposición, mencionada en el cuarto postulado, consiste en subir o bajar la serie original un número determinado de semitonos. Por tanto, no se modifican los intervalos entre las notas, sino solamente la altura a la que está la serie. Ya que consideraremos todas las octavas equivalentes, debemos trabajar módulo 12. La serie transportada k semitonos (con k constante), Tk(σ), se construye sumando k a σ (mod. 12): Tk(σ(m)) = σ(m) + k A su vez, Tk se forma al componer k transposiciones de 1 semitono: Tk = T1 ∘ T1 ∘… ∘ T1, k veces. Debido a que k es en realidad el exponente en la potencia de T, se coloca este número como superíndice. Históricamente, la notación Ψk, Ψk o también Ψ(k) se ha usado en sustitución de la composición de la transposición Tk y otra función Ψ, en el respectivo orden: Ψk = Ψ ∘ Tk = Ψ(Tk). Sin embargo, esta notación es especialmente ambigua y confusa, sobre todo al trabajar con funciones no conmutativas —cuando importa el orden en el que estén T y Ψ—. Por ello, es preferible ceñirse a la notación estrictamente matemática; es decir, a la composición de funciones, aun omitiendo el símbolo ∘, de esta manera: ΨTk. Una posible serie transportada sobre la permutación σ de la Suite para piano Op. 25, con k = 6, es la siguiente serie T6: 3.2.2. Retrogradación La retrogradación consiste en leer la serie original desde la nota final hacia atrás, es decir, aplicar a la serie una simetría especular. De este modo, la primera nota irá al último puesto, la segunda al penúltimo, y así sucesivamente. La serie retrógrada se construye según la siguiente fórmula: R(σ(m)) = σ(11 - m) La serie retrógrada sobre la permutación σ de la Suite Op. 25 es la siguiente serie R: 3.2.3. Inversión La inversión consiste en cambiar la dirección —de ascendente a descendente y viceversa— de los intervalos entre cada nota de la serie. Si el primer intervalo en la serie original σ es de +k, el primer intervalo en la serie invertida I será de -k (siempre módulo 12), por lo que debemos cambiar el signo de σ para construir I. Además, queremos que la primera nota de ambas series, I(σ(0)) y σ(0), coincidan, así que debemos transportar la serie (-σ) un número λ de semitonos para que esta condición se cumpla: I(σ(0)) = -σ(0) + λ = σ(0) ⇒ λ = 2σ(0) Por tanto, la serie invertida se construye de esta forma: I(σ(m)) = - σ(m) + 2σ(0) La serie invertida sobre la permutación σ de la Suite Op. 25 es la siguiente serie I: En total, obtendremos 48 series —aunque no obligatoriamente distintas entre sí— pertenecientes a un solo espectro serial. Hay 12 series originales sobre cada una de las doce notas, 12 series retrógradas, 12 invertidas y 12 series sobre las que se aplica tanto la retrogradación como la inversión. A continuación se muestra la sintaxis simple junto a la matemática: Sintaxis simple T0, T1, T2… R0, R1, R2… I0, I1, I2… IR0, IR1, IR2… Sintaxis matemática T0, T1, T2… R, RT1, RT2… I, IT1, IT2… IR, IRT1, IRT2… 3.3. Matrices dodecafónicas Dada una serie, su matriz dodecafónica es una representación visual de su espectro serial; es decir, del conjunto de series derivadas de esa serie. El espectro serial es todo el material compositivo sonoro del que se dispone para la composición de una obra dodecafónica. Al poder ordenar y disponer la información en una tabla, el compositor puede acceder a toda ella al mismo tiempo sin tener que calcular cada serie individualmente. La matriz se lee en la dirección en la que aparece el nombre de la serie. Las series T se leen de izquierda a derecha, mientras que las series R de derecha a izquierda. Las series I se leen de arriba a abajo y las IR∕RI de abajo a arriba. He creado un programa que devuelve en formato LATEX la matriz correspondiente a cualquier serie dodecafónica que se introduzca en teclado, además de producir la nomenclatura simple para cada serie. El código, escrito en C++, se puede encontrar en el enlace https://gitlab.com/dodecafonismo/cppmatrices. A continuación, se incluye la matriz dodecafónica de la serie P de la Suite Op. 25 de Schoenberg. Mientras que la mayoría de tablas tienen dos filas inferiores, que se corresponden con las distintas nomenclaturas de RI e IR para una misma serie —ya que normalmente no conmutan—, en la matriz de la serie P sí coinciden. Por otro lado, he escrito un comando en el propio lenguaje LATEX que crea esta misma tabla con el comando \dmatrix, y tiene cualquier serie como argumento. Su sintaxis es \dmatrix. El comando se encuentra en el paquete de LATEX ddphonism, disponible en el enlace https://www.ctan.org/pkg/ddphonism. La tabla aparece sin el orlado de nomenclaturas: 4 5 7 1 6 3 8 2 11 0 9 10 3 4 6 0 5 2 7 1 10 11 8 9 1 2 4 10 3 0 5 11 8 9 6 7 7 8 10 4 9 6 11 5 2 3 0 1 2 3 5 11 4 1 6 0 9 10 7 8 5 6 8 2 7 4 9 3 0 1 10 11 0 1 3 9 2 11 4 10 7 8 5 6 6 7 9 3 8 5 10 4 1 2 11 0 9 10 0 6 11 8 1 7 4 5 2 3 8 9 11 5 10 7 0 6 3 4 1 2 11 0 2 8 1 10 3 9 6 7 4 5 10 11 1 7 0 9 2 8 5 6 3 4 También he creado una página interactiva que genera matrices de cualquier serie para cualquier longitud serial, además de generar series aleatorias. Permite escoger entre dos numeraciones y dos nomenclaturas. Está escrita en Elm y el código puede encontrarse en https://gitlab.com/dodecafonismo/matrices. En este enlace se encuentra la aplicación web. Sus instrucciones de uso se encuentran al final de la página: https://matrices.netlify.com/. 4. Análisis de una obra dodecafónica: el opus 25 4.1. Series de la Suite op. 25 Lo primero que hará un compositor dodecafónico antes de empezar a componer será escoger su serie original. Su elección nunca es una simple cuestión de azar; al contrario, ya que las singularidades de la serie darán un carácter especial a toda la obra. Por ejemplo, el compositor puede escoger una serie con simetrías, y así tendrá series repetidas entre su espectro serial. También puede tener simetrías internas solo en un fragmento de tres o cuatro notas, y de este modo podrá el compositor oscilar entre varias series del espectro que se parezcan entre sí. Para un estudio más completo de las relaciones de similitud entre series se recomienda On the Similarity of Twelve-Tone Rows, de Tuukka Ilomäki [10]. En la Suite para Piano Op. 25, Schoenberg escoge su serie σ para resaltar el intervalo de tritono (6 semitonos). A continuación se observan en negrita los intervalos entre las notas de esta serie, en unidad de semitono: Presenta repeticiones triples de los intervalos de tritono (6), de sexta mayor (9) y de segunda menor o semitono (1): los intervalos más disonantes; una repetición doble de cuarta justa (5), y un intervalo de segunda mayor (2); además de una consecución de intervalos repetida: 9–1–9–1. Como se forma el intervalo de tritono al enlazar la serie original con una serie que empiece por la misma nota, se tiene en cuenta el intervalo de tritono (6) al final. En el dodecafonismo se evitan deliberadamente los intervalos de tercera mayor (4), ya que estos son la base de la eludida armonía tonal. El intervalo de tritono tiene la particularidad de no modificarse en la inversión y transportación k = 6, por lo que estos intervalos aparecen en los lugares originales, mientras que en los procedimientos de retrogradación y retrogradación inversa ocupan sus lugares en retrógrado. En particular, Schoenberg utiliza entre los seis movimientos de la Suite solamente las ocho series de todo el espectro serial que cumplen estos requisitos: T0, T6, I, IT6, R, RT6, RI y RIT6, que podemos observar a continuación: Estas series tienen muchos elementos en común: todas comienzan o acaban por mi♮ o por si♭, lo que permite enlazar unas series con otras por medio del unísono o del tritono; se mantienen los intervalos de tritono en sus lugares originales o retrógrados, y coinciden en las dos primeras y las dos últimas notas dos a dos. Se han realizado estudios – como el de Martha Hyde [7] – en los que se limitan las series utilizadas en la Suite a cuatro: T0, T6, I e IT6, pero ya que el objetivo de este texto no es analizar la obra entera se dejará esta cuestión para análisis posteriores. 4.2. Descripción de la Suite op. 25 Schoenberg realiza en la serie σ una partición triple; es decir, la serie se divide en tres tetracordos, y cada uno de ellos contiene un intervalo de tritono. El último tetracordo, si se retrograda, consta de las notas 10–9–0–11, que en notación germánica es la secuencia BACH. Esto puede ser un homenaje al compositor Johann Sebastian Bach (1685—1750), ya que Schoenberg admiraba a los grandes compositores anteriores a él por las estructuras formales de sus obras. Para más información, véase [16]. Otro posible homenaje a Bach y sus contemporáneos barrocos es precisamente la forma de la obra: es una suite, género cultivado durante los siglos XVII y XVIII que se compone de una variedad de danzas. La Suite de Schoenberg está formada por seis danzas: un preludio, una gavota, una musette, un intermezzo —que no tiene influencia barroca sino más bien de Brahms, otro modelo para Schoenberg—, un minueto con trío y una giga. Además, el estilo, la textura —contrapuntística, típicamente barroca—  y la estructura de cada danza se corresponden con los estilos, texturas y estructuras de las danzas homónimas del periodo bachiano. Por ser ésta su primera obra totalmente dodecafónica, Schoenberg la utilizó como una muestra al mundo de las posibilidades de su nuevo método compositivo. Fue también por lo que tomó un formato tan variado como una suite: así podía en una misma obra componer con estilos tan distintos como los de las distintas danzas. Al componer la obra, Schoenberg trata cada tetracordo como una subunidad individual. Los superpone contra otras series del espectro también divididas, o utiliza sus notas como un solo acorde cuatríada. Estas divisiones no sólo sirven para hacer la serie más reconocible o añadir cohesión a la obra, sino que además facilitan el desarrollo de la serie específicamente en el estilo de cada danza. 4.3. Análisis de la Musette En el tercer movimiento de la Suite, la Musette, Schoenberg recrea la danza barroca que toma su nombre del instrumento homónimo: la cornamusa, de la familia de la gaita. La música compuesta para estos instrumentos suele consistir en una melodía acompañada por una nota pedal, que se traduce aquí en la presencia de un bordón sobre el sol♮ (nota 7). Esta nota se extrae de cada una de las series utilizadas y se forma con ella un ostinato rítmico en la mano izquierda del piano. Con el resto de sonidos de cada serie, Schoenberg vuelve a emular el estilo de la danza barroca y articula un discurso polifónico a dos voces con ritmos esencialmente cortos. A partir de la doble barra del compás 9, el re♭ (nota 1) acompaña a sol♮ y ambos crean un doble bordón en la mano izquierda. La elección de esas dos notas está estrechamente relacionada con la tradicional relación de quinta justa formada por sol♮ y re♮ en la música tonal. Schoenberg sustituye las quintas justas tonales por los tritonos dodecafónicos, subrayando aún más su emancipación de la disonancia. Además de las similitudes texturales, rítmicas y armónicas, la Musette de Schoenberg comparte estructura formal con las danzas barrocas. Y esta semejanza es quizás la más notable, ya que fue la búsqueda de estructura formal lo que inspiró a Schoenberg a desarrollar su método compositivo. La Musette barroca, como todos los movimientos de danza, presenta una estructura binaria con simetría tonal: empieza y acaba por la misma tonalidad, mientras que el centro es zona de desarrollo. Schoenberg despoja de funcionalidad tonal a esa simetría, madre de la forma sonata, y la aplica a su composición dodecafónica. En este movimiento se pueden diferenciar a simple vista tres secciones, divididas en los compases 9 y 20, debido a cambios de textura, figuración y tempo. En la segunda sección se le añade melodía a la mano izquierda del piano, dejando más camuflado el bordón que en la primera sección, además de que éste se vuelve doble, mientras que vuelve a aparecer claramente en la tercera sección. También en la segunda sección aparece una nueva figuración, que es la semicorchea; y, por último, en los dos compases de división aparecen dos a tempo, que marcan el final de las dos primeras secciones tras dos zonas de variabilidad rítmica. Para que esta estructura tríptica sea una forma binaria, la primera y la última parte deben mantener un parecido, que se observa a través del análisis de las series utilizadas en el movimiento. Estas series son T0, T6, I e IT6. En la Musette, Schoenberg hace un uso casi absoluto de la tripartición serial, hasta el punto de individualizar los tetracordios por separado y concederles privilegios seriales, como la retrogradación. Por ejemplo, en el compás 7, en la voz inferior de la mano derecha aparece el tetracordio 4–5–2–3, que es o bien el primer tetracordio de RIT6 o la retrogradación del tercer tetracordio de IT6, mientras que los otros dos tetracordios de IT6, 10–9–71 –1 en la voz superior y 8–11–6–0 en la mano izquierda, aparecen en el orden correcto. Entonces no se puede analizar el compás como RIT6, sino indicar que hay una alteración puntual de IT6. Por tanto, es muy complicado analizar esta obra en su totalidad, ya que la flexibilidad en la ordenación de los tetracordios puede generar situaciones muy ambiguas. Debido a estas fragmentaciones y a las variadas combinaciones de tetracordios originales y retrógrados, se escucha un área de desarrollo hacia la sección media del movimiento. En cambio, las series al principio y al final de la pieza se presentan casi íntegramente, como una exposición y reexposición. He aquí un vínculo con la simetría de las formas binarias tonales. Es más, incluso el orden de las series utilizadas en la primera y en la última sección coinciden, exceptuando dos repeticiones consecutivas y las series T0 finales, que actúan como una cadencia serial: A continuación se encuentra el análisis serial completo de la Musette: Figura 4: Análisis de la Musette (I) Figura 5: Análisis de la Musette (II) 5. Definiciones matemáticas 5.1. Conjuntos y grupos Un conjunto es una colección de objetos bien definidos y distintos entre sí que se llaman elementos. Para definir un conjunto se puede o bien listar los objetos uno a uno, o bien describirlos por medio de un predicado: una o varias propiedades que caracterizan a todos los elementos de dicho conjunto. Por ejemplo, el conjunto Ki, formado por las doce notas de la escala cromática de una misma octava i, está bien definido porque podemos hacer una lista con ellas: por ejemplo, K4 =: Por un lado, aun llamando a las notas de distinta manera, el conjunto, conceptualmente, es el mismo. Además, el hecho de listar algún elemento más de una vez no afecta a su definición. Como Do#4 = Re♭4 (ya que trabajamos con temperamento igual), K4 también puede ser listado así: En cambio, el conjunto D, formado por las duraciones rítmicas elementales – sin ligaduras ni puntillos –, es infinito, por lo que no se puede listar de forma completa. Sin embargo, se puede expresar por medio de un predicado: La notación n ∈ ℤ significa que n pertenece a los números enteros. En este caso se han representado las duraciones mediante su ratio con la duración de la negra. Los elementos de un conjunto pueden combinarse mediante operaciones —como la suma o la multiplicación en el caso de los números— para dar otros objetos matemáticos. Se dice que un conjunto G no vacío y una operación binaria (*) forman la estructura de un grupo (G,*) cuando cumplen las siguientes condiciones: 1. Su operación es interna: Si a,b ∈ G, entonces a * b ∈ G. 2. Su operación es asociativa: Si a,b,c ∈ G, entonces (a * b) * c = a * (b * c). 3. Existe un elemento e en G, llamado elemento neutro o identidad, tal que para todo x ∈ G se cumple que e * x = x * e = x. Se puede probar que el neutro es único para cada grupo. A veces se incluye dentro de la definición del grupo: (G,*,e). 4. Cada x ∈ G tiene asociado otro elemento x-1 ∈ G, llamado elemento inverso, tal que x * x-1 = x-1 * x = e. Se puede probar que el inverso de cada elemento es único. (ℤ,+,0) y (ℚ,+,0) son grupos, pero (ℕ,+,0) no porque no existe el inverso de 2 con la suma: -2 ∉ ℕ. En cambio, (ℝ,*,1) y (ℚ,*,1) son grupos, pero (ℤ,*,1) no porque no existe el inverso de 2 con la multiplicación: ½ ∉ ℤ. 5.2. Funciones y permutaciones Una función es una regla que asocia a cada elemento de un primer conjunto, llamado dominio, un único elemento de un segundo conjunto. Si la función se llama f, el dominio A y el segundo conjunto B, se denota f: A → B. El elemento asociado a un x mediante f se denota f(x). Todos los x ∈ A tienen que estar asociados a un f(x) ∈ B, pero no todos los elementos de B tienen un elemento de A asociado. Los elementos de B que sí lo cumplen, es decir, los que se pueden escribir como f(x) para algún x, forman el conjunto imagen de la función: im(f) = . Una función biyectiva es aquella que empareja de manera exacta los elementos de dos conjuntos, de tal forma que cada elemento del dominio está emparejado con exactamente un elemento de la imagen, y cada elemento de la imagen se empareja con exactamente un elemento del dominio. Cuando varias funciones se aplican una detrás de la otra decimos que realizamos la operación de composición de funciones. Se representa con el símbolo ∘. La imagen de la primera función será el dominio de la segunda, y así sucesivamente. Por ejemplo, aplicar una función f(x) y después aplicar una función g(x) se denota g(f(x)) = (g ∘ f)(x). Una permutación σ(X) es una función sobre un conjunto X que asocia sus elementos a los elementos del mismo conjunto X de manera unívoca. Es decir, asocia cada elemento a uno, y solo uno, de los elementos de su mismo conjunto. El conjunto de todas las posibles permutaciones sobre un determinado conjunto X, junto con la operación de composición de funciones (∘), forma un grupo denotado por SX. Para probarlo, se debe comprobar que cumple todas las propiedades de los grupos. 1. Permutar dos veces es también una permutación. 2. La composición de funciones es asociativa. 3. La permutación que asigna un elemento a sí mismo es la función identidad. 4. Como las permutaciones son biyectivas, cada una tiene una inversa que es también una permutación. Cuando X es el conjunto de números naturales desde 1 hasta n, el grupo SX se representa como Sn y se le denomina el grupo simétrico de orden n. El número de elementos en Sn, es decir, de posibles permutaciones de n números es n!. En los ejemplos musicales de este texto, los conjuntos estarán numerados desde 0 hasta n-1, siendo n el número de elementos a permutar, en vez de desde 1 hasta n. Seguirán siendo grupos simétricos de orden n, pero con una numeración distinta. La notación utilizada para representar una permutación σ perteneciente a Sn con la numeración desde 0 y con σ(m) siendo el elemento asociado a m mediante σ, es: 5.3. Aritmética modular Fijado un n ∈ ℕ, se dice que a y b son congruentes (o equivalentes) módulo n si tienen el mismo resto al dividirlos entre n; es decir, que todos los números con el mismo resto se agrupan y se toman como equivalentes. Se expresa como a ≡ b (mod. n). De esta forma se pueden operar entre sí los números del 0 al n-1, ya que se conservan las operaciones de los números enteros, y si un resultado es ≥ n se puede seguir dividiendo entre n para que cumpla 0 ≤ r < n. Se conserva la suma (y la resta), ya que si a = nqa + ra y b = nqb + rb, entonces a + b = (nqa + ra) + (nqb + rb) = n(qa + qb) + (ra + rb), así que el resto de a + b es igual al de ra + rb. La aritmética modular también se llama aritmética del reloj porque funciona de la misma manera que las horas en un reloj. Como el 3 tiene el mismo resto entre 12 que el 15, las 15h son las 3h: 3 ≡ 15 (mod. 12). O, por ejemplo, 2 horas después de las 11 dan las 13, es decir, la 1: 2 + 11 = 13 ≡ 1 (mod. 12). También se conserva la multiplicación: si a = nqa + ra y b = nqb + rb, entonces ab = (nqa + ra)(nqb + rb) = n2qaqb + nqarb + nqbra + rarb = n(nqaqb + qarb + qbra) + rarb, así que el resto de ab es igual al de rarb. En música, la aritmética modular se puede encontrar en las escalas: todas las notas Do se toman como equivalentes, por ejemplo, y al sumarle 12 semitonos (una octava) se vuelve a obtener un Do. Si se asocian los números del 0 al 11 a las notas cromáticas del Do al Si, entonces 0 + 12 = 12 ≡ 0 (mod. 12). Entonces se dice que un número k pertenece al conjunto , con las propiedades indicadas, de esta manera: k ∈ ℤ12.   Nota: 1 La nota 7 aparece como bordón y no en la misma voz que el resto del tetracordio, por lo que su posición es también excepcional. Bibliografía [1] Felipe Aguirre. El concepto de “disonancia” en Adorno y en la nueva música. Enero de 2019. Consultado en agosto de 2019. [2] Pierre Boulez. Schoenberg is dead, 1952. Publicado en la revista The Score originalmente; consultado en línea en agosto de 2019. [3] J. de Aixquivel. Memorias de Historia Antigua. Universidad de Oviedo, 1989. [4] Manuel Domínguez Romero. Las matemáticas en el serialismo musical. Sigma, 41(24):93–98, 2011. [5] Alicia Díaz de la Fuente. Estructura y significado en la música serial y aleatoria. PhD thesis, Universidad Nacional de Educación a Distancia, Departamento de Filosofía, 2005. [6] World Heritage Encyclopedia. Consonance and dissonance, 2017. Consultado en agosto de 2019. [7] Peter Farindon. Dodecaphonism: Schoenberg. In M. Everist and J. Dunsby, editors, Models of Musical Analysis: Early Twentieth-century Music, chapter 4, pages 45–60. Blackwell Pub, Oxford, Inglaterra, 1993. [8] Paco Gómez. Crónica del congreso Mathematics and Computation in Music 2019, julio de 2019. Consultado en agosto de 2019. [9] Paco Gómez. Mathematics and Computation in Music 2019: un congreso interdisciplinar, julio de 2019. Consultado en agosto de 2019. [10] Tuukka Ilomäki. On the Similarity of Twelve-Tone Rows, 2008. Consultado en línea en agosto de 2019. [11] Knud Jeppesen. Counterpoint: The Polyphonic Vocal Style of the Sixteenth Century. (The Prentice-Hall music series). Dover Publications, 1992. [12] James P. Kinney. Twelve-tone Serialism: Exploring the Works of Anton Webern. Master’s thesis, University of San Diego, University of San Diego, 2015. [13] Arnold Schoenberg. Composition with twelve tones, 1923. Publicado en Style and Idea. [14] Arnold Schoenberg. Hauer’s Theories, 1923. Publicado en Style and Idea. [15] Richard Wagner. Oper und Drama, 1851. [16] June Xiao. Bach’s Influences in the Piano Music of Four 20th Century Composers. PhD thesis, Jacobs School of Music, Universidad de Indiana, 2014.

Miércoles, 11 de Septiembre de 2019 | Imprimir | PDF |  Correo electrónico

585. Los secretos de la multiplicación, de los babilonios a los ordenadores

Categoría: Historia de las matemáticas Autor: Raúl Ibáñez Torres Editorial: Catarata. Colección Miradas Matemáticas Año de publicación:  2019 Nº de hojas: 160 ISBN: 978-84-9097-826-9

Lunes, 09 de Septiembre de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

586. 143. SOLUCIÓN CONCURSO DEL VERANO DE 2019

Como siempre, atacando por la espalda, cuando empezamos a disfrutar de las vacaciones, aparece septiembre y el nuevo curso. En fin, que todo cada vez pasa más deprisa. No quiero enrollarme mucho, que la reseña ya es de por si extensa (gracias Nerea por tu comprensión, sobre todo por la dificultad de repasar los símbolos matemáticos con la dificultad añadida de los editores en la red). Simplemente felicitar a todos los participantes e indicar que es el primer año de los quince del concurso que dos de ellos no han dado la película-enigma (uno por confusión con otra con ciertas similitudes, y otro, supongo, porque no ha tenido demasiado tiempo para meterse con ello). Ciertamente intenté que las cuestiones matemáticas fueran más asequibles, y las pistas sobre la película algo más difusas (a lo mejor me pasé, pero es que es, al menos para mí, un título muy conocido). Tenía ganas además de poner algún título de Fritz Lang, uno de mis realizadores favoritos (tengo muchos, pero Lang fue un crack, ya desde la etapa muda). No es su mejor película, obviamente, pero fue la que más me cuadró para esta propuesta “para todos los públicos” (y en este caso me refiero desde el punto de vista de aceptación por la mayor parte de todos; no voy a meter en estas cosas a Bergman o Tarkovski, como cualquiera puede comprender). Cuestiones Matemáticas M – 1.- Si nos dijeran que la suma de un número de cuatro dígitos y sus cuatro dígitos resulta ser 2019. ¿De qué número de cuatro dígitos hablamos? Llamemos n a dicho número. Es obvio que n < 2019. Entonces la cifra de unidad de millar será 1 o 2, y la suma de las tres otras cifras (unidades, decenas y centenas) es como máximo 27 (porque 9 x 3 = 27 en el caso extremo). Por tanto, la suma de los dígitos del número que buscamos es a lo sumo 29, y entonces n ≥ 1990. Llamemos S a la suma de n y los dígitos que lo forman, y sea d un dígito cualquiera. Si n = 2010 + d, entonces S = 2010 + 2 + 1 + 2d; cuando S = 2019, entonces d = 3, posible solución n = 2013. Si n = 2000 + d, entonces S = 2000 + 2 + 2d, con lo que S sería un número par, y nunca podría ser 2019, que es impar. Si n = 1990 + d, entonces S = 2009 + 2d. Cuando S = 2019, d = 5, posible solución. Entonces n = 1995. Si n = 1980 + d, entonces S = 1998 + 2d, y como en el primer caso, S sería par, con lo que nunca podría ser 2019. Si n = 1970 + d, entonces S = 1987 + 2d. Para que S fuera 2019, entonces d debería ser 16, lo cual es absurdo porque d es un dígito. En principio, hay dos posibles soluciones. Después de resolver la siguiente cuestión, la M – 2, deduciremos cuál de los dos valores es el buscado. M – 2.- La diferencia de años entre el número anterior y el año de estreno de la película tiene el mismo número de divisores que el propio año de estreno de la película. ¿Serán suficientes esos datos para determinar dicho año de estreno? Dar un razonamiento a favor o en contra. Adelantándonos un poco, y utilizando información que posteriormente averiguaremos, como el año de estreno de la película es 1955 = 5 • 17 • 23, el número de divisores es 8 de acuerdo con una conocida expresión (si n = p1d1 • p2d2 • …. • prdr, entonces el número de divisores de n es el producto div(n) = (d1 + 1) (d2 + 1) …. (dr + 1) De las dos posibles soluciones del apartado anterior M – 1, como 1995 – 1955 = 40 = 23•5 (que tiene 8 divisores también ya que son (3+1) (1+1), de acuerdo con la fórmula anterior), pero 2013 – 1955 = 58 = 2 • 29, tiene sólo  (1+1) (1+1) = 4 divisores. Por tanto, la solución de M – 1 es 1995. Sin ningún otro dato adicional, no es posible determinar el año x de estreno si no lo supiéramos, ya que, según el enunciado, lo que debe cumplirse es que div(1995 – x) = div(x), y eso lo cumplen un montón de valores de x: 1955, 1957, 1961, 1965, 1969, 1971, 1975, 1981, 1985, 1993. En definitiva, que harían falta más datos para determinar el año. M – 3.- La acción tiene lugar en el siglo de las luces, en un año tal que al ser dividido por 2 y por 4 da resto 1, y al hacerlo por 3 y por 5 da resto 2. ¿A qué año nos referimos? El siglo de las luces es el siglo XVIII, de modo que buscamos un valor entre 1701 y 1800. Al tener los restos y los divisores, parece un claro ejemplo de utilización del conocido como teorema chino de los restos. Veamos si ese resultado nos lleva a la solución. Si n es el número que buscamos, los datos que nos dan son n ≡ 1 mod 2 n ≡ 1 mod 4 n ≡ 2 mod 3 n ≡ 2 mod 5 La primera condición nos indica que n = 2k + 1, para algún valor de k. Sustituyendo ese valor en la tercera condición, tenemos que 2k + 1 ≡ 2 mod 3 Simplificando llegamos a que 2k ≡ 1 mod 3. Para despejar k, basta con multiplicar la congruencia por un valor que nos dé coeficiente uno para k módulo 3. Eso se logra al multiplicar por 5, ya que 10 ≡ 1 mod 3. Eso nos lleva a que k ≡ 5 mod 3, y por tanto k es de la forma k =3t + 5, para algún valor de t. Sustituyendo k en la igualdad que teníamos de n, llegamos a que n = 2(3t + 5) + 1 = 6t + 11 Del mismo modo que en el paso anterior, sustituimos en la cuarta condición, teniendo que 6t + 11 ≡ 2 mod 5, es decir, 6t ≡ 1 mod 5. Multiplicando la ecuación por 6, se concluye que t ≡ 6 mod 5, es decir, que t = 5r + 6, para algún valor de r. Sustituyendo ese valor en la última expresión que habíamos deducido para n, se tiene que n = 6 (5r + 6) + 11 = 30 r + 47 Finalmente, empleando el segundo dato (que me lo he saltado por simple despiste), tendremos que 30 r + 47 ≡ 1 mod 4, o lo que es igual, 30 r ≡ - 46 mod 4, o análogamente, 2r ≡ 2 mod 4, o r ≡ 1 mod 4. De ahí, n = 30(4s + 1) + 47 = 120 s + 77 Para s = 14 encontramos el único valor entre 1701 y 1800, que resulta ser 1757. M – 4.- En un cierto día, la luna se ve con la sombra pasando a través de puntos diametralmente opuestos. Si el centro del arco circular que se está formando se encuentra en la circunferencia de la luna, determinar la proporción exacta de la luna que no está en la sombra. ¿Cuál es dicha proporción (en modo exacto)? Llamemos r al radio de la luna y C su centro. Sea R el radio del arco circular que forma la sombra y O el centro de dicho arco. Sean P y Q los puntos donde la sombra corta a la circunferencia de la luna. Sea x el área del triángulo POQ, y el área de la región entre PQ y el arco que pasa por P y Q centrado en O, y z el área de la región limitada entre los dos arcos (o sea el área de la sombra). Como PC = CQ = r, OP = OQ = R, y el ángulo POQ es de 90 grados (dado que PQ es un diámetro), entonces R = 2r, y por tanto, R = r. Entonces x + y = ¼ π R2 = ¼ π (r)2 = ½ π r2. También se observa que la suma de las superficies y y z es la mitad del área del círculo centrado en C, es decir, y + z = ½ π r2 Entonces x + y = y + z, y de ahí se sigue que x = z. Como x es igual al área del triángulo rectángulo POQ, entonces z = x = ½ (√2 r)2 = r2. El área de la región que no está en la sombra es igual al área del círculo completo centrado en C menos z: π r2 -  r2 = r2 (π - 1) Por tanto, la proporción exacta de la Luna que no está en sombra es . Si se desea en porcentaje, esa fracción es aproximadamente 0.6817…, es decir, un 68.17%. M – 5.- Los carruajes tardaban exactamente tres horas en ir y volver a la ciudad más próxima situada 30 millas al oeste. Llegando octubre, el recorrido se dilataba media hora más. Estimar en ese caso la velocidad del viento. A falta de más datos (tiempo de descanso en el destino, etc.), supondremos que el carruaje circula a velocidad uniforme. Entonces ésta será Vcarruaje = espacio/tiempo = 60/3 = 20 millas por hora. Llamemos w a la velocidad del viento. En uno de los dos trayectos (ida o vuelta), el carruaje circula a favor del viento, de manera que su velocidad será de 20 + w, mientras que en trayecto opuesto será de 20 – w. Entonces el tiempo que tarda en cada trayecto será en un caso , y en el otro , de modo que en todo el trayecto será + = 3 + ½ Resolviendo la ecuación tenemos que la velocidad del viento será w = ≈ 7.56 millas por hora. M – 6.- Si la forma de la suela del zapato (excluyendo el talón, que está más reforzado) sigue la ecuación 4x2 + y2 ≤ 4, con y ≥ 0, y el desgaste del material que conforma la suela se expresa en cada punto (x, y) por la función f(x, y) = 4x2 + y2 + 4x – 3y, determinar en qué punto exactamente se ha hecho el agujero, justificando el resultado. Si el desgaste de material viene dado por f(x, y), parece lógico pensar que el agujero se hará donde mayor desgaste de la suela se produzca (suela que viene dada por la semielipse positiva centrada en (0, 0) y de semiejes 1 y 2, respectivamente, ya que 4x2 + y2 ≤ 4, con y ≥ 0, es lo mismo que x2 + ≤ 1, con y ≥ 0 Por tanto, buscamos el máximo absoluto de la función desgaste, condicionado a la suela del zapato. Dicho máximo se alcanza con seguridad ya que la función de dos variables que describe el desgaste es continua (es polinómica) y la suela del zapato (la semielipse) es un conjunto cerrado (contiene el borde, es decir, los puntos frontera) y acotado (se puede incluir en un entorno de centro (0, 0) y radio 2.1, por ejemplo). En virtud del teorema de Weierstrass, la función desgaste alcanza con seguridad el máximo y el mínimo absolutos dentro de la semielipse. Utilizaremos para localizar el máximo absoluto el método de los multiplicadores de Lagrange. Definimos entonces la función auxiliar de Lagrange F(x, y) = 4x2 + y2 + 4x – 3y + λ(4x2 + y2 – 4) En primer lugar, veamos si los extremos relativos de f(x, y), son posibles candidatos a extremos absolutos. Como las derivadas parciales de f son, respectivamente, 8x + 4 y 2y – 3, el único extremo posible en R2 será (–1/2, 3/2). Como dicho punto se encuentra dentro de la suela del zapato (es decir, está en S, siendo S = ), es un posible candidato a extremo absoluto. Como seguramente el lector recuerde, para poder aplicar el método de los multiplicadores de Lagrange, los puntos obtenidos deben ser regulares de S. Y desgraciadamente, pueden alcanzarse extremos en puntos no regulares (a los que no podemos, insisto, aplicar el método de los multiplicadores de Lagrange). Así que, procedamos a localizar los puntos no regulares de S. Éstos son aquellos para los que el gradiente de la función g(x, y) = 4x2 + y2 – 4 no es máximo, es decir, el rango(∇g) < 1. Como ∇g(x, y) = (8x, 2y), el rango es nulo, si, y sólo si (x, y) = (0, 0). Y (0, 0)∈S, de modo que también es candidato a extremo. Aplicando la condición necesaria de extremo a F, obtenemos el sistema Con un poco de paciencia (despejando y sustituyendo) obtenemos como solución los puntos Ambos están en S, de modo que dos nuevos candidatos. Finalmente debemos considerar los puntos de la frontera y = 0 (los del borde de la elipse, son los anteriores). Estos son (1, 0), (–1, 0), y además aparece el (–1/2, 0), ya que al hacer y = 0, la función desgaste queda h(x) = 4x2 + 4x, y su derivada se anula en –1/2. Al verificarse el teorema de Weierstrass, basta con que evaluemos la función desgaste en todos esos candidatos a extremo. El valor mayor corresponderá al máximo absoluto, y el menor al mínimo absoluto. El primero es en el punto (1, 0) y el segundo en (–1/2, 3/2). Hubiera quedado más acorde con la película que saliera en el medio de la suela, pero el caso es que el máximo absoluto que resulta con estos datos es 8, que se alcanza en el punto (1, 0). M – 7.- Si imagináramos que el protagonista se encuentra en el punto A(0, 0) de un también imaginado plano coordenado, al reiniciar su camino se desplaza 1 unidad a la derecha, después r al norte, r2 a la izquierda, luego r3 al sur, r4 al este, r5 al norte, continuando con ese mismo patrón. Si lo hiciera indefinidamente, y siendo r un número positivo menor que 1, llegaría a un punto B(x, y). Demostrar que AB > 7/10. Denotemos por Pn = (xn, yn) el punto en el que se encuentra después de n movimientos. Así, tenemos que P0 = A = (0, 0), P1 = (1, 0), P2 = (1, r), P3 = (1 – r2, r), …. Es fácil comprobar que, para cada m ≥ 2, x2m-1 = x2m = 1 – r2 + r4 – …. + (–1)m–1 r2m–2 y2m = y2m+1 = r – r3 + r5 – …. + (–1)m–1 r2m–1 Utilizando la suma de los términos de una progresión geométrica, concluimos que Así, AB2 = x2 + y2 = , y como r < 1, M – 8.- ¿Cuántos? Tomando prestado el diagrama de uno de los concursantes, lo que buscamos en realidad es el valor de a + b + c. Tenemos los siguientes datos: Card(I) = 74, Card(A) = 17, Card(N) = 25, Card(I∩A∩N) = 4. Aplicando el principio de inclusión-exclusión, Card(I∪A∪N) = Card(I) + Card(A) + Card(N) – Card(I∩A) – Card(I∩N) – Card(A∩N) + Card(I∩A∩N). Entonces, despejando, se tiene que Card(I∩A) + Card(I∩N) + Card(A∩N) = Card(I) + Card(A) + Card(N) + Card(I∩A∩N) – Card(I∪A∪N) = 74 + 17 + 25 + 4 – 100 = 20. De acuerdo con el diagrama, (4 + a) + (4 + b) + (4 + c) = 20, luego a + b + c = 20 – 12 = 8. M – 9.- Calcular razonadamente el volumen de uno de estos objetos de altura h, sabiendo que se refuerza como vemos en la imagen con seis aros de hierro circulares, tres de ellos de diámetros distintos d1, d2 y d3 (d1 < d2 < d3). hasta la mitad; los otros tres repiten esos valores simétricamente, tal y como se observa en la imagen. El problema de modelización que pongo todos los años en el que el concursante debe “buscarse un poco la vida” aportando los datos que considere pertinentes para encontrar una solución práctica. Prácticamente todos los participantes han utilizado el cálculo integral para determinar el volumen de revolución de una parábola en la que previamente han colocado los valores d1, d2 y d3 que se indicaban. No incluyo las operaciones concretas por no alargar este texto. A todos les he dado la puntuación completa (salvo a los que simplemente dan un valor sin indicar como se obtenía, obviamente). M – 10.- ¿Qué barril se quedó sin comprar? El cliente pagó la misma cantidad (14 libras) por los de mejor calidad y por los de peor, y sabiendo que los primeros valen el doble que los segundos, eso significa que la suma de galones de los de mejor calidad es justamente la mitad que los de inferior. Se trata por tanto de agrupar los galones en dos grupos, uno con el doble de galones que el otro, dejando uno de ellos sin contabilizar. Si uno de esos grupos suma el doble del otro, eso significa que al menos uno de ellos debe sumar una cantidad par de galones. La suma de todos los barriles es 98 galones. Vayamos probando: 1.- Dejamos fuera el barril de 3 galones. El resto suma 95 galones. Hay que dividir 95 en tres partes, ya que una debe ser el doble de la otra. Eso no nos da números enteros, luego no es solución. 2.- Apartamos el barril de 13 galones. El resto suma 85 galones. Tampoco es divisible por 3. 3.- Quitamos el barril de 15 galones. El resto suma 83 galones. Tampoco es posible. 4.- Si eliminamos el de 17 galones, el resto pesa 81 galones. En un grupo por tanto debemos tener 27 galones y en el otro 54. Pero si intentamos sumar 27 galones con los datos de los barriles que tenemos, comprobamos que no es posible. 5.- Descartando el de 19 galones, nos quedarían 79 galones, que no es múltiplo de tres. 6.- Finalmente, apartando el de 31 galones, tendríamos 67 galones, que tampoco es divisible por tres. Por tanto, con esos datos no hay solución. ¿Y cómo puede ser? Pues porque el “listo” que esto escribe, con las prisas, cambió un barril: el de 3 galones, debería haber sido de 8 galones, y entonces, el cliente hubiera comprado los barriles de mejor vino de 13 y 15 galones a 0.50 libras el galón, y los de 8, 17 y 31 galones a 0.25 libras el galón, quedando por tanto sin vender el barril de 19 galones del que no sabríamos si era de vino de mayor o menor calidad. Mil disculpas. Ha habido participantes que lo han razonado perfectamente; al resto se les ha dado una puntuación proporcional al buen planteamiento que hayan realizado. M – 11.- A la entrada de la fiesta, una campana anunciaba con un toque la llegada de los invitados. Cuando llegó el primero, la campana sonó por primera vez. Cada vez que la campana sonó después, el número de invitados que llegaba eran dos más que los que habían llegado la vez que la campana sonó anteriormente. Si la campana tañó n veces, ¿cuántos invitados estuvieron en la fiesta? La cuestión es muy sencilla, a partir de una tabla como la siguiente: Veces que toca la campana    1          2          3          4          …        n Invitados que llegan               1          3          5          7          …        2n - 1 Por tanto, la suma total de invitados es la suma de la segunda fila, es decir, 1 + 3 + 5 + 7 + …. + 2n - 1 Utilizando la suma de los primeros sumandos de una progresión aritmética, se tiene que n = n2. M – 12.- Para juzgarlo, calcúlese la probabilidad de obtener en una mano de 7 cartas (las cinco del reparto inicial más 2 de cambio) cuatro reyes. Comparar con la probabilidad de obtener en las mismas condiciones únicamente tres reyes. Calcular ambas probabilidades es realmente sencillo. Utilizaremos como referencia la baraja francesa de 52 cartas (la que suelen utilizar las películas anglosajonas). Como ir sacando cuatro reyes de la baraja (sin reemplazar las cartas) responde a sucesos independientes, basta con multiplicar las sucesivas probabilidades de extraer un as, luego un segundo as, etc.; una vez obtenidos los cuatro, las restantes nos resultan indiferentes. Ahora bien, los ases pueden salir en cualquier momento de las siete extracciones (es decir, puede ser KKKKXXX, o XKXXKKK), de modo que hay que multiplicar la probabilidad por el número de sucesos posibles. Éstos serán = 35 Por tanto, p(4 reyes) = 35 ≈ 0.0001292824822…. En el caso de tres reyes, la probabilidad se calcula exactamente igual, con la diferencia de que, sacados tres reyes, después necesitamos que salga cualquier carta restante de la baraja, excepto el cuarto rey. Por tanto, p(3 reyes) = 35 ≈ 0.0058177117…., es decir, es mucho más probable, del orden de prácticamente 6 de cada 1000 partidas jugadas, mientras que la de los cuatro reyes, del orden de 1 de cada 10000 partidas. De modo que es bastante acertado concluir que hubo trampas, más aún teniendo en cuenta que su oponente había obtenido ¡¡cuatro reinas!! M – 13.- ¿Qué relación tiene con el emblema de la imagen? M – 14.- El emblema  divide al círculo en tres regiones. ¿Son iguales? ¿Podrían serlo? Atacamos en conjunto ambas cuestiones. Claramente el anillo circular de la película tiene marcada una Y, como indica la figura (es decir, si colocamos como centro O el punto desde el que parten los tres segmentos de la Y, los superiores están sobre las bisectrices del primer y segundo cuadrante, respectivamente). La primera parte de la cuestión M – 14, es inmediata: a simple vista se observa que los sectores circulares AOC y BOC (iguales) son mayores que el AOB. Pero como sabemos, en matemáticas las apreciaciones “a ojo” no son válidas, así que basta con argumentar que para que fueran iguales las regiones el círculo debería ser dividido por ángulos de 120º (porque es 360º entre 3), y el AOB es de 90º (los segmentos son perpendiculares: si OB es la bisectriz del primer cuadrante, el ángulo que forma con el eje de abscisas es de 45º). Entonces para que fueran iguales, deberíamos considerar ángulos (los tres) de 120º. Entonces la figura sería como la de la segunda imagen, que claramente no es la del anillo de la película. He tomado la circunferencia de radio unidad, de modo que el área del círculo sería 2π, y por tanto, cada parte sería de superficie 2π/3. Como ven no hace falta hacer ninguna integral, pero si la hacen, háganla en coordenadas polares que es mucho más rápida y sencilla su resolución. Respecto a la cuestión M – 13 , al tener una raíz cuadrada de dos en liza, lo primero que a uno le viene a la cabeza es involucrar una distancia, o si sus matemáticas son más elementales, la hipotenusa de un triángulo rectángulo (que es una distancia). Tampoco es muy complicado darse cuenta que el punto B, al ser el punto de intersección de la bisectriz del primer cuadrante (o sea, la recta y = x) y la circunferencia unidad (x2 + y2 = 1) tiene por coordenadas (,) (y si no nos percatamos, se resuelve el sistema). ¿Y qué es lo primero que a uno se le ocurre cuando tiene tres puntos A, B, C? Pues es obvio, calcular el área del triángulo. El triángulo ABC tiene por base (ya que es la distancia entre los puntos A(,) y B(,)), y por altura 1 + (la longitud de OC es obviamente 1, al ser el radio del círculo). Por tanto, el área del triángulo ABC (base por altura partido por dos) será: (1 + )  = Algún concursante (más sofisticado y perspicaz que yo), ha recordado que la cantidad dada es la razón o proporción de plata, y ha buscado el rectángulo de plata (aquel cuya proporción entre base y altura es ese valor) que contiene parte del emblema (no es muy complicado, basta darse cuenta del valor de la diagonal BC, por ejemplo). Lo destacable es que lo ha relacionado con el argumento de la película, ya que en ella se dice que las monedas que guardaba el pirata Barbarroja eran precisamente de plata y el medallón del esqueleto de Barbarroja también se dice que es de plata. Excelente observación, que debo reconocer como proponente, en la que nunca pensé, pero que ahí está. Por si fuera poco, otro concursante ha encontrado un curioso juego de palabras. El emblema de los Mohume es una Y (que en inglés se pronuncia “guay”, escribiéndola tal cual), y Why not es el nombre de la taberna del pueblo en la novela (Why también se pronuncia “guay”). M – 15.- El documento está doblado varias veces formando un cuadrilátero ABCD convexo e inscrito en el medallón (es decir sus cuatro vértices tocan la circunferencia que determina el medallón, como aparece en la imagen). Las diagonales AC y BD se cortan en el punto E. Sabiendo que AB = 39, AE = 45, AD = 60 y BC = 56, determinar la longitud de CD. NOTA: En efecto, las medidas de la imagen no están a escala (otro lapsus). No obstante, podemos hacer perfectamente el ejercicio. Empecemos por la semejanza de triángulos: los triángulos AEB y DEC son semejantes (tienen un vértice común y los ángulos en E son opuestos por un vértice). Por tanto, , es decir, (1) Por la misma razón, son semejantes AED y BEC, por lo que (2) De la primera y la tercera de estas fracciones, tenemos que , así que BE = 42. Por otra parte, el teorema de Ptolomeo afirma que AD • CB + AB • CD = BD • AC Sustituyendo los valores conocidos, tenemos que 60 • 56 + 39 • CD = (42 + ED) • (45 + EC)          (3) De (1), se tiene que CD = ED, y de la segunda igualdad de (2) que EC = ED. Entonces la igualdad (3) se transforma en 60 • 56 + 39 • ED = (42 + ED) • (45 + ED) Resolviendo la ecuación, se llega a que ED = 21 (la solución ED = - 75 obviamente la rechazamos), y de ahí, como CD = ED, tenemos que CD = ≈ 18.2. Cuestiones culturales y cinematográficas C – 1.- Es curioso que una película, en apariencia de aventuras, no se estrenara en España hasta pasados 27 años de su estreno internacional, y que además se hiciera por televisión, concretamente el domingo 6 de junio de 1982, por la segunda cadena de televisión española, a las 22:15, aunque se había programado para el sábado 6 de febrero de ese mismo año por la primera cadena, pero “sin ninguna explicación”, el ente público la cambió. En salas comerciales se pudo ver, como nos comentan los concursantes, en circuitos restringidos como salas de arte y ensayo, cine clubs o filmotecas. Así, en Madrid, el cine Bellas Artes la programó el 28 de agosto de 1987, en Sevilla el multicine Cristina la programó el 28 de mayo de 1988, y también el cine club Arquitectura el 15 de marzo de 1990. En Bilbao el 15 de noviembre de 2005 en el cine club FAS, uno de los más antiguos de España en activo, por cierto (seguramente el que más, pero habría que confirmarlo). También nos indican que en Vigo o Gijón se pasó por salas, pero sin prueba que lo demuestre, lo dejamos en el aire. En Valladolid, las salas Casablanca (aún en activo, especializadas en cine de autor) la programó el 7 de abril de 1988 (adjunto el anuncio de esa fecha del periódico El Norte de Castilla); posteriormente el viernes 11 de septiembre de 1988 la filmoteca de la Caja de Ahorros Popular también la pasa en un ciclo dedicado al realizador alemán. Curiosamente, el viernes 30 de agosto (a un día de finalizar el plazo de envío de las respuestas de este concurso) la Filmoteca Española la puso a las 18:00 en el Cine Doré, aunque allí la han programado más veces. C – 2.- Aunque los concursantes han hecho referencia al desplante del director alemán a Goebbles y su huida a Norteamérica, además de su ascendencia judía por parte de madre, y que en España el gobierno de Franco le tendría alguna animadversión, eso implicaría que ninguna película suya se hubiera estrenado por aquí, y eso no fue así. En este caso, nada que ver con la política. Ni a la productora (la Metro-Goldwyn-Mayer), ni al director, les gustó demasiado el producto final, por lo que no tenían demasiado interés en estrenarla en los EE. UU. Esto fue fruto de que al realizador se le impuso un guion, un formato en el que no estaba cómodo (el CinemaScope) y allá donde pudo fue modificando cosas durante el rodaje. Por ello, ni unos ni otros quedaron contentos. Finalmente se estrenó el 12 de mayo de 1955 en sesiones dobles y de cine infantil, sin ningún tipo de promoción, casi avergonzándose de proyectarla. Tampoco hicieron lo mínimo por distribuirla a otros países. En un viaje por Italia, el crítico y cineasta francés Luc Moullet la vio, y escribió una pequeña crítica en la prestigiosa Cahiers du Cinema (en el nº 62, para más detalles) calificándola de genial. Muy cerca de la redacción de la revista se encontraba el cine Mac-Mahon (en la homónima avenida), que se había especializado en estrenar películas que no hubieran llegado a Francia por circuito comercial, en versión original. Y en 1960 logran estrenarla publicitando el hecho como un gran triunfo. ¿Y cómo es posible que no gustara a los yanquis, siendo, porque lo es, una gran película? Hay que verla para descubrirlo, pero se trata de una película (y una novela) incómoda para lo que podríamos llamar, las mentalidades “políticamente correctas”. Nos han hecho a la idea de que a los niños se les debe mostrar un mundo bonito, perfecto, que ya tendrán tiempo de descubrir la realidad cuando crezcan. Hombre, no vamos a poner a los niños ante hechos salvajes o truculentos, eso está claro, pero tampoco podemos estirar el mito de los Reyes Magos al máximo, porque al final la decepción es tan mala como lo que pretendíamos reservar. Es una obra (novela y película) oscura, incómoda, sobre todo para los adultos, y eso, en 1955 costaba. Aunque de 1953 se estrenó Raíces Profundas (Shane, George Stevens, EE. UU.), con la que tiene no pocas similitudes, y sin embargo hasta la “oscarizaron”. Pero claro, no era lo mismo un western (para los que la mayoría no veía más allá de tiros y caballos) con un personaje íntegro hasta la médula, que la lejana costa inglesa con un protagonista vividor cínico, ambicioso y sin escrúpulos. C – 3.- El título original, Moonfleet, lugar inexistente en la realidad, es un compuesto de Moon (Luna) y Fleet (admite varios significados: el más evidente, Flota, pero también hace referencia a un estuario, una ría, una zona de marismas; y como verbo, ondear, ondular, rielar. Todas las acepciones cuadran, tal y como se indica en el párrafo que va a continuación de la novela), aunque el autor indica en la novela que “cuando era un niño pensaba que este lugar se llamaba Moonfleet porque en una noche tranquila, ya sea en verano o durante las heladas invernales, la luna brillaba muy intensamente en la laguna; pero luego aprendí que era la abreviatura de la "flota Mohune", de los Mohunes, una gran familia que una vez fueron los señores de todas estas partes”. C – 4.- Todos los concursantes han descrito que se asusta de una mano que sale de debajo de la tierra, de uñas muy largas, sucia y movimiento lento, tratando de asustar al niño. De un contrabandista en el contexto de la película, obviamente. Sin embargo, a lo que me refería con la cuestión era a quien concretamente pertenece la mano (). Fritz Lang tenía a gala, a modo de marca de fábrica, filmar su propia mano en sus películas. Esta es su mano (maquillada para la ocasión, claro; pensé que bastaba esa insinuación, para que los lectores lo dijeran, pero ya he visto que no). Así que sólo 5 puntos para todos en esta ocasión, excepto para uno que le doy 6 al darse cuenta de que la mano aparece exactamente en el “pinuto” 3:14, ja, ja, ja. C – 5.- Los diez puntos los alcanzan los que hayan indicado que los barriles de contrabando al subir la marea chocaban entre si flotando en la cripta que servía de escondite que se encontraba justamente bajo la iglesia (con esa intención se hizo la pregunta). El sonido se amplificaba a través de las cavidades, percibiéndose en la iglesia con cierto estruendo, que los lugareños atribuían al fantasma de Barbarroja (y obviamente difundido y amplificado por los propios contrabandistas, interesados en que se aceptara la explicación sobrenatural; vamos como algunos otros que hay por ahí que pretenden que creamos en …, bueno mejor me callo y que cada cual concluya). No obstante, los barriles son omnipresentes en toda la trama: el chiquillo se cae de un barrilete y gracias a eso descubre el medallón en el ataúd de Barbarroja, se utiliza medio barril para acceder al pozo donde se halla el diamante, en los barriles se guarda la preciada mercancía de contrabando. Los que hayan indicado alguna de éstas razones, más obvias, tienen cinco puntos. C – 6.- El papel encontrado dentro del medallón de Barbarroja describe varias citas bíblicas que el sacristán/sepulturero Felix Ratsey (buen conocedor de la Biblia) descubre (en la película) al instante que están mal citadas (el versículo no corresponde al texto). Este dato hace pensar a Jeremy Fox que el número incorrecto que sustituye al verdadero debe indicar algo. Tomando de cada cita la palabra que corresponde al número incorrecto (la secuencia es 10 - 6 - 15 -11 – 10) se compone la frase Treasure fourscore feet deep well, cuya traducción sería algo así como Tesoro a 80 pies de profundidad del pozo (obsérvese que fourscore son cuatro veintenas, es decir, ochenta). Eso les lleva al pozo de Hollisbrooke, que se dice el más profundo de Inglaterra, localidad en la que además Barbarroja fue gobernador del castillo. No entiendo por qué los guionistas cambiaron el nombre del lugar original, Carisbrooke, por el imaginario de Hollisbrooke. En este lugar hay un castillo medieval visitable y de cierto interés histórico y turístico, y con una Casa del pozo (Well-House) que data de 1587 y con una curiosa estructura de rueda de tracción animal y eólica para sacar agua. Es una de las mayores atracciones del castillo, donde se forman grandes colas de gente para observar a los burros de Carisbrooke trabajar (recordemos que así se mueve también en la película). C – 7.- Se trata de un símbolo heráldico denominado pall, y es el emblema de la familia Mohune. Uno de los concursantes ha tenido la paciencia de indicar el minuto exacto donde aparece el citado símbolo: Minuto 7:01.- El chico muestra el emblema de los Mohune como prueba de su identidad. Minuto 11:53.- Aparece en la verja de entrada a la mansión de  los Mohune con el Minuto 26:50.- Vuelve a aparecer el símbolo a los pies de la estatua de Barbarroja (un antepasado de los Mohune) dentro de la iglesia. Minuto 31:40.- Tras caer en el escondite de los contrabandistas por el agujero formado bajo el ángel tras la tormenta, se aprecian al menos 4 sarcófagos, todos ellos con el emblema de Mohune. Minuto 32:24.- Vuelve a verse en primer plano el emblema, en otro féretro perteneciente a Barbarroja apartado del resto. Minuto 32:52.- Tras romperse el féretro, sobre el esqueleto se observa un medallón con el símbolo. Minuto 67:22.- En el pozo donde hallan el diamante, se encuentra un ladrillo con el símbolo, marcando el lugar donde está escondido el diamante C – 8.- La caratula del DVD editado en España, el menú de opciones, etc., tienen el título con el que se conoce, Los contrabandistas de Moonfleet, heredada de la versión estrenada en Francia, pero cuando lo reproducimos en la versión doblada al castellano, la voz en off dice Los aventureros de la noche, que es cómo se emitió por televisión española y se anunció en los medios de comunicación. Siendo el año 1982, ya instaurada la democracia y la correspondiente eliminación de la censura desde hacía unos años, no entiendo ese otro título, y no he encontrado por qué en ninguna parte. Sólo cabe la especulación de que quizá no se quería presentar en una película, aparentemente de aventuras, y por tanto para todos los públicos, una actividad ilícita en el título como es el contrabando.  Pero insisto, es pura especulación. C – 9.- La película y la novela tienen muchas diferencias (como decía un participante, casi es más breve indicar las coincidencias). Hago una lista de todas las que nos habéis mandado, aunque como sólo se pedían seis, ese número basta para alcanzar los diez puntos de la pregunta, aunque algunos os habéis explayado: 1.- El Barbarroja de la película es en la novela Barbanegra. 2.- En la novela la posada se llama Why Not, mientras que en la película es The Halberd. 3.- En el libro, es el corpulento Elzevir Block (mesonero encubierto de la taberna) quien se encarga de John Trenchard (llamado John Mohune en el film), mientras que en la película es el galante contrabandista Jeremy Fox (administrador de los bienes de la familia Mohune). 4.- Además, Elzevir Block es el héroe de la novela, pero en el film es un contrabandista sin importancia y uno de los villanos (de hecho, es el que se enfrenta con una enorme lanza a Jeremy Fox en el duelo en la posada). 5.- En la novela, el joven Trenchard es, desde el primer momento, un habitante del pueblo de Moonfleet, y no un recién llegado como ocurre en la película. 6.- John es huérfano, pero en la novela vive con su tía Jane. Este personaje desaparece en la versión cinematográfica, donde solo se menciona la muerte de su madre Olivia. 7.- En la película, John es mucho más aniñado (tiene 11 o 12 años) y temeroso que en la novela (en la que tiene 15 años), y es más adulto y audaz. 8.- En el libro, tras encontrar John el diamante y subir del pozo, Elzevir lucha con el hombre que limpia las instalaciones, quien acaba cayendo al pozo. En la película, se queda inconsciente en el borde del pozo. 9.- En la novela, John se hace con la clave del acertijo gracias a una pista facilitada involuntariamente por la tía, pudiendo localizar así el escondrijo (el castillo donde estuvo retenido el rey Carlos I). 10.- En el libro, John viaja con la biblia de su madre y usa esta para descifrar el mensaje, pero lo hace dentro de la cueva donde se refugian. En la película lo descifran sin la biblia y escondidos en el camino tras unos arbustos. 11.- En la novela, John y Elzevir renuncian al diamante pues un malintencionado joyero holandés les dice que no es auténtico, sino de cristal. Esto no ocurre en la película. 12.- En la novela, Elzevir acoge al muchacho desde el principio, pero en la película, Jeremy tratará por todos los medios de deshacerse del muchacho y la compenetración será progresiva. 13.- John y Elzevir van varios años a la cárcel y después son enviados a Java, pero durante el trayecto, la embarcación naufraga frente a la costa de Moonfleet. Aunque John logra llegar a tierra, Elzevir muere ahogado. En la película no van a la cárcel y Jeremy Fox muere malherido por Ashwood, adentrándose en la mar en un bote. 14.- En el film, el magistrado Maskew no es el padre (como ocurre en la novela), sino el tío de Grace (la niña de quien está enamorado John en la novela). 15.- A diferencia de lo que sucede en el libro, en el film el párroco no interviene en las actividades delictivas de su comunidad, al menos de una forma cómplice. 16.- En la novela, John acaba casándose con Grace y tienen 3 hijos. La película termina con ellos niños. 17.- En la novela a Maskew lo matan accidentalmente sus propios hombres mientras persiguen a los contrabandistas, mientras que en la película Jeremy Fox lo despeña . 18.- La acción en la novela trascurre a lo largo de varios años y en la película sólo en unos pocos días. 19.- En el libro se disfrazan de carreteros, de albañiles y de marineros mientras que en la película Jeremy Fox se disfraza de soldado. 20.- En el libro el que resulta herido es John, en una pierna, mientras que en la película hieren a Jeremy Fox en una mano. 21.- En la película el castillo donde está el diamante se llama Hollysbrooke, en el libro se llama Carisbrooke. C – 10.- Desde hace tres años existe una publicación digital llamada Zenda, Autores, libros & cía. El pasado 10 de abril, Zenda lanzó el sello editorial Zenda Aventuras, con el que pretenden  recuperar novelas del género de aventuras que por diversas razones se han ido olvidando o se conocen mal. El diamante de Moonfleet de John Meade Falkner (el título original es Moonfleet), fue la novela elegida para iniciar este proyecto, disponible desde el 21 de mayo. Los libros de la colección presentan prólogos inéditos de Arturo Pérez-Reverte, portadas diseñadas en exclusiva por el célebre ilustrador Augusto Ferrer-Dalmau, y la traducción está hecha en exclusiva por la escritora Dolores Payás. Una magnífica iniciativa a la que deseamos larga vida. C – 11.- Varios cineastas franceses (ya comentamos antes el aprecio de los críticos de Cahiers por ella) han manifestado su interés y reconocimiento por Fritz Lang. El más conocido que manifestó su devoción por esta película fue François Truffaut, aunque tampoco escatimaron elogios Serge Daney, Jean Luc Godard, Luc Moullet o Bernard Eisenschitz. Cualquiera de estos nombres sirve como respuesta. C – 12.- Hergé (seudónimo de Georges Prosper Remi), autor de la célebre serie de historietas gráficas de Tintín, reconoció que Tintín y el capitán Haddock fueron inspirados en sus características básicas por John Trenchard y Elzevir Block, respectivamente, de la novela. C – 13.- Película: Los contrabandistas de Moonfleet (Moonfleet, Fritz Lang, EE. UU., 1955) Novela: Moonfleet (1898) de John Meade Falkner.   Puntuaciones Es realmente gratificante comprobar el magnífico nivel de todos los participantes (quiero hacer una mención especial a Alba Diez Mariño, que siendo una chica de 14 años solamente, ha resuelto, con las herramientas matemáticas que conoce a esa edad, la mayor parte de las cuestiones; algunas, era imposible que las hiciera, pero ha sido además honesta y no ha pedido a nadie que se las resolviera). Salvo malentendido de algún enunciado, todos han afrontado perfectamente todas las cuestiones matemáticas. Respecto a las de cine, siempre baja un poquillo, pero internet suele suplir las lagunas. 1.- Alejandro Apezteguía.- 274 puntos 2.- Francisco Pi Martínez.- 265 puntos 3.- Marta Pérez Ceballos.- 262 puntos 4.- Pedro Pablo Palacio.- 229 puntos 5.- Alba Diez Mariño.- 196 puntos 6.- Celso de Frutos de Nicolás.- 118 puntos 7.- Alberto Gustavo Colomo.- 10 puntos Agradezco a todos su buenísima disposición, la aceptación de la propuesta, y sus elogios (inmerecidos). Espero que hayan pasado de verdad un buen rato. En breve recibiréis un mail, algunos para pediros una dirección postal a la que enviaros un pequeño obsequio de DivulgaMAT, y los demás para comentaros un poco las puntuaciones de cada cuestión, una vez hayáis leído las soluciones. Alfonso Jesús Población Sáez

Viernes, 06 de Septiembre de 2019 | Imprimir | PDF |  Correo electrónico

587. 174. (Septiembre 2019) Math Casts

Es curioso comprobar cómo las ideas matemáticas originales surgen de las más variadas fuentes y de momentos históricos diversos: no solo entre los profesionales de la materia sino desde el mundo de los aficionados. Ocurre lo mismo con la magia y, por supuesto, con la magia matemática. Ya hemos presentado a lo largo de este rincón a un gran elenco de personajes, del pasado y del presente, tanto aficionados como profesionales, que han contribuido con sus ideas originales al desarrollo de esta disciplina. Si en la última entrega hablamos de un personaje científico actual, Harapan Ong (número 173), esta vez viajaremos en el tiempo para adentrarnos en las ideas mágico-matemáticas de un paisajista y mago aficionado del pasado reciente. Howard Adams nació en 1931 en Buffalo (Nueva York). Fue un prolífico e incansable escritor y publicó grandes enciclopedias de magia, como los 10 volúmenes de O.I.C.U.F.E.S.P. (acrónimo a la inglesa de "Oh, I see you have ESP") o M.I.N.D.E.S.P.A. (una serie de 12 ejemplares dedicados a la magia mental), pero también la colección ESP Card Magic, serie de 20 DVDs recopilados por Aldo Colombini, contiene multitud de juegos con cartas ESP originales de Howard Adams y otros autores. Falleció en 2010 en Laguna Niguel (California). El libro del que hablaremos esta vez es el titulado Mathcasts Aspellonu (H&R Magic Books, 2003), que podemos traducir como "El hechizo de los modelos matemáticos". Esto me recuerda el título del libro de Theoni Pappas, "The magic of mathematics: discovering the spell of mathematics", aunque de contenido completamente distinto. El libro de Howard Adams contiene 12 x 12 = 144 juegos basados en principios matemáticos de combinatoria y propiedades de invariancia y simetrías. Todos se realizan con un pequeño paquete de cartas o con símbolos ESP, a quienes dedicamos los artículos de enero (número 167) y febrero de 2019 (número 168). El propio autor califica estos juegos como solitarios mágicos pues la magia sucede en las propias manos del espectador, sin la intervención del mago. Durante mucho tiempo, el libro ha reposado en mi mesa de noche esperando su oportunidad de salir en nuestro rincón; la cantidad de juegos que contiene ha hecho difícil la elección. Es posible que, en el futuro, otros juegos también tengan cabida. Por el momento, valga mi recomendación como modelo lleno de ideas sobre magia y matemáticas. El juego que hemos elegido como muestra es el titulado MIRAKASTAK, el número 123 de la lista. Su desarrollo te dará una idea del tipo de juegos que contiene el libro, un verdadero filón para la magia pero también para la matemática: la sorpresa del resultado es el objetivo de la primera así como la búsqueda de la solución es la ocupación de la segunda. Separa de la baraja ocho cartas, del as al ocho, de palos mezclados (solo importan sus valores numéricos) y ordénalas de modo que, estando las cartas con las caras hacia abajo, estén en este orden, de arriba abajo (el as será la carta superior y corresponderá al número 1): En la versión original se utilizan también 60 monedas de un céntimo y tres monedas de 25 céntimos. Como no tenemos esas monedas en nuestro sistema eurístico, bastará tener escritas en dos hojas de papel las predicciones que desvelaremos en su momento. Corta el paquete de cartas por cualquier lugar y completa el corte. De este modo, cualquier número puede estar ahora en la parte superior. Reparte sobre la mesa las cuatro cartas superiores, de izquierda a derecha, formando una fila de cuatro cartas, pero colocando cara arriba las que quieras, desde ninguna hasta las cuatro. Un ejemplo: Reparte las cuatro cartas restantes, también de izquierda a derecha, sobre las anteriores, también cara arriba o cara abajo a tu gusto. Vas a recoger ahora todas las cartas. Para ello, gira el paquete de la izquierda y colócalo sobre el siguiente, como cerrando un libro. Gira ahora ese paquete de cuatro cartas y colócalo sobre el siguiente, como antes. Repite la operación anterior con este montón consiguiendo recomponer el paquete de ocho cartas quedando un solo paquete sobre la mesa. Ahora algunas cartas estarán cara arriba y otras cara abajo. Toma las dos cartas superiores del paquete, vuélvelas cara arriba si es necesario y ordénalas de menor a mayor formando así un número de dos cifras (la primera menor que la segunda). Toma las dos siguientes cartas del paquete y repite la operación anterior. Suma los dos números formados y comprueba si mi primera predicción es correcta: Quedan cuatro cartas del paquete mezclado. Recoge las dos primeras, vuelve cara arriba las que estén cara abajo y ordénalas de mayor a menor, formando otro número de dos cifras (ahora la primera cifra es mayor que la segunda). Repite la misma operación con las dos últimas cartas del paquete. Suma ahora los dos números de dos cifras que han salido y comprueba si mi segunda predicción es correcta: Un ejercicio interesante consiste en descubrir el método de adivinación. Más interesante aún es comprobar si hay otra forma de ordenar las cartas inicialmente para obtener resultados diferentes pero también predecibles. Observaciones finales: Habrás observado también que, en todos los casos, la suma de las dos cartas repartidas consecutivamente es igual a nueve. Como solo hay cuatro posibles combinaciones al escribirlas de menor a mayor, 18-27-36-45, la suma de dos parejas de dichos números es 63. Una situación análoga se presenta con los números que se obtienen ordenando las cifras de mayor a menor. Otra propiedad de la ordenación inicial, también descrita en el libro, es la invariancia de la resta: si las dos primeras cartas repartidas se ordenan de mayor a menor y las dos siguientes se ordenan de menor a mayor, la resta de estos números de dos cifras da siempre como resultado 36. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Jueves, 05 de Septiembre de 2019 | Imprimir | PDF |  Correo electrónico

588. 99. (Agosto 2019) Crónica del congreso Mathematics and Computation in Music 2019

El congreso Mathematics and Computation in Music 2019 terminó el pasado 21 de junio. Gracias a la contribución de sus asistentes, el congreso fue un evento extraordinario. Científicamente, tuvimos contribuciones excelentes, profundas, intensas, relevantes. Emocionalmente, según me han hecho llegar muchos conferenciantes, también fue un éxito. Se creo una atmósfera muy amigable en que la gente no competía entre sí, sino que se ayudaba. Por supuesto, hubo crítica y desacuerdo, como ha de ser en toda reunión científica que se precie, pero esa crítica se centró en el contenido y no en la persona, y fue hecha siempre con intenciones de mejora, no de ganancia de poder. Socialmente, también fue un logro. Se hicieron múltiples contactos entre los asistentes como consecuencia del ambiente amistoso de la conferencia así como de la oportunidad de ver en persona a compañeros que trabajan en temas similares a los de uno. Esta efervescencia social fue consecuencia de la generosidad de los asistentes a la conferencia. El congreso se inauguró a las 9:30 de la mañana del 18 de junio por el Rector de la Universidad Politécnica de Madrid (UPM), Guillermo Cisneros. En el acto inaugural intervinieron Agustín Yagüe, Decano de la Escuela de Ingeniería de Sistemas Informáticos (UPM), Paco Gómez (UPM), el organizador local y general (y el humilde autor de esta columna) , Mariana Montiel (Georgia State University), la presidenta del Comité Científico, Guerino Mazzola (University of Minnesota), el Presidente de la Society for Mathematics and Computation in Music, y cerrando el acto el Rector de la UPM, quien ilustró sus ideas con una serie de historias sobre Bach y Euler. En la foto de abajo se ve una instantánea del acto de inauguración. Tras el acto de inauguración, empezó la actividad frenética de las charlas. En la foto de abajo vemos a Moreno Andreatta y Alexandre Popoff respondiendo a las preguntas de los asistentes tras su charla, que fue la primera (la charla tenía de título Groupoids and Wreath Products of Musical Transformations: a Categorical Approach from poly-Klumpenhouwer Networks). En otro momento de la conferencia vemos a Thomas Noll exponer su artículo junto con David Clampitt Exploring the Syntonic Side of Major-Minor Tonality. En la foto de abajo se ve a Paco Gómez junto a Maria Mannone explicando el significado del logo (el oso del logo es del madroño y no Yogui). Los cuatros días de conferencias fueron apasionantes; en particular, la sesión de homenaje a Riemman (Remanaging Riemann: Mathematical Music Theory as “Experimental Philology”?) sobre pedagogía de la Teoría Matemática de la Música (TMM) fueron especialmente productivas y llenas de contribuciones de calidad. La última charla no plenario la dio Jeremy Kastine, quien habló de su trabajo sobre ritmos euclídeos; su charla se titulaba Maximally Even Tilings. No hay que olvidar tampoco las charlas plenarias, que se dieron en el Real Conservatorio Superior de Música de Madrid (RSCMM). En la foto de abajo se ve a Paco Gómez dar la última charla plenaria, que versó sobre la necesidad de la divulgación en el campo de la Teoría Matemática de la Música. En esa charla ocurrió algo que pocas veces, muy pocas veces, he presenciado. El ambiente de aprendizaje, de compañerismo, de buen humor, de cohesión había llegado a tal punto en la conferencia que el turno de preguntas de mi charla se convirtió en un animado y profundo debate sobre múltiples cuestiones de nuestro campo. Se habló largo y tendido de la relación entre los músicos y los científicos, cómo toman unos y otros la presencia del otro, hasta qué punto se aceptan los análisis hechos por matemáticos e informáticos del fenómeno musical, el rechazo que existe en muchos departamentos de música y musicología a los métodos cuantitativos de análisis musical, se habló de la necesidad de que el gran público pero también el público especializado conozca los avances de la TMM, de abrir nuevos canales de comunicación en las redes sociales, se propuso crear canales tales como twitter, canales de Youtube, ¡crear una versión en inglés de esta columna!, escribir libros de divulgación, entre otras muchas ideas. El conserje tuvo que venir a echarnos porque tenía que cerrar el edificio. Otro momento que recuerdo con mucho cariño es el de las pausas para el café. Durante esas pausas los participantes dieron rienda suelta a su vena social. Se hicieron muchas conexiones e incluso se plantaron semillas para colaboraciones y amistades. Además, hubo una exposición interactiva, llamada La La Lab, the Mathematics of Music (https://imaginary.org/exhibition/la-la-lab-the-mathematics-of-music), organizada por Imaginarium. Esta exposición es gratuita —se pueden bajar los materiales desde su web sin coste alguno— y contiene excelente material divulgativo de la TMM. En la foto de abajo vemos a los participantes disfrutando del café y del material de la exposición. El último día nos hicimos la foto de grupo. La cena de gala fue un colofón muy agradable. Muchas risas, francas y abiertas, y un gran ambiente de amistad. Disfrutamos de arroces alicantinos en el restaurante Aynaelda. En la página de Flickr https://www.flickr.com/photos/webpgomez/albums/72157709203649743 se pueden ver muchas más fotos de este fascinante evento. Abajo tenéis fotos de cerca de algunos participantes.

Jueves, 01 de Agosto de 2019 | Imprimir | PDF |  Correo electrónico

589. Monolith

Un homenaje muy geométrico de Shaun Pitz a Stanley Kubrick (1928-1999) en el aniversario de su nacimiento: Ver también La perspectiva con un punto de fuga, explicada a través de Kubrick Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Viernes, 26 de Julio de 2019 | Imprimir | PDF |  Correo electrónico

590. La perspectiva con un punto de fuga, explicada a través de Kubrick

Si quieres saber lo que es la perspectiva con un punto de fuga, no dejes de ver el video Kubrick // One-Point Perspective de kogonada: Una magnífica selección con lo mejor de Stanley Kubrick ayuda a entender el significado de punto de fuga central… Visto en Neatorama Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 25 de Julio de 2019 | Imprimir | PDF |  Correo electrónico