Resultados 611 - 620 de 8471
|
Recursos/Juegos matemáticos
Autor:José Muñoz Santonja
1. Introducción.
Dentro del inmenso universo de juegos que podemos encontrar actualmente, existen algunos en los que, durante el desarrollo del juego, podemos girar o incluso dar la vuelta a las fichas con las que jugamos. Suelen ser fichas que tienen distintos colores o distintas funciones según estén en una posición u otra.
De este tipo de juegos, quizás los más conocidos sean los del tipo Othello o Reversi, en donde disponemos de fichas de dos colores, por una cara blanca y por otra negra, de forma que cuando se capturan las del contrario de les da la vuelta para posicionarlas de nuestro color.
En este artículo veremos juegos en los que tenemos son fichas de este tipo reversi o materiales más usuales y cotidianos.
Cuando realizamos experiencias de matemáticas en la calle, suelen ser muy atractivos los juegos solitarios en los que hay que partir de una determinada situación, e intentar llegar a otra con una serie de pasos, es lo que se suele indicar diciendo que un estado B es accesible desde otro estado A mediante una serie de transiciones, como nos indican en el artículo sobre invariantes que hay en la bibliografía.
En esta ocasión vamos a comenzar planteando una serie de juegos solitarios, en los que intentaremos buscar la solución, si la hay, para acabar con un juego de estrategia dentro del mismo tipo de puesta en escena.
2. Arriba y abajo.
Del artículo que he citado antes he sacado el siguiente enunciado, que nos puede servir de puntos de partida para lo que vamos a trabajar en estas páginas.
Sobre una mesa hay 11 vasos, 5 de ellos boca arriba y 6 boca abajo. Un movimiento consiste en escoger dos vasos cualesquiera y voltearlos simultáneamente. ¿Será posible, mediante una sucesión de estos movimientos, dejar todos los vasos boca arriba? ¿Y dejarlos todos boca abajo?
El planteamiento del reto es indiferente del número de vasos existentes, siempre que haya un número par en un sentido y otro impar en el sentido contrario. Es decir, sería igual partiendo de tres vasos boca arriba y dos boca abajo.
La solución es evidente. En el primer caso, sí es posible conseguir todos los vasos colocados boca arriba, basta realizar tres movimientos de los que están boca abajo para conseguirlo.
Sin embargo, en el segundo supuesto es imposible conseguir, moviendo dos vasos cualesquiera a la vez, que todos estén boca abajo. Si en la distribución que tenemos consideramos que n es el número de elementos boca arriba, en cada movimiento podemos pasar a tres situaciones distintas. Si volvemos boca abajo dos vasos, que estén boca arriba, el número que quedará será n–2. Si volvemos hacia arriba dos que estén boca abajo, tendremos boca arriba n+2 vasos. Por último, si volteamos uno de cada tipo, el número de vasos que quedará boca arriba seguirá siendo n. La única forma de llegar a tenerlos todos boca abajo sería que el número total boca arriba fuesen cero, pero al ser n un número impar y sólo poder volver dos, es imposible llegar a la solución pedida.
Generalizando este problema a un enunciado estándar, si tenemos una fila de vasos todos boca abajo y en cada movimiento le damos la vuelta a dos vasos, sólo se podrá llegar al estado con todos los vasos boca arriba si el número de vasos es par, en caso contrario será imposible.
Si queremos conseguirlo, será necesario añadir alguna regla extra como veremos en el juego último que plantearemos.
Como hemos deducido, volteando dos vasos a la vez, que no tienen por qué estar contiguos, es imposible volver completamente una fila de vasos impar. Pero en el siguiente planteamiento vamos a ver lo que ocurre si podemos volver tres.
3. De tres en tres.
Tenemos una fila de vasos todos boca abajo. Realizamos un movimiento que consiste en voltear tres de los vasos, que no tienen que ser consecutivos. ¿Es posible conseguir que toda la fila de vasos quede boca arriba con ese tipo de movimiento? En caso afirmativo, ¿cuál será el mínimo número de movimientos para conseguirlo?
Como es tradicional en la resolución de problemas, antes de la solución general vamos a estudiar casos más simples. Para ello, vamos a estudiar qué ocurre con los casos en los que hay menos vasos. Antes de seguir leyendo, animamos a los lectores a que intenten hallar la solución.
Vamos a desechar la posibilidad de tener uno o dos vasos pues no podríamos aplicar el movimiento.
a) Con tres vasos.
En este caso es trivial, con un solo movimiento volteamos los tres vasos a la vez.
b) Con cuatro vasos.
Si disponemos de cuatro vasos, veamos cómo es posible dar la vuelta a los cuatro con el movimiento permitido. Los pasos a seguir son:
i. Se mueven tres vasos cualesquiera, por ejemplo, los de lugar 1, 2 y 3. ii. Se mueven el vaso que queda boca abajo y dos de los que están boca arriba, por ejemplo, los vasos 2, 3 y 4. De esa manera nos quedan los dos extremos boca arriba y los dos centrales boca abajo.
Posición inicial
Paso i
Paso ii
iii. Se mueven los dos vasos boca arriba y uno de los que están boca abajo, por ejemplo los de lugar 1, 2 y 4. iv. Después del movimiento anterior quedan exactamente tres vasos boca abajo, los 1, 3 y 4, luego con un último movimiento es posible colocar los cuatro vasos boca arriba.
Paso iii
Paso iv
c) Con cinco vasos.
Cuando se estudian los casos progresivos de un proceso como el que nos ocupa, es normal que a medida que compliquemos el número de elementos, se complique la solución. Sin embargo, en este caso no es así, al trabajar con cinco vasos se simplifica la solución.
Los pasos a seguir son los siguientes vamos a indicar solamente el lugar de los vasos que volteamos, estén como estén en ese momento.
i. Vasos 1, 2 y 3. ii. Vasos 2, 3, y 4. iii. Vasos 2, 3 y 5.
En las imágenes siguientes vemos los tres movimientos.
Posición inicial
Paso i
Paso ii
Paso iiii
d) Con n vasos.
Podemos generalizar, a partir de lo anterior, para cualquier número de vasos mayor o igual que 3.
Si tenemos n vasos, es número puede ser un múltiplo de tres, un múltiplo de tres más uno o un múltiplo de tres más 2. En todos los casos podemos resolverlo, reduciéndolos a los casos anteriores.
i. Si el número de vasos es múltiplo de tres, podemos voltear grupos de tres vasos y con n/3 movimientos hemos conseguido nuestro objetivo. ii. Es el número de vasos es múltiplo de tres más uno, podemos separar 4 vasos y el resto, n–4 será múltiplo de tres. Para estos últimos hay que hacer la tercera parte de movimientos y para los cuatro vasos primeros ya hemos visto en el apartado b que necesitamos 4 movimientos. Luego, si tenemos un número de vasos, n, igual a un múltiplo de tres más uno necesitamos movimientos. iii. Por último, si tenemos un números de vasos que sea múltiplo de tres más dos, separamos 5 vasos y los restantes, n–5, son múltiplos de tres. Por tanto, el número de movimientos es .
4. La vuelta del cuadrado.
Vamos a añadir una dimensión al problema anterior. Ahora en lugar de una línea vamos a tener un cuadrado hecho con vasos. El objetivo, igual que en el caso anterior, será pasar del estado inicial con todos los vasos boca abajo a un resultado final con todos los vasos boca arriba. Para ello el movimiento que se puede hacer es volver tres vasos a la vez, pero en esta ocasión vamos a imponer la obligación de que los tres vasos sean contiguos en línea recta, puede ser horizontal, vertical o diagonal.
Como ya comenzamos a tener muchos elementos a mover, en lugar de utilizar vasos solemos usar fichas del Othello o bien elementos que reciclemos de los que utilizamos normalmente en casa. Así vamos a ver la solución utilizando tapones de botellas o de tetrabrik, basta ir guardando las que vayamos utilizando para poder utilizarlas como fichas en cualquier juego que se utilice al aire libre.
Como en el caso anterior animamos a los lectores a buscar ellos mismos las soluciones antes de continuar leyendo.
a) Cuadrado de lado cuatro.
En un cuadrado de lado cuatro tenemos un total de 16 elementos que hay que volver. Partimos de la posición de la imagen.
Posición inicial
Como en cada movimiento se pueden volver exactamente 3 elementos, se necesitan como mínimo 6 movimientos para conseguir volverlos todos. Vamos a ver que es posible conseguirlo. Hemos señalado, en cada paso, mediante una línea roja los tres tapones que se voltean en ese paso.
Paso 1
Paso 2
Paso 3
Paso 4
Paso 5
Paso 6
b) Cuadrado de lado cinco.
En este caso, el número de elementos de los que disponemos es de 25. Partimos de la posición inicial siguiente.
Posición inicial
Se necesitarían como mínimo un total de 9 movimientos para voltear todos. Yo voy a mostrar una solución en la que se realizan un total de 11 movimientos. Dejo a la investigación de los lectores encontrar un procedimiento con menos pasos.
Para no alargar el proceso los primeros seis pasos lo vamos a hacer directamente. Todos ellos consisten en voltear tres tapones en línea horizontal o vertical. A partir de ese resultado, visto en la imagen del paso 6, continuamos con los siguientes pasos del proceso.
6 primeros pasos
Paso 7
Paso 8
Paso 9
Paso 10
Paso 11
c) Cuadrado de cualquier lado.
Como el razonamiento es similar al visto en el apartado 3, dejamos para nuestros lectores que hagan un estudio de la posibilidad de voltear un cuadrado de cualquier lado y de hallar el número mínimo de movimientos para conseguirlo.
5. El juego de los cinco vasos.
Para terminar con este artículo vamos a ver un juego de estrategia en el que hay que voltear cinco vasos que están boca abajo y conseguir colocarlos boca arriba. Es un juego para dos jugadores y tiene las siguientes reglas.
i. Cada jugador en su turno puede volver uno o dos vasos. ii. Si vuelve un solo vaso, éste tiene que estar boca abajo y se coloca boca arriba. iii. Si vuelve dos vasos, estos deben estar juntos y el de la derecha, al menos, debe estar boca abajo antes de voltearlos.
Vamos a hacer un estudio de la estrategia para ganar. Como es un buen heurístico en la resolución de problemas, vamos a comenzar estudiando un caso más sencillo y después iremos ampliando a casos más complicados hasta llegar a lo que nos proponen.
Como vamos a estudiar muchos casos, para no liarnos lo mejor es consensuar una notación, de forma que podamos fácilmente ver en cada momento en que situación estamos. Para ello hemos a utilizar la C para indicar cuando un vaso está boca abajo, es decir, cuando nos enseña el culo, y por B cuando está boca arriba y nos enseña precisamente la boca del vaso.
Con la notación anterior, queremos pasar del estado CCCCC al estado BBBBB usando las reglas que hemos visto.
Vamos a suponer que los casos en que hay un vaso o dos son triviales, pues el primer jugador gana, y vamos a comenzar a estudiar por la situación de tener tres vasos.
a) Con tres vasos.
En este caso la estrategia ganadora favorece al primer jugador y debe hacer los siguientes procesos.
Comienza volteando el vaso central y pasa a la situación CBC. Esta situación hace que el siguiente en jugar pierda seguro, haga lo que haga. Veamos sus posibles movimientos:
i. Si voltea uno de los vasos boca abajo, el siguiente jugador voltea el otro que está boca abajo y gana la partida. ii. Si voltean a la vez los vasos 2 y 3, llega a la situación CCB, con lo que el siguiente jugador le basta volver los dos primeros y gana la partida.
b) Con cuatro vasos.
Ahora gana siempre el segundo jugador con la siguiente estrategia. Veamos todas las maneras de comenzar el primer jugador.
i. Si voltea dos vasos a la vez, pueden ser el 1 y 2, o el 3 y 4. En ambos casos el segundo jugador voltea los complementarios y gana. Si voltea el 2 y el 3, el segundo jugador basta que voltee los vasos 3 y 4 para llegar a la situación CBCB, que como sabemos por el apartado a, es perdedora para el siguiente jugador, pues el vaso que está a la derecha ya no puede ser movido, y por tanto, la distribución es la misma que CBC. ii. Si voltea el primer vaso, obtiene BCCC, el segundo jugador voltea el 3º llevando la situación a BCBC. El primer jugador puede hacer lo siguiente: a)Voltear uno de los que siguen boca abajo y el segundo jugador voltea el otro y gana. b)Voltear los vasos 3 y 4 quedando la situación en BCCB y el segundo jugador voltea 2 y 3 y gana. c)Voltear los vasos 1 y 2, quedando ahora CBBC. El segundo jugador voltea 3 y 4 llevando a la situación perdedora CBCB que ya hemos visto en el apartado anterior. iii. Volteando el segundo vaso, queda la situación en CBCC. Al segundo jugador le basta voltear el 4º para volver a la situación CBCB perdedora para quien le toque jugar. iv. Volteando el tercer vaso nos encontramos con CCBC. Al segundo jugador le basta voltear el primer vaso para llegar a la situación BCBC, que como hemos visto en el apartado ii es perdedora para quien tenga que jugar. v. Si voltea el cuarto vaso, directamente pasamos a la situación CCCB que es la misma que hemos visto en el apartado a y gana el jugador que le toca jugar.
c) Con cinco vasos.
En este caso el estudio está prácticamente hecho. Basta que el primer jugador voltee el vaso quinto para llegar a la situación CCCCB, que hemos estudiado en el caso anterior, es perdedora para quien le toque jugar. Luego gana el primer jugador.
d) Generalización.
A veces, el estudio que hacemos de un juego nos lleva a una generalización incorrecta, ya que lo obtenido nos lleva a pensar que la generalización es inmediata.
En este juego, en concreto, hemos visto que cuando tenemos tres y cinco vasos, el jugador con estrategia ganadora es el primero, mientras que si tenemos cuatro gana el segundo. Esto nos puede llevar a pensar que en las distribuciones impares gana el primero, mientras que en las pares gana el segundo. Pero nada más lejos de la realidad. Si jugamos con seis vasos, basta que el primer jugador voltee los vasos 5º y 6º para llegar a la misma situación estudiada en b y es evidente que el segundo jugador, que es quien le toca jugar, pierde la partida.
Dejamos aquí abierto, por tanto, el estudio a una generalización del juego o un estudio más exhaustivo según el número de vasos. Que no digan que se lo damos todo hecho.
6. Para acabar, nuevas perspectivas.
En la película “X + Y” dirigida por Morgan Matthews y estrenada en 2014, se desarrollan sesiones de unas olimpiadas internacionales de matemáticas. En la película hay un juego similar al planteado, aunque es un solitario y se realiza con 20 cartas. En cada jugada se vuelve una carta boca abajo hacia arriba y se voltea la que está a su derecha, esté como esté.
En la resolución del problema, que consistía en si el proceso acabaría se utiliza la notación binaria. Así, si consideramos que los elementos boca abajo se corresponderían con un 1 y los boca arriba con un 0, pasaríamos de una situación 111111 a 000000.
Dejo aquí la idea por si algún lector quiere relacionar el sistema binario con alguno de los juegos que hemos visto. Únicamente hay que tener cuidado porque los números binarios que hemos utilizado en estos juegos estarían escritos al revés, comenzando por las unidades y terminando en las posiciones más complejas.
7. Referencia.
NIETO SAID, J.H. (2015): “Invariantes y Problemas de Olimpiadas”. Revista Escolar de la OIM, 53. Enlace activo el 06/08/2018.
https://www.oei.es/historico/oim/revistaoim/numero53/Invariantes.pdf
|
|
Cultura y matemáticas/El rincón matemágico
Autor:Pedro Alegría (Universidad del País Vasco)
El principio de inducción completa es una herramienta matemática tan versátil como intrigante pues permite demostrar infinitas propiedades en solo dos pasos. Para entenderlo, es muy ilustrativo establecer la analogía de este principio con el de la caída de infinitas fichas de dominó (en este video se ven caer un millón de fichas, todavía muy lejos de ser infinitas pero puede servir como aproximación). Como es fácil entender, si numeramos un conjunto infinito de fichas de dominó con los números naturales y los colocamos a una distancia tal que todas las piezas cumplen la condición
"cuando la ficha número n se cae, hace que la ficha número n + 1 también se caiga,"
entonces está claro que, al dejar caer la ficha número 1, las infinitas fichas caerán irremediablemente. No hará falta comprobarlo para la ficha 507 ni para la 4589, ni para ninguna en particular, la condición anterior asegura la caída de todas las fichas.
Esto es precisamente lo que afirma el principio de inducción completa: dada una proposición matemática que depende de un número natural, si queremos asegurar que dicha proposición es válida para todos los números naturales, basta comprobar que es cierta la condición
"cuando la propiedad es cierta para el número n, también será cierta para el número n + 1,"
y, por supuesto, que lo sea también para el número 1.
A pesar de su aparente simplicidad, este principio ha resuelto multitud de problemas matemáticos de todo tipo, incluso es el fundamento de otras técnicas como el método del descenso infinito, muy utilizado en demostraciones clásicas. Sin embargo, a veces nos puede engañar si no observamos con atención todos sus detalles. El gran maestro George Pólya, en el primer volumen de su libro "Mathematics and plausible reasoning" (Princeton University Press, 1954) propone una paradoja que hoy se conoce como teorema de los caballos o de las niñas rubias:
Dado un conjunto de niñas rubias, si al menos una de ellas tiene los ojos azules, entonces todas las niñas tienen los ojos azules.
La versión original con caballos afirma que todos los caballos son del mismo color.
La demostración es la siguiente:
Es evidente que la afirmación es cierta si el conjunto está formado por una sola niña. Supongamos ahora que la afirmación es cierta para cualquier conjunto de n elementos (es decir que, dado un conjunto de n niñas rubias, si una tiene los ojos azules, entonces todas tienen los ojos azules), y consideremos un conjunto de n+1 niñas rubias . Si suponemos que una de ellas, digamos R1, tiene ojos azules, entonces todas las del conjunto tienen ojos azules (por la hipótesis de inducción). En particular, R2 tiene ojos azules de modo que todas las del conjunto tienen ojos azules. En definitiva, todas las del conjunto tienen ojos azules.
A pesar de que la demostración parece correcta, entendemos que no lo es porque la afirmación es falsa. ¿Qué ha fallado? Simplemente, la suposición de que los conjuntos y tienen un elemento común es falsa cuando n = 1.
Hasta aquí la clase de matemáticas. Pasamos al juego de magia, cuya explicación esperamos que descubras, quizá ayudándote del principio de inducción. Realizaremos el juego de este mes con las mismas monedas que usamos la última vez, de momento una cantidad indefinida de ellas.
Saca del bolsillo un puñado de monedas y colócalas en un montón sobre la mesa. Muestra también una predicción, que mantienes a la vista hasta el final pero sin dejar ver lo que contiene.
Entrega un lápiz y una hoja de papel a una persona que quiera colaborar y, contigo de espaldas, pídele que realice las siguientes operaciones:
Separa las monedas en dos bloques, del tamaño que quieras, cuenta el número de monedas que tiene cada bloque y escribe el producto de sus dos valores.
Elige uno de los dos bloques anteriores -tú eliges-, vuelve a separarlo en otros dos bloques, vuelve a contar el número de monedas que tiene cada bloque, vuelve a multiplicar sus valores y escribe el producto.
Repite el mismo proceso del paso anterior: elige uno de los tres bloques, sepáralo en otros dos, cuenta el número de monedas que tiene cada uno y escribe el producto de estos dos valores.
Vuelve a repetir este proceso hasta que todos los bloques tengan una sola moneda. Al final, suma todos los números que habías anotado.
Haz que comprueben que este valor coincide con tu predicción a pesar de la total libertad de elección de los distintos tamaños de los bloques de monedas en cada paso.
Veamos un ejemplo para comprender mejor el proceso:
Sobre la mesa hay diez monedas. Tu colaboradora la separa en dos grupos de 4 y 6 monedas. Por tanto, escribe el número 24.
A continuación, escoge el montón de 4 monedas y lo separa en dos grupos de 3 y una moneda. Escribe el número 3 debajo del 24.
Sobre la mesa hay tres montones, de 6, 3 y 1 moneda. Escoge el montón de 6 monedas y lo separa en dos grupos, de 4 y dos monedas. Escribe el número 8 debajo de los dos anteriores.
Luego escoge el montón de 4 monedas y lo separa en dos grupos, de 2 y 2 monedas. Escribe el número 4.
De momento, hay 5 montones, uno con tres monedas, tres con dos monedas y uno con una moneda. Escoge uno de los montones de dos monedas y lo separa en dos grupos de 1 moneda cada uno. Escribe por tanto el número 1.
Realiza dos veces más esta misma elección: divide el montón de dos monedas en dos grupos de una moneda y escribe el número 1.
Como quedan siete montones con una moneda y un montón con tres monedas, divide este en dos grupos de dos y una moneda y escribe el número 2. Por último, el montón que tiene dos monedas se divide en dos grupos y escribe el número 1.
Un esquema con el resumen de todo el proceso se muestra a continuación:
4
6
4 x 6 = 24
3
1
6
3 x 1 = 3
3
1
4
2
4 x 2 = 8
3
1
2
2
2
2 x 2 = 4
3
1
2
2
1
1
1 x 1 = 1
3
1
1
1
2
1
1
1 x 1 = 1
3
1
1
1
1
1
1
1
1 x 1 = 1
2
1
1
1
1
1
1
1
1
2 x 1 = 2
1
1
1
1
1
1
1
1
1
1
1 x 1 = 1
La suma de las cantidades anotadas es 24 + 3 + 8 + 4 + 1 + 1 + 1 + 2 + 1 = 45.
Las preguntas que debes plantear para saber de antemano el resultado final son: ¿este resultado depende del número inicial de monedas?, ¿depende también de la forma en que se separa cada montón en dos grupos?
Incluso aunque hayas intuido que las respuestas son sí y no, respectivamente, la pregunta final es: ¿cuál es la fórmula con la que se obtiene por adelantado el resultado final de la operación? Pero, más importante aún: ¿cómo demostrar que esa fórmula es la correcta?
Observaciones finales:
Si no has logrado dar con la solución, puedes acudir a la fuente donde he encontrado este juego, el artículo de Franka Brückler titulado "Inductive Magic", aparecido en el blog Mathematics-in-Europe del Comité de Divulgación de la European Mathematical Society.
Ya que hemos comentado el efecto dominó, no está de más sugerir que la caída de las fichas está relacionada también con algunas propiedades físicas, como se explica en este artículo titulado "Domino effect - it's more than just a fall".
Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)
|
|
Cultura y matemáticas/Instantáneas matemáticas
Autor:Ángel Requena Fraile
(Theologiae Christanae Principia Mathematica. 1755. Portada de la segunda edición)
El panfleto Theologiae Christanae Principia Mathematica (1699) del matemático escocés John Craig (1663-1731) fue un libro muy polémico en su época, denostado y olvidado después, para terminar siendo muy citado pero poco leído. Su valor actual viene dado por ser quizá uno de los mejores exponentes de la época hegemónica de la matemática, cuando el more geometrico fue el paradigma de verdad y del pensamiento claro y distinto y, en consecuencia, exportable a todo el saber. Además, la obrita de Craig es una forma curiosa de la integración de la matemática en la cultura.
Dos consagrados pioneros de la historia de la matemática ponen de manifiesto las opiniones contrarias a tal utilización de la disciplina, hasta el punto de considerarlo una chifladura. Por un lado Rouse Ball (1889) habla de un excéntrico sin mérito y por otro Florian Cajori (1919) decía que se hacía un uso absurdo de la matemática.
(Theologiae Christanae Principia Mathematica. 1699. Portada de la primera edición)
Dos hechos han contribuido a la puesta en valor del panfleto de 36 páginas en la edición de 1699. Uno de ellos es por su aportación innovadora para la historia de la estadística como puso de manifiesto el profesor Stephen Stigler en su artículo John Craig and the probability of history (1985). El otro hecho es la interpretación de la obra en su contexto cultural, algo que se muestra parcialmente en la moderna edición, en inglés, de los Principia de Craige realizada por Richard Nash (1991).
(John Craige´s Mathematical Principles. Richard Nash. 1991)
Stigler ha señalado como aspectos importantes la anticipación a Bayes en el cálculo de las probabilidades a posteriori y a Pierce en el uso conceptualista de un logaritmo de probabilidad.
Contenido de Theologiae Christanae Principia Matemática
Los Principia de Craig es un libro que sigue estrictamente el more geometrico de los Elementos de Euclides: diez definiciones, tres axiomas y treinta y cinco proposiciones (14 teoremas, 2 lemas y 19 problemas). Las proposiciones están organizadas en seis apartados:
Sobre la probabilidad histórica de la transmisión oral (1-15)
Sobre la probabilidad histórica de la transmisión a través de los testimonio escritos (16-22)
Sobre el placer uniforme (23-25)
Sobre los placeres de crecimiento uniforme (26-28)
Sobre los placeres cuya intensidad crece con alguna razón exponencial (29-32)
Sobre los placeres finito e infinito comparados uno con el otro (33-35)
Los dos primeros apartados sirven para calcular la fecha del fin del mundo y la resurrección de los muertos según el Apocalipsis de San Juan y los otros cuatro son la expresión matemática del Argumento de la Apuesta de Pascal sobre la existencia de dios: ... Si Dios no existe, el escéptico no pierde nada creyendo en él; pero si existe, el escéptico gana la vida eterna creyendo en él.
Todo parecería delirante si no lo contemplamos en su contexto, pero antes hablaremos del John Craig (o Craige) matemático para poner de manifiesto su valor en el contexto de las matemáticas de la Gran Bretaña.
John Craig, clérigo y matemático
Craig estudió matemáticas en la Universidad de Edimburgo teniendo como profesor a David Gregory. Se graduó en 1687 y había entrado en 1684, el año que Leibniz publica su versión del cálculo infinitesimal. Tras trasladarse a Inglaterra inicia una relación matemática intensa con Newton, y especialmente con De Moivre, Maclaurin y Halley.
Es de resaltar que Craig figura en la historia por ser el primer matemático inglés en usar el análisis infinitesimal de Leibniz y su notación. El primer lugar donde apareció dy/dx es en su obra Methodus figurarum lineis rectis et curvis comprehensarum quadraturas determinand (1685), de igual forma, el símbolo de integración (la S estirada) aparecerá en Tractatus mathematicus de figurarum curvilinearum quadraturis et locis geometricis (1693). Como Newton no había publicado su propio método (el cálculo de fluxiones), Craig solo dispuso de Leibniz, pero al final de su vida, y tras la agria polémica sobre la invención del cálculo, hará uso de la notación newtoniana.
Parece claro que el clérigo escocés no fue un simple aficionado sino un matemático de primer orden que polemiza con Jacob Bernouilli o Tschirnhaus.
El Apocalipsis de San Juan y los matemáticos
La palabra apocalipsis se traduce como revelación. El Libro de Daniel del Antiguo Testamento y el del Apocalipsis del Nuevo son libros que predicen el fin del mundo y el juicio final. Los matemáticos se interesaron por calcular la fecha en que se iba a producir. Craig no actuó como un chalado pues tenía aportaciones anteriores de matemáticos conocidos. De hecho, la Cronología formaba parte de las Matemáticas en la época.
John Napier había publicado Plaine Discovery of the Whole Revelation of Saint John en 1595 como carta al rey. Neper consideraba al Papa de Roma como el Anticristo y por ello pensaba que el fin del mundo debía estar próximo. El documento fue muy importante para la iglesia escocesa.
Isaac Newton fue el que puso de manifiesto con vehemencia que tanto la tradición oral como la escrita habían corrompido la verdadera religión. En su obra An Historical Account of Two Notable Corruptions of Scripture, Observations on Daniel and The Apocalypse of St. John, Newton carga contra Atanasio y la iglesia de Alejandría por su perversión y engaño.
Lo que hizo John Craig fue dar forma matemático probabilística a los argumentos de Newton. De alguna forma Craig fue más newtoniano que el propio Newton.
(Philosophiae Naturalis Principia Mathematica. 1687. Portada de la primera edición)
El argumento probabilístico
Si en los dos primeros apartados de sus Principia, Craig da forma matemática a los planteamientos de Newton en los siguientes hace lo mismo con el argumento de la apuesta segura de Blaise Pascal: Juego en el que existen iguales posibilidades de ganancia o pérdida, y en lo que se puede ganar lo infinito… Esto es demostrativo, y si los hombres son capaces de alguna verdad esta lo es.
Nadie puede mejorar una esperanza matemática infinita. Craig estableció diferentes formas de funciones de placer para hacer su “demostración” y dar envoltura probabilística al argumento de Pascal.
(Blaise Pascal)
Dios demostrable matemáticamente
El Obispo Berkeley arremetió contra los matemáticos incrédulos por su incoherencia de no creer en Díos y si en los infinitésimos. La realidad es que la mayoría de los matemáticos seguían siendo religiosos aunque con creciente heterodoxia. Quizá el caso de Newton muestre la paradoja en la que se vivía: se hace antitrinitario cuando es profesor del Trinity College.
Durante los siglos XVII y XVIII veremos a los matemáticos de primera línea dar forma demostrativa more geometrico a seis pruebas de la existencia de díos. Será Kant, al final de la Ilustración, el encargado de desmontar las pruebas. La prueba probabilística del jugador no la repetimos.
Prueba ontológica. Un ser perfecto tiene que incluir la existencia porque sino no lo sería. El argumento de San Anselmo es usado por René Descartes: Díos, el Ser Perfecto, es o existe como lo puede ser cualquier demostración de la geometría.
Prueba de la contingencia. Todo lo que existe proviene de algo o es movido por algo, así llegamos al primer motor inmóvil. Locke utilizará el mismo triángulo, cuya suma de ángulos es dos rectos, que usó Descartes como argumento euclídeo: la mera nada no puede producir un ser real que sea igual a dos rectos,… lo que no existió desde la eternidad ha tenido que tener un comienzo.
Prueba del designio. El perfecto orden y belleza del universo tiene que provenir de una inteligencia superior (Díos como matemático). Una vez más Newton (comentario en su Óptica): para hacer este sistema solar… la causa no puede ser ciega o fortuita, por el contrario debe estar muy preparada en mecánica o geometría.
Prueba del óptimo. Se trata de una variante de la prueba del designio. Tras desarrollar matemáticamente el Principio de Mínima Acción, Maupertuis dice: ¡Qué satisfacción para el espíritu humano al contemplar estas leyes, que son el principio del movimiento y el reposo de todos los cuerpos del Universo, encontrar la prueba de la existencia de Aquel que lo gobierna!
Prueba axiomática. Deducir de axiomas preestablecidos. Es lo que hace Baruch Spinoza en Ética demostrada al modo geométrico (1677): la proposición XI de la primera parte es Dios existe necesariamente que se deduce del axioma 7, la definición 6 y la proposición 7.
Recapitulando
Tanta inmersión teológica quizá nos haya desviado del principal objetivo: que las matemáticas entre el Renacimiento y la Ilustración jugaron un papel hegemónico como garantía de verdad. Lo que hoy es chaladura no lo fue en su momento. Como hemos expuesto anteriormente usando palabras de François de Gandt:
Me doy cuenta de hasta qué punto son las matemáticas una realidad cultural extraña y compleja, y también, cuán vagos y variables son sus límites según las épocas.
|
|
Publicaciones de divulgación/Matemáticas en los medios de comunicación
Autor:ABC
ABC, 13 de Mayo de 2019 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez
|
|
Publicaciones de divulgación/Matemáticas en los medios de comunicación
Autor:ABC
ABC, 6 de Mayo de 2019 CIENCIA - El ABCdario de las matemáticas Juan Matías Sepulcre Martínez
|
|
Cultura y matemáticas/Cine y matemáticas
Autor:Alfonso Jesús Población Sáez
Con mucha frecuencia las escenas ambientadas en un aula en las películas suelen echar mano de las matemáticas. Añadimos tres más a la larga lista, descubriendo que prácticamente todas son calcadas en cuanto a su propuesta y desarrollo. ¿Será que la metodología del profesorado tampoco ha cambiado sustancialmente? Seguramente.
Durante las pasadas vacaciones de Semana Santa, una cadena de televisión en España proyectó una película no demasiado antigua en la sobremesa de un sábado. No suelo hacer mucho caso a lo que se emite en esa cadena en esa franja horaria, ya que suelen ser producciones televisivas bastante mediocres con temas absolutamente manidos una y mil veces. En este caso, no tener otra cosa mejor en ningún otro sitio, la propia vagancia de no ponerme lo que me apetecía, y observar que se trataba de una producción cinematográfica, hicieron que aguantara cinco minutos de confianza. Y aparecieron las matemáticas. Eso sí, el resto de la película, sin ser tan lamentable como las comentadas previamente, tampoco fue una maravilla, pero resulta entretenida (lo adelanto por si alguien no desea más que ver las escenas de matemáticas; del resto puede prescindir sin provocarse trauma alguno, aunque si le intriga el argumento, tampoco pasa nada, puede terminarla, aunque inicialmente promete más de lo que finalmente es). Para situarnos, como siempre, sus datos básicos:
Ficha Técnica:
Título: Cita a ciegas con la vida. Título Original: Mein Blind Date mit dem Leben. Nacionalidad: Alemania, 2017. Dirección: Marc Rothemund. Guion: Oliver Ziegenbalg y Ruth Toma, sobre la vida de Saliya Kahawatte. Fotografía: Bernhard Jasper, en Color. Montaje: Charles Ladmiral. Música: Michael Geldreich y Jean-Christoph Ritter. Duración: 111 min.
Ficha artística:
Intérpretes: Kostja Ullmann (Saliya Kahawatte), Jacob Matschenz (Max), Anna Maria Mühe (Laura), Johann von Bülow (Kleinschmidt), Alexander Held (Fried), Nilam Farooq (Sheela), Sylvana Krappatsch (Dagmar), Michael A. Grimm (Küchenchef Krohn), Kida Khodr Ramadan (Hamid).
Sinopsis: Basada en la historia real del hoy empresario Saliya Kahawatte (que aparece al final de la película) y autor de la autobiografía en la que se basa la película. Hijo de una alemana y un cingalés (Sri Lanka), a los quince años le diagnosticaron una enfermedad hereditaria en los ojos que le provocaron un desprendimiento progresivo de retina. Como consecuencia perdió el 80% de la visión. A pesar de ello, logró acabar sus estudios de enseñanza secundaria con mucha diligencia y fuerza de voluntad, completó una capacitación como gerente de hotel e hizo carrera en la industria hotelera y gastronómica. Durante años, ocultó su discapacidad, pero sufrió esta mentira cayendo en la depresión (esto ya no lo cuenta la película, ya que, a pesar del drama, intenta mostrar un ejemplo de superación, pareciendo en mucha parte del metraje que estamos ante una comedia).
Las matemáticas
Hacia el minuto 7:21 aproximadamente, el protagonista se encuentra en clase de matemáticas:
Profesor: Otro ejemplo de la regla de la cadena.
Como observamos en la imagen, escribe en la pizarra la función y = e4x+2. A un lado está descrita la citada propiedad (para los que tengan un poco olvidada la regla de la cadena, se trata de la condición necesaria que nos permite derivar la composición de dos o más funciones). Ha escrito ya un ejemplo, bastante típico, con una función exponencial (y = ex^2). Al otro, el profesor tapa un cuadro con las derivadas de las funciones elementales.
Profesor: Si sustituimos esto (señala el exponente, 4x + 2), por u, la función externa queda y = eu.
En ese momento, el docente se para un instante, y se dirige a Saliya, del que suponemos conoce su problema visual. De hecho, echa un vistazo a su cuaderno (nos lo muestra la cámara) y se percata de que está escribiendo las expresiones tremendamente grandes y descolocadas, una encima de otra. El compañero situado a su lado lo observa también y le añade el 2 al exponente, que Saliya no ha escrito.
Profesor: Si voy demasiado deprisa, dígamelo Saliya.
Saliya: Lo haré, señor. Gracias.
Profesor (de vuelta a la pizarra): La derivada externa queda y = eu, mientras que la derivada interna de 4x + 2 es 4.
Saliya (susurrando): … significa que y’ es igual a eu por 4.
Y vemos que, en efecto, esa es la expresión que escribe el profesor en la pizarra.
Con un poco de maldad por mi parte (o un mucho, cada cual que lo interprete como guste), me ha parecido curioso que la cámara, cuando el profesor iniciaba el ejemplo, nos mostraba (como en otros momentos de la película) lo que ve en realidad Saliya (para que nos demos cuenta del progresivo deterioro de su visión), que es la siguiente imagen:
Obviamente lo curioso no es que el protagonista vea eso, sino que me ha dado por pensar que, a lo mejor, se trata de una metáfora sobre lo que los alumnos en general aprecian de las clases de matemáticas, a tenor de lo que escriben en los exámenes con relativa frecuencia. En el caso de Saliya, con una admirable fuerza de voluntad, trata de suplir sus carencias aprendiéndose de memoria los temas. Su hermana diariamente le lee en voz alta los apuntes, y él los repite en voz alta, frase por frase:
Sheela: Otro número como factor…
Saliya: Otro número como factor…
Sheela: … en el denominador …
Saliya: … en el denominador …
En ese momento su madre irrumpe en la habitación con una bandeja con la merienda, instándolos a que descansen un rato
Saliya: Descansaré cuando acabe los exámenes.
Sheela: Dos fracciones …
Saliya: Dos fracciones …
Sin embargo, la escena que más me ha gustado (todo lo anteriormente descrito se ha puesto en escena de manera más o menos similar en otras muchas películas), es la siguiente: El profesor está de nuevo impartiendo clase (ahora la cámara no está colocada desde los pupitres, como la previa, sino desde la pizarra (que no vemos), pero sí observamos los gestos de desagrado del docente cada vez porque cada vez que dice una frase Saliya la repite, en voz baja, pero él lo escucha, y parece molestarle (desde esa posición el espectador ve esas muecas de fastidio, pero no los alumnos ya que está de espaldas a ellos):
Profesor: La suma del arcoseno …
Saliya (susurrando): La suma del arcoseno …
Profesor: … y del arcocoseno ….
Saliya (susurrando): … y del arcocoseno ….
Profesor: … es constante e igual a …
Saliya (susurrando): … es constante e igual a …
Profesor (se da la vuelta y se dirige a Saliya): No se ofenda, Saliya, pero, ¿de verdad funciona eso? ¿El repetir susurrando?
Saliya: La derivada del arco seno de x es 1 dividido por la raíz cuadrada de 1 menos x al cuadrado. Es decir, la suma del arco seno y el arco coseno de x es constante e igual a la mitad de π. Esto es 1.570796327.
Profesor (sorprendido): Bien, continuemos pues.
El resultado que se nos ha contado es la justificación de la igualdad
No he accedido en esta ocasión a la versión original de la película (en alemán) e ignoro si es tal cual se ha traducido, pero, aunque la justificación del protagonista se entiende perfectamente, no está explicada completamente. Saliya habla de la derivada de la función arco seno, y de ahí pasa a indicar que la suma de las funciones arco seno y arco coseno es constante. Esto es así en virtud del resultado que indica que cuando la derivada de una función en nula, entonces la función original es constante. Tampoco dice cómo se calcula dicha constante. Por muy obvio que sea, seguramente algún espectador no sepa por qué. Y aquí aparece la eterna cuestión que algunos de los lectores estarán pensando: ¿Y para qué necesitamos saber eso? Evidentemente no impide continuar viendo la película, no afecta al argumento (ojalá lo hiciera). Este es uno de los asuntos por los que parece que no tiene importancia que algo de carácter científico aparezca como sea en el argumento de una película o en una novela, y no es así. Las matemáticas se utilizan en este tipo de escenas sencillamente porque es la asignatura que más “recuerdos” (no especifico de qué clase conscientemente) traen a todo el mundo a la cabeza, y porque se asocia a complejidad, dificultad, etc. (en el caso de esta película en concreto, un chaval que a pesar de la ceguera es capaz de llevar esta asignatura con buenas calificaciones). Por no hacer referencia al grito en el cielo que pondrían muchos críticos cinematográficos si se deslizara un error geográfico, histórico, literario, etc. Pues miren, honestamente, deberían ser del mismo calibre unos y otros, y no disculpar o hacer la vista gorda ante ninguno de ellos (claro que primero deberían tener ellos ciertos conocimientos, como los demás los tenemos de lo que para estas personas es “cultura”).
Por esas casualidades de la vida, también cayó en mis manos en esos días la tercera temporada de aquella recordada serie española, Curro Jiménez, a mayor gloria de Sancho Gracia (Curro Jiménez), José Sancho (El Estudiante), Álvaro de Luna (El Algarrobo) y Eduardo García (El Gitano). En el último episodio titulado El caballo blanco, dirigido por Mario Camus, el protagonista decide disolver la banda a pesar de los ruegos de sus compañeros, que finalmente comprenden que se ha cerrado un ciclo en sus vidas.
En un momento dado hay una escena en la que aparece una escuela de un pueblo andaluz, y cómo no, la maestra (María José Diez) expone un problema aritmético sencillo (son niños de primaria) (ver imagen): "Supongamos que este es el número de aceitunas que hay en cada árbol, y éste (señala al multiplicando) el número de olivos. Si multiplicamos el número de aceitunas por el número de olivos, ¿qué obtenemos?”
Algunos niños responden olivos, otros aceitunas, en fin que se pone en escena una de las abundantes caricaturas de las clases escolares elementales. Posteriormente, la maestra hace la multiplicación preguntando cada producto parcial, las que se llevan en cada paso, etc., hasta que nuestros héroes la interrumpen. Y al final, la multiplicación queda correcta y perfectamente realizada. Hablamos de una producción de 1979, pero la puesta en escena, salvando el tema, es exactamente igual que la de la primera película de 2017. Quizá sea para pensárselo, no el que el cine las muestre idénticas en la forma, sino el que seguramente sea porque nuestra metodología no ha cambiado demasiado en todos esos años.
Y casualmente, esa misma semana, vi en un Cine Club al que pertenezco, una producción no estrenada en nuestro país, Casa Grande, película brasileña de 2014 dirigida por Fellipe Barbosa sobre la decadencia de una familia acomodada y elitista del país en la que uno de sus hijos, que estudia el último curso del Bachillerato en uno de los mejores institutos de Rio de Janeiro y cuyos padres tratan de encauzar para que entre en una universidad puntera (por cierto, el padre es ingeniero, habla bastante de matemáticas, aunque no ha sabido aplicarlas demasiado bien a su vida porque está sin trabajo y arruinado por invertir su dinero en acciones de empresas que han ido quebrando). Bien, pues en una de las clases del chaval, el profesor explica cuando los sistemas de ecuaciones lineales tienen solución (teorema de Rouché), aunque acaba entrando en cólera porque sus alumnos no lo hacen demasiado caso y no paran de armar jaleo en clase. Misma escenificación que las anteriores (salvo que en la película alemana todos estaban bastante callados) respecto a la forma de impartir clase, a pesar de ser países muy diferentes. Desgraciadamente, no he encontrado imagen de esta última en el que aparezca la pizarra y los sistemas.
Concurso del verano
Como desde hace algunos años (dieciséis concretamente), la reseña de junio consistirá en la propuesta de un concurso para entretener el verano en la que hay que resolver algunas cuestioncillas matemáticas y responder algunas preguntas de tipo cultural relacionadas con una película-enigma (o varias) que hay que tratar de descubrir. Entre que nos encontramos a final de curso y que idearlo todo lleva su tiempo, dicha reseña no aparecerá hasta finales de mes en esta ocasión. Pero seguro que la espera, merecerá la pena…
Alfonso Jesús Población Sáez
|
|
Publicaciones de divulgación/Matemáticas en los medios de comunicación
Autor:ABC
ABC, 9 de Mayo de 2019 CIENCIA Rosalía Sánchez
|
|
Publicaciones de divulgación/Matemáticas en los medios de comunicación
Autor:EL DIARIO VASCO
El Diario Vasco, 6 de Mayo de 2019 SOCIEDAD
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Macroarmonía y centralidad
Esta es la última entrega de la serie Geometría y Música, serie que ha consistido en una revisión exhaustiva del libro A Geometry of Music [Tym18], redactado por el compositor y teórico de la música Dimitri Tymoczko. Este autor se ha caracterizado por ser un ferviente partidario de los métodos geométricos del análisis musical. En varios textos suyos aboga por este tipo de métodos y argumenta que son más potentes a la hora de analizar música tonal, atonal y jazz. En la primera entrega [Góm18d] estudiamos las cinco características principales de la música tonal según Tymoczko (el movimiento melódico por grados conjuntos, la consonancia acústica, la consistencia armónica, la macroarmonía limitada y la centralidad). En el segundo artículo [Góm18b] describimos a fondo los modelos matemáticos que usa Tymoczko para el análisis musical. En la tercera entrega [Góm18c] se estudiaron los modelos geométricos de progresiones de acordes y conducciones de voces para acordes de dos y tres voces. En la cuarta entrega [Góm18a] se trataron la construcción de escalas, las operaciones sobre escalas y la relación entre escala y modulación y conducción de voces.
En el capítulo cinco de Geometría y Música, el autor analiza el concepto de macroarmonía. Lo define como el efecto musical que tiene una sucesión de acordes en su conjunto. No cabe duda de que el efecto que tiene un acorde depende de los acordes que se hayan tocado en los compases anteriores. Tymoczko plantea cuatro cuestiones acerca de la macroarmonía:
La música en cuestión ¿articula una macroarmonía clara aparte del total cromático?
¿Cuán rápido se producen los cambios de armonía?
¿Son las macroarmonías de la pieza similares estructuralmente hablando? Otra manera de plantear esta cuestión es si las macroarmonías se pueden relacionar a través de las operaciones estudiadas en las series anteriores.
¿Son las macroarmonías consonantes o disonantes?
2. Cambios de clases de alturas
Una cuestión que interesa a Tymoczko es cómo cuantificar la macroarmonía. Para ello, investiga el cambio de clases de alturas en piezas de varias tradiciones musicales. Toma un número fijo de notas, al que llama ventana, y se cuentan los cambios de clases de alturas dentro de dicha ventana. El tamaño de la ventana va desde una nota hasta la pieza entera. Así, por ejemplo, en la invención a dos voces en fa mayor de Bach de la figura siguiente, vemos las ventanas de tamaño 3 y 4 para el tema principal. Para tamaño 3, la media es 2,4 y para tamaño 4 es 2,9.
Figura 1: Cambios de clases de altura en función del número de notas (figura tomada de [Tym11])
En la figura siguiente se tienen el número medio de clases en función del tamaño de la ventana así como su histograma. Este gráfico nos da una idea aproximada de cuán rápido cambian las armonías a lo largo de la pieza.
Figura 2: Histograma del cambio de clases de alturas (figura tomada de [Tym11])
La siguiente figura muestra una serie de piezas que recorren varios periodos de la música, desde el Renacimiento con la música de Palestrina (la misa del Papa Marcelo) hasta el opus 27 de Webern, pasando por obras de Mozart, Beethoven, Brahms y Wagner. Las curvas de Palestrina y Webern tienen un cierto parecido; ambas indican que los compositores usaron exhaustivamente ciertas colecciones de notas en un periodo de tiempo relativamente corto. Sin embargo, en el caso de Palestrina se trata de las notas de la escala diatónica y en el caso de Webern las notas de la escala cromática. El hecho de que la curva de Webern se acerque al valor de 12 tan pronto y tan pronunciadamente nos habla del carácter dodecafónico del opus 27. Webern recorre cíclicamente todas las armonías que son posibles dentro de la escala cromática. Viendo estos gráficos se concluye que las piezas son estáticas desde un punto de vista de la macroarmonía.
Figura 3: Comparación entre los cambios de clases de alturas de varios compositores (figura tomada de [Tym11])
La figura 3 confirma empíricamente un hecho bien conocido en la historia de la música y es que el cromatismo gradualmente fue aumentando con el tiempo. Empezó con tímidas exploraciones en la época del Barroco, fue a más durante el Clasicismo, aumentó fuertemente en el Romanticismo y desembocó en el atonalismo a principios del siglo XX.
Los histogramas se puede usar también para estudiar obras de un mismo autor y ver cómo se comportan los cambios en las clases de alturas. En la figura 4 se ve las curvas de cambio de clases de alturas para nueve estudios de Chopin. El opus 10, número 2, es un estudio con un gran cromatismo, que tras 40 compases ya ha visitado prácticamente el universo cromático. En cambio, el estudio opus 10, número 4, es menos cromático y no pasa de ocho clases de alturas.
Figura 4: Cambios en las clases de alturas en los estudios de Chopin (figura tomada de [Tym11])
Un análisis similar podemos ver en la figura siguiente, esta vez referido a las clases de alturas en el primer libro de preludios de Debussy. Se puede ver que en el caso de esta obra la tendencia hacia al cromatismo ocurre más lentamente que en el caso de Chopin. Se observa que las curvas se acercan al valor 12 (cromatismo total) para valores mayores de la ventana y también que hay varias obras que no alcanzan ese valor, sino otros inferiores.
Figura 5: Cambios en las clases de alturas en el primer libro de preludios de Debussy (figura tomada de [Tym11])
Por último, tomemos un compositor menos tonal como puede ser Igor Stravinsky. Abajo tenemos las curvas de cambios de clases de alturas para La consagración de la primavera. Se ha analizado cada sección. Vemos que el Cortejo del sabio es mucho más cromática que las Rondas primaverales. También observamos que los cambios de altura se producen pronto.
Figura 6: Cambios en las clases de alturas en La consagración de la primavera de Stravinsky (figura tomada de [Tym11])
Sin embargo, estos histogramas no reflejan un hecho importante. Informan de cuán rápido cambian las clases de alturas, pero no informan de las macroarmonías en sí mismas. Estos histogramas no pueden distinguir entre piezas en que se modula rápidamente y piezas no diatónicas, por poner un ejemplo. Hace falta otro tipo de instrumentos de análisis. Dicho instrumento es el perfil macroarmónico global. Dada una pieza se pueden tabular todos los acordes de tres notas, de cuatro notas, y así sucesivamente. Para ilustrar el uso de estos perfiles, consideremos dos piezas de dos autores bastante distintos, Schoenberg y Coltrane. Las piezas a comparar son el opus 11, número 1, del primero y el solo de Giant steps, del segundo. En la figura 7 vemos los perfiles para acordes de seis y siete notas. El eje x del perfil corresponde a la codificación de los acordes de Forte; véase [For77] para una descripción general de los mismos. En realidad, lo que importa es la forma de las curvas en los perfiles. Se puede ver que en ambos perfiles, la música de Schoenberg muestra una distribución más regular de los acordes que la música de Coltrane. Schoenberg no enfatiza ningún acorde en particular, mientras que Coltrane sí lo hace. Desde este punto de vista se puede decir que la pieza de Coltrane es más consistente macroarmónicamente que la pieza de Schoenberg.
Figura 7: Cambios en las clases de alturas en La consagración de la primavera de Stravinsky (figura tomada de [Tym11])
3. Centralidad
En su libro, Tymoczko reconoce que el concepto de centralidad es elusivo. En muchos pasajes musicales se percibe una nota o una serie de notas como más estables, importantes o destacadas que otras. Es lo que llamamos el centro tonal. Esta definición, aunque popular, no es todo lo operativa que sería deseable. En parte se debe a que el concepto de centralidad comprende dos fenómenos relacionados entre sí: las notas fundamentales y la tonicidad. La nota fundamental de un acorde se suele asignar a la nota más grave del mismo cuando el acorde se dispone como una sucesión de terceras ascendentes. No en todos los contextos es así. Por ejemplo, en el siguiente pasaje vemos una serie de repeticiones de dos acordes superpuestos, do-mi-sol y fa♯-re-mi♭. En este contexto es difícil argumentar que la nota fundamental es fa♯ solo porque es la más grave. La dinámica del pasaje nos hace percibirlo como una transición desde el acorde fa♯-re-mi♭ hasta el acorde do-mi-sol. Esta situación aparece con frecuencia en la música del siglo XX.
Figura 8: El problema de la determinación de la fundamental de un acorde (figura tomada de [Tym11])
En análisis musical ha empezado a usarse los perfiles de clases de alturas para representar las diferencias en importancia entre las notas de un acorde. El esquema para construir los es asignar el valor 0 a las notas fuera de la macroarmonía, 1 a las notas dentro de la macroarmonía que son centrales y 2 a las notas que sí son centrales. Por centrales aquí se quiere decir que presenta algún tipo de prominencia musical (discutiremos esto más adelante) . Por ejemplo, el perfil asociado a la música en la figura 8 sería una interpolación entre los dos perfiles siguientes:
Figura 9: Perfiles de clases de alturas (figura tomada de [Tym11])
En la figura 10 se puede ver el perfil de clases de alturas para la frase inicial de la sinfonía Júpiter de Mozart. Esta distribución de alturas recuerda claramente a la de la escala de do mayor. Este tipo de histogramas reflejan, sin embargo, solo una parte del fenómeno. Es posible crear sensación de centralidad no solo en base a la repetición de notas, sino a través de otros mecanismos.
Figura 10: Perfil de clases de alturas para la frase inicial de la sinfonía Júpiter de Mozart (figura tomada de [Tym11])
Tymockzko sostiene en su libro que hay dos tipos de explicaciones para la centralidad, las explicaciones externas y las internas. Las explicaciones externas identifican los mecanismos por los cuales los compositores hacen que ciertas notas sean más importantes que otras. Por ejemplo, esos mecanismos pueden ser tener notas que aparecen con más frecuencia, acentos rítmicos, dinámicos o poniendo énfasis en la textura. Las explicaciones internas, en cambio, se centran en el fenómeno y basta un análisis de la música para determinar qué notas son más importantes que otras. En las explicaciones internas se suele asumir dos principios: (1) una nota es más prominente que otra si es la más grave y forma un intervalo consonante; (2) una nota es más prominente que otra si no forma una disonancia fuerte con ninguna otra nota en la macroarmonía (como una segunda menor o un tritono).
Bibliografía
[For77] Allen Forte. The Structure of Atonal Music. The Yale University Press, Madison, WI, 1977.
[Góm18a] Paco Gómez. La geometría de la música (iv), consultado en abril de 2018.
[Góm18b] Paco Gómez. La geometría de la música (ii), consultado en diciembre de 2018.
[Góm18c] Paco Gómez. La geometría de la música (iii), consultado en enero de 2018.
[Góm18d] Paco Gómez. La geometría de la música (i), consultado en octubre de 2018.
[Tym11] Dimitri Tymoczko. A geometry of music: harmony and counterpoint in the extended common practice. Oxford University Press, 2011.
[Tym18] Dmitri Tymoczko. Página web de Dmitri Tymoczko, consultado en diciembre de 2018.
|
|
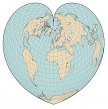
Noticias/Noticias en DivulgaMAT
Autor:Nerea Diez
El ser humano ha sentido siempre la necesidad de representar tanto el territorio que habitaba, como los que iba descubriendo. Estas representaciones planas reflejaban el mundo que conocía y la imagen que tenía del mismo. Los mapas son objetos cotidianos que están presentes en nuestro día a día. El objetivo del cuaderno, escrito con motivo del Día Escolar de las Matemáticas 2019, es intentar conocer un poco más esos objetos cotidianos que son los mapas, y en especial, la geometría que se esconde detrás de los mismos.
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |