631. ¡Pum! ¡Pum! ¡Pum!… PI

En el trabajo [1] se calcula una aproximación del número pi… a ‘tiro limpio’. En efecto, se calcula una aproximación por el método de Monte Carlo del número pi, usando un muestreo –por importancia– con los disparos producidos por una escopeta Mossberg 500. El principio es sencillo: se toma un cuadrado de lado 1 m, que contiene un arco de circunferencia dibujado entre dos esquinas opuestas para formar un cuarto de círculo. El área del cuadrado es 1 m2, mientras que el área del cuarto de círculo es π/4. A continuación, se dispara la escopeta, de manera que se agujerea el cuadrado con una ‘distribución aleatoria’ de impactos. Si se cuenta el número de agujeros en el interior del cuarto de círculo y el número total que cubre el cuadrado, la relación de estos dos números es una estimación de la relación entre el área del cuarto de círculo y del cuadrado, es decir, π/4. https://medium.com/the-physics-arxiv-blog/c1eb776193ef Al realizar el experimento –como se explica en [1] y [2], tuvieron que tener en cuenta otros aspectos como la altura de la escopeta, etc.– los investigadores obtuvieron una aproximación de pi de… 3,131. ¡No está del todo mal! Más información: Vincent Dumoulin and Félix Thouin, A Ballistic Monte Carlo Approximation of π, arXiv:1404.1499v2, 2014 How Mathematicians Used A Pump-Action Shotgun to Estimate Pi, The Physics arXiv Blog, 2014 Visto en Improbable Research Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Miércoles, 10 de Abril de 2019 | Imprimir | PDF |  Correo electrónico

632. Germinal Pierre Dandelin y sus esferas

El matemático Germinal Pierre Dandelin (1794–1847) nació un 12 de abril. Levan su nombre las esferas de Dandelin, las esferas interiores a un cono que son simultáneamente tangentes a un plano –que corta de manera no degenerada al cono– y al cono. El teorema de Dandelin (1822) prueba que si se corta un cono por un plano, los focos de la cónica obtenida son los puntos donde este plano toca a las esferas de Dandelin. Este trabajo lo realizó en colaboración con Lambert Adolphe Jacques Quetelet. Teorema de Dandelin: Las esferas focales G1 y G2 tocan al plano π que se interseca con el cono en F1 y F2 respectivamente, cayendo siempre estos puntos en la zona (azul claro) interior al cono. En 1826, generalizó su teorema para un hiperboloide de revolución, en lugar de un cono. En colaboración con Eduard Heinrich Gräffe, desarrolló un método numérico de solución de ecuaciones algebraicas llamado de Dandelin-Gräffe. También publicó estudios sobre la proyección estereográfica, álgebra y teoría de la probabilidad. Más información (fundamentalmente, sus publicaciones): Germinal Pierre Dandelin, Géométrie descriptive solution à ces deux questions, Correspondance sur l’École Royale Polytechnique à l’usage des élèves de cette école 3, 203-205, 1816 Germinal Pierre Dandelin, Mémoire sur quelques propriétés remarquables de la focale parabolique, Nouveaux mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles 2, 171-202, 1822 Adolphe Quetelet, Sur l’emploi des projections stéréographiques en géométrie, Correspondance mathématique et physique 1 (1), 256-264, 1825 Adolphe Quetelet,  Suite et fin du mémoire sur l’emploi des projections stéréographiques en géométrie, Correspondance mathématique et physique, 1 (1), 316-322, 1825 Germinal Pierre Dandelin, Recherches sur la résolution des équations numériques, Nouveaux mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles 3, 7-71, 1826 Germinal Pierre Dandelin, Mémoire sur l’hyperboloide de révolution, et sur les hexagones de Pascal et de M. Brianchon, Nouveaux mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles 3, 3-86, 1826 Germinal Pierre Dandelin y C.F. de Nieuport, Sur une question relative au calcul des probabilités, Nouveaux mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles 3, 141-159, 1826 Germinal Pierre Dandelin, De la sphère tangente à quatre sphères, Correspondance mathématique et physique 2, 13, 1826 Germinal Pierre Dandelin, Problème du plus court crépuscule, Correspondance mathématique et physique 2, 97, 1826 Germinal Pierre Dandelin, Sur les intersections de la sphère et d’un cône du second degré, Nouveaux mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles 4, 1-11, 1827 Germinal Pierre Dandelin, Mémoire sur l’emploi des projections stéréographiques en géometrie, Nouveaux mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles 4, 11-48, 1827 Germinal Pierre Dandelin, Propriétés projectives des courbes du second degré, Correspondance mathématique et physique 3, 9, 1827 Germinal Pierre Dandelin, Sur quelques applications de la théorie des polaires, Correspondance mathématique et physique 3, 277, 1827 Germinal Pierre Dandelin, Note sur les vaisseaux insubmersibles nouvellement construits en Angleterre, Correspondance mathématique et physique 3, 311, 1827 Germinal Pierre Dandelin, Leçons sur la mécanique et les machines, 1827 Germinal Pierre Dandelin, Sur une difficulté mécanique relative au professions exercées sur un plan, Correspondance mathématique et physique 4, 241, 1828 Germinal Pierre Dandelin, Sur la détermination géométrique des orbites cométaires, Nouveaux mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles13, 1-41, 1839 Germinal Pierre Dandelin, Mémoire sur quelques points de métaphysique géométrique, Nouveaux mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles 17, 1-44, 1844 Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Viernes, 12 de Abril de 2019 | Imprimir | PDF |  Correo electrónico

633. Dorothy Lewis Bernstein (1914-1988)

La matemática Dorothy Lewis Bernstein (1914-1988) nació un 11 de abril. Es conocida por su trabajo en matemática aplicada, estadística y programación, y por su investigación sobre la trasformada de Laplace. Su tesis The Double Laplace Integral fue publicada en Duke Mathematical Journal en 1939. Fue la primera mujer en ser elegida presidente de la Mathematics Association of America. Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 11 de Abril de 2019 | Imprimir | PDF |  Correo electrónico

634. Solucionan el diabólico acertijo matemático que no ha podido ser resuelto en 64 años

ABC, 8 de Abril de 2019 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 08 de Abril de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

635. 170. (Abril 2019) Las tarjetas perforadas

Recordemos que el mes pasado (rincón matemágico 169) presentamos una secuencia de juegos descrita por Javier Serrano donde los protagonistas eran varias cartas que tenían unas ranuras y perforaciones en diversos lugares. Queremos en esta ocasión entender el funcionamiento de estos juegos pero también rastrear su origen y posterior evolución. Parece evidente que la dualidad ranura/agujero pone de manifiesto la clásica representación binaria sí/no, 1/0, ON/OFF, y las distintas posiciones en las que están hechas las ranuras y los agujeros reflejan a su vez la característica posicional del sistema binario. De este modo, cada carta se caracteriza por su valor en este sistema binario, escrito en esta ocasión como combinación de agujeros (para representar la cifra 0) y ranuras (que representan la cifra 1). Si repasamos las imágenes de las cartas, podemos darnos cuenta cómo las incisiones determinan su valor, en código binario, salvo el ocho que identificamos con el cero porque, en caso contrario, tendría cuatro cifras. Entendemos entonces que, al atravesar la posición de las unidades con el clavo, solo se desprenden las cartas que tienen un uno en dicha posición: las impares; al atravesar la posición que representa las decenas, las cartas que se desprenden son el 2, 3, 6 y 7; por último, al atravesar con el clavo la posición de las centenas, las únicas cartas que se desprenden son el 5, 6, 7 y 8. Al hacer las separaciones en este orden -derecha, centro, izquierda- colocando cada vez las cartas separadas detrás de las que han quedado atrapadas (con las caras a la vista), el resultado final es que las cartas se han ordenado, empezando por el 8 que representa el cero. Puedes seguir el proceso paso a paso: la primera vez han quedado encima los números pares, en cualquier orden; la segunda vez quedará una secuencia de dos pares (el cuatro y el ocho), dos impares (el uno y el cinco), dos pares y dos impares; la tercera vez ya estarán todas alternadas, par (el ocho), impar (el uno), par (el dos), etc. ¿Recuerdas algún juego similar donde la posición de los unos y ceros en la representación binaria de los números permite hacer adivinaciones? Cierto, el de las tarjetas binarias que citamos allá por el año 2005 (rincón matemágico 13) y sus numerosas secuelas (rincón matemágico 49, rincón matemágico 51, rincón matemágico 104, rincón matemágico 163). La novedad de esta versión es que los números se sustituyen por las correspondientes incisiones en las tarjetas, como se hacía en los albores de la informática. Fue Martin Gardner, por lo que sabemos, el primero en presentar esta variante de las tarjetas binarias. El primer capítulo del libro "Nuevos pasatiempos matemáticos", traducción de "New mathematical diversions" (publicado por primera vez en 1966), reproduce el artículo titulado "Some recreations involving the binary number system", aparecido en el número 203 (diciembre de 1960) de la revista Scientific American. En este artículo se muestra un conjunto de 32 cartulinas (claro, una potencia de dos) que presentan ranuras y perforaciones según el esquema que hemos indicado antes (la ranura corresponde a la cifra "1" y el agujero corresponde a la cifra "0"), de modo que están representados todos los números del cero al 31 en su notación binaria. Después de mezclar todas las cartulinas, se cuadran para que queden las perforaciones alineadas, se pasa un clavo o una varilla por el hueco de la derecha dejando que caigan las tarjetas que no tienen agujero; se colocan estas tarjetas en la mesa, letras hacia abajo, y sobre ellas se colocan las que habían quedado sujetas. Se repite esta operación con el resto de perforaciones, de derecha a izquierda, siempre colocando las tarjetas que queden sujetas sobre las que queden sueltas. Al final del proceso, las letras escritas en las tarjetas se habrán ordenado para formar un mensaje, en inglés, que seguro compartes. En realidad, el proceso anterior solo ordena los valores numéricos asignados a las cartulinas, de modo que es fácil preparar un conjunto de cartulinas con cualquier mensaje y hacer algún juego de predicción. Es también interesante el uso que Martin Gardner hace de estas tarjetas como "simulador" de tablas de verdad en lógica. Basándose en el ábaco lógico o piano lógico (como el ilustrado en la figura adjunta) ideado por el economista británico William S. Jevons, se puede establecer si un razonamiento lógico es verdadero o falso. Veamos a grandes rasgos el funcionamiento del sistema: todo razonamiento consta de un conjunto de premisas, que se suponen ciertas, y una conclusión, que debe ser consecuencia de las premisas. Si cada premisa involucra no más de cinco proposiciones simples, se puede representar por un conjunto de nuestras tarjetas perforadas. Insertando adecuadamente la varilla por las tarjetas, se van eliminando aquellas que hacen que las premisas sean falsas quedando al final un pequeño grupo de tarjetas. Si alguna de ellas contiene la negación de la conclusión de nuestro razonamiento, deduciremos que dicho razonamiento es falso. La figura con el modelo de tarjetas de Gardner ya contempla esta opción porque, además de las letras con las que se ha formado el mensaje, se señalan las cinco proposiciones A, B, C, D y E, así como sus negaciones A, B, C, D y E. Por ejemplo, la tarjeta con tres ranuras y dos agujeros, que corresponde al número binario 11100, indica que las proposiciones A, B y C son ciertas, mientras que las proposiciones D y E son falsas. Si has estudiado lógica proposicional en algún momento (si no, seguro que puedes encontrar en la red bastante material para empezar), puedes jugar con las tarjetas realizando las comprobaciones de los razonamientos básicos: ¿te suenan las frases PONENDO PONENS, TOLLENDO TOLLENS, ...? No profundizaremos sobre el tema en este rincón pero el artículo citado de Martin Gardner contiene algunos ejemplos para practicar. Comentarios finales: El juego de las tarjetas perforadas también está explicado por el mago y matemático Carlos Vinuesa en su artículo "Matemagia básica", publicado en La Gaceta de la RSME (2011). En este artículo aprenderás también otros juegos basados en la aritmética binaria. Mucho más sencilla y recomendable es la versión de tarjetas lógicas que el mismo Martin Gardner presenta en el artículo titulado "Logic Machines" para la revista Scientific American, publicado en marzo de 1952 (unos años antes de empezar su colaboración regular para la sección Mathematical Games) y posteriormente incluido en el libro "Logic Machines and Diagrams", publicado en 1958. Este juego ha sido desarrollado recientemente por el equipo de Divermates, bajo el título "Tarjetas lógicas". Junto con la explicación de su funcionamiento, puedes descargar y fabricarte tus propias tarjetas. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Martes, 02 de Abril de 2019 | Imprimir | PDF |  Correo electrónico

636. El hombre que ha propuesto más de 300 problemas de matemáticas

ABC, 1 de Abril de 2019 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 01 de Abril de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

637. 53. (Abril 2019) La Geometría, acceso para la humanidad

(Lorenzo Lotto. Alegoría de la virtud y del vicio. 1505. Washington. Galería Nacional de Arte) Huellas del hombre en la Playa de Rodas El filósofo Aristipo, discípulo de Sócrates, víctima de un naufragio, fue arrojado a las costas de la isla de Rodas y al advertir unas figuras geométricas dibujadas en la arena, cuentan que gritó a sus compañeros: « Alegrémonos, pues observo huellas humanas» (Vitruvio, De architectura, Libro VI) La Geometría como portal civilizador El célebre naufragio de Aristipo se enmarca en la tradición platónico-pitagórica del frontispicio de la Academia: no entre quien no sepa geometría. En el medioevo se mantiene esa situación de privilegio de la matemática: puerta y llave del conocimiento diría Roger Bacon. La renovación renacentista de la cultura se realiza en muchas dimensiones y en una de ellas se rescata el pensamiento matemático como paradigma de civilización contra barbarie, de humanidad frente a bestialidad, y de virtud frente a vicio. Las representaciones iconográficas son deliciosas. Observemos la evolución desde el primer Renacimiento con Lorenzo Lotto, pasando por los manieristas Federico Zuccari y Bartholomäus Spranger, para terminar en el siglo XIX con un panel de azulejos valencianos. Alegoría de la virtud y del vicio La geometría como modelo de civilización y humanidad frente al vicio tiene una de sus primeras y más logradas manifestaciones en la Alegoría de la virtud y del vicio (1505) de Lorenzo Lotto. La pintura al óleo sobre madera se encuentra en el Museo Nacional de Arte en Washington y proviene de la donación del filántropo Samuel Kress. La madera pintada servía para proteger el retrato del obispo de Treviso que por entonces era el mecenas de Lotto. (Lorenzo Lotto. Alegoría de la virtud y del vicio. 1505. Detalle) Lo que fue una simple tapadera se ha convertido con el tiempo en la obra principal. Un paisaje tormentoso, un barco naufragando y dos figuras contrapuestas: un sátiro con pezuñas que encarna la bestialidad y un niño que hace geometría nos muestra a la naciente humanidad, virtud frente a vicio. La virtud es diligente. El vicio va unido a la ebriedad y el abandono. Los instrumentos que se representan son un compás en la mano, otro en el suelo, una escuadra y un cuadrante. Los libros y una flauta de Pan completan el cuadro de la virtud. Porta Virtutis La puerta sapiencial en taracea del Palacio Ducal de Urbino va acompañada por otra puerta alegórica: Porta Virtutis (1581), pintura cargada de mensajes de Federico Zuccari. La Galleria Nazionale delle Marche muestra con esta pintura manierista las inquietudes del final del Renacimiento: arte, virtud y ciencia matemática. (Federico Zuccari . Porta Virtutis. 1581 Palacio Ducal de Urbino) Vemos a Minerva guardando la entrada al mundo de la virtud que está separado del mundo de los vicios representado por seres más bestiales que humanos. Un gran arco votivo divide los dos mundos. Dentro hay inventiva, inteligencia, diseño, decoro, colorido… mientras que fuera proliferan la envidia, los vicios y la brutalidad. Abajo a nuestra izquierda, un ser se está preparando para librarse de la bestialidad con una escuadra y un compás en la mano, una tablilla sujeta por una mujer (¿alegoría de la aritmética?) y unos pinceles en el suelo. Los rasgos van siendo cada vez más humanos. A ambos lados de la entrada y parcialmente ocultas, se vislumbran dos alegorías de la Inteligencia cuyos  atributos son la escuadra, el compás y la esfera armilar: los de la geometría. La escena reproduce visualmente el no entre quien no sepa geometría del portal de la Academia de Atenas. (Federico Zuccari. Porta Virtutis. 1581 Detalles) Minerva victoriosa frente a la ignorancia La alegoría de Zuccari es reconstruida por el sensual artista flamenco Bartholomäus Spranger, uno de los pintores preferidos por la corte imperial de Rodolfo II en Praga. La idea es similar: Minerva triunfa sobre la barbarie con las virtudes de la civilización: la escritura y la geometría. Curiosamente Spranger cambia el orden de los instrumentos: la esfera armilar está a la izquierda y el compás emerge a la derecha. Minerva victoriosa frente a la ignorancia (1591) se encuentra en el Museo de Arte e Historia de Viena: las ricas colecciones de Rodolfo fueron trasladadas desde Praga cuando la corte imperial regresa a Viena. La bestialidad está representada en la figura de largas orejas que queda inmovilizada por la diosa de la guerra y la inteligencia. La geometría resalta aún más como veremos en la segunda versión que hace Spranger del mismo tema. (Bartholomäus Spranger. Minerva victoriosa frente a la ignorancia. 1591. Viena, Kunsthistorisch Museum) La geometría contra la ignorancia en  D´Azay-le-Rideau Uno de los castillos más bellos del Valle del Loira es D´Azay-le-Rideau, que ocupa un islote del río Indre a unos kilómetros al sur de Tours. El château suele ser citado como una de las más logradas realizaciones de la arquitectura renacentista en Francia. La escalera monumental es especialmente destacable. El castillo fue erigido por el tesorero estatal de Francisco I que no llega a ocuparlo al ser acusado de malversación. Situémonos en la Cámara del Rey de la planta principal (llamada así pese a que el rey apenas pasó alguna noche en ella). La decoración se limita a una gran chimenea y unos deliciosos escritorios. Aunque no sea el de más calidad, nos fijamos en uno de madera tallada del lado derecho de la chimenea. El tallador ha reproducido en la puerta superior la alegoría de Minerva victoriosa contra la ignorancia. La pintura original es una segunda versión del manierista flamenco Bartholomäus Spranger y el grabador Egidio Sadeler la reproduce. (Grabado de Egidio Sadeler sobre dibujo de Bartholomäus Spranger. Minerva victoriosa frente a la ignorancia II) Minerva doblega a un sátiro (con largas y bestiales orejas) y en su entorno se encuentran las artes que son atributos de la diosa: a un lado y otro destacan una esfera armilar y una mano con escuadra y compás. Spranger ha vuelto a personalizar el tema de Federico Zuccari en Porta Virtutis: la geometría como puerta de entrada a la virtud y a la civilización. El ebanista del mueble de D´Azay-le-Rideau, además, escribe Geome para que no queden dudas. (Minerva victoriosa frente a la ignorancia II. Castillo de D´Azay-le-Rideau) Geometría contra ignorancia en un panel cerámico valenciano del XIX El Museo Nacional de la Cerámica Gonzalez Martí de Valencia conserva un bonito panel de azulejos de M. Molla realizado a mitad del siglo XIX. La geometría como antídoto contra el error y la ignorancia vuelve a aparecer con los mismos instrumentos. El panel valenciano procederá de un dibujo que cristianiza el tema pagano: Minerva y Mercurio aparecen en el centro pero por encima de ellos están las deidades cristianas. La idea sigue siendo la misma pero con algún elemento singular: La ignorancia, otra vez con largas orejas, trata de convencer a un hombre para que se dispare flechas contra sí mismo. El compás y la esfera está en el suelo como muestra de que el ser está a punto de volver a la barbarie. La figura alegórica femenina de la derecha está desnuda como la verdad y tiene un espejo como la prudencia.  Sería la representación de la virtud. El Museo cataloga el panel como Valencia ante la disyuntiva del error y la verdad. (Panel del error y la verdad. 1850. Museo Nacional de la Cerámica. Valencia)

Lunes, 01 de Abril de 2019 | Imprimir | PDF |  Correo electrónico

638. Marzo 2019: Bingo de Funciones

1. El bingo como recurso matemático. Hace más de medio siglo, un juguete muy habitual en los Reyes Magos, era una lotería infantil, un juego muy entretenido con el que después jugaba toda la familia en las largas tardes predigitales. Cuando pasaron los años, el juego comenzó a denominarse bingo, y se considera que apareció, tal como lo conocemos actualmente, en el siglo XVI en Italia, aunque hay autores que remontan su aparición a la antigua Roma. Aunque sigue siendo un juego educativo habitual en la niñez, en la actualidad, suele relacionarse más con los juegos de azar en los que se apuestan determinadas sumas de dinero para conseguir suculentos premios. Incluso en la actual era digital, es posible perder los dineros jugando en línea sin necesidad de moverse del sillón de casa. Desde nuestro punto de vista, como docentes, el bingo tiene la ventaja de ser un juego atractivo, cuya dinámica es fácil de aprender, en el supuesto de que no se conozca. Estaría, en la clasificación de recursos, considerado un juego de procedimiento conocido, pues su puesta en práctica se supone que es conocida en la vida social exterior a la escuela. Se presupone que se han jugado fuera de la escuela este tipo de juegos, como pueden ser las cartas, los dominós, los rompecabezas, etc… aunque cada vez nos encontramos con más alumnado que no conocen determinados juegos tradicionales. Se pueden utilizar didácticamente de dos maneras diferentes. Por un lado, podemos trabajar directamente con el juego original, por ejemplo, podemos jugar al dominó tradicional y construir figuras geométricas con las fichas cumpliendo una determinada propiedad, como construir cuadrados con fichas de forma que los lados del cuadrado sumen lo mismo. Otra manera de trabajar con ellos es modificando alguno de sus elementos, aunque el método de juego se mantenga. Seguro que casi todos habremos jugado en la infancia con dominós donde los puntos tradicionales han sido sustituidos por dibujos, formas, colores, etc… De este segundo método de trabajo es el que vamos a presentar en este artículo algún ejemplo. El juego del bingo tiene además una ventaja que lo hace atractivo al alumnado: depende directamente del azar, y ya sabemos que el azar es caprichoso, como dice una reciente campaña publicitaria. El azar no distingue entre guapos o feos, ricos o pobres, torpes o inteligentes, ... Por ello, puede ocurrir que un alumno con menos conocimientos que otro pueda superarlo en este juego, lo que favorece la autoestima y  la participación de aquellas personas que suelen estar en clase descolgados. En el artículo de hoy quería presentar un par de juegos para practicar o repasar conceptos de funciones, a utilizar una vez vistos en clase los contenidos básicos de este bloque, y así sirven para afianzarlos y manejarlos de una manera más lúcida. 2. Modificar las preguntas. Una primera manera de jugar al bingo, como recurso didáctico, en el aula de matemáticas es mantener el cartón habitual con números pero cambiar las “bolas” con los números que se extraen del “bombo”. En general, se pueden preparar una serie de tarjetas con preguntas cuyo resultado pertenezcan al rango de números que aparecen en los cartones con números. Para no tener que construir o copiar un gran número de cartones, que en algunos casos plantea problemas como veremos más adelante, yo suelo utilizar un método que es muy cómodo y fácil de realizar. Intento que las preguntas tengan un mínimo de resultados posibles, por ejemplo de 1 a 20 y se les pide a los alumnos que se creen su propio cartón, dibujando un cuadrado de 3x3 o un rectángulo de 4x3 y lo rellenen de números entre los comprendidos en el rango fijado, lógicamente sin repetir, y que los vayan tachando a medida que se van planteando los resultados. Vamos a ver un ejemplo con funciones de primer grado. Se les pide a los alumnos un cuadrado de 3 filas y tres columnas con números comprendidos entre 1 y 16. Se escriben en la pizarra dos funciones: f(x) = 2 · (x - 1) + 3                           g(x) = 10 + 2 · (3 - x) Y las preguntas son el valor de esas funciones para los números desde 0 hasta 7, ambos inclusive. La función f nos da todos los impares y la g todos los pares. El profesor, de forma aleatoria elige una de las funciones y uno de los valores y lo plantea a la clase. El alumno realiza la operación y tacha, en su cartón, el resultado de la operación. El profesor puede tener una serie de tarjetas con las preguntas (por ejemplo: f(5), g(1), ..) y tras barajarlas, va diciendo la propuesta de la tarjeta. Esto tiene la ventaja de que se puede sacar a algún alumno para que sea el encargado de “sacar las bolas del bingo”. También puede decirlas aleatoriamente. En este caso, yo lo que hago es tener una tabla con las posibilidades y los resultados de cada caso, y escoger aleatoriamente señalando cuál es la cuestión que ya ha salido. Sería por ejemplo un recuadro como el siguiente: Pregunta f(0) g(7) f(1) g(6) f(2) g(5) f(3) g(4) Resultado 1 2 3 4 5 6 7 8   Pregunta f(4) g(3) f(5) g(2) f(6) g(1) f(7) g(0) Resultado 9 10 11 12 13 14 15 16 Esta forma de trabajar tiene la ventaja de que es muy fácil hacer una adaptación al alumnado y a los contenidos que queramos repasar. Podemos simplificar o complicar las funciones, introducir alguna más, ampliar el rango de números resultados posibles, etc… Pero además, podemos trabajar con otros bloques temáticos, como operaciones simples o combinadas, expresiones algebraicas, ecuaciones de primer grado, figuras geométricas, cálculo de máximo común divisor y mínimo común múltiplo, etc… El enfoque que le hemos dado tiene la ventaja de ser un juego muy rápido, por lo que es posible tener preparados varios grupos de funciones y repetir el juego dos o tres veces, no llegando a ocupar ni la mitad de la clase. 3. Modificar preguntas y cartones. Otra forma de afrontar la modificación de un bingo es cambiar los cartones con las soluciones. Esto lleva una gran dificultad porque es necesario realizar cartones diferenciados para cada alumno, y según el tema elegido, en este caso funciones, puede ser laborioso realizar un mínimo de 30 cartones para trabajar con una clase completa. El bingo que presento lo construí hace ya tres lustros y no recuerdo bien si las imágenes las hice con Cabri o con un incipiente GeoGebra, pero hoy en día, utilizando este último programa, es fácil dibujarse las funciones que a uno le interese. Los contenidos que pretendía repasar eran las funciones cuyas gráficas eran líneas, parábolas o hipérbolas. En la mayoría de cartones aparecen 4 rectas, tres parábolas y dos hipérbolas. Las tarjetas con las preguntas que plantea el profesor llevan la imagen correspondiente para poder posteriormente comprobar el bingo. 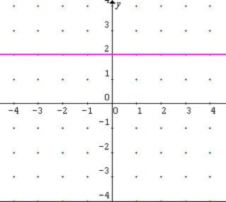Esas tarjetas son las siguientes: Una función constante.   y=2 La función lineal de pendiente 1.   y=x   La bisectriz del primer cuadrante La función lineal de pendiente –½.   y= - ½ x Función afín creciente que pasa por el punto (0,2).   y=2x+2 Función afín de pendiente 3 y ordenada en el origen –2.   y= 3x-2 Función afín que forma con los ejes coordenados un triángulo isósceles.   y= - x+2 y = - 2x +3   Función afín de ordenada en el origen igual a 3. x·y=1   Su dominio son todos los reales menos el 0 y pasa por el punto (1,1). Función siempre creciente que no es lineal ni afín.   x·y=-1 Función de proporcionalidad inversa cuyo eje vertical es x=2. y = x²   Función cuadrática con vértice en (0,0). Función opuesta de y=x²-1   Función cuadrática con valor máximo 1.   y = - x² + 1 Función polinómica de segundo grado cuyo valor mínimo es 2.   y = x² + 2 y = (x-2)²   Función cuadrática cuya gráfica tiene por eje la recta x = 2. y = (x-3)² + 1   Función cuadrática cuyo valor más bajo es 1. Función cuadrática cuyo vértice es el punto (-2,2).   y= - (x+2)²+2 Se puede apreciar que en las tarjetas aparecen a la izquierda una serie de preguntas posibles para reconocer la gráfica de la derecha. El objetivo es que el profesor elija una de esas posibilidades para indicarla en clase. Si se quiere simplificar o ayudar más a aquellos alumnos con dificultades se pueden indicar más de una pregunta. Para completar, reproduzco las 30 tarjetas cuadradas de 3x3 donde aparecen las gráficas de las funciones. Lo ideal es imprimir en color y plastificar, tanto los cartones como las tarjetas. De esa manera resisten mejor el paso del tiempo y podemos utilizarlos sin problemas un curso tras otro. La forma efectiva de jugar es repartir a cada alumno un cartón y nueve fichas, de forma que a medida que descubre una gráfica que corresponde a la función planteada, coloque encima una ficha para capturar esa gráfica. Como en las tarjetas están las imágenes de las distintas funciones se pueden construir cartones alternativos, por ejemplo con menos gráficas, o incluir sólo lineales y cuadráticas.

Jueves, 28 de Marzo de 2019 | Imprimir | PDF |  Correo electrónico

639. ¿Quién resolverá el teorema de Fermat llevado al cubo?

ABC, 25 de Marzo de 2019 CIENCIA - El ABCdario de las matemáticas Pedro Alegría

Lunes, 25 de Marzo de 2019 | Imprimir | PDF |  Correo electrónico | Leer más

640. Los misterios del número Pi aún sin resolver

ABC, 14 de Marzo de 2019 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Jueves, 14 de Marzo de 2019 | Imprimir | PDF |  Correo electrónico | Leer más