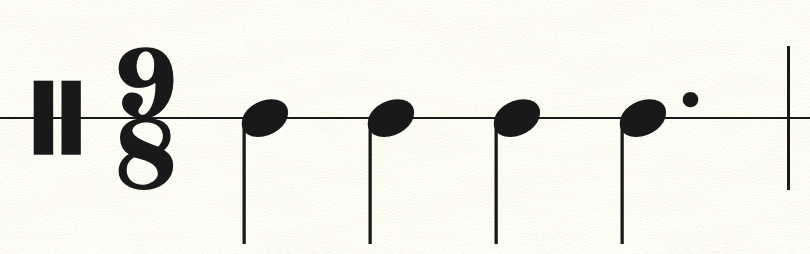71. 125. (Junio 2022) Modelos computacionales de ritmo y métrica (III)

1. Introducción Seguimos con la serie Modelos computacionales de ritmo y métrica y en la columna de este mes vamos a examinar la combinatoria de palabras aplicada a la música, en particular a la teoría del ritmo. En el primer artículo [Góm22a] de esta serie tratamos la definición de ritmo desde un punto de vista conceptual así como la presentación de diversos métodos de notación rítmica. En el segundo artículo [Góm22b] se estudiaron métodos de generación y recuento de ritmos, sobre todo los ritmos aksak. La combinatoria de palabras —combinatorics on words en inglés —es una rama de la matemática discreta que pertenece a su vez al campo de la combinatoria. El campo de la combinatoria de palabras es relativamente nuevo y su objeto de estudio son las palabras y los lenguajes formales, con especial atención a los patrones. La combinatoria de palabras como tal se formaliza modernamente en el libro Combinatorics on words [Lot83], libro escrito por un grupo de matemáticos que tomó el nombre de Lothaire. Sin embargo, hay precedentes tan tempranos como Bernouilli en 1771 con su estudio de las fracciones continuas o los trabajos de Christoffel (1829–1900), de donde toman el nombre las palabras de Christoffel que estudiaremos en la columna de este mes. Para un buen examen histórico de la combinatoria de palabras, véase el artículo de Berstel y Perrin The origins of combinatorics on words [BP07]. La teoría de las palabras de Christoffel empieza a finales del siglo XIX, pero el término no se acuña oficialmente hasta 1990, y es Berstel [Ber90] quien lo hace por primera vez. Desde entonces, las palabras de Christoffel se han estudiado a fondo y hay muchas caracterizaciones y resultados, algunos de los cuales veremos aquí. 2. 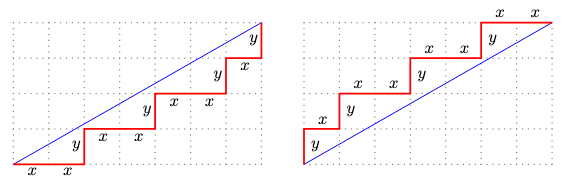Palabras de Christoffel Empezaremos con la definición geométrica de las palabras de Christoffel. Sean a,b dos números naturales tales que su máximo común divisor es 1, esto es, que, salvo el 1, no tienen divisores comunes. Cuando esto ocurre decimos que a y b son primos relativos entre sí o coprimos y es costumbre en el campo de la combinatoria de palabras escribir a ⊥ b. Consideremos a continuación la recta que une (0,0) y (a,b) en el retículo ℤ × ℤ (en lugar de en ℝ2). Llamemos (0,0) → (a,b) al segmento dirigido que une (0,0) y (a,b). El camino inferior de Christoffel, o simplemente el camino inferior, es el camino que se ve en rojo en la parte izquierda de la figura 1. Está definido como sigue: Es una poligonal de lados paralelos a los ejes que empieza en (0,0) y acaba en (a,b). La región interior comprendida entre el segmento (0,0) → (a,b) y la poligonal no contiene ningún punto del retículo ℤ × ℤ. Figura 1: Definición geométrica de las palabras de Christoffel (figura tomada de [BLRS08]) De manera análoga, se define camino superior de Christoffel. En todo lo que sigue, solo consideraremos el camino inferior, por lo que por camino siempre entenderemos el camino inferior de Christoffel. Si ahora asociamos a cada segmento horizontal unidad la letra x y a cada segmento vertical unidad la letra y, obtendremos una sucesión. Esta sucesión es una palabra de Christoffel sobre el alfabeto A = . El conjunto de las palabras formadas con elementos del alfabeto se designa por * y en dicho conjunto está la sucesión vacía, designada por ε. El número de elementos de una sucesión se llama la longitud de la palabra; la longitud de ε es cero y la de una palabra arbitraria la suma del número de símbolos x e y. Si miramos la figura 1 de nuevo, vemos que (a,b) = (7,4) y que la palabra de Christoffel asociada es C(a,b) = xxyxxyxxyxy; donde C(a,b) es el símbolo para dicha palabra. Obsérvese que la pendiente de la recta que pasa por el segmento (0,0) → (a,b) es 4∕7. C(0,1) = y es la palabra de Christoffel de pendiente +∞; C(1,1) = xy; y la palabra vacía ε no es una palabra de Christoffel porque 0 no es relativamente primo consigo mismo. Las palabras de Christoffel tienen la bonita propiedad de que toda palabra de longitud 2 o más es la concatenación de dos únicas palabras de Christoffel; véase [BLRS08] para una prueba de este resultado. Para los lectores amantes de la computación, a continuación presentamos un algoritmo para generar palabras de Christoffel; aparece en el capítulo 6 del libro de Boenn [Boe18]. Figura 2: Algoritmo de generación de palabras de Christoffel (tomado de [Boe18]) 3. Generación de ritmos a partir de palabras de Christoffel 3.1. Conversión de palabras en ritmos La manera de generar ritmos a partir de palabras de Christoffel es bastante directa. Escojamos como alfabeto el conjunto A = , donde haremos que 1 represente una nota y 0 un silencio. Las palabras de Christoffel son ahora sucesiones formadas de por ceros y unos (por bits), que no son otra cosa que representación de ritmos, como vimos en la primera columna de esta serie. Por ejemplo, la palabra C(5,7) es la sucesión xyxyxyyxyxyy, pero cuando se la transforma en un ritmo es [1 0 1 0 1 0 0 1 0 1 0 0] (por claridad de lectura, pondremos los ritmos entre corchetes). Este ritmo no es sino la conocida clave son 6/8 de la tradición musical afrocubana. Un ritmo que proviene de una palabra de Christoffel se llamará ritmo de Christoffel. 3.2. Operaciones sobre ritmos de Christoffel Matemática y musicalmente, vienen a la mente varias operaciones. La primera es el complementario, esto es, intercambiar los ceros por los unos y viceversa. Si C(a,b) es un ritmo de Christoffel, su complementario se designará por ¬C(a,b). Por ejemplo, si C(3,5) = [1 1 0 1 1 0 1 0], entonces el complementario será ¬C(3,5) = [0 0 1 0 0 1 0 1]. Otra operación, menos obvia de concebir, es la operación ν, que lleva un recuento de las repeticiones en dos elementos consecutivos. ν(C(a,b)) se define como sigue: El primer bit del ritmo se queda como está en ν(C(a,b)); Si en C(a,b) el k-ésimo bit es igual al anterior, con k = 2,…,a + b, entonces el k-ésimo bit de ν(C(a,b)) es 0; en otro caso, es 1. Abajo tenemos ejemplos de las operaciones anteriores: C(3,5) = [1 1 0 1 1 0 1 0]; ¬C(3,5) = [0 0 1 0 0 1 0 1]; ν(C(3,5) = [1 0 1 1 0 1 1 1] ¬ν(C(3,5) = [0 1 0 0 1 0 0 0] Otras operaciones son posibles tales como las operaciones lógicas de o lógico ∨ o de y lógico ∧ (siempre que los ritmos tengan la misma longitud). La rotación de ritmos de Christoffel es otra operación muy común. La rotación a la izquierda de k posiciones de un ritmo C(a,b), donde 0 ≤ k ≤ a + b, consiste en leer el ritmo desde la posición k hacia la izquierda volviendo al principio cuando se llega a la última posición del ritmo. La rotación a la izquierda de 3 posiciones de C(3,5) es el ritmo [1 1 0 1 0 1 1 0]. Análogamente, se pueden definir las rotaciones a la derecha. Las rotaciones a la izquierda de k posiciones se designan por ϱk(C(a,b)), donde k puede ser positivo o negativo. Por último, una operación muy natural es la inversión del ritmo, que no consiste en otra cosa que en leer el ritmo de derecha a izquierda empezando por el último bit. Se usa la notación R(C(a,b)) para designar la inversión de C(a,b). La inversión de C(3,5) es R(C(3,5)) = [0 1 0 1 1 0 1 1]. No es muy difícil probar la igualdad: C(b,a) = R(¬C (a,b)) 4. Ritmos de Christoffel en música Los ritmos de Christoffel se encuentran en la música y en la poesía griega. La poesía griega se basaba en un sistema de pies métricos. Un pie es la unidad de medida métrica y está compuesto por combinaciones de sílabas largas y cortas. Esto se traslada a la música combinando notas largas y cortas. Este sistema de pies métricos se ha usado con frecuencia para analizar la música occidental. La siguiente tabla muestra algunos ejemplos. En la primera columna se encuentra el nombre de los pies rítmicos, después su notación moderna, seguido por la notación SNMR y, por último la correspondiente palabra de Christoffel. Ritmo Notación Notación SNMR Palabra de Christoffel Yambo X C(1,2) = 110 Troqueo > ϱ(C(1,2)) = ν(C(1,2)) = 101 Tribaco i C(0,3) = 111 Espondeo II C(2,2) = 1010 Anapesto :I C(1,3) = 1110 Tabla 1: Ritmos de Christoffel en los pies métricos de la poesía griega También encontramos ritmos de Christoffel en las claves de las tradiciones musicales africanas y afro-americanas. Una clave es un ritmo que se toca a lo largo de una pieza y que tienes varias funciones, entre ellas la de estabilizador rítmico, marcar el fraseo o establecer referencia temporal. Para más información sobre las claves, véanse [Lon04] o [DGMM+09] y las referencias allí contenidas. La tabla siguiente muestra varias claves de diversas culturales musicales que son ritmos de Christoffel. Los ritmos están escritos en compás de 4/2. El punto en la segunda fila significa concatenación de ritmos. Ritmo Notación Notación SNMR Palabra de Christoffel Clave son 2-3 - H - - - ϱ4(C(11,5) = 0010100010010010 Clave rumba 3-2 - H - I H ϱ(C(7,3)) ⋅ C(1,1) ⋅ C(3,1) = 1001000100101000 Bossa Nova - - H - - ϱ2(C(11,5) = 1001000100100100 Soukous - -H XI C(7,3) ⋅ ν(C(5,1)) = 1001001000110000 Tabla 2: Ritmos de Christoffel en los pies métricos de la poesía griega En la música turca, los ritmos de Christoffel aparecen con mucha frecuencia. La tabla siguiente muestra unos cuantos de esos ritmos. Figura 3: Ritmos de Christoffel que se encuentran en la música turca (lista tomada de [Boe18]) Para acabar esta columna, vamos a explorar la relación entre los ritmos de Christoffel y los ritmos euclídeos. La siguiente sección es una breve exposición de los ritmos euclídeos y sus propiedades. 5. Ritmos euclídeos En lo que sigue vamos a seguir la exposición del trabajo Si Euclides lo supiese... se sentiría orgulloso [Góm09] del propio autor de estas líneas. Los ritmos euclídeos reciben este nombre porque provienen de la aplicación del algoritmo de Euclides. Este algoritmo lo inventó Euclides para calcular el máximo común divisor de dos números y consiste en hacer divisiones sucesivas para hallar el máximo común divisor de dos números positivos (m.c.d. de aquí en adelante). Si queremos hallar el m.c.d. de dos números a y b, suponiendo que a > b, primero dividimos a entre b, y obtenemos el resto r de la división. Euclides se dio cuenta de que el m.c.d. de a y b era el mismo que el de b y r. Para verlo, observemos que al dividir a entre b, hallamos un cociente c y un resto r de tal manera que se cumple que: a = c⋅b+ r,  0 ≤ r ≤ b- 1 Esta ecuación nos dice que todo divisor común de a y b tiene que serlo también de r. En particular, el m.c.d. de a y b es el m.c.d. de b y r. En efecto, si d es un divisor común de a y b, entonces y, por tanto, r divide a d. Esto implica que m.c.d(a,b) = m.c.d.(b,r). Pero ¿por qué parar aquí? Aplicamos el mismo argumento a b y r y obtenemos una sucesión de restos estrictamente decreciente. En algún momento esa sucesión alcanza el 0. Se puede probar que el último resto no nulo es precisamente el máximo común divisor de a y b. Por ejemplo, calculemos el máximo común de 17 y 7. Como 17 = 7 ⋅ 2 + 3, entonces el m.c.d.(17, 7) es igual al m.c.d.(7, 3). De nuevo, como 7 = 3 ⋅ 2 + 1, entonces el m.c.d.(7, 3) es igual al m.c.d.(3, 1). Aquí es claro que el m.c.d. entre 3 y 1 es simplemente 1. Por tanto, el m.c.d entre 17 y 7 es 1 también. ¿Cómo se transforma el cálculo del máximo común divisor en un método para generar patrones distribuidos con regularidad máxima? Ilustraremos el proceso con un ejemplo de ritmos. Supongamos que tenemos 17 pulsos y queremos distribuir de forma regular 7 notas entre los 17 pulsos. Sigamos los pasos dados en la figura 4. Primero, alineamos el número de notas y el número de silencios (siete unos y diez ceros); véase la figura 4-paso (1). A continuación, formamos grupos de 7, los cuales corresponden a efectuar la división de 17 entre 7; obtenemos, pues, 7 grupos formados por [1 0] (en columnas en el paso (2) de la figura 4). Sobran tres ceros, lo cual indica que en el paso siguiente formaremos grupos de 3. Tras formar el primer grupo —véase el paso (3) de la figura 4— nos quedamos sin ceros. Continuamos agrupando de 3 en 3 tomando los grupos de la otra caja, en la que quedan 4 columnas (figura 4-paso (4)). Procedemos así que queden uno o cero grupos; de nuevo, esto es equivalente a efectuar la división de 7 entre 3. En nuestro caso, queda un solo grupo y hemos terminado (paso (5)). Finalmente, el ritmo se obtiene leyendo por columnas y de izquierda a derecha la agrupación obtenida (paso (6)). Figura 4: El algoritmo de Euclides para generar ritmos regulares. Aquí cada 1 representa una nota [x] y cada 0, un silencio [.]. El ritmo que hemos generado con nuestra notación se escribe entonces como [x . . x . x . . x . x . . x . x .]. Los ritmos generados por este método se llaman ritmos euclídeos. El ritmo euclídeo de k notas y n pulsos se designa por E(k,n). Otra manera útil de designar un ritmo es mediante las duraciones de las notas en términos de pulsos. El ritmo euclídeo que acabamos de obtener con esta notación se escribe E(7,17) = [x . . x . x . . x . x . . x . x .]= (3232322). Para más información sobre ritmos euclídeos, véase el artículo Si Euclides lo supiese... se sentiría orgulloso [Góm09] del propio autor de estas líneas. Demain y sus coautores [DGMM+09] probaron formalmente que este algoritmo proporciona, salvo rotaciones, la única manera de distribuir k objetos entre n del modo más regular posible. Aún más, había varios algoritmos propuestos de manera independiente y ellos probaron que, en realidad, eran todos equivalentes al viejo algoritmo de Euclides. Damos a continuación una pequeñísima muestra de ritmos euclídeos que se encuentran en las músicas tradicionales del mundo. E(5,8) =[x . x x . x x .]= (21212) es el cinquillo cubano, así como el malfuf de Egipto, o el ritmo coreano para tambor mong P’yon. Si el ritmo se empieza a tocar desde la segunda nota aparece un popular ritmo típico de Oriente Próximo, así como el timini de Senegal. Si se empieza en la tercera nota tenemos el ritmo del tango. E(5,12) =[x . . x . x . . x . x .]= (32322) es un ritmo muy común en África central que tocan los pigmeos aka. Cuando se toca desde la segunda nota es, entre otros, la clave columbia de la música cubana y el ritmo de la danza chakacha de Kenya. E(5,16) =[x . . x . . x . . x . . x . . . ]= (33334) es el ritmo de la bosa-nova de Brasil. Este ritmo se toca a partir de la tercera nota. Existen cerca de dos centenares de ritmos de músicas del mundo documentados que son generados por el algoritmo de Euclides. De nuevo, véase el artículo The distance geometry of music de Demain y sus coautores [DGMM+09]. He aquí una lista de las principales propiedades de los ritmos regulares o ritmos euclídeos: Los ritmos euclídeos tienen solo una o dos duraciones. En el caso de dos duraciones, estas difieren exactamente en una unidad. Por ejemplo, en este ritmo euclídeo (21212) hay dos duraciones de valor 2 y 1. Cuando el número de notas no es primo relativo del número de pulsos, los ritmos euclídeos están formados por la repetición de un patrón. En caso contrario, el ritmo está compuesto por un patrón repetido un número máximo de veces más un único patrón más pequeño, que además es subpatrón del patrón que se repite. Los patrones que forman los ritmos euclídeos son a su vez euclídeos. Esto crea una jerarquía de ritmos euclídeos anidados. La rotación de un ritmo euclídeo es también euclídeo. Esto es consecuencia de que los ritmos euclídeos maximizan las distancias intercordales entre las notas y dichas distancias no cambian con las rotaciones. Tomar el complementario de un ritmo euclídeo (esto es, intercambiar ceros por unos) devuelve un ritmo euclídeo. 6. Ritmos de Christoffel y ritmos euclídeos Boenn prueba en su libro [Boe18] que si, dados a,b con a ⊥ b, existe un k ∈ ℕ tal que a-kb = 1, entonces el ritmo de Christoffel C(a,b) es igual al ritmo euclídeo E(b,a + b). Aquí por E(b,a + b) nos referimos al ritmo obtenido directamente del algoritmo de Bjorklund expuesto más arriba en la figura 4. En el caso en que no se cumpla la condición anterior, el ritmo de Christoffel C(a,b) es igual a una rotación del ritmo euclídeo E(b,a + b). Boenn presenta la siguiente tabla de ritmos euclídeos y sus correspondientes ritmos de Christoffel para ilustrar los resultados mencionados. Figura 5: Ritmos euclídeos que son ritmos de Christoffel (figura tomada de [Boe18]) 7. Notación SNMR Cuadro con la notación SNMR: Figura 6: La codificación SNMR (figura tomada de [Boe18])   Bibliografía [Ber90] Jean Berstel. Tracé de droites, fractions continues et morphismes itérés. Mots, pages 298–309, 1990. [BLRS08] Jean Berstel, Aaron Lauve, Christophe Reutenauer, and Franco Saliola. Combinatorics on Words: Christoffel Words and Repetition in Words. American Mathematical Society, Rhode Island, USA, 2008. [Boe18] Georg Boenn. Computational Models of Rhythm and Meter. Springer, New York, Berlín, 2018. [BP07] Jean Berstel and Dominique Perrin. The origins of combinatorics on words. European Journal of Combinatorics, pages 996–1022, 2007. [DGMM+09] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, and David R. Wood. The distance geometry of music. Computational Geometry: Theory and Application, 42(5):429–454, 2009. [Góm09] Paco Gómez. Si Euclides lo supiese... se sentiría orgulloso. http://www.upm.es/sfs/Rectorado/Vicerrectorado\%20de\%20Investigacion/Oficina\%20de\%20Transferencia\%20de\%20Resultados\%20de\%20Investigacion\%20(OTRI)/Divulgacion/documentos/Si_Euclides.pdf, Noviembre, 2009. [Góm22a] P. Gómez. Modelos computacionales de ritmo y métrica (I). https://www.divulgamat.net/index.php?option=com_content&view=article&id=18789&directory=67, abril de 2022. [Góm22b] P. Gómez. Modelos computacionales de ritmo y métrica (II). https://www.divulgamat.net/index.php?option=com_content&view=article&id=18810&directory=67, abril de 2022. [Lon04] Justin London. Hearing in Time. Oxford University Press, Oxford, England, 2004. [Lot83] M. Lothaire. Combinatorics on words. Addison-Wesley Publishing Co., Reading, Massachusetts., 1983. Encyclopedia of Mathematics and its Applications, vol. 17.

Viernes, 10 de Junio de 2022 | Imprimir | PDF |  Correo electrónico

72. ¿Seguro que no necesitas las matemáticas?

ABC, 30 de Mayo de 2022 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 30 de Mayo de 2022 | Imprimir | PDF |  Correo electrónico | Leer más

73. El problema del huerto o cómo los matemáticos plantan árboles sin azada

ABC, 23 de Mayo de 2022 CIENCIA - El ABCdario de las matemáticas Alfonso Jesús Población Sáez

Lunes, 23 de Mayo de 2022 | Imprimir | PDF |  Correo electrónico | Leer más

74. 84. (Junio 2022) Matemáticas sobre marfil

(Astrónomo. Cáliz de las Artes Liberales. Museo del Duomo. Milán) El marfil es un material noble fácil de moldear y que ha sido muy apreciado. Los huesos han servido desde la prehistoria como utensilio o como decoración. La matemática no ha sido ajena a estos usos. Los compases de proporción ingleses, llamados sectores, se solían hacer con marfil, como las reglas de precisión o los conocidos huesos de Neper para la computación. A los delicados poliedros de marfil del gusto de las cámaras de arte y curiosidades de los Príncipes del Renacimiento ya hemos dedicado una instantánea anterior. Ahora destacamos otros objetos artísticos con representaciones matemáticas. El Cáliz Gótico de las Artes Liberales del Duomo de Milán Iniciamos con un cáliz gótico del siglo XIV, perteneciente a la Catedral de Milán, formado por diez gallones de marfil representando las Artes Liberales y la Medicina. La joya se encuentra en la Sala del Tesoro, en la oscura entrada al Museo del Duomo, un edificio situado a la derecha de la catedral. Museo que   permite apreciar en detalle y disfrutar la decoración del edificio principal. (Alegoría de la Geometría. Cáliz de las Artes Liberales. Museo del Duomo. Milán) El Cáliz ya aparece mencionado en 1440 como parte del Tesoro de la Capilla Ducal de San Gottardo. El trabajo en marfil se considera alemán (Colonia). El pie metálico y su pedrería son de manufactura lombarda posterior. El bello objeto ha sido restaurado recientemente con esmero usando como referencia su gemelo: la copa de Madrid. La iconografía es la clásica en el gótico tardío: Medicina con ampolleta, Música con las campanas (tintinabulum), Geometría con escuadra y compás, Aritmética con tablilla de números arábigos y Astronomía con astrolabio plano. (Cáliz de las Artes Liberales. Museo del Duomo. Milán) El cáliz milanés tiene un pariente próximo en Madrid. Si una pieza es valiosa, las dos redoblan el placer. No se conocen otros trabajos similares. Copa de las Artes Liberales del Lázaro Galdiano El Museo Lázaro Galdiano de la Calle Serrano de Madrid no solo tiene el encanto de su extensa colección y la diversidad de objetos que alberga, también flota en el ambiente la gran pasión con la que se realizó la recopilación. La Copa gótica en marfil de las Artes Liberales es una muestra elocuente de los tesoros del museo. El cáliz de Milán que se exhibe en todo su esplendor con un único objeto acompañante y levemente resaltado en una sala en tinieblas. La escenografía de la Copa del Lázaro es, en cambio, muy modesta: se encuentra en una gran vitrina rodeada y bien acompañada por el resto de los marfiles y huesos, como un dado real.   (Copa de las Artes Liberales. Museo Lázaro Galdiano. Madrid) La copa madrileña es más completa que la lombarda pues tiene doce gallones en lugar de diez. El interior de los arcos ojivales de la copa está trilobulado. Los dos gajos adicionales se utilizan para ampliar las escenas de la Medicina y  la Dialéctica. Ambas le dan más encanto al conjunto. La Dialéctica en solitario se limita a su discurso, mientras que con las dos escenas se nos presenta la disputatio dialectica, elemento clave en la educación escolástica. La escena de la Medicina se amplia a una posible mujer médico, justo reconocimiento a las mulieres salernitanae que como Trotula de Ruggiero, Rebeca Guarda Abella Salernitana, Mercuriade, o Costanza Calenda sentaron las bases de la futuras facultades de Medicina. La Geometría está personificada por una figura barbada con compás y posible escuadra desaparecida pero en distinta mano que la de Milán. La Aritmética con tablilla no marca ningún número reconocible. El Astrónomo del Lázaro tiene un astrolabio plano con indicadores de giro pero sin la alidada, uno es el reverso del otro. (Astrónomo. Copa de las Artes Liberales. Museo Lázaro Galdiano. Madrid) La Alegoría de la Astronomía en un bargueño de Burdeos (Alegoría de la Astronomía. Museo de Artes Decorativas. Burdeos) Los museos de Artes Decorativas son también lugares interesantes para encontrar objetos de interés matemático. Una confirmación destacable de lo mucho que merecen la pena es el Museo de Artes Decorativas de Burdeos. Dos bargueños (cabinet, en francés) nos permiten encontrarnos con la Astronomía, uno en su forma alegórica y otro con su aplicación práctica. Nos centramos en el alegórico, un hermoso arca de Amberes de 1610, construido en ébano, marfil y hueso. La decoración exterior de las dos puertas muestra una alegoría de la Justicia, a la derecha, y otra de la Astronomía, a la izquierda. La alegoría es una deliciosa imagen clásica con globo terráqueo sobre el hombro y compás en la otra mano; el diseño proviene de un grabado de Lukas Kilian (1579–1637). (Cabinet de las Artes Liberales. Museo de Artes Decorativas. Burdeos) El cabinet de la Aritmética en Bruselas Los Museos Reales de Arte e Historia del Cincuentenario exhiben un cabinet de inicios del siglo XVII decorado con cinco de las siete alegorías de las Artes Liberales. Solo son visibles las dos exteriores: la Aritmética y la Lógica. El cabinet es de las mismas características que el del Museo de Artes Decorativas de Burdeos. El mueble fue ejecutado en madera de ébano y marfil. Las alegorías están pintadas con tinta negra sobre las láminas de marfil. Los dibujos se ajustan a los grabados de Crispijn de Passe el Viejo (1610) que son diseños de los pintores manieristas flamencos Frans Floris y Maarten de Vos. La Aritmética aparece calculando sobre una tablilla y la Lógica se representa con su doble serpiente enrollada. (Alegoría de la Aritmética. Museo Reales de de Arte de Historia. Bruselas) Las Artes con Minerva en el Liebieghaus El Liebieghaus es una villa de finales del siglo XIX a orillas del río en Fráncfort del Meno que alberga un museo de esculturas, la Städtische Galerie Liebieghaus, que forma parte del conjunto museístico de la ciudad. (Minerva con las Artes Liberales. Museo Liebieghaus. Fránfort) El conjunto en marfil de Minerva y las Artes Liberales es una obra delicada de finales del XVII que pertenecería a una Kunstkammer, un gabinete de curiosidades principesco. La Geometría tiene un compás metálico y un globo terrestre dorado, la Astronomía lleva una esfera armilar y la Aritmética calcula con una tablilla. (Detalle de las Artes Matemáticas. Museo Liebieghaus. Fránfort) El joven matemático de la peluca empolvada del Victoria and Albert El Museo V&A de Londres tiene, entre su extensísimas colecciones, una placa del siglo XVIII en marfil que representa a un joven matemático con sus instrumentos sobre la mesa. Puede tratarse de la representación de un futuro marino con sus útiles de geometría y cálculo. La placa fue tallada por David Le Marchand en 1720. Sobre la mesa hay un compás, un sector inglés (compás de proporción), un cuadrante y un papel con figuras geométricas. (Joven matemático. Museo V&A. Londres)

Miércoles, 01 de Junio de 2022 | Imprimir | PDF |  Correo electrónico

75. Las figuras imposibles de Guido Moretti

El genial artista Miguel Ángel decía que sólo hay dos maneras de crear esculturas: quitando o añadiendo. Sin embargo,  Guido Moretti compone sus esculturas separando. Así se presenta la obra este físico y escultor en su página web, antes de introducirnos en un sorprendente mundo de figuras imposibles. Aunque parezca mentira, estas tres imágenes corresponden a un mismo objeto creado por Moretti… En este video puedes ver algunas de sus obras: y en su página web explica las diferentes técnicas que utiliza, todo ello acompañado de diagramas y animaciones. ¡Realmente singular y bello! Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com

Lunes, 23 de Mayo de 2022 | Imprimir | PDF |  Correo electrónico

76. 124. (Mayo 2022) Modelos computacionales de ritmo y métrica (II)

1. Introducción En esta segunda columna de la serie Modelos computacionales de ritmo y métrica, vamos a tratar el recuento y la generación de ritmos con técnicas combinatorias.. En la primera columna [Góm], hicimos una breve recensión de los dos primeros capítulos del libro Computational Models of Rhythm and Meter de Boenn [Boe18]. En el primer capítulo se examinaba la definición de ritmo desde un punto de vista abstracto y filosófico; en el segundo, se definió la notación SNMR. 2. Recuento de listas Esta sección tendrá un carácter indagatorio y orgánico. Empezamos considerando un entero positivo n > 1. Este entero representará el número total de pulsos de nuestro ritmo. Asociado a todo ritmo, tenemos k, otro entero positivo con 1 ≤ k ≤ n, que representa las notas del ritmo o ataques. Así, el ritmo lo representamos por la lista R1 = (2,2,2,3). Marcamos en negrita la palabra lista como definición, la cual quiere decir que el orden de los elementos es importante y distingue entre listas (ritmos). Así, el ritmo R2 = (3,2,2,2) tiene un orden distinto de los elementos y es, por tanto, una lista y un ritmo distintos. 2.1. Permutaciones sin y con repetición Investiguemos las listas un poco más en abstracto (el lector se lo merece). Tomemos un conjunto A = de n elementos donde los elementos son distintos entre sí (esto es, ai≠aj si i≠j). ¿Cuántas listas distintas se pueden formar con los elementos de A? Este es un argumento clásico. Para el primer elemento de la lista, tenemos n posibilidades, los n elementos de A. Para el segundo elemento, dado que no podemos usar el elemento de la primera posición, hay n - 1 posibilidades. Razonando así hasta completar la lista entera, llegamos a que hay n ⋅ (n - 1) ⋅… ⋅ 2 ⋅ 1. El número anterior se llama factorial de n y se escribe Este argumento se puede ilustrar con el siguiente árbol, donde hemos hecho que A = : El número de listas formadas por un conjunto de n elementos no repetidos se llama permutaciones sin repetición y se designa por Pn. Por lo visto antes, Pn = n!. ¿Qué ocurre si a continuación eliminamos la restricción de la repetición? Supongamos que tenemos un conjunto A de n elementos formado como sigue: donde n = k1 + k2 + … + km. ¿Cuántas listas distintas se pueden formar con los elementos de A? Si hay repetidos, esto quiere decir que las permutaciones entre los elementos repetidos del mismo tipo dará lugar a la misma selección. Las repeticiones se quitan dividiendo por las permutaciones de la repetición. Por tanto, el número de listas ordenadas formadas con elementos de A, donde hay m grupos de elementos repetidos es: Este número se designa por PRnk1,…,km, donde k1,…,km son los elementos repetidos En el caso del ritmo de arriba R1 = (2,2,2,3), está claro que el conjunto de listas distintas es: de las cuales hay 4. Si calculamos ese número, obtenemos PR43 = = = 4, como era de esperar. 3. Los ritmos aksak Los ritmos aksak son ritmos que tienen solo dos duraciones posibles en términos de distancias, 2 o 3, y han de contener al menos un 2 y al menos un 3. Este tipo de ritmos aparecen en varias tradiciones musicales, entre ellas la música turca o la música búlgara. Autores como Simha Arom [Aro04], Brăiloiu [Bra51], Cler [Cle94], y en conexión con los ritmos euclídeos Demain y coautores [DGMM+09]. Arom clasificó los ritmos aksak para valores del número de pulsos n entre 5 y 29 y proporcionó una clasificación teórica. En su clasificación de ritmos aksak delinea tres categorías: Un ritmo aksak se dice que es auténtico si n es primo. Cuando n es impar pero no es primo, el ritmo aksak es llamado quasi-aksak. En caso de que n sea par, el ritmo aksak se denomina pseudo-aksak. A continuación listamos algunos ritmos aksak junto con sus categorizaciones (los representamos con la notación de notas y silencios, la notación de distancias y la notación SNMR): Ritmos aksak auténticos: [×⋅×⋅ ⋅ ]= (23))=I-, ritmo que se encuentra en la música clásica y en la música de entre otros Grecia, Macedonia, Namibia o Ruanda. [×⋅×⋅×⋅ ] = (223)=II-, ritmo que se encuentra en la música de Bulgaria, Grecia, Sudán y Turquía. [×⋅ ⋅×⋅ ⋅×⋅ ⋅×⋅ ]=(3332)=—I, ritmo que puede oír en la música del sur de la India. [×⋅×⋅×⋅×⋅×⋅ ⋅ ]= (22223), ritmo que se encuentra en Bulgaria, el norte de la India y en Serbia, por nombrar unos pocos ejemplos. Los ritmos [×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ⋅ ]=(32323)=-I-I- y [×⋅×⋅×⋅×⋅×⋅×⋅ ⋅ ]=(222223)= =IIIII- se encuentran en la música de Macedonia. Otros ritmos aksak auténticos de la tradición búlgara son: (3232322), (22222223), (32232232), o (323232323). Como ejemplos de ritmos quasi-aksak tenemos: [×⋅×⋅×⋅×⋅ ⋅ ]=(2223)=III-, que se pueden escuchar en la música de Grecia, Macedonia, Turquía o Zaire. El ritmo búlgaro [×⋅×⋅×⋅×⋅×⋅×⋅×⋅ ⋅ ]=(2222223)=IIIIII-. Por último, los siguientes son ritmos pseudo-aksak: [×⋅ ⋅×⋅ ⋅×⋅ ]=(332)=–I, ritmo que se encuentra con frecuencia, por ejemplo, en la música de África central, Grecia, India, Latinoamérica, África del oeste o Sudán. [×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ]=(32322)=-I-II, que se encuentra en música de Macedonia o Sudáfrica. Sea R un ritmo aksak de n pulsos con r doses y s tres. El número de ritmos aksak que hay con esos r doses y s treses es: Además, se cumple la siguiente relación entre n,r y s: Esta última relación es una ecuación diofántica y se puede usar para generar y contar ritmos aksak. Una ecuación diofántica es una ecuación de la forma c = ax + by, donde a,b,c son números enteros. El siguiente teorema determina cuándo hay solución y cuando existen cómo se calculan las soluciones. Cuando hay solución, existen infinitas soluciones como vemos en el enunciado del teorema. Teorema. Resolución de ecuaciones diofánticas. Sean a,b,c tres números enteros, y sea d = mcd(a,b). Se considera la ecuación diofántica c = ax + by. Entonces: (1) Si d no divide a c, entonces la ecuación diofántica no tiene solución. (2) Si d divide a c, entonces la ecuación diofántica tiene infinitas soluciones de la forma x = x0 + m, y = y0 -m donde m ∈ ℤ y x0,y0 son soluciones particulares de la ecuación diofántica. Aplicando el teorema a la relación (1) de arriba, vemos que el máximo común de 2 y 3 es 1 (son primos ambos números) y, por tanto, la ecuación (1) siempre tiene solución por el apartado (2) del teorema. La solución particular es, por ejemplo, x0 = -n,y0 = n, ya que 2x0 + 3y0 = -2n + 3n = n. Se sigue que la solución general es: Fijado n, basta encontrar los valores de m que dan valores positivos de x,y (recuérdese que un ritmo aksak exige que haya al menos un 2 y un 3). Pongamos el ejemplo de los ritmos aksak de n = 17 pulsos. Según el teorema, las soluciones de x e y son, respectivamente, x = -17 + 3m,y = 17 - 2m. El valor m = 6 es el primer valor para el que x e y son positivos. La taba siguiente muestra los resultados: m x = -17 + 3m y = 17 - 2m Ritmo SNMR 4 1 5 (233333) I- - - - - 5 4 3 (2222333) I I I I - - - 7 1 2 (22222223) I I I I I I I - Tabla 1: Ritmos aksak de 17 pulsos 4. Combinaciones sin y con repetición La diferencia entre una lista y un conjunto es que en la primera el orden importa y en el segundo no. En los conjuntos el orden no importa; de hecho, la definición de conjunto habla de una colección no ordenada de elementos. Sea A = un conjunto de n elementos distintos. El número de listas de tamaño n es, como sabemos, Pn = n!. Si ahora queremos contar el número de subconjuntos tenemos que usar argumentos adicionales para contarlos. En primer lugar, vamos a estudiar cómo contar el número de listas de tamaño k, donde 1 ≤ k ≤ n. Usando el argumento de más arriba, tenemos n posibilidades para la primera posición de la lista, n - 1 para la segunda y, siguiendo este proceso, tendremos n - k + 1 para la posición número k. Por tanto, el número final será n ⋅ (n - 1) ⋅… ⋅ (n - k + 1). Este número se llama variaciones sin repetición de n tomados de k en k o más corto V n,k. Este número se puede escribir como: Continuemos. Sea L = (ai1,…,aik) una de esas listas. Cuando esta lista se transforma en un subconjunto, cualquier permutación de L da lugar al mismo subconjunto. Hay k! permutaciones de L y, por tanto, el número de subconjuntos de tamaño de k de A, al que llamaremos Cn,k, es: Se llaman combinaciones sin repetición de conjuntos a los subconjuntos de tamaño k formados con los elementos de un conjunto dado, donde se supone que en el conjunto no hay elementos repetidos. Se designarán por Cn,k o por (n k) . Por último, pedimos al lector que trate de resolver la ecuación donde n,k son números enteros no negativos. ¿Alguna idea? He aquí una ingeniosa idea para resolverla. Consideremos el conjunto formado por un palote ∣ y un signo +. Queremos formar todas las listas distintas con n palotes y k - 1 signos más. Como los palotes y los signos más son indistinguibles entre sí, las listas difieren en la posición de los palotes y signos más. Cada lista da lugar a la solución de la ecuación x1 + x2 + … + xk = n sin más que contar los palotes entre dos signos más consecutivos. Y viceversa, una solución de x1 + x2 + … + xk = n da lugar a una lista de palotes y signos más. Vamos a contar esas listas pues. En vista de lo aprendido arriba, hay Pn+k-1 = (n + k - 1)! listas. Como se repiten los palotes, de los que hay nk, y las signos más, de los que hay k - 1, tendremos que dividir por n! y (k - 1)!. Así que el número de las listas es: que son las combinaciones de n + k - 1 tomadas de k - 1 en k - 1. 5. Particiones de enteros y ritmos Dado un ritmo de n pulsos, las soluciones positivas de la ecuación x1 + x2 + … + xk = n nos da todos los ritmos de k notas. La sucesión de distancias de ese ritmo sería sencillamente R = (x1,x2,…,xk). La siguiente tabla muestra cómo se generan ritmos a partir de esta ecuación: x1 x2 x3 x4 x5 Ritmo SNMR 5 (5) H˜- 4 1 (41) H- 3 2 (32) - I 3 1 1 (311) - . . 2 2 1 (221) I I . 2 1 1 1 (2111) I . . . 1 1 1 1 1 (11111) . . . . . Tabla 2: Las particiones de 5 y los ritmos asociados Dado un ritmo R = (x1,x2,…,xk), donde los xi son positivos todos, hay ritmos posibles con esa configuración de distancias. Por ejemplo, del cuarto ritmo de la tabla de arriba (3,1,1) hay 3!∕2! = 3 ritmos distintos, que son (3,1,1),(1,3,1),(1,1,3). Obsérvese que aquí k = 3 porque x4 = x5 = 0. Cuando todas las xi son diferentes, el número de ritmos es simplemente k!.   6. Notación SNMR Cuadro con la notación SNMR: Figura 1: La codificación SNMR (figura tomada de [Boe18]   Bibliografía [Aro04] Simha Arom. L?aksak: Principes et typologie polyphony and polyrhythm. Cahiers de Musiques Traditionnelles, pages 12–48, 2004. [Boe18] Georg Boenn. Computational Models of Rhythm and Meter. Springer, New York, Berlín, 2018. [Bra51] C. Brailoiu. Le rythme aksak. Revue de Musicologie, pages 71–108, 1951. [Cle94] J. Cler. Pour une théorie de l?aksak. Revue de Musicologie, pages 181–210, 1994. [DGMM+09] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, and David R. Wood. The distance geometry of music. Computational Geometry: Theory and Application, 42(5):429–454, 2009. [Góm] P. Gómez. Modelos computacionales de ritmo y métrica (I)

Martes, 17 de Mayo de 2022 | Imprimir | PDF |  Correo electrónico

77. Flatland: The Movie

Flatland: The Movie es una película de animación inspirada en la novela Flatland de Edwin A. Abbott. Ambientada en un mundo de sólo dos dimensiones –habitado por formas geométricas y dominado por los déspotas círculos–, la historia tiene como protagonistas al cuadrado Arthur Square y su nieta –un hexágono– Hex que descubren la tercera dimensión. Flatland, el mundo en el que vive Hex Flatland: The Movie es un corto de una media hora de duración cuyos responsables son Seth Caplan –productor–, Dano Johnson –director de la animación– y Jeffrey Travis –realizador y director–. Los protagonistas principales –y los actores y actrices que les doblan son– Arthur Square (Martin Sheen), Hex (Kristen Bell),  Spherius (Michael York), Abbott Square hermano de Arthur (Joe Estevez–que es casualmente el hermano de Martin Sheen–) y Arlene Square esposa de Arthur (Danu Uribe). Hex, la joven hexágono protagonista, vive en su mundo bidimensional –Flatland o Planilandia– con sus abuelos, Arthur y Arlene: su madre y su padre fueron ajusticiados por creer en la existencia de la tercera dimensión, enfrentándose a las ideas impuestas por los círculos dictadores. En este mundo, cada nueva generación nace con una arista más que la anterior –Arthur y Arlene son cuadrados y los desaparecidos padres de Hex eran pentágonos–. Se rigen por un sistema de castas: cuantas más aristas tiene un polígono, más valorado está en la escala social. Por ejemplo, los triángulos son los vigilantes de las leyes, mientras que los círculos son los legisladores que dominan Planilandia. Cuando un polígono quebranta la ley, se le castiga eliminando una de sus aristas. Los círculos –que caricaturizan a la clase política– conocen la existencia de la tercera dimensión, pero deciden mantenerlo en secreto para sustentar su poder sobre los habitantes del mundo plano. Arthur intenta explicar al Rey de Rectilandia que existe una dimensión más que la suya Arthur viaje en sueños a Puntilandia y a Rectilandia –mundos de cero y una dimensión, respectivamente– e intenta explicar al Rey de Rectilandia la existencia de una dimensión más que la suya. Spherius –¿un profeta?, ¿un ‘extra-planilandio’?– contacta desde Espacilandia con Arthur y le muestra la tercera dimensión, en un emocionante viaje descubriendo extrañas formas. Arthur comprende –aunque Spherius se resiste a creerlo– que debe de haber mundos de cuatro, seis,… de cualquier dimensión. Spherius explica a Arthur la tercera dimensión del mismo modo en que Arthur argumentó con el Rey de Rectilandia: le muestra sucesivas trazas de sí mismo con Planilandia. Hex se escapa de casa, intentando entender las ideas de sus padres. Encuentra un lugar conocido como Área 33h –metáfora del Área 51– en el que se realizan –y ocultan– experimentos secretos. Es apresada, pero su abuelo acude al rescate enviándola a Espacilandia. Spherius se muestra finalmente a los habitantes de Planilandia, que terminan liberándose de la opresión de los círculos, comenzando una nueva era. Spherius se deja ver ante las y los habitantes de Planilandia La película finaliza con Spherius desbarrando ante la idea de una cuarta dimensión y una evocadora imagen que deja una puerta abierta… Visualizando la cuarta dimensión El cortometraje es una delicia, con preciosa música, bellísimas imágenes, una buena historia, sentido del humor –por ejemplo, los pentágonos-periodistas entrevistando casi al final al héroe Arthur son una divertida parodia de lo que pasa en nuestro mundo– y unas magníficas explicaciones del concepto de dimensión. Más información: Página oficial de la película Flatland: The Movie Alfonso J. Población Sáez,  Planilandia (y III), DivulgaMAT, mayo de 2007 Marianne Freiberger, Flatland: The movie, Plus Magazine, 2007 Ian Stewart, Flatland: The movie, Notices of the AMS, november 2007, 1317-1321 Fernando Q. Gouvêa, Flatland: The movie, MAA Hemant Mehta, Review of Flatland: The Movie, Skeptical Inquirer, 2010 Continuará… Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Lunes, 16 de Mayo de 2022 | Imprimir | PDF |  Correo electrónico

78. Los cuatro templos de las matemáticas en España

ABC, 16 de Mayo de 2022 CIENCIA - El ABCdario de las matemáticas Robert Escribano, Mª Carmen Perea, Víctor Manero, Fernando Blasco y Alfonso Jesús Población

Lunes, 16 de Mayo de 2022 | Imprimir | PDF |  Correo electrónico | Leer más

79. Día Escolar de las Matemáticas 2022: Matemáticas en los caminos de Santiago

El día 12 de mayo se celebra el Día Escolar de las Matemáticas, dedicado este año a las matemáticas que hay en los diferentes «caminos de Santiago». En esta edición el profesor Julio Rodríguez Taboada nos ha preparado un material al respecto que se ha publicado en la revista SUMA 97, y que se puede descargar en el siguiente enlace.

Miércoles, 11 de Mayo de 2022 | Imprimir | PDF |  Correo electrónico | Leer más

80. Día Escolar de las Matemáticas 2022: Matemáticas en los caminos de Santiago

El día 12 de mayo se celebra el Día Escolar de las Matemáticas, dedicado este año a las matemáticas que hay en los diferentes «caminos de Santiago». En esta edición el profesor Julio Rodríguez Taboada nos ha preparado un material al respecto que se ha publicado en la revista SUMA 97, y que se puede descargar en el siguiente enlace.

Miércoles, 11 de Mayo de 2022 | Imprimir | PDF |  Correo electrónico | Leer más